2. 山东科技大学 交通学院,山东 青岛 266590;
3. 青岛黄海学院,山东 青岛 266555
2. College of Transportation, Shandong University of Science and Technology, Qingdao 266590, China;
3. Qingdao Huanghai University, Qingdao 266555, China
自主式水下航行器(AUV)是在无人驾驶的情况下,依靠自身携带的动力自主地完成复杂海洋环境中预定任务的机器人[1]。海底环境建模是AUV进行全局路径规划进而完成自主巡航的关键一环[2],主要任务是把AUV所处海底环境描述为计算机识别的形式,它是利用路径规划算法寻找最优路径的基础[3-4]。
目前,在水下机器人环境建模方面已有许多研究成果,如美国Bluefin Robotics公司的Bluefin-21 AUV就具有非常出色的环境建模算法能力,该AUV根据需要装载了包括如410 kHz侧扫声呐系统在内的多种探测设备,以最高7.5 cm的分辨率勘测地貌,完成了海底建模[5],在2014年搜寻马航MH370失联客机过程中发挥了重大作用;由Hydroid公司研制的REMUS-6000也具备利用配备的侧扫声呐收集水下环境数据并进行海底建模的能力[6];美国研发的深井热探测器(DEPTHX)[7]直径约2.5 m,用来探索未知的水下洞穴和隧道,对海底进行三维映射,将海底数据转化为环境参数并进行立体建模,可以较为准确地还原沼穴外形;中国沈阳自动化所和海洋所联合研制的“探索4500”具备了基于前视声呐信息的自主碰撞技术,提高其对复杂环境的适应能力,对大面积冷泉区进行精细海底建模,保证近海域海底路径规划的安全[8]。这些AUV研究成果均已完成湖上或海上的功能试验。
水下航行器全局路径规划过程受水下航行器探测能力、水下航行器的机动性能和障碍物特性的影响,研究存在的挑战和难点主要有以下两点:
1)海底环境较为复杂,当障碍物密集时环境建模精度较低。
2)海流因素对环境建模后续算法的影响较大,将海流因素转化为参数数据,考虑进建模及算法过程中时,会大幅度提升算法的复杂度。
本文在分析AUV自主巡航技术背景的基础上,对AUV全局路径规划环境建模算法及研究热点展开综述,重点讨论海流对AUV全局路径规划环境建模影响方面的研究进展,为研究和发展AUV全局路径规划环境建模算法提供参考。
1 全局路径规划环境建模方法概述适用于水下全局路径规划环境建模的主要方法有栅格法,拓扑法,可视图法等。
1.1 栅格法栅格法最早由Elfes和Moravec等学者提出,即利用栅格法进行环境建模即将环境等分为方格,以栅格为单元表示该区域环境信息,然后在环境地图上使用路径规划算法[10]。Wang等[11]针对海底环境特征将栅格图中的障碍物分为3类,分别是静态障碍物、动态障碍物和准静态障碍物,其中准静态障碍物具有固定中心和随时间变化的不确定半径,如珊瑚、藻类等。再通过对障碍物的连续观测进行海底环境建模,提高路径规划精度。为降低计算复杂度,传统栅格法仅将AUV所在栅格的周围8个栅格作为下一时刻可选位置,但会降低规划路径的质量,如平滑度。针对这一缺点,姚鹏等[12]扩大了备选邻居栅格的层数,即下一时刻AUV不仅可移动至周围8个栅格,还可移动至更远处的栅格,从而提高路径质量。
由于海底环境是三维环境,近年来众多研究人员用栅格法对海底进行三维建模。
文献[13]用栅格法对海底环境进行三维建模,但此建模只能基于AUV下潜深度变化范围较小的前提下,将AUV在三维空间内的运动分解为2个二维平面的运动,对海底栅格模型的水深范围进行简化处理,利用声呐探测的信息实现对障碍物的3D重建,局部避障效果较好,此建模并不是真正意义上的三维建模。文献[14]将生物启发神经网络引入三维栅格模型,把具体的动态环境和AUV前后时刻的航行位置联系起来综合决策出AUV的下一个航行位置,缩短了搜索时间,降低路径规划的重复率。文献[15]引入多个AUV协同作业,将任务分解到水下平面的不同深度,达到三维建模的效果,原理与文献[13]有相似之处,但实际路径规划中,单AUV并不能跨层进行搜索。文献[16]在二维栅格建模的基础上,拓展到三维空间,对比了二维、三维栅格建模对AUV巡航过程的影响,二维栅格建模算法复杂度低,AUV面对障碍物时可更快做出决策;三维栅格建模可降低AUV巡航过程中的转向幅度与转角次数,一定程度上避免AUV进入死区。
综上,栅格法海底环境建模多数基于二维建模,建模结构简单,易于管理、存储和检索,且发展较成熟,但不利于在密集障碍物环境中规划最优路径。网格尺寸的规划也与传感器性能和AUV体积有关。栅格法易于向三维拓展[17],但对环境分辨清晰度需求较高,环境信息存储量大且决策速度慢,降低系统实时性,发展尚不成熟。在三维栅格建模中,过于精细的栅格划分虽可以保证精度,但带来了计算时间的级数增长,然而过大的栅格尺度又无法保证障碍物的精确建模。两者之间的平衡问题一直是难点。
1.2 拓扑法拓扑法是由清华大学张钹教授等于1984年提出的路径规划算法,基本思想是:将规划空间分割成拓扑特性一致的子空间,并建立拓扑网络,在拓扑网络上寻找起点到终点的拓扑路径,并由拓扑路径求出几何路径[18]。随后张钹教授对其进行改进,用图形方法实现拓扑路径规划算法,将复杂的几何计算问题转化为图形的一些简单处理,将问题变得更直观灵活,缺点是如果局部障碍物发生变化,整个拓扑空间需要重新构造,极为费时。
拓扑法和栅格法的区别在于,拓扑法是天生三维的环境建模法,能更好地适用于水下环境,可完全描述海底地形的结构特征,并具有较高的存储效率,在得不到精确环境信息情况时,也可以依靠环境特征信息与传感器检测信息匹配确定AUV的方位[19]。但拓扑法因建模模型复杂,占用大量空间,无法灵活处理局部障碍物发生变化的情况,故国内外应用较少,研究进展缓慢。
1.3 可视图法可视图法于1979年由麻省理工学院的Tomas Lozano-Perez和IBM研究院的Michael A.Wesley提出[20]。最大特点是用多边形描述环境边界及障碍物轮廓,且将AUV视作大小形状可忽略的质点。把AUV的起点、每个障碍物的顶点及目标点通过直线连接在一起,而连接直线不能穿越障碍物,由此获得一张无碰撞路径图,即为可视图。可视图法的缺点有2个:一是规划冗余路径过多;二是将移动目标视作质点可能会出现与障碍物碰撞的现象。
针对冗余路径过多的问题,可将切线法运用到路径规划中,把障碍物的切线图形化,大大减少无用路径规划量[21]。采用“方向偏差最小”策略对切线法路径规划进行全局路径优化,可避免AUV转向过大,有效防止AUV进入“死区”。
针对移动目标与障碍物碰撞的问题,王芳[22]将维诺图[23]运用到路径规划中,统计离障碍物较远的路径,当AUV偏离路径时,也可避免碰撞障碍物。夏娜等[24]将维诺图与二分图结合起来,经仿真实验证明该方法规划的路径较短且规划效率高。
对于可视图在路径规划中的运用,一般是将障碍物矩形化,提高路径规划的效率,但只能保证局部最优路径,无法得到全局最优解。2017年张雪莲[25]分析了障碍物矩形化的缺陷,提出了将障碍物膨化,避免AUV采用绕行方向使生成路径不理想,改进对比如图1所示,左图为改进前,右图为改进后。

|
图 1 改进对比图 Fig. 1 Improved comparison chart |
3种全局路径规划方法优缺点对比如表1所示。
|
|
表 1 优缺点对比 Tab.1 Advantages and disadvantages comparison |
合理的环境建模有利于减少路径规划中的计算量。可视图法与二维栅格适用于障碍物较少的简单海底环境,此环境对建模精度要求较低。三维海底建模的计算复杂度随维度增加,利用拓扑法及三维栅格为AUV建立精确的海底模型具有挑战性,但随着计算速度的提高和对建模精度的需求,水下三维建模将取代二维建模成为主流。
2 考虑海流影响的AUV全局路径规划环境建模算法研究AUV在有海流的海域中航行时,会受到海流产生的压力,使AUV运动或转向的阻力增大,并偏离预定的轨迹和航向[26],甚至转向,增大AUV的能耗[27]。因此,在规划AUV的巡航路径时,应考虑海流对航向造成的影响。与直线轨迹相比,AUV在处于小流向角的情况下航行可以减少推力器的功率,并使AUV处于可控状态[28]。同时需要考虑航行中能量消耗的问题,尽量利用海流助力,使AUV顺着海流的流向运动,减少逆流航行造成的能量消耗[29]。在模拟海流环境中寻找最优路径如图2所示,图中圆圈表示障碍物,线段为规划路径。

|
图 2 海流环境模型 Fig. 2 Ocean current environment model |
考虑海流因素的巡航策略研究,主要从2个方面入手:一是将海流信息引入环境建模;二是将海流信息引入路径规划算法。
2.1 将海流引入环境建模文献[30]利用声呐传感器采集信息,建模时通过凸算法和贝塞尔插值简化障碍物边界,使AUV快速响应各种障碍物环境。考虑到AUV在海流情况下前进,航迹存在旋转偏差时用一定半径的圆弧代替,避免AUV进入“死区”,与文献[16, 21]相比,此方法耗能低,可同时保证AUV航行的安全性与节能性。文献[17]分析了海流对AUV航行的影响,将不利于AUV航行安全的海洋因素转化为约束条件加入三维栅格中,后续路径规划时则可避免进入危险海洋环境。此方法可大幅度提升AUV巡航过程中的安全性,但以损失最优路径为代价,规划出的路径较长,AUV能耗相对较高。为降低AUV能耗,文献[31]将海流模型栅格做离散处理,对海流数据进行建模,综合考虑路径长度和海流对能源消耗的影响,在能耗最小的前提下实现路径最优化,且在较短路径下,大幅度降低路径的转角,可改善文献的高能耗问题。但该文献为追求算法复杂度低,划分栅格模型时并不精细,未来可做进一步改进。文献[32]针对大型复杂海洋环境,引入了具有学习能力的群体超启发式算法,考虑了能量及时间消耗、转弯半径限制,海洋环境及海流影响,在B样条曲线建模算法中添加相应的约束来限制轨迹的生成空间,将全局路径规划与局部路径规划结合起来,全局路径规划出AUV的大致巡航路径,当遇到动态障碍物时,利用局部路径规划避障。该算法在计算时间、自主优化能力、稳定性方面具有显著优势。
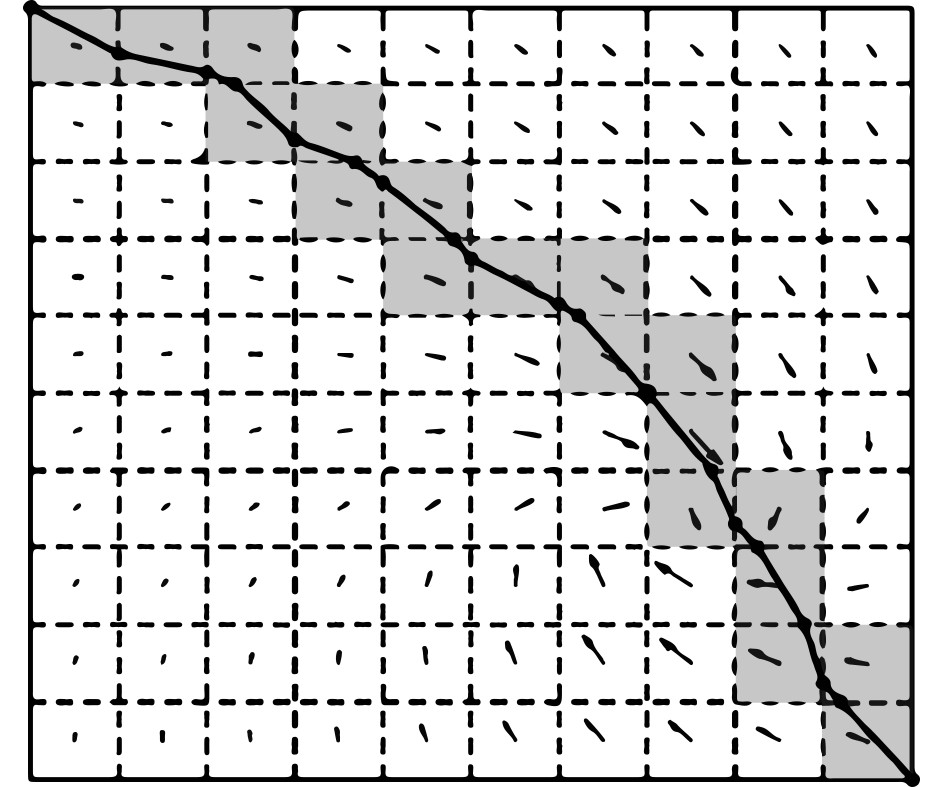
综上,采用栅格法进行海底环境建模时,更易将海流信息化为参数导入,如图3所示。
|
图 3 将海流信息导入栅格图 Fig. 3 Import current information into raster |
栅格法可根据每个网格存储的海洋环境信息判断网格的适航性,当网格中存在对AUV航行的不利影响时,选择该网格的概率降低。地形、水压力等影响因素同样可作为参数加至网格,使规划路径更优。环境建模的难点在于海洋生物对AUV的威胁,潮汐对AUV航行的影响难以转化为数学模型。
2.2 将海流引入环境建模后续路径规划算法文献[33]采用狼群算法进行AUV的路径规划,结果证明该算法具有较强的收敛性与全局寻优能力,虽然算法相对复杂,但可设置更多参数,例如将海流、温度、海水盐度等转化为数据导入算法。针对算法复杂度高这一缺点,文献[34]对狼群算法进行优化,利用杜宾曲线满足AUV转向角的控制约束,并可调整AUV的转弯半径,避免AUV转弯时剐蹭障碍物。仿真结果证明改进后的狼群算法局部规划能力强,精度高,在规划路径不变的情况下,将规划时间减少了6.3%。但结合狼群算法的规划技术实时避障能力较弱,为弥补这一缺点,文献[35]采用遗传算法(GA)进行路径规划,结果证明结合遗传算法的动态实时避障能力较好,缺点是局部寻优能力较差,稳定性不强。遗传算法在早期阶段具有快速的全局搜索能力,而在后期阶段规划速度较慢。然而,遗传算法易与其他算法结合,文献[36]将遗传算法与狼群算法结合起来,使遗传算法在迭代过程中提高规划能力。仿真结果证明,将二者算法结合后,与文献[33-35]相比,其算法收敛速度与路径规划时间均有大幅度改善,且路径规划精度不变。
快速扩展随机树算法(RRT)[37]也是常用的路径规划算法之一,即将海底环境采样为一组节点作为依据规划路径。规划速度快,但规划出的路径通常是次优的,且难以在狭窄的通道中规划路径[38]。文献[39-40]分别用RRT算法在二维、三维建模的前提下进行路径规划,仿真结果证明传统RRT算法的计算复杂度与自由度呈指数关系,不适合解决多自由度AUV在复杂海底环境中的路径规划。针对AUV自由度过高导致算法复杂这一缺陷,文献[41]提出一种改进RRT算法,增加了对AUV旋转角的约束,降低AUV的自由度,改善了扩展树的生长点与探索点,满足规划路径的最优解。仿真结果表明,该算法规划效率高,且安全性较强。
文献[42]利用人工势场法进行路径规划,效果并不理想。当航行路段通过狭窄通道时,由于海流不断干扰AUV,AUV会不断发生摆动陷入“自锁”模式。传统的人工势场法不能消除海流带来的影响。文献[43]采用克隆选择优化算法对人工势场法进行优化,可以避免算法陷入局部最小值,使AUV摆脱“自锁”模式。对比文献[16, 21, 30]可知,解决AUV陷入“死区”最常用的方法,即采用各种手段减少AUV巡航过程中的转角次数与转角幅度,若先利用栅格法对海底环境进行三维建模,将“方向偏差最小”策略引入建模过程,再采用后续算法进行优化,可有效解决AUV陷入“死区”这一问题。
针对AUV路径规划中的时间最优问题,文献[44]提出了一种基于粒子群优化算法(PSO)的二维路径规划算法。通过分析AUV的航行特点与海流运动规律,推导出计算航行时间的函数。仿真结果表明,该算法鲁棒性强且能够找到最短距离的安全路径。缺点是没有进行三维路径规划,且算法的实用性与适应性尚未在实际海洋环境中得到验证,虽在算法过程中加入海流参数,但并未考虑如何应对海流干扰。针对这一缺陷,文献[45]对PSO算法提出改进,将粒子群分为全局搜索粒子与局部搜索粒子对海流进行综合评估,规划路径使AUV尽可能随着海流前进,避免盲目克服海流干扰,从而使航行过程更加稳定。文献[46]比较了量子粒子群算法与遗传算法的优缺点,同时将海流速度方向等参数加入算法中,将二者结合进行路径规划,仿真后证明该组合算法比单一算法有更好的寻优能力和更少的计算时间,可针对海流因素使收敛次数达到理想状态。但文献[46]只研究了在海流大小方向均不变情况下的路径规划,并且没有考虑海流横向推动AUV造成的误差应如何修正。文献[11]采用GA与PSO双层规划算法,先用GA进行路径规划,后用PSO进行路径优化,在保证全局最优的同时解决了传统基于栅格的路径规划算法中AUV运动方向受限的问题,使AUV顺着有利海流流向航行,最后进行实验仿真证明了该算法在可接受的精度下显著提高了计算效率,AUV可进行实时规划,并不断修正海流推动AUV造成的偏离规划路径。文献[47]对文献[11]进行改进,在海流过大时对AUV的速度进行限制,且最终以Kongsberg/Hydroid REMUS 600s型水下机器人为模型,对路径规划算法进行实验验证。以上几种经典算法的优缺点对比如表2所示。
|
|
表 2 优缺点对比 Tab.2 Advantages and disadvantages comparison |
除上述热门经典算法外,还有一些规划效果不错的算法。例如文献[48]提出一种结合速度合成方法的自组织映射算法,当海流发生变化AUV随机移动时,只要给出AUV和目标的位置及海流的速度和方向,就可以计算出AUV前进的方向,规划出后续路径。但此文献只是假设固定在垂直方向上的传感器可以探测到洋流的信息,没有讨论获取海流方向和速度的方法,可与文献[30]中声呐传感器的探测方法相结合,提高规划精度。文献[49]提出一种动态规划算法,将近似时变海流作为参数引进算法,对协同合作的AUV进行路径规划,经过仿真证明算法的可行性。但模拟海流值与实际海流存在差异,难以投入实际使用。文献[50]是在传感器存在噪声及海流存在的情况下跟踪海底电缆,给AUV增加了一个动力控制器,在航线偏离过大时对路径实行重新规划,与文献[46]相比,可在一定程度上修正横向流推动AUV造成的航线偏离,缺点是AUV的动力控制器需要实时计算输入航行方向,且每次修正航线时需要重新规划路径,计算量过大。文献[51-52]分别设计了一种考虑海流影响的二维、三维路径规划方法。该方法结合海流速度与AUV速度修正水平集的偏微分方程,然后对方程进行数值求解,水平集不断迭代以收敛于目标,最后通过反向迭代得到最优路径。基于模拟海流数据和真实地形的仿真实验表明,该方法能够在海流和障碍物连续的海洋环境中找到安全可行的路径。
由于实验条件限制,多数研究处于实验模拟阶段,虽然一些研究在真实水下环境中进行,但还未达到可在实践中应用的鲁棒性水平。目前,成熟的传统算法很难适用复杂的水下环境,部分智能算法存在不成熟、鲁棒性差、运行速度慢等问题。后续研究可融合多种算法,将各种算法的优点融合为改进算法,以提高路径规划的实时性与可靠性。
3 总结与展望AUV的自主水下巡航是一个十分重要的研究领域,具有广泛的应用前景。本文对海底环境的全局路径规划方法进行综述,并对3种全局路径规划方法进行优缺点对比。栅格法多是基于二维建模,目前发展较为成熟。三维栅格法海底建模近几年起步,仍存在诸多缺陷,如环境建模精度低、规划路径安全性不强。二维空间并不能完全体现海洋环境的所有三维信息,栅格法应更多地向三维发展。拓扑图法是一种天生三维的建模法,但因算法复杂,普及度不高。可视图法仅支持二维建模,但因算法简单,易与路径搜索算法相结合。
考虑到海流因素对AUV巡航过程中的影响,本文针对巡航过程中能量消耗的角度对路径规划算法的发展进行了综述。在目前的研究中,海流模型相对简单,多是以二维海底建模为主,如可视图法与栅格法。其中栅格法易离散化,可视图法的建模过程简单,二者均可在建模过程中加入海流参数,在能耗最小的前提下实现路径最优化。关于考虑海流因素的路径规划算法,多数研究采用2种算法结合,利用算法优势对路径进行筛选,最后得出能耗少的最优路径。针对海流动态随机这一特点,研究人员对路径规划算法进行改进,增强算法鲁棒性,以应对突变海流带来的紧急情况,且成功以水下机器人为模型进行了水下实验。
虽然当前AUV自主水下巡航已经取得了丰富的研究成果,但大多数研究将海流因素加入AUV水下巡航的过程中仅考虑单一方面,少数研究在环境建模与路径规划中均加入对海流因素的考虑。例如文献[17],建模时考虑到AUV在海流情况下前进,航迹存在旋转偏差时用一定半径的圆弧代替,路径规划时考虑到AUV在实际水下环境中存在涡流造成的陷阱问题,采用视线制导机制预测巡航轨迹,当前置声呐传感器检测到涡流时,激活回避算法避开涡流陷阱。后续研究可在环境建模与路径规划算法中均加入对海流因素的考虑。
1)栅格法环境建模易于向三维拓展,环境信息精确,空间表达力好,鲁棒性强,且每个网格中均可存储信息,容易将海流速度、流向等这些约束条件加入路径规划算法中规划路径。PSO与GA双层路径规划算法融合性较好,加入约束条件时计算效率高,且易与栅格法相结合。未来研究可将栅格法环境建模与双层规划算法相结合,同时加入海流约束条件,提高水下巡航任务完成度与完成精度。
2)可视图法建模过程简单,能有效避免AUV在海流存在的情况下进入“死区”,易与路径规划算法相结合,一定程度上可消解传统人工势场法的固有缺陷。人工势场法原理简单,反应迅速,易于实现和扩展。经国内外专家学者对人工势场法的不断改进,已经改善了局部极小值问题,将海流因素考虑进人工势场法中是保证该算法适用于AUV水下巡航避障的关键,国内外学者也针对定常海流和涡流的影响,对势场法进行了相应改进。若将可视图环境建模与人工势场法相结合,可进一步提高路径规划的效率,使AUV的巡航过程更具实时性。
4 结 语随着海洋考察范围的逐步扩大,AUV向着智能化方向发展,这就要求AUV必须具有感知海洋环境并准确进行海底建模的能力,只有在了解环境的基础上,才可能让AUV进行智能算法的学习,以及在未知环境中进行适应环境的训练,从而提高AUV的灵活性、稳定性与鲁棒性。
本文在对AUV海底环境建模技术的相关概念和算法进行深入研究的基础上,对3种环境建模方法进行了综述和优缺点对比,并详细阐述了AUV环境建模后续规划算法的研究进展。未来研究中,对于建模技术精度与复杂度的平衡,仍需众多研究人员的不懈努力。
| [1] |
朱大奇, 胡震. 深海潜水器研究现状与展望[J]. 安徽师范大学学报(自然科学版), 2018, 41(3): 205-216. |
| [2] |
郭银景, 刘琦, 鲍建康, 等. 基于人工势场法的AUV避障算法研究综述[J]. 计算机工程与应用, 2020, 56(4): 16-23. |
| [3] |
ZHANG Honghan, GONG Liming, CHEN Tao, et al. Global path planning methods of UUV in coastal environment[C]//2016 IEEE International Conference on Mechatronics and Automation, Harbin, 2016, 1018−1023.
|
| [4] |
LI Daoliang, WANG Peng, DU Ling. Path planning technologies for autonomous underwater vehicles-A review[J]. IEEE Access, 2019, 7: 9745-9768. DOI:10.1109/ACCESS.2018.2888617 |
| [5] |
曹俊, 胡震, 刘涛, 等. 深海潜水器装备体系现状及发展分析[J]. 中国造船, 2020, 61(1): 204-218. DOI:10.3969/j.issn.1000-4882.2020.01.021 |
| [6] |
SAHOO A, DWIVEDY S K, Robi P S. Advancements in the field of autonomous underwater vehicle[J]. Ocean Engineering, 2019, 181: 145-160. DOI:10.1016/j.oceaneng.2019.04.011 |
| [7] |
张世童, 张宏伟, 王延辉, 等. 自主水下航行器导航技术发展现状与分析[J]. 导航定位学报, 2020, 8(2): 1-7. DOI:10.3969/j.issn.2095-4999.2020.02.001 |
| [8] |
李硕, 唐元贵, 黄琰, 等. 深海技术装备研制现状与展望[J]. 中国科学院院刊, 2016, 31(12): 1316-1325. |
| [9] |
ZHAO Yijing, ZHENG Zheng, LIU Yang. Survey on computational-intelligence based UAV path planning[J]. Knowledge-based SYSTEMS, 2018, 158: 54-64. DOI:10.1016/j.knosys.2018.05.033 |
| [10] |
SONG Y S, ARSHAD M R. Coverage path planning for underwater pole inspection using an autonomous underwater vehicle[C]//IEEE International Conference on Automatic Control and Intelligent Systems(I2CACIS), Shah Alam, Malaysia, 2016, 230−235.
|
| [11] |
YAO Xuliang, WANG Feng, WANG Jingfang. Bilevel optimization-based time-optimal path planning for AUVs[J]. Sensors, 2018, 18(12): 1-16. DOI:10.1109/JSEN.2018.2828619 |
| [12] |
姚鹏, 王琨. 基于最小一致性的自治式水下机器人路径规划[J]. 无人系统技术, 2019, 2(4): 8-14. |
| [13] |
邢炜. 基于前视声呐的AUV避障方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [14] |
孙奥林, 曹翔, 肖旭, 等. 基于生物启发神经网络的多AUV目标搜索[J]. 舰船电子工程, 2019, 39(3): 32-36. |
| [15] |
SUN Bing, ZHU Daqi, TIAN Chen, et al. Complete coverage autonomous underwater vehicles path planning based on glasius bio-inspired neural network algorithm for discrete and centralized programming[J]. IEEE Transactions on Cognitive and Developmental Systems, 2018, 11(1): 73-84. |
| [16] |
张楠楠. 水下机器人路径规划与路径跟踪方法研究[D]. 镇江: 江苏科技大学, 2019.
|
| [17] |
夏卫星, 杨晓东. 水下平台三维航路多约束多指标规划的蚁群策略研究[J]. 兵工学报, 2018, 39(9): 1795-1803. DOI:10.3969/j.issn.1000-1093.2018.09.017 |
| [18] |
CHIEN R T, ZHANG L, ZHANG B. Planning collision-free path for robotic arm among obstacles[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1984, 1(6): 91-96. |
| [19] |
陈中悦. 分布式水声网络状态一空间建模与目标检测跟踪[D]. 杭州: 浙江大学, 2019.
|
| [20] |
TOMAS L P, MICHAEL A W. An algorithm for planning collision-free paths among polyhedral obstacles[J]. Communications of the ACM, 1979, 22(5): 436-450. |
| [21] |
包昕幼. 浅水区域无人探测艇编队巡航路径规划研究[D]. 广州: 华南理工大学, 2018.
|
| [22] |
王芳. 基于量子蚁群算法的多无人机协同航迹规划研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [23] |
CANDELORO M, LEKKAS A M, SORENSEN A J. A Voronoi-diagram based dynamic path-planning system for underactuated marine vessels[J]. Control Engineering Practice, 2017, 61: 41-54. DOI:10.1016/j.conengprac.2017.01.007 |
| [24] |
夏娜, 束强, 赵青, 等. 基于维诺图和二分图的水面移动基站路径规划方法[J]. 自动化学报, 2016, 42(8): 1185-1197. |
| [25] |
张雪莲. 基于深度学习的无人水下航行器动态规划方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [26] |
LIU Xing, ZHANG Mingjun, ROGERS E. Trajectory tracking control for autonomous underwater vehicles based on fuzzy re-planning of a local desired trajectory[J]. IEEE Transactions on Vehicular Technology, 2019, 68(12): 11657-11667. DOI:10.1109/TVT.2019.2948153 |
| [27] |
苗润龙, 庞硕, 姜大鹏, 等. 海洋自主航行器多海湾区域完全遍历路径规划[J]. 测绘学报, 2019, 48(2): 256-264. |
| [28] |
CAO Xiang, Sun Changyin, CHEN Mingzhi. Path planning for autonomous underwater vehicle in time-varying current[J]. IET Intelligent transport systems, 2019, 13(8): 1265-1271. DOI:10.1049/iet-its.2018.5388 |
| [29] |
马焱, 肖玉杰, 陈轶, 等. 基于改进烟花-蚁群算法的海流环境下水下无人潜航器的避障路径规划[J]. 导航与控制, 2019, 18(1): 51-59. DOI:10.3969/j.issn.1674-5558.2019.01.007 |
| [30] |
LI Juan, ZHANG Jianxin, ZHANG Honghan, et al. A predictive guidance obstacle avoidance algorithm for AUV in unknown environments[J]. Sensors, 2019, 19(13): 2862. DOI:10.3390/s19132862 |
| [31] |
张楠楠, 姜文刚, 窦刚. 改进蚁群算法在AUV三维路径规划中的研究[J]. 计算机工程与应用, 2019, 55(11): 265-270. DOI:10.3778/j.issn.1002-8331.1805-0298 |
| [32] |
WEI Dunwei, WANG Feiran, MA Hongjiao. Autonomous path planning of AUV in large-scale complex marine environment based in swarm hyper-heuristic algorithm[J]. Applied Sciences-basel, 2019, 9(13): 1-22. |
| [33] |
SHEN Jian, SHI Jing, XIONG Lu. A route planning method for underwater terrain aided positioning based on gray wolf optimization algorithm[C]//Intelligent Data Engineering and Automated Learning, Yangzhou, 2016: 126−133.
|
| [34] |
ZHANG Lanyong, ZHANG Lei, LIU Sheng, et al. Three-dimensional underwater path planning based on modified wolf pack algorithm[J]. IEEE Access, 2017, 5: 22783-22795. DOI:10.1109/ACCESS.2017.2765504 |
| [35] |
KHAN F A, KHAN S A, TURGUT D, et al. Optimizing resurfacing schedules to maximize value of information in UWSNs[C]// IEEE Global Communications Conference, Washington, DC, 2016: 1−5.
|
| [36] |
YAO Peng, ZHAO Shiqiang. Three-dimensional path planning for AUV based on interfered fluid dynamical system under ocean current(June 2018)[J]. IEEE Access, 2018, 6: 42904-42916. DOI:10.1109/ACCESS.2018.2861468 |
| [37] |
CHAO Nan, LIU Yongkuo, XIA Hong. Grid-based RRT* for minimum dose walking path-planning in complex radioactive environments[J]. Annals of Nuclear Energy, 2018, 115: 73-82. DOI:10.1016/j.anucene.2018.01.007 |
| [38] |
JANSON L, ICHTER B, PAVONE. Deterministic sampling-based motion planning: Optimality, complexity, and performance[J]. International Journal of Robotics Reserch, 2018, 37(1): 46-61. DOI:10.1177/0278364917714338 |
| [39] |
CARRERAS M, HERNANDEZ J D, VIDAL E. Online motion planning for underwater inspection[C]//IEEE/OES Autonomous Underwater Vehicles, Tokyo, Japan, 2016: 335−341.
|
| [40] |
CARRERAS M, HERNANDEZ J D, VIDAL E. Sparus II AUV-A hovering vehicle for seabed inspection[J]. IEEE Journal of Oceanic Engineering, 2018, 43(2): 344-355. DOI:10.1109/JOE.2018.2792278 |
| [41] |
YU Lijun, WEI Zhizhong, WANG Zhengan, et al. Path optimization of AUV based on smooth-RRT algorithm[C]//IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 2017: 1498−1502.
|
| [42] |
FRANCO S, ALEJANDRO R, SEBASTIAN V A, et al. Artificial potential fields for the obstacles avoidance system of an AUV using a mechanical scanning sonar[C]//IEEE/OES South American International Symposium on Ocean Engineering. Buenos Aires, Argentina, 2017: 1−6.
|
| [43] |
DAS B, SUBUDHI B, PATI B B. Co-operative control of a team of autonomous underwater vehicles in an obstacle-rich environment[J]. Journal of Marine Engineering and Technology, 15(3): 135−151.
|
| [44] |
冯炜, 张静远, 王众, 等. 海洋环境下基于量子行为粒子群优化的时间最短路径规划方法[J]. 海军工程大学学报, 2017, 29(6): 72-77. |
| [45] |
WANG Xiaowei, YAO Xuliang, ZHANG Le. Path planning under constraints and path following control of autonomous underwater vehicle with dynamical uncertainties and wave disturbances[J]. Journal of Intelligent and Robotic Systems, 2020 Article in Press.
|
| [46] |
ZENG Zheng, SAMMUT K, LAMMAS A, et al. Imperialist competitive algorithm for AUV path planning in a variable ocean[J]. Applied Artificial Intelligence, 2015, 29(4): 402-420. DOI:10.1080/08839514.2015.1004614 |
| [47] |
姚绪梁, 王峰, 王景芳, 等. 一种时变洋流场下AUV最优能耗路径规划方法[J/OL]. 控制与决策: 1−9[2020-06-10]. https://doi.org/10.13195/j.kzyjc.2019.0072.
|
| [48] |
HUANG Huan, ZHU Daqi, DING Feng. Dynamic task assignment and path planning for multi-AUV system in variable ocean current environment[J]. Journal of Intelligent and Robotic Systems, 2013, 74(3): 999-1012. |
| [49] |
LIU Mingyong, XU Baogui, PENG Xingguang. Cooperative path planning for multi-AUV in time-varying ocean flows[J]. Journal of System Engineering and Electronics, 2016, 27(3): 612-618. DOI:10.1109/JSEE.2016.00065 |
| [50] |
YU Caoyang, XIANG Xianbo, LAPIERRE L, et al. Robust magnetic tracking of subsea cable by AUV in the presence of sensor noise and ocean currents[J]. IEEE Journal of Oceanic Engineering, 2018, 43(2): 311-322. DOI:10.1109/JOE.2017.2768105 |
| [51] |
孙天龙. 考虑海流影响的AUV航路规划方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [52] |
刘厂, 孙天龙, 张志强. 基于改进水平集的AUV时间最优航路规划方法[C]//第36届中国控制会议论文集, 辽宁, 2017: 784−789.
|
 2021, Vol. 43
2021, Vol. 43
