2. 郑州市科学技术情报研究所,河南 郑州 450007
2. Zhengzhou Institute of Science and Technology Information, Zhengzhou 450007, China
某舰炮在射击时,炮尾与身管定位块位置出现断裂缺口,造成自动机停射。对该炮尾部位进行测量后发现炮尾抓钩尺寸偏小,结构壁厚偏薄弱。
为了查找炮尾裂口原因,校核炮尾强度是否足够,分别建立炮尾名义尺寸和实测尺寸模型,对炮尾-身管耦合模型进行非线性接触分析,对炮尾抓钩进行强度分析。
1 炮身轴向载荷理论计算由火炮内弹道相关理论[1-3],弹丸膛内运动时期炮膛合力分为3部分:
1)火药气体作用在膛底的力
2)作用在药室锥面上的力
3)弹丸作用在膛线上的力r。
膛内时期炮膛合力示意图如图1所示。

|
图 1 膛内运动时期炮膛合力作用示意图 Fig. 1 Schematic diagram of gun bore resultant force during interior ballistics process |
膛内火药气体膛底压力
| ${p_{\rm{t}}} = \dfrac{{1 + \dfrac{1}{2}\dfrac{w}{{{\phi _1}q}}}}{{1 + \dfrac{1}{3}\dfrac{w}{{{\phi _1}q}}}}p \approx \dfrac{1}{\phi }\left({\phi _1} + \dfrac{1}{2}\frac{w}{q}\right)p\text{。}$ | (1) |
式中:q为弹丸质量;w为装药质量;φ1为仅考虑弹丸旋转和摩擦两种次要功的计算系数,φ1≈1.02;φ为次要功计算系数。
| $\phi = K + \frac{1}{3}\frac{w}{q} \approx {\phi _1} + \frac{1}{3}\frac{w}{q}\,,$ | (2) |
用St表示膛底断面积,作用在膛底的力为:
| ${P_{\rm{t}}} = {p_{\rm{t}}}{S_{\rm{t}}} \approx \frac{1}{\phi }\left({\phi _1} + \frac{1}{2}\frac{w}{q}\right)p{S_{\rm{t}}}\,{\text{。}}$ | (3) |
膛内压力分布是不均匀的,火药气体压力沿药室长度分布也不均匀。作用在药室锥面上的轴向分力为:
| ${P_{{\rm{zm}}}} = {p_{{\rm{zm}}}}({S_{\rm{t}}} - S) \approx {p_{\rm{t}}}({S_{\rm{t}}} - S)\,{\text{。}}$ | (4) |
式中:pzm为整个药室锥面上所受火药气体压力的平均值,pzm与pt相差不大;
膛内时期弹丸的弹带对膛线作用力的轴向分力r又称为弹丸膛线阻力。用
| ${\phi _1}q\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = {p_{\rm{d}}}S\,,$ | (5) |
将式(5)代入式(6),考虑
| $r = \frac{1}{\phi }({\phi _1} - 1)pS\,{\text{。}}$ | (6) |
将相关内弹道参数代入式(4)和式(6),即可得到
基于PTC Creo 2.0建立炮尾、身管三维模型,基于Ansys Workbench 18.0进行有限元分析。
2.1 炮尾材料参数有限元分析轴向载荷由前文所述方法求得,约束条件由舰炮射击时工况确定。炮尾材料为炮钢,其屈服极限用σs表示,热处理后其屈服极限超过1300 MPa,有限元计算时所用材料参数见表1。
|
|
表 1 结构钢材料参数 Tab.1 Structural steel material parameters |
炮尾抓钩强度校核不需分析炮闩和炮尾的非线性接触,将炮尾和炮闩接触部分切除。射击时只有一个炮膛进行点火击发,其他炮膛和对应身管不受射击载荷作用。
计算建立2种三维模型,一是根据名义尺寸建立的三维模型;二是根据炮尾抓钩实测尺寸建立的三维模型。由于工况相同,两模型的边界条件相同,有限元模型的约束及载荷情况如图2所示。炮尾后断面为固定约束,滚珠滚道为轴向位移约束,身管前端台座与六面体贴合处为法向位移约束,膛底为均布压力,施加沿发射方向的药室锥面轴向力Pzm和内膛壁面轴向力r。

|
图 2 约束和载荷加载情况示意 Fig. 2 Schematic diagram of constraint and load |
基于大量的理论研究和实验验证,目前已经提出了上百个强度模型或准则,按照剪应力分类,可以将强度理论划分为单剪强度理论(SSS理论,Single-Shear Strength Theory)、双剪强度理论(TSS理论,Twin-Shear Strength Theory)和八面体剪应力强度强度理论(OSS理论,Octahedral-Shear Strength Theory)三大系列强度理论[5-6]。Tresca屈服条件是SSS强度理论的单参数准则,Mises屈服条件是OSS强度理论的单参数准则,最大偏应力屈服条件是TSS理论的单参数准则。
对炮尾抓钩分别按照Tresca屈服条件、Mises屈服条件和最大偏应力屈服条件进行校核,提取炮尾Tresca等效应力、Mises等效应力、最大偏应力等效应力云图。
炮尾抓钩内侧圆角被抓钩侧壁挡住,在观察其应力分布时难以直接观察到圆角根部,对炮尾进行切片处理,在炮尾前端镜面前进行剖切,便于观察圆角根部和抓钩侧壁处应力分布。
1)Tresca等效应力结果
为表述简便,将名义尺寸模型Tresca等效应力记为

|
图 3 抓钩Tresca等效应力云图 Fig. 3 Nephogram of grapnel Tresca equivalent stress |
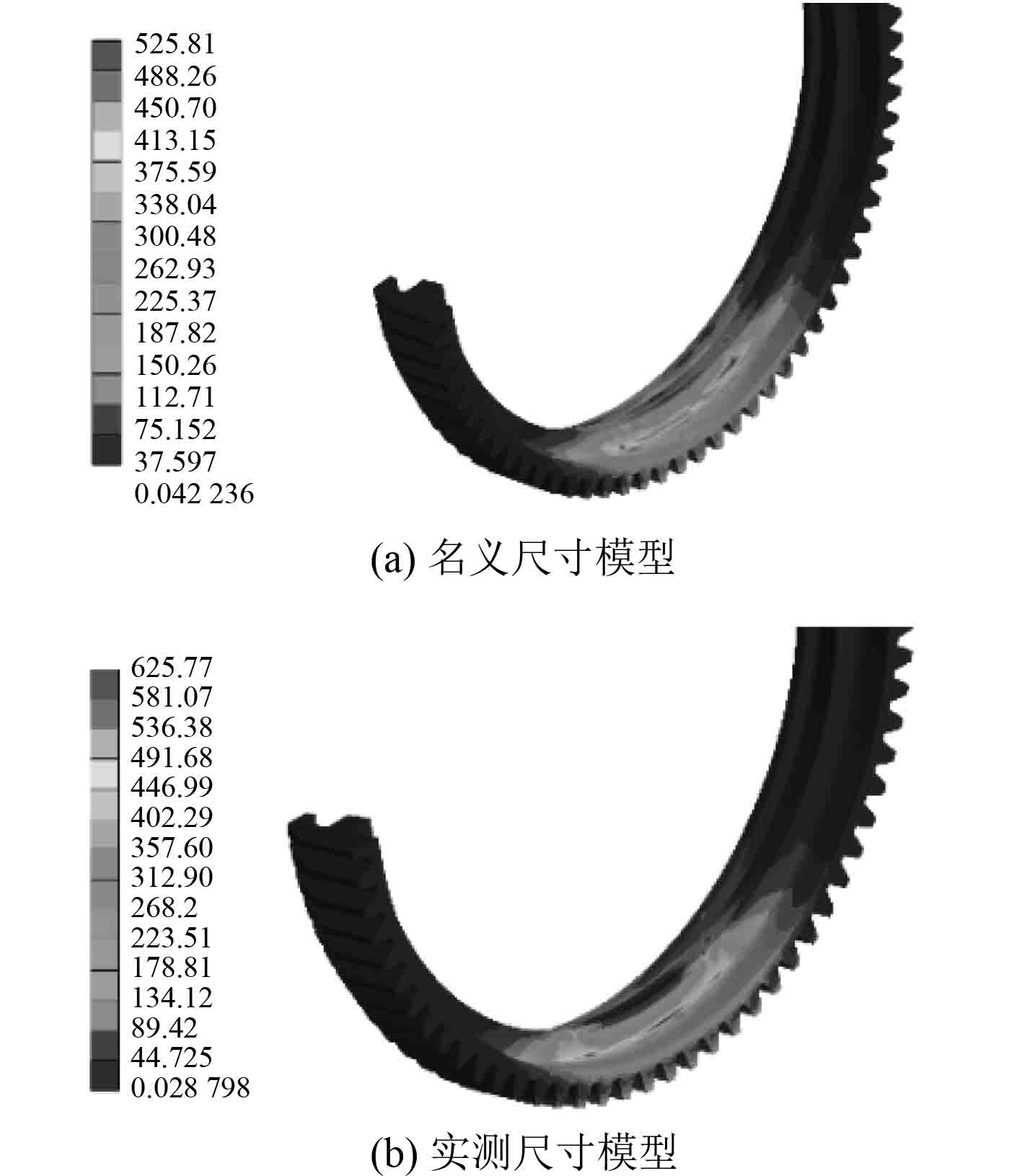
2)Mises等效应力结果
名义尺寸模型Mises等效应力记为
|
图 4 抓钩Mises等效应力云图 Fig. 4 Nephogram of grapnel Mises equivalent stress |
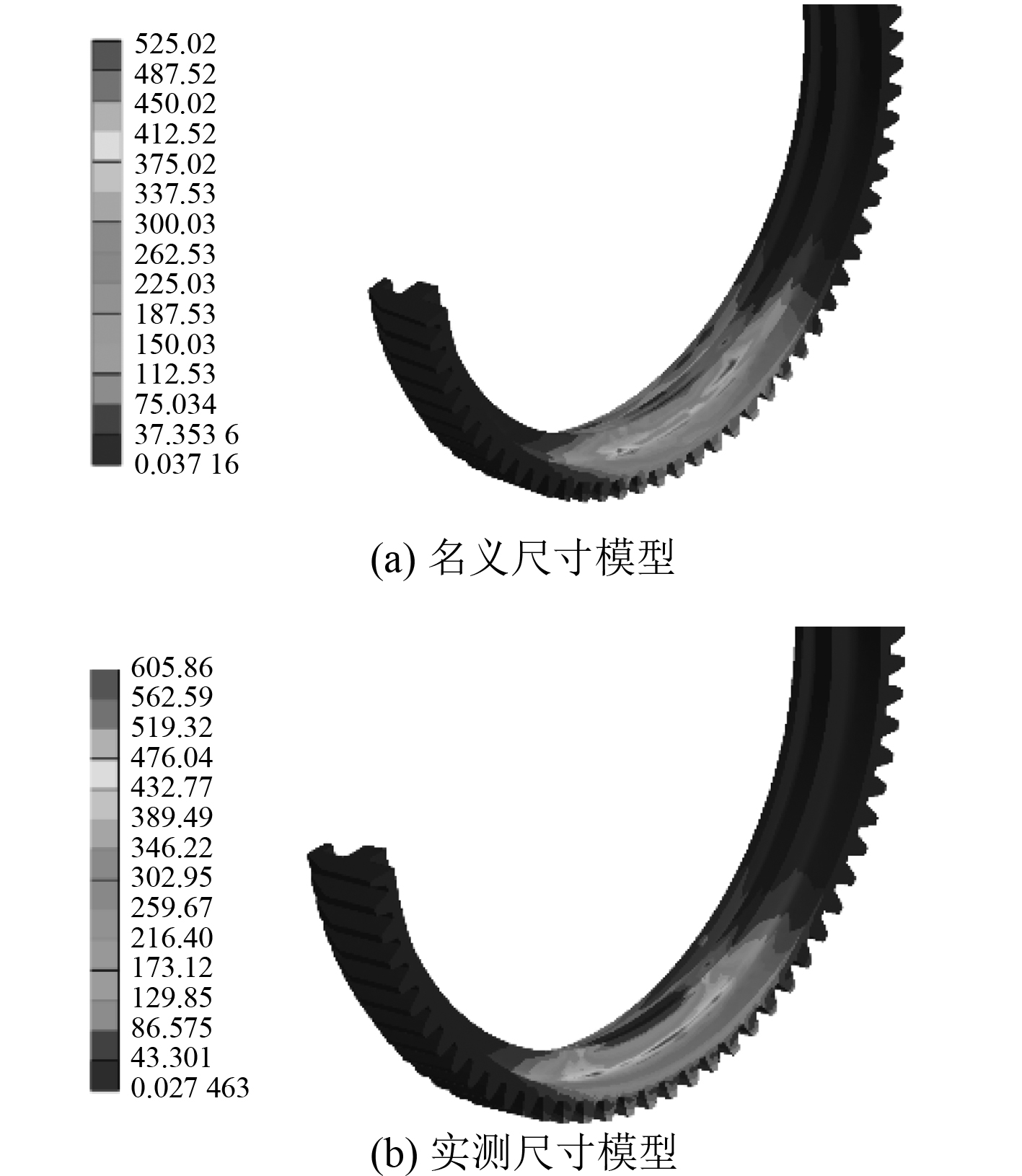
3)最大偏应力等效应力结果
名义尺寸模型最大偏应力等效应力记为
|
图 5 抓钩最大偏应力等效应力云图 Fig. 5 Nephogram of grapnel maximum deviatoric stress equivalent stress |
4)抓钩根部等效应力沿路径的分布
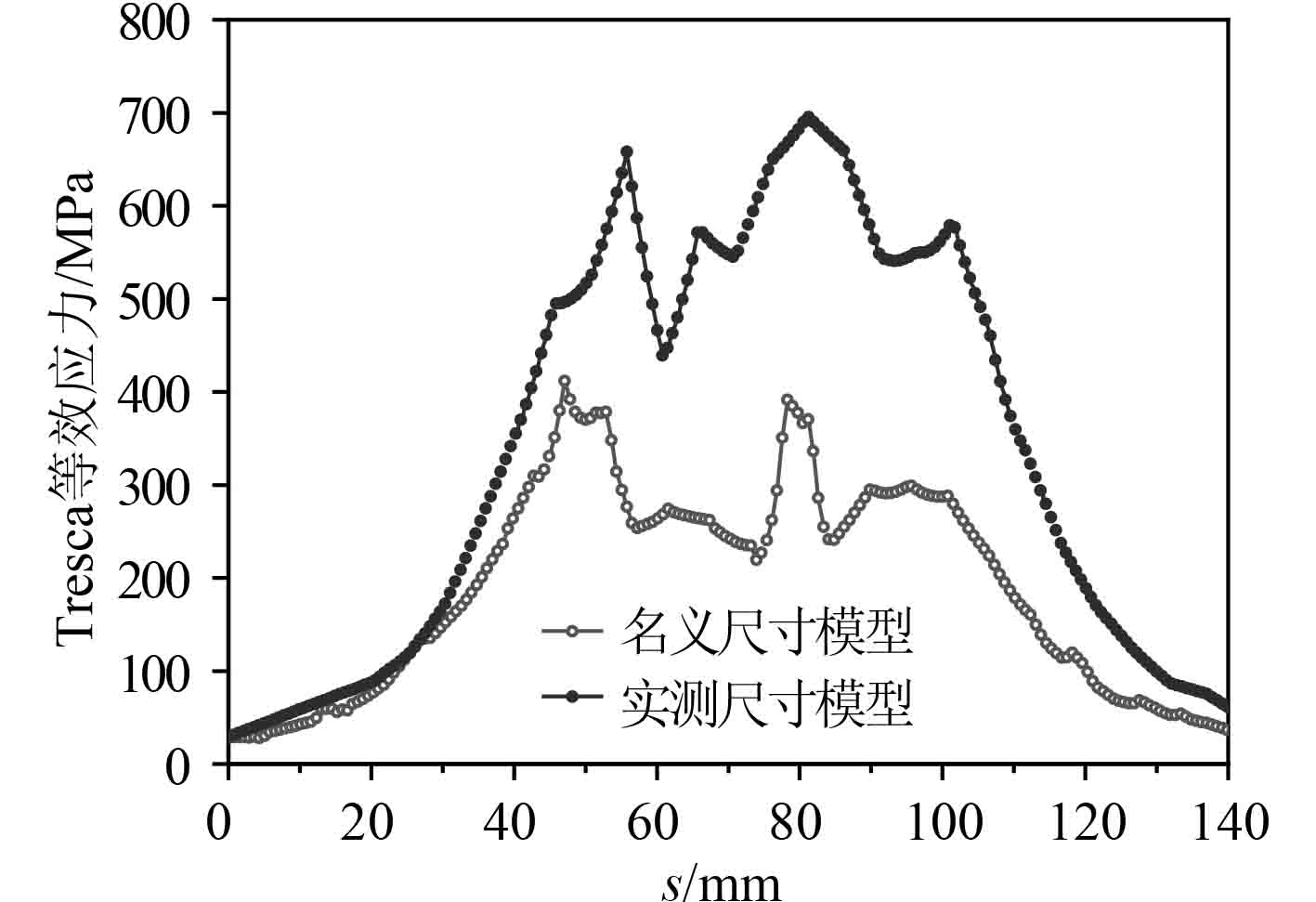
取抓钩圆角根部路径(Path),由3种屈服条件求得的等效应力随路径的分布曲线如图6~图8所示。可知等效应力在倒角根部两侧和中间点附近达到峰值,抓钩在此3处承受较大的周期性交变载荷作用,此3处易成为疲劳源,裂纹易在此处形核扩展,进而造成炮尾抓钩断裂失效。
|
图 6 抓钩根部Tresca等效应力沿路径的变化 Fig. 6 Curve of grapnel chamfer Tresca equivalent stress along the path |

|
图 7 抓钩根部Mises等效应力沿路径的变化 Fig. 7 Curve of grapnel chamfer Mises equivalent stress along the path |

|
图 8 抓钩根部最大偏应力等效应力沿路径的变化 Fig. 8 Curve of grapnel chamfer maximum deviatoric stress equivalent stress along the path |
复杂应力状态下结构屈服条件为应力空间中的曲线、曲面或超曲面。初始屈服条件一般可表示为:
| $f({\sigma _{ij}},{k_i}) = 0\,,$ | (7) |
对各向同性材料,屈服条件与坐标无关,可用应力张量不变量表示为:
| $ f({I}_{1}\text{,}{I}_{2}\text{,}{I}_{3}\text{,}{k}_{i})=0\,,$ | (8) |
炮钢应用于火炮自动机,实验数据表明静水压力对其屈服的影响可以忽略不计[7],忽略其影响,屈服条件可用应力偏张量不变量表示为:
| $f({J_2},{J_3}) = 0\,,$ | (9) |
法国工程师H. Tresca提出的Tresca屈服条件[8]的一般应力表达式为:
| $f({J_2},{J_3}) = \frac{{\sqrt {{J_2}} }}{{{k_1}}}\cos \left\{ {\frac{1}{3}\arcsin \left[ { - \frac{{3\sqrt 3 {J_3}}}{{2{{({J_2})}^{\frac{3}{2}}}}}} \right]} \right\} - 1 = 0\,,$ | (10) |
它是非正则的,由6个线性函数构成,几何上是一个不光滑曲面,在数学处理上不方便。
德国力学家R. Von Mises提出用圆柱面代替Tresca正六边棱柱面,即为Mises屈服条件,它的一般应力表达式为:
| $f({J_2},{J_3}) = {J_2} - k_2^2 = 0\,,$ | (11) |
最大偏应力屈服条件[8](又称双剪应力屈服条件)最早由R.Schmidt提出,后由俞茂宏用双剪应力的概念对该屈服条件进行了说明,其一般表达式为:
| $\begin{split}f({J_2},{J_3}) = &\frac{{2\sqrt {{J_2}} }}{{\sqrt 3 }}\frac{1}{{{k_3}}}\max \left\{ \left| {\sin \left({\theta _\sigma } + \frac{{2{\text{π}}}}{{\rm{3}}}\right)} \right|,\right.\\ &\left.\left| {\rm{sin}}\left({\theta _\sigma } - \frac{{2{\text{π}}}}{{\rm{3}}}\right) \right| \right\} - 1 = 0\,{\text{。}}\end{split}$ | (12) |
其中,
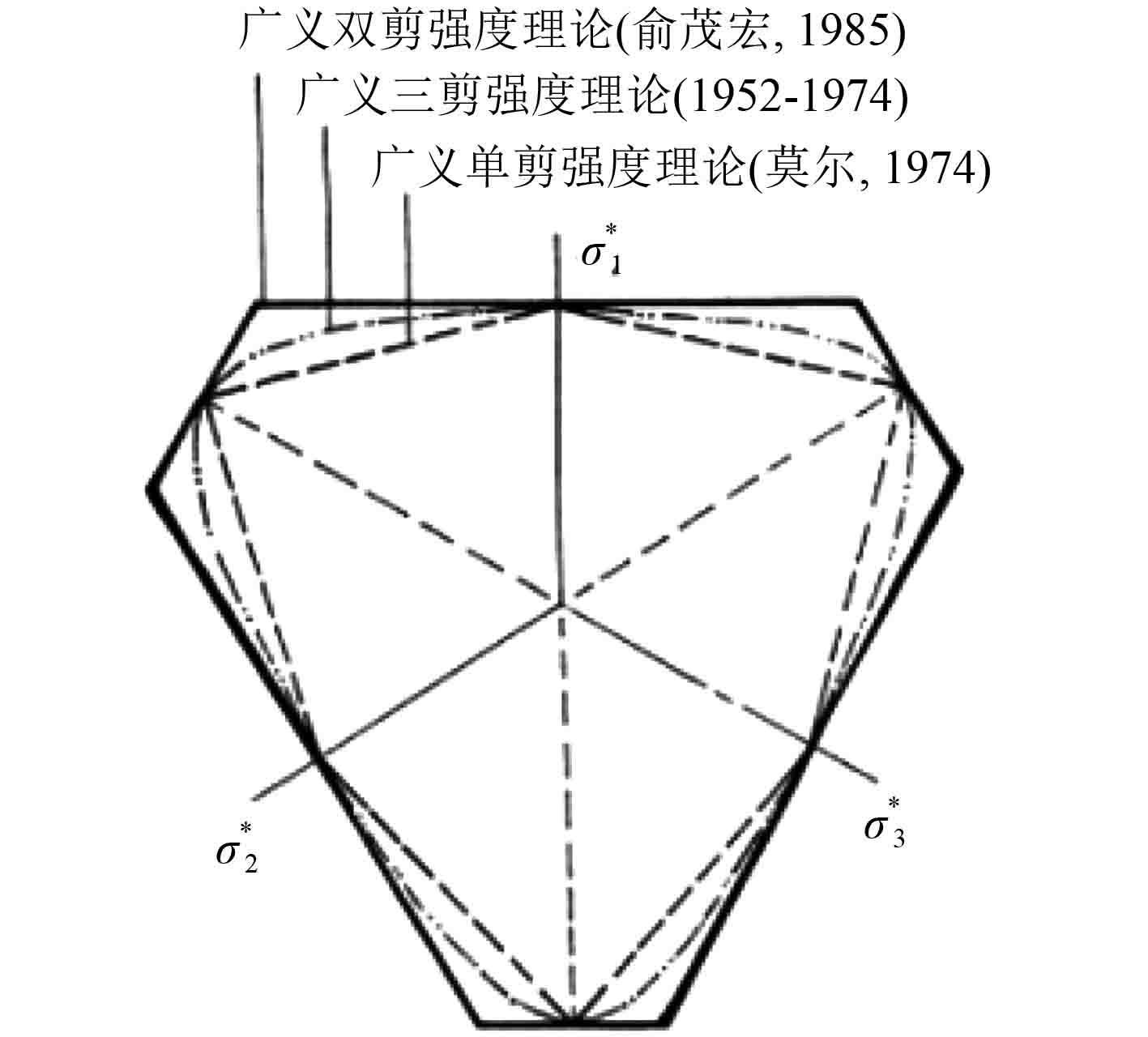
单剪强度理论的极限面为所有外凸极限轨迹的内边界,双剪强度理论的极限面为所有外凸极限轨迹的外边界,八面体剪应力强度理论的极限面居中[6],如图9所示。
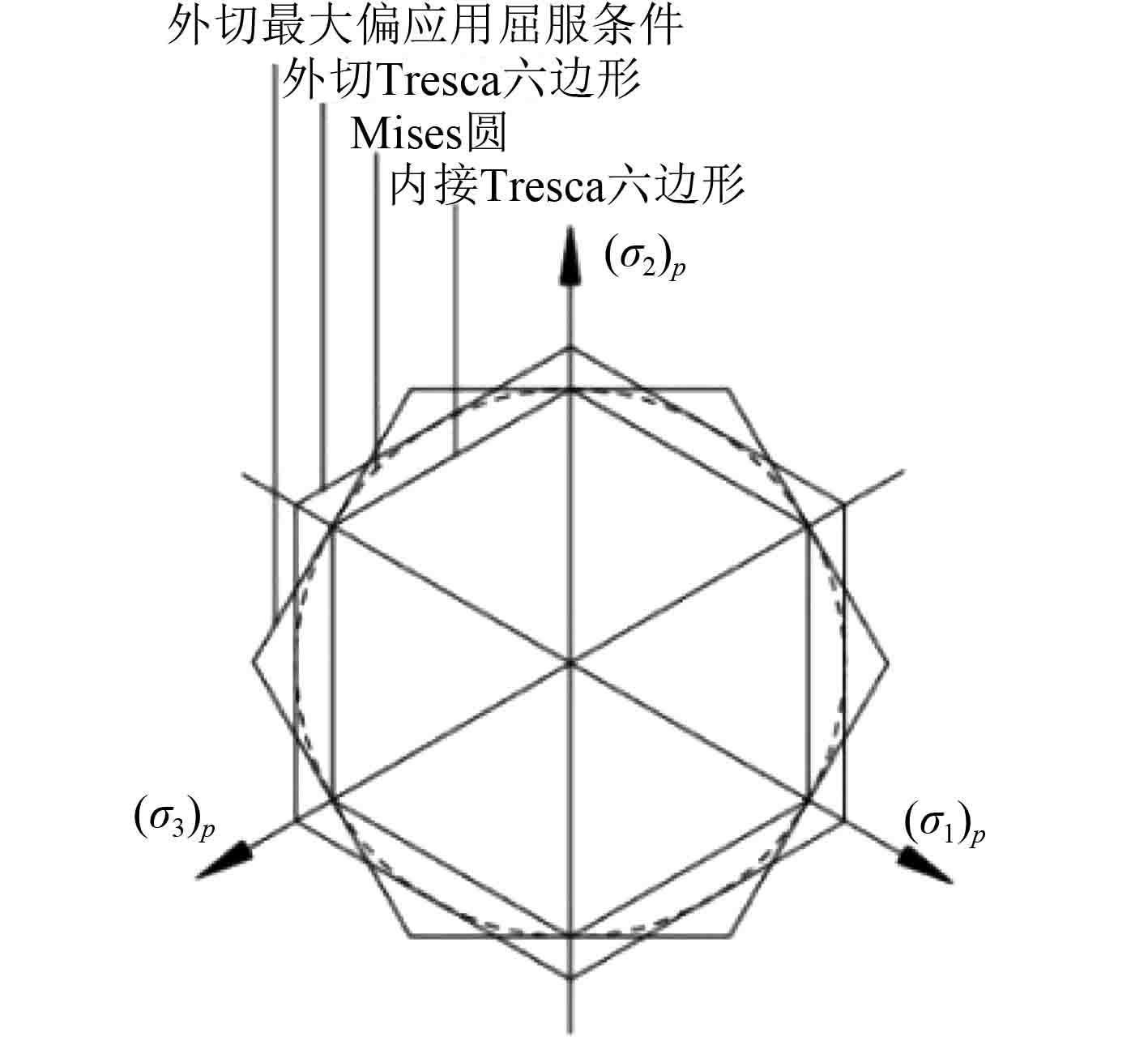
作为三大系列强度理论的单参数准则,在π平面(或偏平面)上,若假定单轴拉伸时2个屈服面重合,则Tresca六边形内接于Mises圆,此时2个屈服面在纯剪切状态时差别最大为33.33%。若假定纯剪切时2个屈服面重合,则Tresca六边形外切于Mises圆,此时2个屈服面在单轴拉伸(或压缩)状态时差别最大为33.33%。最大偏应力屈服条件在π平面上为一外切于Mises圆的正六边形,相对于内接Tresca正六边形旋转30°,如图10所示。
3.2 3种强度理论校核结果及分析 3.2.1 3种屈服条件校核结果分别按Tresca屈服条件、Mises屈服条件、最大偏应力屈服条件校核该炮尾抓钩处的强度。
名义尺寸模型计算结果为:
| $\left\{ {\begin{array}{*{20}{l}} {\sigma _{{\rm{tresca}}}^{{\rm{my}}} \leqslant \left[ \sigma \right] = {\sigma _{\rm{s}}}/2}\,, \\ {\sigma _{{\rm{mises}}}^{{\rm{my}}} \leqslant \left[ \sigma \right] = {\sigma _{\rm{s}}}/2}\,, \\ {\sigma _{{\rm{yu}}}^{{\rm{my}}}\;\;\; \leqslant \left[ \sigma \right] = {\sigma _{\rm{s}}}/2}\,, \end{array}} \right.$ | (13) |
实测最小尺寸计算结果为:
| $\left\{ {\begin{array}{*{20}{l}} {\sigma _{{\rm{tresca}}}^{{\rm{sc}}} \geqslant \left[ \sigma \right] = {\sigma _{\rm{s}}}/2}\,, \\ {\sigma _{{\rm{mises}}}^{{\rm{sc}}} \leqslant \left[ \sigma \right] = {\sigma _{\rm{s}}}/2}\,, \\ {\sigma _{{\rm{yu}}}^{{\rm{sc}}}\;\;\; \leqslant \left[ \sigma \right] = {\sigma _{\rm{s}}}/2}\,{\text{。}} \end{array}} \right.$ | (14) |
3种强度理论分析结果整理后如表2所示。
|
|
表 2 安全系数计算结果 Tab.2 Calculation results of safety factor |
抓钩按Tresca屈服条件校核时,名义尺寸模型满足2倍安全系数,不满足2.5倍安全系数,实测尺寸模型不满足2倍安全系数,此时其安全系数(n)降为1.84,强度不足。
抓钩按Mises屈服条件和最大偏应力屈服条件校核时,名义尺寸模型均近似满足2.5倍安全系数,实测尺寸模型均满足2倍安全系数,不满足2.5倍安全系数。且由表2可知,不论是名义尺寸模型还是实测尺寸模型,均有最大偏应力屈服条件安全系数最大,Tresca屈服条件安全系数最小,Mises屈服条件安全系数居中,计算结果与理论预测结果一致。
各种屈服理论的可靠性需要由实验加以验证,据此可对比分析Tresca屈服条件、Mises屈服条件、最大偏应力屈服条件与实验结果的吻合程度。
Lode薄壁圆筒拉伸-内压实验结果如图11(a)所示[10],实验结果与Mises屈服条件更接近,与Tresca屈服条件偏离较远。如前文所述,若拉伸时各屈服条件重合,剪切时最大偏差可达33.33%,由于未考虑剪应力的影响,此实验结果的验证并不充分。

|
图 11 各屈服条件和实验数据对比 Fig. 11 Comparison of yield conditions and experimental data |
Taylor等[11]又进行了薄壁圆筒拉伸-扭转联合作用实验,结果如图11(b)所示。实验结果显示,铝和铜与Mises屈服条件吻合较好,而软钢实验结果更接近最大偏应力屈服条件,且所有实验结果都与Tresca屈服条件偏离较远。
Tresca屈服条件在材料力学中经过处理,被称为最大剪应力理论,其强度条件在材料力学中被表述为:
| ${\sigma _{{\rm{xd}}3}} = {\sigma _1} - \sigma {}_3 \leqslant \left[ \sigma \right]\,,$ | (15) |
其只考虑最大和最小主应力的作用,未考虑中间主应力的作用,大量理论研究和试验研究结果表明,中间主应力对材料屈服确实存在一定的影响,其对材料失效破坏的影响在很多应力状态下是不能忽略的[12-13]。根据Tresca屈服条件得到的强度条件偏保守,由此设计的结构重量偏大,较为笨重,经济性偏低,不适合对重量要求较高的结构设计。
Mises屈服条件认为引起材料屈服的主要因素是畸变能,其强度条件在材料力学中被表述为:
| ${\sigma _{{\rm{xd}}4}} = \sqrt {\frac{{{{({\sigma _1} - {\sigma _2})}^2} + {{({\sigma _2} - {\sigma _3})}^2} + {{({\sigma _3} - {\sigma _1})}^2}}}{2}} \leqslant \left[ \sigma \right]\,,$ | (16) |
式(16)中的等效应力考虑了3个主应力的综合影响,也更符合大量试验验证的结果。对于塑性材料,其结果相对于Tresca屈服条件校核结果更为精确。但Mises屈服条件并不能够对高三轴应力状态下材料易于脆断的现象予以解释[14]。
双剪应力强度理论认为当作用于单元体上的2个较大主剪应力之和达到某一极限值时,材料开始发生屈服,俞茂宏将其表述为:
| $ \left\{\begin{array}{*{20}{l}}{c}f={\tau }_{13}+{\tau }_{12}={\sigma }_{1}-\dfrac{1}{2}({\sigma }_{2}+{\sigma }_{3})=c\rm{\hspace{0.17em}},\rm{\hspace{0.17em}}({\tau }_{12}\geqslant {\tau }_{23})\,,\\ {f}^{\rm{'}}={\tau }_{13}+{\tau }_{23}=\dfrac{1}{2}({\sigma }_{1}+{\sigma }_{2})-{\sigma }_{3}=c\rm{\hspace{0.17em}},\rm{\hspace{0.17em}}({\tau }_{12}\leqslant {\tau }_{23})\,{\text{。}}\end{array}\right.$ | (17) |
它比Tresca强度理论多考虑了中间主剪应力的影响(见图10),在不同的应力状态下二者相差最大可达33.33%。在某些应力状态下其理论值与实验结果吻合非常好,文献[15]展示了其实验结果和理论预测的对比。
3.2.3 主应力分布的影响分析对炮尾抓钩有限元分析的3个主应力进行对比分析。
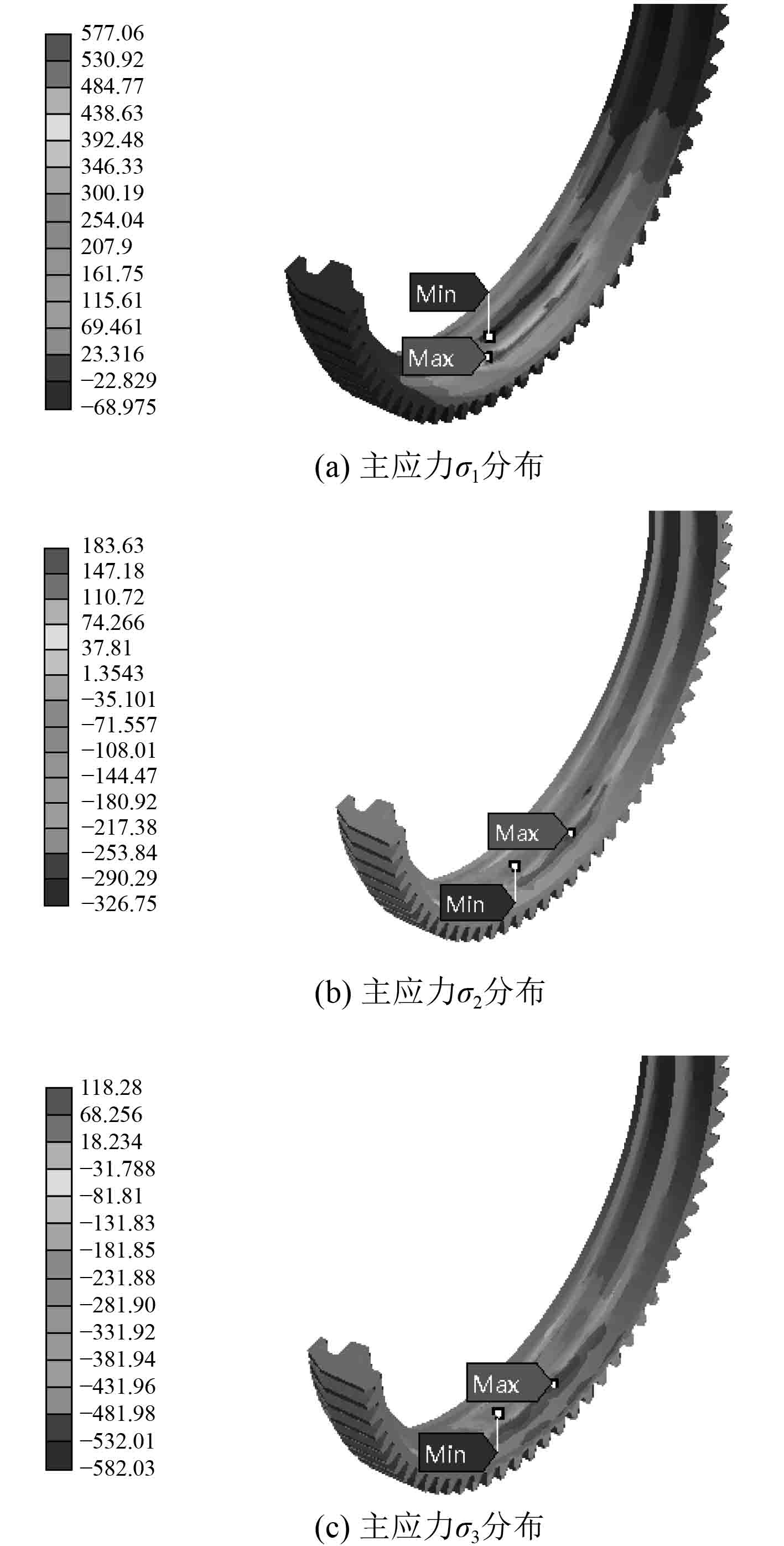
由主应力分布云图(见图12和图13),结合前述等效应力云图以及抓钩倒角根部路径处等效应力变化曲线,可以清晰地看出中间主应力对等效应力的影响,其不但影响了等效应力的大小,而且影响了等效应力极值的分布。
|
图 12 名义尺寸模型主应力分布 Fig. 12 Principal stress distribution of nominal size model |
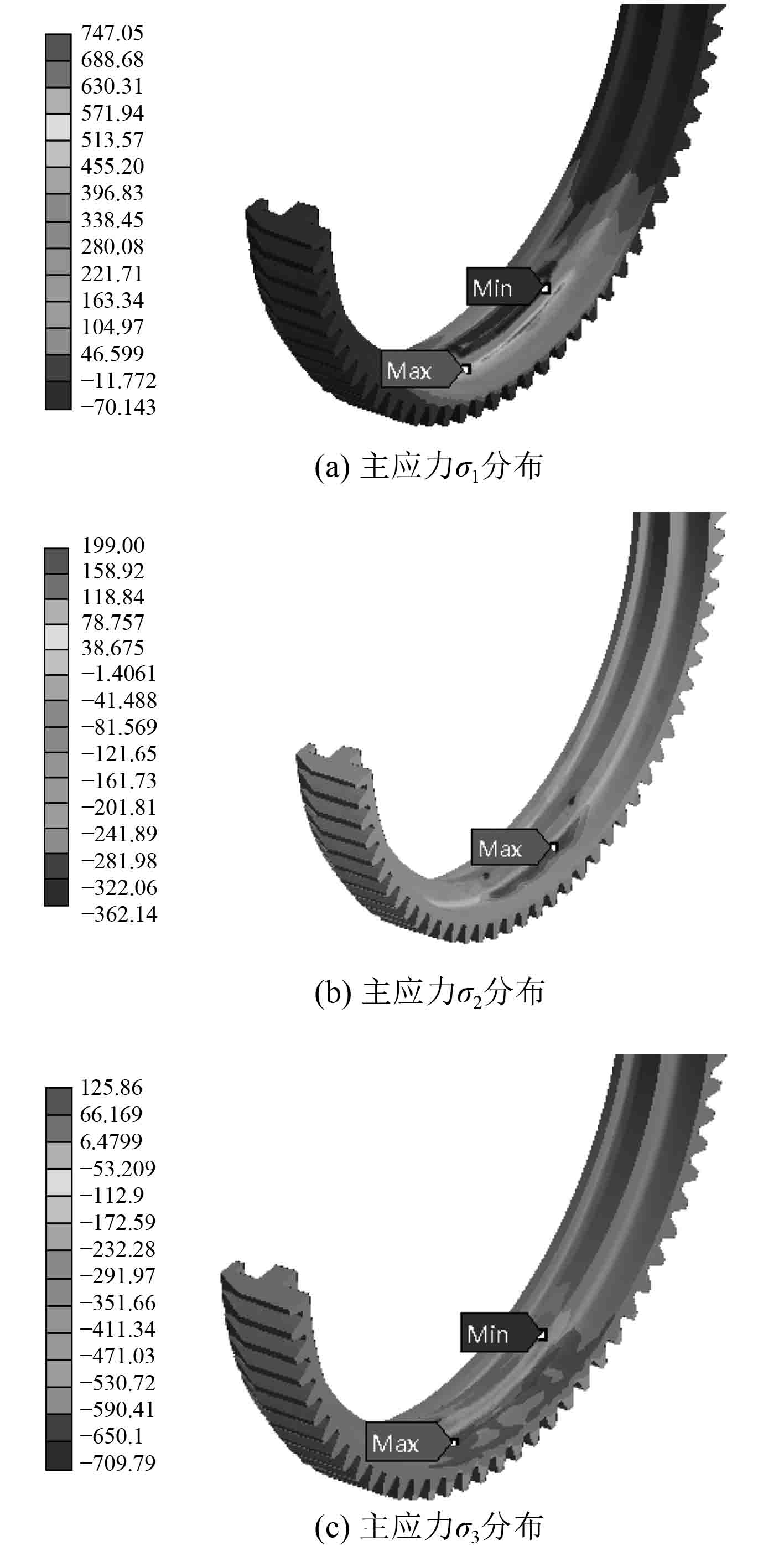
|
图 13 实测尺寸模型主应力分布 Fig. 13 Principal stress distribution of measured size model |
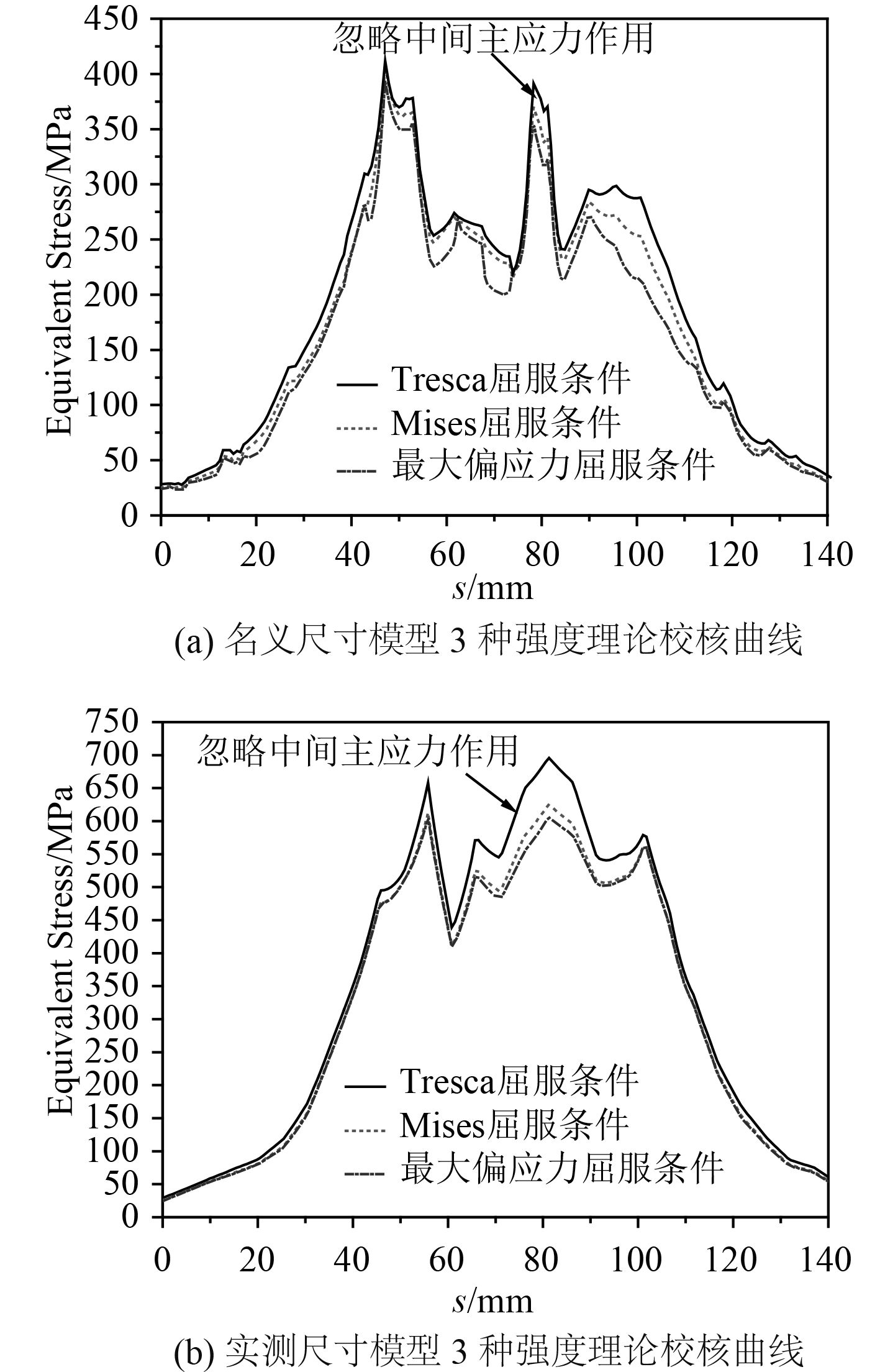
中间主应力在抓钩圆角根部是最大拉应力,在抓钩侧壁边缘处是最大压应力,考虑其影响和忽略其影响会对强度校核结果产生较大差异,从而导致不同强度理论下最大等效应力的显著差异,2种尺寸三维模型在不同强度理论下的校核结果对比如图14所示。2种模型在忽略中间主应力的影响时,得到的等效应力均为最大值,由此得到的结构安全系数较低,设计结构偏保守,考虑中间主应力的影响后,2种模型的等效应力下降,且基于双剪强度系列理论的最大偏应力等效应力下降最多,结构的安全系数最大,材料利用更充分,结构的潜能得到最大程度的发挥。
|
图 14 3种强度理论校核曲线 Fig. 14 Intensity check curves of three kinds of strength theory |
根据本文分析,可以得出如下结论:
1)名义尺寸模型按Tresca强度理论校核满足2倍安全系数,达到2.3倍安全系数,不满足2.5倍安全系数,按照Mises强度理论和最大偏应力强度理论校核时均近似满足2.5倍安全系数,抓钩设计强度足够。
实测尺寸模型抓钩壁厚变薄,按Tresca强度理论校核时炮尾抓钩安全系数仅为1.84,不足2倍安全系数,强度不足。按Mises强度理论和最大偏应力理论校核满足2倍安全系数,不满足2.25倍安全系数,强度不足。炮尾抓钩断裂由机加超差引起。
2)Tresca强度理论较为保守,位于屈服面的下限,由于忽略了中间主应力的影响,导致结构计算得到的静强度不满足要求,由此强度准则设计的结构较为保守,结构较粗笨,偏安全,但经济性较差。而Mises强度理论和最大偏应力强度理论均考虑了中间主应力的影响,材料利用率更高,结构更轻巧更合理,经济性和灵活性更佳。
3)由计算结果来看,Mises屈服条件校核结果和最大偏应力校核结果相差不大,二者很接近,在对炮钢进行强度校核时,二者均可选用,视具体情况而定。最大偏应力屈服条件是线性方程,Mises屈服条件是非线性方程,对数学处理上的解析分析而言,最大偏应力屈服条件应用起来更加方便,在解析分析中有独特的优点。
| [1] |
张相炎, 郑建国, 袁人枢. 火炮设计理论[M]. 北京: 北京理工大学出版社, 2014.
|
| [2] |
高跃飞. 火炮反后坐装置设计[M]. 北京: 国防工业出版社, 2010.
|
| [3] |
高树滋, 陈运生, 张月林, 等. 火炮反后坐装置设计[M]. 北京: 兵器工业出版社, 1995.
|
| [4] |
张小兵. 枪炮内弹道学[M]. 北京: 北京理工大学出版社, 2014.
|
| [5] |
俞茂宏. 强度理论百年总结[J]. 力学进展, 2004, 34(4): 529-560. |
| [6] |
俞茂宏, M. YOSHIMINE, 强洪夫, 等. 强度理论的发展和展望[J]. 工程力学, 2004, 21(6): 1-20. DOI:10.3969/j.issn.1000-4750.2004.06.001 |
| [7] |
朱兆祥. 材料本构关系理论讲义[M]. 北京: 科学出版社, 2015.
|
| [8] |
米海珍, 胡燕妮. 塑性力学[M]. 北京: 清华大学出版社. 2014.
|
| [9] |
陈明祥. 弹塑性力学[M]. 北京: 科学出版社, 2012.
|
| [10] |
VON W. LODE. Versuche über den Einfluß der mittleren Hauptspannung auf das Fließen der Metalle Eisen, Kupfer und Nickel[J]. Z. Physik, Bd. 36(1926). p. 913−939.
|
| [11] |
TAYLOR G. I., QUINNEY H. The plastic distortion of metals[J]. Trans. Roy. Soc. (London), Series A, vol. 230 (1931) p. 323−362.
|
| [12] |
RICE J R. Limitations to the small scale yielding approximation for creak tip plasticity[J]. Mech. Phys, Solid, 1974, 22: 17-26. DOI:10.1016/0022-5096(74)90010-6 |
| [13] |
MOGI K. Effect of the intermediate principal stress on rock failure[J]. Journal of Geophysical Research, 1967, 72: 5117-5131. DOI:10.1029/JZ072i020p05117 |
| [14] |
张俊善. 材料强度学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014.
|
| [15] |
YU MAOHONG. Twin shear stress yield criterion[J]. Inter. J. Mech. Sci., 1983, 25(1): 71-74. DOI:10.1016/0020-7403(83)90088-7 |
 2021, Vol. 43
2021, Vol. 43