0 引　言

弹丸起始扰动是评价射击精度的重要指标，减小弹丸起始扰动有利于提高大口径火炮射击精度。火炮发射是一个多物理场耦合的复杂过程，弹丸在火药气体推力下向炮口移动同时，弹丸和火药气体还会与身管内壁产生径向作用，致使身管和整炮都会产生剧烈振动，这些复杂过程中弹丸出炮口时刻的初始扰动的因素众多，例如火炮系统等效刚度，弹丸质量偏心，身管内膛磨损，身管热变形，弹体结构变形等。其中身管磨损是火炮使用过程最普遍的现象，磨损后弹炮间隙增大，各种不均衡因素会增大弹丸运动不规则性，对弹丸初始扰动具有重要的影响。

关于火炮起始扰动的影响因素、各因素对射击精度的影响等，目前已有较多文献及研究成果。文献[1]根据Bernouli-Euler初等梁理论研究了弹炮碰撞对身管动力响应的影响，结果显示考虑弹管间隙后身管振动幅度比不考虑间隙时要大得多；文献[2]从身管自身变形和热因素分析了身管弯曲的产生机理，在此基础上建立了身管弯曲度与火炮跳角的数学模型，研究了身管弯曲对火炮射击精度的影响；文献[3]基于刚体动力学建立了弹炮耦合运动模型，分析了弹炮间隙的存在对膛内运动姿态和起始扰动结果的影响；文献[4]建立了考虑弹管间隙的多管火箭发射动力学方程,对某多管火箭武器弹管间隙与起始扰动及密集度进行了仿真,分析了弹管间隙与起始扰动及射击密集度的关系；文献[5]运用 Ansys软件建立了某型舰炮的后坐部分动力学模型，分析了弹炮耦合对炮口振动的影响，得出炮口处的振幅从开始逐渐增大，在弹丸出膛瞬间到达最大值的结论；文献[6]通过建立弹炮耦合有限元模型，研究了后坐体质量、质心位置、动力偶臂变化对弹丸起始扰动的影响；文献[7]研究了火炮回转质心变化对弹丸初始扰度的影响，并利用遗传算法对火炮回转部分质心位置进行了优化；文献[8]通过多刚体和刚柔耦合发射动力学仿真研究了细长比较大倾斜发射的火箭弹弹性变形引起的横向振动对起始扰动的影响；文献[9]建立了某大口径牵引火炮有限元模型，对火炮各参数对初始扰动影响的灵敏度进行了分析，指出摇架壁板厚对起始扰动影响显著。

目前，身管磨损因素对弹丸起始扰动的影响研究成果较少。本文以实际测量的身管磨损依据为基础，建立弹炮耦合发射动力学仿真模型，研究身管磨损对弹丸膛内运动姿态的影响规律，并通过弹丸起始扰动归一化函数定量分析了弹丸起始扰动随磨损量的变化关系。

1 磨损内弹道弹丸运动分析^[10]

弹丸在膛内运动的理想情况是，弹丸轴线与身管轴线重合，并以此轴旋转着向炮口方向运动。身管磨损后弹炮间隙增大，弹丸质偏、火药气体不均匀作用等不均衡因素会增大弹丸与身管的不同轴度。因此，弹丸除向炮口运动的速度及沿膛线旋转外，其质心旋转产生一个侧向分速度，称为第一侧方速度，如图1所示。

设弹丸的质量为 $m$ ，不均衡质量为 ${m_1}$ 和 ${m_2}$ ，弹丸定心部半径为 $r$ ，则弹丸质心相对于轴线的偏心距为：

${\xi ^{}} = \dfrac{{m_1 + m_2}}{m}r + \frac{\Delta }{{{l_y}}}b\,,$

(1)

则第一侧方速度为：

${W_1} = \left(\dfrac{{m_1 + m_2}}{m}r + \dfrac{\Delta }{{{l_y}}}b\right)\dfrac{{\text{π}} }{{\eta r}}{v_d}\,{\text{。}}$

(2)

式中： $\xi $ 为弹丸偏心距； ${l_y}$ 为弹丸定心部长度； $b$ 为弹丸质心到弹带中心距离； $\Delta $ 为弹炮单边间隙； $\eta $ 为膛线缠度； ${v_d}$ 为弹丸轴向速度。

由于较大的弹炮间隙，不均衡力使弹丸在垂向平面内绕弹带中心旋转，使弹丸质心产生第二侧方速度，如图2所示。

以弹带为支点，弹丸偏转的运动方程为：

$({J_y} + m{b^2}) = \dfrac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{t^2}}} = K{l_y}\,,$

(3)

将上式对时间 $t$ 积分，得

$({J_y} + m{b^2}) = \dfrac{{{\rm{d}}\delta }}{{{{\rm{d}}}t}} = K{l_y}t\,{\text{。}}$

(4)

其中 $t$ 在数值上等于弹丸从上定心部到弹带运动所需时间，即

$t = \dfrac{{{l_y}}}{{{v_d}}}\,,$

(5)

将式（5）代入式（4），求出弹丸回转角速度为：

$\frac{{{\rm{d}}\delta }}{{{\rm{d}}t}} = \dfrac{{K{l_y}^2}}{{({J_y} + m{b^2}){v_d}}}\,,$

(6)

故弹丸的第二侧方速度为：

${W_2} = \dfrac{{Kb{l_y}^2}}{{({J_y} + m{b^2}){v_d}}}\,{\text{。}}$

(7)

弹丸在膛内运动过程中，横向平面内除了第一侧方速度 ${W_1}$ 外，还存在由于横向摆动产生的第三侧方速度 ${W_3}$ ，分析与求解方法同 ${W_2}$ ，这3个速度是引起弹丸散布的主要原因。

2 弹丸起始扰动函数

以弹丸出炮口时刻垂直和水平方向的角位移、角速度、速度表征弹丸起始扰动，以弹丸出炮口时刻垂直方向的角位移、角速度、速度表征弹丸垂直方向弹丸起始扰动，以弹丸出炮口时刻水平方向的角位移、角速度、速度表征弹丸水平方向弹丸起始扰动，并采用线性加权和归一化处理，建立表征弹丸起始扰动的函数为^[7]：

$f = {f_{VD}} + {f_{HD}}\,,$

(8)

${f_{VD}} = {\alpha _1}\left| {\dfrac{{{\theta _z}}}{{\theta {}_{z0}}}} \right| + {\beta _1}\left| {\dfrac{{{\omega _z}}}{{{\omega _{z0}}}}} \right| + {\gamma _1}\left| {\dfrac{{{v_z}}}{{{v_{z0}}}}} \right|\,,$

(9)

${f_{HD}} = {\alpha _2}\left| {\dfrac{{{\theta _y}}}{{\theta {}_{y0}}}} \right| + {\beta _2}\left| {\dfrac{{{\omega _y}}}{{{\omega _{y0}}}}} \right| + {\gamma _2}\left| {\dfrac{{{v_y}}}{{{v_{y0}}}}} \right|\,{\text{。}}$

(10)

式中： ${f_{VD}}$ 为垂直方向弹丸起始扰动函数， ${f_{HD}}$ 为水平方向弹丸起始扰动函数； ${\theta _Z}$ ， ${\theta _y}$ 为弹丸质心的垂直方向角位移和水平方向角位移； ${\omega _Z}$ ， ${\omega _y}$ 为弹丸质心的垂直方向角速度和水平方向角速度； ${v_Z}$ ， ${v_y}$ 为弹丸质心的垂直方向速度和水平方向速度； ${\theta _{Z0}}$ ， ${\omega _{Z0}}$ ， ${v_{Z0}}$ ， ${\theta _{y0}}$ ， ${\omega _{y0}}$ ， ${v_{y0}}$ 为相应的弹丸扰动参考值，文中取正常身管工况的弹丸扰动为参考值； ${\alpha _1}$ ， ${\ \beta _1}$ ， ${\gamma _1}$ ， ${\alpha _2}$ ， ${\ \beta _2}$ ， ${\gamma _2}$ 分别为各弹丸参量在归一化函数F中所占比值，且 ${\alpha _1} + {\beta _1} + {\gamma _1} + {\alpha _2} + {\beta _2} + {\gamma _2} = 1$ 根据火炮设计经验，取 ${\alpha _1} = {\alpha _2} = 0.2$ ， ${\beta _1} = {\beta _2} = 0.25$ ， ${\gamma _1} = {\gamma _2} = 0.05$ 。

3 发射过程数值模拟 3.1 基本假设

弹丸与身管膛线之间的作用机理十分复杂，本文研究在建立某大口径火炮弹炮耦合有限元动力学模型时作如下假设^[7]:

1）弹带密封良好，不考虑火药气体泄漏；

2）忽略火药燃气高温对弹带的影响；

3）考虑身管与弹丸所受重力场作用，即考虑身管预弯对弹丸起始扰动的影响；

4）动力学模型只含有弹丸和后坐体，不考虑其他结构对弹丸起始扰动的影响。

3.2 弹炮耦合发射动力学有限元模型

身管建模较为复杂，首先，在creo软件中，根据身管截面建立不带缠角的身管膛线的几何特征，导入到有限元软件中划分网格。然后，根据膛线空间曲线方程通过移动节点的方法建立最终身管模型，如图3所示，具体建模方法参考文献[11]。对于磨损工况身管，把身管磨损曲线数据代入到参数化建模程序，通过节点偏移建立磨损身管有限元模型。

根据实际尺寸建立了弹丸整体有限元模型，在保证弹丸重量及质心与设计一致的前提下，对预制破片、引信等结构进行简化，如图4所示。

将弹丸模型装配至输弹到位时的初始位置，弹丸定心部与身管内壁面、弹带与身管内壁面分别设置接触，由于弹带大变形和损伤效应，弹带自身定义自接触，形成弹炮耦合的有限元模型，如图5所示，计算模型中包含了弹丸挤进过程。

3.3 材料本构模型

实际射击过程中，身管及弹体主要为弹性变形，因此身管及弹体均采用线弹性本构模型。弹带材料为纯铜，弹丸在挤进过程中经历弹塑性变形及损伤，最终发生局部化韧性断裂，涉及到弹带材料的应变硬化、应变率硬化和温度软化，采用在冲击动力学中应用广泛的Johson-Cook本构模型，即

$\sigma = \left(A + B{\varepsilon ^n}\right) \left[1 + C\ln \left( \frac{{\dot \varepsilon }}{\dot \varepsilon }_0\right)\right]\left[1 - {\left(\frac{{T - {T_0}}}{{{T_M} - {T_0}}}\right)^m}\right]\,,$

(11)

式中： $\sigma $ ， $\varepsilon $ ， ${\dot \varepsilon _0}$ 为等效应力、塑性应变、参考应变率（一般为准静态试验下的材料应变率，常见值为1×10^-3）； $A$ ， $B$ ， $C$ ， $m$ 和 $n$ 为材料常数； ${T_0}$ 为试验参考温度、 ${T_M}$ 材料熔点温度、 $T$ 为无量纲温度。

经过分离式Hopkinson压杆试验，拟合得到纯铜的Johson-Cook本构，如下式：

$\sigma =\left (122 + 179.9{\varepsilon ^{0.33}}\right)\left[1 + 0.085\ln \left(\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}\right)\right]\left[1 - {\left(\dfrac{{T - {T_0}}}{{{T_M} - {T_0}}}\right)^m}\right]\,{\text{。}}$

(12)

3.4 摩擦模型

弹丸在膛内高速运动，弹丸与内膛存在较大的相对滑移速度及接触压力，用经典的库伦摩擦定律计算弹丸与内膛摩擦力存在较大误差，采用文献[12]中弹炮摩擦模型，即

$\mu (\sigma ,v) = {\left[\frac{{{\rho _1}{\eta ^2}{v^2}({e_L} + c({t_p} - {t_0}))}}{{k{l^2}{\sigma ^3}}}\right]^{\frac{1}{4}}}\,{\text{。}}$

(13)

式中， ${\ \rho _1}$ 为弹带材料密度， $\eta $ 为熔融态弹带动力黏度， ${e_L}$ 为弹带融化潜热， $c$ 为弹带比热容， ${t_p}$ 为弹带熔点， ${t_0}$ 为室温， $k$ 为动坐标下熔融层位置， $l$ 为弹带宽度， $\sigma $ 为接触压力。

根据上式编写了VFRIC的Abaqus子程序来模拟摩擦系数随压应力和速度的变化，计算过程中根据上一步速度与压应力计算结果实时调整模型中摩擦系数。

3.5 载荷与边界条件

弹丸在膛内运动过程中受到的主动力为火药气体燃烧产生的压力，发射药燃烧与弹丸运动是相互关联的双向求解过程。通过Abaqus用户子程序接口引入内弹道方程组，以方程组解出的弹底压力压P作为有限元模型中弹丸运动的推力，同时以有限元模型中求解的弹丸位移、速度值、次要功等作为内弹道方程组下一增量步计算的初始条件，直至弹丸出炮口。边界条件为约束身管尾部六自由度，约束位置保持与身管在炮尾本体实际安装位置一致。

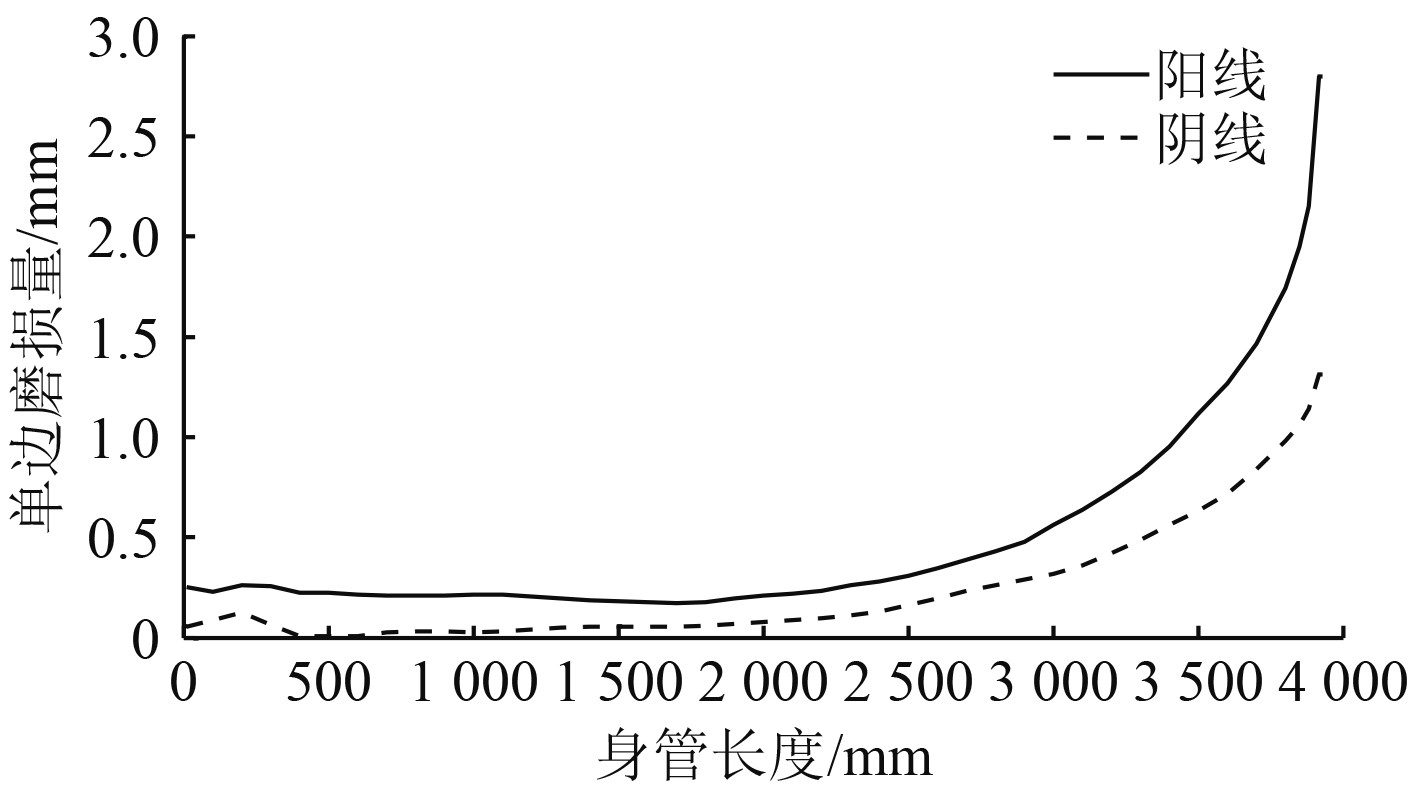
4 计算结果及分析 4.1 计算工况

选择正常、一般磨损和严重磨损身管3种典型内膛磨损工况进行分析计算。按照身管工程尺寸建立正常身管模型，参照弹道寿命结束期（≥2000发）内径测量数据建立严重磨损身管模型，如图6所示。取严重磨损工况磨损量的50%建立一般磨损身管内膛模型。

4.2 计算结果分析

线膛炮发射时弹丸膛内运动的理想状态是，弹丸轴线与身管内膛轴线重合，并以此轴作为旋转轴，边前进边旋转。但是，随着身管发射弹数增加，膛线磨损，阳线变浅，弹炮间隙增大，膛线对弹丸导转和对定心部约束都会减弱，使得弹丸不能严格沿膛线旋转运动，势必增大弹丸运动过程的径向运动与摆动。图7为弹带变形的仿真结果，由图可知，弹带变形随着磨损增大而增大，达到严重磨损时，弹带出现削光，与上述分析结果吻合。

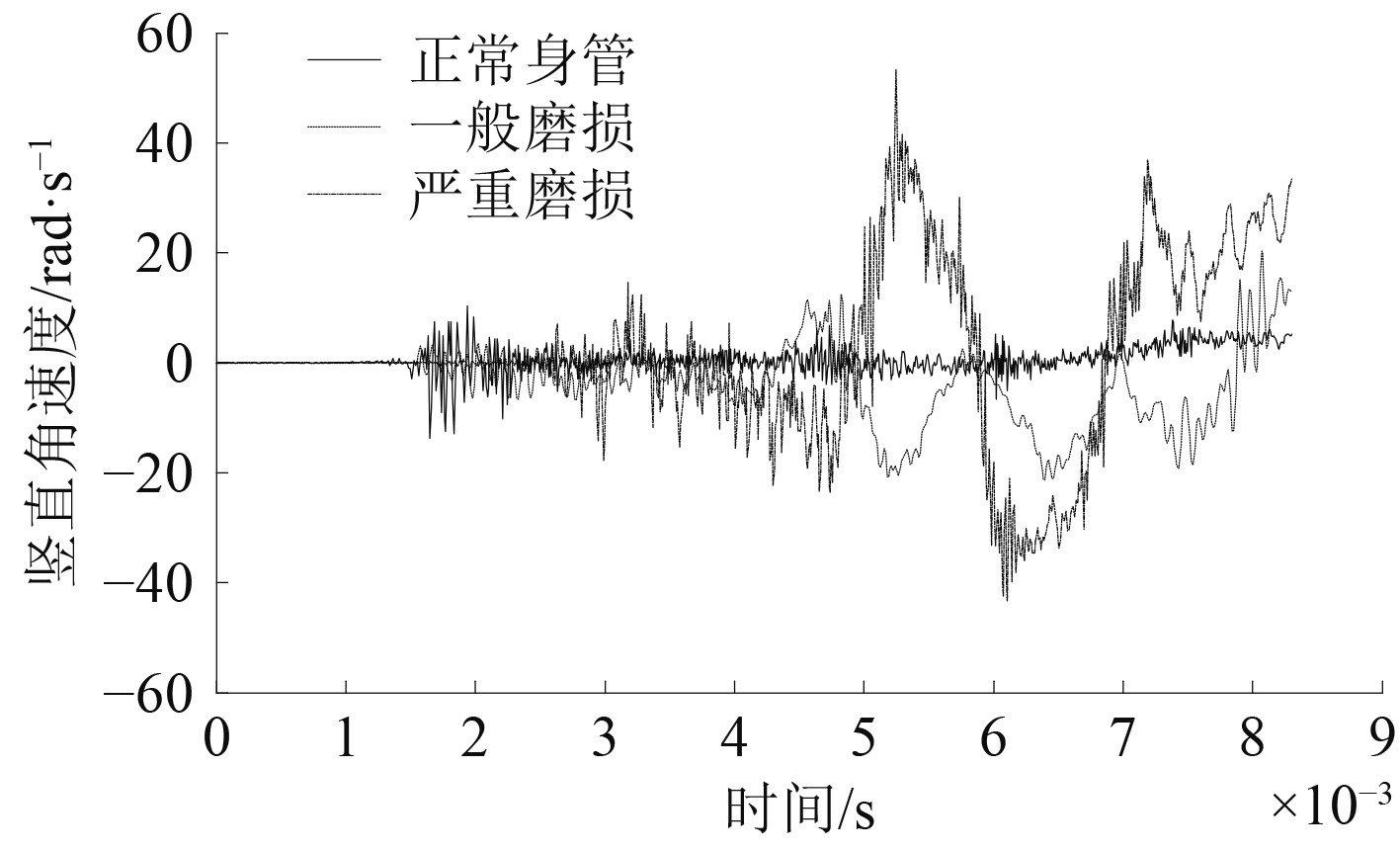
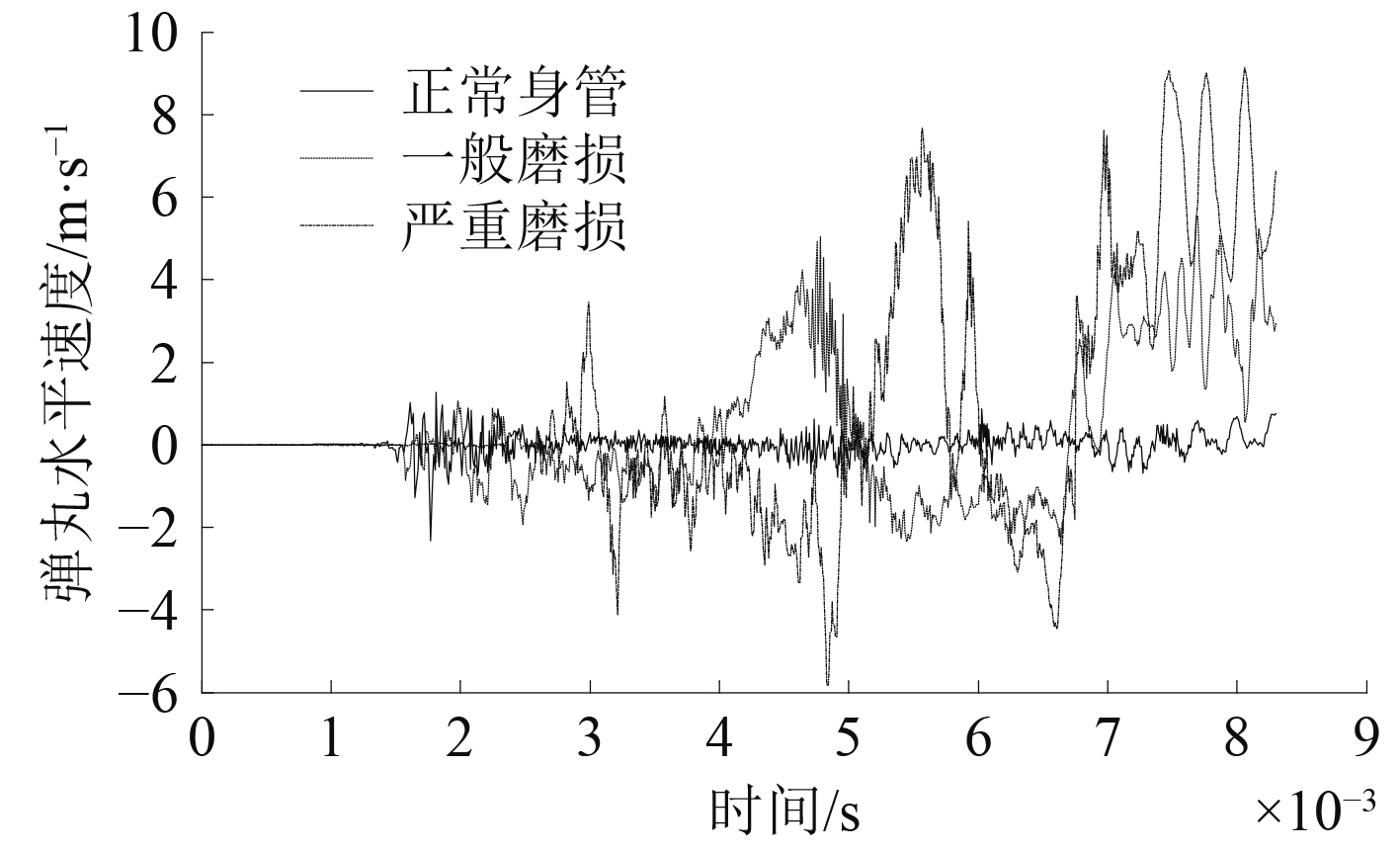
图8～图13为不同磨损工况下弹丸水平和竖直2个方向的角位移、角速度和速度对比曲线。由图可知，弹丸膛内运动过程中的径向扰动量随着磨损增大而增大，且增长速率有增大趋势。这是因为磨损后期，弹带被削光，弹丸停止加速旋转，稳定性降低，加剧了弹丸径向扰动。

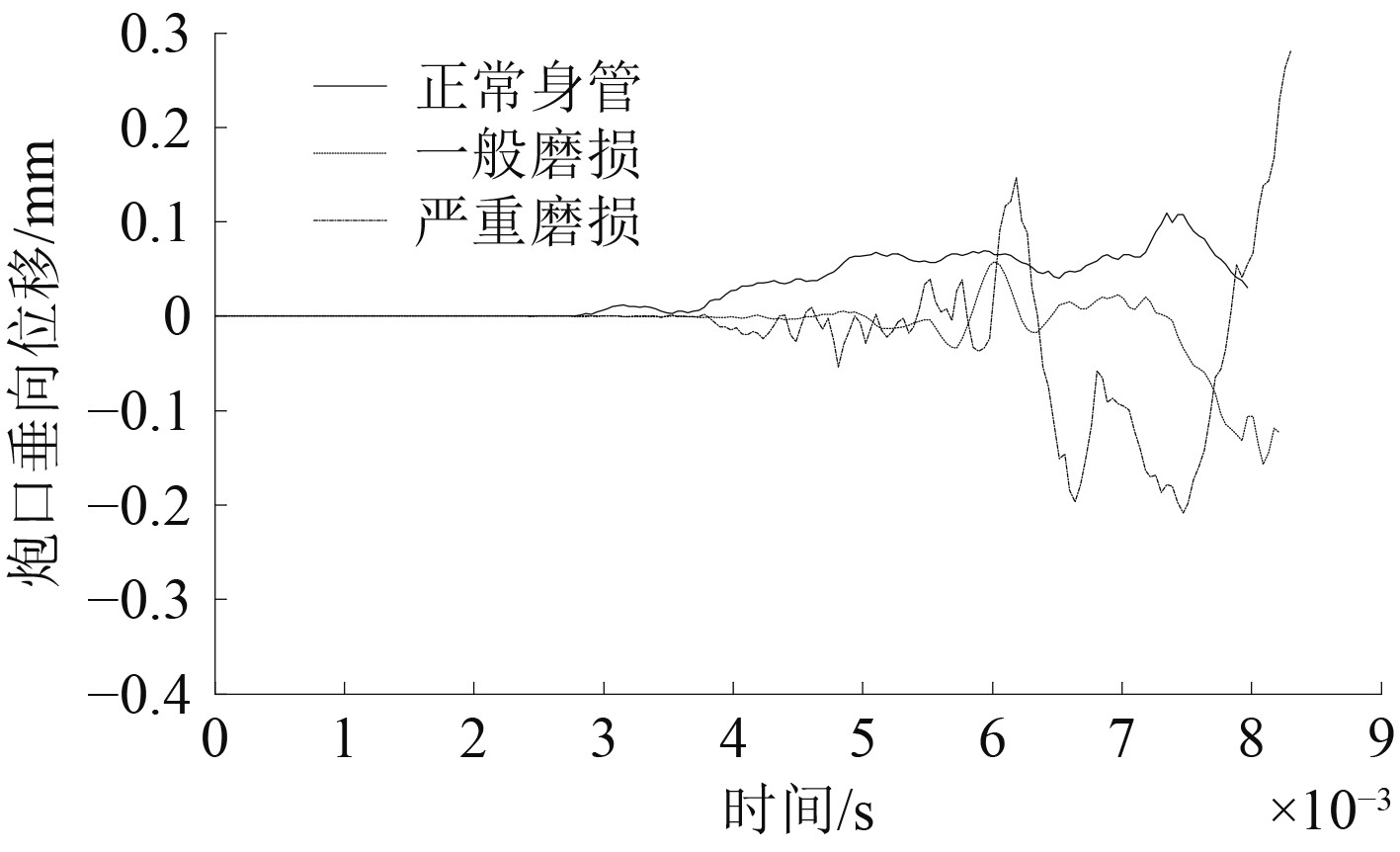
图14为炮口垂向位移的对比曲线。由图可知，炮口垂向的位移随着磨损增大而增大，一般磨损工况和严重磨损身管相对于未磨损身管工况，炮口位移增大了299%，805%，说明磨损加剧了弹丸与身管的接触碰撞，导致炮口位移明显增大，炮口的振动对弹丸的起始扰动有重要影响。

分别取3种磨损工况下弹丸出炮口时刻起始扰动参数列于表1所示。

将3种工况计算的弹丸起始扰动参量代入式（7）得到弹丸起始扰动函数值 $f$ ，如表2所示。

由表2可知，身管磨损后，弹丸起始扰动显著增大，一般磨损工况和严重磨损身管达到了2.07和4.87，相对于未磨损身管工况，弹丸起始扰动增大了107%，387%。文献[6]研究结果显示，后坐体质量、质心位置、动力偶臂变化到极限值后弹丸起始扰动分别达到1.06，1.15，1.05；文献[13]研究结果显示某车载炮上架刚度提高70%，弹丸起始扰动达到2.186。由此可见，相对于炮架刚度、后坐质量参量、动力偶臂、弹丸质心偏心等因素，身管磨损后对弹丸起始扰动的影响更加明显。

5 结　语

通过建立弹炮耦合仿真模型，研究了弹丸在不同程度磨损线膛炮身管中发射过程的运动特性。通过不同磨损工况的仿真计算，分析了身管磨损对弹丸起始扰动的影响。结果表明，弹丸初始扰动与膛线磨损量成正相关，弹带磨光后，起始扰动增幅尤为明显。在火炮使用过程中，应尽量减小膛线磨损。