什么是时间?什么是空间?时间与空间存在怎样的关系?这是自人类文明出现以来,一直困扰人们的基本问题。从爱因斯坦在狭义相对论中提出的钟慢尺缩推断(即当物体运动速度等于光速时,时间就会停止,空间就微缩为点),到广义相对论的时间-空间的边界理论(大爆炸开始,大挤压终结),再到现代物理学公认的由巴克哈德·海姆创立的八维空间理论。有人问:我们生活在同一的时空下,为什么还要进行时空配准呢?事实上,由于受到人类自身感知能力和手段的限制,我们只能感知局部的时空信息。在很多情况下,对客观世界较为“全面”认知,必须依赖于他人(或其他手段)获取的信息进行补充。但由于获取手段的差异,在综合这些信息时,相互间的偏差在所难免,当这种偏差超过一定范围时,就无法将这些原本“共同”信息融合在一起,即出现所谓的“时空失配”问题。
本文在总结和借鉴了国内外相关研究成果基础上,给出对该问题的研究思考。尽管现代物理学已经证明时间和空间是一个整体,但是为了叙述方便,下面讨论中,仍将它们分开,分别称为时间同步和空间配准问题。
1 时间同步美专家认为[1],在GPS出现之前,在全球范围内,试图将无线电台、雷达等系统同步到很高的精密度和准确度不可能。同样正因为GPS的出现,使得能够采用非常廉价的手段实现全球范围的平台和目标的精确定位、武器的精确制导,进而引起军事行动中作战方式的革命。另一方面,美军最先意识到GPS卫星下传链路结构及其低信号功率的本质特性,也给军用用户带来极大的风险。因此,保持时钟和振荡器在自主模式下具有确定的性能,即便是在很短的时间内,以增强GPS接收系统的性能、备份其功能,是非常必要的。
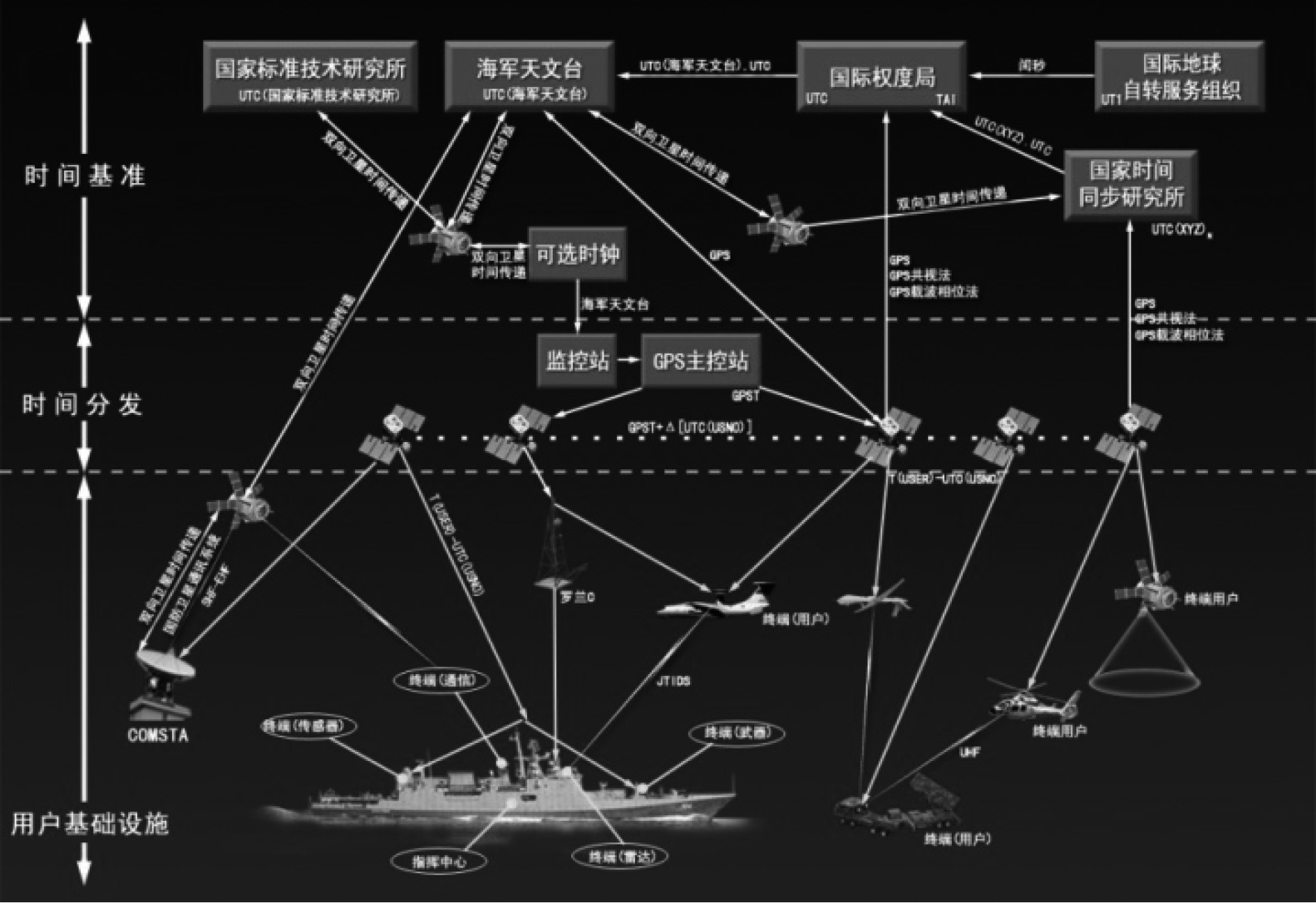
1.1 美军公共时间基准体系美军公共时间基准体系结构由3部分构成[2]:时间基准、时间分发和用户基础实施,如图1所示。这一分布式基准体系结构能够满足如下基本需求:提供一个具有较低相位噪声、高准确性、连续的公共基准频率源;提供一个具有长期时间准确度的连续的时间基准;提供采用各种信号和编码格式的时间和频率分发能力;提供自动诊断和频率标准的评估能力,并能在出现异常情况时,保持准确地连续输出;优化使用现有的时间资源;在因分发链路导致信息延迟时,仍然能够建立起一个鲁棒、持久准确的时间和频率源。
|
图 1 美军公共时间基准体系结构图 Fig. 1 The structure diagram of the U.S. military's public time reference system |
同时,美军也已经意识到GPS不能彻底解决所有作战单元的时间同步问题,完全依赖于GPS甚至有非常大的风险。因此,为了确保在任何电磁环境下对GPS的增强能力,维持性能最优,应当采用一种具有独立或半自治的技术,即通过组合所有时间资源,独立于GPS建立一种公共的基准。由此,美军制订了一系列系统/设备定时和时间同步的主要标准和规范,包括:规定UTC(USNO)为国防部所有设施的统一的标准时间和时间间隔;规定了单个网络系统的内部定时、外部定时,以及定时所花费的通信负载等;强调定时信息对USNO的主钟的可追踪性。
1.2 时间同步协议目前,有线网络各节点间的时间同步很多采用NTP(Network Time Protocol)协议[3]实现。NTP发明人Mills基于互联网环境10万台主机持续6天的统计结果表明:在Internet环境下基于NTP时间同步误差均值约为几毫秒、最大值为50 ms(滤波结果)。Mills认为未来可以通过改善频率估计算法和子网的同步监控方法提高基于NTP的网络时间同步性能。事实上,NTP已经成为大多数有线网络环境中时间同步的标准。
为了满足电力、金融、银行交易和军事领域更高精度的时间同步需求,IEEE在2008发布的IEEE 1588协议版本2[4],所谓精确时间同步协议(Precision Time Protocol,PTP),在原理上可以实现分布式网络系统中的亚微秒级的同步精度。目前已经实现的方案中基于硬件可以达到微秒级精度。美国军方也同步舰艇作战系统中采用PTP协议,并确认在以太网应用中,其同步精度比NTP高1~2个数量级。
在时间同步方法研究方面,也有一些美国专家提出事件发生时间可以采用事件的“年龄”而不是事件发生的绝对时间进行描述,采用这种方式在一些非常强自适应传感器网络中精度可以达到1 ms。
1.3 思考建议无论是民用或是军用,从卫星上天到和平时期的应急救灾、反恐行动,到战争时期的军事行动,对时序过程的严格控制、记录、应用,均离不开精密而准确的时间基准。
当前,我国北斗导航系统正在逐渐缩小与美军GPS之间的差距,但总体上可用的时间资源也不少:北斗系统、移动通信(4G,5G)、数字电视、“长河二号”导航链系统、国家授时中心等单位多台原子钟资源,以及无处不在的有线光缆构成的互联网,由此,完全可以通过资源整合,建立起我国特有的原子时系统,进一步通过研发主时钟优选策略、高精度时间比对算法、优化时间传递途径,实现依赖自主时间资源的高精度时间体系。一个可用性好的时间同步体系,可追踪的溯源链构建和成体系的节点状态动态监控是关键。
谋划建立各自独立且协同的军用和民用时间体系,应明确2种体系之间的关系,可互相融合又可独立运行,民用体系尽可采用国际上廉价的商用技术,通过商用技术优势促进时间比对、传递和同步技术的发展。建立独立的军用时间体系,借鉴民用技术,通过整合现有的军用时间和频率资源,补强薄弱环节,满足国防战略的需求。
2 多传感器空间配准当战场上或空管系统中只有1部雷达传感器时,目标(飞机等)的相对位置比较重要。此时,距离和方位角上的系统偏差对于所有的目标都一样,因而从总体上不会对跟踪系统的性能造成很大的影响。但随着侦察、预警和监视范围的扩大或者电子对抗或者可靠性等方面的考虑,人们需要把多个互相重叠的传感器的信息综合成更加完整的态势图像,此时每个传感器的系统偏差来源就必须逐一分析,并尽可能消除,否则将会产生歧义或冗余目标,从而极大地影响指挥员的决策的稳定性。其中传感器测量误差源分析见表1[5]。
|
|
表 1 传感器配准主要误差源分析 Tab.1 Analysis of main error sources of sensor registration |
对于安装在运动平台上的传感器而言,传感器测量可能叠加的误差还有姿态误差,比如舰艇的纵摇角、横摇角和偏航角误差,飞机的俯仰角、横滚角和航向角误差,当然可能还有平台安装带来的误差等。实际上对于舰艇和飞机平台而言,在很多应用场合,对于传感器的探测,姿态偏差可能影响更大。
本文主要探讨运动平台传感器探测信息中系统误差的估计和消除方法。考虑到平台姿态误差与传感器对目标探测误差叠加在一起,并且惯导设备提供姿态数据,与探测器的目标数据,在采样频率上存在着不一致性,也使得惯导设备的误差在很多情况下,很难及时修正。这里重点讨论动平台传感器配准问题,为简化起见,只涉及舰艇平台及其三坐标(方位、距离、俯仰)、两坐标(方位、距离)传感器。
配准误差来源可分2类:一类是称为传感器的校准误差,传感器在开始使用前都要标校,以消除此类误差,随着时间的推移,标校的效果将退化,但由于地球曲率等环境气象因素的影响,也会加大这类误差;另一类为传感器基准引起的误差,称为定向误差或姿态误差,该类误差由传感器的惯性测量基准引起。
空间配准方法可以分为2类:绝对配准[6]和相对配准,具体取决于基准的性质。相对配准指在多传感器跟踪系统中,选择其中一个传感器为主传感器,其他传感器以主传感器为基准,估计偏差,然后均向主传感器配准;绝对配准以地心坐标系为基准,不同传感器的探测数据全部转换到该基准参考系,估计偏差并进行校准。绝对配准又可分为基于公共目标绝对配准和基于协同目标的绝对配准。
公共目标配准法[7-10],目的消除三维传感器及其平台之中存在的姿态和探测绝对偏差。具体思路是:以地心坐标系为处理坐标系,将2个传感器对公共目标的探测数据变换到地心坐标系中;然后根据2个传感器对公共目标的探测数据迭合条件,利用一次泰勒展式可以导出偏差估计方程。最后可利用卡尔曼滤波和最小二乘估计出姿态和探测偏差值。这种情形下,当传感器缺维时,可采用极大似然估计法求解。此时得到的似然方程的解是否存在,将更加依赖于公共目标航路数据的特性。
合作目标配准法实质是更广泛意义的标校,通过在合作目标和探测平台上,安装类似GPS的定位设备,测量出目标和平台的位置信息,作为真值数据。此时,传感器探测到的目标信息为不稳定坐标系中的数据,经转换到稳定坐标系后,同样采用一次泰勒展式,可以导出偏差估计方程,估计出传感器和姿态信息中存在的偏差。目前,国内外,在工程界,在多平台(特别是涉及动平台)组网时,对于如何对探测偏差进行估计和修正,仍然处在边研究边试用的阶段,不存在普遍实用的处理方法。
2.1 偏差建模考虑位于不同运动平台上多部雷达的系统误差估计问题。雷达观测数据中的系统误差,表现为雷达输出的目标航迹数据在稳定地理坐标系下的距离、方位和/或俯仰上的偏差,而平台姿态偏差和雷达安装位置的形变,会使距离、方位误差产生不同程度的变化。本节通过求解系统误差参数与目标真实状态参数的非线性优化问题,导出不含目标真实状态参数的系统误差参数伪观测方程,从而建立基于公共目标配准和基于合作目标配准2种配准方法。
当雷达有系统误差时,其观测状态可表示为观测值与偏差参数的非线性向量函数:
| $\begin{split}{f_{ik}} =& {T_{ik}}\left( \begin{array}{l} ({r_{ik}} + \Delta {r_i})\sin ({\beta _{ik}} + \Delta {\beta _i})\cos ({\varepsilon _{ik}} + \Delta {\varepsilon _i}) \\ ({r_{ik}} + \Delta {r_i})\cos ({\beta _{ik}} + \Delta {\beta _i})\cos ({\varepsilon _{ik}} + \Delta {\varepsilon _i}) \\ ({r_{ik}} + \Delta {r_i})\sin ({\varepsilon _{ik}} + \Delta {\varepsilon _i}) \end{array} \right) + \\ &\left( \begin{array}{l} {u_{ik}} \\ {v_{ik}} \\ {w_{ik}} \end{array} \right) \approx {X_{ik}} + {{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}}{b_i}{\text。}\end{split}$ | (1) |
其中:
| $\mathop {\min }\limits_{{X_k},b} \sum\limits_i {{{({X_k} - {X_{ik}} - {{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}}{b_i})}^{\rm{T}}}{\boldsymbol{P}}_{ik}^{ - 1}({X_k} - {X_{ik}} - {{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}}{b_i})}{\text。} $ | (2) |
其中:
根据目标函数的最优性条件,对
| $\sum\limits_i {P_{ik}^{ - 1}{X_k}} = \sum\limits_i {P_{ik}^{ - 1}{X_{ik}}} {\text,}$ | (3) |
令
| ${X_k} = {P_k}\sum\limits_i {{\boldsymbol{P}}_{ik}^{ - 1}\left( {{X_{ik}} + {{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}}{b_i}} \right)}{\text。} $ | (4) |
关于偏差向量bi(
| $\begin{split}&{({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}})^{\rm{T}}}P_{ik}^{ - 1}({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}}{b_i} - {P_k}\sum\limits_s {P_{sk}^{ - 1}{T_{sk}}{J_{sk}}{b_s}} ) = \\ &\qquad{({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}})^{\rm{T}}}{\boldsymbol{P}}_{ik}^{ - 1}({\hat X_k} - {X_{ik}}){\text,}\end{split}$ | (5) |
其中,
将式(5)写成矩阵形式,可得:
| ${Q_k}b = \left( \begin{array}{c} {({T_{1k}}{J_{1k}})^T}P_{1k}^{ - 1}({{\hat X}_k} - {X_{1k}}) \\ \vdots \\ {({T_{mk}}{J_{mk}})^T}P_{mk}^{ - 1}({{\hat X}_k} - {X_{mk}}) \end{array} \right){\text,}$ | (6) |
其中:
| $\begin{split}{Q_k} =& {\rm{diag}}\left\{ {{{({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}})}^{\rm{T}}}{\boldsymbol{P}}_{ik}^{ - 1}({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}})} \right\} - \\ &\left( \begin{array}{c} {({T_{1k}}{J_{1k}})^{\rm{T}}}P_{1k}^{ - 1} \\ \vdots \\ {({T_{mk}}{J_{mk}})^{\rm{T}}}P_{mk}^{ - 1} \end{array} \right){P_k}(P_{1k}^{ - 1}({T_{1k}}{J_{1k}}), \cdots ,P_{mk}^{ - 1}({T_{mk}}{J_{mk}})){\text。}\end{split}$ | (7) |
假设
| ${P_{ik}} = ({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}}){\Sigma _i}{({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}})^{\rm{T}}} + {{\boldsymbol{O}}_{ik}} = ({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}}){\Sigma _{ik}}{({{\boldsymbol{T}}_{ik}}{{\boldsymbol{J}}_{ik}})^{\rm{T}}}{\text,}$ | (8) |
其中,
| ${M_k}{\rm{diag}}(\Sigma _{_{ik}}^{ - 1/2})b = \left( \begin{array}{c} \Sigma _{_{1k}}^{ - 1/2}{({T_{1k}}{J_{1k}})^{ - 1}}({{\hat X}_k} - {X_{1k}}) \\ \vdots \\ \Sigma _{_{mk}}^{ - 1/2}{({T_{mk}}{J_{mk}})^{ - 1}}({{\hat X}_k} - {X_{mk}}) \end{array} \right){\text。}$ | (9) |
其中:
| $\begin{split}{{\boldsymbol{M}}_k} = &I - \left( \begin{array}{c} \Sigma _{_{1k}}^{ - 1/2}{({T_{1k}}{J_{1k}})^{ - 1}} \\ \vdots \\ \Sigma _{mk}^{ - 1/2}{({T_{kk}}{J_{mk}})^{ - 1}} \end{array} \right)\times\\ &{P_k}\left({\left({T_{1k}}{J_{1k}}\right)^{ - {\rm{T}}}}\Sigma _{_{1k}}^{ - 1/2}, \cdots ,{\left({T_{mk}}{J_{mk}}\right)^{ - {\rm{T}}}}\Sigma _{mk}^{ - 1/2}\right){\text。}\end{split}$ | (10) |
容易证明,
由此得到各雷达的距离、方位和/或俯仰系统误差的伪观测方程为:
| ${\boldsymbol{b}} = \left( \begin{array}{c} {({T_{1k}}{J_{1k}})^{ - 1}}({{\hat X}_k} - {X_{1k}}) \\ \vdots \\ {({T_{mk}}{J_{mk}})^{ - 1}}({{\hat X}_k} - {X_{mk}}) \end{array} \right){\text。}$ | (11) |
相应的方差矩阵为
对于合作目标,若
| ${b_k} = {({T_k}{J_k})^{ - 1}}({\hat X_k} - {X_k}){\text,}$ | (12) |
式(12)与式(11)具有相同的表达形式。
当
由此可见,合作目标配准、绝对/相对配准的偏差观测方程,均可统一用式(11)来表示,只是相应“观测”向量的方差矩阵不同。
上述分析推导过程,只考虑各传感器在稳定地理坐标系中的距离、方位、俯仰系统误差。根据等效偏差参数模型[11],可将式(11)的右端向量表示为待估计的多类偏差参数的观测方程:
| ${z_k} = {C_k}{b_k}{\text。}$ | (13) |
其中,
由于式(13)的左端向量不是传感器的直接观测结果,而是对各传感器的观测状态
根据观测方程(13)及其“观测”方差矩阵,可得到常值的系统误差向量b的广义最小二乘估计为:
| $\mathop {\min }\limits_b \sum\limits_k {{{({C_k}b - {z_k})}^{\rm{T}}}{G_k}({C_k}b - {z_k})} {\text,}$ | (14) |
其中,
对上式进行求解,得到最小二乘解
| $\begin{split}\hat b =& {\left[ {\sum\limits_k {C_k^{\rm{T}}{\rm{diag}}(\Sigma _{ik}^{ - 1/2}){{\boldsymbol{M}}_k}{\rm{diag}}(\Sigma _{ik}^{ - 1/2}){C_k}} } \right]^{ - 1}}\times\\ &\left( {\sum\limits_k {C_k^{\rm{T}}{\rm{diag}}(\Sigma _{ik}^{ - 1}){z_k}} } \right){\text。}\end{split}$ | (15) |
在总的系统偏差向量b中,距离偏差通常在百米量级,方位和纵横摇等角度偏差量通常在毫弧度量级。这种量级上的差异,使得上式中的系数矩阵条件数很大,为此可采用尺度变换的方法来提高计算的稳定性。
假设b的测量误差方差为
| $\begin{split}\Sigma _b^{ - 1/2}\hat b =& {\left( {\sum\limits_k {\Sigma _b^{1/2}C_k^T{\rm{diag}}(\Sigma _{ik}^{ - 1/2}){{\boldsymbol{M}}_k}{\rm{diag}}(\Sigma _{ik}^{ - 1/2}){C_k}\Sigma _b^{1/2}} } \right)^{ - 1}}\times\\ &\left( {\sum\limits_k {\Sigma _b^{1/2}C_k^T{\rm{diag}}(\Sigma _{ik}^{ - 1}){z_k}} } \right){\text。}\\[-20pt]\end{split}$ | (16) |
对于可观测性较差情形下的系统误差估计求解,还可进一步采用ML、正则化、岭估计等方法来提高估计精度。
下面给出2部传感器仿真结果,ECEF直角坐标系采用WGS-84坐标系,2部传感器采样间隔均为1 s,目标1初始位置
传感器1偏差参数:传感器探测偏差
传感器2偏差参数:传感器探测偏差
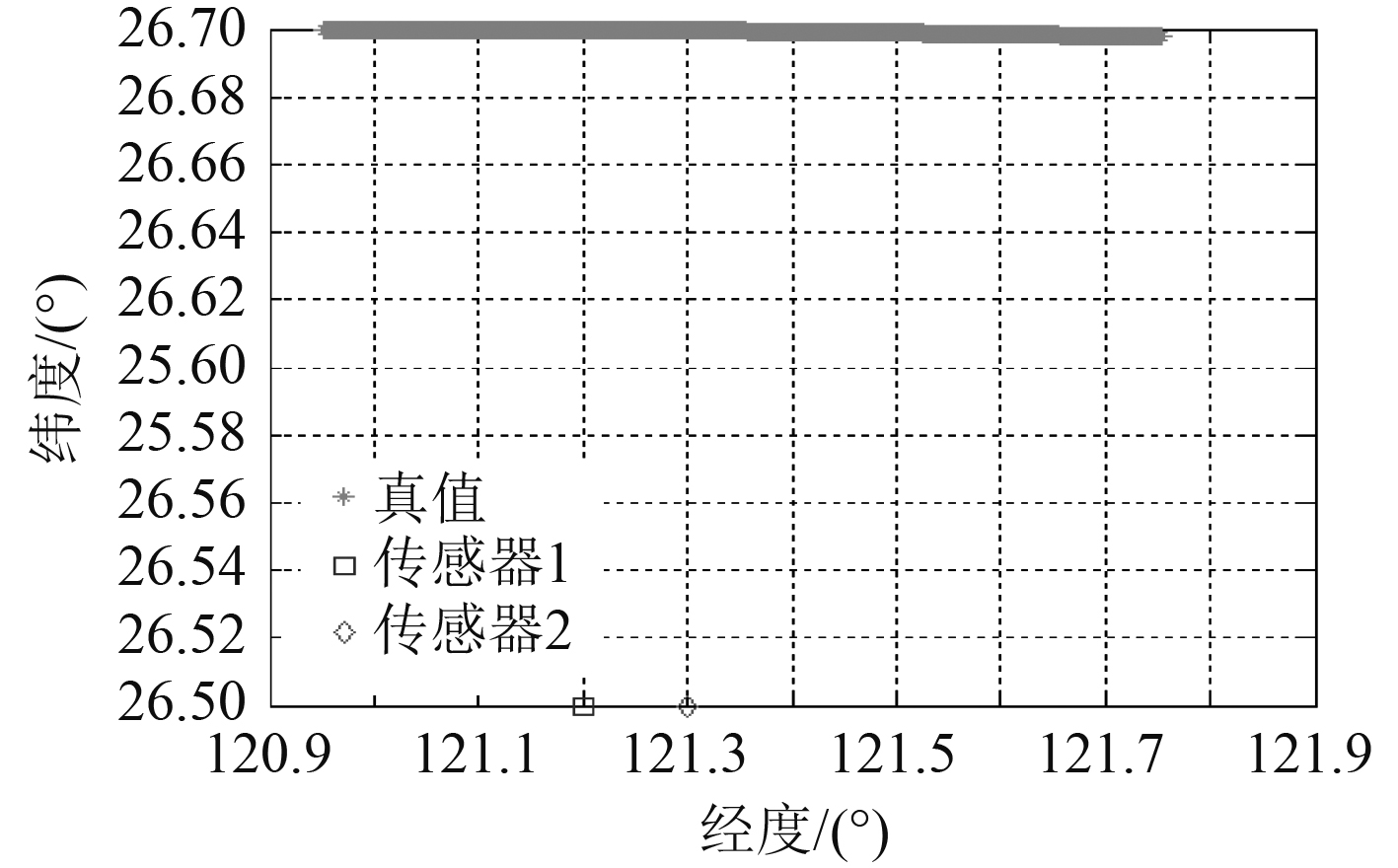
|
图 2 仿真场景 Fig. 2 Simulation scenario |
偏差估计结果如图3所示。
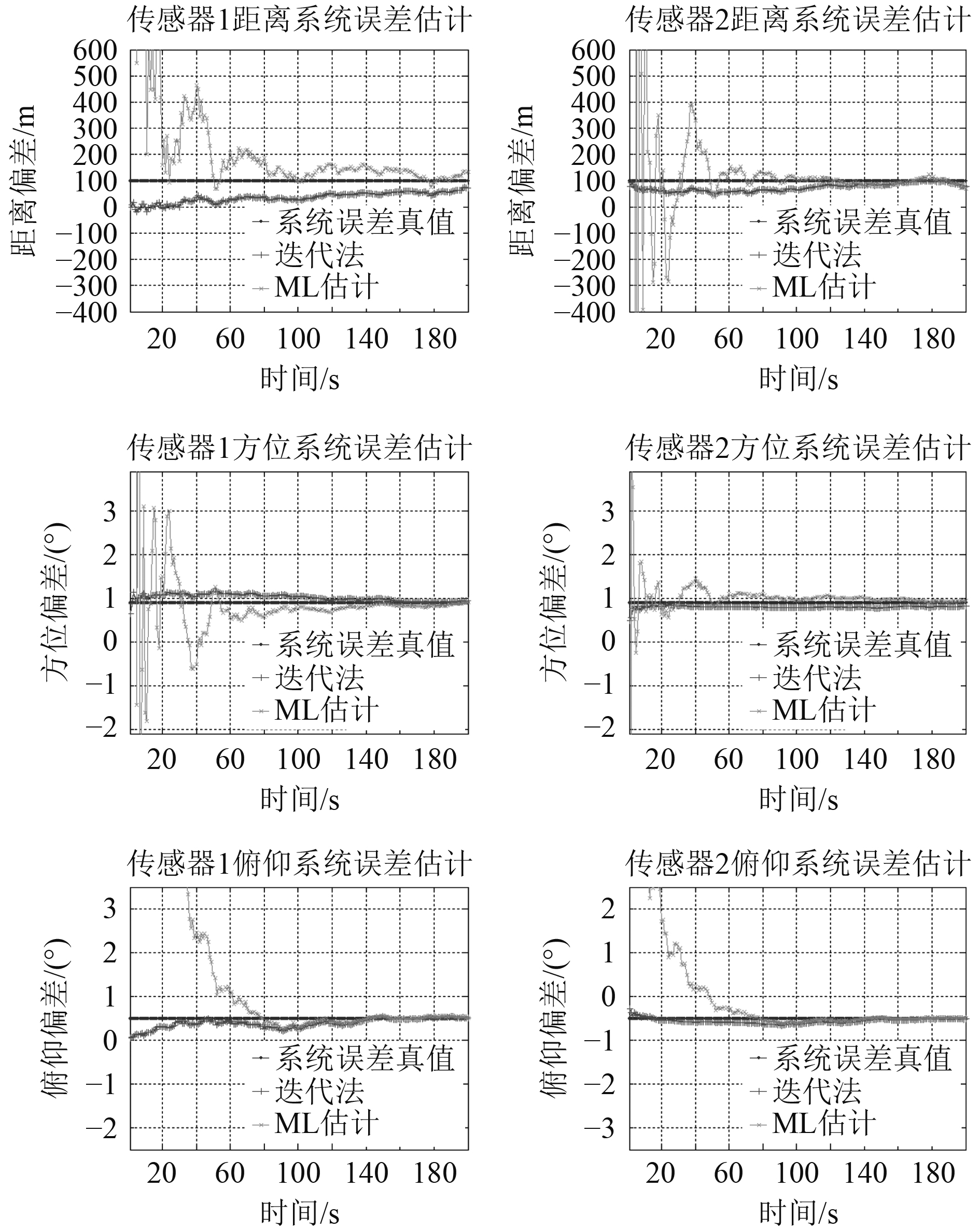
|
图 3 偏差估计结果 Fig. 3 Bias estimation result |
可以看出,迭代法比极大似然配准方法估计结果更快、更稳定。
2.3 合作目标配准通常情况下,海上舰艇编队各平台之间的距离不是太远,处于各自传感器的探测范围之内。根据编队内其他平台报知的GPS/北斗定位信息或者民用AIS/ADS信息(统称为合作目标),以此为真值来估计传感器探测的系统误差。估计的偏差结果可对该传感器报告的其他目标航迹进行修正。
由等效偏差模型可知,不考虑平台定位误差,对舰载传感器采用如下简化模型:
| $\left(\!\!\!\! \begin{array}{l} \Delta {r_s} \\ \Delta {\beta _s} \\ \Delta {\varepsilon _s} \end{array} \!\!\!\! \right) + \left( \!\!\!\!\begin{array}{l} 0 \\ \cos {\beta _s}\tan {\varepsilon _s} \\ - \sin {\beta _s} \end{array} \!\!\!\!\right)\Delta \theta + \left( \!\!\!\!\begin{array}{l} 0 \\ \sin {\beta _s}\tan {\varepsilon _s} \\ \cos {\beta _s} \end{array} \!\!\!\! \right)\Delta \psi = \left(\!\!\!\! \begin{array}{l} \hat r - {r_s} \\ \hat \beta - {\beta _s} \\ \hat \varepsilon - {\varepsilon _s} \end{array} \!\!\!\!\right){\text,}$ | (17) |
其中,
由于姿态的转换不会对距离测量产生影响,因此距离偏差和测角偏差可以分别估计。
1)径向距离测量偏差估计
利用最小二乘法,可以得到径向距离测量偏差的估计为:
| $\Delta r = \frac{{\displaystyle\sum\limits_{i = 1}^N {\left( {{{\hat r}_i} - {r_i}} \right)} }}{N}{\text。}$ | (18) |
2)测角偏差估计
假设传感器的方位、俯仰和纵横摇测量精度分别为
| $\left( {\begin{array}{*{20}{c}} {{A_1}} \\ {{A_2}} \\ \vdots \\ {{A_N}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\Delta \beta /{\sigma _\beta }} \\ {\Delta \varepsilon /{\sigma _\varepsilon }} \\ {\Delta \psi /{\sigma _\psi }} \\ {\Delta \theta /{\sigma _\theta }} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{z_1}} \\ {{z_2}} \\ \vdots \\ {{z_N}} \end{array}} \right){\text。}$ | (19) |
其中:
| $\begin{split} & {A_k} = \left[ {\begin{array}{*{20}{c}} 1&0&{\dfrac{{{\sigma _\psi }}}{{{\sigma _\beta }}}\sin {{\hat \beta }_k}\tan {{\hat \varepsilon }_k}}&{\dfrac{{{\sigma _\theta }}}{{{\sigma _\beta }}}\cos {{\hat \beta }_k}\tan {{\hat \varepsilon }_k}} \\ 0&1&{\dfrac{{{\sigma _\psi }}}{{{\sigma _\varepsilon }}}\cos {{\hat \beta }_k}}&{ - \dfrac{{{\sigma _\theta }}}{{{\sigma _\varepsilon }}}\sin {{\hat \beta }_k}} \end{array}} \right] {\text,}\\ & {z_k} = \left( \begin{array}{l} ({{\hat \beta }_k} - {\beta _k})/{\sigma _\beta } \\ ({{\hat \varepsilon }_k} - {\varepsilon _k})/{\sigma _\varepsilon } \end{array} \right) {\text。}\\[-20pt] \end{split} $ | (20) |
由此可得最小二乘估计结果为:
| $\Sigma _b^{ - 1/2}\hat b = {\left( {\sum\limits_{k = 1}^N {A_k^T{A_k}} } \right)^{ - 1}}\left( {\sum\limits_{k = 1}^N {A_k^T{z_k}} } \right){\text,}$ | (21) |
若令
| $\begin{split}\sum A_k^T{A_k} =& \sum\limits_k \left( \begin{array}{*{20}{c}} 1&0&\!\!\!\!\!\!\!\!{{\lambda _1}\sin {{\hat \beta }_k}\tan {{\hat \varepsilon }_k}} \\ 0&1&\!\!\!\!\!\!{{\lambda _2}\cos {{\hat \beta }_k}} \\ *&*&\!\!\!\!\!\!{\lambda _1^2{{\sin }^2}{{\hat \beta }_k}{{\tan }^2}{{\hat \varepsilon }_k} + \lambda _2^2{{\cos }^2}{{\hat \beta }_k}} \\ *&*&* \end{array}\right.\\ &\left. \begin{array}{*{20}{c}} {{\delta _1}\cos {{\hat \beta }_k}\tan {{\hat \varepsilon }_k}}\\ { - {\delta _2}\sin {{\hat \beta }_k}}\\ {({\lambda _1}{\delta _1}{{\tan }^2}{{\hat \varepsilon }_k} - {\lambda _2}{\delta _2})\sin {{\hat \beta }_k}\cos {{\hat \beta }_k}}\\ {\delta _1^2{{\cos }^2}{{\hat \beta }_k}{{\tan }^2}{{\hat \varepsilon }_k} + \delta _2^2{{\sin }^2}{{\hat \beta }_k}} \end{array} \right){\text。} \end{split}$ | (22) |
据此可以看出:
1)对于低空目标,因为
2)当传感器对多个合作目标或同一目标的测量数据关于平台呈对称分布时,上述系数矩阵的非对角元素趋近于0;
3)一般情况下,要保证姿态偏差的估计精度,必须使系数矩阵的对角元素
根据上述分析可知,即使对于合作目标,要有效地估计姿态偏差,必须保证较大的方位覆盖区域和较大的俯仰测量值,并尽可能使测量数据保持对称分布。这一结论与装备应用中广泛使用的水平度测量方法的基本原理是一致的。
以下通过2种典型的仿真场景对比来验证上述结论。
仿真场景1:合作目标围绕传感器平台做圆周运动,目标距离平台35 km,目标高度3 km。
仿真场景2:合作目标相对校正传感器平台做匀速直线运动,初始位置
主要的仿真参数设置均为:
传感器测量偏差:

|
图 4 场景1估计结果 Fig. 4 Scenario 1 estimation result |
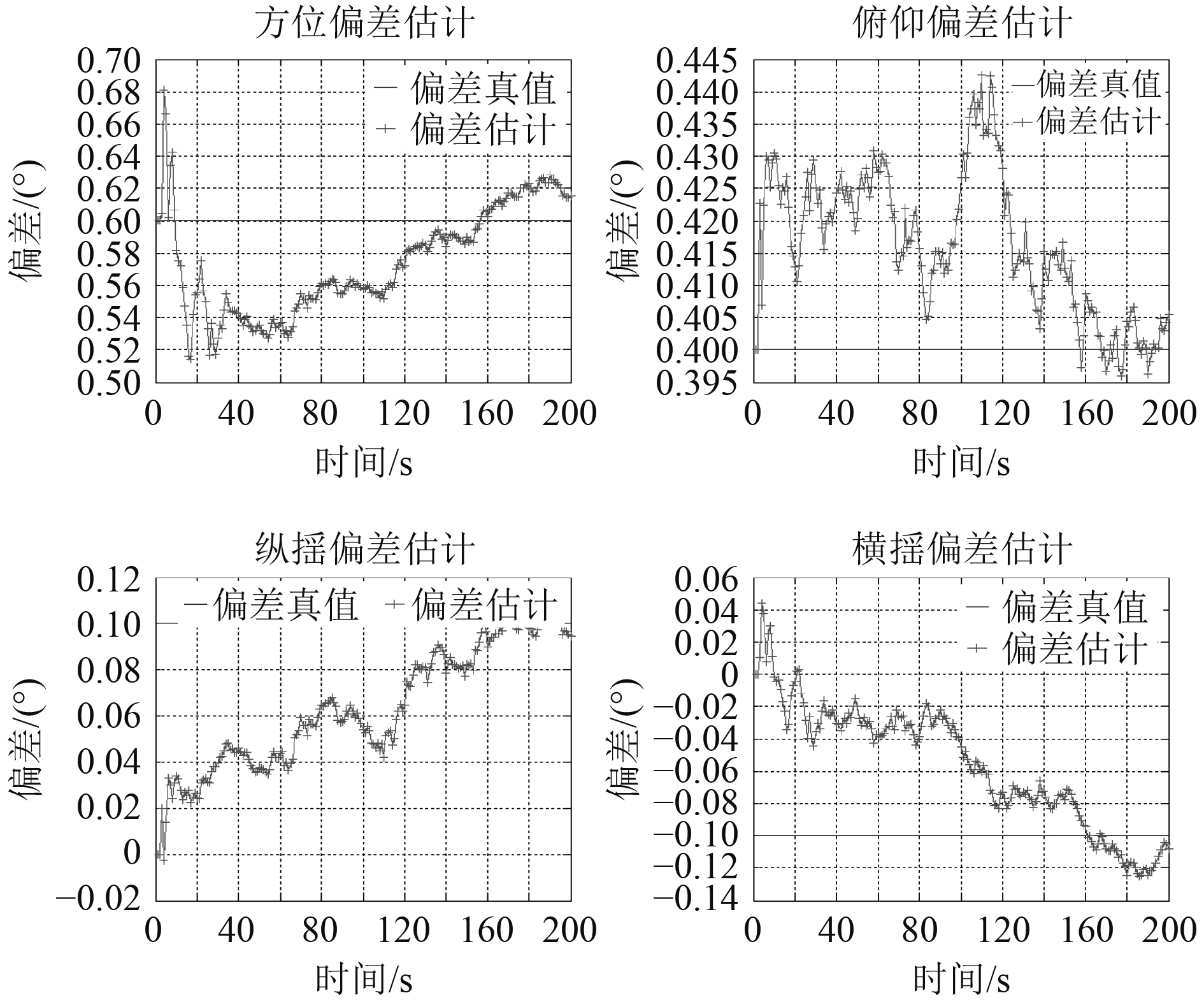
|
图 5 场景2估计结果 Fig. 5 Scenario 2 estimation results |
通过上述2种不同场景的估计结果可以看出,在同样的传感器参数设置和采样条件下,场景1明显比场景2的方位和俯仰角偏差估计结果要稳定,收敛更快。
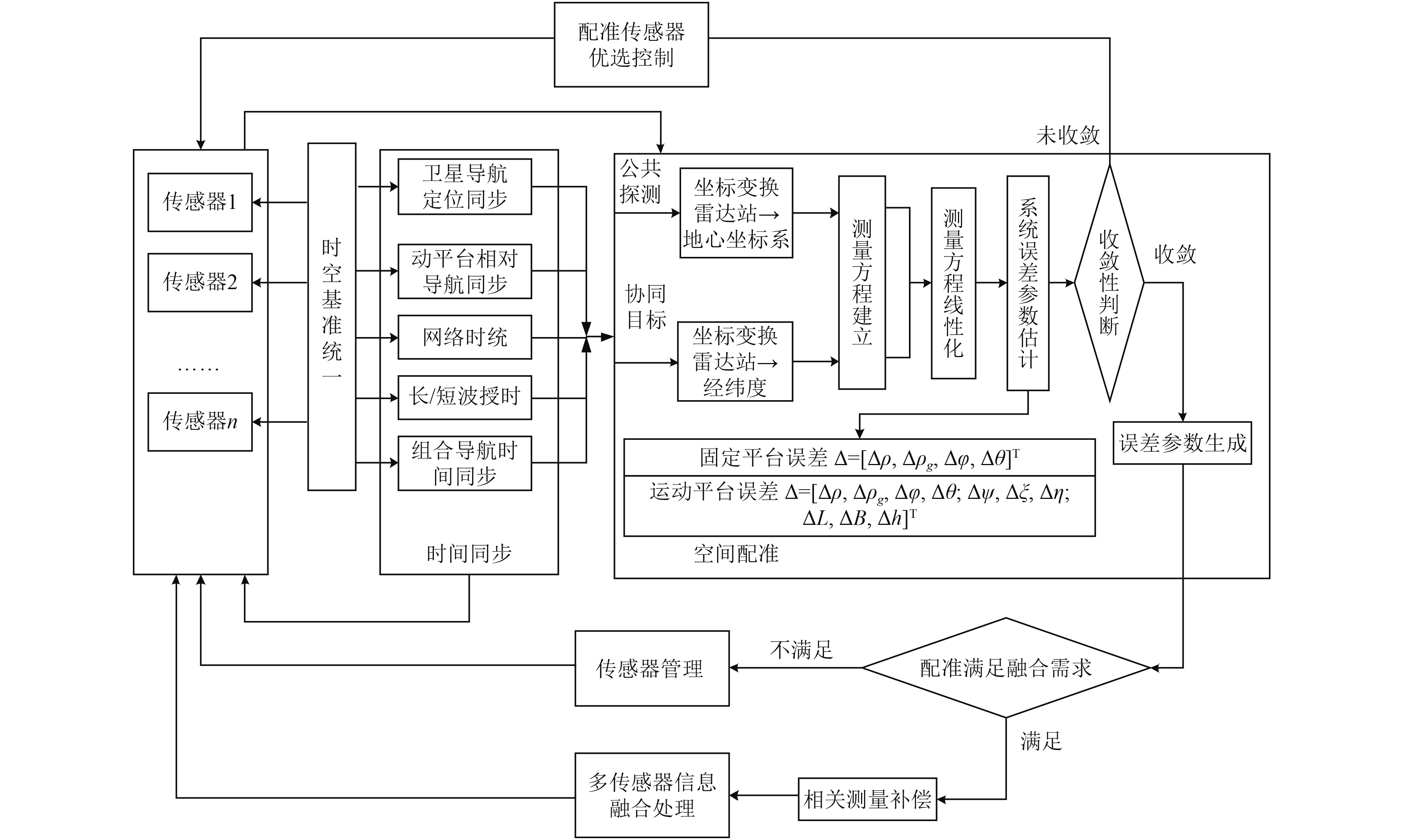
3 时空配准统一架构前文讨论应当构建时间同步体系解决战场各类系统和设备的时间同步问题,但对具体的有线和无线时间方法并没有深入讨论;在空间配准问题中,重点对公共目标配准和协同目标配准中的2种最典型的配准策略进行建模,同时给出了配准模型和特定情形的仿真结果,但并未涉及解的存在性、收敛性等难点问题。特别是公共目标配准问题,其解的存在性非常强地依赖于目标和传感器之间的空间关系。其是对一些更加复杂的情况,当目标信息不完整、偏差分布更加复杂时,估计将更加困难。由此,认为应当构建起如图6所示的时空配准的统一架构,处理上述问题。
|
图 6 时空配准的统一处理架构 Fig. 6 Unified processing architecture of spatio-temporal registration |
时空配准问题一直没有得到足够的重视,难度只是问题一个方面,更重要的原因是研究人员的“偏见”。正如大家将系统性误差视为“偏差”一样,此时更多情况归因于“差错”,认为只要消除“差错”,就能消除“偏差”。
根据海森堡的“测不准原理”:即不可能同时知道一个粒子的位置和它的速度,“测不准原理”从某种程度上说是自然界的客观规律。猜想其中根本性的问题还是“时间”存在着某种“不可测”成分,对“时间”认知的偏差,引起对速度和位置测量的偏差。军事行动中常常更是有意为之,复杂环境加上“虚实与真假”并存,正兵法所言[11]“战势不过奇正,奇正之变,不可胜穷也。”这进一步增加了战场目标时空配准问题的复杂度。
| [1] |
COOPER R S, CHI A R. 郑运广译. 卫星时间传递技术—成就及未来的应用[J]. Radio Science, 1969, 14(4): 605-619. |
| [2] |
BEARD R L, WHITE J D, DETOMA A, et al. Common time reference for naval systems[R], Naval Research Laboratory, AD A427684.
|
| [3] | |
| [4] |
IEEE Std. 1588TM-2008.1588 IEEE Standard for a precision clock synchronization protocol for networked measurement and control system[S]. 2008.
|
| [5] |
FISHER W L, MUEHE C E, CAMERON A G. Registration errors in a netted air surveillance system[R], MIT Lincoln Laboratory, AD A093691. Sept, 1980.
|
| [6] |
HELMICK R E, CONTE J E, RICE T R. Absolute sensor alignment using GPS[J]. Proceedings of SPIE Acquisition, Tracking, and Pointing XVI, 1996, 27(39): 168-179. |
| [7] |
OKELLO N N, RISTIC B. Maximum likelihood registration for multiple dissimilar sensors[J]. IEEE Transactions Aerospace and Electronic Systems, 2003, 39(3): 1074-1082. DOI:10.1109/TAES.2003.1238759 |
| [8] |
HELMICK R E, RICK T R. Removal of alignment errors in integrated system of two 3-D sensors[J]. IEEE Transactions Aerospace and Electronic Systems, 1993, 29(4): 1333-1343. DOI:10.1109/7.259537 |
| [9] |
吴卫华, 江晶. WGS-84坐标系下多空基无源传感器最大似然配准[J]. 系统工程与电子技术, 2015, 37(2): 304-309. DOI:10.3969/j.issn.1001-506X.2015.02.12 |
| [10] |
李洪梅, 潘江怀, 何佳洲, 等. 舰载雷达探测误差传递与灵敏度分析[J]. 数据采集与处理, 2012, 27(4): 474-479. DOI:10.3969/j.issn.1004-9037.2012.04.013 |
| [11] |
中国人民解放军军事科学院战争理论研究部《孙子》注释小组注[M]. 孙子兵法新注, 中华书局, 1977.1(2005.1重印), 北京.
|
 2021, Vol. 43
2021, Vol. 43

