2. 江苏省绿色船舶技术重点实验室,江苏 无锡 214082
2. Jiangsu Key Laboratory of Green Ship Technology, Wuxi 214082, China
某海洋平台在试航时发现有部分甲板区域出现振动超标,该甲板位于主设备舱上方并受到舱内2台主机振动传递的激励。当甲板结构的固有频率与主机激振力的频率一致时,会产生结构共振。结构共振不但会妨碍平台上设备、仪表和人员的正常工作,也容易引起局部结构产生疲劳损伤。为了查出结构振动超标的原因,本文采用理论解析结合数值仿真的计算方法,对平台甲板板架结构及其组成单元,包括甲板板格、加筋板的固有频率进行计算研究,以确定异常振动是因哪部分结构共振引起,为振动超标区的治理提供理论依据。
在进行甲板结构动力分析时,规范一般将其边界约束简化为四边简支的板架,参照规范计算公式可计算其固有频率 [1]。张硕等[2]对比采用经验公式法和有限元法计算船体甲板固有频率的不同,分析各种经验计算方法的适用范围,提出计算甲板固有频率的有限元法边界条件设置方法,并采用实船测试结果对计算方法进行验证。龚郝等[3]采用有限元计算方法对船体板架固有频率的计算模型进行简化,讨论某实船甲板板架计算模型的范围、边界条件的选择对计算结果的影响,研究认为采用边界约束为简支的单舱段局部模型或单舱段模型进行板架固有频率分析与频率储备校核有利于保证计算精度。郭列等[4]对船舶结构局部振动计算模型进行了研究,探讨了建立振动计算模型的一些关键性问题,如结构振动是采用硬设计还是软设计、确定计算结构边界条件时相邻结构的选取问题、结构的力学模拟问题以及计算模型的精细程度等;王维等[5]采用直接简化计算的方法对船上常见的局部板架结构的固有频率进行计算和分析研究,在此基础上从调整板厚、骨材形状、局部范围的强梁跨距等方法在初步设计阶段避免局部板架与附近激励源的共振问题。曾文源等[6]对某舰船机舱区域底部板架振动进行了计算研究,建立了不同的振动区域计算模型,通过计算分析和比较,探讨不同计算模型范围、边界条件对计算结果的影响。
论文针对某海洋平台振动超标区的结构进行振动理论分析,分别研究了甲板板格、加筋板单元固有频率的解析计算方法,重点研究了预报甲板板架振动固有频率的数值计算方法,给出了板架振动有限元模型的取值范围的建议。通过研究预报了平台甲板板架区域中板格、加筋板单元及整体甲板板架结构的固有频率,并进行了试验验证,得出了结构异常振动的原因并给出了结构振动超标的一般分析流程。
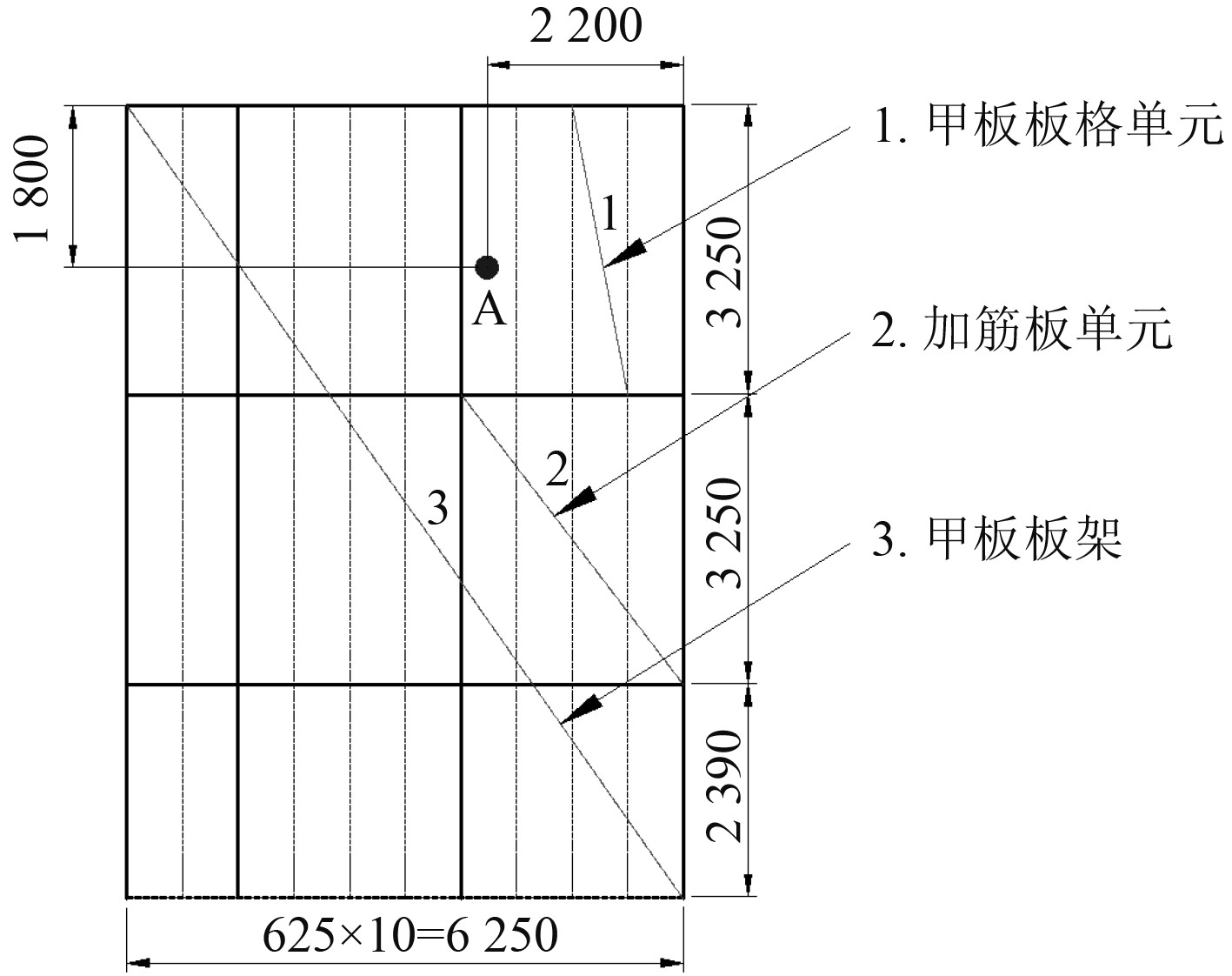
1 计算方法振动超标区域的甲板板架结构单元可分为甲板板格、加筋板,如图1所示。这些结构单元与整体板架固有频率之中的任何一个与外加激励频率相重合都有可能引起结构共振,从而使振动出现异常。因此,需要对板格、加筋板以及板架整体结构固有频率进行研究分析。
|
图 1 振动超标区域结构图 Fig. 1 Structure diagram of excessive vibration area |
在船舶与海洋平台结构局部振动计算中,计算矩形板格首阶固有频率时,对于承受较大中面力作用,四边简支边界条件下的板格的固有频率计算公式为[7]:
| $\omega _{_{nij}}^2 = \frac{{D{\text{π} ^4}}}{{\rho h{b^4}}}\left[\Biggr(1 + \frac{{{b^2}}}{{{a^2}}}\right]^2 + \left.\dfrac{{({\sigma _y} + {\sigma _x}\dfrac{{{b^2}}}{{{a^2}}}){b^2}h}}{{{\text{π} ^2}D}}\right]{\text{。}}$ | (1) |
式中:
若忽略中面力影响,板的材料为钢材,可得无中面力作用下四边简支矩形板的理论解如下:
| ${f_{01}} = 2.45 \times {10^6}h\left(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}}\right){\text。}$ | (2) |
式中:
加筋板由板和梁结构组成,在计算其垂向弯曲振动时,把此板梁结构看成梁系结构,板的影响采用引入梁剖面的附连翼板的形式来考虑,不仅符合结构的力学模拟原则,保证计算精度,还可以简化计算。对于四边简支、沿一个方向有平行加筋的加筋板,首阶固有频率计算公式为:
| ${f_{01}} = \frac{{8.1}}{{{L^2}}} \times {10^5}\sqrt {\frac{{KIn}}{{{t_e}s(n + 1)}}}{\text{。}} $ | (3) |
式中:n为加强筋数量,K为折减系数(加强筋截面为对称形时取1.0,非对称形时取0.85),
| ${t_e} = h + \frac{{An}}{{s(n + 1)}}{\text。}$ | (4) |
式中:
由于海洋平台甲板板架上可能还有甲板敷料、浮动地板等,计算时假定这些附加的功能结构仅以质量的形式参与振动计算而不影响板架本身的刚度特性,因此根据构件振动固有频率的以下简化计算公式,附加质量对构件固有频率的影响仅体现在质量因子上:
| $f = \frac{1}{{2\text{π} }}\sqrt {\frac{K}{M}}{\text。} $ | (5) |
式中:K为构件的弯曲、扭转、剪切刚度等。
附加质量的折减因子为:
| $ \lambda =\sqrt{\frac{{M}_{\text{构件}}}{{M}_{\text{构件}}+{M}_{\text{附加}}}}{\text,}$ | (6) |
则带有附加质量的板格或加筋板的固有振动频率为:
| ${f_m} = \lambda {f_0}{\text。}$ | (7) |
式中:
由于甲板板架结构的复杂性,其固有频率计算需要采用数值方法对结构进行离散。板架结构离散后的自由振动方程为:
| $M\mathop x\limits^{..} + Kx = 0{\text,}$ | (8) |
根据微分方程理论,式(8)的解为:
| $x = X\sin ({\omega _n}t + \varphi ){\text,}$ | (9) |
式中:M为结构质量阵;K为结构刚度阵;
| $[K - \omega _n^2M]\left\{ X \right\} = 0{\text{。}}$ | (10) |
式(10)为一齐次的线性代数方程组,存在非零解的条件为系数行列式为零:
| $\left| {K - \omega _n^2M} \right| = 0{\text。}$ | (11) |
式(11)即为结构振动系统的频率方程或特征方程。对于n个自由度的系统,频率方程(11)必有n个正实根,即有n个圆频率,每个圆频率均有相对应的固有振型
根据上述理论,首先仅对“目标区域”板架进行有限元建模,板架模型均在舱壁处断开。由于板架结构受到舱壁的弹性支持,结构的固有频率介于四周简支与刚性固定之间,本文分别采用四边简支和四边固支边界条件进行计算。甲板板架有限元模型如图2所示。

|
图 2 甲板板架有限元模型 Fig. 2 Finite element model of deck plate frame |
为考虑舱壁结构对甲板板架固有频率计算的影响,建立含目标区域甲板的单舱段有限元模型,考虑甲板板架上部舱室以及下部舱室结构的影响。有限元模型如图3,模型的边界条件为舱段底端简支。

|
图 3 单舱段模型 Fig. 3 Single compartment model |
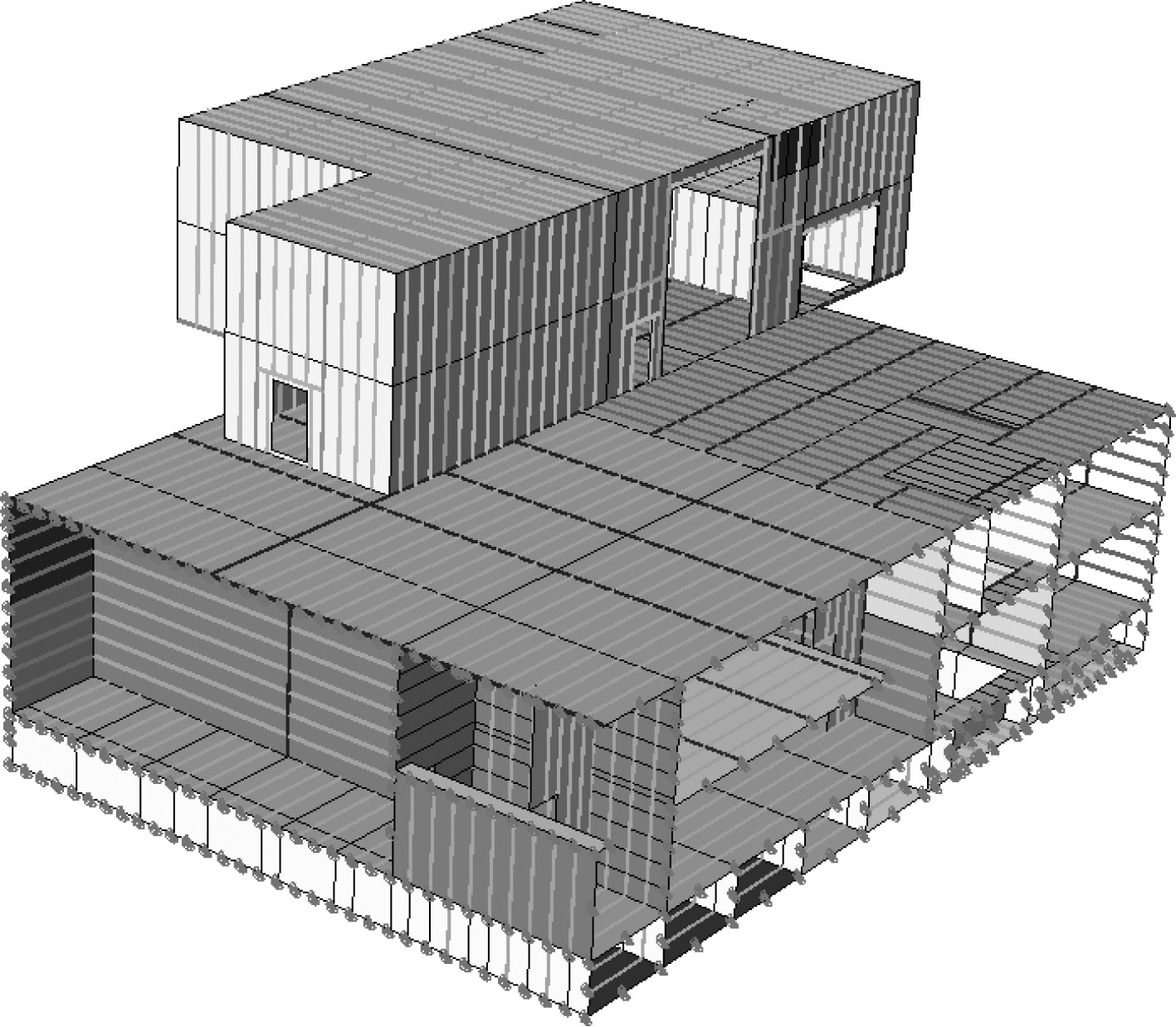
为了更逼近真实边界条件,将该甲板板架周围的舱室进行建模,并考虑前后舱段结构对甲板板架固有频率计算的影响,将舱段有限元模型向四周各延伸一个舱段形成三舱段模型,并尽可能在强支撑构件处断开,并在断开处采用简支边界条件,有限元模型如图4所示。
|
图 4 三舱段模型 Fig. 4 Three-compartments model |
以上有限元模型中,舱室的甲板、舱壁板采用Abaqus中的S4R壳单元模拟,强梁、加强筋等均采用B31梁单元模拟。由于平台设备运行所引起的结构振动主频率主要集中在100 Hz范围内,有限元分析的频段选取为5 ~100 Hz,频率间隔为1 Hz。
2 计算结果及分析 2.1 甲板板格固有频率的计算结果图1中振动超标区域甲板板格(编号1)长为3250 mm,宽为625 mm,厚度为15 mm,质量为239 kg,并考虑板格上甲板敷料的附加质量63.1 kg,根据式(6),
建立该甲板板格的有限元模型,并考虑附加质量,得到四边简支约束板的1阶固有模态如图5所示。

|
图 5 甲板板格1阶振动频率及振型 Fig. 5 The first order modal frequency and shape of deck plate |
有限元计算得到的含附加质量的四边简支板的固有频率为87.6Hz,与解析法计算得到的结果相差不到1%,证明解析计算式(2)、式(7)可作为预测板格振动固有频率的理论方法。
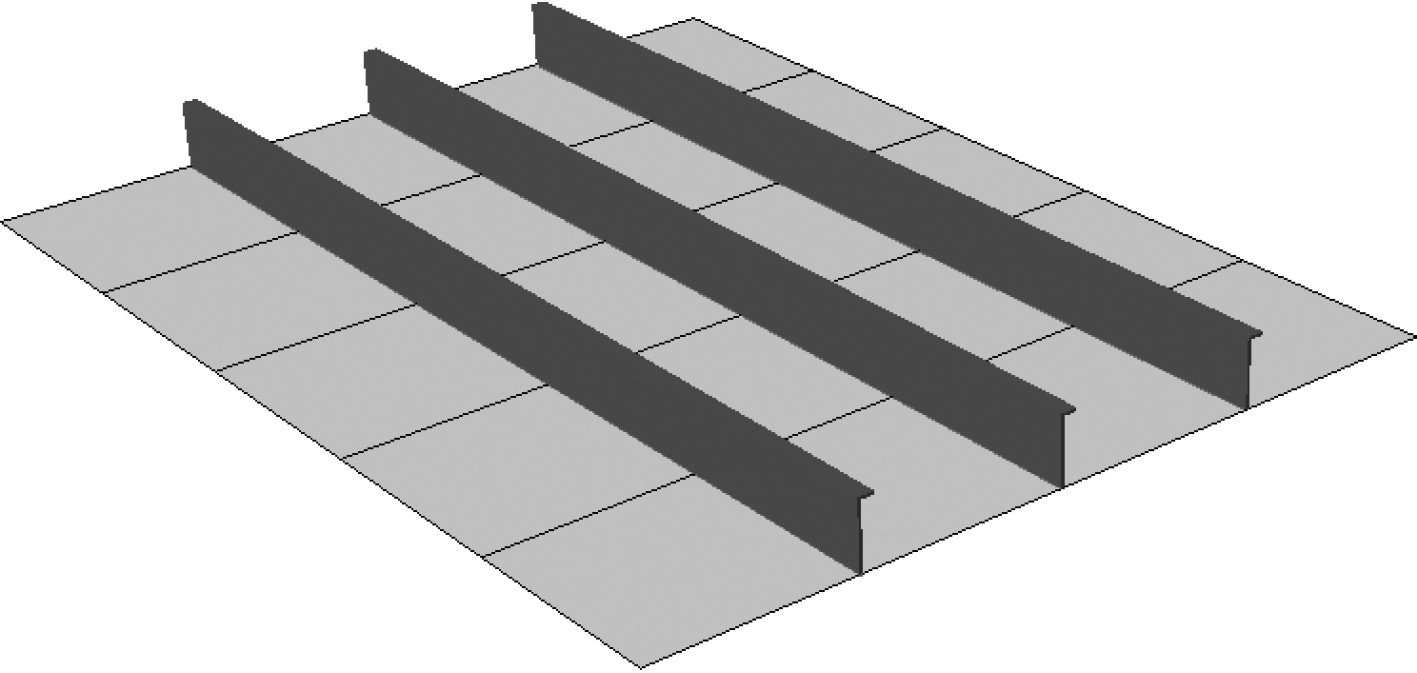
2.2 加筋板固有频率的计算图1中振动超标区域加筋板(编号2)长度为3250 mm,宽度为2500 mm,板的厚度为15 mm,沿着长度方向均匀布置有3条纵向加强筋,加强筋尺寸为HP200 × 10的球扁钢,加筋板分析模型如图6所示。总质量为1166 kg,甲板敷料的附加质量为252 kg。根据公式(6),
|
图 6 加筋板模型 Fig. 6 Stiffened plate model |
|
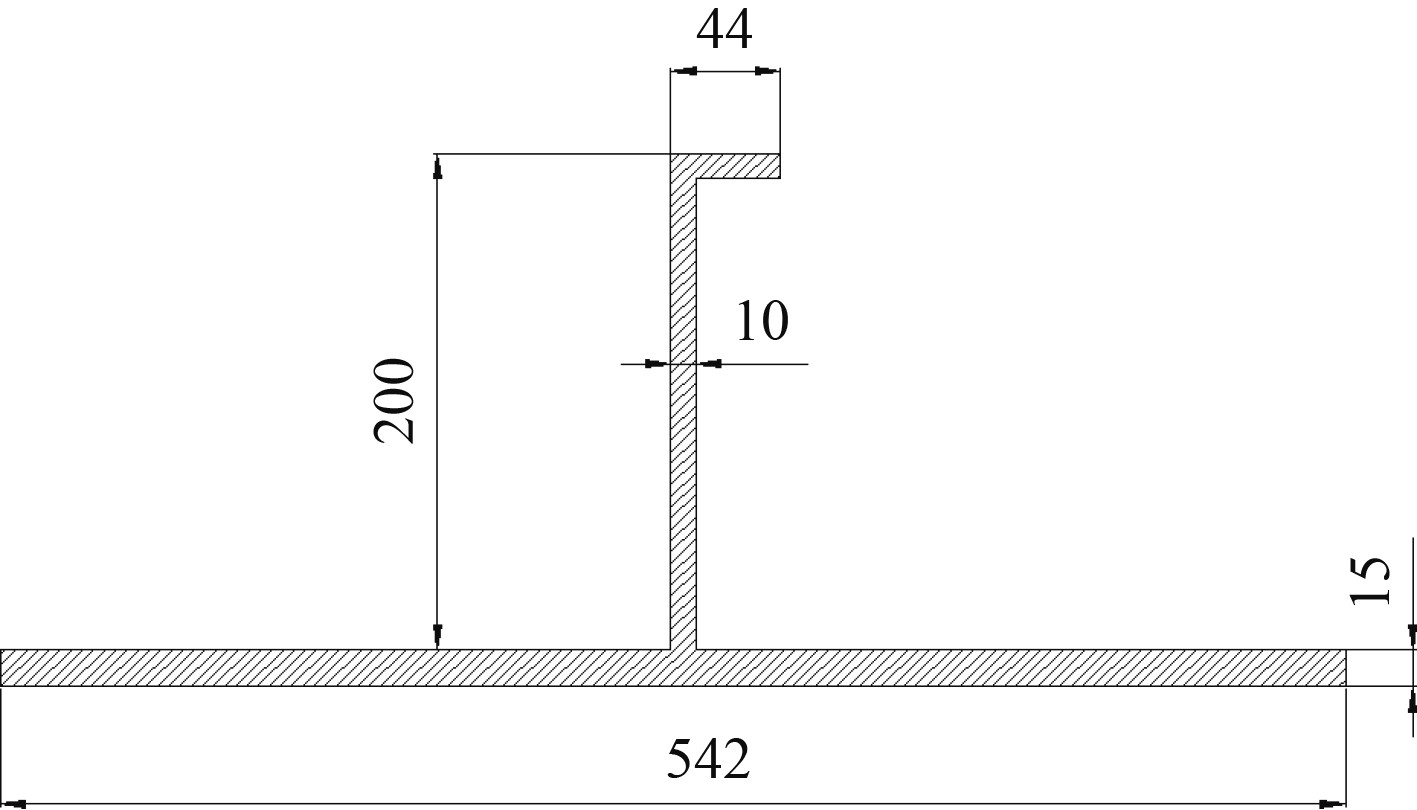
图 7 加筋板惯性矩计算剖面 Fig. 7 Moment of inertia profile of stiffened plate |
建立加筋板有限元模型进行有限元分析,板采用Abaqus中的S4R壳单元,加强筋采用B31梁单元,并考虑甲板敷料附加质量的影响,得到四边简支约束下加筋板的1阶固有模态如图8所示。

|
图 8 加筋板1阶振动固有频率及振型 Fig. 8 The first order modal frequency and shape of stiffened plate |
由计算结果可知,有限元计算得到的含附加质量的加筋板的固有频率为36.9 Hz,与解析法计算得到的结果34 Hz相差约为8.5%,证明解析计算式(3)、式(7)可作为预测加筋板振动固有频率的理论方法。
2.3 板架固有频率的计算结果分别采用单板架有限元模型、单舱段有限元模型、三舱段有限元模型对板架的固有频率进行计算,并考虑板架上的附加质量746.5 kg,其中单板架有限元模型的模态计算结果如图9和图10所示。
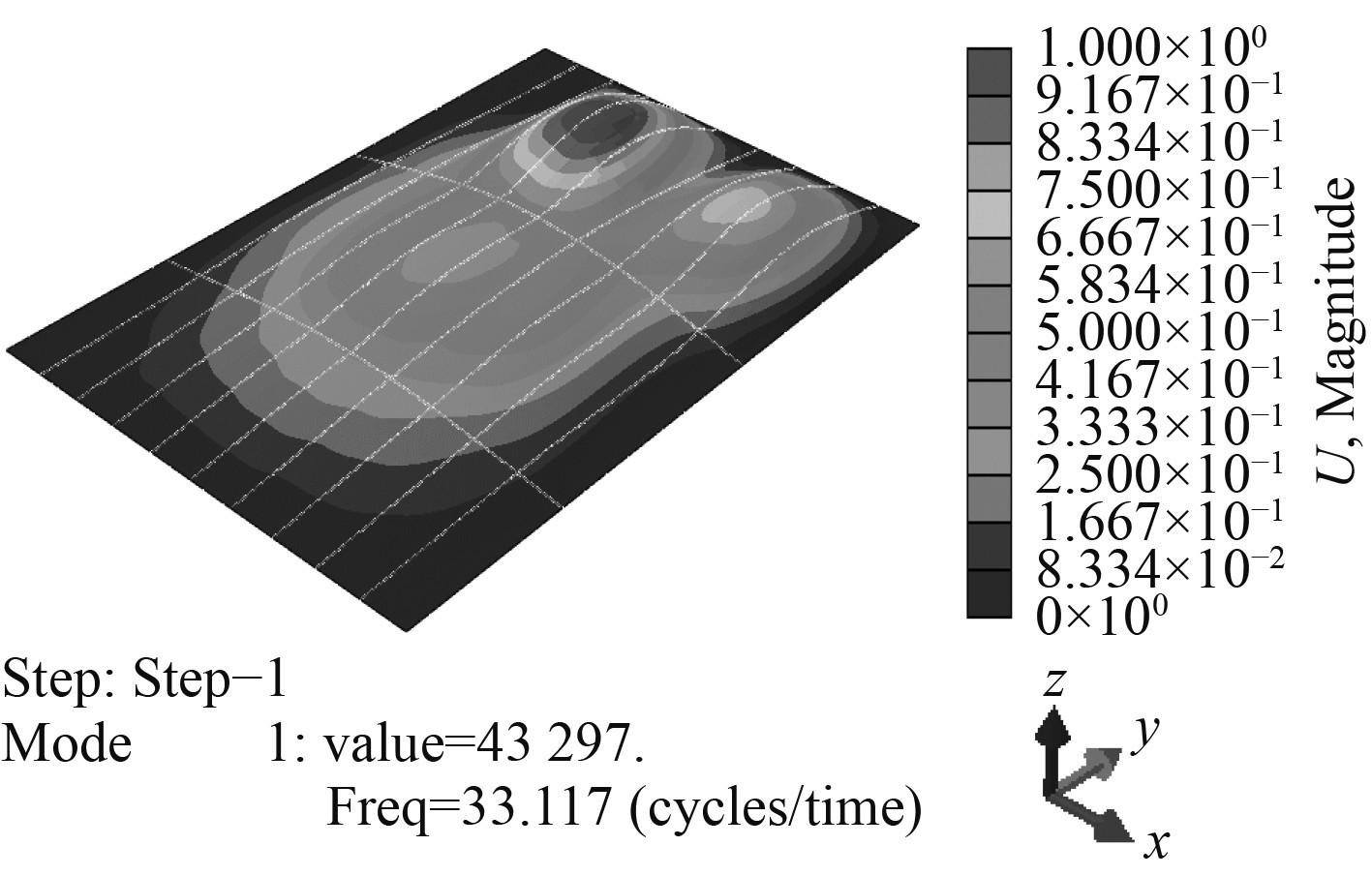
|
图 9 板架模型简支模态结果 Fig. 9 Modal results of the simply supported frame model |
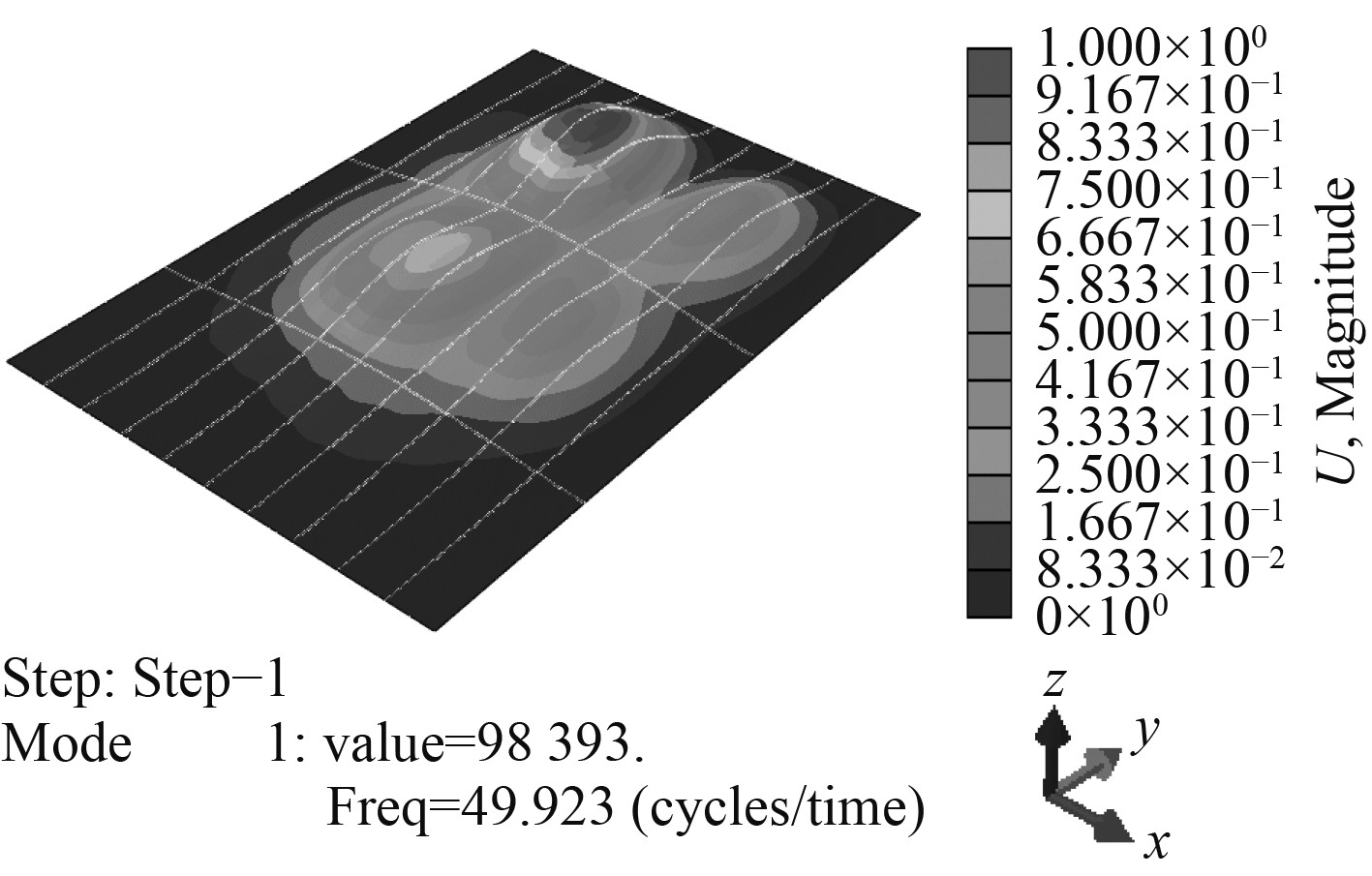
|
图 10 板架模型固支模态结果 Fig. 10 Modal results of the clamped frame model |
从计算结果可以看到,采用单板架模型计算时,第1阶模态结果即是板架主模态,板架垂向弯曲振动简支和固支边界条件下固有频率约为33.1 Hz和49.9 Hz,板架主弯曲模态可以从表1中板架该模态下的模态质量占比得出。表1中模态质量为整体模型质量在某模态代表的不同自由度方向上是如何分布的,模态质量的理论计算公式为:
|
|
表 1 甲板板架振动多级有限元计算结果对比 Tab.1 Comparison of multi-stage finite element calculation results of deck plate frame vibration |
| $m_{i j}=m_{i}\left(\Gamma_{i j}\right)^{2}{\text,}$ | (12) |
式中:
| ${m_{i}} = \phi _i^{\rm{T}} M \phi _i{\text,}$ | (13) |
| ${\Gamma _{ij}} = \frac{1}{{{m_i}}}\phi _i^{\rm{T}}M{T_j}{\text。}$ | (14) |
式中:M为质量阵;
通过模态质量可以识别哪阶振型(模态)对所要研究的荷载作用方向是有作用的,表1中单板架模型在该模态下模态质量与模型总质量的比值分别达到62.3%和53%,证明图9和图10中该阶模态即为单板架模型的垂向弯曲振动主模态。
单舱段有限元模型的模态计算结果如图11所示。为了方便显示所关注的甲板板架区域,隐掉了板架上方舱室壁板的显示。
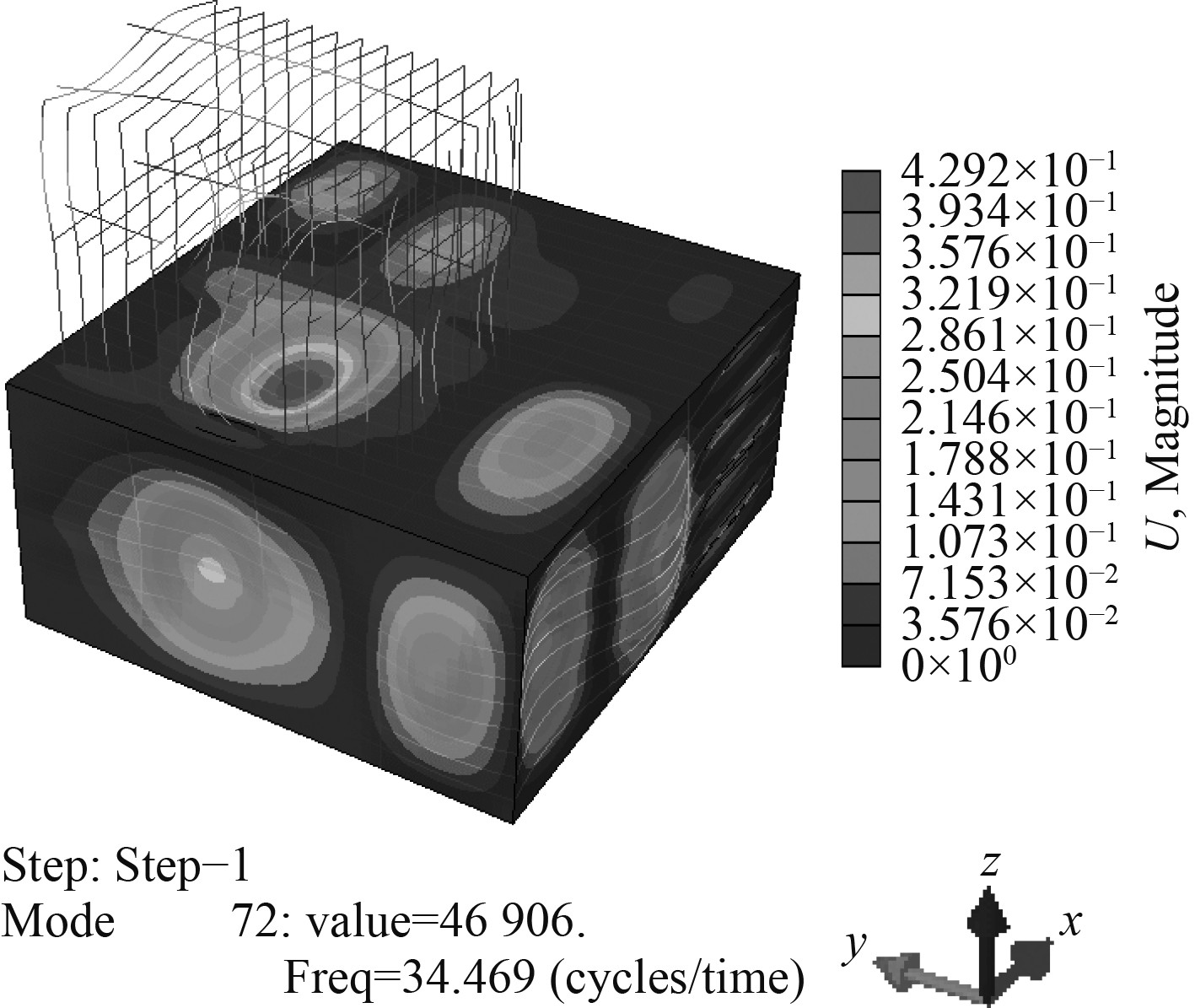
|
图 11 单舱段模型模态结果 Fig. 11 Modal results of the single compartment model |
从图11可以看出,采用单舱段模型计算时,板架垂向弯曲振动的首阶固有频率 约为34.5 Hz,比四边简支约束下单板架模型计算的固有频率结果大4.2%。由于单舱段模型考虑了板架周围结构的约束,计算结果相对四边简支的单板架模型结果更为准确。从表1可以看出,在该模态下,单舱段模型弯曲振动方向的模态质量占比较小,并且是以局部振动为主。而在其它阶模态计算结果下,也未能发现“目标区域”有垂向弯曲振动主模态的出现。
三舱段有限元模型的模态计算结果如图12所示。同样为了方便显示所关注的甲板板架区域,隐掉了板架上方舱室壁板的显示。

|
图 12 三舱段模型板架模态计算结果 Fig. 12 Modal results of the three-compartments model |
从图12和表1的计算结果可以看出,采用三舱段模型计算时,随着“目标板架”的边界条件更一步逼近真实结构,板架垂向弯曲振动的首阶固有频率计算结果进一步增加,但是增加幅度较小,所得固有频率35.4 Hz较单舱段模型仅有2.6%的增加。
同时也可以看到,建立的三舱段模型由于模型规模的进一步扩大以及模型自由度的大幅度增加,将引入更多的局部振动模态,使得寻找“目标区域”固有模态的难度也随之增加。综合计算精度、建模工作量、模态识别的难易程度,工程计算中可以选用单舱段模型。
比较表1各模型计算结果可以看出,采用边界约束为固支的单板架模型固有频率计算结果明显偏大,甲板板架的固有频率偏向于简支。
3 计算结果试验验证为分析平台振动噪声超标原因并验证本文的计算方法,在平台停靠码头时对超标区域进行了振动测试[8]。在主机舱内2台主机分别单独开启和同时开启的状态下,在主机舱舱室的顶部振动超标区域甲板上布置振动加速度测点A1(见图1),测试甲板结构振动。
振动测试系统由ICP振动加速度计和BK 3650数据采集仪组成,参试的所有仪表均计量合格,满足测试要求,振动测量物理量为速度,测量频率范围为5~100 Hz,频率分辨率为0.1 Hz。图13~图15为甲板测点的振动频谱图。
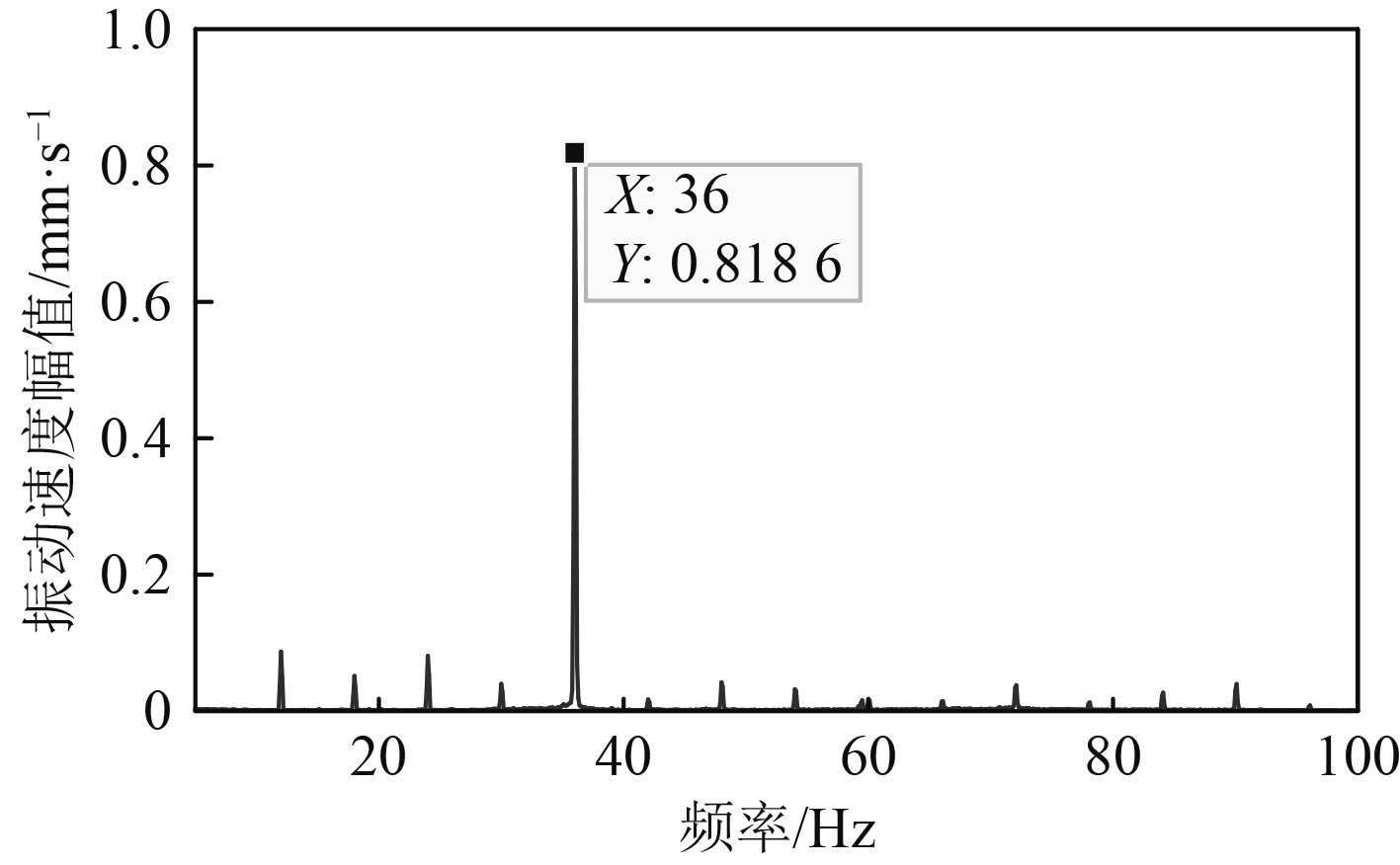
|
图 13 主机1开启下甲板测点的振动 Fig. 13 Vibration of the measured points on the deck under main engine 1 opened |
|
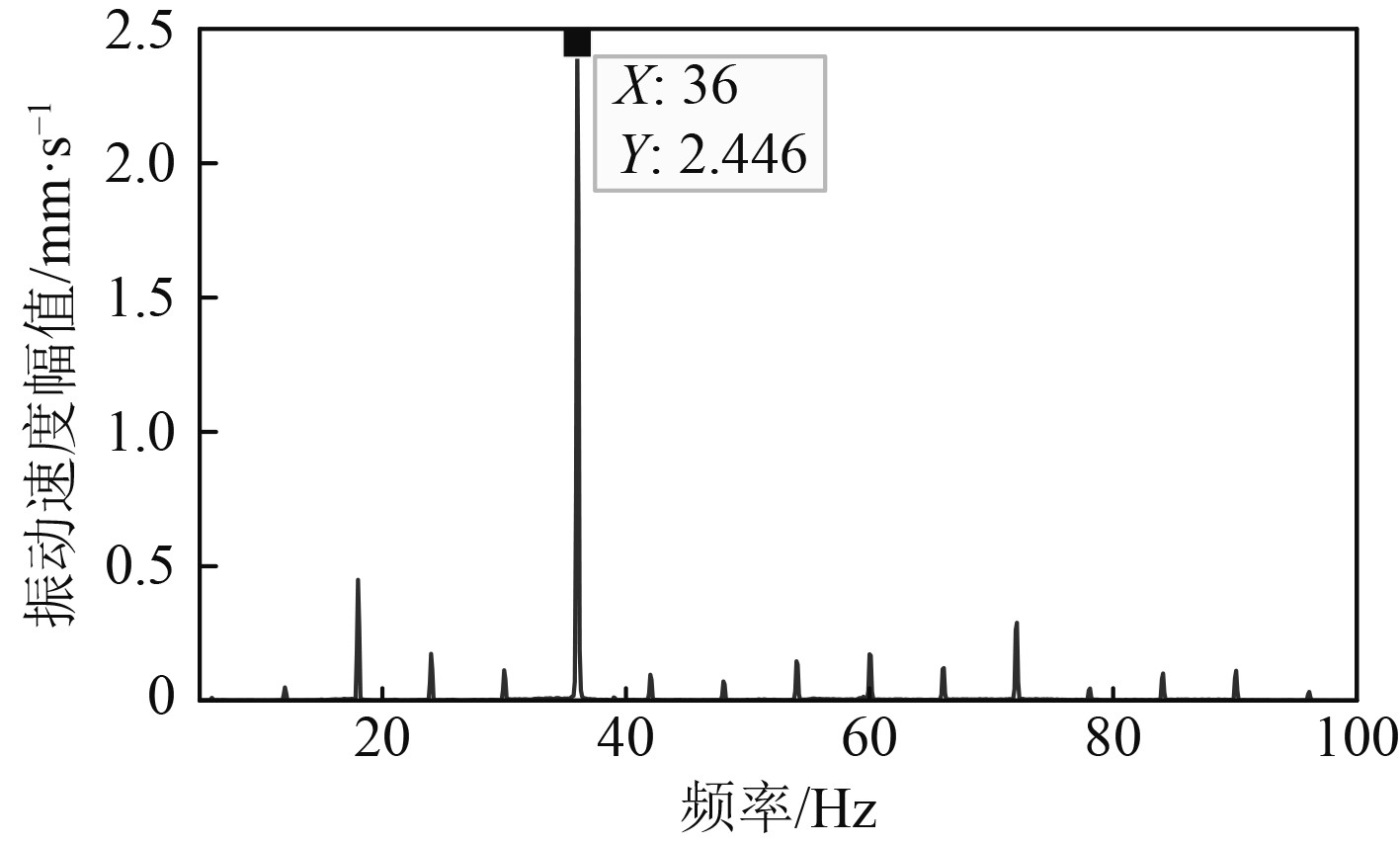
图 14 主机2开启下甲板测点的振动 Fig. 14 Vibration of the measured points on the deck under main engine 2 opened |
|
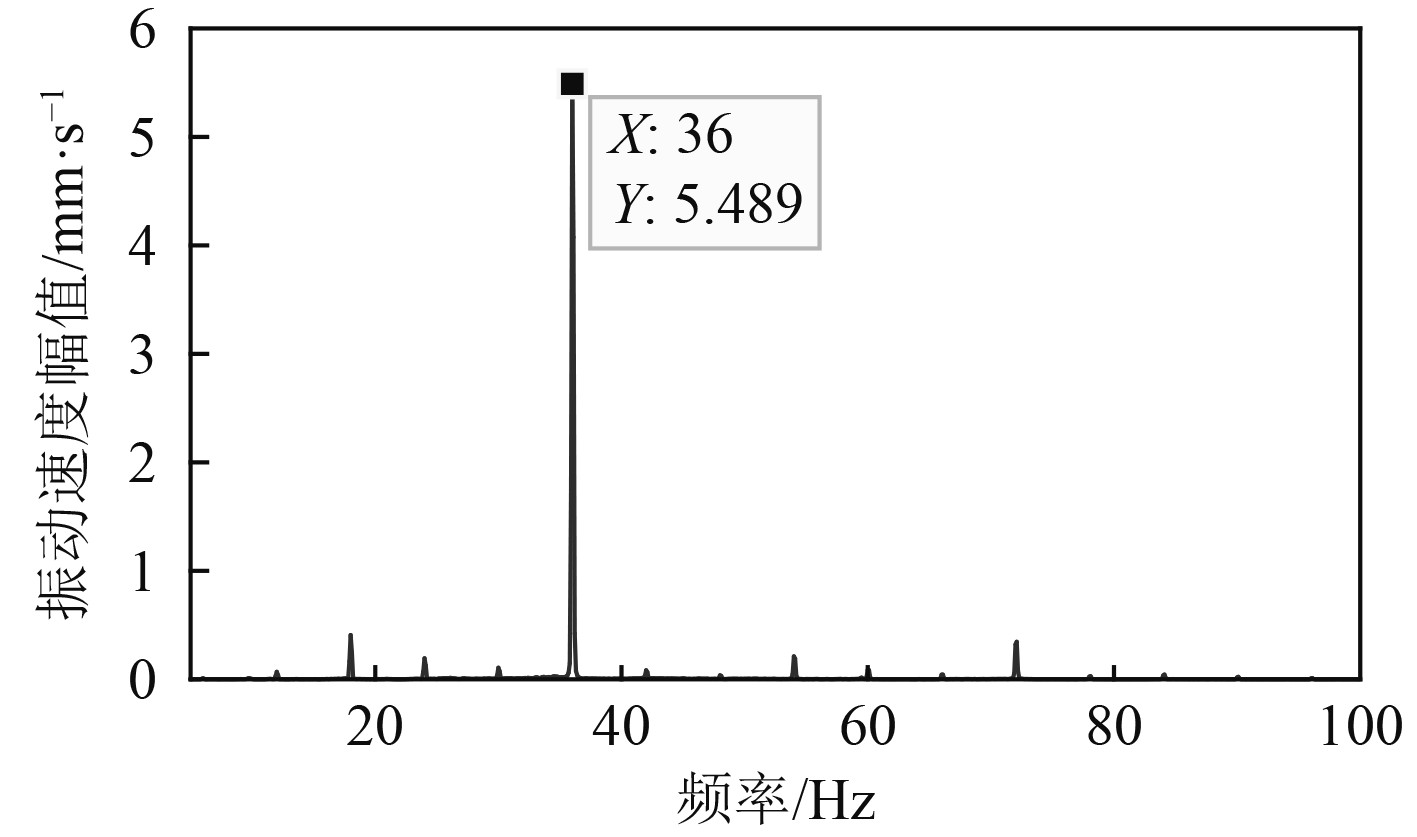
图 15 主机同时开启下甲板测点的振动 Fig. 15 Vibration of the measured points on the deck under main engine 2 opened |
主机的转速为720 r/min,因此轴频为12 Hz。由图13~图15可以看出,甲板板架结构在主机轴频12 Hz所对应的振动峰值并不大,最大的峰值对应的频率是3倍的轴频即36 Hz,是导致结构振动超标的激励频率。
对前文各种计算模型及方法得到的振动超标区域结构固有频率的计算结果汇总于表2。
|
|
表 2 振动超标区甲板结构固有频率计算结果 Tab.2 Natural frequency results of deck structures in abnormal vibration region |
可以看出,通过加筋板单元计算模型以及单舱段、三舱段数值计算模型得到的结构局部振动频率均在36 Hz附近,与实船测试结果非常接近,因此可以认为结构振动超标的主要原因是甲板板架局部加筋板单元的固有频率与主机36 Hz的激励频率相重合引起的。对于本文,采用局部加筋板模型即可迅速分析出振动超标的原因,并且分析高效、简便、快捷。
4 振动超标计算流程对潜在或存在振动超标区域的板架结构设计或计算分析时,应依次选取结构中的板格单元、加筋板单元以及整体板架进行分析,并与激励源的激励频率进行比较,确定振动超标是因哪部分结构引起,并采取相应的振动控制措施或者是结构改进。
对于板格单元和加筋板单元,采用文中的理论解析公式即可得到较为精确的固有频率解答;对于板架模型,建议选用边界约束为简支的单舱段模型进行固有频率分析。
5 结 语本文对海洋平台甲板振动超标区域结构振动进行研究分析,采用理论解析与数值方法计算甲板板格及加筋板单元的固有频率,采用不同有限元模型计算整体甲板板架结构的固有频率,从而依次获得振动超标区域甲板板格、加筋板单元以及整体甲板板架结构的固有频率计算结果,并与实船试验结果进行对比,得出以下结论:
1)平台甲板结构振动超标的主要原因是加筋板单元的振动固有频率与激励频率重合引起的结构局部共振;
2)对于甲板板格单元和加筋板单元,采用本文的理论解析公式即可得到较为精确的计算结果,可以用于振动超标区结构单元的固有频率快速预报和评估;
3)为保证甲板板架固有频率的计算精度,避免因模型计算规模的扩大引入更多的局部振动模态,造成结构主模态难以辨识、固有频率难以获取的问题,建议采用边界约束为简支的单舱段模型进行板架结构的固有频率分析;
4)本文以甲板板架振动超标区为研究对象,提出的振动超标分析方法和流程可以推广至船舶与海洋工程中结构底部板架、舷侧板架等类似板架结构的振动固有频率分析。
| [1] |
中国船级社. 船上振动控制指南[M]. 北京: 人民交通出版社, 2012.
|
| [2] |
张硕, 施惟奇, 贺华, 等. 船体局部甲板固有频率计算方法比较[J]. 噪声与振动控制, 2015, 35(6): 52−55.
|
| [3] |
龚郝, 张世联. 船体板架固有频率计算模型的简化[J]. 船海工程, 2016, 3: 47-54. DOI:10.3963/j.issn.1671-7953.2016.03.011 |
| [4] |
郭列, 吴士冲, 何富坚. 舰艇结构局部振动计算模型研究[J]. 船舶工程, 2000, 2: 21-29. DOI:10.3969/j.issn.1000-6982.2000.01.005 |
| [5] |
王维, 孙雪荣. 局部板架振动的计算研究[J]. 船舶, 2010, 3: 16-24. DOI:10.3969/j.issn.1001-9855.2010.06.004 |
| [6] |
曾文源, 郑宏宇, 陈雷厉, 等. 机舱区域底部板架振动计算研究[J]. 船舶, 2006, 12(6): 18-20. ZENG WENYUAN, ZHENG HONGYU, CHEN LEILI, et al. Vibration Calculation of Bottom Plate Frame in Engine Room Area[J]. Ship, 2006, 12(6): 18-20. DOI:10.3969/j.issn.1001-9855.2006.06.005 |
| [7] |
金咸定, 赵德有. 船体振动学[M]. 上海: 上海交通大学出版社, 2000.
|
| [8] |
陶沙, 李泽成. 支持平台超标区域振动噪声测试分析报告[R]. 中国船舶科学研究中心科技报告, 2017.
|
 2021, Vol. 43
2021, Vol. 43
