在双浮筒防波堤试验与应用中发现,当波浪经过防波堤双浮筒之间上下贯通的围壁腔体时,波浪在腔体内部位能升高,并周期性上下振荡。这一运动特性与海工结构物月池内流体活塞振动相似,且二者均为上下贯通的腔体,结构特性相同,二者的不同点在于海工平台月池内流体严重影响平台安全性,而浮式防波堤腔体内部振荡有利于其消波效果。在对浮式防波堤腔内流体展开研究时可以参考海工平台月池结构的研究成果。目前关于月池结构的研究重点关注月池内流体振荡对平台运动响应的影响规律以及推演流体振荡频率的理论公式。Faltinsen[4]使用解析的方法对月池内部活塞晃荡式运动展开研究,将月池内部发生活塞式振动的流体化为质量—弹簧系统,从而得到振荡频率的表达式。ZHOU等[6]运用势流理论,研究分析了带月池型柱状结构的运动响应,结果发现,月池对垂荡运动具有较大影响。本文基于此考虑不同工况浮式防波堤腔体内部波浪振荡变化规律及其对消波效果的影响,并对不同腔体模型腔内波浪振荡与消波效果的影响进行分析。
1 基本理论 1.1 计算流体力学基本方程流体的运动可以通过连续性方程和动量守恒方程来表达,假定流体为不可压缩流体,其连续性方程及动量守恒方程表达式为:
连续性方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0, $ | (1) |
式中:
动量方程(Navier-Stokes方程)
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{u_j}} \right){\rm{ }} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_i}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \overline {\rho u_i^\prime u_j^\prime } + \rho {g_i}} \right), $ | (2) |
式中:
湍流模型使用RNG k-ε湍流模型,其耗散率中的ε为:
| $ \varepsilon {\rm{ = }}\frac{\mu }{\rho }\overline {\left( {\frac{{\partial u_i'}}{{\partial {x_k}}}} \right)\left( {\frac{{\partial u_i'}}{{\partial {x_k}}}} \right)}, $ | (3) |
式中:
| $ {u_i} = \rho {C_\mu }\frac{{{\kappa ^2}}}{\varepsilon }\text{。} $ | (4) |
式中:
| $\begin{split} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] +\\ &{G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k}\end{split}, $ | (5) |
| $\begin{split} \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = &\frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{\sigma \varepsilon }}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] +\\ &({G_k} + {C_{3\varepsilon }}{G_b}) - {C_{2\sigma }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon }\end{split}\text{。} $ | (6) |
为使模拟接近真实海况,在进行CFD模拟造波时选用Stokes五阶波作为波面造波,它的速度势为:
| $ \varphi = \frac{L}{{kT}}\sum\limits_{n = 1}^5 {{\varphi _n}ch(nks)\sin (n\theta )}\text{。} $ | (7) |
式中:L为波长;k为波数;T为波浪周期;s为自由面至底部距离;
浮式防波堤的透射系数Kr可以直观反映浮式防波堤的消波性能,是浮式防波堤最重要的指标之一。其表达式为:
| $ {K_r} = \frac{{{H_t}}}{{{H_i}}}\text{。} $ | (8) |
式中:Ht表示堤后的透射波高;Hi表示入射波高。
数值计算时在腔体内部与堤后一个波长(L)距离处插入数值浪高仪监测腔体内部波高与堤后透射波高,由于消波区域设置足够大,可以忽略水槽尾部反射波的影响,直接使用Origin软件对计算数据进行拟合。
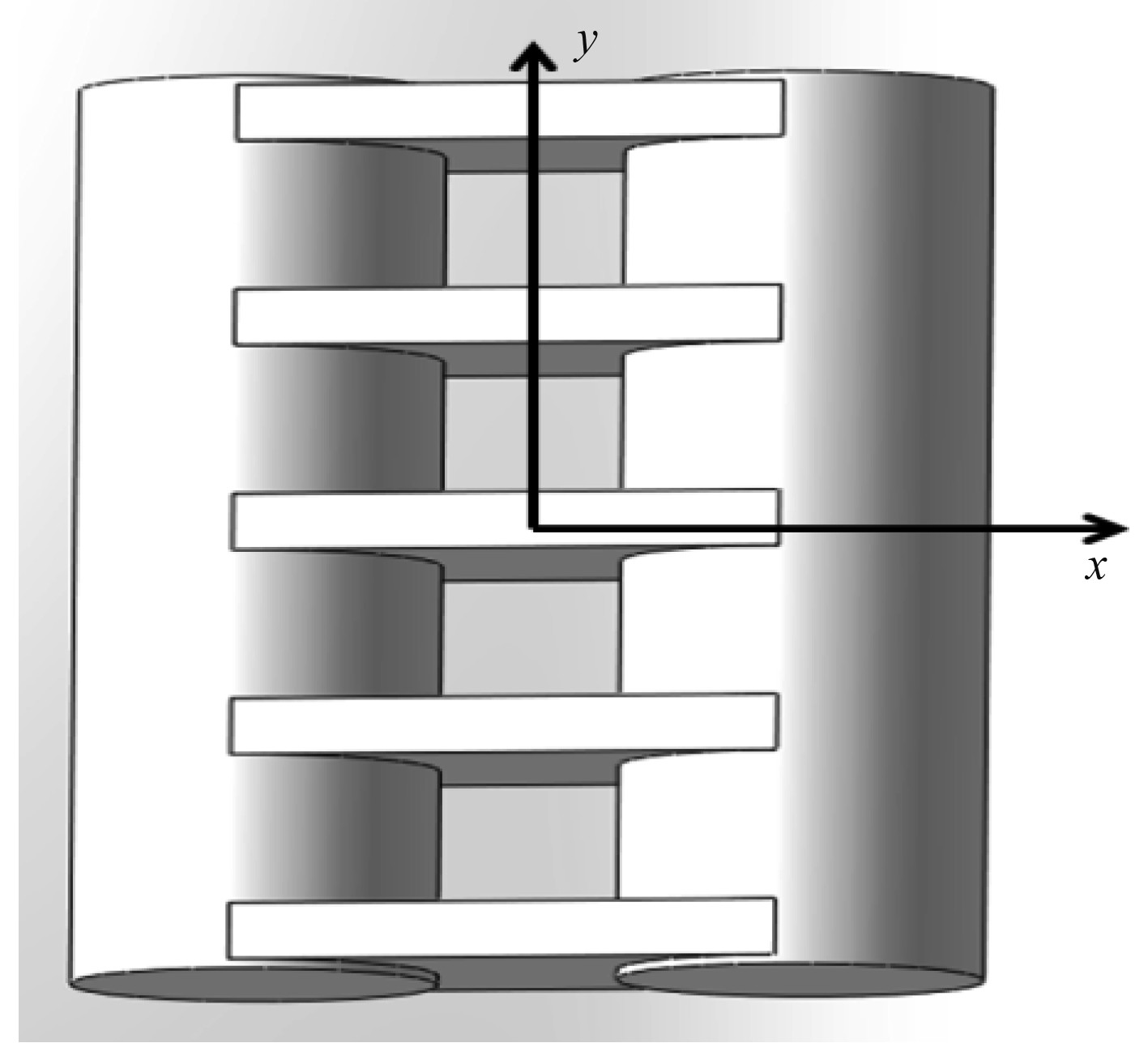
2 浮式防波堤水动力响应数值算例 2.1 浮式防波堤数值算例基本参数选取二维水槽中开展模型试验的浮式防波堤作为数值计算算例模型,该浮式防波堤为双圆筒型,双圆筒之间由连接舱连接,并将双圆筒中间区域分隔为4个局部开口腔室结构,其数值模型与坐标定义如图1所示,定义来流方向为X轴方向,浮筒轴向为Y轴方向。其主尺度如表1所示。
|
图 1 数值模型 Fig. 1 Numerical model |
|
|
表 1 浮式防波堤主尺度表 Tab.1 Principal scale table of floating breakwater |
计算域边界选用速度入口与压力出口边界,水深设置40 m。采用欧拉两相流模型模拟气态与液态流体。自由液面通过VOF法追踪。压力出口边界设置阻尼消波,消波长度为2个波长(L)距离。计算域设置如图2所示。

|
图 2 数值水槽 Fig. 2 Numerical pool |
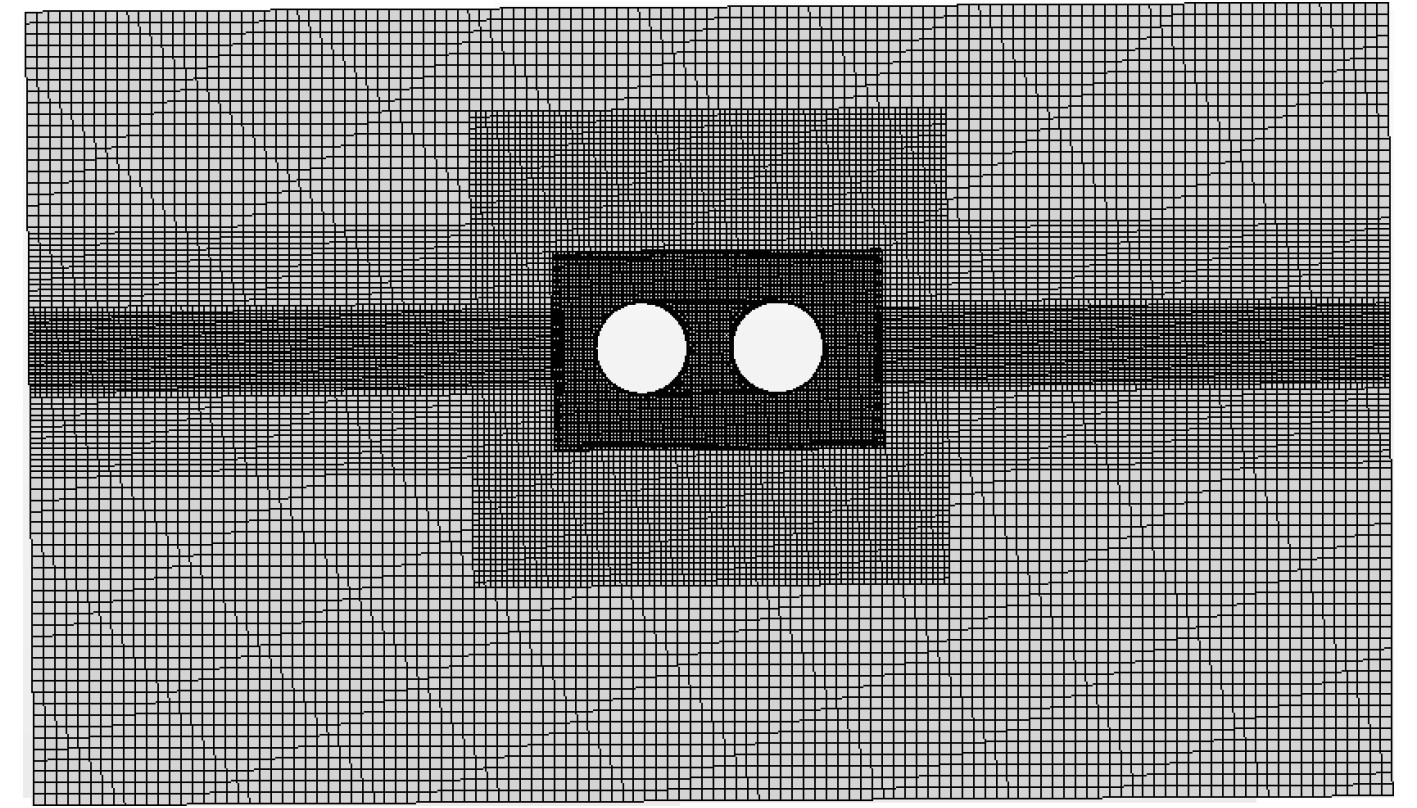
网格基础值设置为0.5 m。将浮式防波堤置于计算域坐标原点,使用重叠网格技术对浮体周围网格进行处理。背景网格内运动区域网格大小为0.5 m,网格向外部逐渐增大至400%的网格基础值。对波浪波动区域进行加密,波动区域内最密集一层网格量随环境改变,保证一个波长(L)80个网格分辨率,一个波高(Hi)20个网格分辨率。网格模型如图3所示。
|
图 3 流域局部网格图 Fig. 3 Grid diagram |
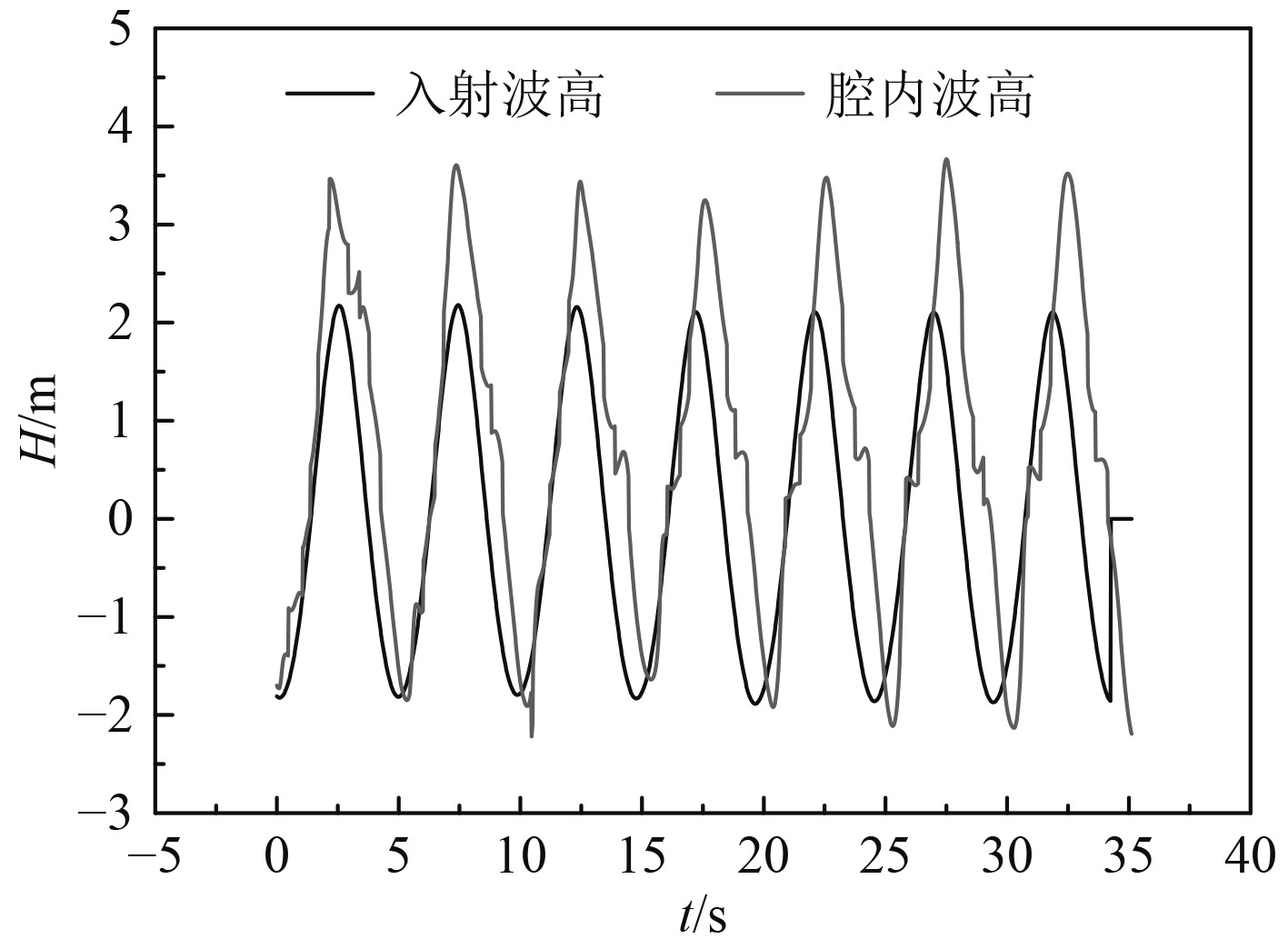
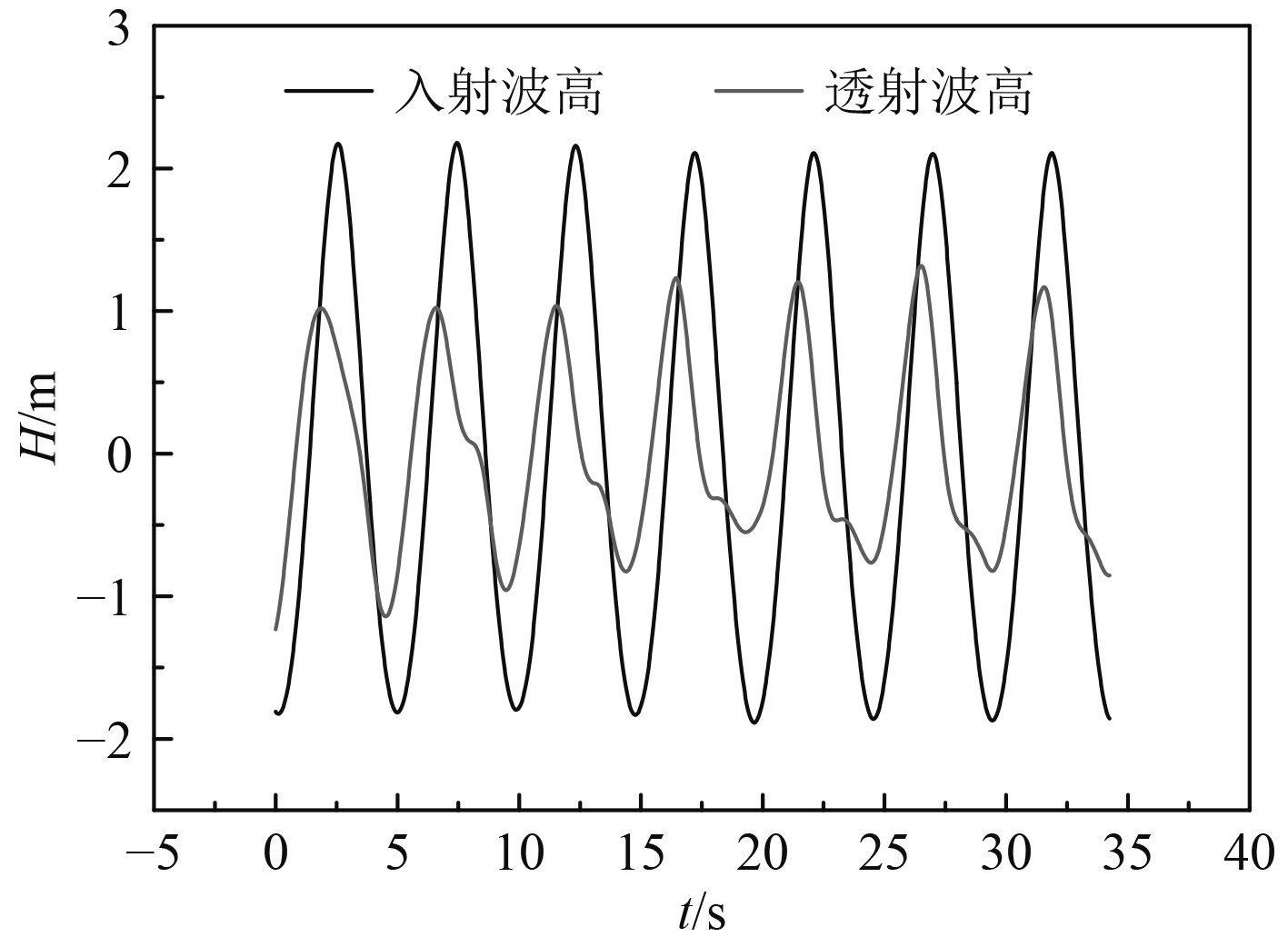
选取Hi=4 m,T=5.1 s工况为例进行数值计算,图4给出了腔体内部波高与入射波高的时历曲线对比,此时浮式防波堤腔体内部波高约为5.32 m,波高增幅约为入射波的33%。图5给出了Hi=4m,T=5.1 s工况时,浮式防波堤堤后透射波高与入射波高的时历曲线对比,此时堤后透射波高约为1.84 m,其透射系数为0.46。上述数值计算结果表明,基于CFD技术,可以实现对局部有开口的浮式防波堤内外流场的数值计算并获得波浪的透射性能。
|
图 4 腔内波高时历对比图 Fig. 4 Time comparison of wave height in cavity |
|
图 5 透射波高时历对比图 Fig. 5 Time comparison of transmitted wave height |
试验模型选用

|
图 6 试验模型 Fig. 6 Experimental model |
|
|
表 2 浮式防波堤模型主尺度表 Tab.2 Principal scale table of floating breakwater |

|
图 7 试验中腔内波浪振荡现象 Fig. 7 Wave resonance in cavity |
实验室波浪水槽长40 m,宽0.8 m,最大水深1 m。本文选取试验中发生了明显腔内波浪振荡现象的工况进行数值计算,并与试验中结果进行对比分析,工况设置如表3所示。
|
|
表 3 数值与试验对比工况表 Tab.3 Worktable of comprison between number and test |
考虑不同周期要素影响下腔室内部波高与消波效果的变化,并将计算值与试验值共同绘制于图8。图8(a)中横坐标为无因次周期L/h,其中L为入射波长,h为水深;纵坐标为腔体内部无因次波高Hj/Hi;图8(b)中横坐标为无因次周期L/h,纵坐标为透射系数Kr

|
图 8 试验结果与数值结果对比 Fig. 8 Comparison between test results and numerical results |
由图8可以看出,腔内无因次波高计算值与试验值具有相同的变化趋势,随着周期增大,腔内波浪振荡幅值减小。透射系数计算值与试验值变化趋势一致,随着周期增大,透射系数随之增大。试验值与计算值的平均误差约为14%,这是由于数值计算基于线性波理论,未考虑波浪的喷涌与翻卷等非线性作用。图8中试验值与计算值吻合良好,误差较小,证明了本文数值计算方法的准确性。
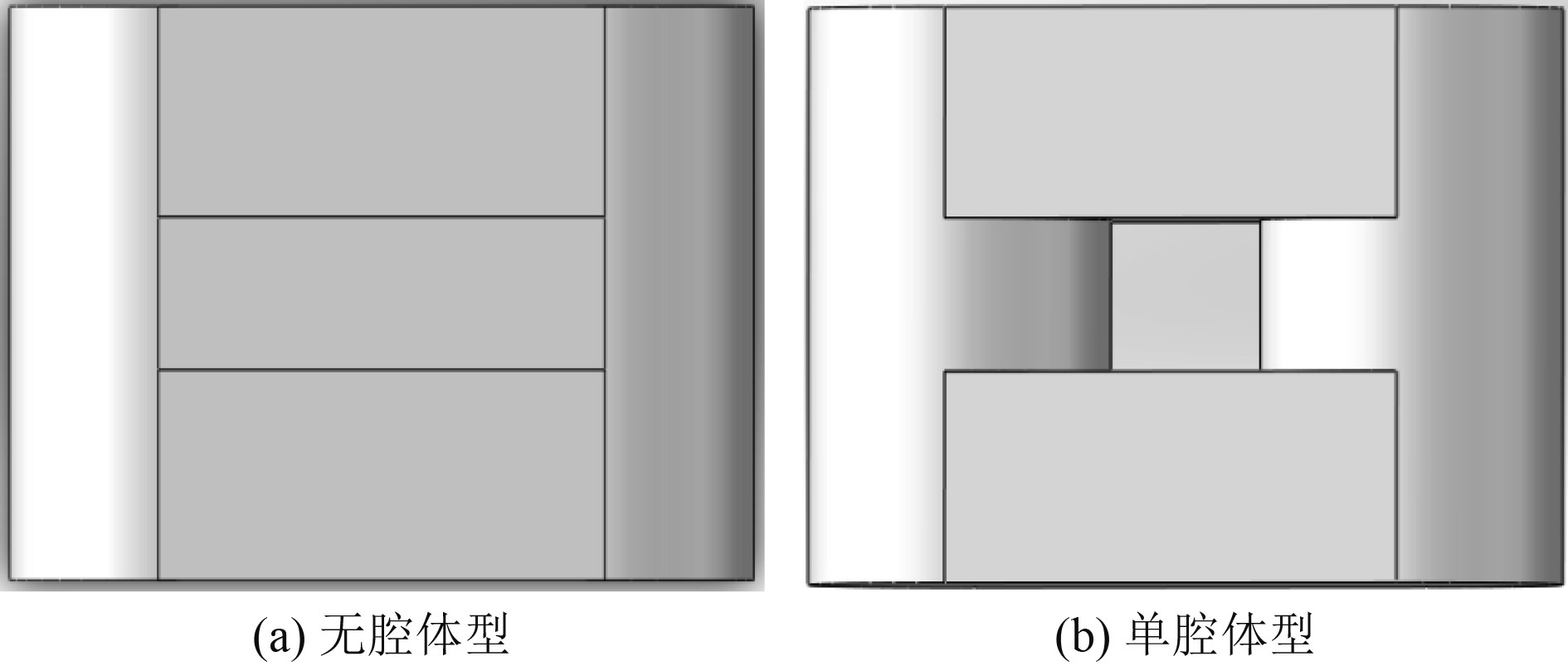
4 局部波浪振荡规律与消波性能数值分析 4.1 局部波浪振荡对消波效果的影响分析 4.1.1 数值模型设计本文设计了2种浮式防波堤模型用以验证浮式防波堤腔体内部波浪振荡对其消波性能的影响。如图9所示,2种模型分别为无腔体型浮式防波堤与单腔体型浮式防波堤。其中,无腔体型为单腔体型上下开口处加隔板构成。2种模型均为圆筒形浮式防波堤,其主尺度相关参数见表4所示。
|
图 9 浮式防波堤模型 Fig. 9 Floating Breakwater model |
|
|
表 4 浮式防波堤主尺度 Tab.4 Main dimensions of floating breakwater |
考虑不同入射周期和不同入射波高的影响,入射周期分为T=4 s,T=4.5 s,T=5 s,T=5.5 s,T=6 s,T=6.5 s,T=7 s;入射波高分为Hi=2 m,Hi=2.5 m,Hi=3 m。结果如图10所示,腔内无因次波高随周期先增大后减小,在入射周期T=6 s时与模型垂荡共振周期相近,此时腔内出现大幅波浪共振现象,无因次波高出现极值点。当入射周期小于此共振周期时,腔内无因次波高随周期增大而单调递增,当入射周期大于共振周期时,腔内无因次波高随周期增大而单调递减。入射周期远离此共振周期时,入射波高对腔内无因次波高的影响较小;当入射周期接近共振周期,随着波高增大,腔内无因次波高下降明显,这是由于浮式防波堤对大波幅入射波具有较强的反射作用。

|
图 10 不同工况腔内波浪振荡 Fig. 10 Wave oscillation in cavity under different working conditions |
图11给出了单腔体型浮式防波堤与无腔体型浮式防波堤消波性能对比图。其中图11(a)固定入射波高Hi=2 m,考虑入射周期的影响。结果表明,随着周期增大,2种模型透射系数均呈现增大趋势。在T=6 s时,单腔体模型透射系数出现极值,这是由于入射周期接近模型共振周期,模型运动增大,消波效果变差。单腔体模型消波效果总体优于无腔体模型,仅在入射周期T=6 s时二者的消波效果差别不大。

|
图 11 消波性能对比 Fig. 11 Comparison of wave attenuation performance |
图11(b)固定入射周期T=5 s,考虑入射波高的影响。结果表明,随着入射波高增大,2种模型消波性能均发生一定程度的恶化。可以看出,单腔体模型消波效果总体优于无腔体模型,且在较大波高工况时,优势更为明显。
总而言之,浮式防波堤腔内波浪振荡对其消波效果具有优化作用,优化效果与腔体模型有关,但当腔内发生大幅波浪共振时,其消波性能急剧降低。
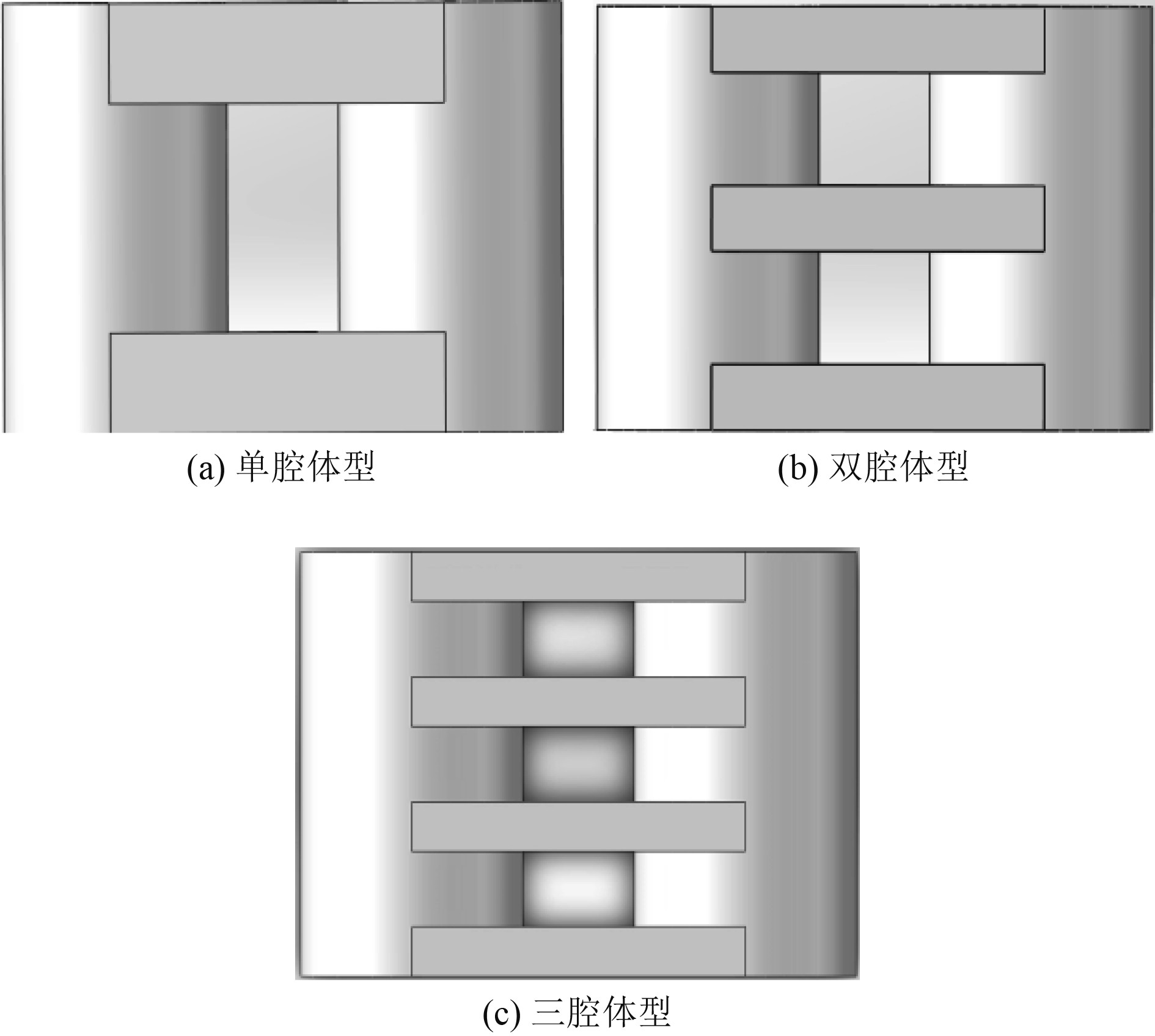
4.2 不同腔体数量对消波效果的影响分析 4.2.1 数值模型设计本文设计了3种浮式防波堤模型,对其腔室内部波高与堤后透射波高进行监测分析。数值模型如图12所示,腔体开口总尺度保持不变,根据腔体开口个数浮式防波堤模型分别为单腔体型、双腔体型和三腔体型。各模型堤长与堤宽相同,分别为15 m和20 m,浮筒直径均为8 m,双浮筒间距均为4 m。其他主尺度如表5所示。
|
图 12 不同腔体个数模型 Fig. 12 The model of different number of cavities |
|
|
表 5 主尺度表 Tab.5 Principal scale table |
表6给出了数值计算工况表,考虑同一入射周期,不同入射波高,计算分析不同模型腔内波浪振荡与透射系数的变化规律。
|
|
表 6 工况表 Tab.6 Worktable |
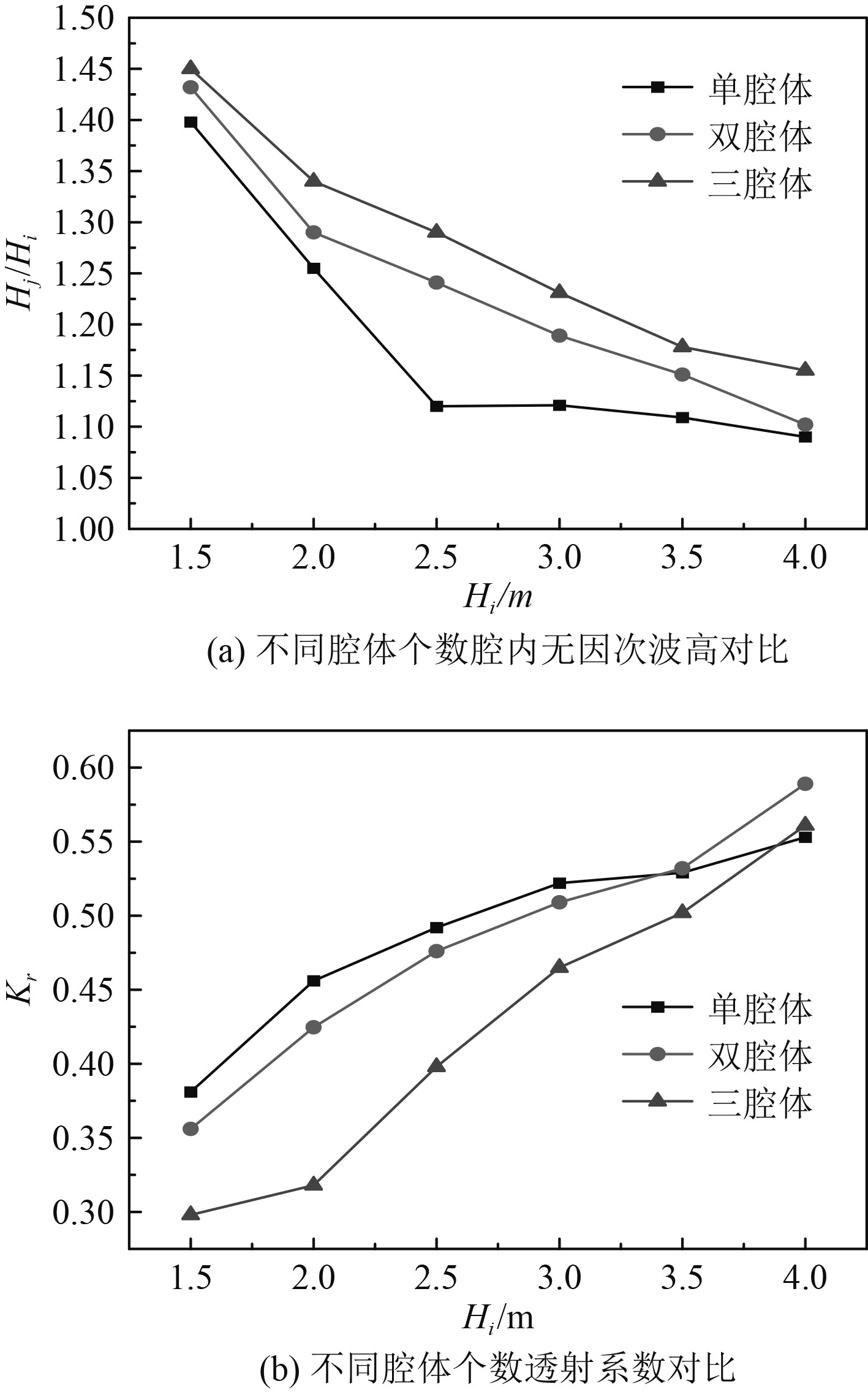
图13给出了腔内无因次波高与透射系数随波高要素的计算结果。固定入射周期T=5 s,随着入射波高的增大,3种腔体模型腔内无因次波高均呈现减小趋势,透射系数均呈现增大趋势,这一结果与上文吻合。在腔体开口总尺度不变的情况下,随着腔体个数增多,腔内无因次波高上升,透射系数减小。结果表明,浮式防波堤腔内波浪振荡与透射系数在数值上具有相关性,并呈现反比趋势;相同外部条件下,腔内波浪振荡越明显,则透射系数越小,防浪消波性能越好。综上所述,适当增加腔体个数是提高浮式防波堤消波效果的有效手段。
|
图 13 不同腔体个数数值结果 Fig. 13 Numerical results of different number of cavities |
本文基于二维数值水槽相关理论对局部波浪振荡与浮式防波堤消波性能的关系进行计算分析。通过数值计算与试验结果比对,验证数值计算的准确性;利用数值计算方法分析了不同工况下腔内波浪振荡规律以及腔内波浪振荡对浮式防波堤消波性能的影响,并探讨了不同腔体模型对腔内无因次波高和消波性能的影响。结论如下:
1)腔内波浪振荡与入射周期和入射波高均有关系。随着周期增大,腔内无因次波高先增大后减小。当入射周期接近浮体共振周期时,腔内波浪振幅激增,浮式防波堤发生局部波浪共振现象,此时,入射波高对腔内无因次波高影响显著,随着入射波高的增大,腔内无因次波高下降明显。
2)对比分析单腔体模型和无腔体模型的消波性能发现,单腔体模型消波效果总体优于无腔体模型,仅在入射周期接近单腔体模型固有振动周期时,二者消波效果差别较小。腔内波浪振荡对浮式防波堤消波具有促进作用,但当腔内发生大幅波浪共振时,消波效果较差。
3)腔体开口个数对腔内波浪振荡和消波性能均有影响。在本文模型数据范围内,随着腔体个数增多,腔内波浪振荡增强,消波性能提升。浮式防波堤腔内无因次波高与透射系数在数值上呈现负相关性,相同外部条件下,腔内波浪振荡越明显,则透射系数越小。
| [1] |
CHUN-YAN JI, KE Y, YONG C, et al. Numerical and experimental investigation of interactions between free-surface waves and a floating breakwater with cylindrical-dual/rectangular-single pontoon[J]. 中国海洋工程(英文版), 2018. |
| [2] |
陈力. 浮式防波堤的试验研究[D]. 上海: 上海交通大学, 2008.
|
| [3] |
沈雨生, 周益人, 潘军宁, 等. 浮式防波堤研究进展[J]. 水利水运工程学报, 2016(5): 124-132. |
| [4] |
FALTINSEN OM. Sea loads on ships and offshore structures[M]. Cambridge: Cambridge University Press, 1990.
|
| [5] |
BARREIRA R, SPHAIER S H, MASETTI I Q. Behavior of a mono-column structure (monobr) in waves[C]//In: Proceedings of 24th International Conference on Offshore Mechanics and Arctic Engineering. New York: American Society of Mechanical Engineers, 2005: 867−873.
|
| [6] |
ZHOU Huawei, ZHANG Hongsheng. Radiation and diffraction analysis of a cylindrical body with a moon pool[J]. Journal of Hydrodynamics, 2013, 25(2): 196-204. DOI:10.1016/S1001-6058(13)60354-6 |
| [7] |
刘利琴, 邱雨, 张永恒, 等. Spar平台垂荡-纵摇与月池内流体垂向振动的耦合运动研究[J]. 振动与冲击, 2016, 35(19): 113-118. |
| [8] |
邹康, 桂满海, 罗良. 月池水动力特性及其对船舶运动的影响研究[J]. 船舶与海洋工程, 2017(5). |
| [9] |
康庄. 月池流噪声及水动力特性的试验研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [10] |
王鑫, 刘亚东. 船体垂荡运动及环境波高对月池内流体的影响[J]. 船舶工程, 2019(5).
|
| [11] |
姜胜超, 宗智, 邹丽. 波浪对并联双箱作用的耦合水动力共振分析[J]. 海洋工程装备与技术, 2017(3). DOI:10.3969/j.issn.2095-7297.2017.03.012 |
| [12] |
刘春阳. 波浪作用下双浮体系统水动力特性的实验和数值研究[D]. 大连: 大连理工大学.
|
| [13] |
苏绍娟, 王有志, 王天霖, 等. 数值波浪水槽波浪传递性能研究[J]. 舰船科学技术, 2020, 42(9): 61-65. DOI:10.3404/j.issn.1672-7649.2020.09.011 |
 2021, Vol. 43
2021, Vol. 43
