2. 海军航空大学,山东 青岛 266000
2. Naval Aviation University, Qingdao 266000, China
航迹规划[1]是USV研究领域中最主要的研究方向之一。USV航迹规划指规划出一条安全快速到达目标位置的路径。
航迹规划主要研究避障问题。目前,传统的航迹规划算法有模拟退火算法[2]、禁忌搜索算法[3]、A*算法[4]、人工视场法[5-6]等。随着智能仿生学算法的发展和应用,逐渐将遗传算法[7]、粒子群算法[8]以及蚁群算法[9]等用于航迹规划。其中,A*算法具有较强的全局搜索能力,在低密度避障环境中能够快速高效地规划出到达目标点的合理路径,但当避障环境密度较高时,A*算法容易陷入局部死区。蚁群算法具有较强的鲁棒性,在高密度环境下亦能找到合理路径,但其收敛速度较慢。因此本文将水面环境进行分割,在高密度环境中设置过度目标点,在低密度环境下采用A*算法进行航路规划,当目标到达过度目标点,则采用蚁群算法进行搜索规划航路。从而提高了USV全局和局部航路规划能力。
1 航行环境模型栅格(grid)法[1],即用编码的栅格来表示地图,把包含障碍物的栅格标记为障碍栅格,反之则为自由栅格,以此为基础作路径搜索。栅格法是目前研究最为广泛的空间规划方法。构建路径规划环境,令障碍物的栅格状态为1,自由栅格状态为0。环境矩阵为:
| ${\rm{Environment}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&1&1&1 \\ 0&0&0&0&0&0&0&1&1&1 \\ 0&0&0&0&0&0&0&0&1&1 \\ 0&0&0&0&1&1&0&0&0&0 \\ 0&0&0&0&1&1&0&0&0&0 \\ 0&0&0&0&0&0&0&1&1&1 \\ 0&0&0&0&0&0&0&1&1&1 \\ 0&0&1&1&0&0&0&0&0&0 \\ 1&1&1&1&0&0&0&0&0&0 \\ 1&1&1&1&0&0&0&0&0&0 \end{array}} \right]\text{。}$ |
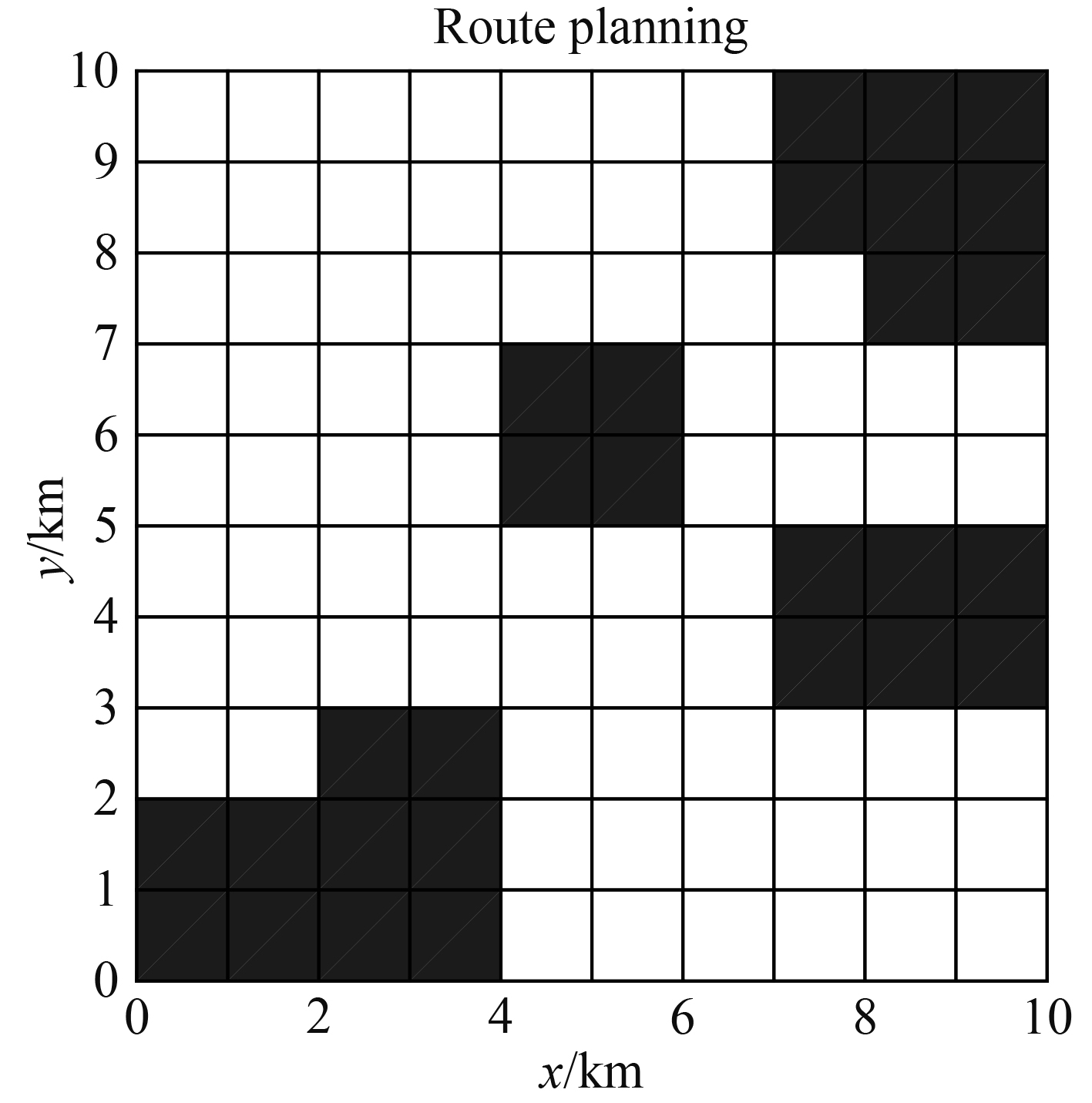
模拟空间环境如图1所示。
|
图 1 模拟的空间环境 Fig. 1 Simulated space environment |
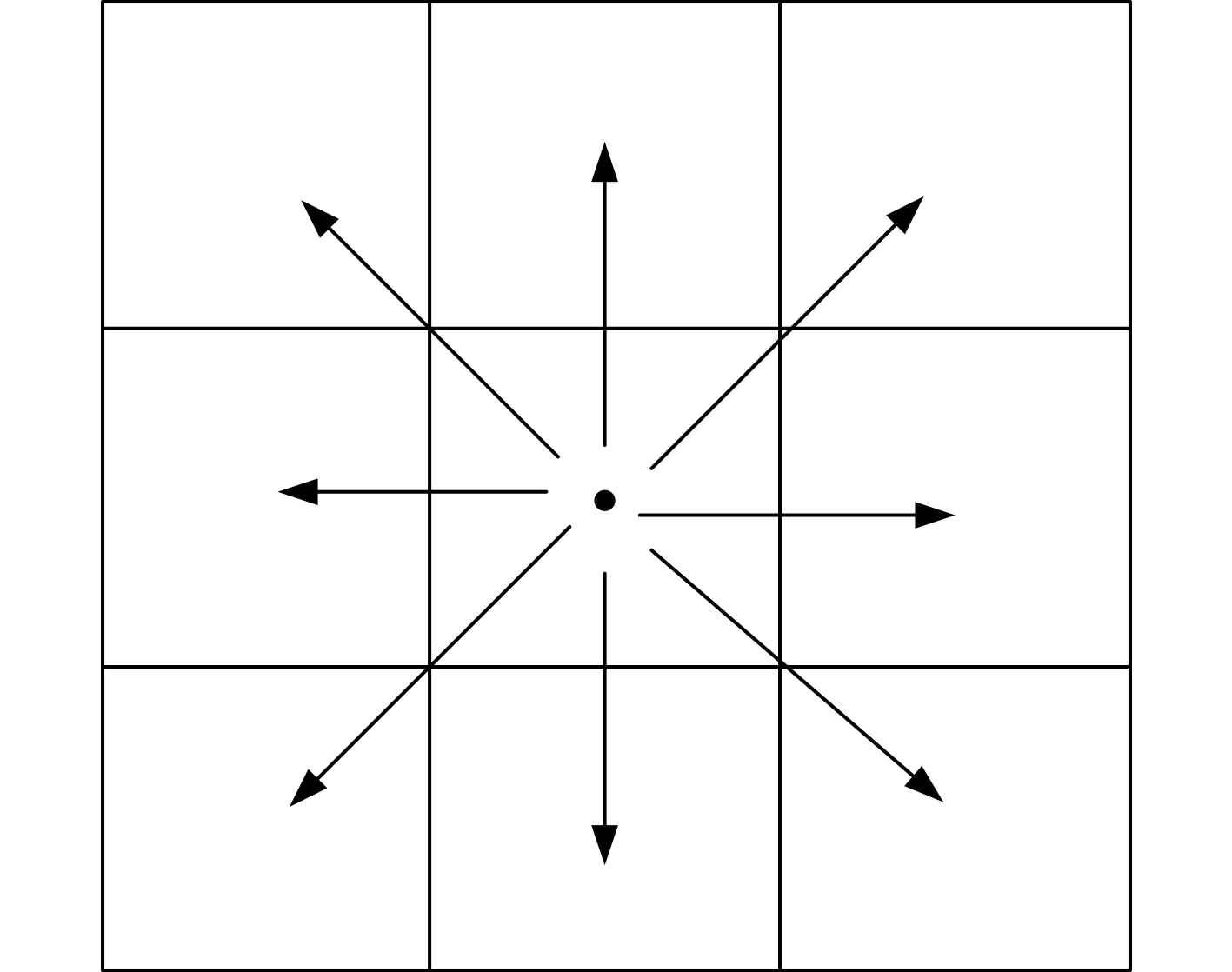
无人航行器节点的位置移动方式如图2所示。
|
图 2 位置移动模式 Fig. 2 Position movement mode |
A*算法[4]的估价函数为:
| $f(n) = g(n,s) + h(n,e) \text{。}$ | (1) |
式中:
| $g(n,s){\rm{ = }}\sum\limits_{i = 2}^n {\sqrt {{{({x_i} - {x_{i - 1}})}^2} + {{({y_i} - {y_{i - 1}})}^2}} }, $ | (2) |
| $h(n,e){\rm{ = }}\sqrt {{{({x_e} - {x_n})}^2} + {{({y_e} - {y_n})}^2}} \text{。} $ | (3) |
在传统的蚁群算法[10-11]中,当所有蚂蚁完成一次迭代后,对路径上
| $ {\tau }_{ij}(t+n)=(1-\rho )\cdot {\tau }_{ij}(t)+\Delta {\tau }_{ij}(t),$ | (4) |
| $\Delta {\tau _{ij}}(t){\rm{ = }}\sum\limits_{k = 1}^m {\Delta \tau _{_{ij}}^k} (t),$ | (5) |
| $\Delta \tau _{_{ij}}^k(t) = Q/{L_k} \text{。}$ | (6) |
式中:
为增强蚁群算法的快速性和有效性,本次改进了信息素的更新模型,增强了可行路径中最优路径的信息浓度,减弱了最差路径的信息浓度,并通过调整信息素浓度总和比例,增强算法的寻优能力。
| $ {\tau }_{ij}(t+n)=(1-\rho )\cdot {\tau }_{ij}(t)+\rho \Delta {\tau }_{ij}(t),$ | (7) |
| $\Delta \tau _{_{ij}}^k(t) = Q/{L_k}{\rm{ + }}Q/{L_{\min }}{\rm{ - }}Q/{L_{\max }} \text{。}$ | (8) |
式中:
USV的航路规划分为全局规划和局部规划。算法首先利用A*算法进行全局规划,当遇到高密度环境,则采用蚁群算法,通过蚁群信息素搜索原理,进行障碍的规避。
根据环境栅格图的特点在高密度局部图中设置过渡节点,过渡节点的总代价函数要小于USV所处节点的代价。目标先采用A*算法朝向目标节点进行全局规划,到达过渡节点时采用蚁群搜索算法进行局部规划。在USV的全局航行过程中,不断采用蚁群算法进行局部高密度避障在,可有效地提高航行器在复杂环境中的航路规划能力,避免陷入局部死锁。算法流程如图3所示。

|
图 3 改进的A*-蚂蚁混合算法流程图 Fig. 3 Flow chart of improved A * - ant hybrid algorithm |
为了验证本文所提改进型A*-蚁群混合算法的有效性和优势性,进行仿真实验比较。
3.1 低密度简单环境下的仿真比较分析本仿真试验选取22 km×22 km的正方形水域,采用栅格法划分该区域为22×22的网格,各网格表示1 km×1 km区域。黑色表示障碍物区或禁航区,白色表示自由航行区。分别采用传统A*算法、蚁群算法、改进型蚁群算法、改进型A*-蚁群混合算法进行航路规划。蚁群规模为M=50,最大迭代次数为N=100;信息素重要程度因子
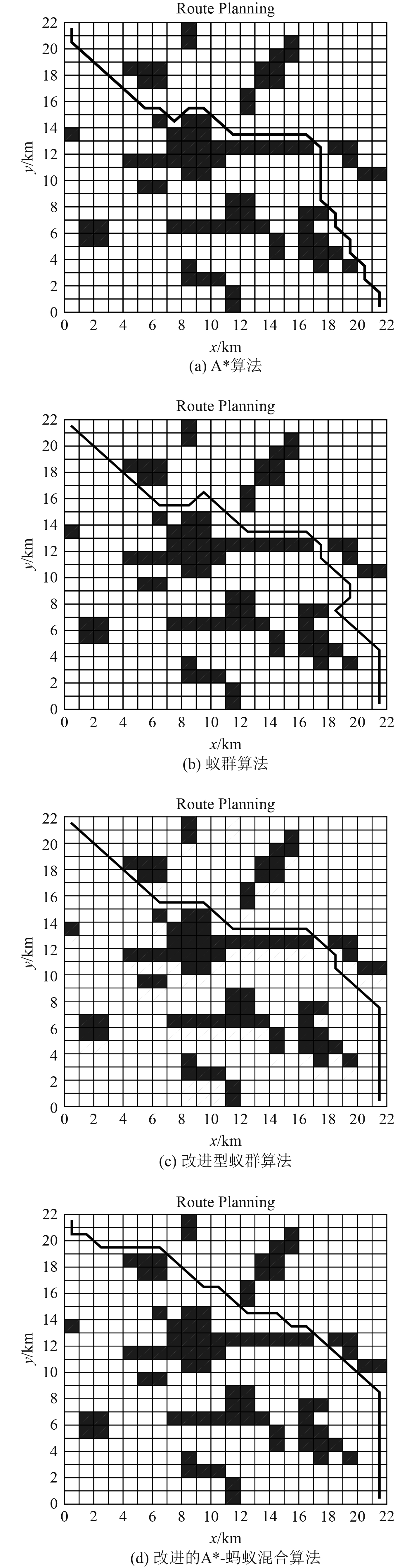
|
图 4 四种算法的仿真结果 Fig. 4 Simulation results of four algorithms |
|
|
表 1 四种算法的数据统计 Tab.1 Data statistics of four algorithms |
根据图4和表1比较分析,4种方法的路径长度比较为改进型蚁群算法<本文算法<A*<传统蚁群算法,运行时间比较A*<本文算法<改进型蚁群算法<传统蚁群算法。A*算法的运算时间是最快的,而改进型蚁群算法路径规划最优,但本文算法路径规划长度相近。由此可知,在低密度、小规模的环境下,A*算法可以快速进行路径规划,得到合理的优化路径。此外,在运算时间基本相同的情况下,改进型蚁群算法路径规划优于传统蚁群算法。而本文提出了一种改进的A*-蚂蚁混合算法,其路径规划长度接近于改进型蚁群算法,但运算时间较短。综上所述,本文提出的算法在低密度、小规模环境下的运行时间比A*算法要长,且路径规划的优势不明显,但本文提出的算法比传统的和改进的蚂蚁混合算法要好,证明了算法的有效性。
3.2 高密度复杂环境下仿真比较分析为了进一步证明该算法的优越性和有效性。选取面积为45 km×45 km的正方形水域,采用栅格法将面积划分为45×45个网格,每个网格代表1 km×1 km的面积。分别采用传统A*算法、蚁群算法、改进型蚁群算法、改进型A*-蚁群混合算法进行航路规划。仿真参数不变,增加了障碍的复杂性。仿真结果如图5所示。
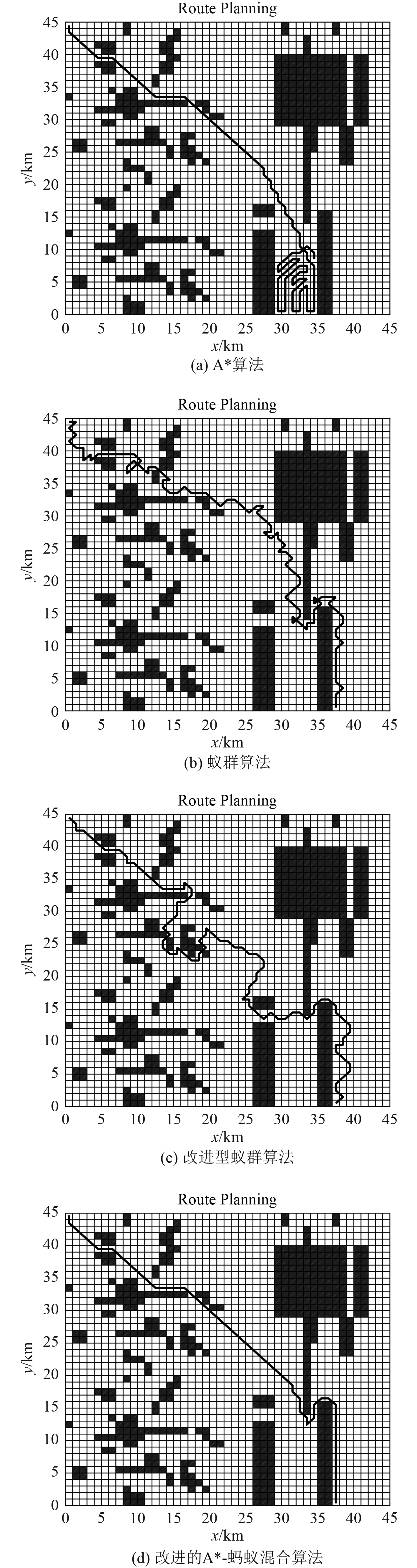
|
图 5 四种算法的仿真结果 Fig. 5 Simulation results of four algorithms |
|
|
表 2 四种算法的数据统计 Tab.2 Data statistics of four algorithms |
根据图5和表2的比较分析,4种方法的路径长度比较为:本文算法<改进型蚁群算法<传统蚁群算法<A*,这里路径长度越短表示路径规划越优。运行时间比较为:本文算法<改进型蚁群算法<传统蚁群算法。A*算法陷入死区,则认为路径规划失败,而本文算法路径规划最优,且运行时间最短,路径规划效率高。改进的蚁群算法在运行时间和路径质量上都优于传统算法。由此可知,在高密度和复杂环境下,本文算法在路径规划效率上明显优于其他算法,大大提高了路径规划能力,有效地证明了该算法的有效性和优越性。
仿真结果表明,A*算法在低密度、小规模环境下具有较强的路径规划能力和较短的运行时间。然而,在高密度、复杂的环境中,A*算法容易陷入死区。与传统蚁群算法和A*算法相比,本文提出的算法大大提高了路径规划的质量和效率,能够快速有效地完成OSV的路径规划。
4 结 语针对高密度复杂环境下的无人水面航行器(USV)航迹规划问题,本算法有效地增强USV航迹规划能力,解决了传统蚁群算法和A*算法各自使用不能兼顾全局和局部规划的问题。通过仿真比较分析,本算法能够有效地平衡全局和局部规划,提高在复杂环境下的USV航迹规划能力。本文方法将为USV大规模复杂的环境任务提供研究依据。
| [1] |
邱晨, 周海峰, 王荣杰, 等. 改进蚁群的无人求生船航迹规划[J]. 集美大学学报 (自然科学版), 2019, 24(5): 358-363. |
| [2] |
陶重犇, 雷祝兵, 李春光, 等. 基于改进模拟退火算法的搬运机器人路径规划[J]. 计算机测量与控制, 2018, 26(7): 182-185. |
| [3] |
KARIM B, ZHU Q. A fuzzy logic behavior architecture controller for a mobile robot path planning in multi-obstacles environment[J]. Research Journal of Applied Sciences Engineering & Technology. 2013, 5(14), 38353842. |
| [4] |
BING F, LIN C, ZHOU Y, et al. An improved A* algorithm for the industrial robot path planning with high success rate and short length[J]. Robotics and Autonomous Systems, 2018, 106: 26-37. DOI:10.1016/j.robot.2018.04.007 |
| [5] |
ZHANG T, ZHU Y, SONG J. Real-time motion planning for mobile robots by means of artificial potential field method in unknown environment[J]. Industrial Robot, 2013, 37(4): 384-400. |
| [6] |
刘砚菊; 代涛; 宋建辉. 改进人工势场法的路径规划算法研究[J]. 沈阳理工大学学报, 2017(1): 61-65. DOI:10.3969/j.issn.1003-1251.2017.01.015 |
| [7] |
XU X, LIANG R S, YANG H Z. Path planning for agent based on improved genetic algorithm[J]. Computer Simulation, 2014, 31(6): 357-361. |
| [8] |
DUAN H, QIAO P. Pigeon-inspired optimization: a new swarm intelligence optimizer for air robot path planning[J]. International Journal of Intelligent Computing and Cybernetics, 2014, 7(1): 24-37. DOI:10.1108/IJICC-02-2014-0005 |
| [9] |
ZHAO Q, ZHEN Z, CHEN G, et al. Path planning of UAVs formation based on improved ant colony optimization algorithm[C]//Proceedings of IEEE Conference on Guidance, Navigation and Control, 2015: 1549−1552.
|
| [10] |
康冰; 王曦辉; 刘富. 基于改进蚁群算法的搜索机器人路径规划[J]. 吉林大学学报(工学版), 2014, 44(4): 1062-1068. |
| [11] |
刘洋, 章卫国, 李广文, 等. 一种三维环境中的无人机多路径规划方法[J]. 西北工业大学学报, 2014, 32(3): 412-416. DOI:10.3969/j.issn.1000-2758.2014.03.016 |
 2021, Vol. 43
2021, Vol. 43
