极区是地球球体的两端,临近地理极的区域,是地理纬度最高的区域。随着世界各大国间经济互通、航运交往的频繁,跨越极区的航路越来越受到重视,极区的军事、经济、自然资源等战略意义及重要性越发凸显。目前,各国在极区的科研活动都在加强。
极区内水下对准及导航技术的研究,可使水下航行器具备全球导航能力,为实现极区内经济和军事战略提供理论支撑和技术储备。因此有必要开展水下航行器在极区内的导航及对准技术研究与关键技术探索,深入研究适应极区环境的对准和导航策略。
水下航行器主要采用惯性导航。针对水下航行器惯性导航系统在极地的使用,存在的问题主要有以下几点[1-6]:
1)航向角定义失效
在水下航行器导航计算中,通常采用的是地理坐标系实现在地球表面的导航。根据航向角定义,航行器纵轴水平面投影与北向的夹角为航向角,而在极地附近,原本是一条指向线的“北向”变成一个点,航向角失去定义。
2)经典惯性导航力学编排失效问题
在经典惯性导航力学编排中,存在对地球自转角速率的跟踪指令。在高纬度地区,天向指令将趋于无效。这与传统的指北方位平台惯导力学编排在高纬度地区存在计算溢出和方位陀螺施矩困难的问题是一致的。
3)航向角无法提取
在极地附近,当航行器穿过极地附近(例如经度由0°直线驶向180°,10°驶向190°等),航向角速度未发生变换,而航向角却将发生180°跳变,惯导解算无法提取。
4)初始对准算法失效
与非极区相比,极区存在的经线收敛问题会导致常规的基于地理北向方向参考线的导航算法失效,与之相应的主惯导对子惯导系统的传递对准算法也将失效。必须通过分析其导航误差模型,建立适应极区内传递对准的卡尔曼滤波算法。
5)定位计算失效
在极地附近,由于地理纬度接近±90°,当有定位计算要求时,经度解算中存在除纬度余弦的算法,定位计算提取误差很大。
针对上述水下航行器极区导航存在的问题,本文提出一种利用格网坐标系直接获得格网航向,进而优化惯导系统导航性能的方法,研究格网惯性导航算法编排方案,以满足水下航行器在极区航行时的导航需要。同时,对格网惯性导航的误差进行建模,并据此设计格网导航系统的“速度匹配”传递对准算法,利用卡尔曼滤波器,实现对子惯导误差的估计和校正。
1 极区格网惯性导航编排 1.1 格网坐标系格网导航坐标系
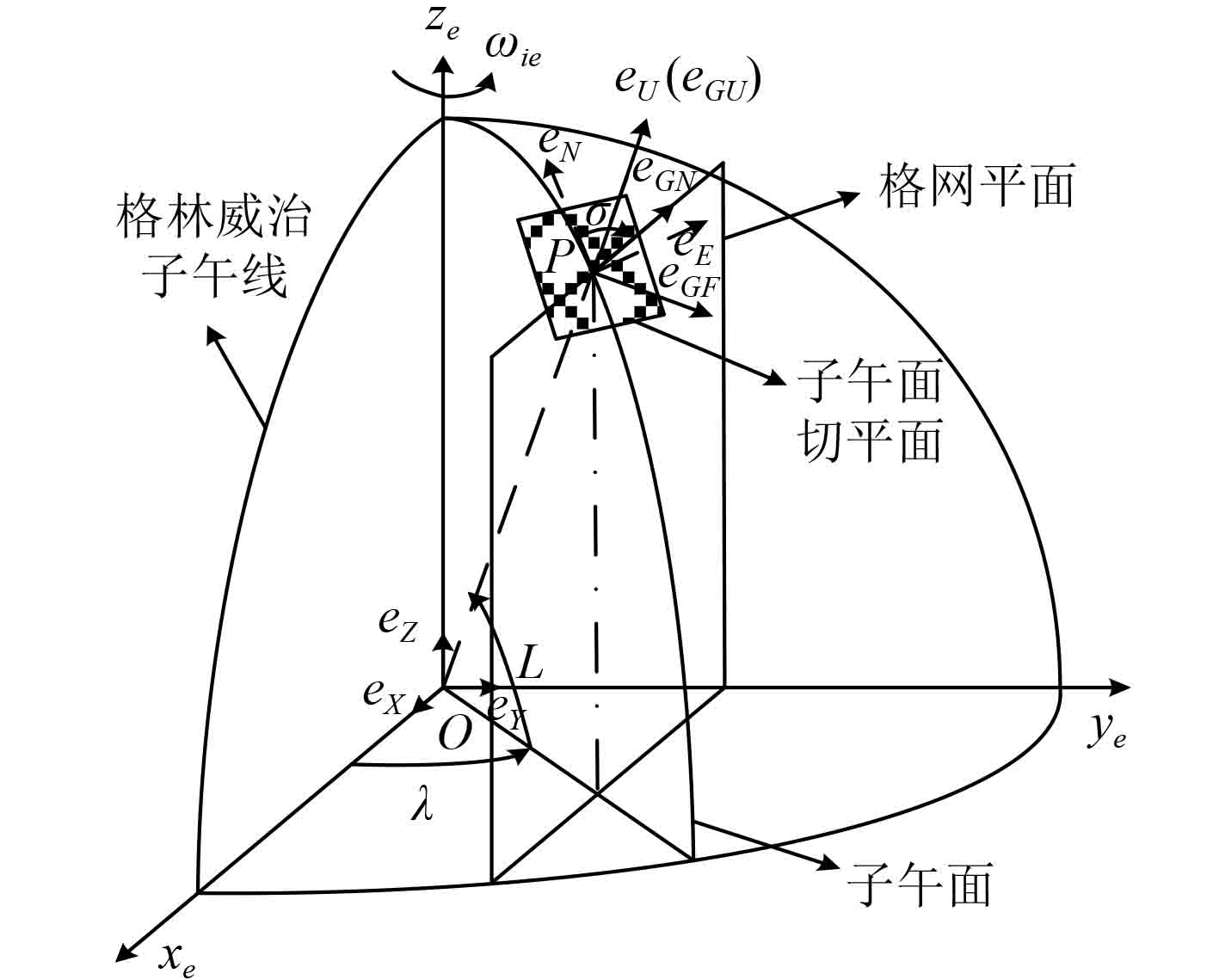
|
图 1 格网坐标系 Fig. 1 Grid coordinate system |
根据格网坐标系定义,地理和格网坐标系间的转换关系为:
| $\left[ {\begin{array}{*{20}{c}} {{e_G}_E} \\ {{e_G}_N} \\ {{e_G}_{\rm{U}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \sigma }&{ - \sin \sigma }&0 \\ {\sin \sigma }&{\cos \sigma }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{e_E}} \\ {{e_N}} \\ {{e_U}} \end{array}} \right],$ | (1) |
即由地理坐标系到格网坐标系的方向余弦矩阵为:
| ${\mathbf{C}}_g^G = \left[ {\begin{array}{*{20}{c}} {\cos \sigma }&{ - \sin \sigma }&0 \\ {\sin \sigma }&{\cos \sigma }&0 \\ 0&0&1 \end{array}} \right]\text{。}$ | (2) |
同样的,由地球坐标系到格网坐标系的方向余弦矩阵
| ${\mathbf{C}}_e^G = \left[ {\begin{array}{*{20}{c}} { - \cos \sigma \sin \lambda + \sin \sigma \cos \lambda \sin L} \\ { - \sin \sigma \sin \lambda - \cos \sigma \sin L\cos \lambda } \\ {\cos L\cos \lambda }\end{array}}\right.$ |
| $\left.{\begin{array}{*{20}{c}} {\cos \sigma \cos \lambda + \sin \sigma \sin \lambda \sin L}&{ - \sin \sigma \cos L} \\ {\sin \sigma \cos \lambda - \cos \sigma \sin L\sin \lambda }&{\cos \sigma \cos L} \\ {\cos L\sin \lambda }&{\sin L} \end{array}} \right]\text{。}$ | (3) |
由图1可以看出单位向量
| ${e_{{G_N}}} \cdot {e_Y} = 0,$ | (4) |
其中,单位向量
| ${e_{{G_N}}} = \sin \sigma {e_E} + \cos \sigma {e_N} + 0{e_U},$ | (5) |
| ${e_Y} = \cos \lambda {e_E} - \sin L\sin \lambda {e_N} + \cos L\sin \lambda {e_U}\text{。}$ | (6) |
由此可得:
| $\sin \sigma = \frac{{\sin \lambda \sin L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }},$ | (7) |
| $\cos \sigma = \frac{{\cos \lambda }}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}\text{。}$ | (8) |
将
| ${\mathbf{C}}_e^G =\left[ {\begin{array}{*{20}{c}} {\dfrac{{ - {{\cos }^2}L\sin \lambda \cos \lambda }}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}} \\ {\dfrac{{ - \sin L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}} \\ {\cos L\cos \lambda }\end{array}}\right.$ |
| $\left.{\begin{array}{*{20}{c}} {\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }&{\dfrac{{\sin \lambda \sin L\cos L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}} \\ 0&{\dfrac{{\cos L\cos \lambda }}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}} \\ {\cos L\sin \lambda }&{\sin L} \end{array}} \right]\text{。}$ | (9) |
格网导航坐标系内的惯导力学编排同游移方位惯导系统有许多相同的地方,在计算指令角速度的时候略有不同。选取格网坐标系
1)姿态更新微分方程
| ${{\dot C}}_b^G = {{C}}_b^G\Omega _{Gb}^b,$ | (10) |
| $\omega _{Gb}^b = \omega _{ib}^b - \omega _{iG}^b = \omega _{ib}^b - {\mathbf{C}}_G^b\omega _{iG}^G\text{。}$ | (11) |
其中,
| $C_b^G(0) = C_g^G(0)C_b^g(0)\text{。}$ | (12) |
位置速率
| $\omega _{eG}^G = \left[ {\begin{array}{*{20}{c}} {\omega _{eGx}^G} \\ {\omega _{eGy}^G} \\ {\omega _{eGz}^G} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{T_{{f_G}}}}}}{ - \dfrac{1}{{{R_{yG}}}}} \\ {\dfrac{1}{{{R_{xG}}}}}{ - \dfrac{1}{{{T_{fG}}}}} \\ {\dfrac{{{k_G}}}{{{T_{fG}}}}}{ - \dfrac{{{k_G}}}{{{R_{yG}}}}} \end{array} } \right]\left[ {\begin{array}{*{20}{c}} {{V_{GE}}} \\ {{V_{GN}}} \end{array}} \right]\text{。}$ | (13) |
其中:
| $\frac{1}{{{R_{xG}}}} = \frac{{{{\sin }^2}\sigma }}{{{R_{Mh}}}} + \frac{{{{\cos }^2}\sigma }}{{{R_{Nh}}}},$ | (14) |
| $\frac{1}{{{R_{yG}}}} = \frac{{{{\cos }^2}\sigma }}{{{R_{Mh}}}} + \frac{{{{\sin }^2}\sigma }}{{{R_{Nh}}}},$ | (15) |
| $\frac{1}{{{T_{fG}}}} = \left(\frac{1}{{{R_{Mh}}}} - \frac{1}{{{R_{Nh}}}}\right)\sin \sigma \cos \sigma ,$ | (16) |
| ${k_G} = \frac{{\sin \lambda \cos L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}\text{。}$ | (17) |
2)速度微分方程
参照文献[1-5]比力方程,可类推出格网导航坐标系下的比力方程:
| ${{{\dot V}}^G} = {{C}}_b^G{{{f}}^b} - \left(2{{C}}_g^G{{\omega }}_{ie}^g + {{\omega }}_{eG}^G\right) \times {{{V}}^G} + {{{g}}^G},$ | (18) |
| ${{\mathbf{g}}^G} = {\left[ {\begin{array}{*{20}{c}} 0&0&{ - g} \end{array}} \right]^{\rm{T}}}\text{。}$ | (19) |
3)位置微分方程
指北方位惯导力学编排和游移方位惯导力学编排的位置求解都是通过位置方向余弦矩阵微分方程的数值积分获得经纬高定位信息,而在高纬度地区采用经纬高的定位策略不再适用,此处采用ECEF坐标表示航行器的实时位置
| $\dot R = C_G^e{V^G},$ | (20) |
由地球坐标和直角坐标间关系可得:
| $\cos L = \frac{{\sqrt {{x^2} + {y^2}} }}{{{R_{Nh}}}},$ | (21) |
| $\sin L = \pm \sqrt {1 - \frac{{{x^2} + {y^2}}}{{{R^2}_{Nh}}}},$ | (22) |
| $\sin \lambda = \frac{y}{{{R_{Nh}}\cos L}} = \frac{y}{{\sqrt {{x^2} + {y^2}} }},$ | (23) |
| $\cos \lambda = \frac{x}{{{R_{Nh}}\cos L}} = \frac{x}{{\sqrt {{x^2} + {y^2}} }}\text{。}$ | (24) |
式(22)中当
1.2节是完整的格网导航力学编排形式,是在地球为椭球模型的基础上推导的。为简化分析,在推导格网导航误差方程的过程中假设地球是圆球模型。考察完整格网导航力学编排方程可知式(13)是与地球模型相关的,在圆球模型下位置速率
| $\begin{split}\omega _{eG}^G = &\left[ {\begin{array}{*{20}{c}} {\omega _{eGx}^G} \\ {\omega _{eGy}^G} \\ {\omega _{eGz}^G} \end{array}} \right] =\left[ {\begin{array}{*{20}{c}} 0&{ - \dfrac{1}{{{R_{eh}}}}} \\ {\dfrac{1}{{{R_{eh}}}}}&{0} \\ 0&{ - \dfrac{{{k_G}}}{{{R_{eh}}}}} \end{array} } \right]\times\\ &\left[ {\begin{array}{*{20}{c}} {{V_{GE}}} \\ {{V_{GN}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \dfrac{{{V_{GN}}}}{{{R_{eh}}}}} \\ {\dfrac{{{V_{GE}}}}{{{R_{eh}}}}} \\ { - \dfrac{{{V_{GN}}}}{{{R_{eh}}}} - \dfrac{{\sin \lambda \cos L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}} \end{array}} \right]\end{split}\text{。}$ | (25) |
相应的由式(20)计算的直角坐标位置
则格网惯性导航的速度误差方程:
| $ \begin{split} \delta \dot{\boldsymbol{v}}^{G}= &\boldsymbol{f}^{G} \times \phi^{G}+\left[v^{G} \times C_{\omega G v}-\left(2 \boldsymbol{\omega}_{i e}^{G}+\omega_{e G}^{G}\right) \times\right] \delta \boldsymbol{v}^{G}+ \\ &v^{G} \times\left(C_{\omega G p}+2 \boldsymbol{C}_{\text {wep }}\right) \delta \boldsymbol{p}+\boldsymbol{C}_{b}^{G} \nabla^{b}\text{,} \end{split} $ | (26) |
姿态误差方程:
| $\dot \phi = - \left(\omega _{iG}^G \times \right){\phi ^G} + {C_{wGv}}\delta {V^G} + \left({C_{weR}} + {C_{wGR}}\right)\delta {R^e} - C_b^G{\varepsilon ^b},$ | (27) |
位置误差方程:
| $\delta {\dot R^e} = C_G^e\delta {V^G} - C_G^e({V^G} \times ){C_R}\delta {R^e},$ | (28) |
另外将陀螺漂移
| ${\varepsilon ^b} = \varepsilon _b^b + \varepsilon _w^b \quad {\nabla ^b} = \nabla _b^b + \nabla _w^b,$ | (29) |
| $\dot \varepsilon _b^b = 0, \quad \dot \nabla _b^b = 0\text{。}$ | (30) |
格网惯性导航的误差状态取为
| $\dot x = \left[\!\! {\begin{array}{*{20}{c}} { - (w_{iG}^G \times )}&{{C_{wGV}}}&{{C_{13}}}&{ - C_b^G}&{{0_3}} \\ {({f^G} \times )}&{{C_{22}}}&{{C_{23}}}&{{0_3}}&{C_b^G} \\ {{0_3}}&{C_G^e}&{{C_{33}}}&{{0_3}}&{{0_3}} \\ {{0_3}}&{{0_3}}&{{0_3}}&{{0_3}}&{{0_3}} \\ {{0_3}}&{{0_3}}&{{0_3}}&{{0_3}}&{{0_3}} \end{array} }\!\! \right]x + \left[\!\! {\begin{array}{*{20}{c}} { - C_b^G\varepsilon _\omega ^b} \\ {C_b^G\nabla _\omega ^b} \\ {0_{3,1}} \\ {0_{3,1}} \\ {{0_{3,1}}} \end{array} } \!\!\right],$ | (31) |
其中:
| ${C_{13}} = {C_{\omega eR}} + {C_{\omega GR}} \;\;\; {C_{22}} = {V^G} \times {C_{\omega GV}} - \left[ {(2\omega _{ie}^G + \omega _{eG}^G) \times } \right],$ | (32) |
| ${C_{23}} = {V^G} \times (2{C_{weR}} + {C_{wGR}}), \;\;\; {C_{33}} = - C_G^e({V^G} \times ){C_R},$ | (33) |
| $ {C_{weR}} = \frac{{{w_{ie}}}}{{{R_{eh}}{{(1 - {{\cos }^2}L{{\sin }^2}\lambda )}^{\frac{3}{2}}}}} \times \left[ {\begin{array}{*{20}{c}} {2{{\cos }^2}L\sin L\sin \lambda \cos \lambda } \\ {{{\sin }^2}L} \\ { - \sin L\cos L\cos \lambda } \end{array}}\right.$ |
| $\left. {\begin{array}{*{20}{c}} \begin{gathered} ( - \sin L[{\cos ^2}\lambda+ \\ {\sin ^2}\lambda ({\sin ^2}L - {\cos ^2}L)]) \end{gathered} &{{{\sin }^2}L\cos L\sin \lambda }\\ 0&{ - \sin L\cos L\cos \lambda } \\ {{{\sin }^2}L} \\ { - \sin L\cos L\sin \lambda }&{{{\cos }^2}L} \end{array}} \right] ,$ | (34) |
| ${C_{wGR}} = \dfrac{1}{{{R_{eh}}^2}} \times \left[ {\begin{array}{*{20}{c}} {{V_{GN}}\cos L\cos \lambda } \\ { - {V_{GE}}\cos L\cos \lambda } \\ {\dfrac{{2{V_{GN}}{{\cos }^2}L\sin \lambda \cos \lambda }}{{{{(1 - {{\cos }^2}L{{\sin }^2}\lambda )}^{\frac{3}{2}}}}}}\end{array}}\right.$ |
| $\left. {\begin{array}{*{20}{c}} {{V_{GN}}\cos L\sin \lambda }&{{V_{GN}}\sin L} \\ { - {V_{GE}}\cos L\sin \lambda }&{ - {V_{GE}}\sin L} \\ { - {V_{GN}}\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }&{\dfrac{{2{V_{GN}}\sin L\cos L\sin \lambda }}{{{{(1 - {{\cos }^2}L{{\sin }^2}\lambda )}^{\frac{3}{2}}}}}} \end{array}} \right],$ | (35) |
| ${C_{wGv}} = \left[ {\begin{array}{*{20}{c}} 0&{ - \dfrac{1}{{{R_{eh}}}}}&0 \\ {\dfrac{1}{{{R_{eh}}}}}&0&0 \\ 0&{ - \dfrac{{\cot L\sin \sigma }}{{{R_{eh}}}}}&0 \end{array}} \right],$ | (36) |
| $\begin{split}&{C_R} = \frac{1}{{{R_{eh}}}}\times\\ &\left[\!\!\!\! {\begin{array}{*{20}{c}} {\dfrac{{\sin L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}}&0&{\dfrac{{ - \cos L\cos \lambda }}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}} \\ {\dfrac{{\sin \lambda \cos \lambda {{\cos }^2}L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}}\!\!\!\!\!\!&{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }\!\!\!\!\!\!&{\dfrac{{ - \sin L\sin \lambda \cos L}}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}} \\ {\dfrac{{\cos L\sin L\sin \lambda }}{{1 - {{\cos }^2}L{{\sin }^2}\lambda }}}&0&{ - \dfrac{{{{\cos }^2}L\sin \lambda \cos \lambda }}{{1 - {{\cos }^2}L{{\sin }^2}\lambda }}} \end{array}} \!\!\!\!\right]\text{。}\end{split}$ | (37) |
取子惯导姿态误差
| $x = \left[ {\begin{array}{*{20}{c}} {{\phi ^G};}&{\delta {V^G};}&{\delta {R^e};}&{{\varepsilon ^b};}&{{\nabla ^b}} \end{array} } \right],$ | (38) |
选取主惯导速度输出与子惯导速度之差作为量测量,即
| $z = \left[ {\delta {V^G}} \right] = \left[ {V_m^G - V_b^G} \right],$ | (39) |
则量测方程为:
| $z = \left[ {\begin{array}{*{20}{c}} {{0_3}}&{{I_3}}&{{0_3}}&{{0_3}}&{{0_3}} \end{array} } \right]x + {v^e}\text{。}$ | (40) |
式(33)组成了“速度匹配”传递对准算法的卡尔曼滤波模型。
3 仿真分析 3.1 格网导航有效性验证为了验证极区格网导航算法的有效性,仿真生成一条沿着某条固定的经线穿越极点然后驶出极区的轨迹。
仿真过程具体仿真参数设置如下:
1)轨迹起始点[89.7°N 108°E 300 m];
2)航行速度和时间为沿着108°E经线以50 m/s速度向极点航行,穿越极点后沿着72°W驶离极点,共航行1000 s;
3)惯性器件误差为陀螺随机常值漂移
整个航行过程航行器无航向机动,航行轨迹在地球上如图2所示,整个轨迹过程的位置真值如图3所示。

|
图 2 极区导航仿真轨迹 Fig. 2 Simulation track for polar navigation |
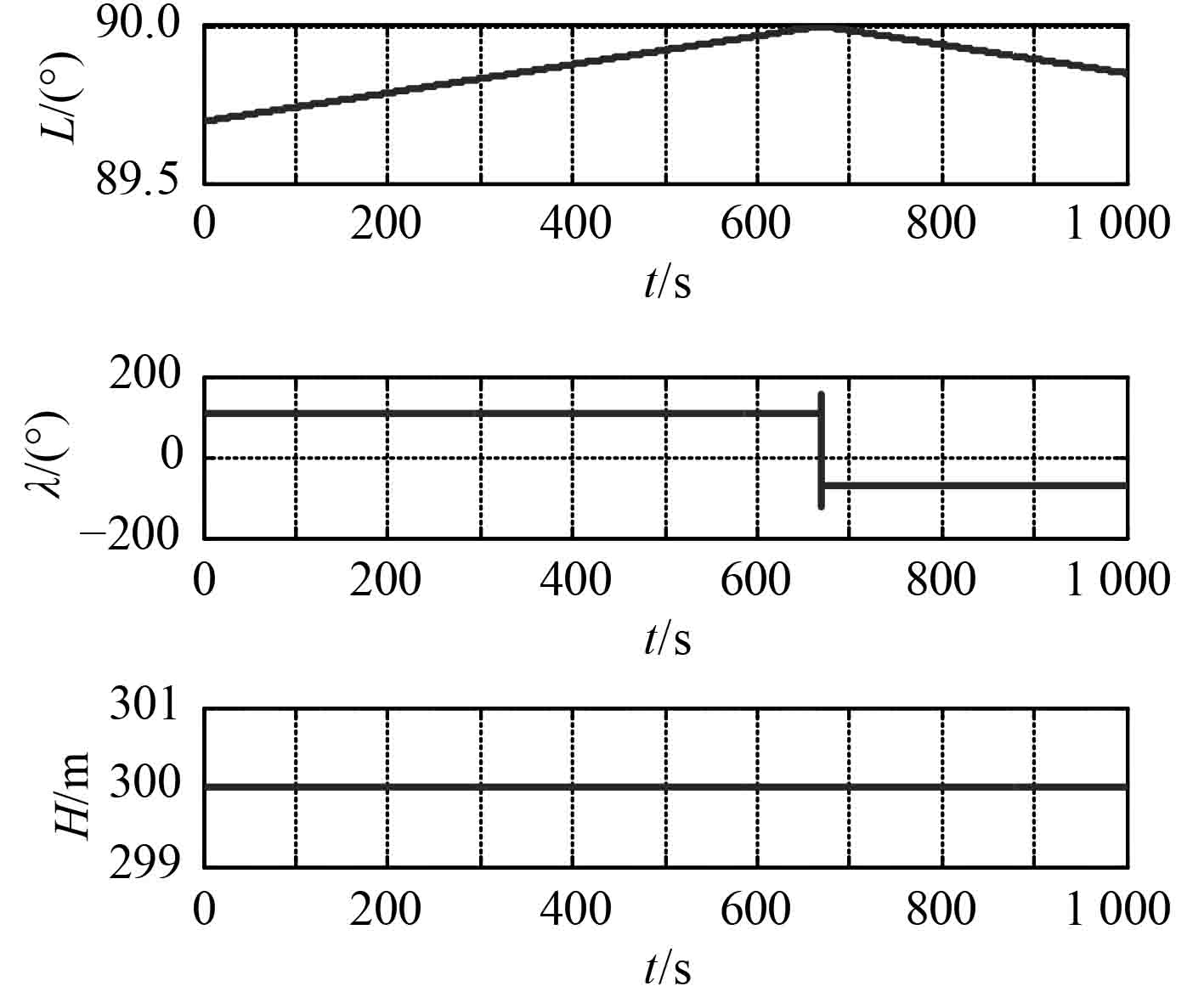
|
图 3 极区导航仿真轨迹真实经纬高 Fig. 3 Real longitude and latitude of simulation track for polar navigation |
东北天坐标系编排下姿态角误差、速度误差和位置误差如图4~图6所示。
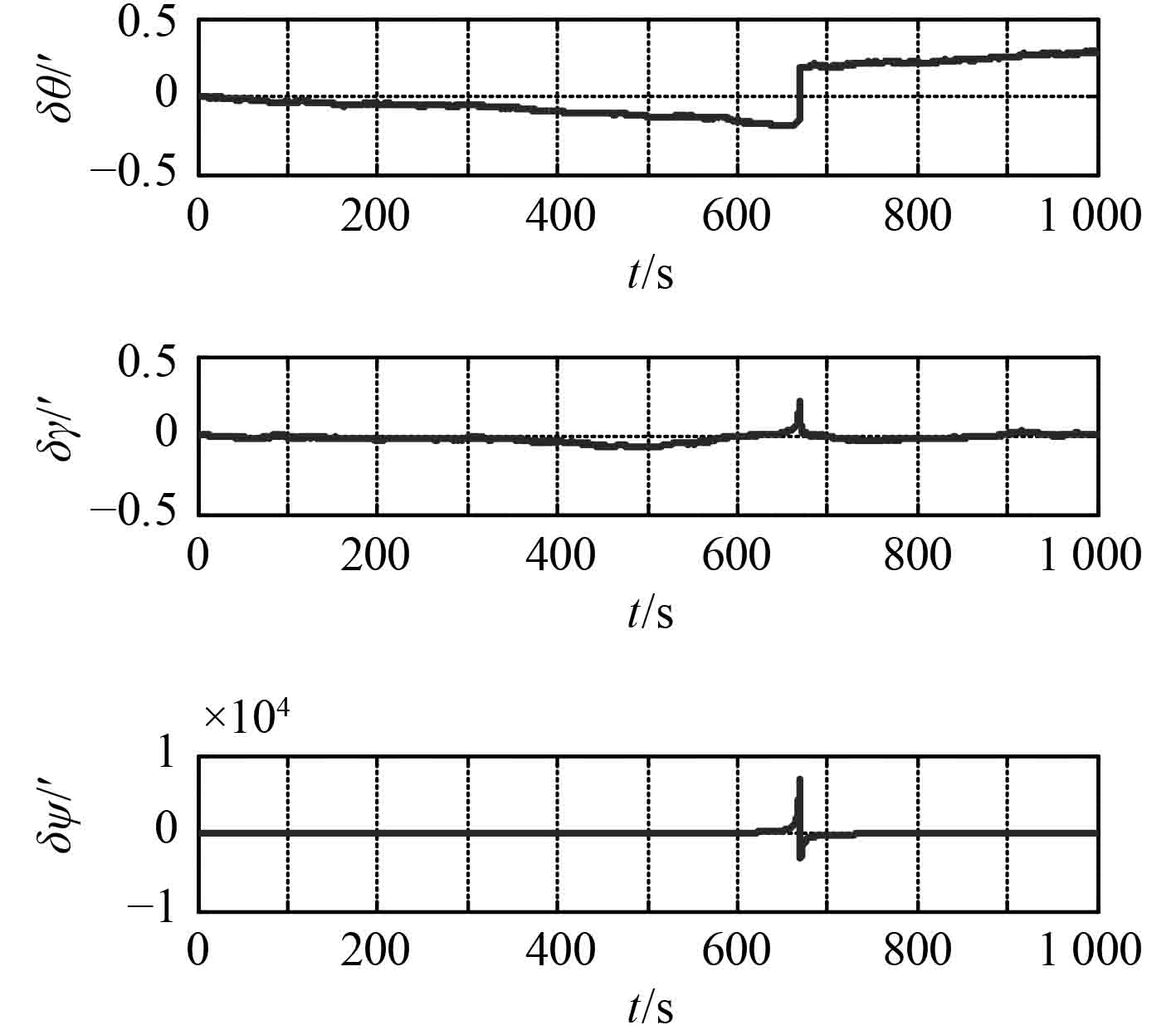
|
图 4 东北天坐标系下姿态角误差 Fig. 4 Attitude errors of ENU coordinate system |

|
图 5 东北天坐标系下速度误差 Fig. 5 Velocity errors of ENU coordinate system |
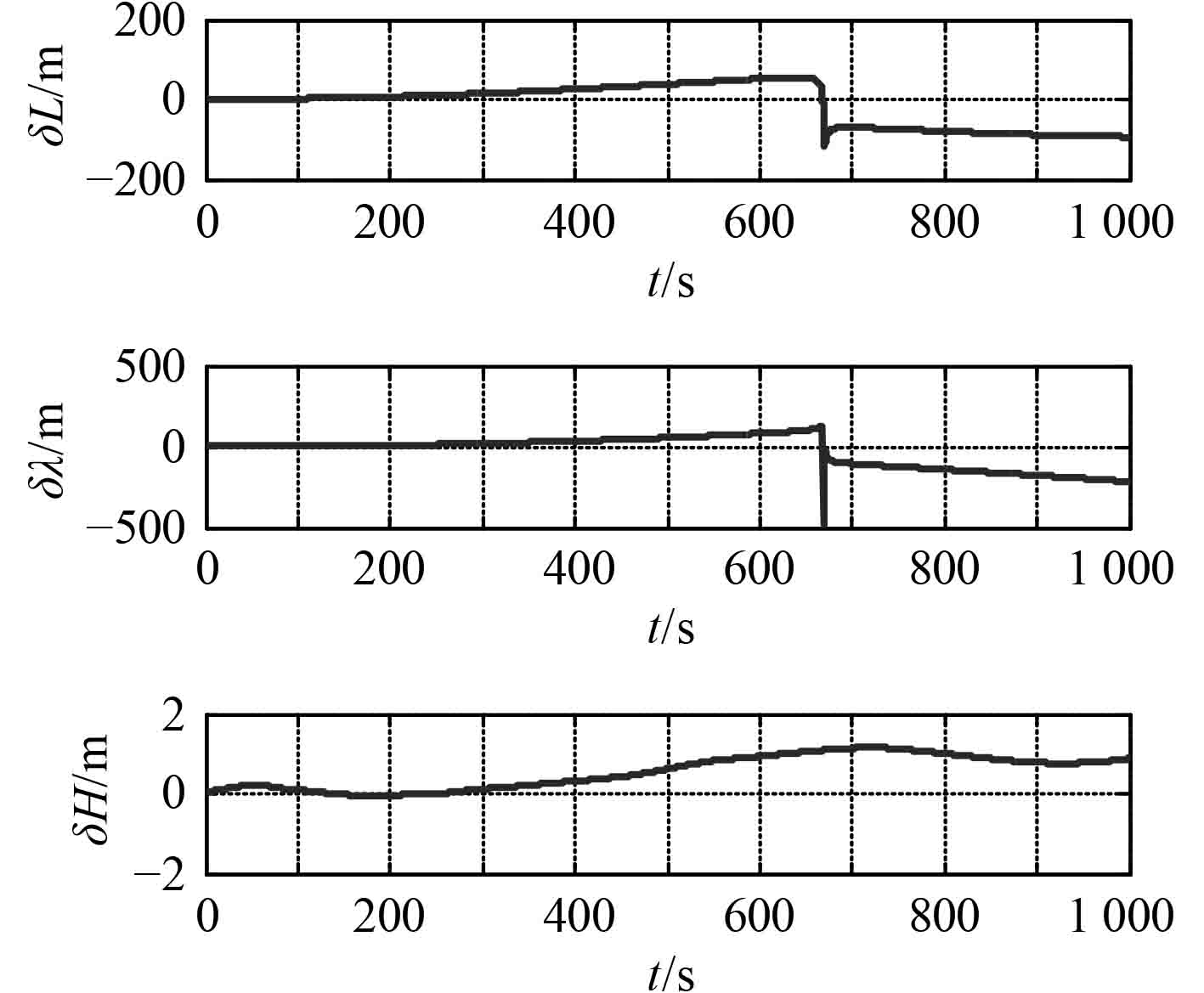
|
图 6 经纬高位置误差 Fig. 6 The errors of longitude and latitude |
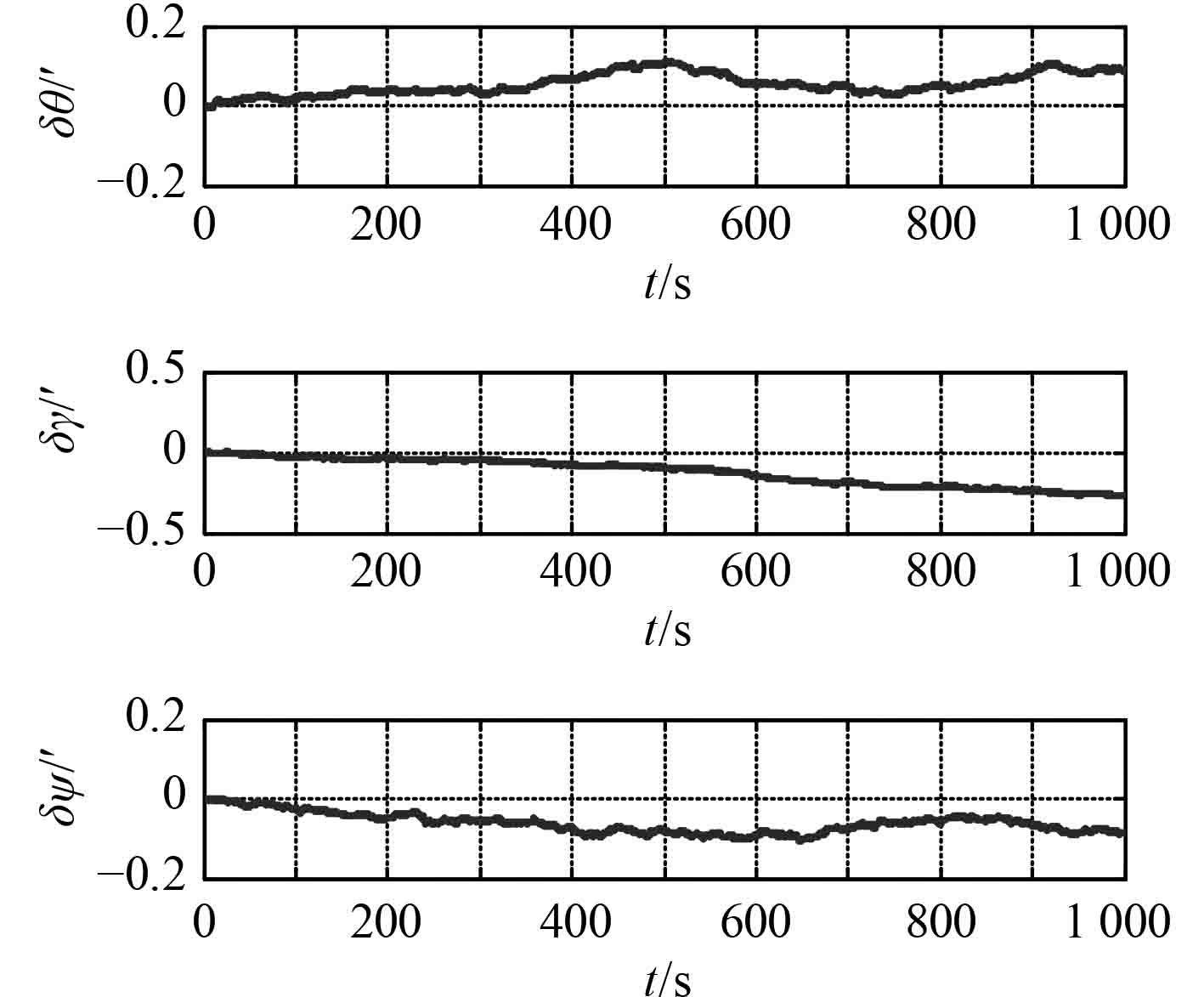
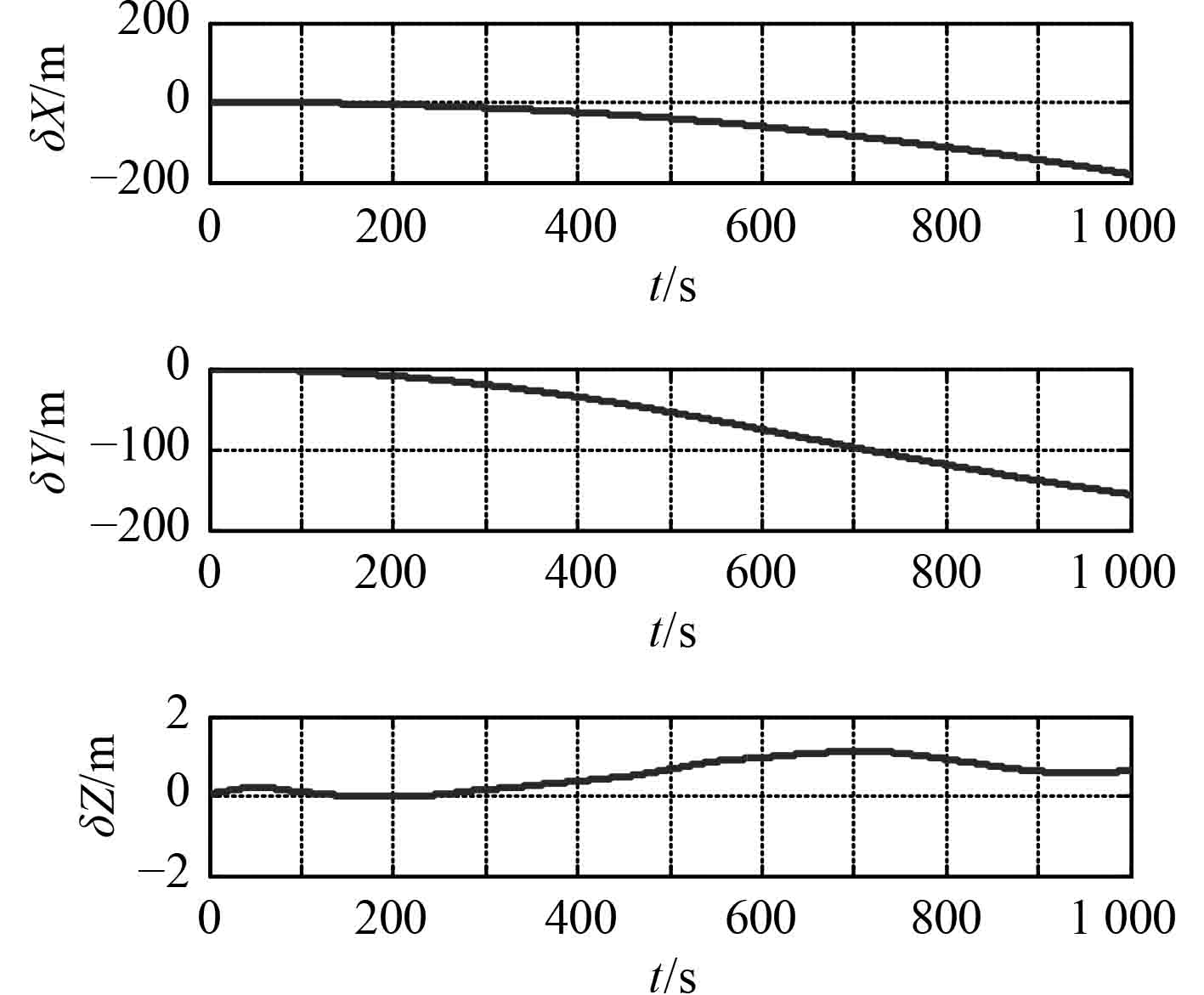
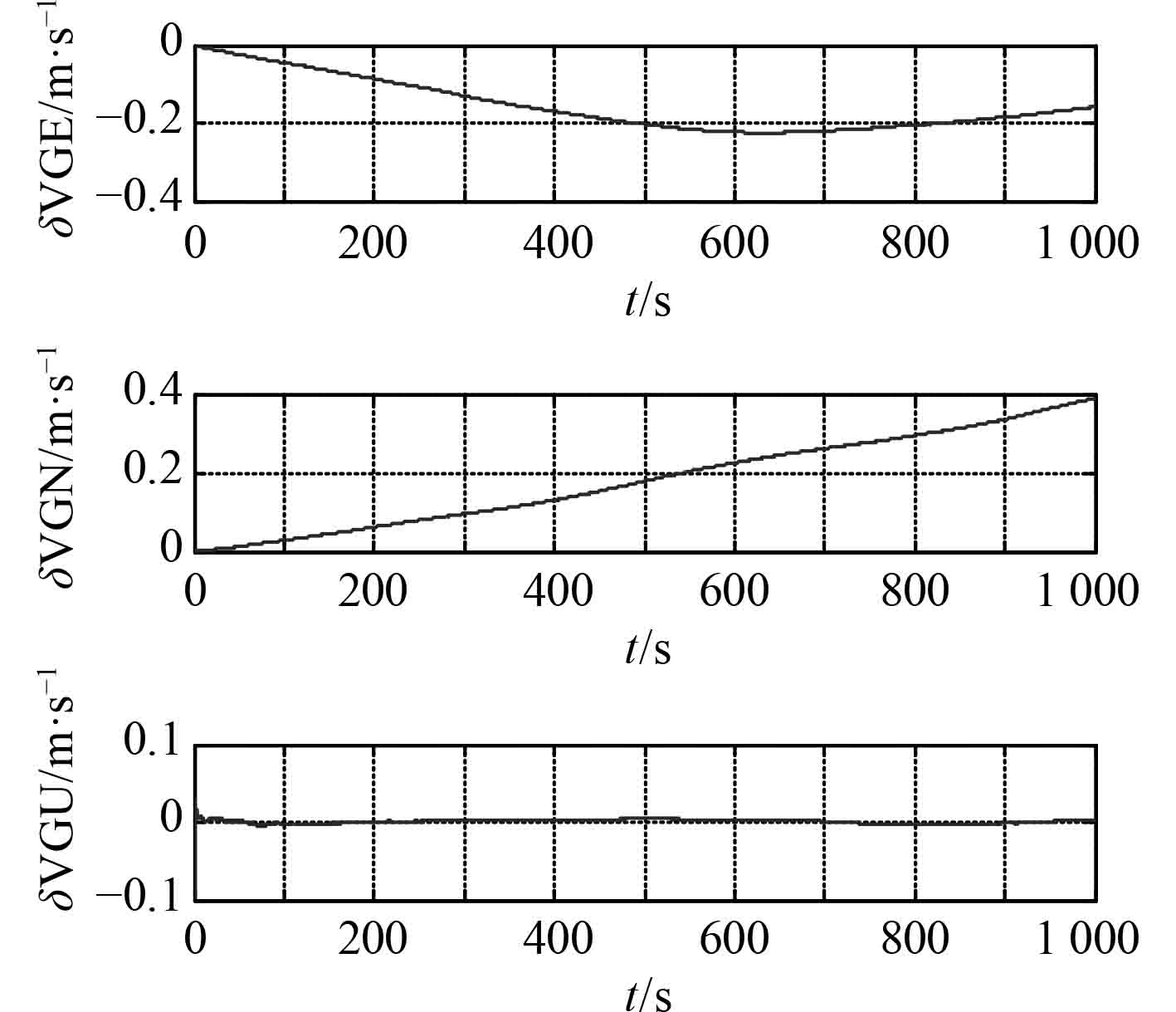
格网导航解算下姿态角误差、速度误差和位置误差如图7~图9所示。
|
图 7 格网坐标系下姿态角误差 Fig. 7 Attitude errors of grid coordinate system |
|
图 9 ECEF坐标系下位置误差 Fig. 9 The error of position in ECEF coordinates |
由图7~图9可以看出,格网导航在15 min内由惯性器件误差引起的水平姿态角误差小于0.5′,方位失准角误差小于0.2′,水平速度误差小于0.5 m/s,图8所示水平位置误差小于200 m。
|
图 8 格网坐标系下速度误差 Fig. 8 Velocity error of grid coordinate system |
图4~图6中,传统惯导解算方法下姿态角误差、速度误差以及经纬度误差在极点附近存在跳变。因此,在极区不适合采用经纬度作为定位输出参数,而应输出地心地固坐标下位置参数。
3.2 “速度匹配”传递对准算法有效性验证对上述提出的“速度匹配”传递对准算法进行仿真验证,仿真参数设置及仿真轨迹如下:
1)惯性器件误差设置
陀螺仪:常值漂移0.01o/h,随机游走系数为
2)惯导初始误差
初始姿态误差为
3)导航解算周期为0.01 s,仿真时间100 s。
4)卡尔曼滤波器参数
状态估计初值设置为0,初始方差阵取为真实均方误差阵的5倍,卡尔曼滤波周期取为0.01 s,速度量测噪声0.1 m/s。
设置2种航行轨迹:匀速直航、加速直航。航行器以30 m/s的初始速度匀速航行,如表1所示。
|
|
表 1 航行轨迹设置 Tab.1 Setting of torpedo track |
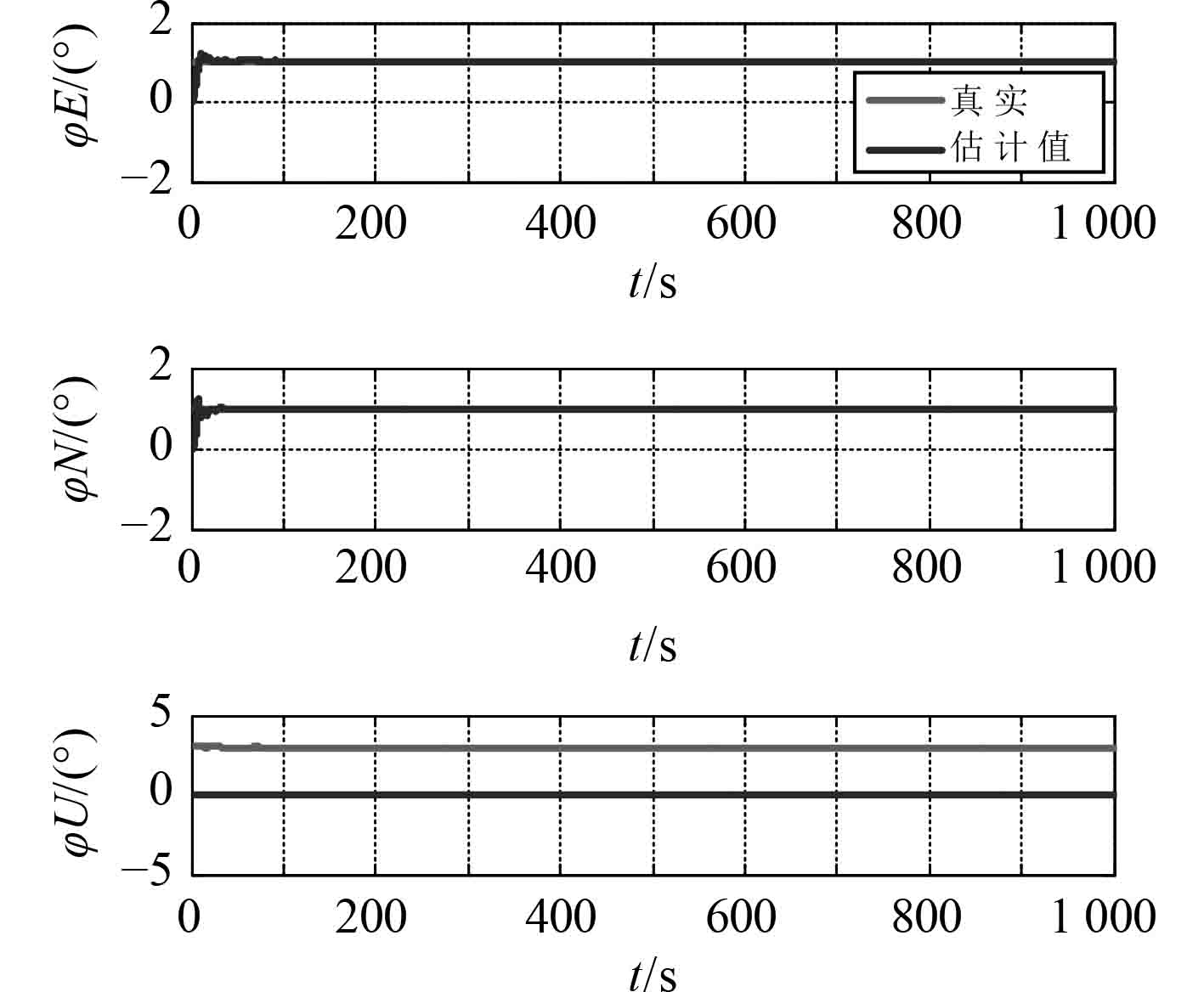
分别在2种轨迹下进行仿真,失准角估计误差如图10和图11所示。
|
图 10 匀速直航下失准角估计误差 Fig. 10 The estimate error of misalignment angle in direct navigation and uniform speed |
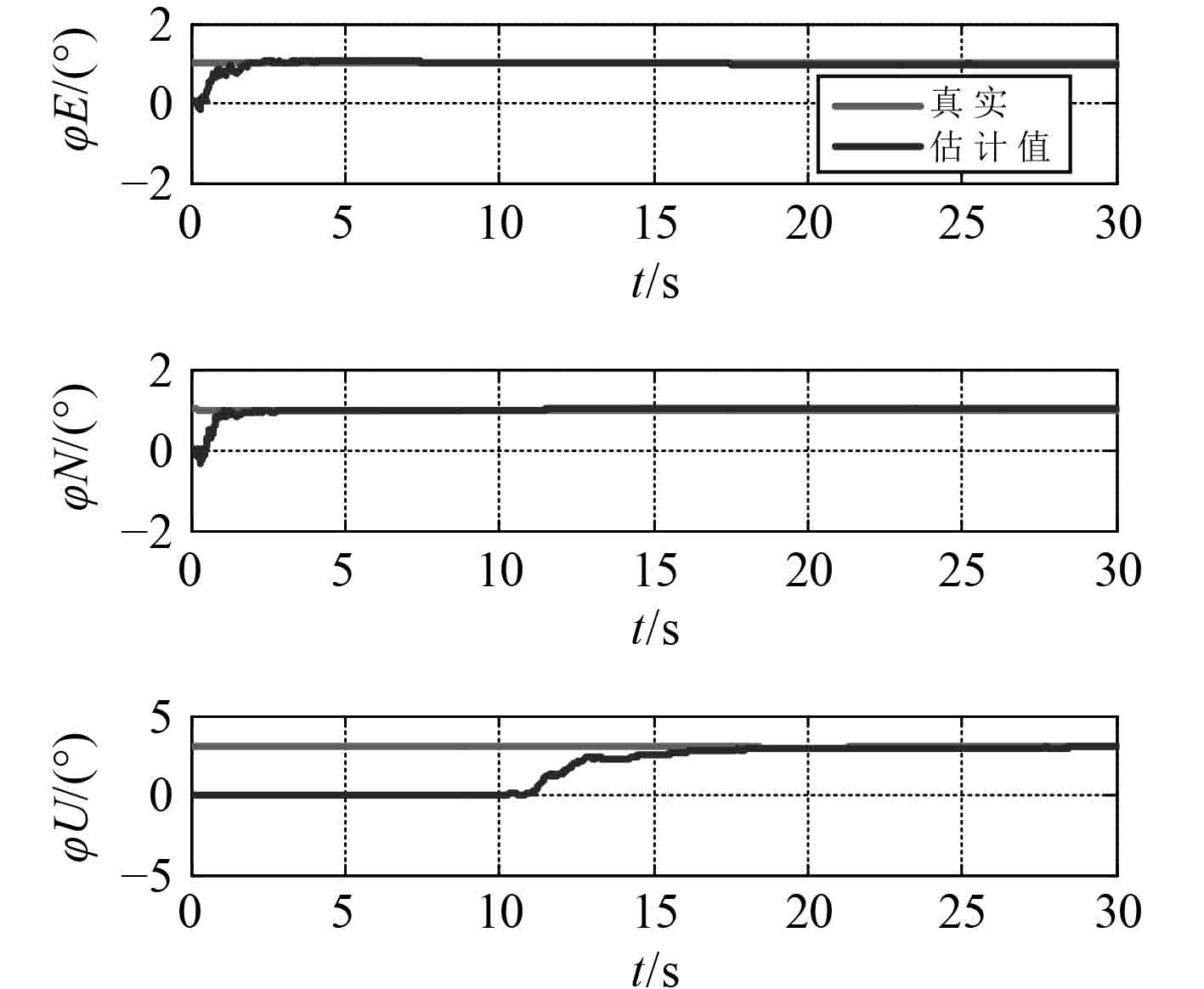
|
图 11 加速直航下失准角估计误差 Fig. 11 The estimate error of misalignment angle in direct navigation and acceleration |
由图10和图11可得,采用“速度匹配”传递对准算法,速度误差与惯导水平失准角直接相关,因此该对准方法水平失准角的收敛速度相对较快,当航行器匀速直航时,水平失准角
本文针对水下航行器惯导系统在极区因地理经线快速收敛导致无法精确定位定向的问题,提出一种利用格网坐标系直接获得格网航向,进而优化惯导系统导航性能的方法,研究了格网惯性导航算法编排方案,以满足水下航行器在极区航行时的导航需要。仿真结果表明,在格网惯性导航下,采用高精度惯性器件,15 min内水平姿态角误差小于0.5′,方位姿态角误差小于0.2′,水平速度误差小于0.5m/s,ECEF坐标系下的位置误差全程小于200 m。
针对水下航行器在极区内的对准问题,对格网惯性导航的误差进行建模,并据此设计了格网惯导系统的“速度匹配”传递对准算法,利用卡尔曼滤波器,实现对子惯导误差的估计和校正。仿真结果表明,采用该传递对准算法,水平失准角在10 s内即可收敛到1.5′以内,同时,加速机动对方位失准角有激励作用,30 s内方位对准精度在4′以内。
| [1] |
CHARLES BROXMEYER. Inertial navigation systems[J]. New York: McGraw Hill, 1964. |
| [2] |
秦永元. 惯性导航[M]. 北京: 科学出版社, 2006.
|
| [3] |
PAUL G. SAVAGE. strapdown analytic[J]. Minnesota: Strapdown Associates, Inc, 2000. |
| [4] |
MYRON KAYTON, WALTER R. FRIED. avionics navigation systems[J]. New York: John Wiley, 1996. |
| [5] |
ESMAT BERKIR. Introduction to modern navigation systems[J]. New Jersey: World Scientific, 2007. |
| [6] |
周琪, 秦永元, 付强文, 等. 极区飞行格网惯性导航算法原理[J]. 西北工业大学学报, 2013, 31(2): 210-217. DOI:10.3969/j.issn.1000-2758.2013.02.010 |
 2021, Vol. 43
2021, Vol. 43
