0 引　言

水下滑翔机本身属于弱控制系统，浮力驱动系统是其动力来源，水翼上产生的升力将一部分动力转换为前向驱动力，实现锯齿状的剖面滑翔运动^[1-2]。航向控制主要依赖横滚调节，如果受到横向洋流干扰，水下滑翔机将产生横滚坡度并开始改变航线进行转弯运动。过弱的横向静稳定性会延长恢复平衡状态的时间，导致更大的航向偏差。参考飞机的空气动力学理论，由侧滑产生的横滚力矩是横向静稳定性的主要影响因素^[3]，一方面，水翼后掠角的存在能改变两边水翼上的有效速度分量，产生升力差使机身发生横滚；另一方面，垂尾上产生侧向力，作用点相对机身偏高，也会产生相应的横滚力矩，故通过优化水翼后掠角及垂尾展弦比进一步提高水下滑翔机横向静稳定性。

关于附体水动力参数对横向静稳定性的影响，目前开展的研究较少，大多局限在对滑翔经济性及纵向静稳定性的探讨上，武建国^[4]采用极差分析法分析了标准翼型4因素（水翼弦长、安装位置、后掠角及展弦比）对经济性及纵向稳定性影响所占的比重；Liu等^[5]借助CFD仿真，优化水翼布局，提出了弦长对经济效率影响最大，后掠角对机体纵向稳定性影响较大的论点；赵宝强^[6]利用Javafoil软件获得多攻角、多雷诺系数下不同水翼参数的极曲线图，基于升阻比优化平板水翼翼型，并考虑稳定性因素，提出并设计了柔性水翼；徐世勋^[7]以NACA翼型为基础，通过改变水翼厚度和水翼弯度，提高了滑翔机的经济性及纵向稳定性，并提出了变后缘柔性机翼的概念。国外方面，Masahiko Nakamura^[8]选取不同尺寸的平板水翼和垂尾进行水槽实验，根据测量得到的水动力值来判断最优的水动力附体外形；Christian Aage^[9]通过配备有平面运动机构的拖曳水池牵引，测量出比目鱼型自主水下航行器的附加质量、升阻力及各项阻尼系数，并且还进行了自由航行测试，讨论了水下航行器外形可能的优化方案；Muhammad Yasar Javaid^[10]通过数值模拟及水槽实验的方法对比了梯形翼和矩形翼的水动力性能和动态稳定性，结果表明矩形翼虽然能提供更大的升力但稳定性较差；Zhang等^[11]计算了某鱼型水下机器人不同水翼展弦比下的升阻比，研究发现较大展弦比水翼导致较浅的滑翔路径和较长的水平航程。

本文以中国海洋大学研制的声学水下滑翔机为研究对象，选取适当的水翼后掠角及垂尾展弦比参数，参考飞机横向运动原理，提出了应用于水下滑翔机的横向静稳定性判据，并在此基础上分析了水翼后掠角及垂尾展弦比的作用机理，最后借助数值计算方法^[12]，综合考虑经济性指标，研究了不同水翼后掠角及垂尾展弦比对横向静稳定性指标的影响，从而设计优化水动力参数。

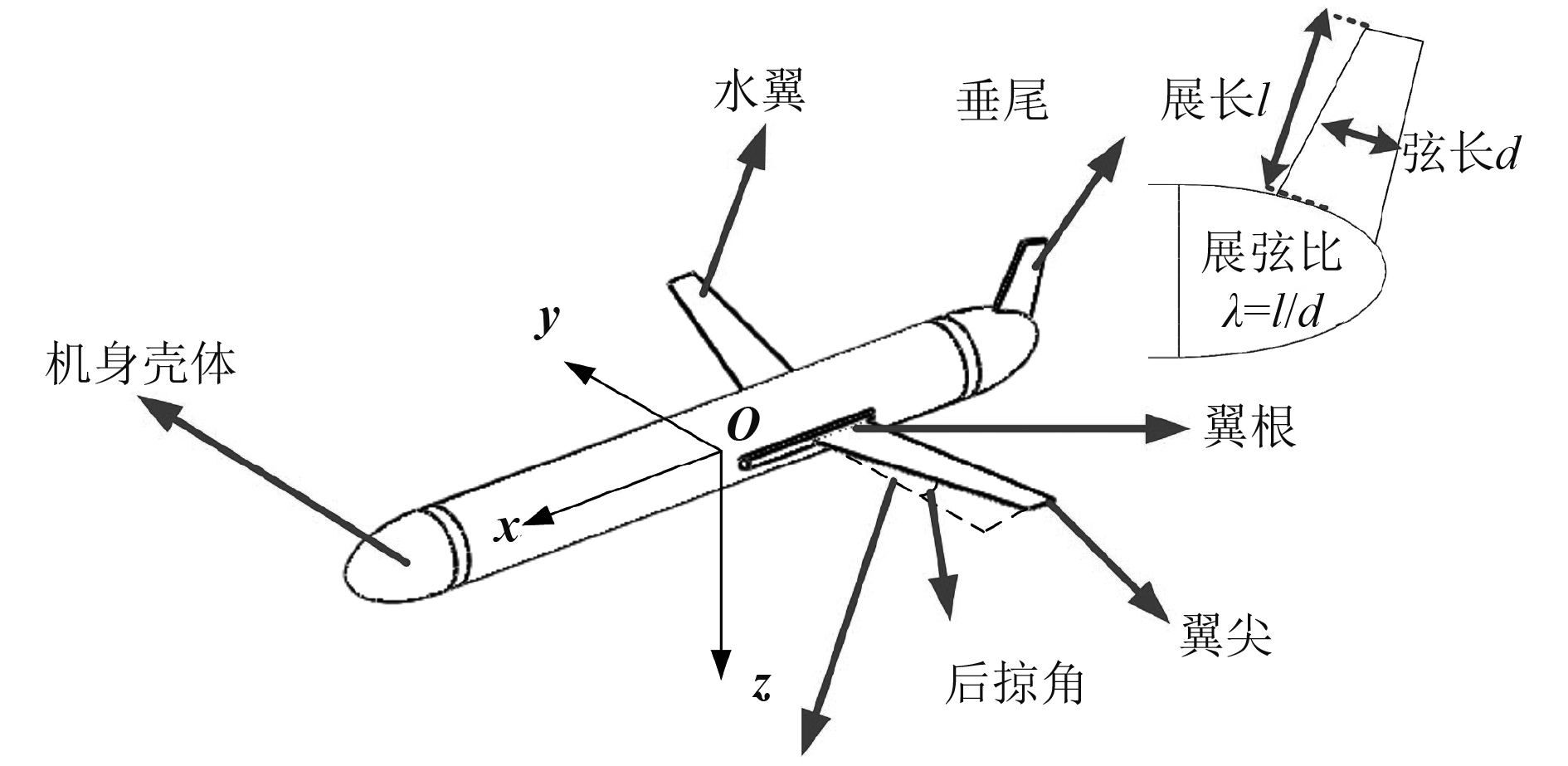
1 水下滑翔机附体水动力参数 1.1 水翼翼型参数

在考虑实用性的基础上，水下滑翔机通常配置为平板翼型^[13]。本文分析中，讨论了水翼后掠角在一定滑翔经济性的基础上，对横向静稳定性的影响，受到水下滑翔机本身机械结构和重量的限制，后掠角的改变必然会影响其余翼型参数，其中展弦比及弦长对滑翔效率的影响最大。为了保证现有水翼的滑翔经济性，该数值被固定，而根梢比随着后掠角的增加而增加。本文将选取6组翼型进行仿真试验，翼型参数如表1所示。

1.2 垂尾翼型参数

为了研究垂尾展弦比对水下滑翔机横向静稳定性的影响，选取3组垂尾翼型进行仿真试验，参数如表2所示。

2 CFD数值计算方法 2.1 几何模型和计算域建立

计算模型为自主研制的声学水下滑翔机模型，主要以主体筒体、首尾导流罩、水翼及垂尾组成，略去了首部导流罩中的传感器、尾部天线等流体特征明显的区域，对一些微小的孔洞和凸起进行了修补，如图1所示。机身全长为2.616 m，主体直径为0.25 m，水翼展长为0.7 m，平均弦长为0.15 m，完全按照实体模型1∶1建立。

为保证机体周围流场的充分发展，计算域选取圆柱状的外流场，流场入口距机体艏部约三倍主体长度，出口距机体艉部约4倍主体长度，直径被设置为水下滑翔机圆形中段直径的10倍。通过旋转圆柱形外流域调整水下滑翔机的空间位置，从而获取相应的斜航运动状态^[7]。

2.2 网格划分

采用前处理软件ICEM提供的非结构网格自动划分技术。边界层区域采用三棱柱网格捕捉流动特征细节，其余流动区域采用四面体非结构网格。近壁区第一层网格节点高度定义在对数层区域，选取y⁺值为30～300。经计算，边界层第一层网格高度取2.7 mm，设置6层边界层，总厚度 $\delta $ 约为20 mm，最大面网格取20 mm，最大体网格取500 mm。

2.3 FLUENT求解设置

采用基于压力的隐式分离求解器，采用RNG k-ε湍流模型，求解方法为SIMPLE算法，压力项为标准差值格式，对流项及扩散项均为二阶迎风格式^[8]。

入口边界采用速度入口（velocity inlet）；出口边界设置为自由出流（outflow），不；圆柱侧面边界设置为对称边界（symmetry），假定经过此面的对流通量为零，相应的剪应力也为零；水下滑翔机其他壁面设置为无滑移壁面（no slip wall）。

3 经济性分析 3.1 经济性指标

水下滑翔机的滑翔效率综合考虑前进动力来源及阻力因素，一般通过升阻比^[16]来衡量，可表示为：

$\tan \phi = {{{F_D}} /{{F_L}}}\text{。} $

(1)

其中： $\phi $ 表示水下滑翔机的滑翔角； ${F_D}$ 为水阻； ${F_L}$ 为升力；当升阻比增加时，滑翔角减小，进而使水平航程更远。有研究表明，水翼后掠角的变化会一定程度上改变水下滑翔机的升阻比^[17-18]，所以本文首先通过求解不同水翼后掠角参数下的斜航运动升阻比，作为研究横向静稳定性指标的前提条件，进而在优化水翼后掠角时做出必要取舍。

3.2 水下滑翔机斜航升阻比试验

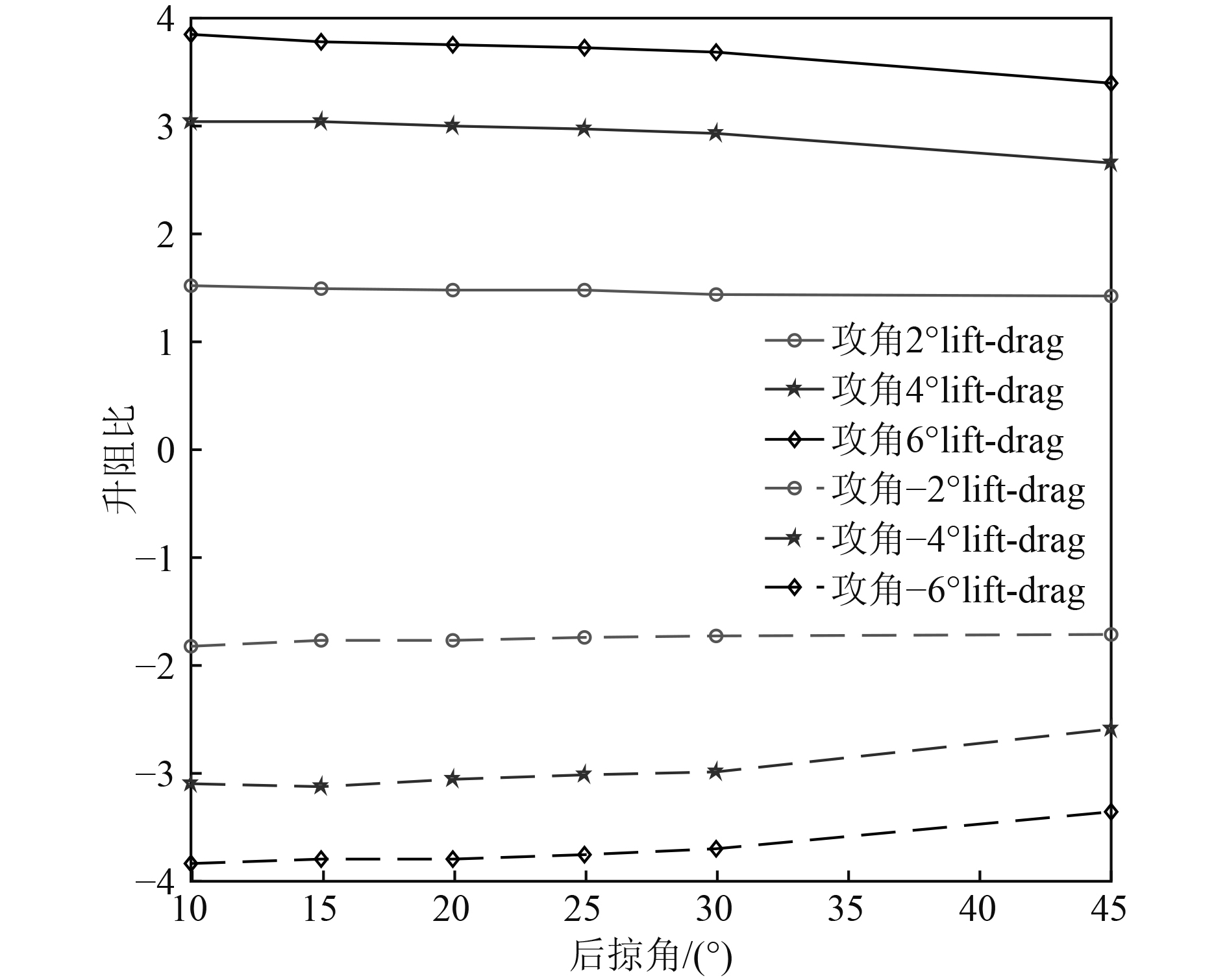
斜航升阻比试验主要模拟水下滑翔机垂直面内运动，通过转动圆柱形外流域来改变攻角，求解不同水翼后掠角下对应攻角的升力、阻力值。选取攻角 $\alpha $ 范围为−6°～6°，攻角为正值时表示下潜状态，取稳态滑翔速度V=0.4 m/s，对水翼翼型a～f进行数值仿真模拟，绘制升阻比与后掠角的相关曲线，如图2所示。

由图2可知，在正负攻角航行时，升阻比变化趋势基本一致，细微的取值差别主要来源于水下滑翔机上下并非严格对称，符号相反主要是因为升力方向的改变。随着攻角绝对值增加，各翼型升阻比的绝对值也在增加。对 ${\rm{ - }}{{\rm{2}}^ \circ } \leqslant \alpha \leqslant {{\rm{2}}^ \circ }$ 范围内的攻角，水翼后掠角的变化对升阻比基本无影响，而 $\alpha \leqslant {\rm{ - }}{{\rm{4}}^ \circ }$ 或 $\alpha \geqslant {{\rm{4}}^ \circ }$ 范围内的攻角，当后掠角处于阈值30°以下时，升阻比变化较缓，而增加至阈值30°以上时，升阻比的绝对值有明显的下降趋势。以−4°攻角曲线为例，分析2段曲线拟合的斜率，后掠角在10°～30°时，其斜率为0.005995，30°～45°时，其斜率为0.0263，后者远大于前者，说明继续增加后掠角将会较大程度上降低水下滑翔机的升阻比。尽管展弦比及弦长一定，为了保证滑翔经济性，不宜采用过大的后掠角。故在横向静稳定性的研究中均以阈值30°为上限，来探讨水翼后掠角对其影响。

4 横向静稳定性分析 4.1 横向静稳定性指标

水下滑翔机的横向静稳定性主要与侧滑角有关，由侧滑角引起的横滚力矩表达式如下：

${m_x}(\beta ) = \frac{K}{{\dfrac{1}{2}\rho {V^2}{S_w}{l_w}}}\text{。}$

(2)

式中： ${m_x}(\beta )$ 为横滚力矩系数； $K$ 表示侧滑角引起的横滚力矩; $\ \rho $ 表示海水密度； $V$ 为来流速度； ${S_w}$ 在这里取水翼投影面积; ${l_w}$ 取水翼展长。因为本文主要研究翼型影响，所以相关的无因次化也应取和翼型相关的特征参数。通过线性假设，横滚力矩系数可以表示为侧滑角 $\ \beta $ 的线性函数：

${m_x}(\beta ) = {m_x}(0) + m_x^\beta \beta \text{，}$

(3)

右边第一项表示侧滑角为零时的横滚力矩系数，可忽略不计，横向静稳定性的判定指标由静稳定导数 $m_x^\beta $ 来决定，取决于 ${m_x}(\beta )$ 随 $\ \beta $ 变化曲线的斜率。

$m_x^\beta = \frac{{\Delta {m_x}(\beta )}}{{\Delta \beta }}\text{。}$

(4)

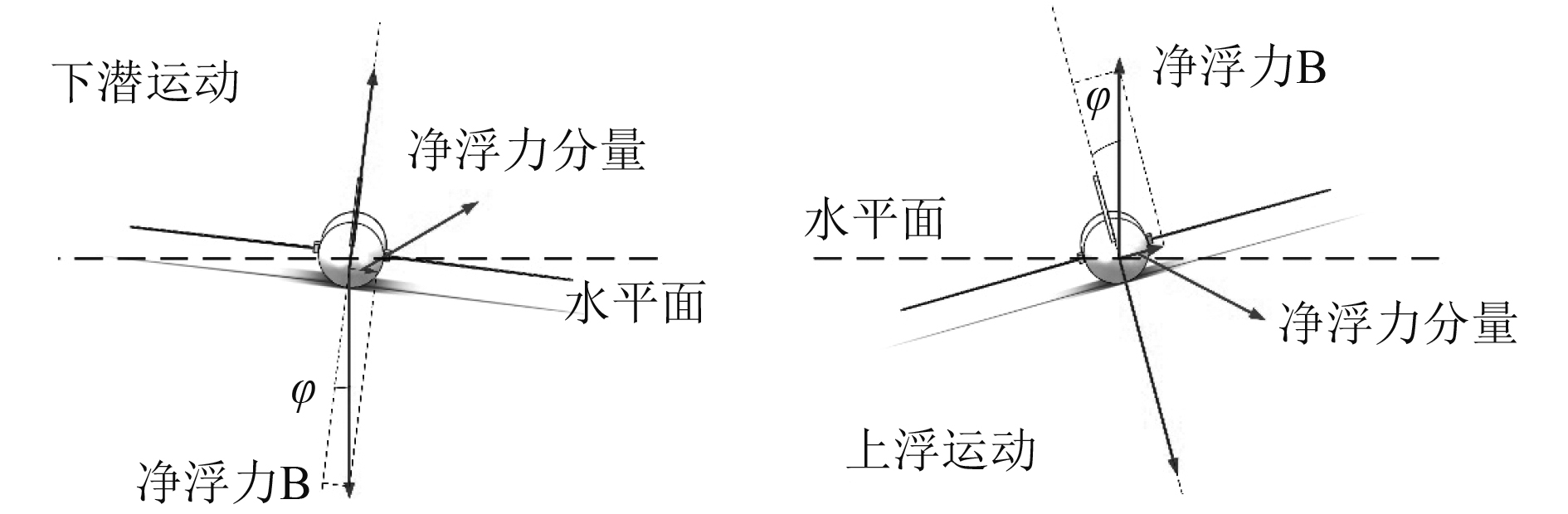
水下滑翔机的上浮、下潜为2种截然不同的运动状态，其受力情况也不同，以下针对这2种情况讨论其横向静稳定性，如图3所示。

下潜运动时，升力作用向上，净浮力向下，在其分量的作用下，同方向横滚扰动导致同方向的侧滑，如果 $m_x^\beta < 0$ ，侧滑角变化产生使滑翔机恢复水平趋势的横滚力矩，横滚坡度减小，这种情况被称为横向静稳定；当 $m_x^\beta > 0$ 时，侧滑角变化所产生的横滚力矩则会使横滚运动继续加剧，这种情况被称为静不稳定。最后当 $m_x^\beta = 0$ 时，属于临界静稳定情况。

上浮运动时，升力作用向下，净浮力向上，其分量作用下横滚扰动导致相反方向的侧滑，此时如果当 $m_x^\beta > 0$ ，侧滑角变化产生恢复水平趋势的横滚力矩，横滚坡度减小，最终稳定下来，被称为横向静稳定；当 $m_x^\beta < 0$ 时，侧滑角变化所产生的横滚力矩则会使横滚运动继续加剧，不会产生回归水平的趋势，这种情况被称为静不稳定。最后当 $m_x^\beta = 0$ 时，属于临界静稳定情况。所以，对于不同运动状态的水下滑翔机，横向静稳性的判定标准不同。

4.2 水翼后掠角影响分析

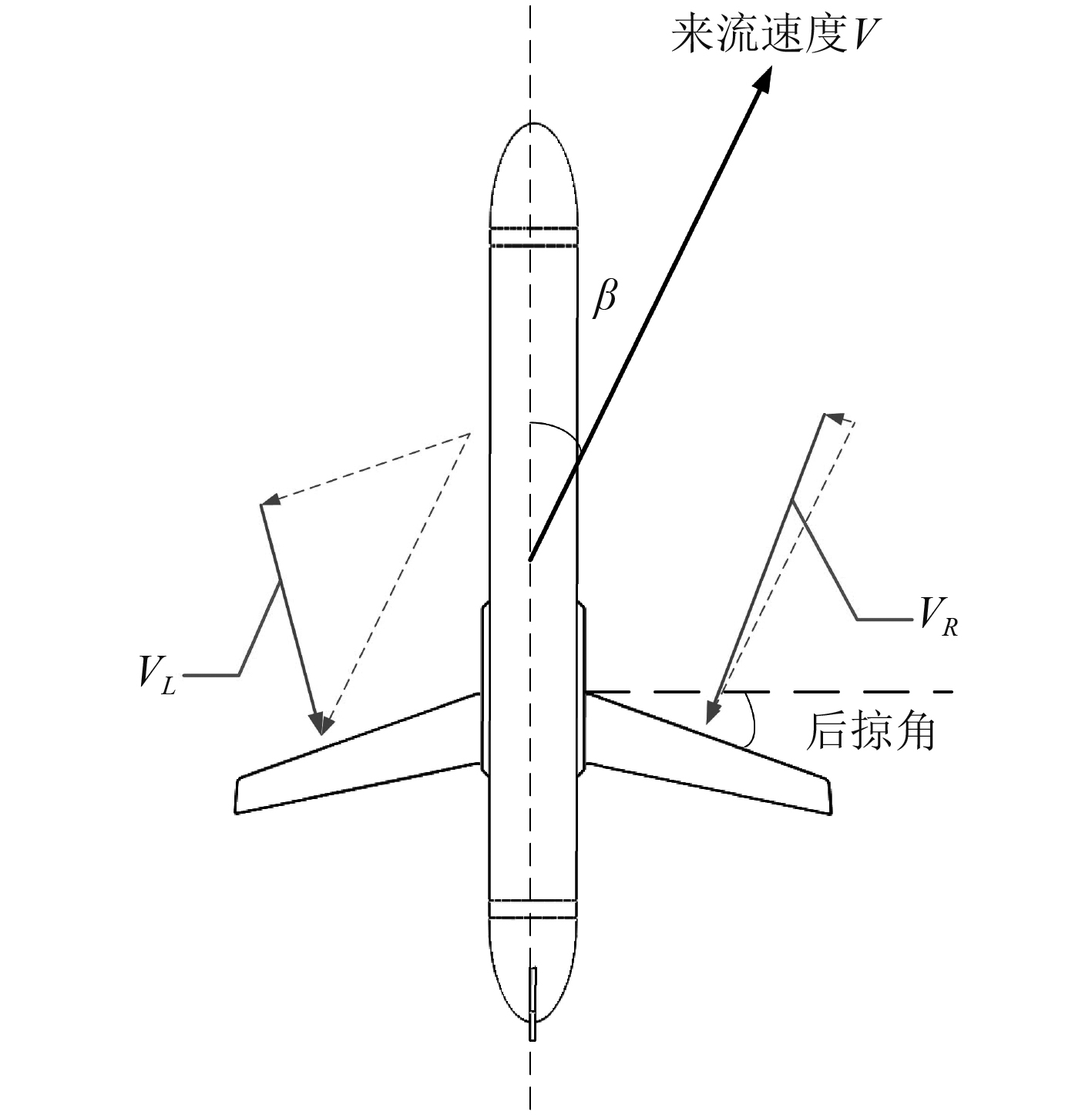
对于平板水翼下滑翔运动，由于攻角的存在，后掠角的作用得以体现，以图4为例说明。假设水下滑翔机处于右侧滑状态，后掠角的存在使水翼两边产生不均等的有效速度分量 ${V_R} > {V_L}$ ，产生的升力差使得机身发生横滚，配合垂尾产生横滚合力矩。

4.3 垂尾展弦比影响分析

如图5所示，侧滑角的作用下，使垂尾上产生相应的侧向力，由于水下滑翔机的重心C偏低，而垂尾上受到的侧向力Y作用点相对于机身偏高，所以会产生使机身绕纵轴转动的横滚力矩（考虑到重浮心相距不大，将以浮心为原点的横滚力矩近似等效于以重心为原点的横滚力矩）。垂尾展弦比变化会改变侧向力的大小及横滚力矩的力臂长度 ${z_{ap}}$ 。

4.4 水下滑翔机横向静稳定性试验 4.4.1 水翼后掠角影响下的横向静稳定性

仿真中从水下滑翔机下潜及上浮运动两方面考虑，选取合适攻角 $\alpha = \pm {{\rm{4}}^ \circ }$ ，来流速度0.4 m/s，侧滑角 $\ \beta $ 分别取 ${\rm{0}}^{\circ }\text{，}\pm {\rm{2}}^{\circ }\text{，}\pm {\rm{4}}^{\circ }\text{，}\pm {\rm{6}}^{\circ }$ ，右侧滑对应正值，对30°以内后掠角水翼进行数值仿真，求解侧滑角对应的横滚力矩系数 ${m_x}(\beta )$ ，计算出横向静稳定导数 $m_x^\beta $ 。

1）下潜运动

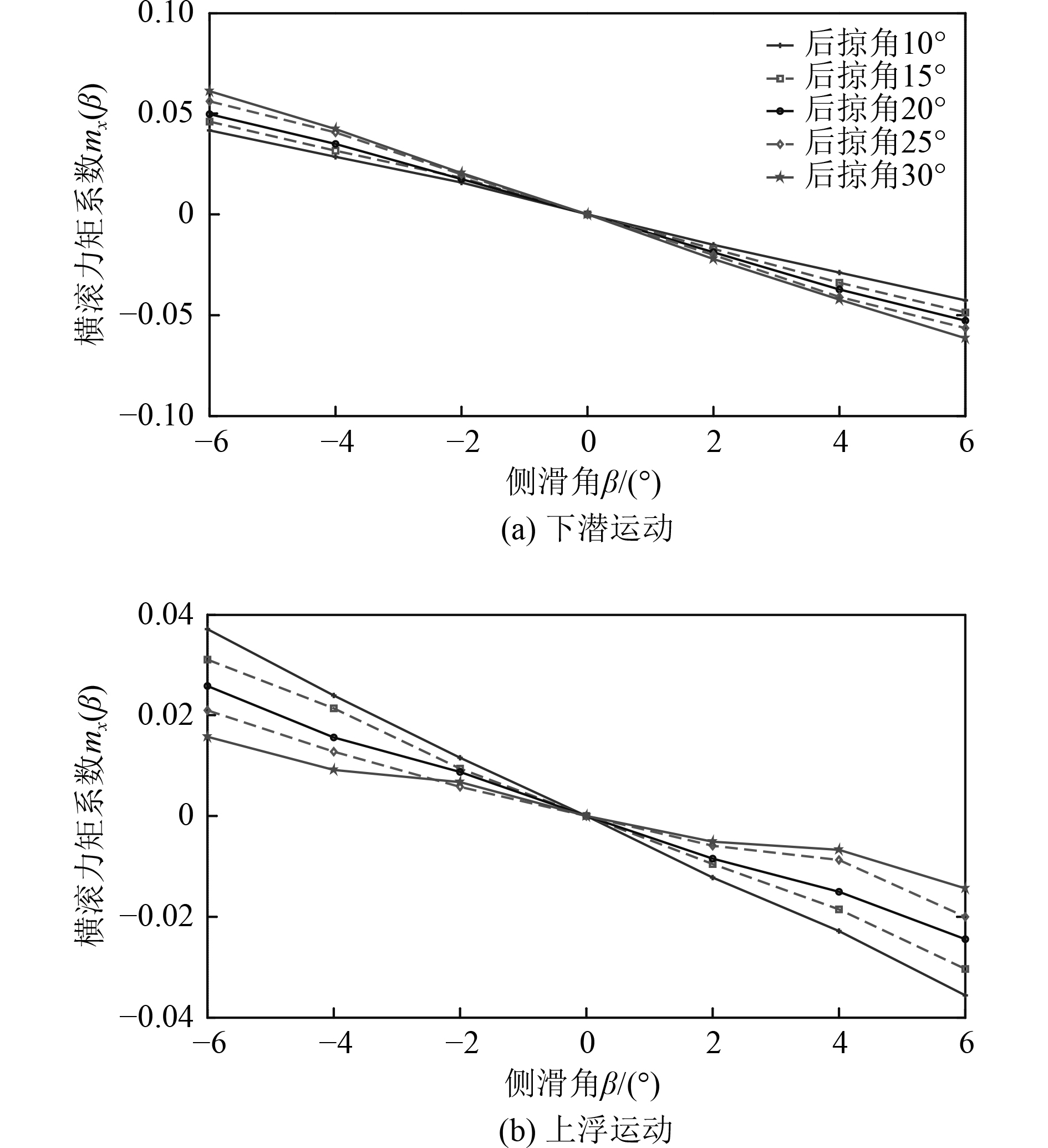
图6（a）为下潜状态下各水翼翼型在不同侧滑角下的横滚力矩系数仿真结果。由图可知，各条曲线的斜率（即横向静稳定导数 $m_x^\beta $ ）均小于零，此水下滑翔机在各翼型下均是横向静稳定的，且随着后掠角的增加，其 $m_x^\beta $ 逐渐偏离零值，即横向静稳定性越强，各水翼翼型对应 $m_x^\beta $ 值如表3所示。

2）上浮运动

图6（b）为上浮状态下各水翼翼型在不同侧滑角下的横滚力矩系数仿真结果。如图所示，各种翼型下曲线的斜率同样小于零，均处于静不稳定状态，但随着后掠角的增加，斜率值趋向于零值，即向着静稳定的方向发展，各翼型对应 $m_x^\beta $ 值如表4所示。

由实验数据可知，一定范围内水翼后掠角的增加对下潜上浮状态的滑翔运动横向静稳定性都起到了促进作用，下潜状态下，增加了静稳定力矩的绝对值，增强了横滚扰动的恢复能力；上浮状态下，减小了静不稳定力矩的绝对值，降低了主动控制单元的能耗。

从水翼流场的静压云图分析，可进一步得知后掠角对横滚力矩的影响，仿真图均取正视图，机头向外，以 $\ \beta = {{\rm{6}}^ \circ }$ 为例，比较分析水翼翼型a和e的周围流场。

由图7可知，翼型a后掠角小，侧滑状态下，左右水翼的有效速度分量相差不大，两边水翼的静压差基本相同，产生的升力也基本一致，无明显升力差值，对横滚力矩的影响不大；翼型e增加足够的后掠角后（见图8），右边水翼出现更大的静压差，产生的升力大于左边水翼，且方向向上，产生向左的横滚力矩，力图使水下滑翔机恢复水平状态。

由图9可知，上浮运动中，翼型a后掠角过小，同样两边水翼的静压差基本一致，对横滚力矩影响不大；对于翼型e（见图10），右边水翼出现更大的静压差，升力大于左边水翼，且方向向下，产生向右的横滚力矩，力图使水下滑翔机恢复水平状态。

4.4.2 垂尾展弦比影响下的横向静稳定性

讨论水下滑翔机垂尾展弦比对横向静稳定性的影响，同样分为下潜及上浮状态，其余变量保持一致，对不同垂尾展弦比翼型进行数值分析，计算横向静稳定导数 $m_x^\beta $ 。

1）下潜运动

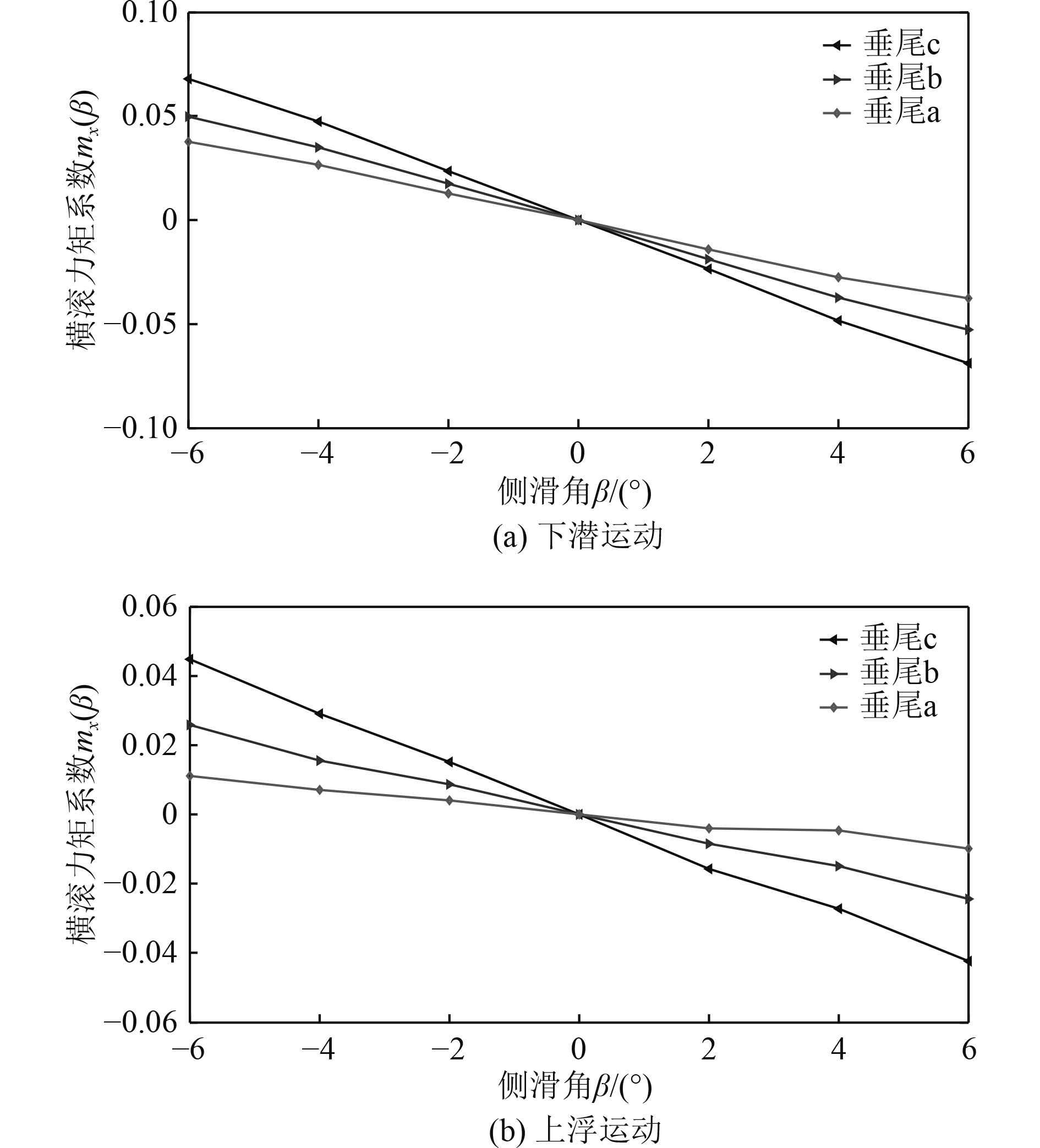
图11（a）为下潜状态下各垂尾翼型在不同侧滑角下的横滚力矩系数仿真结果，各条曲线的斜率均小于零，滑翔机在各垂尾展弦比下均是横向静稳定的，随着展弦比的增加，其 $m_x^\beta $ 逐渐偏离零值，横向静稳定性越强，各垂尾翼型对应 $m_x^\beta $ 值如表5所示。

2）上浮运动

图11（b）为上浮状态下各垂尾翼型在不同侧滑角下的横滚力矩系数仿真结果，滑翔机在各垂尾展弦比下均处于静不稳定状态，且随着垂尾展弦比的增加，斜率更加偏离零值，即朝着静不稳定的方向发展，各垂尾翼型对应 $m_x^\beta $ 值如表6所示。

由实验数据可知，垂尾展弦比对水下滑翔机横向静稳定性的影响具有双重性，处于下潜时，垂尾展弦比的增加促进了静稳定；上浮时，垂尾展弦比的增加会阻碍机身的恢复。

同样取侧滑角 $\ \beta = {6^ \circ }$ ，分析比较垂尾翼型a和c的周围流场。

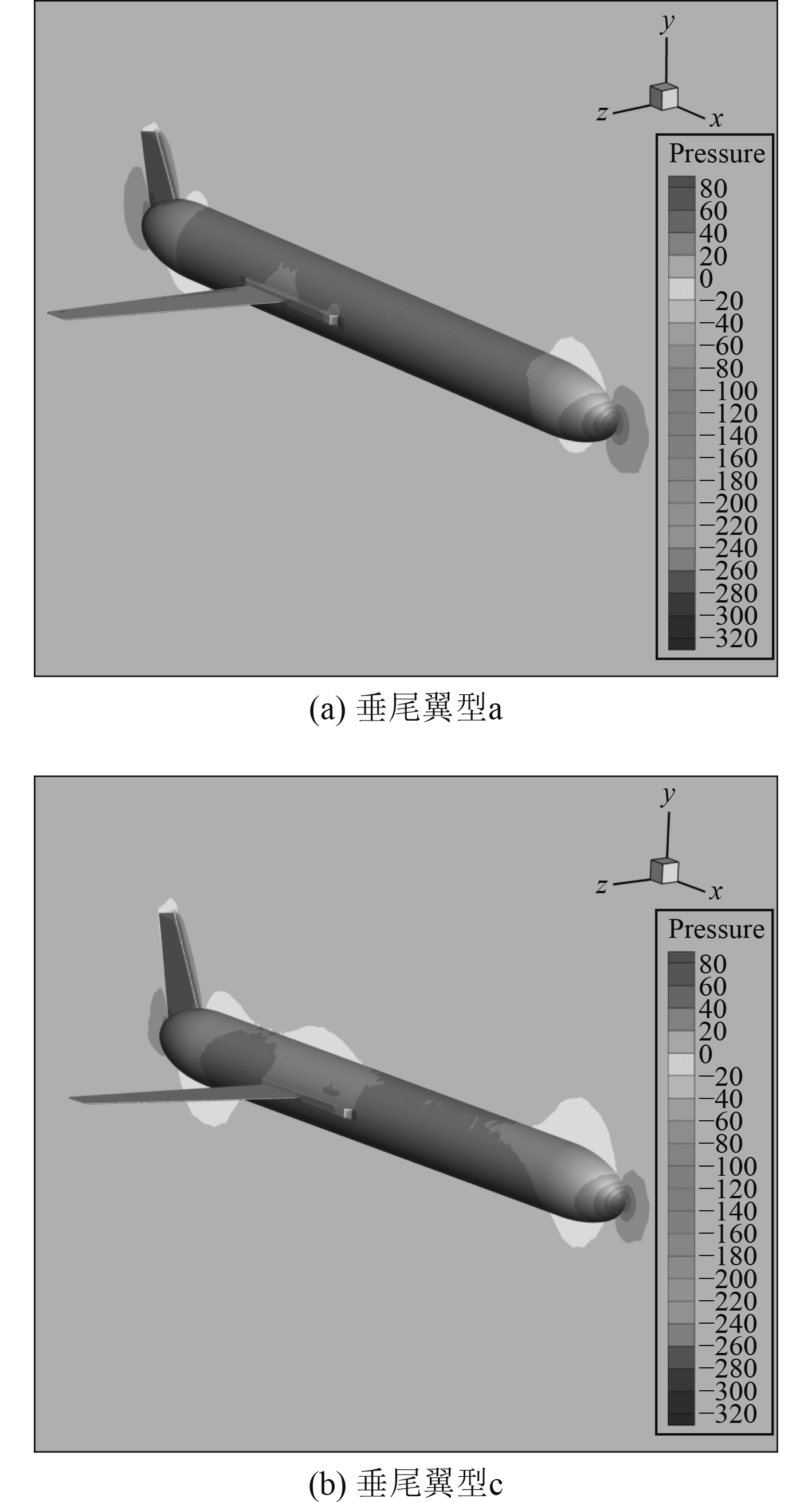
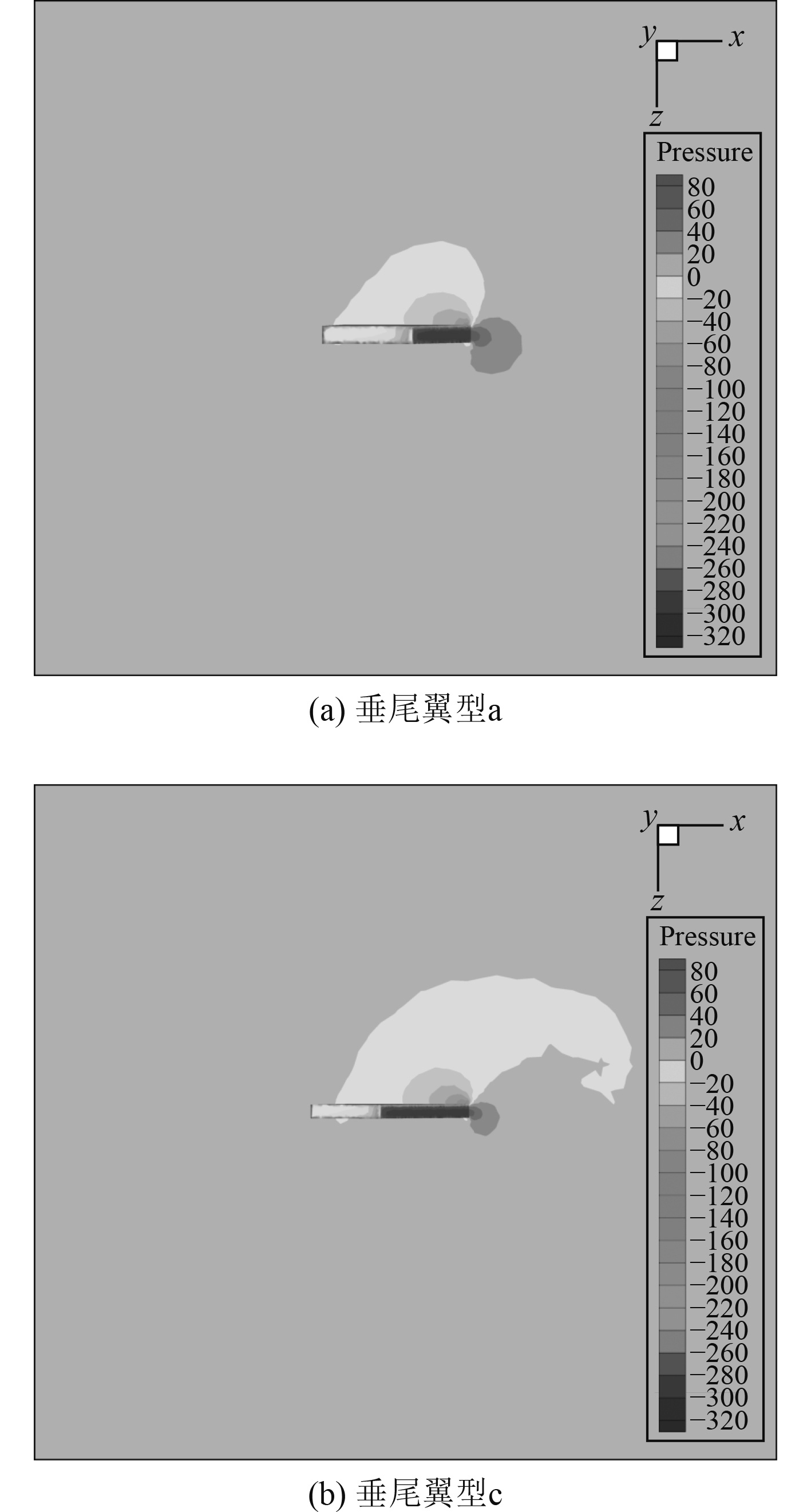
图12（a）和图12（b）分别为下潜运动中不同垂尾翼型下水下滑翔机右侧整体静压云图。由图可知，垂尾展弦比的增加使侧向力作用点偏离重心，力臂增加，但右侧整体静压并未发生太大变化。图13（a）和图13（b）分别为不同垂尾翼型下距离滑翔机横剖面200 mm处垂尾周围的局部流场，下方表示水下滑翔机的右侧。由图可知，2种垂尾翼型下左右两侧静压差基本一致。那么，综合考虑垂尾受力面积及力臂长度，随着展弦比的增加，使水下滑翔机向左侧发生横滚的力矩增大，有利于平衡状态的恢复。

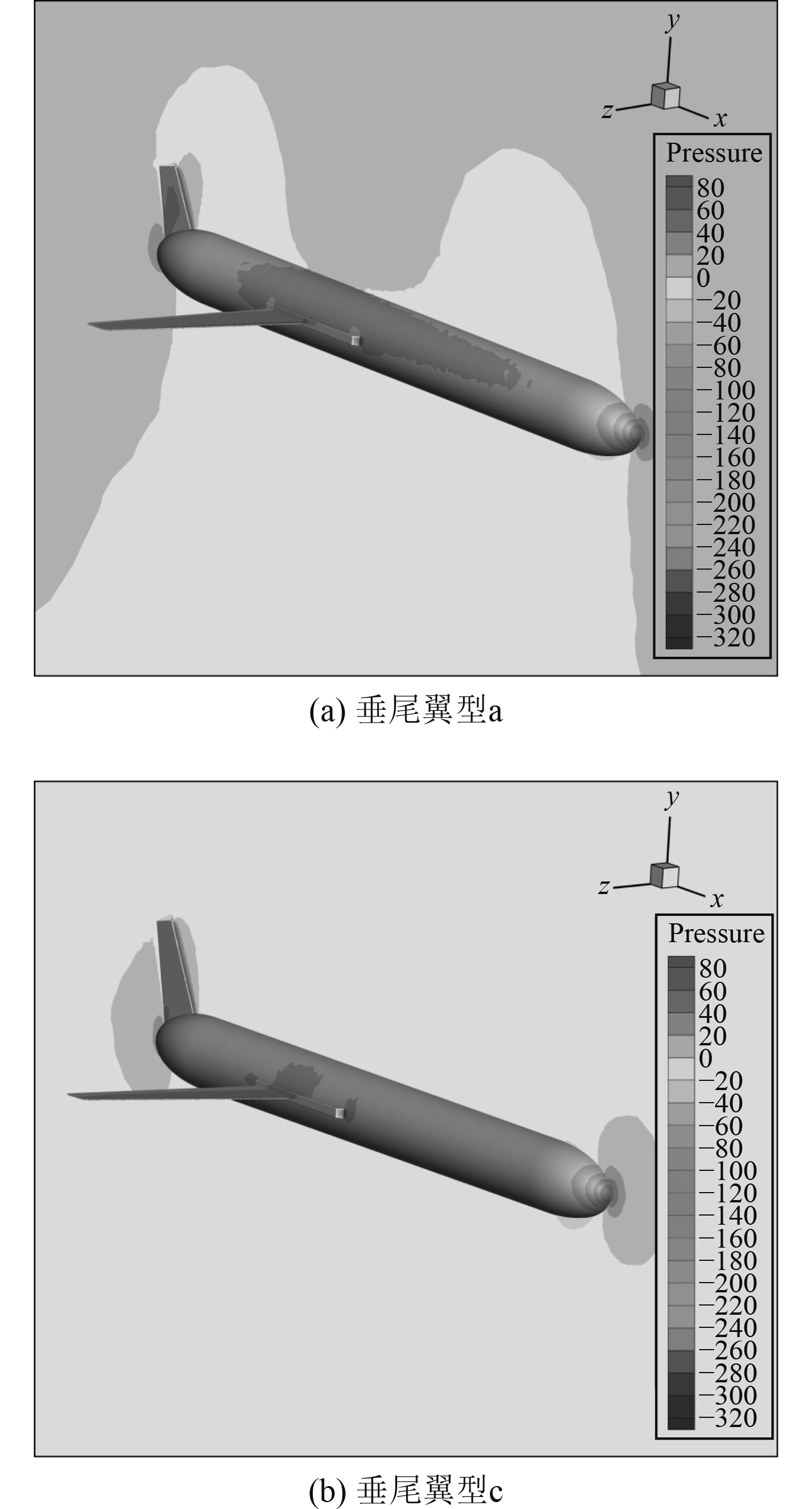
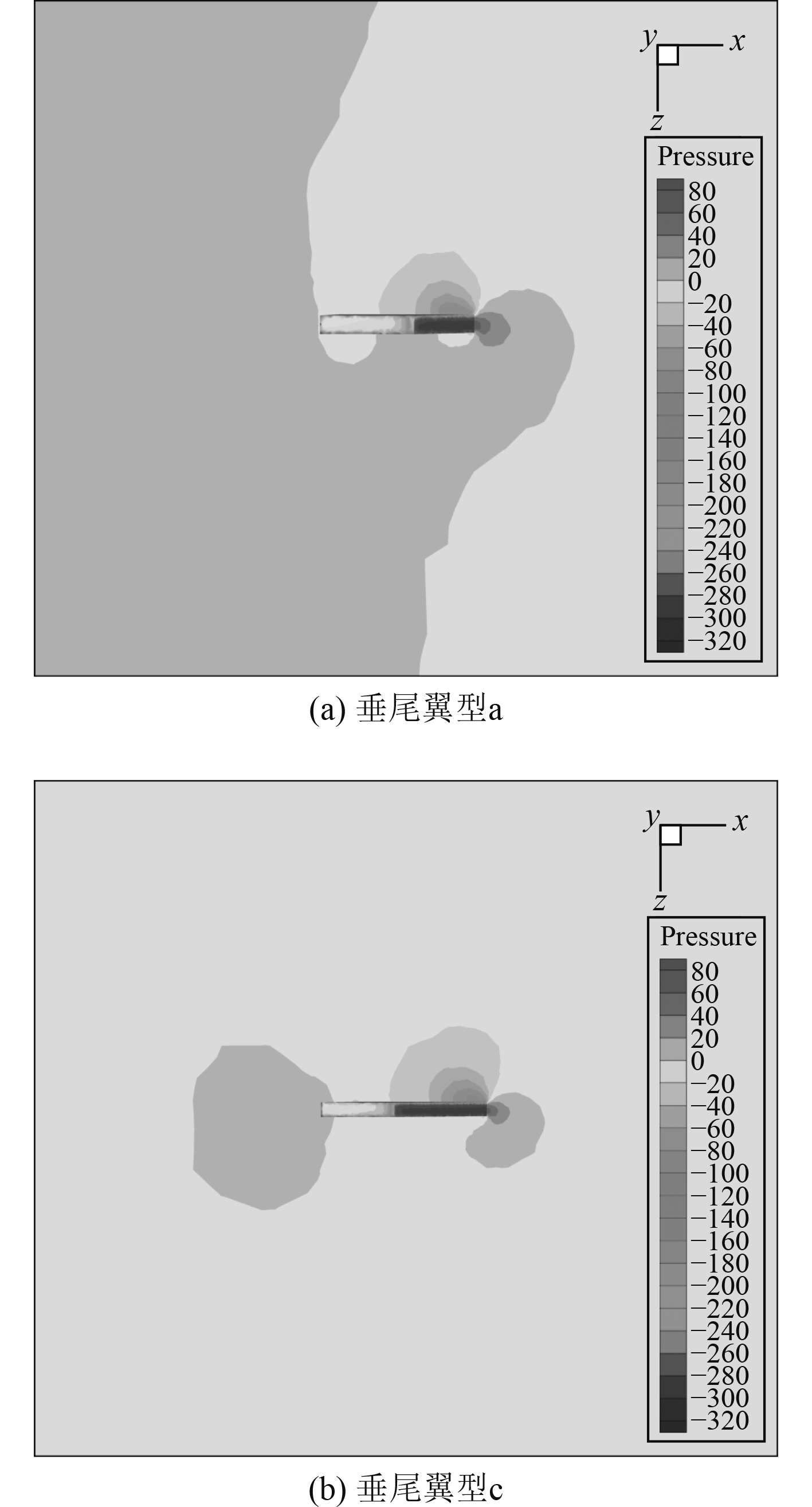
图14（a）和图14（b）分别为上浮运动中不同垂尾翼型下水下滑翔机右侧的整体静压云图。由图可知，垂尾展弦比的增加使侧向力作用点偏离重心，力臂增加，而垂尾展弦比过小，会造成受力面静压分布不均的现象。图15（a）和图15（b）分别为不同垂尾翼型下距离滑翔机横剖面200 mm处垂尾周围的局部流场，下方表示右侧，2种垂尾翼型下左右两侧静压差有轻微变化，展弦比过小的垂尾受力面静压分布不均，容易造成横滚的失稳。那么，综合考虑垂尾受力面积、力臂长度及左右两侧静压差等因素，随着垂尾展弦比的增加，使水下滑翔机向左侧发生横滚的力矩增大，机身朝着静不稳定的方向发展。

4.5 影响比重分析

综合水翼后掠角及垂尾展弦比对水下滑翔机横向静稳定性影响，为了提升水下滑翔机在横向洋流干扰下的自恢复特性，采用一次变化法进行影响比重分析，由此来确定水下滑翔机的附体水动力参数选型。影响比重因子定义为：

${S_i} = \Delta {y_j}/\Delta {x_i}(i = 1,2\;j = 1)\text{。}$

(9)

其中， ${S_i}$ 表示第i个参数对第j个目标参数的影响程度系数， $\Delta {x_i}$ 表示第i个参数的变化率， $\Delta {y_j}$ 表示第j个目标参数的变化率，分别分析下潜及上浮2个运动状态下不同水动力参数对横向静稳定性影响的比重。

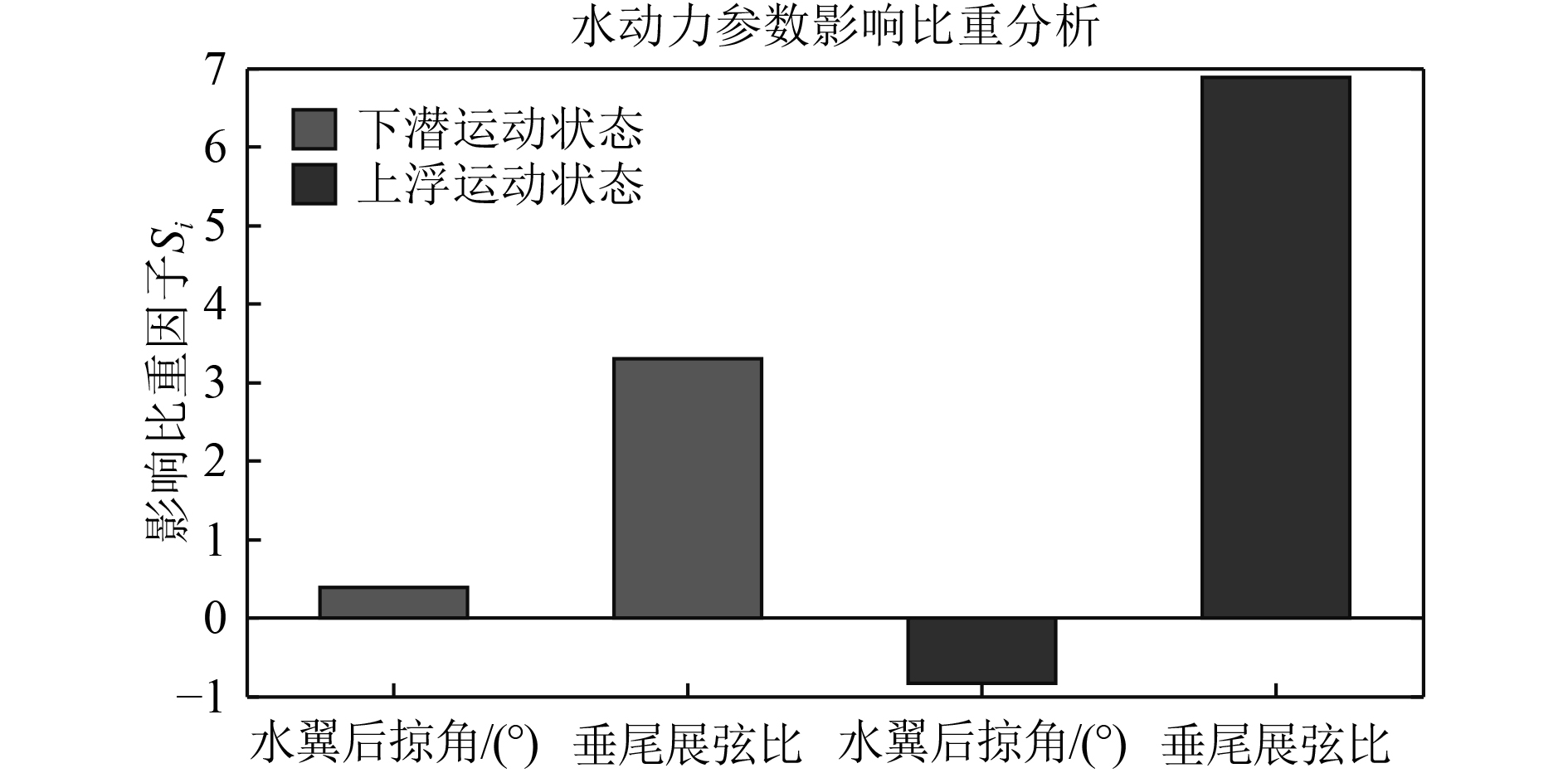
结果分析如图16所示，处于下潜运动状态时，横向静稳定导数的变化率受水翼后掠角变化率的影响程度系数为0.3908，而受垂尾展弦比变化率的影响程度系数为3.037，说明水翼后掠角及垂尾展弦比的增加会使横向静稳定导数减小并偏离零值，增强了下潜状态的横向静稳定性，但增强幅度有明显差异，垂尾展弦比对横向静稳定性的影响比重更大；处于上浮运动状态时，横向静稳定导数的变化率受水翼后掠角变化率的影响程度系数为−0.8292，而受垂尾展弦比变化率的影响程度系数为6.889，说明水翼后掠角的增加会使横向静稳定导数增大并趋近零值，增强了上浮状态的横向静稳定性，垂尾展弦比的增加会使横向静稳定导数减小并偏离零值，降低了上浮状态的横向静稳定性，且影响比重上仍然是垂尾展弦比占主导因素。为了保证水下滑翔机在下潜及上浮阶段都具备一定的横向静稳定特性，水动力参数的选型上应该更偏向增加水翼后掠角而选取适中的垂尾展弦比，如水翼翼型e及垂尾翼型b。

5 结　语

本文主要基于水下滑翔机的水动力参数，开展改善横向静稳定性的研究，并通过数值仿真及真实海上试验初步验证了水动力参数设计的合理性，主要结论如下：

1）通过对水下滑翔机不同水翼后掠角进行升阻比仿真试验，说明在水翼展弦比一定的情况下，后掠角对滑翔经济性的影响较小，但超过一定范围后继续增加后掠角，在较大攻角下，后掠角的增加会导致滑翔效率降低，此仿真结论可以作为研究横向静稳定性的前提条件，对水翼后掠角作出范围上限界定。

2）无论是下潜运动还是上浮运动，水翼后掠角的增加对水下滑翔机横向静稳定性起到了促进作用。下潜状态中，后掠角的增加会使横向静稳定性不断增强，有利于平衡状态的恢复；上浮状态中，后掠角的增加会改善横向静不稳定状态，向着横向静稳定的趋势发展。

3）垂尾展弦比对横向静稳定性的影响具有双重性，下潜状态中，增加垂尾展弦比有利于平衡状态的恢复，起到了促进静稳定的作用；上浮状态中，垂尾展弦比的增加会增加静不稳定力矩的绝对值，以至于水翼后掠角无法减缓横滚继续转动。

4）研究了水翼后掠角及垂尾展弦比对横向静稳定性的影响比重，结果表明，无论是下潜状态还是上浮状态，垂尾展弦比始终占主导因素。