2. 华南理工大学 土木与交通学院,广东 广州 510640
2. School of Civil and Transportation Engineering, South China University of Technology, Guangzhou 510640, China
大型海上结构物的运输方式,有采用拖轮通过系缆直接拖曳浮于水面上结构物的湿拖方式以及将结构物装载于半潜船甲板上的干拖方式。由于运输船舶的运动响应复杂且难以精准预测,因此如何准确地预报和模拟船舶的运动响应,尤其是船舶的横摇,是水动力学研究的前沿课题之一。文献[1]采用单纯型算法,研究如何获得优化船舶运动响应的水动力系数。文献[2]基于矢量分析方法,进行船舶运动响应轨迹分析和预测。文献[3]研究了船舶不同舭龙骨配置对船舶在波浪中横摇阻尼及响应的影响。文献[4]研究对比了动态和静态工况下横摇复原力矩,计算在不同横浪规则波下的横摇阻尼。文献[5]采用人工智能机械学习方法,预测驳船横摇运动响应幅值算子。文献[6]应用重叠网格方法及RANS方法开展了船模在顶浪条件下运动响应的数值模拟。文献[7]利用Fluent软件和势流理论计算得到不同吃水船舶在波浪中升沉、纵摇运动响应和附加阻力值。
在针对半潜船干拖运输大型海工结构物的运动响应方面,文献[8]采用软件Hydrostar,对某大型半潜船进行了波浪载荷的直接计算。文献[9]基于势流理论对浮式平台干拖式运输方案进行了数值分析,针对运输绑扎固定系统的特性开展了研究。文献[10]基于源汇分布法的装载平台半潜驳船运动响应与波浪荷载的计算方法,并分析了波浪周期、浪向对装载半潜驳船运动响应的影响。文献[11]研究某5万吨级半潜船航行耐波特性,分别通过耐波性模型试验、实船试验和三维水动力数值模拟方法研究该半潜船在不同海况下的水动力运动响应。以往研究或关注精确预测船舶运动响应及横摇阻尼理论方法,或关注货物干拖运输时半潜船自身的运动响应和载荷,而对于半潜船运输超大型结构物过程中,船舶运动响应和干拖结构物所受加速度在不同海运参数下的影响规律,则鲜有研究。为此,本文利用利用波浪势流理论及运动响应控制条件的数值模拟方法,以迄今为止世界规模最大半潜式“海上渔场”从中国青岛干拖运输至挪威为例,研究不同海况、航行吃水及系统重心高度等参数下,半潜船运动响应和超大型结构的加速度特性,获得不同参数的影响规律。
1 基本理论由于受到波浪载荷的作用,船舶除了恒速前进运动外,还有6个自由度的摇荡运动,即纵荡
| $M\frac{{{{\rm{d}}^2}X}}{{{\rm{d}}{t^2}}} + C\frac{{{\rm{d}}X}}{{{\rm{d}}t}} + KX = {F_{}} {\text{。}}$ | (1) |
式中:
在不规则的波浪中,船体对波浪的响应,可看作是线性时不变系统。由随机过程理论可知,在海浪的作用下(输入),其响应——波浪载荷(输出)亦将是均值为零的平稳正态随机过程。输入与输出满足下式:
| ${S_r}({\omega _e}) = {H^2}({\omega _e}){S_w}({\omega _e})\,{\text{。}}$ | (2) |
式中:
利用响应谱的各阶矩可计算出波浪载荷的各种特征值,船舶响应谱的各阶矩表示为:
| ${m_n} = \int_0^\infty{{S_r}({\omega _e})} \omega _e^n{\rm{d}}{\omega _e}, n = 0,1,2\cdots \,{\text{。}}$ | (3) |
平均跨零周期为:
| ${T_z} = 2\text{2π} \sqrt {\frac{{{m_0}}}{{{m_2}}}}\,\,\,,$ | (4) |
响应有义幅值表示为:
| ${A_{1/3}} = 2\sqrt {{m_0}} \,\,\,,$ | (5) |
响应极值表示为:
| $MPE = \sqrt {2{m_0}\ln \left[ {\frac{{{t_e}}}{{{T_z}}}} \right]}{\text{。}}$ | (6) |
式中:
求得荡位移矩阵和波浪载荷后,船舶上关注点的纵向加速度可表示为:
| $ \begin{split}{a}_{longitudinal}=&{\stackrel{··}{x}}_{G}-({y}_{p}-{y}_{G})\cdot \stackrel{··}{\psi }+\\ &({z}_{p}-{z}_{G})\cdot \stackrel{··}{\theta }-g\cdot \mathrm{sin}\theta \end{split}\,\,\,,$ | (7) |
船舶上关注点的横向加速度可表示为:
| $ \begin{split}{a}_{transverse}=&({x}_{p}-{x}_{G})\cdot \stackrel{··}{\psi }+\stackrel{··}{{y}_{G}}-\\ &({z}_{p}-{z}_{G})\cdot \stackrel{··}{\varphi }-g\cdot \mathrm{sin}\varphi \end{split}\,\,\,,$ | (8) |
船舶上关注点的垂向加速度可表示为:
| $ {a}_{vertical}=-({x}_{p}-{x}_{G})\stackrel{··}{\cdot \theta }+({y}_{p}-{y}_{G})\cdot \stackrel{··}{\varphi }+\stackrel{··}{z}\,\,\,{\text{。}}$ | (9) |
式中:
“海上渔场”是迄今为止世界上规模最大的半潜式智能海上渔场,其主体是一个由12根黄色立柱所组成的巨大型圆柱结构,其中6个立柱下面布置有6个圆锥形压载舱,并在最下面布置有6个圆柱。立柱间采用桁架结构连接,并布置有渔网。托运前,使用浮装的方式,将其装载至半潜运输船的载货甲板上。“海上渔场”及承担拖航半潜运输船“华海龙”的主要结构参数见表1。
|
|
表 1 干拖运输方案主要参数 Tab.1 Main parameters of dry tow transportation |
由于“海上渔场”结构庞大、超宽,“华海龙”装载该“海上渔场”后,货物外飘悬出船舷两侧各39.5 m,结构最高点72 m,因此采用了在渔场结构底部增加支撑梁的方式,以减小“海上渔场”实际垂悬宽度及增大“海上渔场”距水面空隙,最后的装载布置三维模型如图1所示。
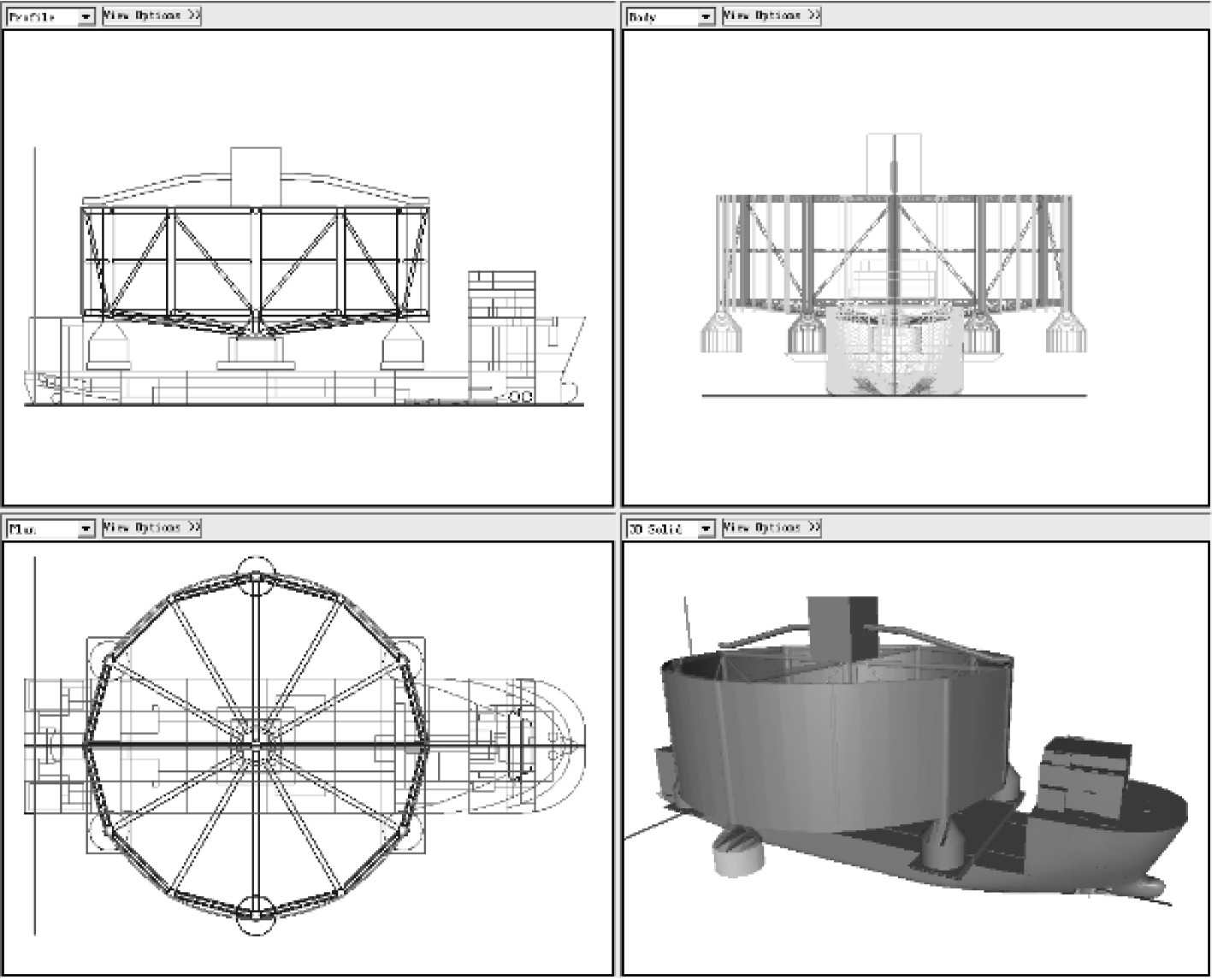
|
图 1 配载三维模型示意图 Fig. 1 Schematic diagram of loading 3d model |
渔场的巨大悬垂、超高及结构单薄,且跨洋从青岛到挪威共航行15500多海里,这样的主体结构超宽外飘海运在半潜船运输史上也是首次。而运输过程中恶劣海况导致船舶运动产生的动载荷,对其结构强度破坏具有一定风险,因此对海运过程中的特性分析就成为能否成功运输“海上渔场”的关键。
2.2 计算模型本文采用Octopus软件建立干拖运输的三维运动响应数值模拟模型,如图2所示。根据“海上渔场”干拖运输各种工况数据(如吃水、重心高度、惯量半径及加速度关注点坐标等),输入到计算模型中,以保证模拟的真实有效性。

|
图 2 数值模拟的水动力模型 Fig. 2 The Hydrodynamic model for numerical simulation |
中国青岛经好望角至挪威的航线,跨越了不同的海区,遭遇的海况也会因季节及航向不同而有很大的区别,因此模拟船舶运动响应(主要为横摇、纵摇及垂荡)和渔场薄弱结构点(因货物及船舶左右对称,关注点坐标只建左舷结构薄弱处,其坐标为
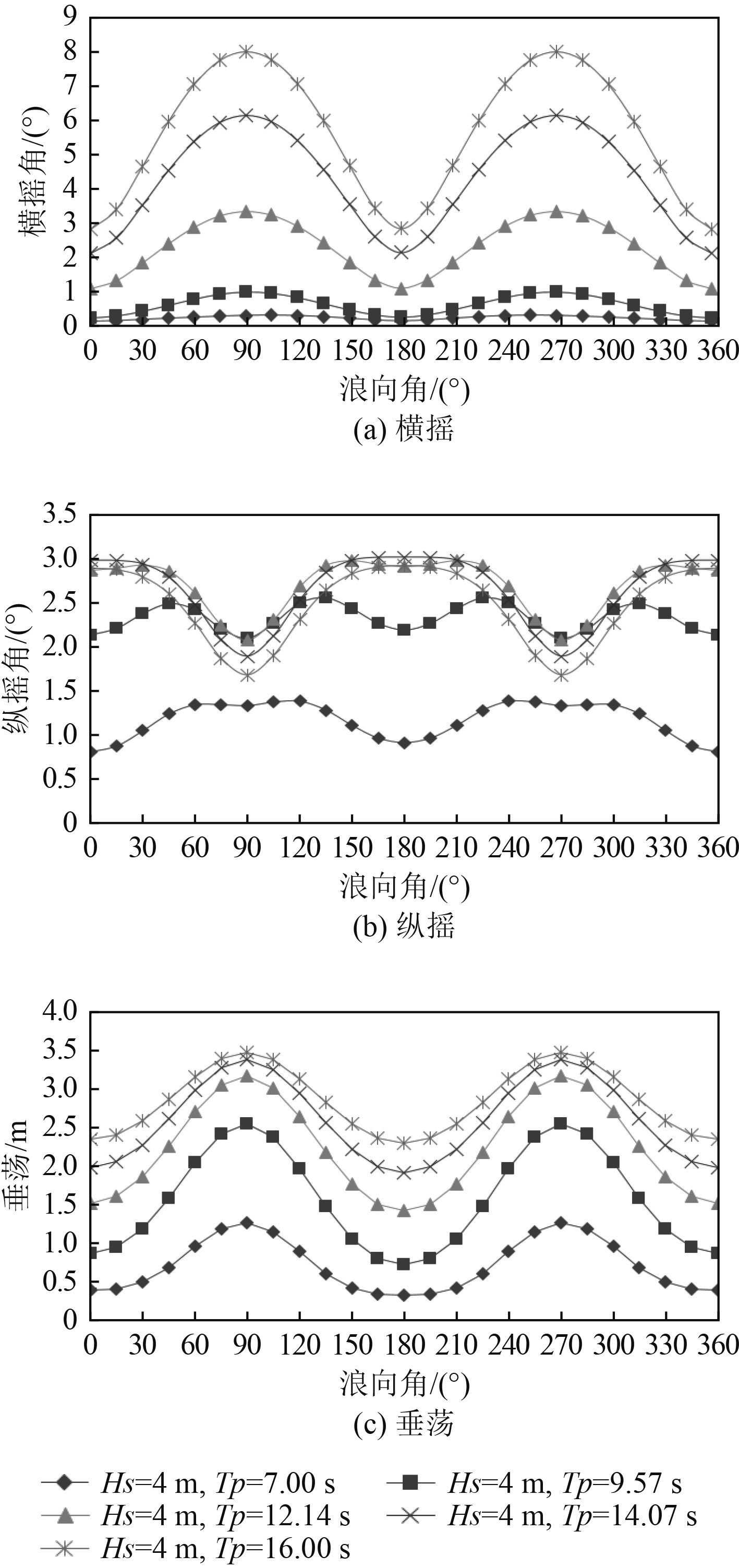
|
图 3 船舶的运动响应随海况变化规律 Fig. 3 The motion responses of the ship under different the sea states |
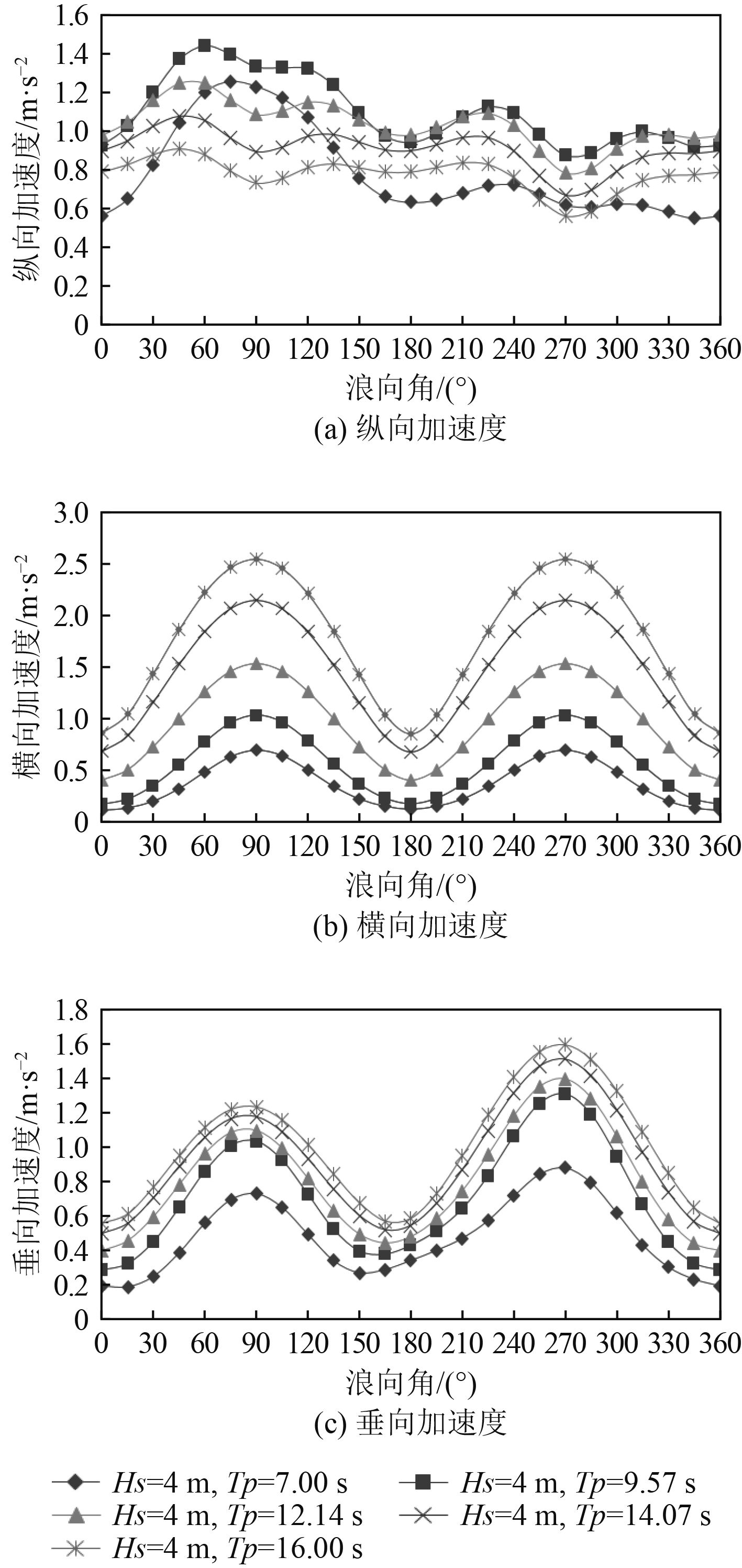
|
图 4 渔场关注点的加速度随海况变化规律 Fig. 4 The accelerations of the weak point under different sea states |
由图3可知,横摇和垂荡在首浪和尾浪响应最小,在横浪响应最大,均随遭遇海况谱峰周期的增加而增加;横摇随谱峰周期增加而逐渐显著增大,垂荡随谱峰周期增加而逐渐显著减小;纵摇在谱峰周期较小时随浪向角的变化不明显,在谱峰周期较大时随浪向角的变化与横摇角的变化趋势基本相反。
从图4关注点横向和垂向加速度变化随浪向角趋势基本一致,在首浪和尾浪响应最小,在横浪响应最大;横向加速度随谱峰周期增加而逐渐显著增大,垂向加速度随谱峰周期呈线性增加,且同侧横浪(左舷来浪,浪向角270°)增加更明显;纵向加速度随浪向角变化趋势不明显,在横浪时有减小趋势,随谱峰周期增加的整体变化趋势为缓慢减小。
3.2 航行吃水变化的影响干运航行的干舷越大,吃水就越小,整体的船舶排水量也会随之变小,航行中船舶的运动响应和“海上渔场”的加速度可能会加剧,但是如果吃水太大,也会导致渔场外飘结构砰击发生的概率增大,因此对船舶运动响应和渔场关注点加速度在不同船舶航行吃水工况下的变化情况进行模拟分析,计算结果见图5和图6。
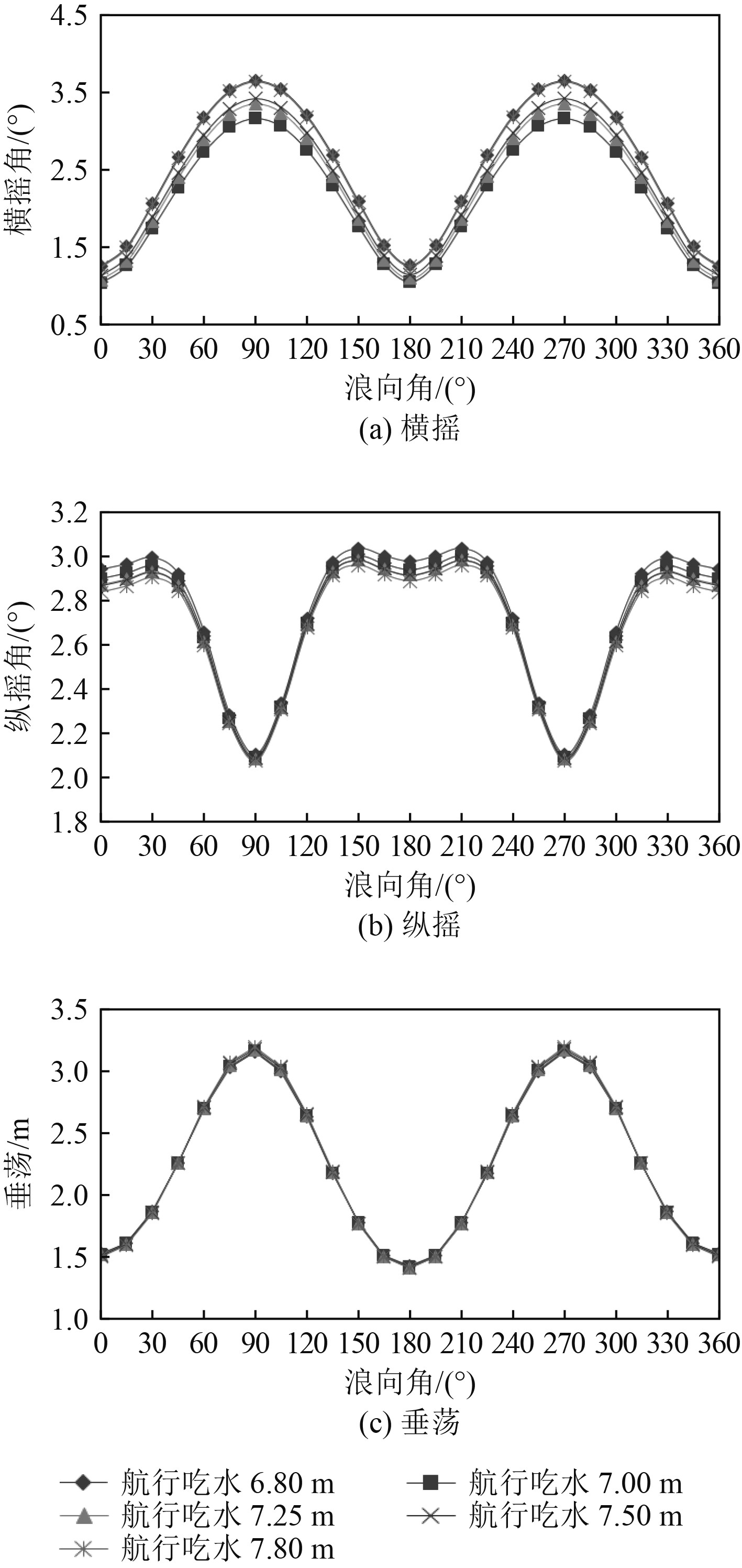
|
图 5 船舶的运动响应随吃水变化规律 Fig. 5 The motion responses of the ship varies with the draft |
|
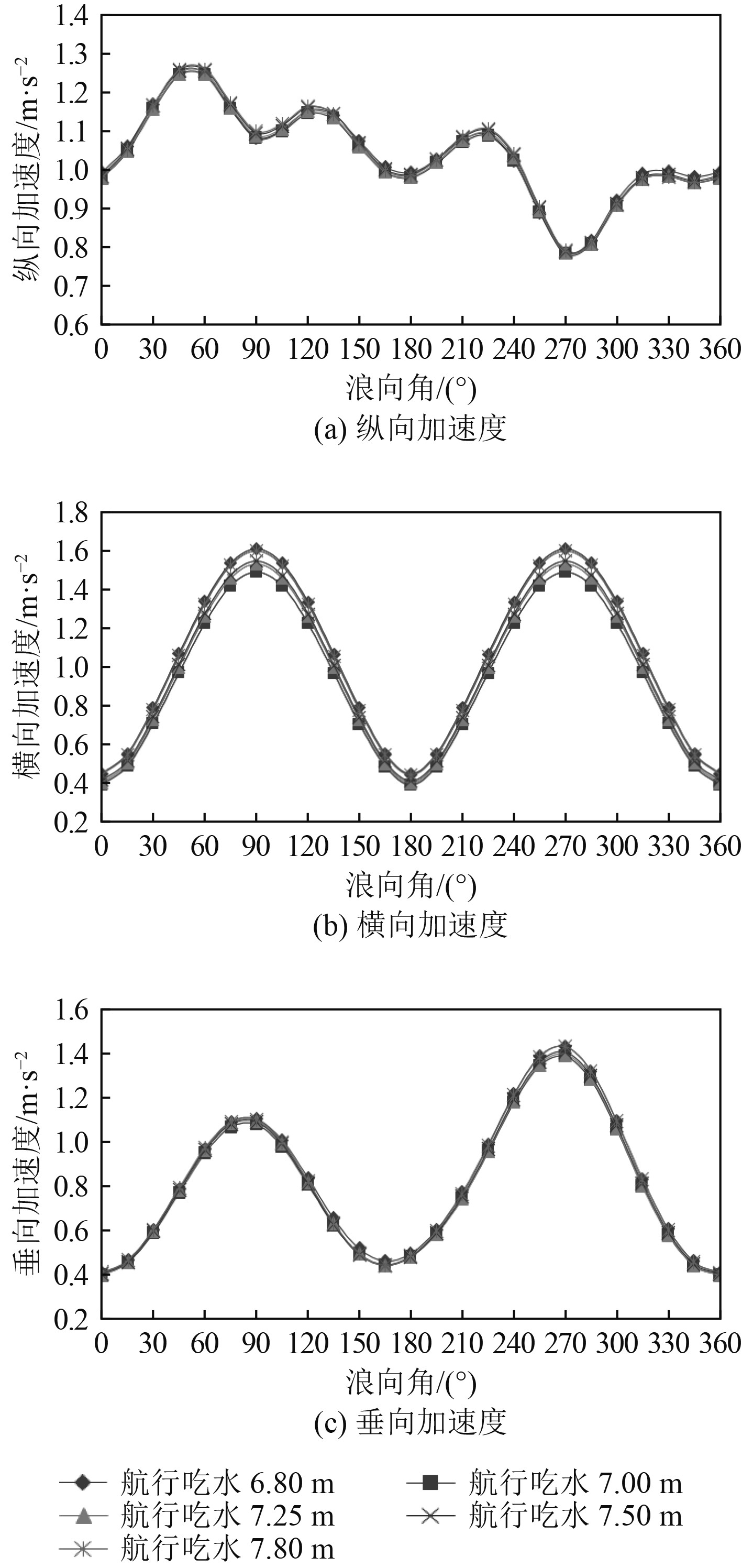
图 6 渔场关注点的加速度随吃水变化规律 Fig. 6 The accelerations of the weak point varies with the draft |
由图5可知,横摇和垂荡在横浪时响应最大,首浪和尾浪时响应最小,横摇随航行吃水的增加而稍微增大,但不明显;垂荡随航行吃水增加而几乎不变;纵摇在横浪时减小很显著,但在横浪时随航行吃水变化不明显,在随除横浪附近的其他浪向角下,变化不明显,但随航行吃水的增大而稍微减小。
由图6可知,横向和垂向加速度随浪向角趋势基本一致,在首浪和尾浪响应最小,在横浪响应最大,垂荡加速度在同侧横浪(左舷来浪,浪向角270°)增加更明显;纵向和垂向加速度基本不随航行吃水的变化而变化,横向加速度随航行吃水的增大而稍微增大,纵向加速度在斜浪时有增大趋势。
3.3 系统重心变化的影响在干拖运输中,通常利用调整船舶和货物压载水的方式,来控制船舶系统重心,进而控制船舶的运动响应,由于调整系统重心影响了船舶的稳性以及横摇周期等,因此模拟船舶运动响应和渔场关注点加速度在不同系统重心下的变化规律,十分有必要,计算结果见图7和图8。
|
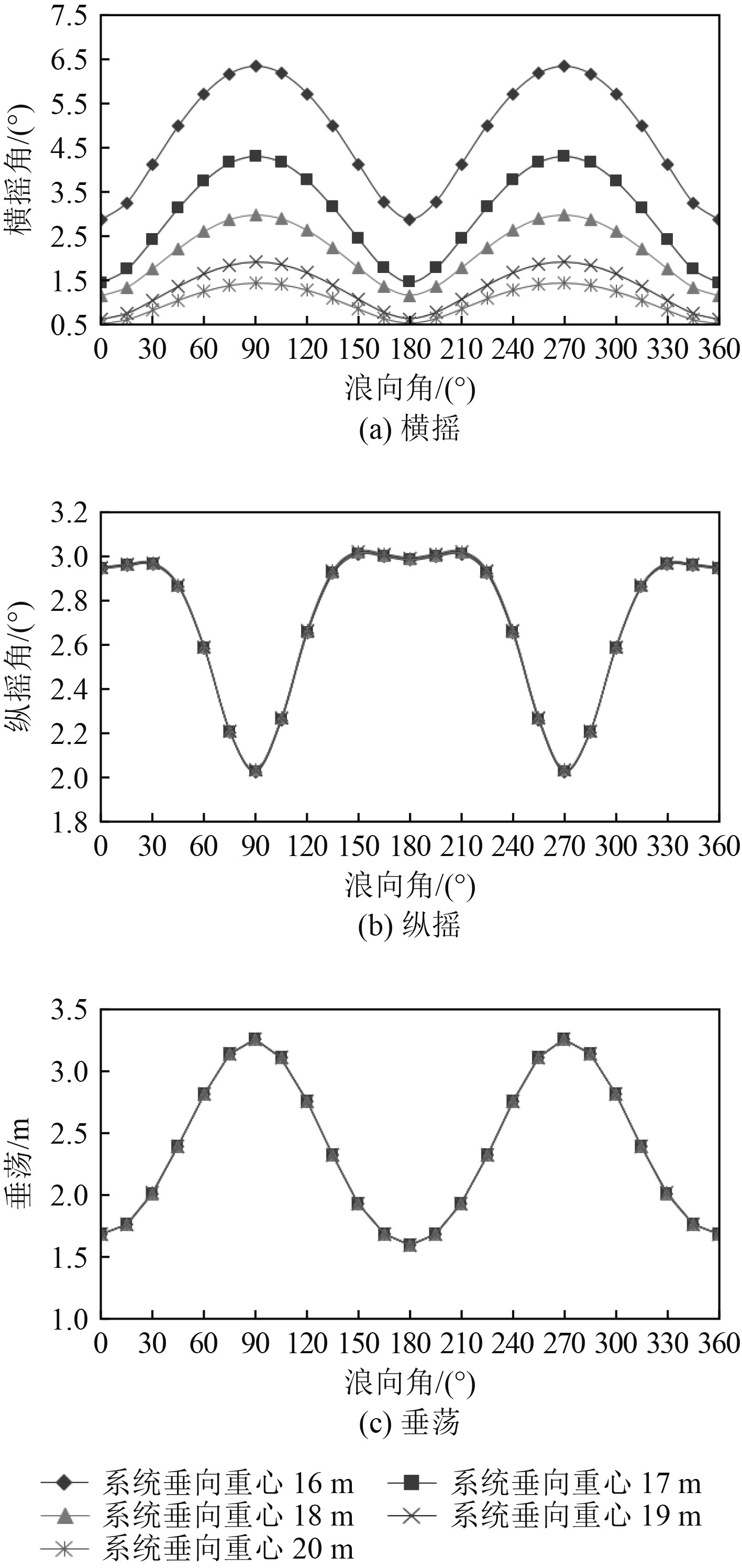
图 7 船舶的运动响应随系统重心变化规律 Fig. 7 The motion responses of the ship varies with the center of gravity |
|
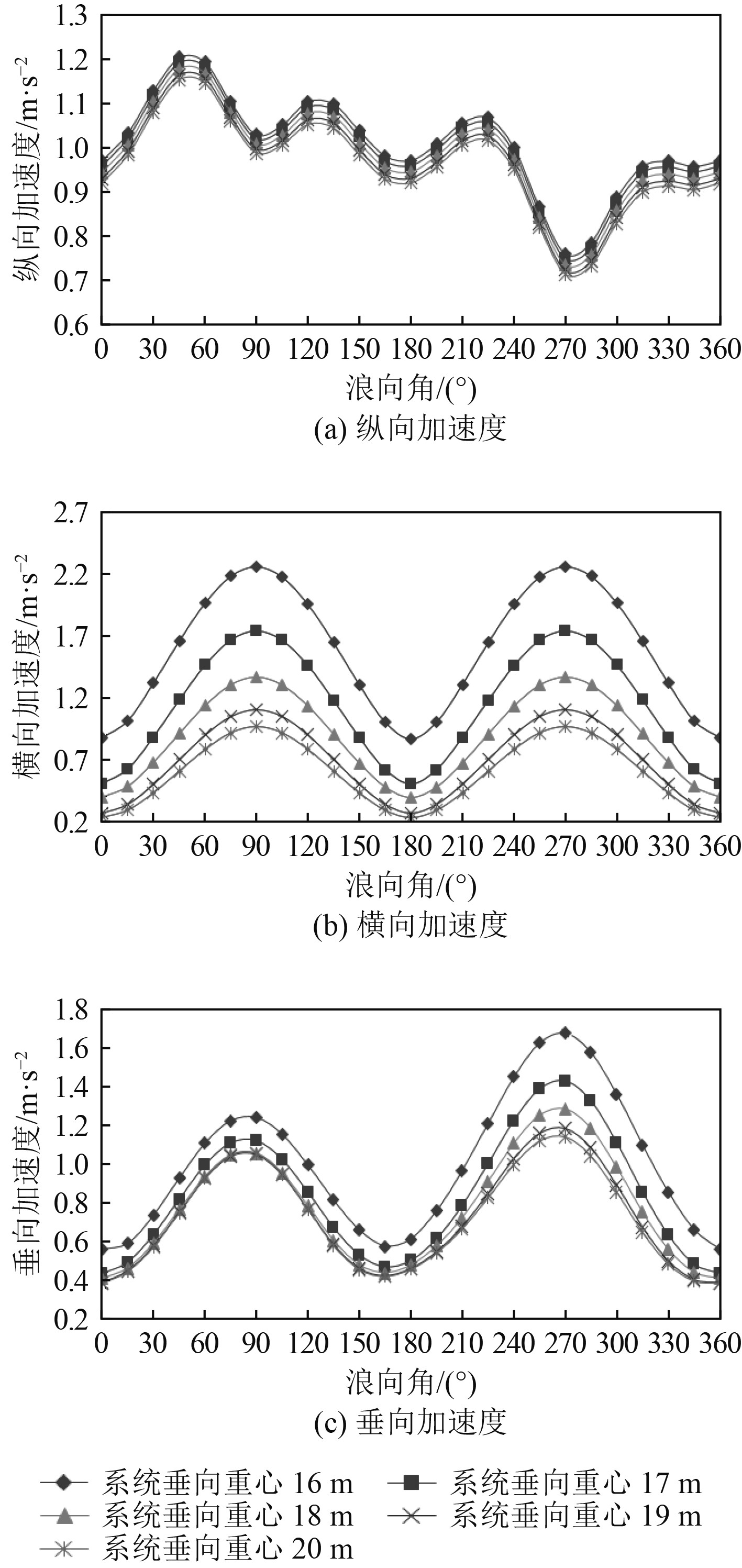
图 8 关注点的加速度随系统重心变化规律 Fig. 8 The accelerations of the weak point varies with the center of gravity |
由图7可知,纵摇和垂荡垂荡基本不受系统重心变化的影响,垂荡和横摇在横浪时响应最大,首浪和尾浪时响应最小;纵摇在横浪时减小很显著,但在横浪时随系统重心变化不明显;横摇随系统重心的增加而减小,尤其是在横浪时,减小的趋势显著。
横向和垂向加速度随浪向角趋势基本一致,在首浪和尾浪响应最小,在横浪响应最大,垂荡加速度在同侧横浪(左舷来浪,浪向角270°)增加更明显;纵向、横向及垂向加速度均随系统重心的增大而减小,且横向加速度减小显著,垂向加速度减小次之,纵向加速度减小最不明显。
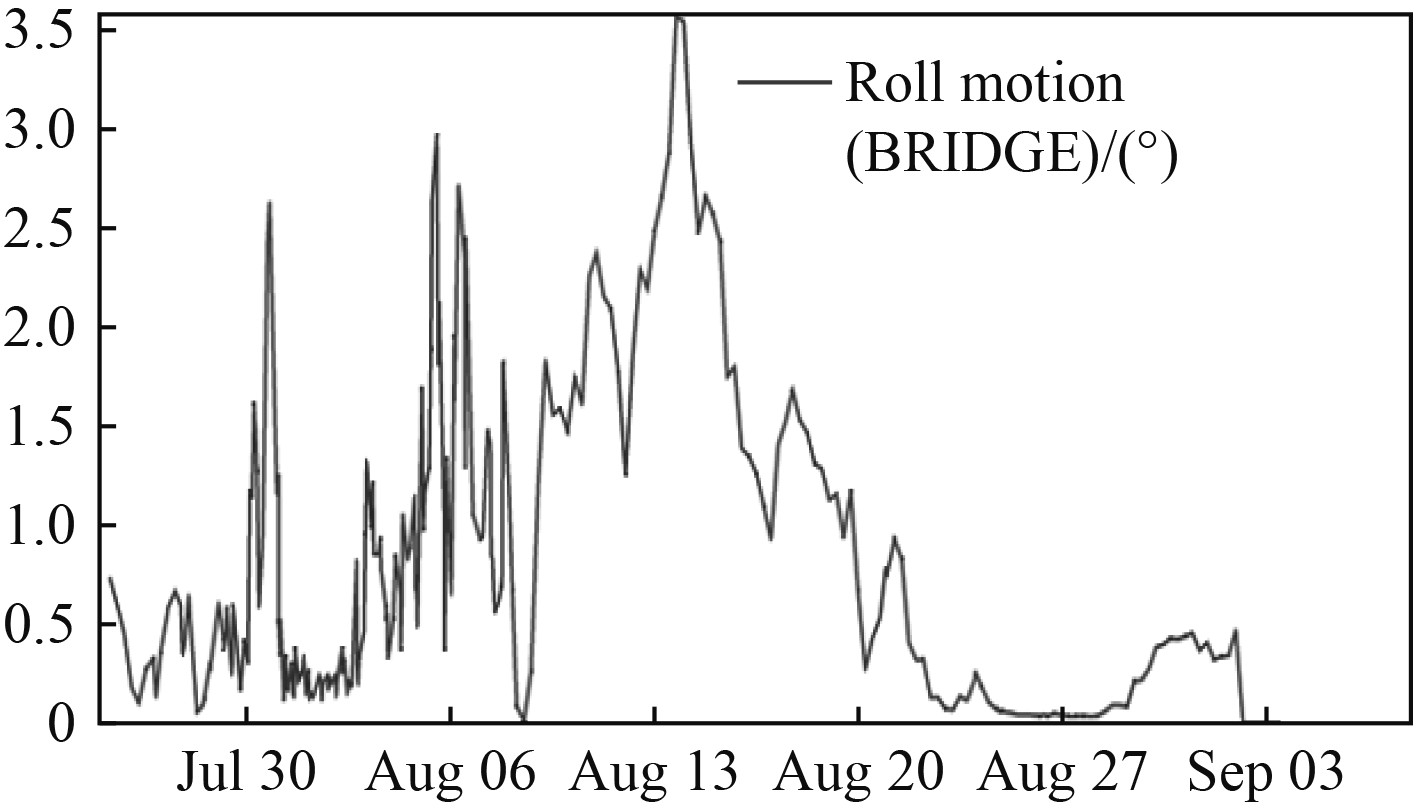
4 数值模拟结果与工程实践对比分析渔场干拖运输是根据运输特性的数值分析结果进行干拖的控制,即在满足规范条件下,尽量减小航行吃水、增大系统重心,同时进行航行首向控制,航行过程中的船舶运动用船载船舶传感器等实时记录数据,其中横摇记录结果如图9所示。
|
图 9 结果对比图 Fig. 9 Comparison of the results |
通过将干拖运输运动响应数据与数值模拟计算结果进行对比,船舶运动响应极值统计情况与本文计算结果高度吻合,船舶横摇方面误差在8%的范围内,证明数值模拟方法是有效可靠的。
5 结 语通过对超大型渔场干拖运输特性的数值模拟分析,研究海况、航行吃水及系统重心等不同参数下船舶响应及渔场加速度等变化情况,数值计算与分析表明:
1)横摇、垂荡、关注点横向加速度、垂向加速度随浪向角基本呈“m”字形,即在首浪和尾浪下最小,在横浪时最大,且随遭遇海况谱峰周期增加而增加,纵摇在横浪时减小较显著,因此干运过程中需根据气象预报气进行首向控制,减少船舶的遭遇横浪情况;
2)纵摇、横摇、垂荡、关注点横向、垂向加速度随航行吃水变化不明显,因次航行吃水的控制主要是看干舷以及航行阻力的要求;
3)横摇、横向加速度及垂向加速度随系统重心的增加则减小显著,因此在满足稳性前提下,尽可能提高系统重心,渔场结构的加速度也会显著降低。
| [1] |
NGUYEN M C, TRAN K T. Applying simplex algorithm for ship's motion simulation optimization by using maneuvering tests data[J]. International Journal on Advanced ence Engineering and Information Technology, 2020, 10(2): 491. DOI:10.18517/ijaseit.10.2.11252 |
| [2] |
LUO Weidong, ZHANG Guojun. Ship motion trajectory and prediction based on vector analysis[J]. Journal of Coastal Research, 2020, 95(S1). |
| [3] |
JIANG Yichen , DING Yunfeng , SUN Yuan , et al. Influence of bilge-keel configuration on ship roll damping and roll response in waves[J]. Ocean Engineering, 2020, 216. |
| [4] |
SADRA KIANEJAD, HOSSEIN ENSHAEI, JONATHAN DUFFY, et al. Calculation of ship roll hydrodynamic coefficients in regular beam waves[J]. Ocean Engineering, 2020, 203. |
| [5] |
JAE HWAN LIM, HYO JAE JO. Prediction of barge ship roll response amplitude operator using machine learning techniques[J]. Journal of Ocean Engineering and Technology, 2020, 34(3). |
| [6] |
陶志奇, 王慧, 徐伟光, 等. 船舶在顶浪不规则波中的运动响应数值分析[J]. 船舶力学, 2020, 24(9): 1134-1141. DOI:10.3969/j.issn.1007-7294.2020.09.005 |
| [7] |
余建星, 于佳晖, 余杨, 等. 不同吃水条件下船舶运动及附加阻力的研究[J/OL]. 哈尔滨工程大学学报: 1-7[2020-12-11]. http://kns.cnki.net/kcms/detail/23.1390.U.20201105.1203.002.html.
|
| [8] |
杨索贤, 李伟, 凌芳芳. 基于HYDROSTAR的大型半潜船波浪载荷预报研究[J]. 船舶工程, 2016, 38(S1): 5-7. |
| [9] |
吴波, 赵珍强, 程小明, 等. 浮式平台干拖式运输特性的数值模拟研究[J]. 船舶力学, 2020, 24(1): 63-69. |
| [10] |
于本福, 闫相祯, 蒋将, 等. 装载平台半潜驳船的运动响应和波浪荷载分析[J]. 中国科技论文, 2017, 12(19): 2236-2240. DOI:10.3969/j.issn.2095-2783.2017.19.015 |
| [11] |
刘旭, 陈晓明, 蔡连财. 5万吨级半潜船航行耐波性[J]. 中国航海, 2019, 42(4): 29-32+37. DOI:10.3969/j.issn.1000-4653.2019.04.006 |
 2021, Vol. 43
2021, Vol. 43
