2. 江苏现代造船技术有限公司,江苏 镇江 212003;
3. 广州文冲船舶修造有限公司,广东 广州 511462
2. Jiangsu Modern Shipbuilding Technology Co., Ltd., Zhenjiang 212003, China;
3. Guang zhou Wenchong Shipbuilding Co., Ltd., Guangzhou 511462, China
由于铝合金材料的焊后屈服强度相对钢材较低,且铝的密度是2.7 t/m3,若船体采用铝合金为建造材料,相比钢制船有很多的优点,如结构重量轻、耐海水腐蚀能力,且在相等航速下所需要的推进功率比钢船要低[1-2]。双体船不同于单体船,双体船利用连接桥连接的独特双片体结构,使其有了较大宽度的甲板,因此不能像分析单体船那样分析双体船了[3]。由于双体船其宽度大长度小的特点,在遭遇到横浪和斜浪时,它的总纵强度影响不大,但是会受到横向弯曲和扭转,这是双体船结构强度研究的重点,目前常采用有限元的分析方法来研究双体船的结构强度[4]。
1 模型概述 1.1 船体结构分析及属性船体的结构模型可以通过有限元分析软件MSC.Patran进行船体建模并设置相关属性,然后运用Nastran得到船体的应力分布和变形规律变化图[5]。
在进行有限元分析之前要先建立全船的有限元结构模型,由于连接桥是其承受应力的关键结构,本文结构调整主要对连接桥的结构进行研究分析[6]。采用国际单位制,即长度为mm,力为N,质量为t,密度为t/mm3,应力为MPa[7]。
1.2 全船有限元模型建立以某高速风电运维船为研究对象,其主尺度参数为总长19.88 m,型宽8 m,水线长19.38 m,片体宽2.60 m,型深3.20 m,设计吃水1.20 m,肋距#−1~#39均为0.50 m,航速25 kn,续航力150 nmile,航区为沿海航区。建立全船的有限元模型,对船体的总横强度、总扭转强度进行分析研究,特别是对双体船连接桥的强度进行调整分析[8]。
模型取全船范围内船体结构构件,全船构件尺寸均为设计尺寸。本文根据文献资料建立了2种结构骨架型式,即纵骨架式结构和全横骨架式结构。其中纵骨架式结构模型节点总数为27352,单元总数38698,有限元模型图如图1所示。全横骨架式结构模型节点总数27450,单元总数38061,有限元模型图如图2所示。材料为耐蚀高强度铝合金,模型结构质量见表1。
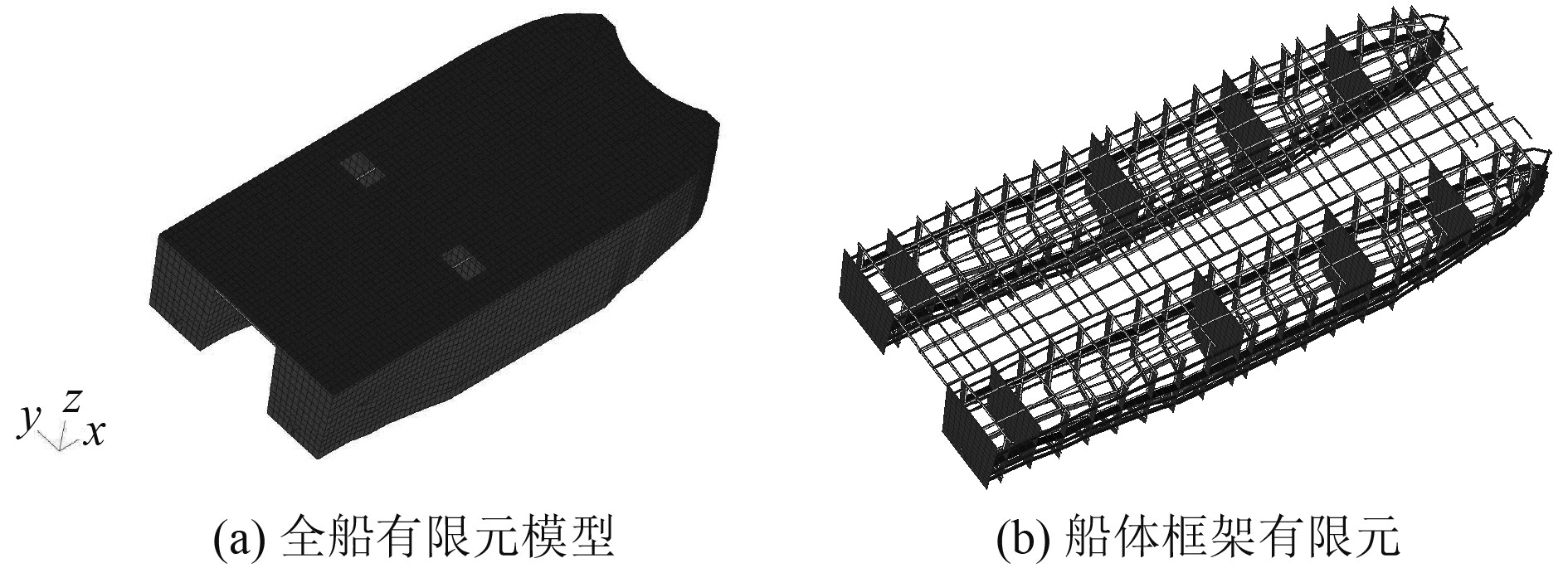
|
图 1 纵骨架式全船有限元模型 Fig. 1 Longitudinal frame type whole ship finite element model |
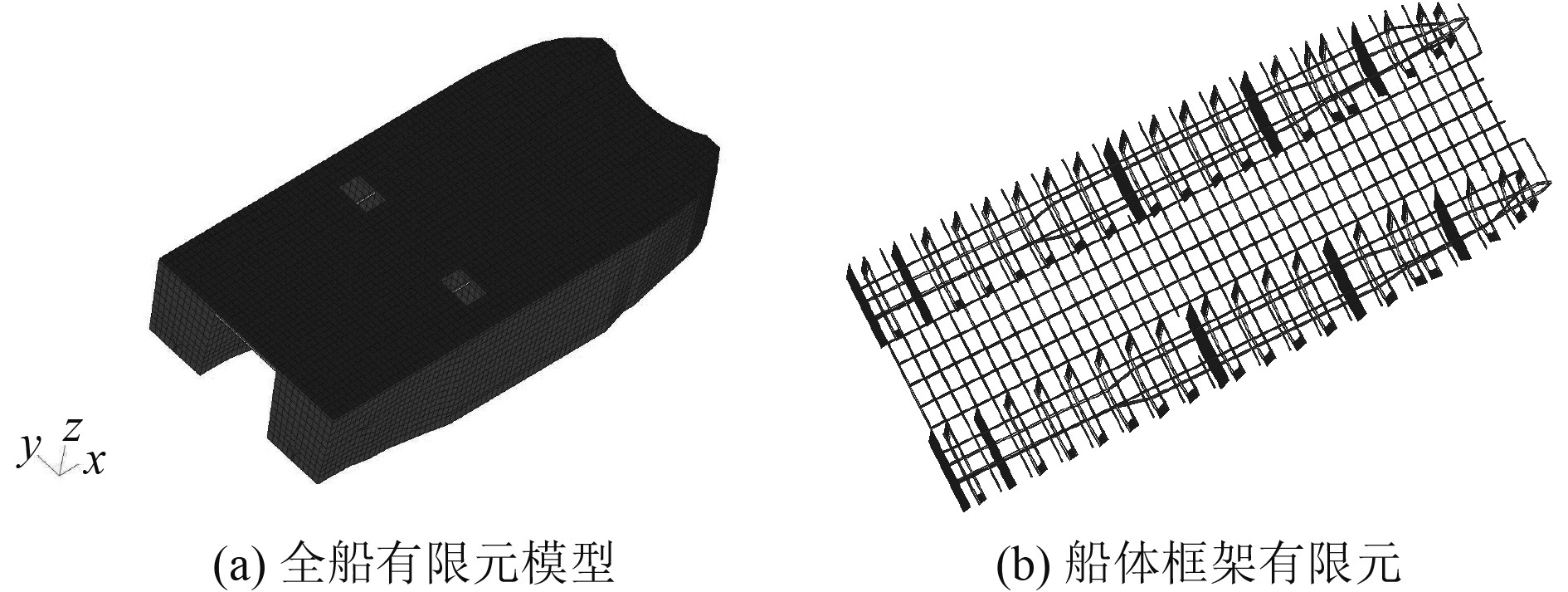
|
图 2 全横骨架式有限元模型 Fig. 2 Full transverse skeleton type finite element model of the whole ship |
|
|
表 1 模型结构质量 Tab.1 Model structure quality |
双体船在横浪作用下受到总横弯矩,其计算公式如下:
| $ {M}_{BX}={C}_{1}\Delta {a}_{cg}b\;{\rm {kN}}\cdot {\rm m}\text{,}$ | (1) |
式中:
总横弯矩
| ${F_y} = \frac{{{M_{BX}}}}{{Z + 0.5d}}\;{\rm{kN}}\text{。}$ | (2) |
计算时,将
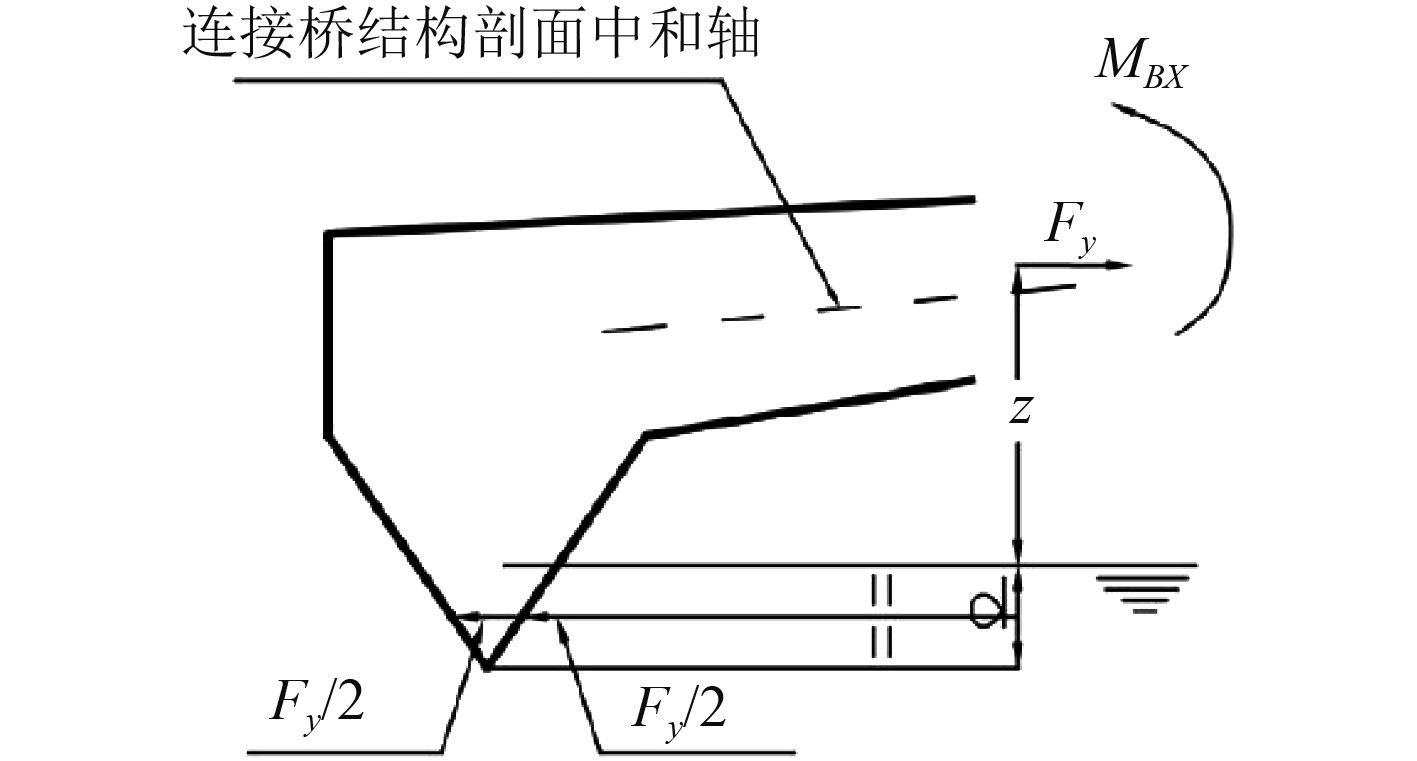
|
图 3
横向对开力
|
计算得横向对开力
双体船在海上高速航行时,会引起总横弯矩和垂向剪力,其计算公式如下:
| ${Q_t} = {C_2}\Delta {a_{cg}}\;{\rm{kN}}\text{。}$ | (3) |
式中:C2为航区系数,沿海航区
双体船在斜浪中航行时,受到横向Y轴的扭矩,其计算如下:
| $ {M}_{ty}={C}_{3}\Delta {a}_{cg}L\;{\rm{kN}}\cdot {\rm m}\text{,}$ | (4) |
其中:
计算得
对纵向X轴(即船长方向)的扭矩计算公式如下:
| $ {M}_{tx}=2{C}_{3}\Delta {a}_{cg}b\;{\rm{kN}}\cdot {\rm m}\text{。}$ | (5) |
计算得
双体船结构强度分析中,还要充分考虑弯扭组合情况,按CCS规范要求,本船结构分析中计算的载荷组合工况如表2所示。
|
|
表 2 双体船计算工况 Tab.2 Calculation conditions of catamaran |
根据参照《小水线面双体船指南》确定边界条件,可以在双体船的船首和船尾连接桥结构上选取3个点约束边界条件。各工况的边界条件的约束情况如表3~表5和图4~图6所示。表中,Cons表示固定,--表示自由,下同;
|
|
表 3 边界条件1支点约束情况 Tab.3 Boundary condition 1 fulcrum constraint |
|
|
表 5 边界条件3支点约束情况 Tab.5 Boundary conditions and 3 fulcrum constraints |
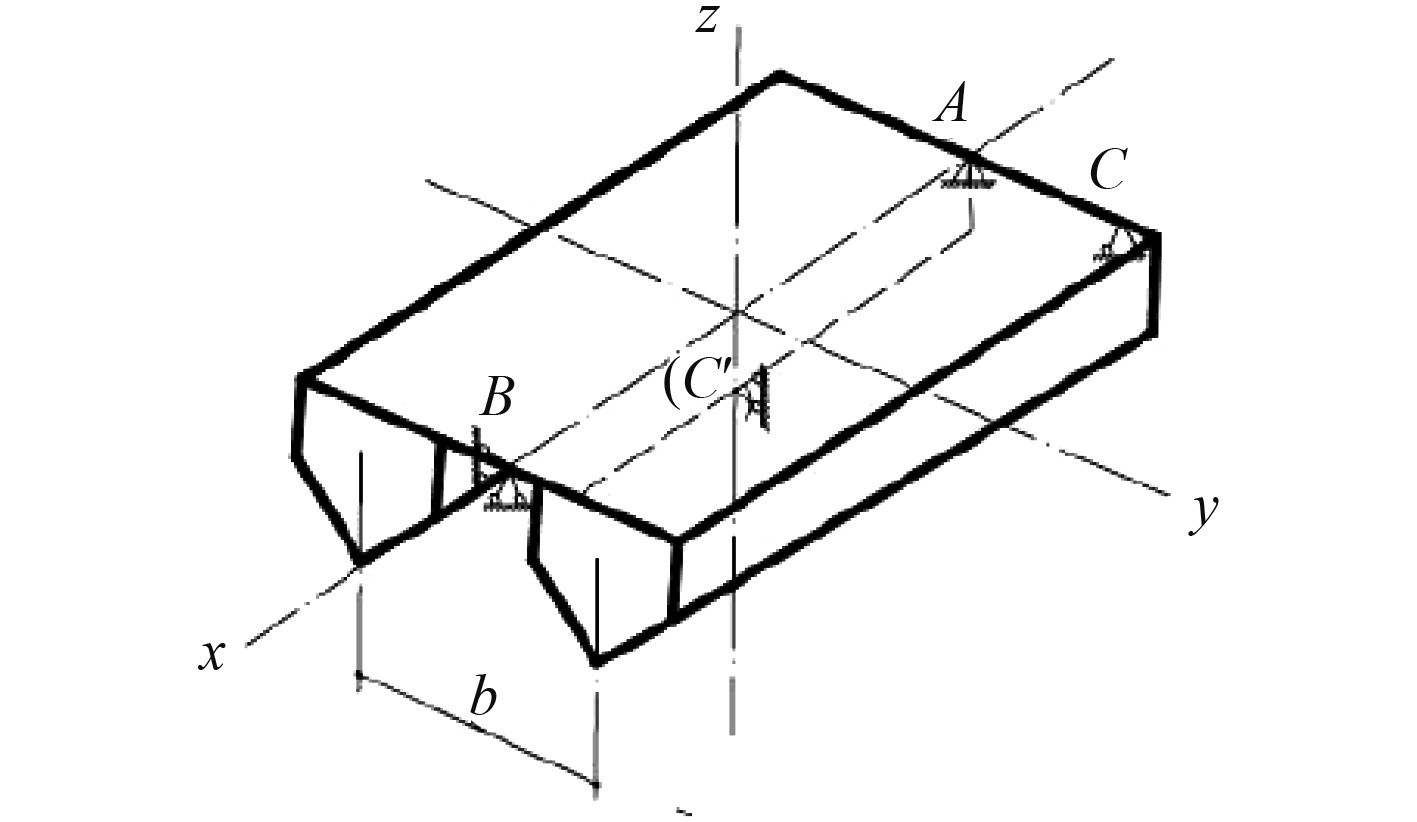
|
图 4 边界条件1支点约束示意图 Fig. 4 Schematic diagram of boundary condition 1 fulcrum constraint |
|
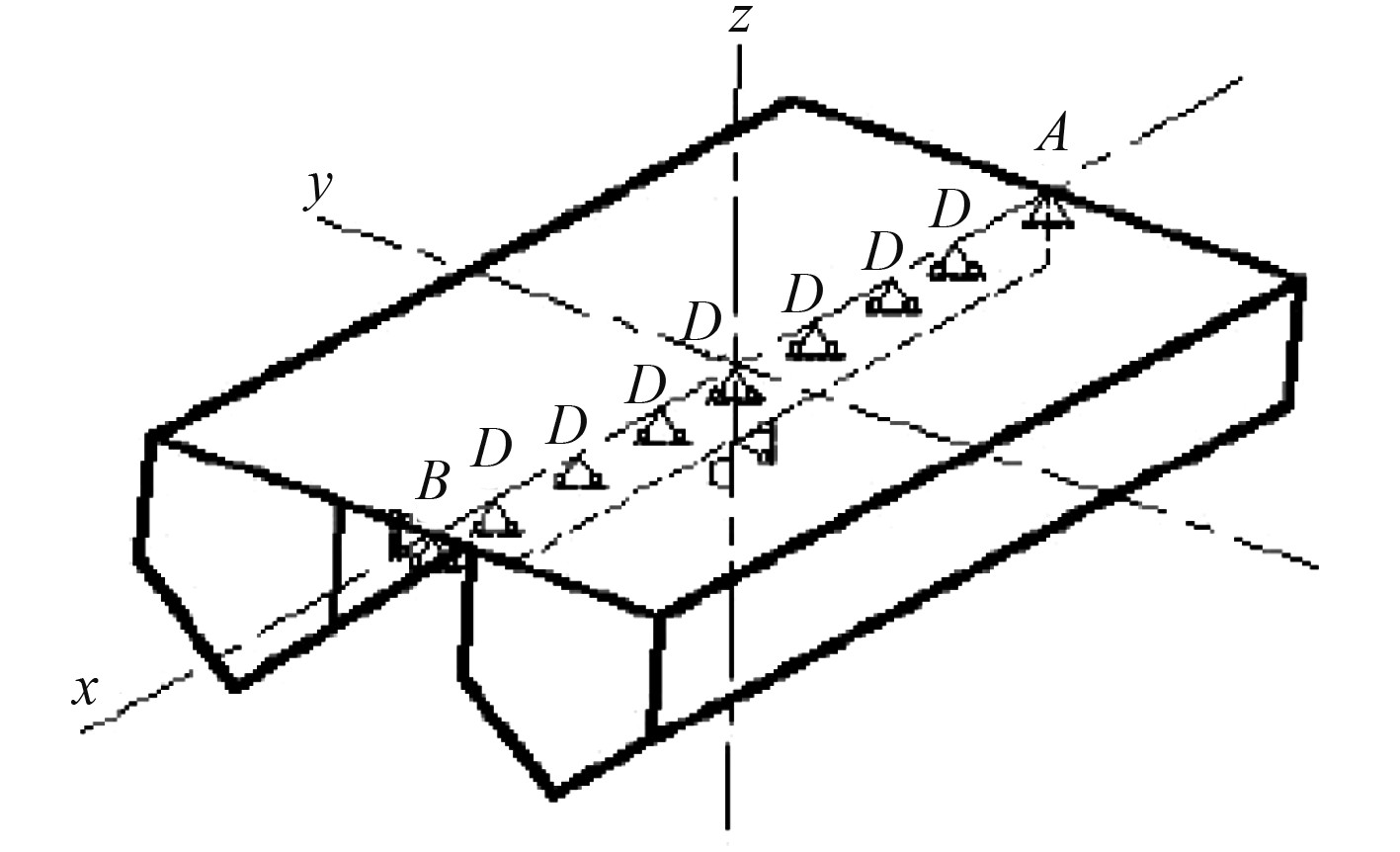
图 6 边界条件3支点约束示意图 Fig. 6 Schematic diagram of boundary condition 3 pivot constraint |
1)工况1和工况2边界条件如表3所示;
2)工况3~工况6边界条件如表4所示;
|
|
表 4 边界条件2支点约束情况 Tab.4 Boundary conditions 2 fulcrum constraints |
|
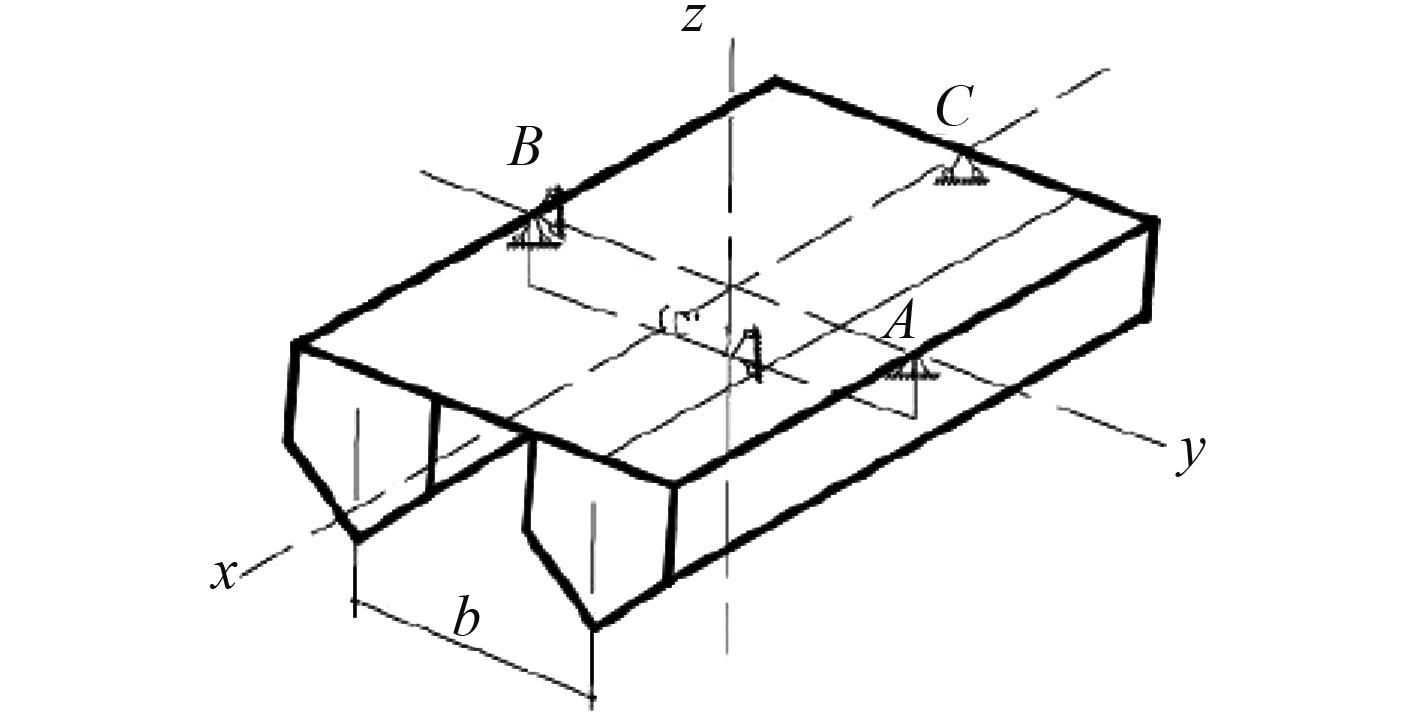
图 5 边界条件2支点约束示意图 Fig. 5 Schematic diagram of boundary condition 2 fulcrum constraint |
3)工况7边界条件如表5所示。
2.3 计算结果分析根据CCS规范要求,对于双体船铝合金结构强度计算应满足表6中许用应力。
|
|
表 6 总强度许用应力 Tab.6 Total strength allowable stress |
通过有限元分析,对双体船具体的计算应力结果见表7和表8,横骨架式船体结构部分应力云图如图7所示。
|
|
表 7 纵骨架式模型相当应力和剪切应力 Tab.7 Equivalent stress and shear stress of longitudinal frame model |
|
|
表 8 全横骨架式模型相当应力和剪切应力 Tab.8 Equivalent stress and shear stress of the full transverse skeleton model |
|
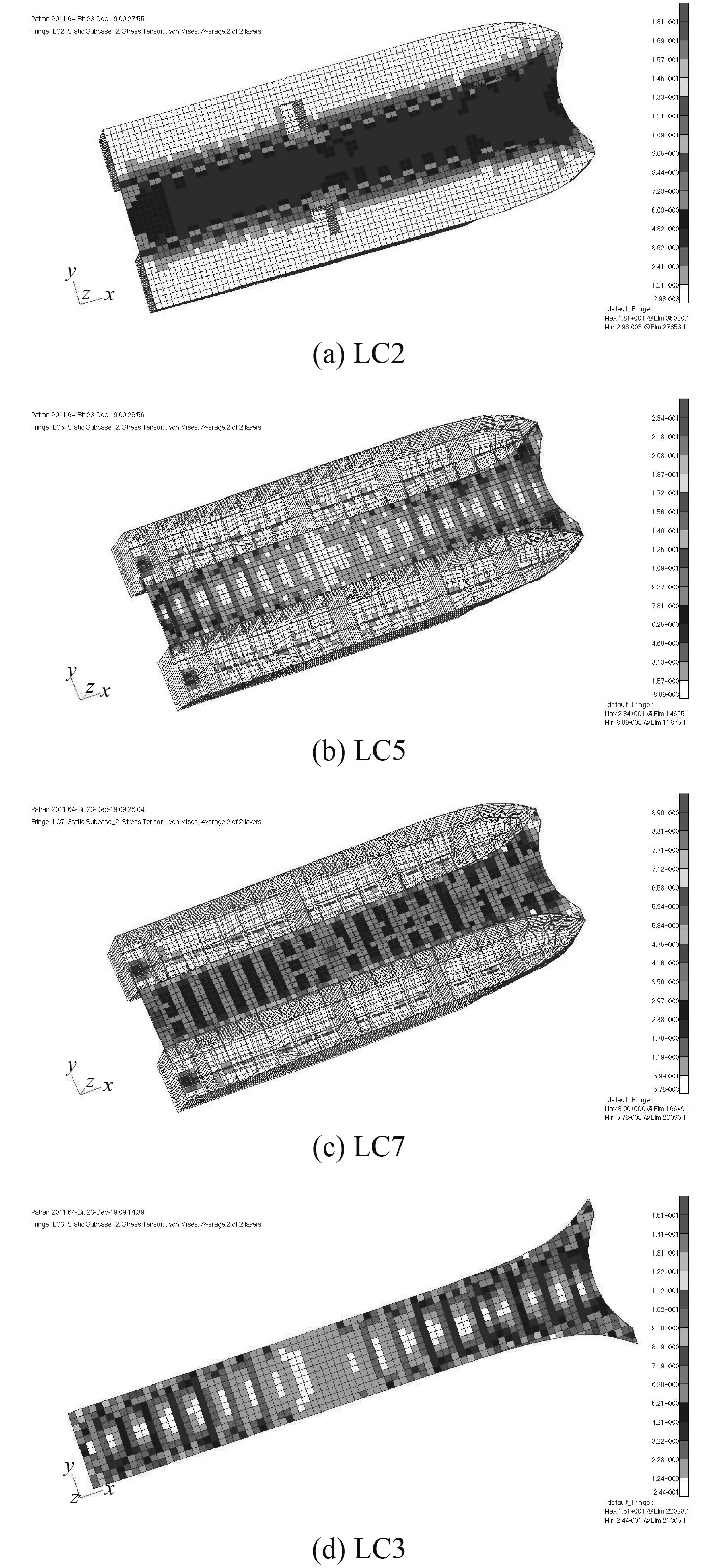
图 7 横骨架式船体结构合成应力分布图 Fig. 7 The composite stress distribution diagram of the transverse frame hull structure |
通过以上对双体运维船纵骨架式和横骨架式的计算结果分析可以看出,2种结构架式的结构设计均满足规范要求,最大应力位置出现在连接桥甲板艏艉与横框架连接处。且在纵骨架式和横骨架式连接桥板厚一样的情况下,全横骨架式连接桥甲板的相当应力略低于纵骨架式的相当应力,其他2种构架的各部分构件应力相当。另一方面全横骨架式结构的质量比纵骨架式的结构质量轻,所以选用质量较轻的全横骨架式结构方案。
3 连接桥结构方案调整及分析比较 3.1 连接桥结构方案调整为使风电运维船在工作时具有较高的安全性,且考虑到本文研究的风电运维船船型小,其海上风电场风浪比一般海域大的情况,需要提高船体的结构强度。而连接桥结构的强度对于提高整船的结构是至关重要的,所以,为了提高该船的结构性和安全性,需要对该船的连接桥结构进行调整改进。
由于全横骨架式结构方案的质量较轻,而且考虑到高速船的质量问题,选择全横骨架式结构进行结构的调整计算对比,对其连接桥结构区域设计了3种不同的结构调整方案,并进行分析对比。
方案1:甲板加强型-仅将连接桥甲板厚度增加;
方案2:首尾端区域强横梁-将首尾端连接桥普通横梁改为强横梁;
方案3:全强横梁制-将连接桥甲板结构隔一肋位设置的强横梁改为每一肋位设置。
1)甲板加强型方案
连接桥甲板是连接桥结构的重要组成,通过有限元分析计算,得出连接桥甲板的计算应力相比其他部位的应力值较小,尝试将连接桥甲板厚度由5 mm增加到8 mm/12 mm/16 mm。
2)首尾端区域强横梁方案
由于原结构方案中最大应力主要集中在连接桥首尾端位置,因此,通过把首尾端普通横梁改为强横梁来增强连接桥强度,其有限元模型如图8所示。

|
图 8 首尾端区域强横梁方案 Fig. 8 Strong beam scheme for the head and tail area |
3)全强横梁制方案
由于原结构方案中最大应力主要集中在连接桥强横梁的端部位置,再加上小型双体船连接桥甲板的具体情况,将连接桥甲板强横梁由原来的隔一肋位设置增加为每一肋位设置强横梁,其结构尺寸保持不变,其有限元模型如图9所示。

|
图 9 全强横梁连接桥模型方案 Fig. 9 Full-strength beam connecting bridge model scheme |
对上述3种结构方案进行强度应力分析,其模型结构质量见表9,方案1模型质量取连接桥甲板厚度为5 mm,计算应力结果见图10,方案1和方案2计算结果见表10和表11,部分应力云图见图11。
|
|
表 9 调整方案模型结构质量 Tab.9 Structural quality of adjustment plan model |
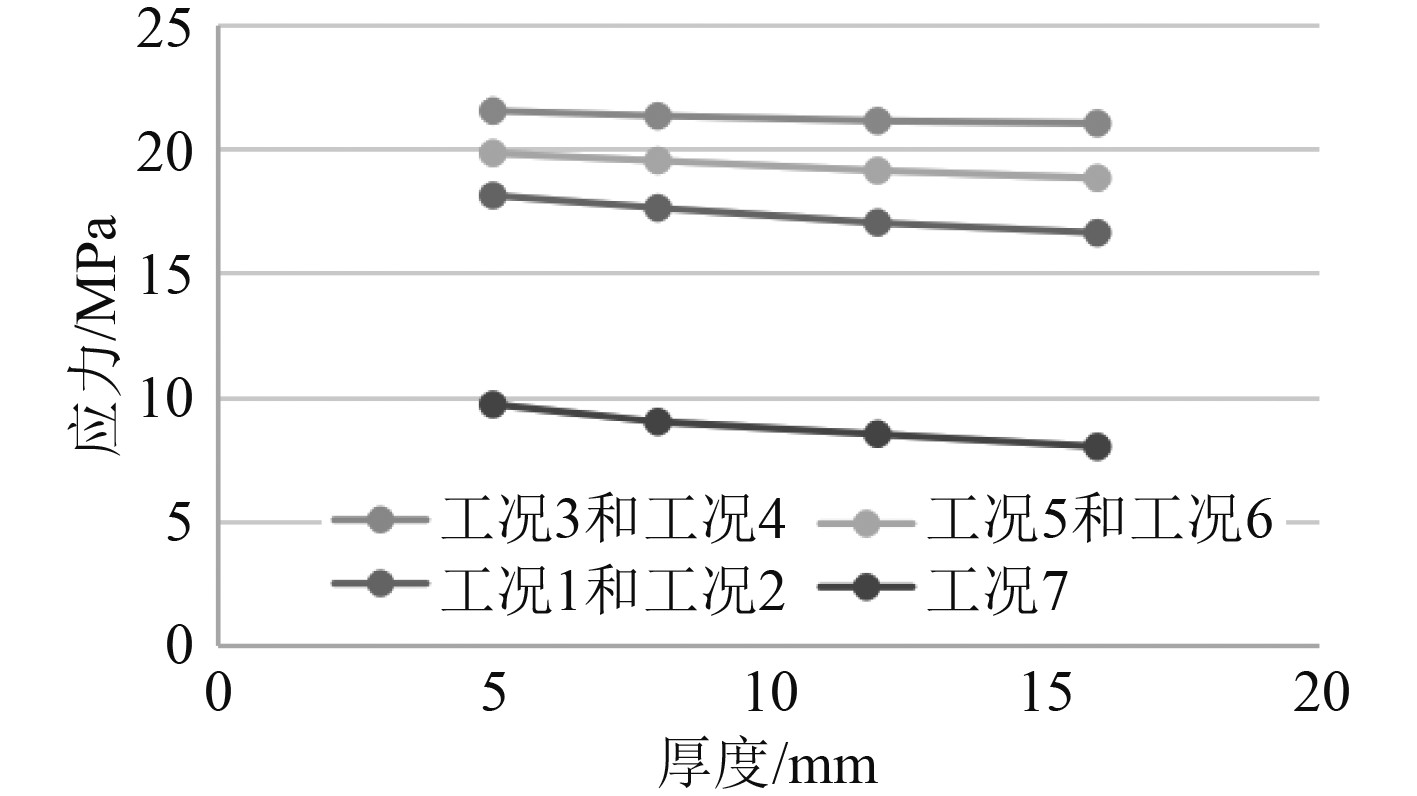
|
图 10 甲板加强型模型相当应力值 Fig. 10 The equivalent stress value of the reinforced deck model |
|
|
表 10 首尾端区域强横梁模型最大计算应力 Tab.10 The maximum calculated stress of the strong beam model at the head and tail regions |
|
|
表 11 全强横梁制模型最大计算应力 Tab.11 Maximum calculated stress of the full-strength beam system model |
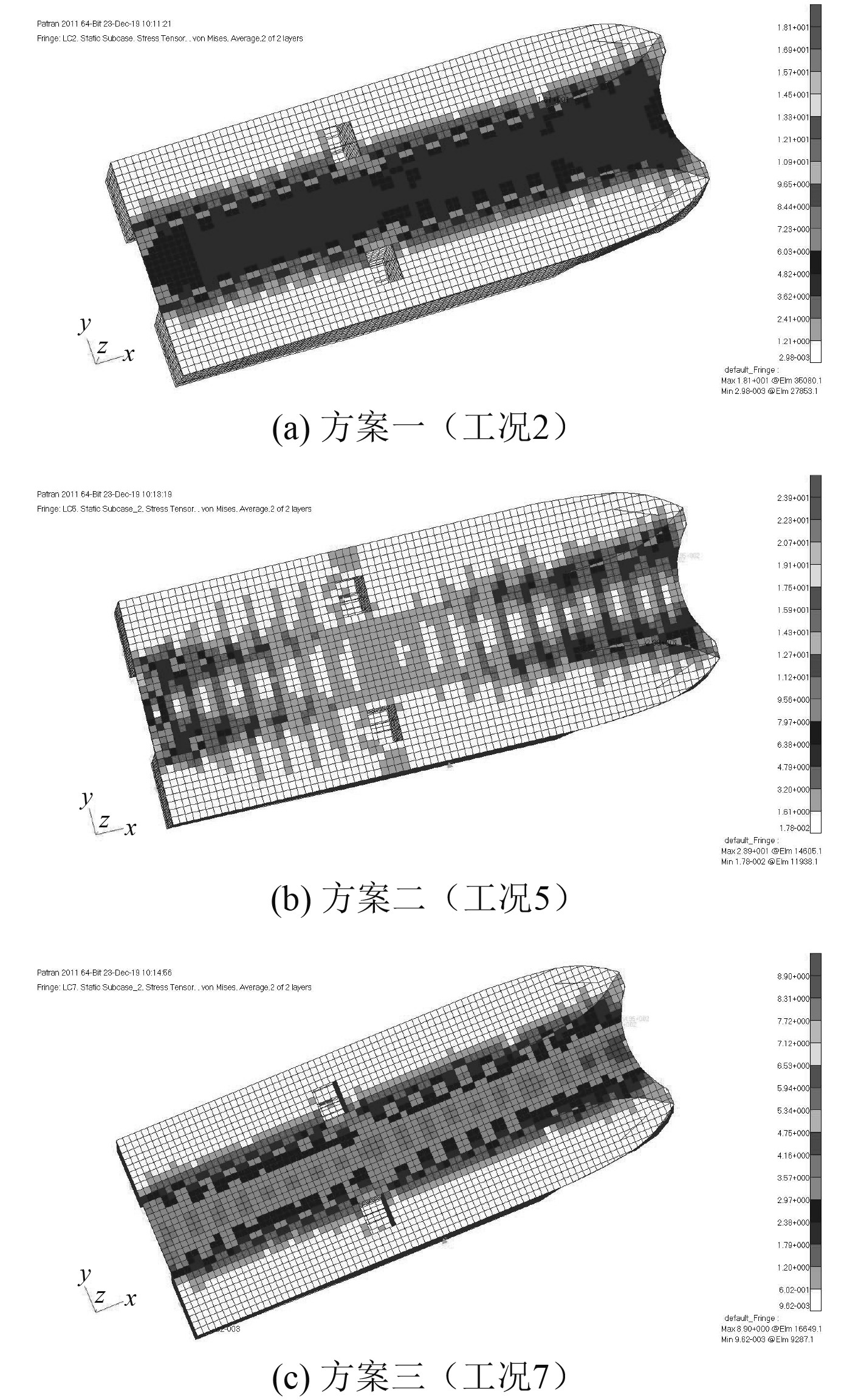
|
图 11 船体结构合成应力云图 Fig. 11 Synthetic stress cloud diagram of hull structure |
通过仅增加连接桥甲板厚度,其相当应力值表明:原厚度改为8 mm/12 mm/16 mm时,应力变化并不明显,各个工况值相比原模型的值略有降低,但幅度很小。从连接桥增加板厚应力计算结果来看,船体的整体结构强度趋于平稳。而且增加连接桥板厚一方面对板厚过渡处理增加了难度,另一方面也会增加船体的整体质量。所以,通过加厚连接桥甲板这一方案来提高船体整体结构强度并不是一个合理可行的方法。
4 结 语通过对上述双体船连接桥的强度计算结果分析,得到:
1)在原结构方案的基础上,通过对设计的3种结构方案进行强度计算,其相当应力均有所降低,但是降低幅度不大,其中甲板加强型方案降低幅度最不明显,全强横梁制方案降低最明显,但各工况下最大应力小于许用应力,均满足强度要求。
2)通过对3种结构方案的调整,其强度计算应力分析表明,3种方案在横浪状态(LC1,LC2)下所受的最大应力相当,均为18.1 MPa上下,但在斜浪状态(LC3,LC4,LC5,LC6)下,方案1的最大相当应力为40.3 MPa,方案2和方案3的最大相当应力均为23.9 MPa,方案2和方案3的应力明显比方案1降低很多。
3)对比全船应力云图,在上述计算的各工况下,全强横梁制方案最大剪切应力位置出现在双体船连接桥与强构件相连接处,所以,最大应力的位置也有可能出现连接桥与强构件的连接处。因此,在双体船设计时对其连接桥与强构件相接的构件位置也应注意进行加强。
4)比较3种调整方案,在连接桥甲板板厚相同时,甲板加强型方案的质量最小,全强横梁制方案的质量最大,但是连接桥首尾端区域强横梁方案和全强横梁制方案的应力水平相差不大,甲板加强型方案的应力水平最差,所以为了结构的安全性和提高航速,选择质量及结构较优的首尾端区域强横梁方案。
| [1] |
中国船级社(CCS), 国内航行海船建造规范[S]. 北京: 人民交通出版社, 2015.
|
| [2] |
管义锋, 黄涣青, 谷家扬, 等. 双体铝合金高速客船强度有限元分析研究[J]. 船舶工程, 2011, 6: 14-17. DOI:10.3969/j.issn.1000-6982.2011.05.004 |
| [3] |
杨平, 黄乐华. 双体船结构的直接计算分析[J]. 船海工程, 2006, 35(5): 4-7. DOI:10.3963/j.issn.1671-7953.2006.05.002 |
| [4] |
吴鑫鑫, 大型半潜船船体强度有限元分析[D], 广州: 华南理工大学, 2015.
|
| [5] |
杜庆喜. 船体结构强度直接计算方法研究[D]. 武汉: 武汉理工大学, 2007.
|
| [6] |
李培勇, 鄢慧敏, 杨辉杰, 等. 双体采沙船结构有限元计算分析[J]. 船海工程, 2009(1): 1-3. DOI:10.3963/j.issn.1671-7953.2009.01.001 |
| [7] |
李国强. 江海直达散货船疲劳强度直接计算研究[D]. 舟山: 浙江海洋学院, 2014.
|
| [8] |
魏利, 海上风电场维护船的结构设计及结构强度研究[D], 镇江: 江苏科技大学, 2014.
|
 2021, Vol. 43
2021, Vol. 43
