2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
逐步破坏分析法是由Smith[1]基于平断面假设提出的构件逐步破坏的增量曲率法。而后,Paik[2]计算了箱形梁结构单元应力-应变关系刚度矩阵。Gannon[3]基于Smith方法对考虑焊接残余应力与初始变形的船体梁极限强度进行对比分析。在非线性数值分析方面,骆文刚[4]计算得到加筋板单元平均应力应变关系,为逐步破坏法提供应力应变关系等。Kim[5] 计算计及腐蚀影响的老龄集装箱船进行船体梁纵向极限承载能力。Shi[6]研究在扭转载荷作用下初始裂纹长度、初始裂纹位置等因素对箱型梁剩余极限强度的影响。Saad-Eldeen[7]分析2个不同腐蚀程度的箱型梁结构的垂向极限强度。Yamada[8]研究散货船碰撞之后的剩余极限强度,提出了合适的破损后数值方法。赵南[9]采用Abaqus开展超大型浮体结构极限强度研究。同时,根据第十四届国际船舶与海洋工程结构会议对各种方法的评分可以看出,目前极限强度评估最有力的方法为逐步破坏分析方法和数值仿真分析方法。因此,本文主要采用这2种方法对某船结构进行极限强度分析,同时对比2种计算分析方法,验证本文分析方法的正确性。
1 逐步破坏法逐步破坏法依据平断面假定,认为横向构件具有足够的结构强度,船体纵向构件失效发生在相邻的单个框架内部,整体结构具有比框架间更高的失稳崩溃能力,并认为这些单元之间无相互作用。将横剖面进行离散成加筋板单元和硬角单元两类单元,加筋板单元由筋和带板组成,是船体梁甲板与船底板上板架结构承载总纵弯矩的主要构件单元;而舷顶列板、纵舱壁与甲板相交的结构连接处结构由于刚度相对比较大,假定为硬角单元。
1.1 加筋板格失效模式加筋板受压缩载荷作用下逐渐发生屈曲崩溃失效,其失效模式主要包含加筋板格失效和整个加筋板格失效。前者由于加强筋翼缘在压缩时发生屈曲或屈服失效,后者因为带板在压缩作用下发生屈曲或屈服破坏。在结构承受压缩和弯曲载荷共同作用下,加强筋面板厚度中心的总应力由4类应力合成,分别为初始变形产生的残余应力、面内纵向载荷产生的拉压应力、侧向载荷产生的应力以及弯矩产生的应力。加筋板带板受压可能引起加筋板格失效模式,即失效模式1,在该失效模式中,加强筋整体承受纵向面内压缩载荷,且还能继续承载外在拉压引力,但带板已无法继续承载,因为已处于极限应力状态。而当总应力等于加强筋屈服应力时,加强筋翼缘首先发生破坏,此时发生加强筋翼缘压缩失效模式,即失效模式2。
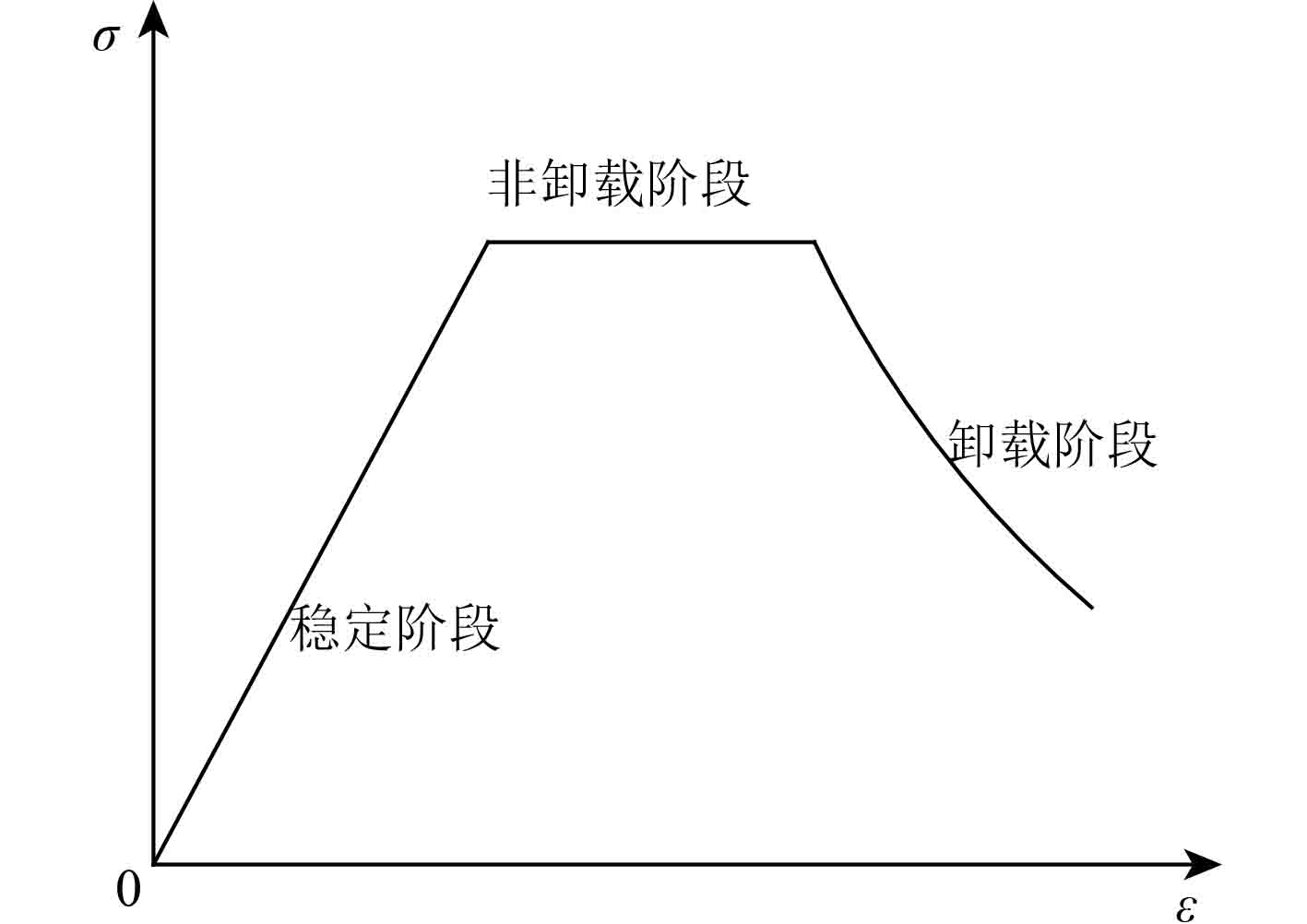
1.2 单元应力-应变关系对于加筋板的应力-应变关系,采用一定的简化方法来求解,求解精度决定了Smith方法的计算精度。硬角单元与承受拉应力的加筋板单元假定为理想弹塑性力学响应,与选用的材料属性一致,其应力-应变关系如图1所示。对于承受逐渐增大的压应力直至失稳崩溃的加筋板单元,根据其应力应变关系特征分为3个阶段,即开始上升阶段的线弹性阶段稳定状态、由塑性流动产生的稳定非卸载阶段、塑性铰形成后载荷下降的卸载阶段,相应的单元应力-应变曲线关系如图2所示。

|
图 1 拉伸和硬角单元 Fig. 1 Element of stretching & hard angle |
|
图 2 压缩单元 Fig. 2 Element of compression |
弯曲载荷作用下船体极限承载能力计算流程如图3所示。

|
图 3 极限强度计算流程图 Fig. 3 Flow sheet of ultimate strength |
随着计算技术的飞速发展,非线性有限元方法是评估结构极限强度的一个重要方法,其不仅可以考虑初始变形、焊接残余应力等结构初始缺陷的影响,同时又可计及几何非线性、材料非线性等非线性因素,还可求解多轴载荷共同作用下的各种失效模式(如屈服、线性与非线性屈曲等)及其结构极限强度。非线性有限元分析是解决复杂工程结构问题强有力的工具,专用有限元法常用于早期船体结构极限强度计算中。近年来计算机性能、内存和数值分析方法飞速发展,越来越多地应用商业有限元程序进行船舶结构的非线性计算分析,如Ansys,Abaqus,MSC.MARC、MSC.NASTRAN等大型通用有限元程序,已经频繁地应用到船舶结构的极限承载能力计算中。本文主要采用非线性有限元方法对某船模型结构进行计算分析,以便获得其极限承载能力及失效模式等。
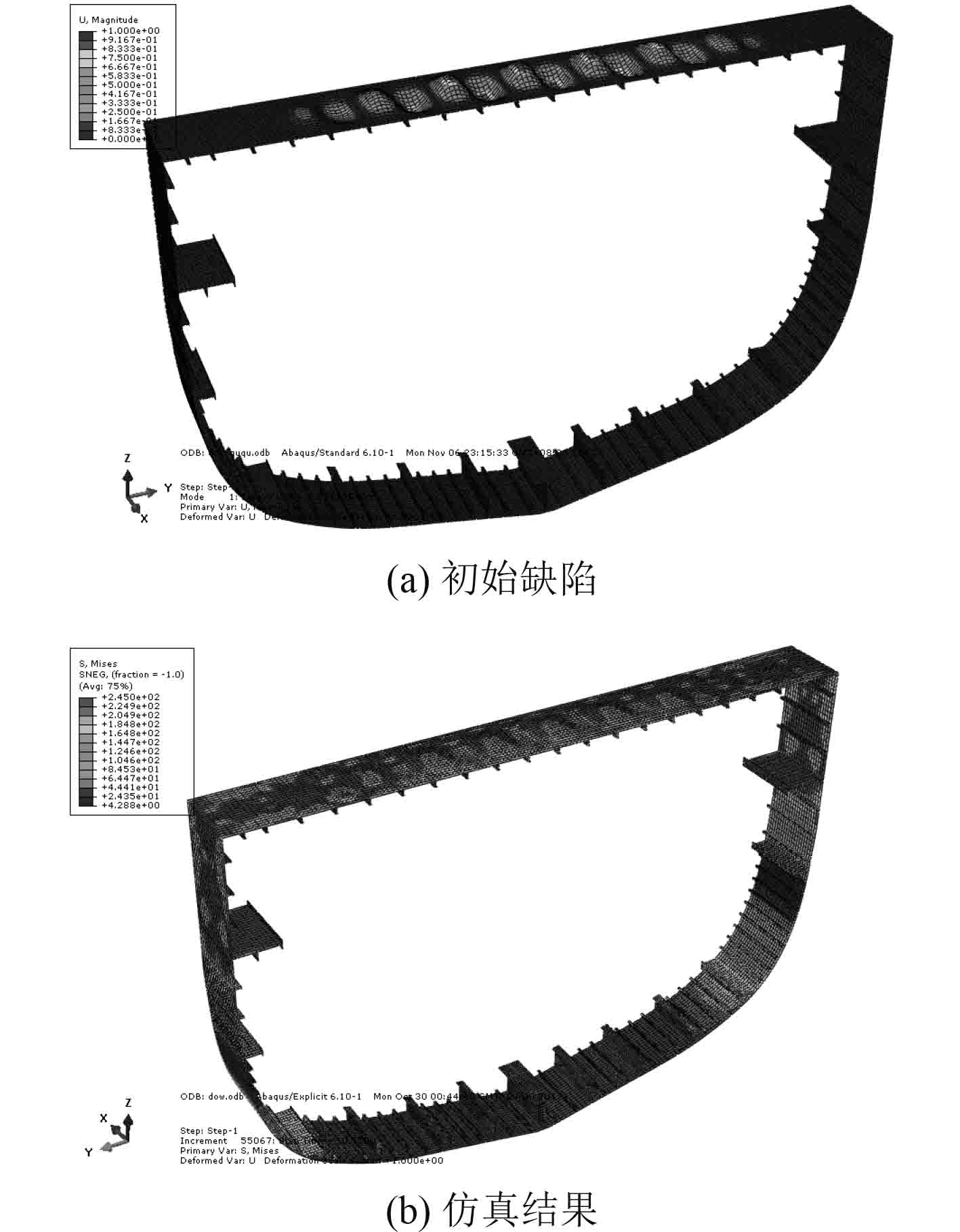
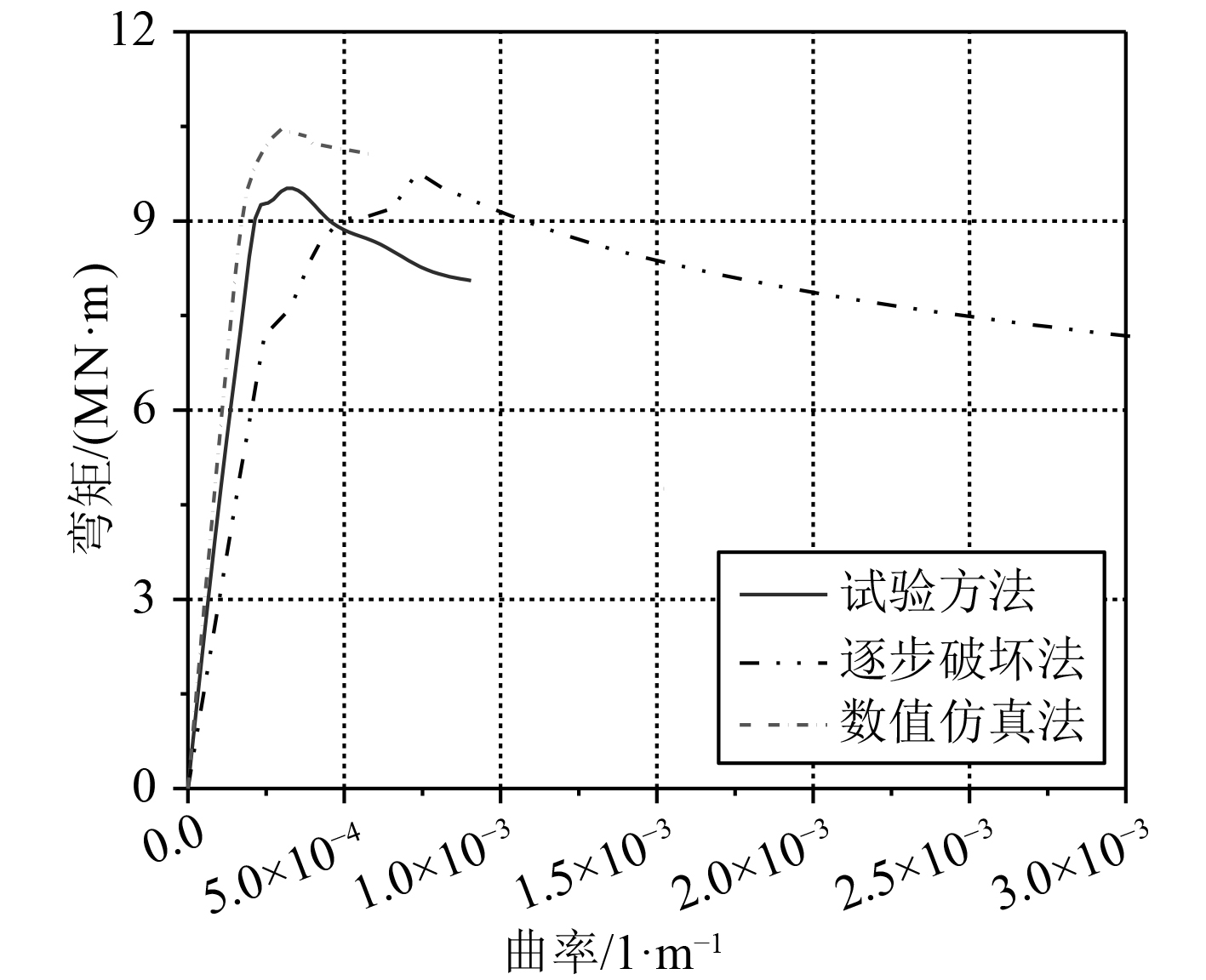
3 研究对象参数本文研究对象为Dow’s 1/3 Test Hull模型,该船取自著名的极限强度缩比船模试验,用1/3比例模型做中垂情况下的某船破坏试验,模型的长×宽×型深为18 m×4.1 m×2.8 m,构件尺寸和属性及参数见表1和表2,船体舯剖面结构形式如图4所示,数值仿真中初始缺陷和极限状态如图5所示,图6给出了本文逐步破坏法和数值仿真与试验结果的对比曲线。其中试验结果为9.47 MN·m,逐步破坏法计算结果为9.77 MN·m,相比于试验结果误差为3.2%;数值仿真计算结果为10.46 MN·m,相比于试验结果误差为10.5%。通过对比可以发现逐步破坏法相比于数值仿真更加接近试验结果,主要是由于逐步破坏法中计及初始变形和焊接残余应力,而数值仿真过程中未计及焊接残余应力影响。
|
|
表 1 Dow’s Test Hull构件尺寸和属性 Tab.1 Scantling & property of Dow’s Test Hull |
|
|
表 2 Dow’s Test Hull构件参数 Tab.2 Component parameters of Dow’s Test Hull |

|
图 4 Dow’s Test Hull剖面图 Fig. 4 Section plan of Dow’s Test Hull |
|
图 5 Dow’s Test Hull剖面图 Fig. 5 Section plan of Dow’s Test Hull |
|
图 6 计算结果与试验结果对比 Fig. 6 Comparison of computing result & test result |
本文采用逐步破坏方法和Abaqus数值仿真软件开展某船结构极限承载能力分析,并将2种方法计算结果与试验结果进行对比分析,获得不同方法获得的极限承载能力。通过研究分析得出相关的主要结论可为某船结构设计及强度校核等提供参考,具体包括:1)本文中的逐步破坏法可以计及焊接残余应力和初始变形影响,可以更好模拟船体结构失效模式;2)数值仿真方法和逐步破坏法均满足工程实用精度要求。
| [1] |
Smith C S. Influence of local compressive failure on ultimate longitudinal strength of a ship hull[A]. PRADS 77(C), 1977: 73−79.
|
| [2] |
Jeom kee paik, Bong ju kim. Progressive collapse analysis of thin-walled box columns[J]. Thin-Walled Structures, 2008, 46: 541-550P. DOI:10.1016/j.tws.2007.10.004 |
| [3] |
Liam Gannon, Yi Liu, Neil Pegg, Malcolm J. Smith.. Effect of welding-induced residual stress and distortion on ship hull girder ultimate strength[J]. Marine Structures, 2012, 28: 25-49. DOI:10.1016/j.marstruc.2012.03.004 |
| [4] |
骆文刚, 杨平, 崔虎威, 等. 内河船舶极限强度计算的逐步破坏法程序设计[J]. 中国舰船研究, 2013, 8(2): P58-64. |
| [5] |
Do Kyun Kim, Dae Kyeom Park, Han Byul Kim, et al. The necessity of applying the common corrosion addition rule to container ships in terms of ultimate longitudinal strength[J]. Ocean Engineering, 2012, 49: 43-55. DOI:10.1016/j.oceaneng.2012.04.012 |
| [6] |
Gui-jie Shi, De-yuWang. Residual ultimate strength of cracked box girders under torsional loading[J]. Ocean Engineering, 2012, 43: 102-112. DOI:10.1016/j.oceaneng.2011.12.028 |
| [7] |
S. Saad-Eldeen, Y. Garbatov, C. Guedes Soares.. Ultimate strength assessment of corroded box girders[J]. Ocean Engineering, 2013, 58: 35-47. DOI:10.1016/j.oceaneng.2012.09.019 |
| [8] |
Yasuhira Yamada. Numerical study on the residual ultimate strength of hull girder of a buck carrier after ship-ship collision[C]//Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, OMAE2014-23811, June 8−13, 2014, San Francisco, California, USA.
|
| [9] |
赵南. 复杂载荷作用下超大型浮体结构极限强度研究[D]. 北京: 中国舰船研究院, 2018.
|
 2021, Vol. 43
2021, Vol. 43
