0 引　言

舰艇在平日航行或执行作战任务时，由于操作失误可能发生舰艇碰撞或遭受武器攻击，这些情况均会导致舰艇大面积破损进水，进水后的舰艇将会出现横摇运动，并且横摇运动是不规则的、非线性的，直接影响舰艇是否倾覆。若破损进水舱为Ⅱ类舱，舱内进水产生的自由液面与舱内的自由液面影响基本一致，在线性范围内可能引起舰艇的稳定中心高减少，稳性降低，导致舰艇倾覆沉没^[1]。若破损进水舱为Ⅲ类舱^[1]，舱内进水量会随横摇运动不断增减，并且舱内进水会随舰艇不停晃动，因此Ⅲ类舱的破损进水将使舰艇的横摇运动更加复杂，目前Ⅲ类舱破损进水的研究较少^[2]。由于具有Ⅱ类进水舱和Ⅲ类进水舱的舰艇会加剧横摇运动的混沌状态，也是舱室破损进水研究的重点。

舰艇破损进水产生的横摇运动具有复杂的非线性和混沌现象，包括由水动力载荷的复杂性和大幅横摇运动引起的不可忽略的非线性，以及不同运动形式之间耦合形成的具有参数激励的非线性动力^[3]。学者们开展了大量舰艇进水舱内液体运动的理论分析和实验研究，如处理破损船在波浪中横摇运动的问题时，Yildiy.A^[4]利用Hamilton变分原理，建立了具有Ⅱ类进水舱破损船在波浪中的横摇运动微分方程，并利用李亚普诺夫的稳定性理论来讨论破损船的横摇运动响应的稳定性条件。日本东京大学的Murashige等^[5]对部分液舱进水的舰艇运动进行了详细研究。本文在构建破损进水舰艇非线性横摇运动数学模型基础上，对破损进水舱为Ⅲ类舱时舰艇的横摇运动状态进行数值仿真求解，讨论不同系统参数和激励参数对破损舰艇横摇运动的影响，预报具有Ⅲ类进水舱破损进水舰艇的运动形式。

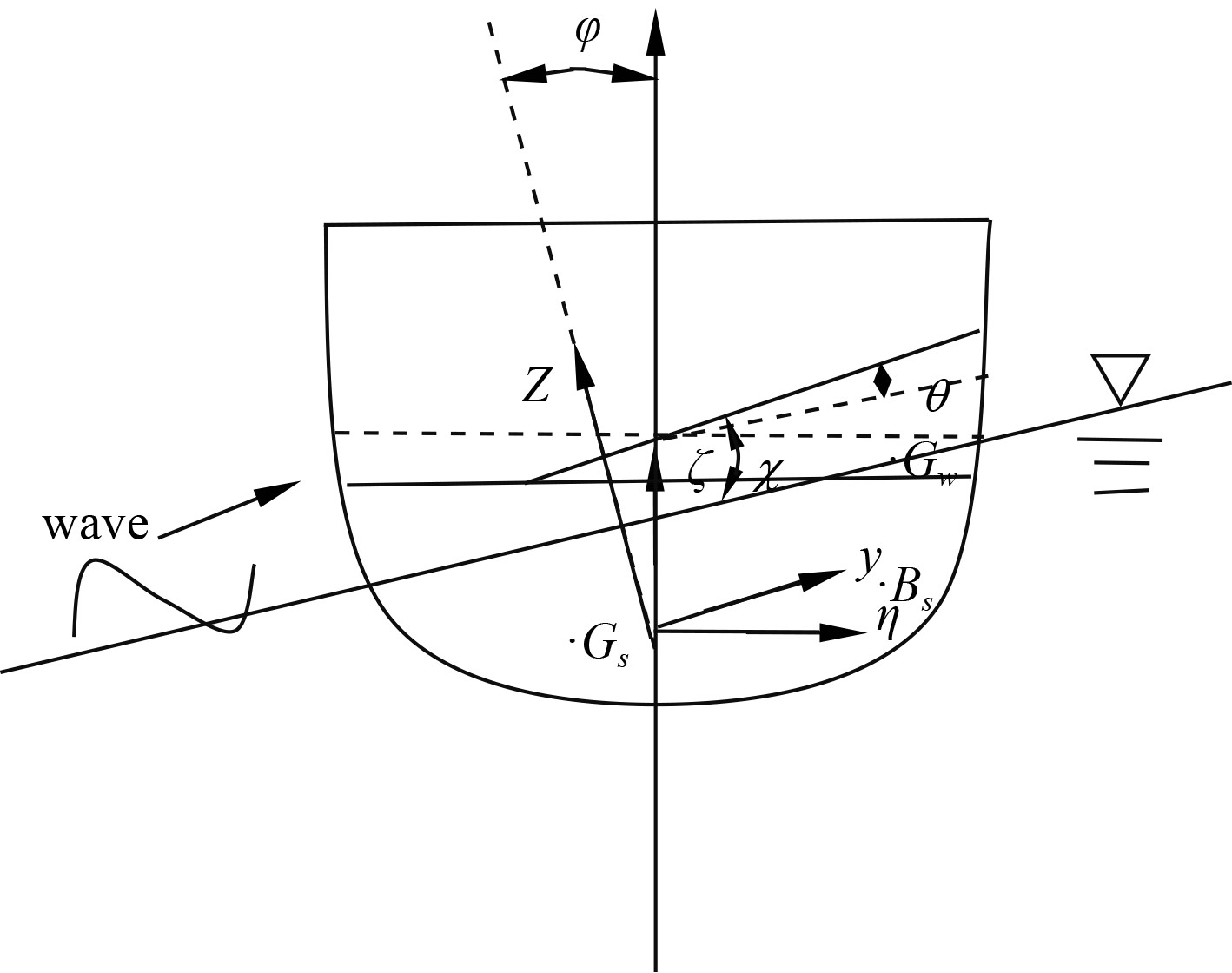
1 舰艇破损进水的非线性横摇运动模型 1.1 坐标系

为更好研究和描述舰艇的运动过程，建立如图1所示的大地惯性坐标系 $Oxyz$ 和舰艇运动坐标系 $O\xi \eta \zeta $ 2个坐标系。

图中： ${G_s}$ 为舰艇的重心； ${B_s}$ 为舰艇的浮心； ${G_w}$ 为进水容积的中心； $\varphi $ 为舰艇的横摇角； $\,\chi $ 为进水舱内液面与 $\eta $ 轴的夹角； $\theta $ 为进水舱内液面与 $y$ 轴的夹角。原点O设在舰艇的重心 ${G_s}$ 处，当舰艇的横摇角 $\varphi $ 为0时，两坐标系重合， $\xi $ 轴与 $x$ 轴重合， $\eta $ 轴与 $y$ 轴重合， $\zeta $ 轴与 $z$ 轴重合。

1.2 舰艇破损进水横摇运动的能量分析

舰艇由于破损出现横摇运动后，舱内进水和舰艇同时运动，假设舰艇和舱内进水的横摇耦合运动是主要的，忽略垂荡和纵摇运动对舰艇的影响^[6]。舰艇横摇运动产生能量主要包括舰艇本身的动能和势能、破损进水产生的动能和势能、阻尼耗能和外界激励力矩。

1）舰艇的动能和势能

假设不考虑舰艇的垂荡运动和横荡运动，则舰艇的动能仅为绕其重心的转动动能，即

${K_s} = \frac{1}{2}{I_0}{\dot \varphi ^2}{\text{，}}$

(1)

式中， ${I_0}$ 为舰艇的转动惯量 ${I_0} = {I_0}(\dot \varphi ,\varphi )$ 。

若以正直漂浮位置为势能零点，则在任一倾角时，舰艇的势能即为从正直位置开始舰艇的回复力矩所作的功：

${P_s} = \int_0^\varphi {{M_f}{\rm d}\varphi } = {C_{ - 1}}(\varphi )\text{，}$

(2)

式中， ${M_f}$ 为舰艇回复力矩，可表示为横倾角 $\varphi $ 的多项式函数^[7]，令其多项式系数为 $C$ ，则 ${M_f} = {C_0}(\varphi ) = $ $ {c_0}{\varphi ^{}} + {c_2}{\varphi ^3} + {c_4}{\varphi ^5} + {c_6}{\varphi ^7}$ 。

2）破损进水产生的的动能和势能

若不考虑舱内水的转动及激荡，假设舱内进水水的运动为平动，则

$\begin{split} {K_w} = &\frac{1}{2}m\left(\dot y_w^2 + \dot z_w^2\right) = \frac{1}{2}\rho {D_0}\Big[{\left(\dot \chi {E_1} + \dot \varphi {F_0}\right)^2} + \\ & {(\dot \chi {F_1} - \dot \varphi {E_0})^2}\Big] \text{，} \end{split} $

(3)

$\left( \begin{array}{l} {y_w} \\ {Z_w} \end{array} \right) = \left( {\begin{array}{*{20}{c}} {\cos \varphi }&{\sin \varphi } \\ { - \sin \eta }&{\cos \varphi } \end{array}} \right){\rm{ }}\left( {\begin{array}{*{20}{c}} {{\eta _w}} \\ {{\zeta _w}} \end{array}} \right)\text{。}$

(4)

式（3）和式（4）中 $ {y}_{w}$ ， ${z}_{w}$ 分别为大地惯性坐标系进水容积中心的横坐标和垂坐标， ${\eta _w},{\zeta _w}$ 分别为进水容积中心在Oξηζ坐标系中的横坐标和垂坐标。

$\begin{split} &{\eta _w} = {e_0} + {e_1}\chi + {e_2}{\chi ^2} + {e_3}{\chi ^3} + {e_4}{\chi ^4} = {E_0}(\chi )\text{，}\\ &{\zeta _w} = {f_0} + {f_1}\chi + {f_2}{\chi ^2} + {f_3}{\chi ^3} + {f_4}{\chi ^4} = {F_0}(\chi )\text{，}\\ &\frac{{{\rm d}{\zeta _w}}}{{{\rm d}x}} = {e_1} + 2{e_2}\chi + 3{e_3}{\chi ^2} + 4{e_4}{\chi ^3} = {E_1}(\chi )\text{，}\\ &\frac{{{\rm d}{\eta _w}}}{{{\rm d}\chi }} = {f_1} + 2{f_2}\chi + 3{f_3}{\chi ^2} + 4{f_4}{\chi ^3} = {F_1}(\chi )\text{。} \end{split}$

(5)

舱内水的势能即为其重力势能，则

$\begin{split} {P_w} =& mg{z_w} = \rho {D_0}g{z_w}( - {\xi _w}\sin \varphi + {\eta _w}\cos \varphi ) = \\ &\rho g{D_0}({F_0}\cos \varphi - {E_0}\sin \varphi ) {\text{。}} \end{split} $

(6)

3）激励力矩做功

${P_f} = {M_w}\varphi = \frac{1}{{19.59}}MhH{\omega ^2}\cos \omega t.\varphi \text{，}$

(7)

式中， $M$ 为舰艇模排水量， $h$ 为舰艇初稳心高， $H$ 为波高， $\omega $ 为波频。

4）阻尼产生的耗能

${D_\nu } = \frac{1}{2}{\nu _s}{\dot \varphi ^2} + \frac{1}{2}{\nu _w}{\dot \chi ^2}\text{。}$

(8)

1.3 舰艇非线性横摇运动微分方程的推导与构建

对舰艇运动产生的能量进行综合分析，建立拉格朗日方程如下：

$L = {K_s} + {K_w} + {P_s} + {P_w} + {P_f}\text{，}$

(9)

$\left\{ {\begin{array}{*{20}{c}} {\dfrac{{\rm{d}}}{{{\rm{d}}t}}\left(\dfrac{{\partial L}}{{\partial \dot \varphi }}\right) - \dfrac{{\partial L}}{{\partial \varphi }} + \dfrac{{\partial {D_v}}}{{\partial \dot \varphi }} = 0} \text{，}\\ {\dfrac{{\rm{d}}}{{{\rm{d}}t}}\left(\dfrac{{\partial L}}{{\partial \dot \chi }}\right) - \dfrac{{\partial L}}{{\partial \chi }} + \dfrac{{\partial {D_v}}}{{\partial \dot \chi }} = 0} \text{。} \end{array}} \right.$

(10)

将式（1）～式（8）代入式（9）和式（10）中，推导简化可得：

$\begin{split} {C_{11}}\ddot \varphi +& {C_{12}}\ddot \chi + {C_{13}}{{\dot \varphi }^2} + {C_{14}}{{\dot \chi }^2} + {C_{15}}\dot \varphi \dot \chi + \\ & {C_{16}}\dot \varphi + {C_{17}}\dot \chi + {C_{18}} = 0 \text{，}\\ {C_{21}}\ddot \varphi +& {C_{22}}\ddot \chi + {C_{23}}{{\dot \varphi }^2} + {C_{24}}{{\dot \chi }^2} + {C_{25}}\dot \varphi \dot \chi + \\ & {C_{26}}\dot \varphi + {C_{27}}\dot \chi + {C_{28}} = 0 \text{。} \end{split} $

(11)

对两自由度运动方程进行解耦，使两自由度问题化为单自由度问题，将式（11）展开并经过复杂的推导过程^[7-8]，考虑船体运动的阻尼项、非线性项及内部水对船体影响的非线性耦合项，得到舰艇破损进水作用下的舰艇横摇运动非线性微分方程。

$\begin{split} & \left[ {M + {G_1}(\omega t) + {I_1}{\varphi ^2}} \right]\ddot \varphi + \left[ {D + {G_2}(\omega t)} \right]\dot \varphi + \\ &\qquad \left[ {C + {G_3}(\omega t)} \right]\varphi + \left[ {Q + {G_5}(\omega t)} \right]{\varphi ^2} + \\ &\qquad \left[ {N + {G_4}(\omega t)} \right]{\varphi ^3} = F(\omega t) \text{，} \end{split} $

(12)

$\begin{split} [1 +& {a_2}\cos (2\omega t) + {a_4}\cos (4\omega t) + \\ &{{a_6}\cos (6\omega t) + {b_1}\sin (\omega t) + {b_3}\sin (3\omega t) + }\\ &{{b_5}\sin (5\omega t) + {a_0}{\theta ^2}]\ddot \theta + [{d_0} + {d_1}\cos (\omega t)}+\\ &{ {d_3}\cos (3\omega t) + {d_5}\cos (5\omega t) + {e_2}\sin (2\omega t)}+\\ &{ {e_4}\sin (4\omega t) + {e_6}\sin (6\omega t)]\dot \theta + ( \pm \theta + {\theta ^3}) + }\\ &{[{f_2}\cos (2\omega t) + {f_4}\cos (4\omega t) + {g_1}\sin (\omega t) + }\\ &{{g_3}\sin (3\omega t)]\theta + [{h_2}\cos (2\omega t) + {h_4}\cos (4\omega t)}+\\ &{ {i_1}\sin (\omega t) + {i_3}\sin (3\omega t)]{\theta ^3} + [{p_0} + {p_2}\cos 2\omega t}+\\ &{ {p_4}\cos 4\omega t + {q_1}\sin \omega t + {q_3}\sin 3\omega t]{\theta ^2}}=\\ &{ j + {k_2}\cos (2\omega t) + {k_4}\cos (4\omega t) + {l_1}\sin (\omega t)}+\\ &{ {l_3}\sin (3\omega t) + {l_5}\sin (5\omega t)}\text{。} \end{split}$

(13)

式中：阻尼系数 ${d_0}$ ；参激系数 ${i_1}$ ， ${q_1}$ 和外激系数 ${l_1}$ 的数值比其他系数量阶大，引入小量 $\varepsilon $ ，获得简化的舰艇横摇运动非线性运动微分方程。

$\begin{split} \ddot \theta +& \varepsilon \cdot {d_0}\dot \theta + ( - \theta + {\theta ^3}) + \varepsilon \cdot {i_1}\sin \omega t{\theta ^3}+ \\ & \varepsilon \cdot {q_1}\sin \omega t{\theta ^2} = \varepsilon \cdot {l_1}\sin \omega t \text{。} \end{split} $

(14)

2 舰艇非线性横摇运动数值仿真 2.1 研究对象

为更好验证数值仿真结果，以通过试验验证的船模为研究对象^[9]，对具有Ⅲ类进水舱的破损舰艇在不同规则正横浪激励下的运动进行了数值仿真。

1）船模参数

$M = 37.75\;{\rm{kg}}$ ， ${Z_g} = 15.75\;{\rm{cm}}$ ， $T = 8.56\;{\rm{cm}}$ ， $r = $ $ 11.61\;{\rm{cm}}$ ， ${Z_C} = 5.17\;{\rm{cm}}$ ， $h = 1.22\;{\rm{cm}}$ ，无因次等效阻尼系数 ${v_s} = 0.114$ 。

2）舱室破损进水参数

2个Ⅱ类舱对称进水，总进水量2 kg，3个Ⅲ类舱，正浮时的进水量为18.6 kg，舱内水重量及容积中心随进水液面倾角的变化规律如下式：

$D = 20.6 + 2.741\;5{\chi ^2} + 4.216\;8{\chi ^4}\text{，}$

(15)

$\xi = 0.118\;6\chi - 0.032\;4{\chi ^3}\text{，}$

(16)

$\eta = 0.07 + 0.063\;8{\chi ^2} + 0.004\;3{\chi ^4}\text{。}$

(17)

2.2 数值仿真流程

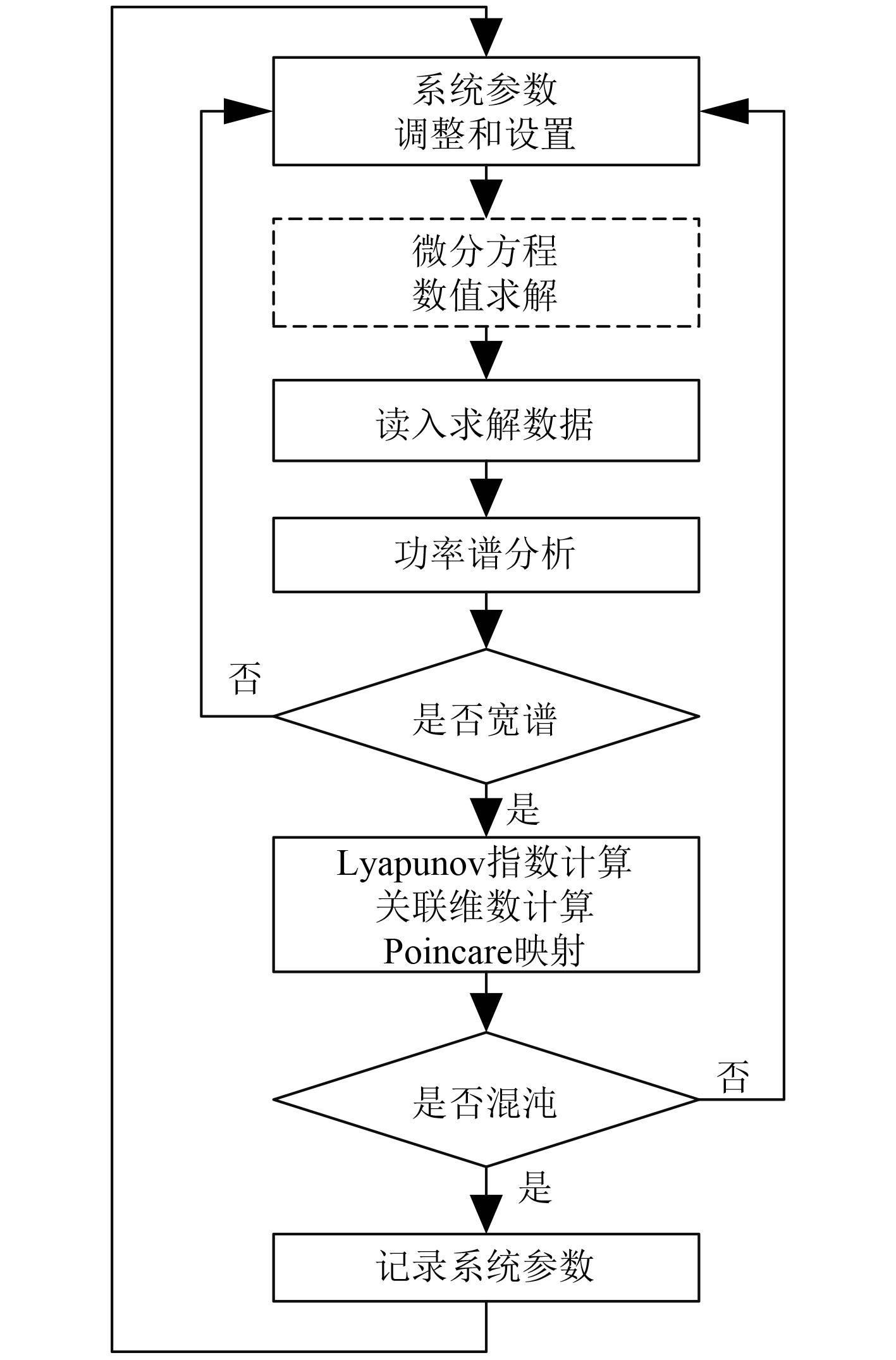
利用数值仿真计算方法对建立的舰艇非线性横摇运动微分方程进行求解，讨论不同激励参数条件对破损舰艇非线性运动的影响规律，预报舰艇横摇运动是处于周期运动还是处于混沌运动范围。采用定步长4阶Runge-Kutta方法对运动微分方程进行数值求解，具体求解计算过程如图2所示。

仿真计算中，假设舰艇破口足够大，出现横摇运动时，舱内进水与舷外海水的交换是完全自由的，不受破口大小的限制，即交换率为100%。在给定的船模参数条件下，改变激励力（即波浪力）的幅值（波高）和频率（波长），进行数值仿真确定使舰艇处于混沌运动状态的区域^[10]。在此基础上，改变舱内进水与舷外水的交换率进行仿真，讨论交换率的变化对混沌参数区域的影响。同时采用功率谱分析方法对数值仿真结果进行分析，判断舰艇横摇运动是否为混沌运动。

2.3 数值仿真结果

图3中 ${A_\omega }/{I_0}$ 表示为船模横摇角幅值与无量纲激励力矩幅值之比，显示了具有Ⅲ类进水舱的破损舰艇在不同规则正横浪波激励下运动响应的几种典型形式的历程、相图和功率谱。从仿真结果看，在规则正横浪激励下的频率响应特性与具有Ⅱ类进水舱的破损舰艇的频率响应特性相似，Ⅲ类进水舱的破损舰艇横摇具有非常丰富的运动形式，随船模参数、进水参数和波浪激励力矩等激励参数的不同，其运动可能是单频的，也可能包含超谐波、次谐波以及组合频率成分，还可能为混沌的。

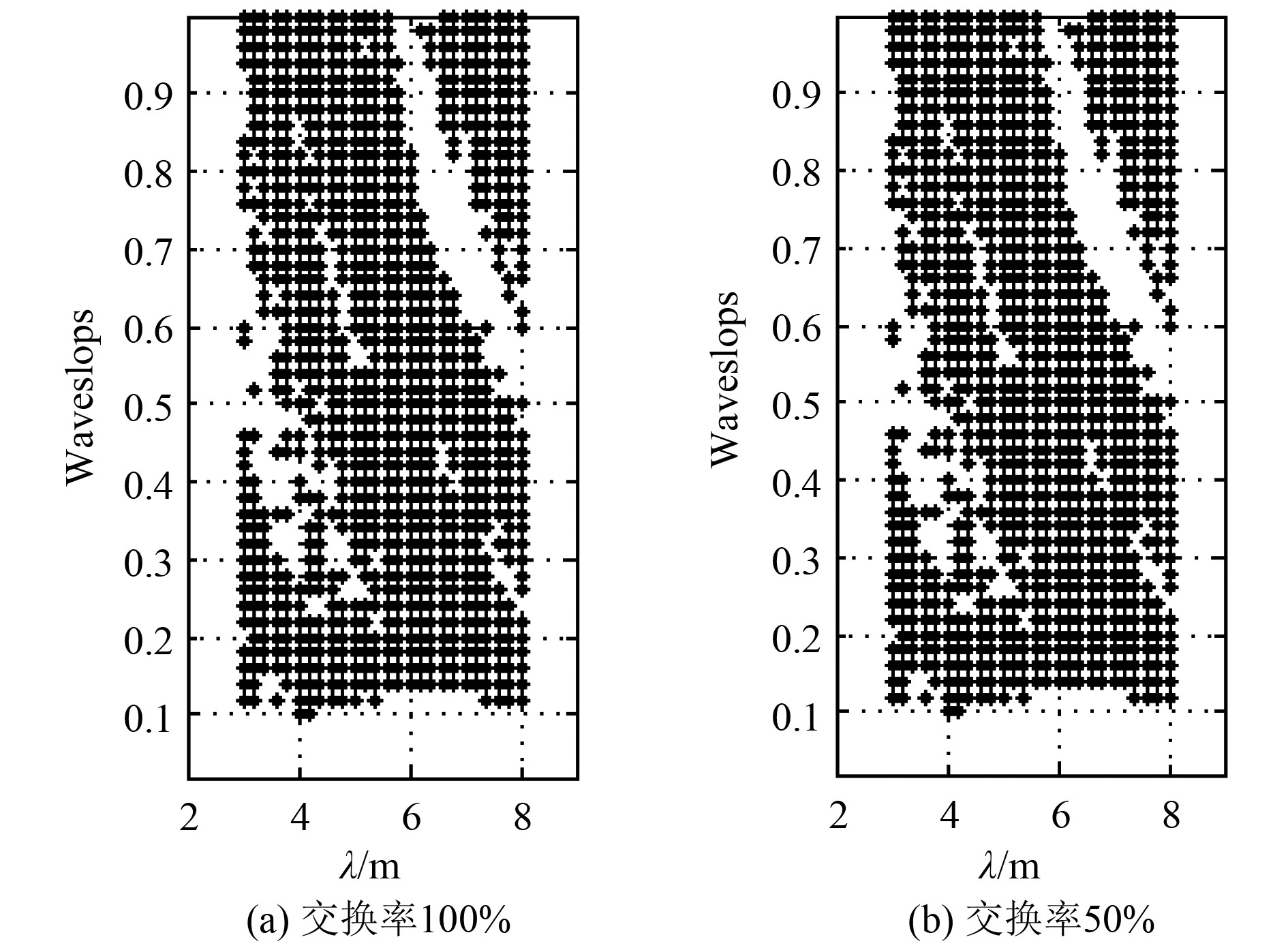
图3所示结果中，均假设Ⅲ类进水舱的破口为无限大，即横摇过程中舱内进水与舷外水的交换是完全自由的，不受破口大小的限制。在实际的破损舰艇中，由于破口面积是有限的，因而横摇过程中进水舱内的进水与舷外水不可能完全自由的交换，尤其当进水舱存在气垫时，舱内水和舷外水的交换率更小。本文对不同交换率的舱内进水进行了数值仿真，图4仿真结果显示具有Ⅲ类进水舱的破损舰艇的混沌运动参数区域超出了实际能达到的激励力矩参数范围，因而在实际条件下不可能出现混沌现象，并且舱内水与舷外水的交换率对具有Ⅲ类舱进水舱的破损舰艇受激横摇混沌运动参数区域基本没有影响。主要原因是在Ⅲ类舱进水情况下，舱内水与舷外水相通，相对Ⅱ类进水舱而言，舱内水与舰艇之间的动力耦合更弱，因而舱内水的运动对舰艇横摇运动的影响更小。上述数值仿真的结果与相同船模的试验结果相一致^[9]。

3 结　语

本文在分析舰艇破损进水后在波浪中运动产生的能量，微分推导构建了舰艇破损进水情况下的非线性横摇运动数学模型基础上，对具有Ⅲ类进水舱的破损船模进行了数值仿真。结果表明，具有Ⅲ类进水舱的破损舰艇运动过程中出现混沌现象时需要的波浪激励力矩幅值很大，超出舰艇实际运动中能达到的波浪激励力范围，并且舱内进水与舷外水的交换率对舰艇受激横摇运动参数区域没有影响，因此具有Ⅲ类进水舱的破损舰艇在横摇运动中不会出现混沌现象，与船模横摇试验结果相吻合。

对比Ⅱ类进水舱，由于Ⅱ类进水舱的舱内水与舷外水隔离，进水产生的自由液面和大进水量对舰艇的横摇运动有很大的影响，具有大自由液面、大进水量的破损舰艇出现混沌运动的参数区域越大，出现混沌运动时的波浪激励力矩幅值越小。因此，具有Ⅱ类进水舱的舰艇横摇运动的形式非常丰富，可能为单频的，也可能包含超谐波、次谐波以及组合频率成分，在一定参数条件下，其运动还可能为混沌的。