随着船舶行业的发展,船舶的舒适性已成为主要考核指标之一。伴随着ISO振动横准的不断更新,要求更加严格[1],促使振动预报成为船舶设计中的重要环节。同时近年来,船舶大型化的趋势,使得在振动预报中,三维建模、加载及计算分析的工作量巨大,导致快速准确的预报振动特性及响应水平十分困难。尤其是在设计阶段,若能快速分析出船舶整体或局部的振动特性,可及时对结构设计或布置带来指导与建议。
因此,针对组合模型的特点及油船的自身特点(货舱区结构连续性一致且没有大开口)提出组合模型应用到油船振动分析中,在船舶设计阶段,可有效缩短振动分析周期,同时在设计初期即可进行振动预报分析。以某11.5万吨油船为例,分别采用组合模型与全船三维模型对其振动特性及响应水平进行评估,并研究与讨论了组合模型的特点及预报精度。
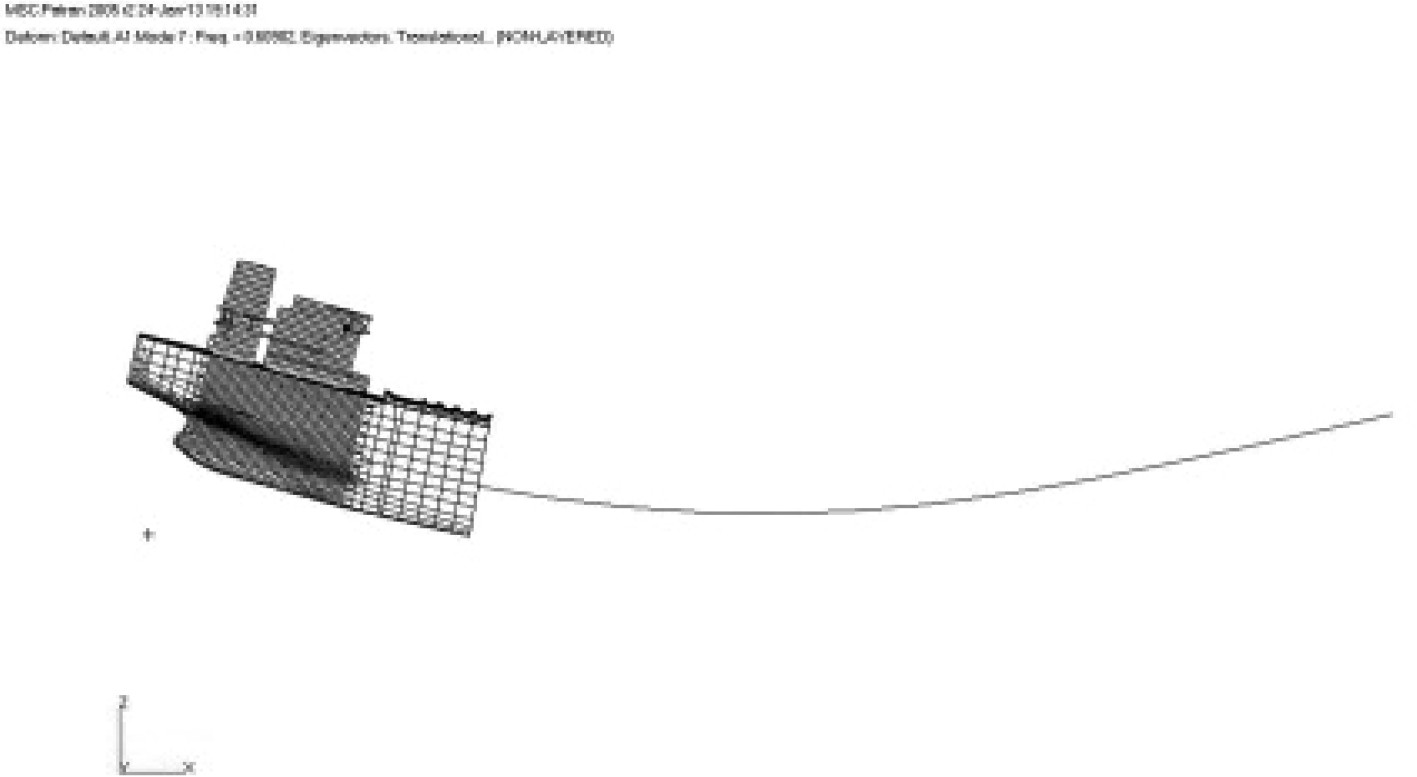
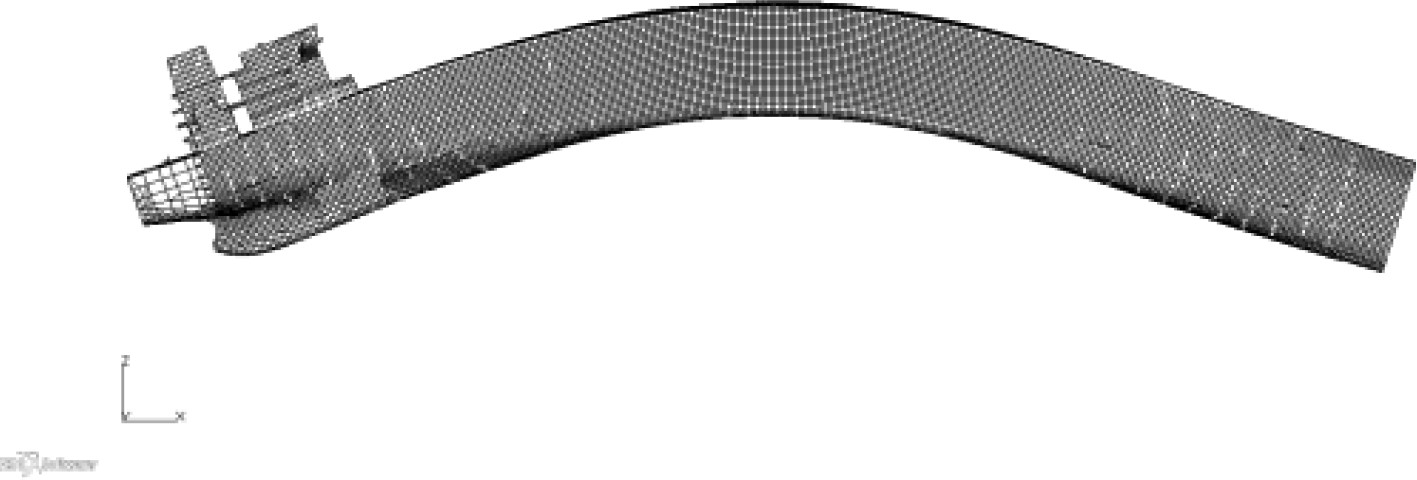
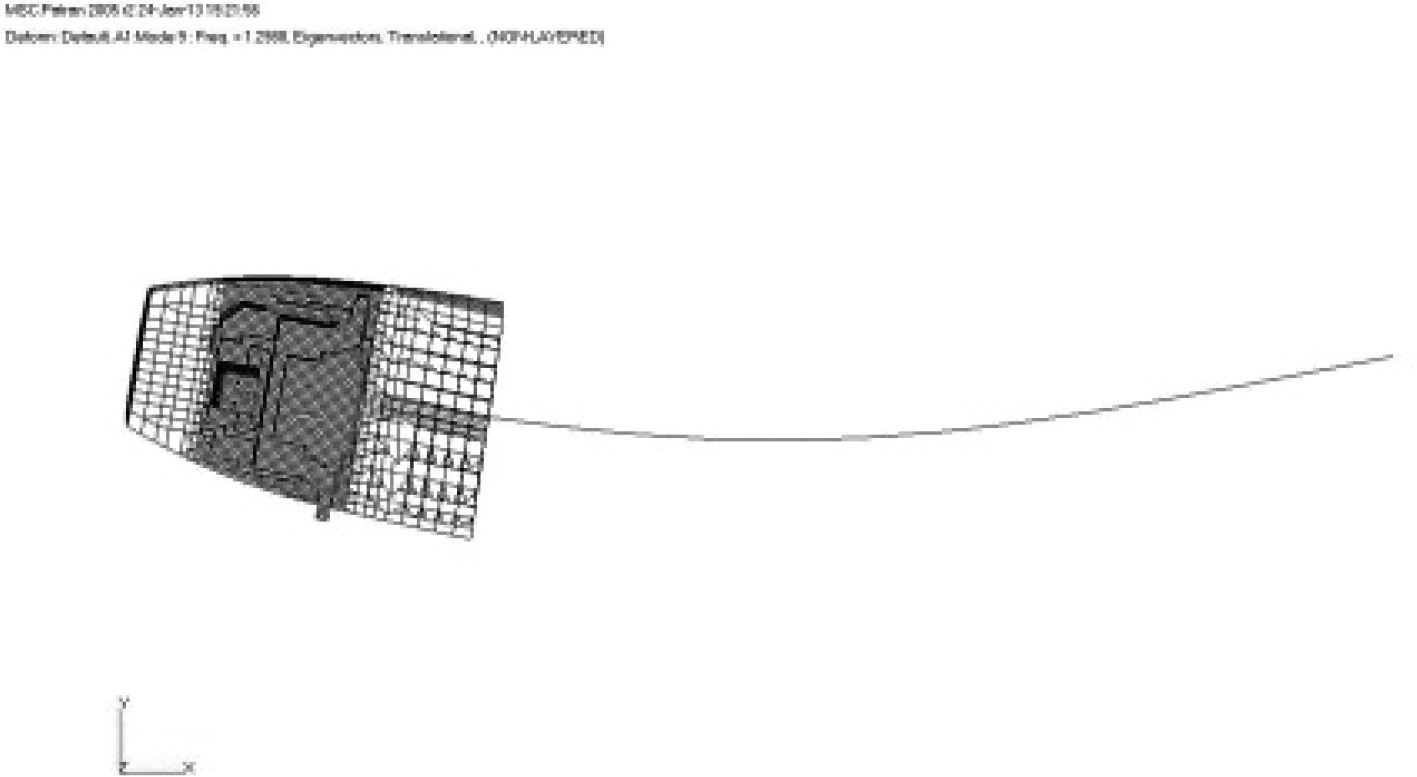
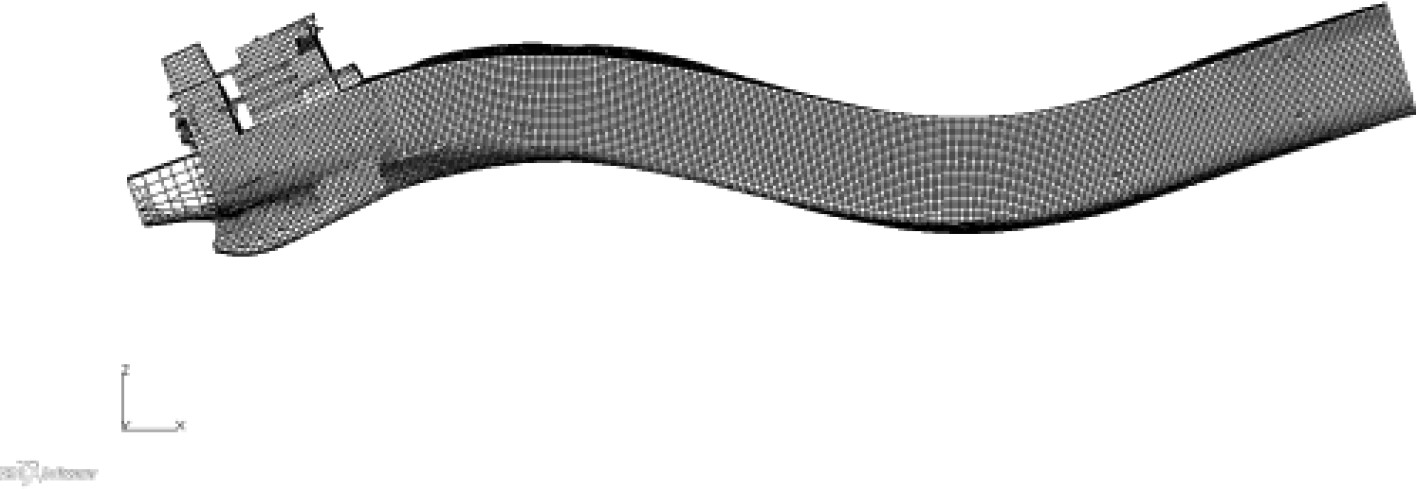
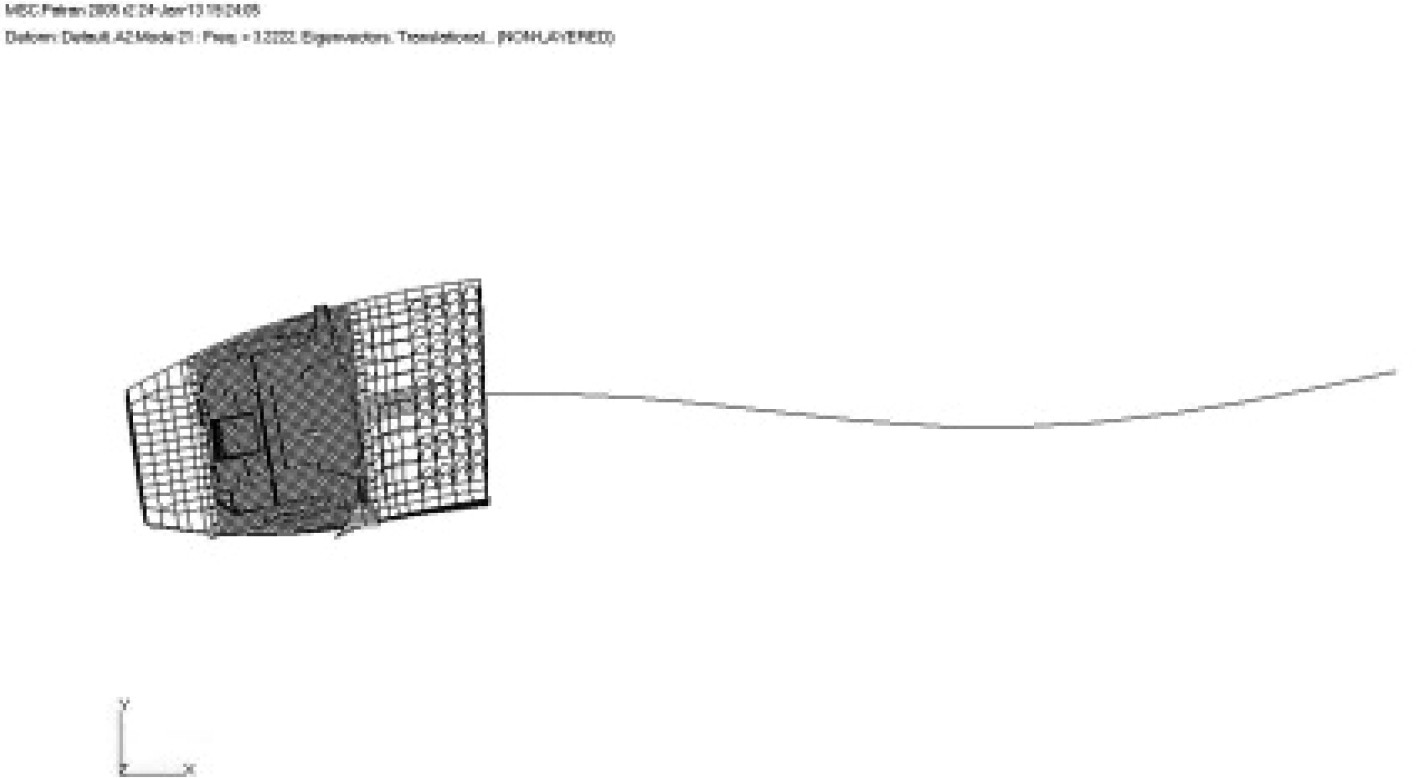
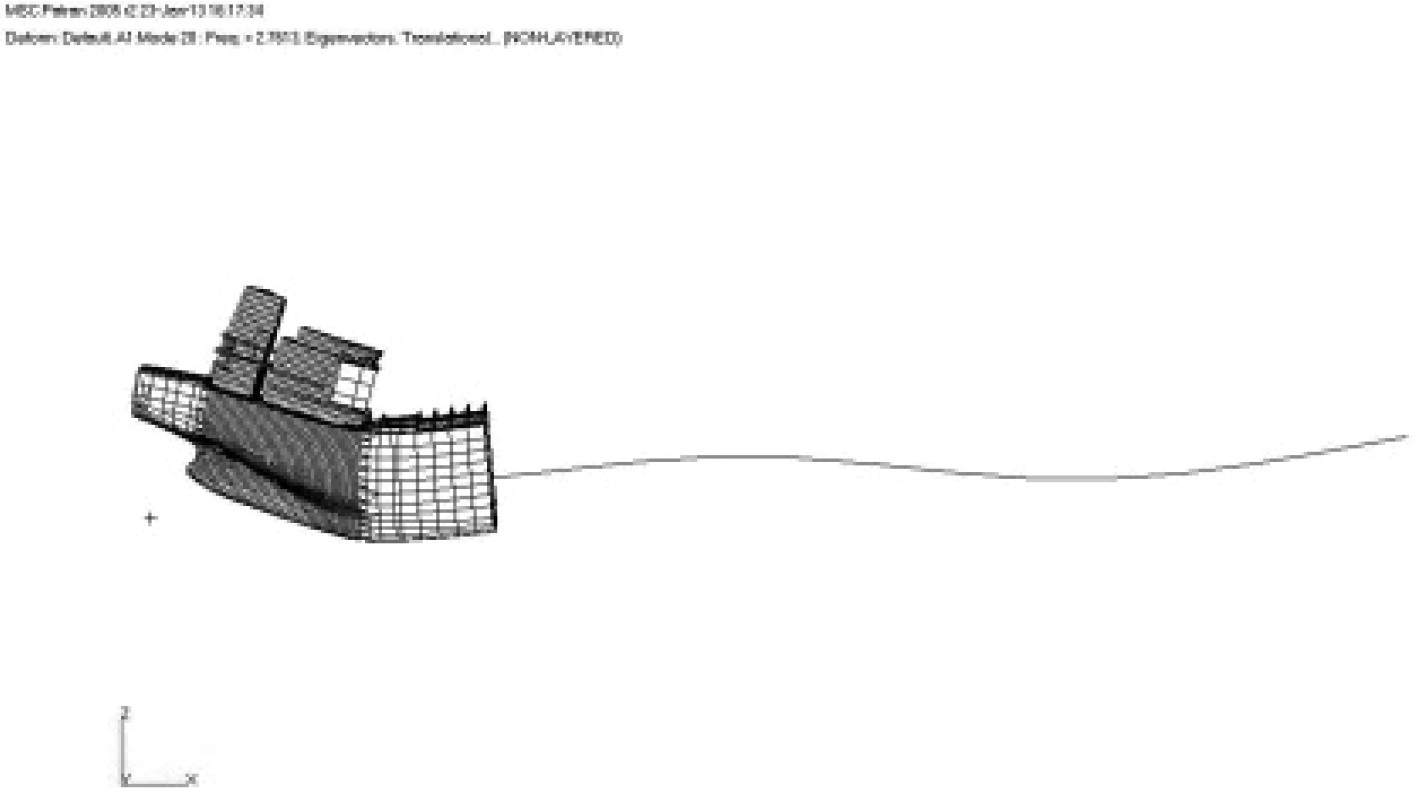
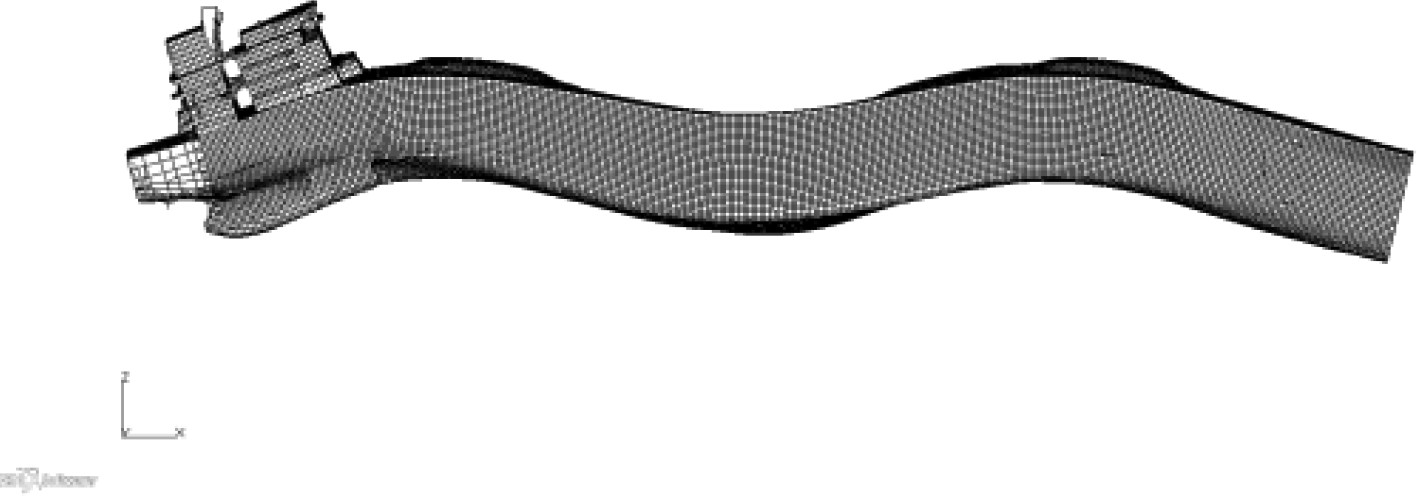
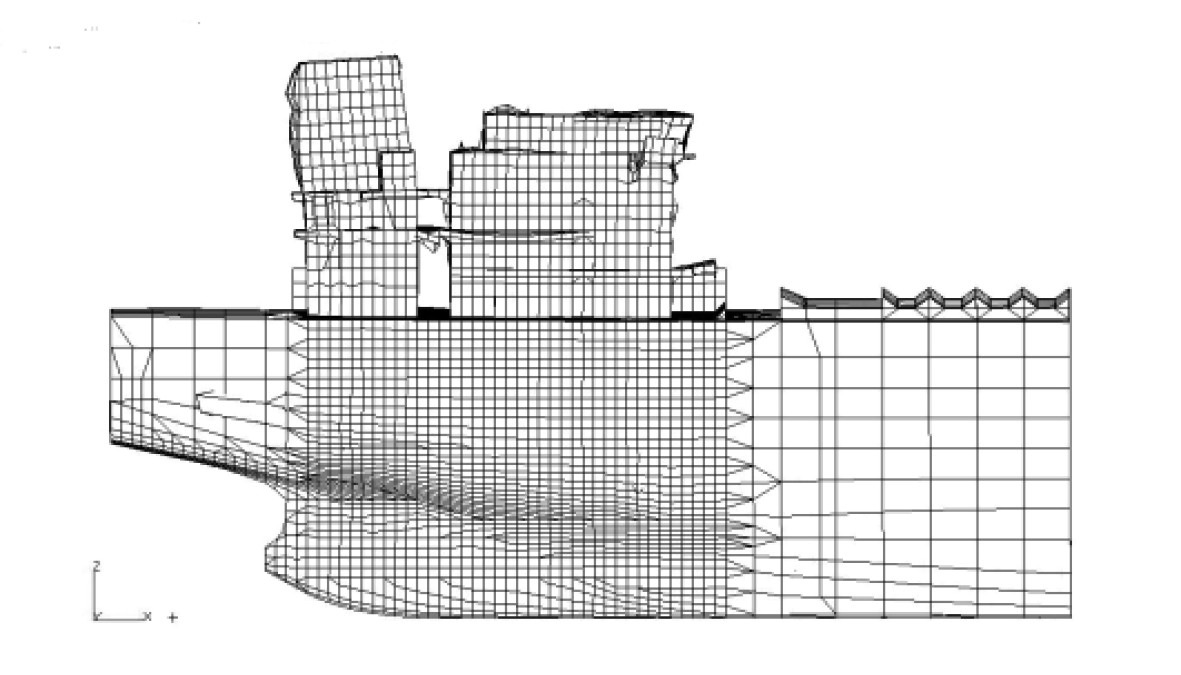
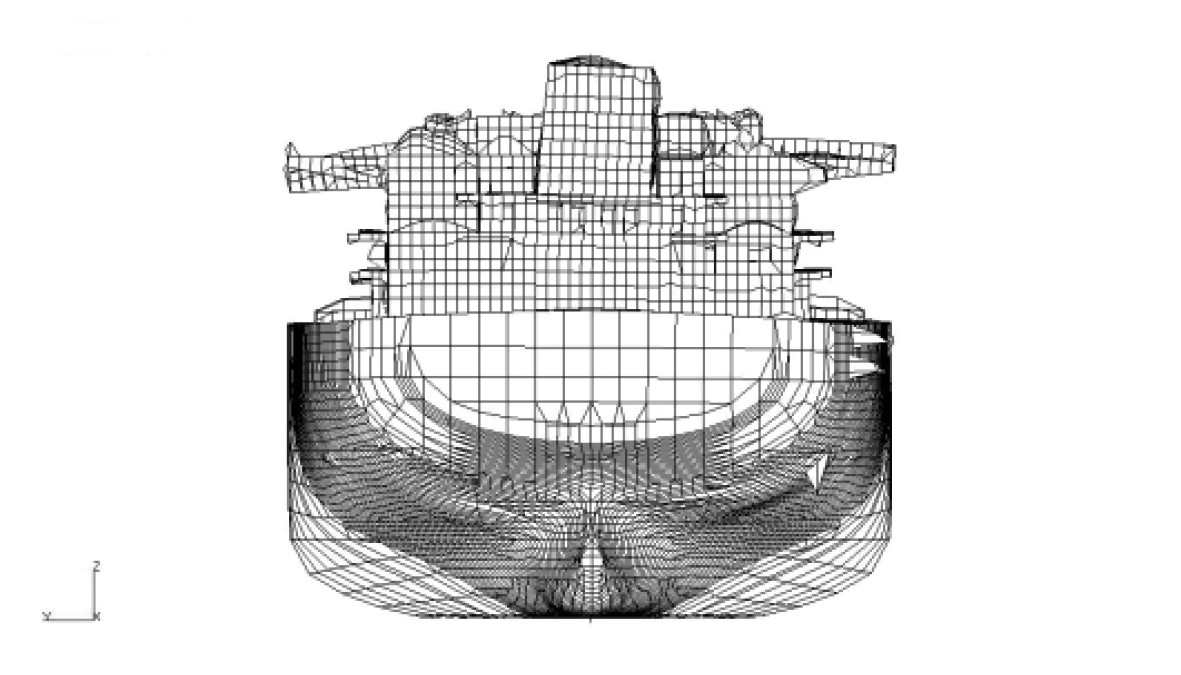
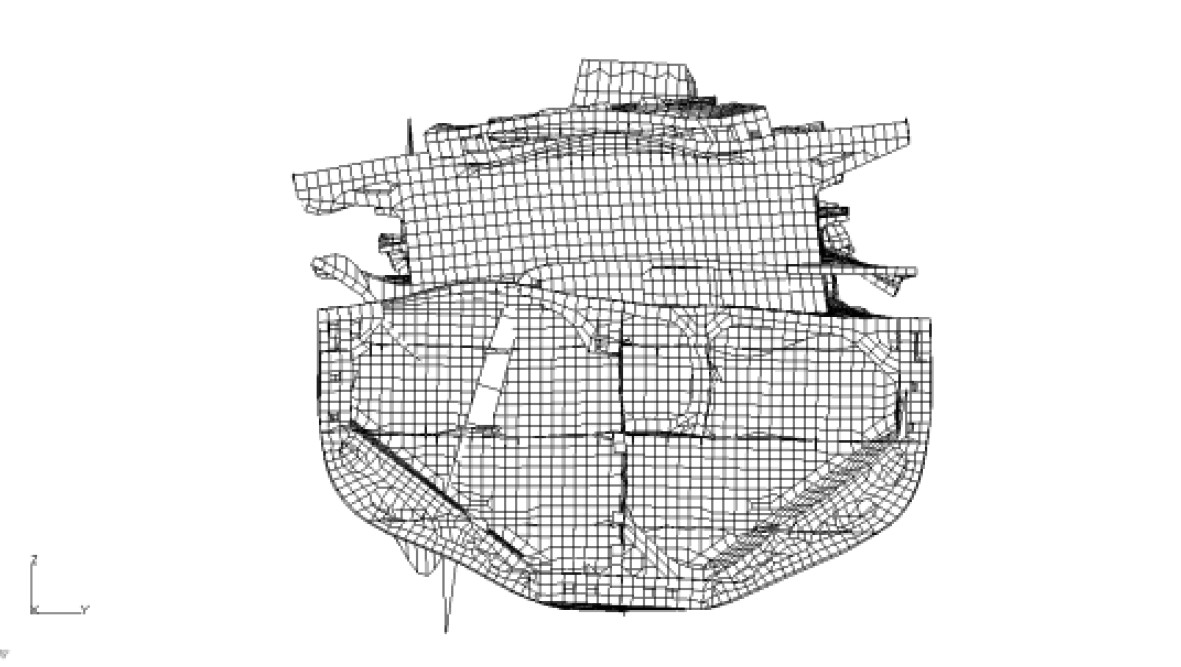
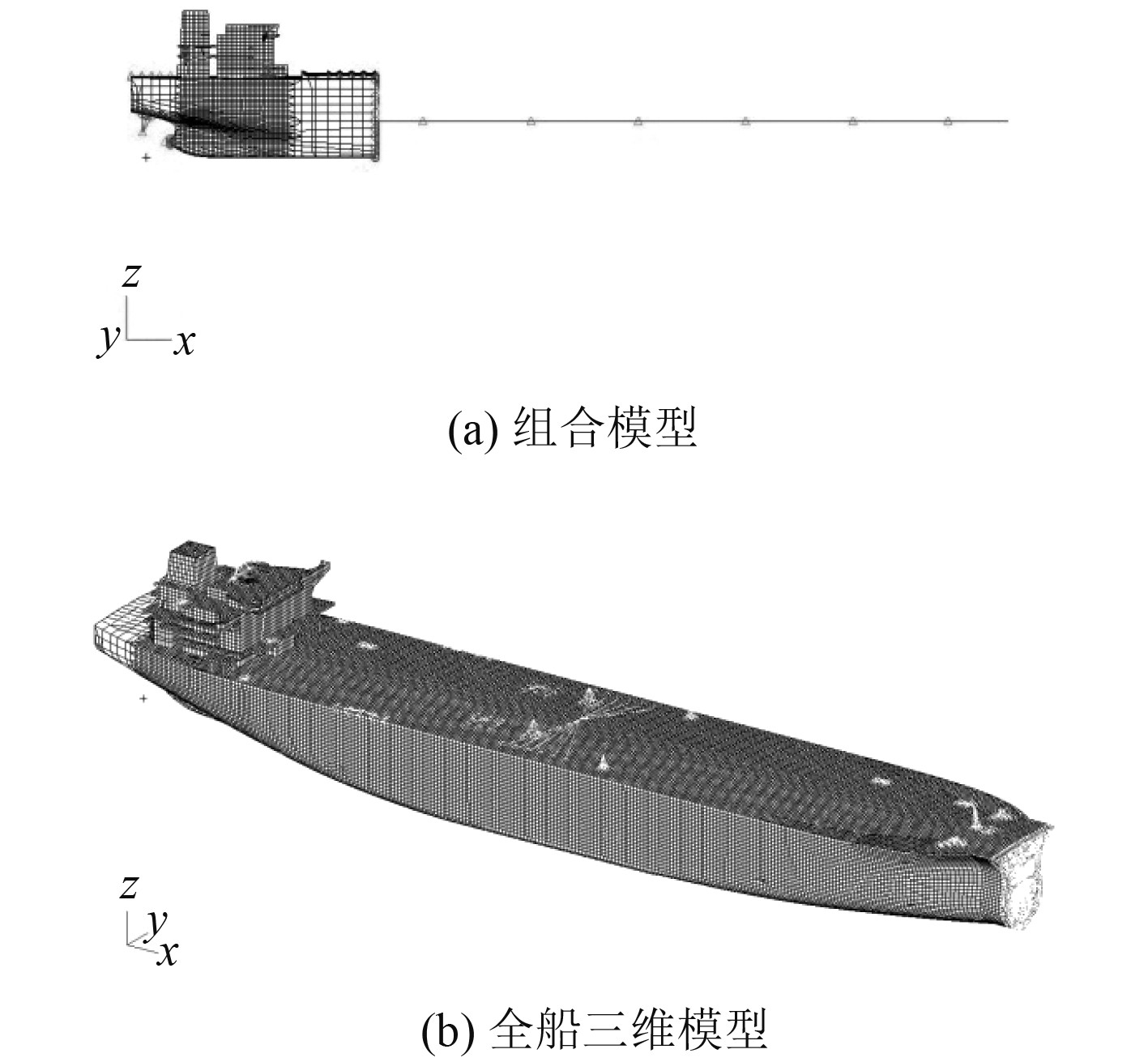
1 组合模型 1.1 模型模拟方法通常情况下,组合模型的上建、尾部、机舱及部分尾货舱采用三维模型模拟,其他货舱区及首部采用梁单元模拟,并通过MPC将梁单元模型与三维模型连接。该模拟方法可准确反映上层建筑及机舱尾部主要振动关注区域的振动特性,同时方便螺旋桨与主机激励力的施加。针对油船的货舱区结构布置及连续性基本一致,没有大开口,近似箱型梁等特点,所以可采用梁单元模拟货舱区域。通常每个货舱采用一段梁单元模拟,并将该货舱中部的剖面属性(面积、惯性矩等)赋予梁单元,梁单元的高度按货舱重心高度确定。具体模型见图1所示,同时为了方便对比,也给出了全船三维模型。
|
图 1 振动模型 Fig. 1 Vibration model |
质量分布的准确与否是决定船体振动分析准确性的关键因素之一。对于组合模型,三维模型部分(尾部、机舱与上建)通过施加质量点及非结构质量等方法真实模拟设备、管系等的质量分布;对于梁单元部分,首先横舱壁的质量需通过质量点施加在相应的位置,各货舱的货物质量可通过调整对应梁单元的密度实现。
2 船体梁振动特性对比基于目标船的装载手册,选取压载工况进行振动预报。通过模型模拟,质量分布调整等,保持2个模型的质量分布及重量重心基本一致,并采用有限元法分别对组合模型与全船模型进行振动特性分析。
2.1 附连水计算附连水对船体梁振动的影响是一个特殊且重要的问题,当船体梁振动时,在它周围的水也会随之运动,这部分的水相当于增加了船体梁的质量,且与船体本身质量相当,对船体梁振动的影响较大。
船体在水中作垂向振动时,各计算剖面处单位长度上的附连水质量按下式计算[2-3]:
| $ m_{a v}=\frac{1}{2} \alpha_{v} K C_{v} \rho \text{π} b^{2} \; {\rm t} / {\rm m}\text{。} $ | (1) |
式中:
船体在水中作水平振动时,各计算剖面处单位长度上的附连水质量按下式计算[2-3]:
| $ m_{a h}=\frac{1}{2} \alpha_{h} K C_{h} \rho \text{π} d^{2} \; {\rm t} / {\rm m}\text{。} $ | (2) |
式中:
为了对比组合模型与全船模型的振动特性分析结果的异同,对2个模型均采用上述方法施加附连水质量。同时,由于附连水质量的计算与固有频率阶数有关,所以,需计算出各阶振型对应的附连水质量。表1列出了船体梁前3阶船中某剖面处单位长度的附连水质量。
|
|
表 1 船体梁附连水质量 Tab.1 Added mass for ship hull |
另外,需要特别注意振动频率越大,附连水质量越小;对于有限水域或浅吃水情况,附连水质量计算公式需进行修正[4]。
2.2 计算结果船体梁固有频率分析的目的在于校核其是否与激励频率错开,所以对于组合模型,其分析精度是否到达设计需要和工程要求至关重要。为了方便对比组合模型的分析精度,表2与表3分别列出了组合模型与全船模型的船体梁前5阶的固有频率及振动模态。
|
|
表 2 船体梁振动固有频率 Tab.2 Ship hull vibration natural frequency |
|
|
表 3 船体梁振动模态 Tab.3 Ship hull vibration mode shapes |
1)组合模型船体梁固有频率及模态与全船模型基本一致,误差较小;
2)随着船体梁模态阶数的升高,组合模型的误差随之增大,由于高阶振动时船体剪切变形的影响变大所导致[5]。对于运输船,通常采用低速机,所以确保低阶船体梁固有频率错开激励频率即可;
3)对于组合模型,由于采用梁单元模拟货舱区域,所以扭转振动模态无法体现出来。但对于油船货舱区域没有大开口,上层建筑偏矮且固有频率较高,一般不会出现船体梁振动耦合情况,所以船体梁扭转振动通常情况下不是主要的关注点。
3 上层建筑振动特性对比上层建筑作为居住生活区域,其振动特性为主要关注点,同时横准要求也更严格。通常首先需分析得出上层建筑整体固有频率及模态,并判断其是否与主要激励频率错开,然后再分析其各层甲板及板架的固有频率。作为甲板及板架等局部区域,其固有频率受到船体梁模型的影响几乎可以忽略不计,因此,本文仅列出上层建筑整体振动固有频率及模态。为了方便对比,表4与表5分别列出了基于组合模型与全船模型分析得到的上层建筑横向、纵向固有频率及振动模态。
|
|
表 4 上层建筑振动固有频率 Tab.4 Deckhouse vibration natural frequency |
|
|
表 5 上层建筑振动模态 Tab.5 Deckhouse vibration mode shapes |
从表4和表5可以看出,基于组合模型与全船模型,所得结果基本吻合,误差可忽略不计。对于上层建筑的固有频率的计算,无论是组合模型还是全船模型,只是起到模拟弹性支撑的作用。所以组合模型已完全可达到上建振动特性分析的精度要求。
4 振动响应对比船体梁振动响应分析预报主要在于获得船体梁在主要激励载荷作用下的响应值,从而在设计阶段把握全船及主要关注区域的响应水平。评估结果对照横准ISO 20283–5[6],必要时需采取相应的减振措施。
4.1 计算方法通常情况下,求得船体梁的固有频率与振型后,可采用模态叠加法计算船体梁在主要激励载荷下的振动响应值。
由于附连水质量随着阵型而变化,对于全船三维模型可通过边界源法自动施加到船体外板上。而对于组合模型,附连水质量的确定是主要问题之一。基于船体梁阻尼随着阶数的增高而增大,在求解强迫振动响应时仅仅考虑前几阶振型的贡献就有足够的精度。为确保振型的正交性,选取激励频率最接近固有频率对应阶的附连水质量作为各阶共用的附连水质量,也不失计算的精度,因为振动响应的主要贡献来自最接近阶的响应[2]。
4.2 激励源、阻尼及计算位置1)激励源
船体振动激励源主要为螺旋桨和主机,螺旋桨脉动压力根据模型试验得到;主机激励力由设备商提供。选取船型的CSR转速为75.8 r/min,螺旋桨为四叶桨,压载工况下试验最大脉动压力为2.1 kPa;主机为六缸机,2阶垂向不平衡力矩(1 232 kNm)与6阶横向倾覆力矩(1 319 kNm)为主要激励力。
2)阻尼
在船体振动响应分析时,需考虑阻尼的影响。通常情况下,阻尼系数很大程度上依赖于实船测试来进行确定。根据目标船的船型及吨位,本文阻尼系数取为0.015[2]。
3)计算位置
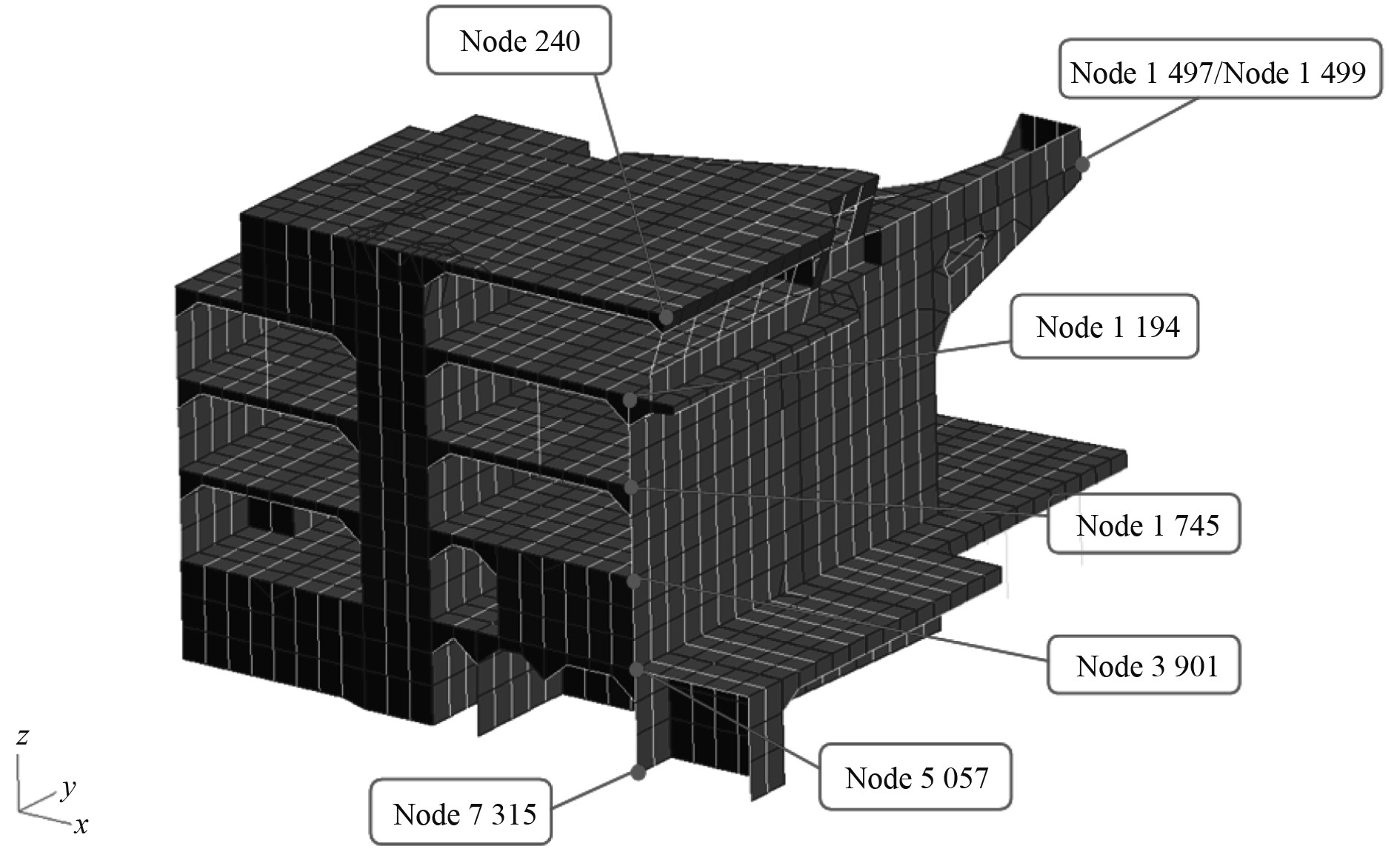
对于螺旋桨或主机激励下的油船振动响应分析,评估其振动响应的具体位置,主要选取船员工作、休息区域及重要设备场所,如各层甲板前端中点和边缘、翼桥端部等,具体计算位置如图2所示。
|
图 2 响应计算位置 Fig. 2 Forced vibration calculation locations |
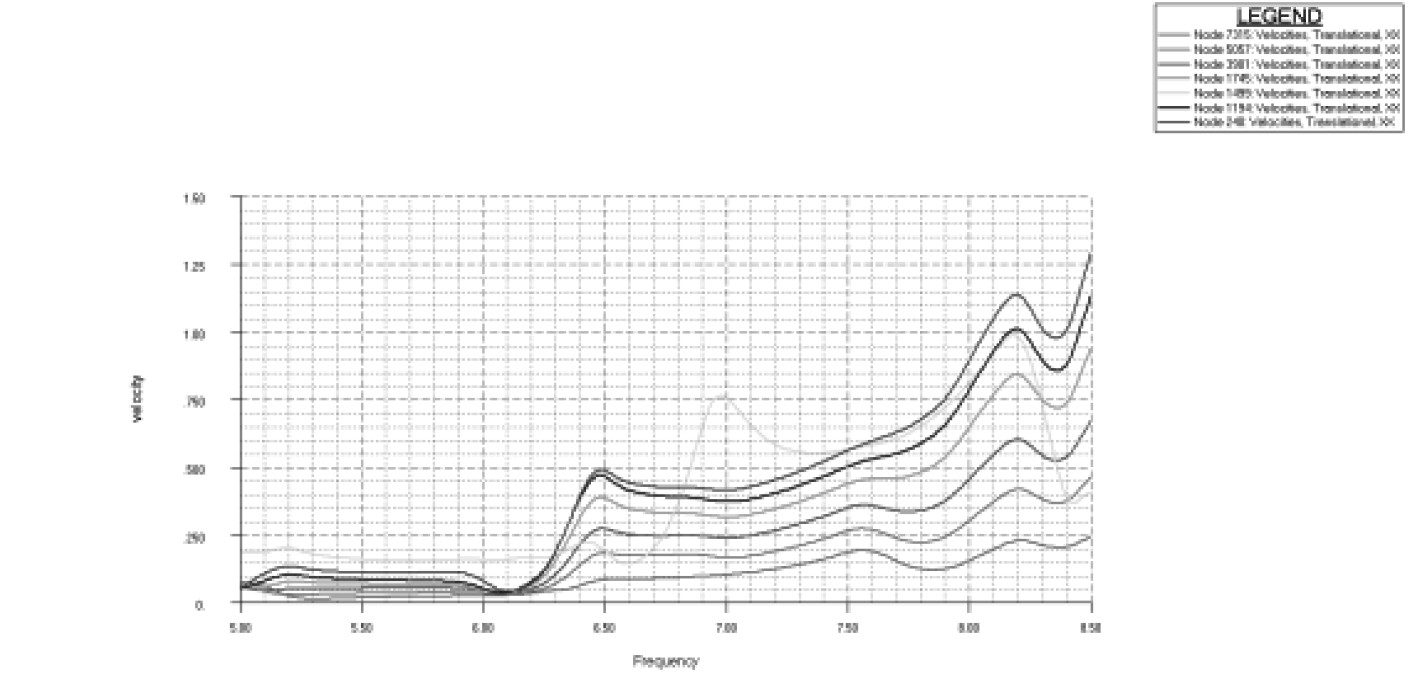
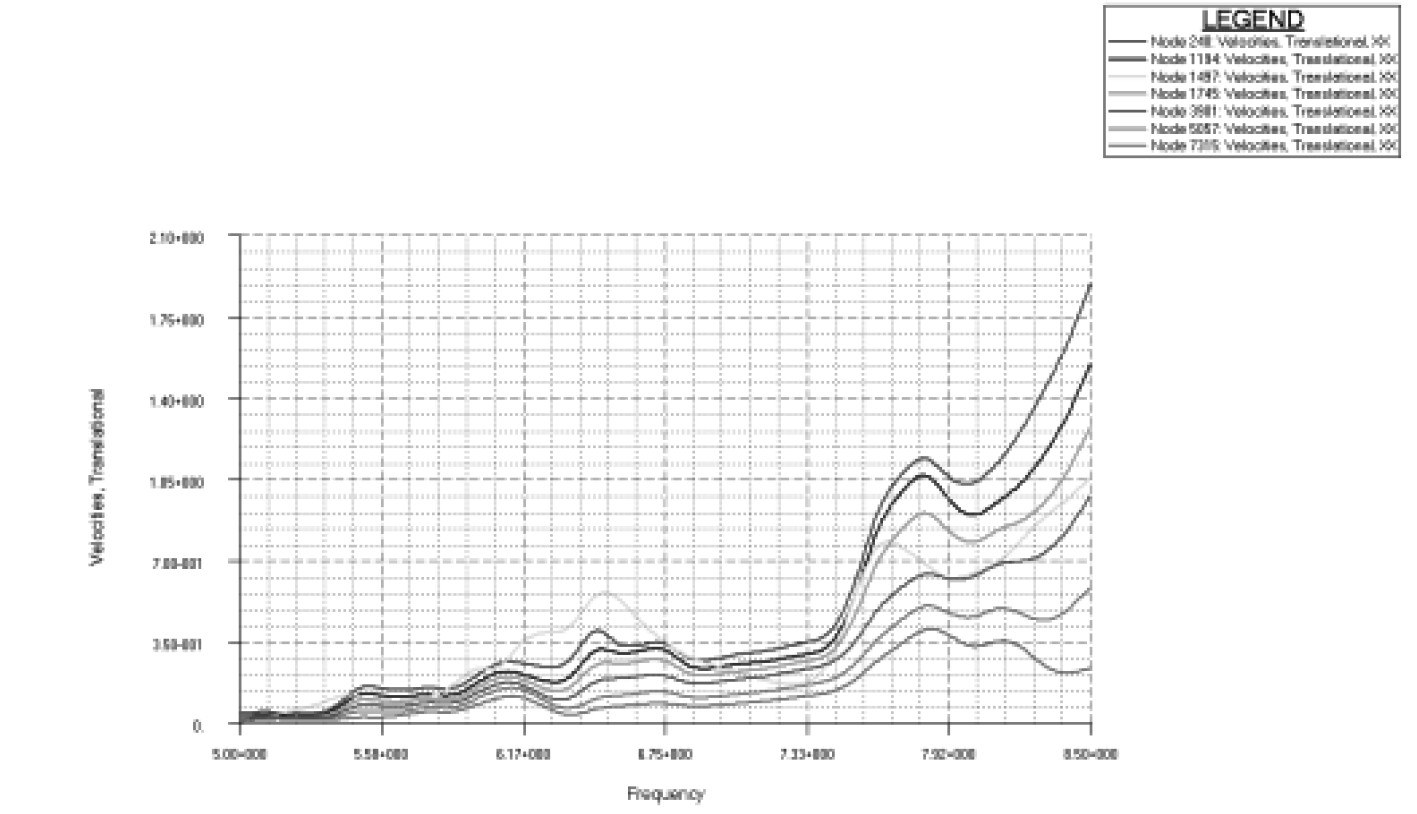
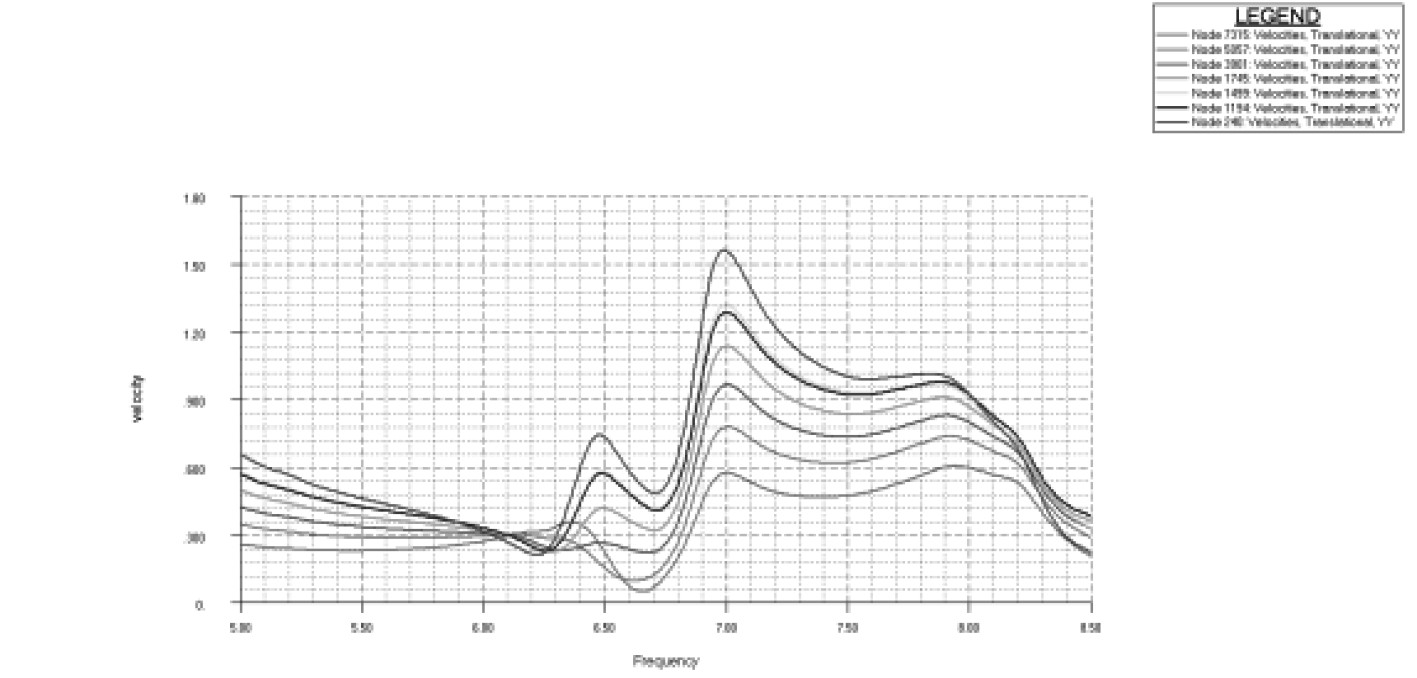
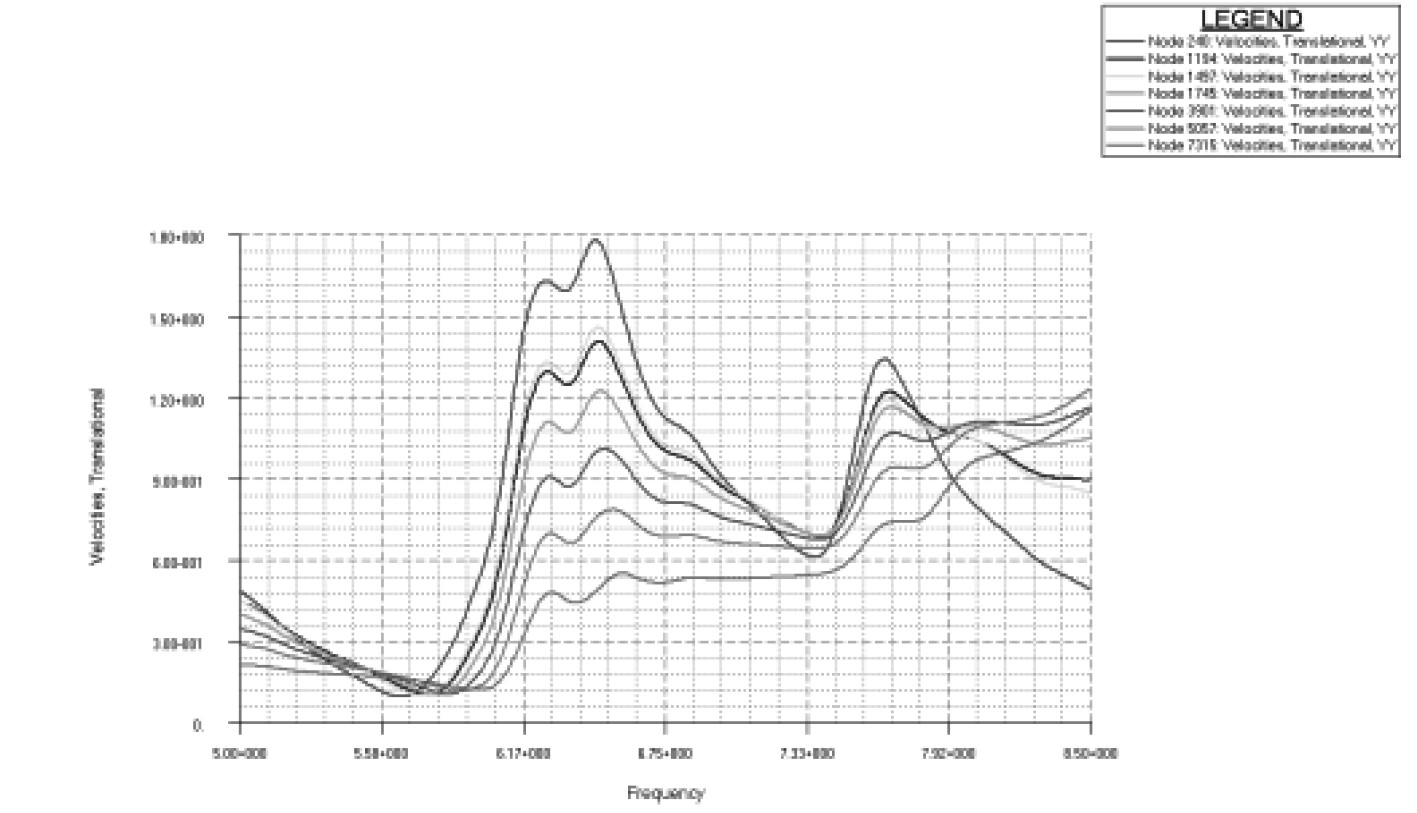
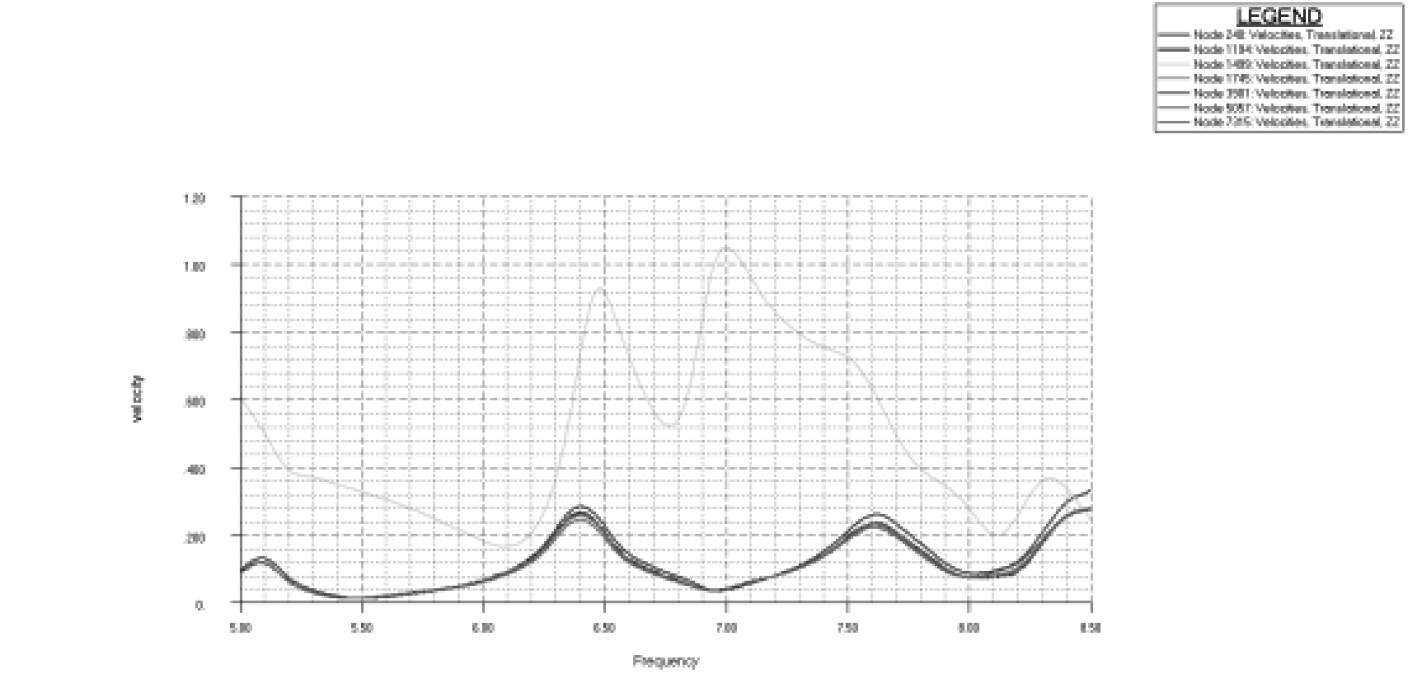
根据以往分析经验及实船振动测试数据,通常情况下,对于运输船,主机横向倾覆力矩对船体及上层建筑的振动响应水平影响最大,所以本文选取主要激励源主机6阶倾覆力矩进行响应分析。为了更好分析组合模型响应分析的精度,同时也基于全船模型进行响应分析,频响曲线如表6所示。
|
|
表 6 响应计算结果对比 Tab.6 Forced vibration calculation results comparison |
由表6可以看出:
1)响应值大小方面,基于2个模型的计算结果在激励频率附近考察区域(一般取激励频率前后10%范围)各方向的响应值大小基本一致;
2)频响曲线方面,响应值随频率变化的趋势比较复杂,但是整体趋势基本一致,横向相对偏差较大一些;
3)与全船三维模型对比,基于组合模型计算所得的响应值基本满足精度要求。
5 结 语基于油船货舱区结构连续,没有大开口,类似箱型梁等特点,本文以某11.5万吨油船为例,通过与全船三维模型对比,分析并研究了组合模型在油船振动分析预报中的应用,主要结论如下:
1)组合模型的模拟需按照正确的方法模拟,准确反映船体梁质量分布、重量重心以及三维模型与梁模型的连接;
2)船体梁固有特性方面,在低价范围组合模型计算结果与全船三维模型结果基本一致,随着船体梁固有频率阶数的增加差距增大;
3)船体振动响应方面,基于组合模型的计算结果在响应值大小和响应曲线整体趋势等方面与全船三维模型结果基本一致;
4)组合模型在油船振动分析中的应用,可保证设计要求精度,同时可有效节省建模与分析周期,在设计初中期阶段即可采用此方法。
| [1] |
付佳, 徐智言, 王铭. 船舶振动ISO 20283-5新标准研究[J]. 噪声与振动控制, 2018, 38(4): 239-242. |
| [2] |
中国船级社. 船上振动控制指南[S]. 北京: 人民交通出版社, 2012.
|
| [3] |
金咸定, 夏利娟. 船体振动学[M]. 上海: 上海交通大学出版社, 2011.
|
| [4] |
尚鹏飞, 车驰东. 基于振动测量的刚体附连水质量研究[J]. 舰船科学技术, 2015, 37(12): 7-12. |
| [5] |
张晓, 陈克强, 杨和振. 船舶总振动固有频率实用算法[J]. 中国舰船研究, 2007, 2(1): 56-58. |
| [6] |
ISO 20283-5: Mechanical vibration- Measurement of vibration on ships- Guidelines for measurement, evaluation and reporting of vibration with regard to habitability on passenger and merchant ships[S]. 2016(E).
|
 2021, Vol. 43
2021, Vol. 43