潜艇作为各国海军杀手锏武器,航行过程中将产生“声指纹”特征明显的辐射噪声,这将极大地影响潜艇隐身性能。美国海军在《2000-2035年海军技术—潜艇平台技术》报告中,已将潜艇声隐身作为关键技术之首。实际上,该技术也是各军事大国极为重视和大力发展的技术之一。
隔振作为降低设备振动的有效措施,可分为被动隔振和主动控制。前者因设计简单、无外置能源、方便安装及价格经济等优点,应用较为广泛。目前,美国核潜艇推进系统使用浮筏隔振后,艇体结构噪声降低了15~20 dB,而其“洛杉矶”级和“海狼”级攻击型核潜艇辐射噪声已分别降至118 dB和90~100 dB,己低于3级海况海洋背景噪声(110~120 dB)。被动隔振优点较多但也有不足之处,例如低动刚度和失稳之间尚存矛盾,主要对高频振动有较好控制效果[1-2],200 Hz以下低频隔振效果还不够理想。
主动控制是在被动隔振中引入次级能量,通过执行装置与隔振器串联或并联实现振动消减,往往可具有较好的低频控制效果[3]。美国新型海狼级核潜艇列装有源隔振系统后,具备良好的声隐身性能[4],其还研发主动隔振缓冲装置,可降低攻击型核潜艇50%~70%冲击载荷[5]。瑞典Karlskrona大学设计惯性主动隔振装置,能有效降低护卫舰壳体结构振动所致辐射噪声[6]。与此同时,国内何琳等[7]、杨铁军等[8]、张志谊等[9]在隔振元件及主动控制方面也开展了诸多研究。实际上,主动控制重点就是设计适宜的控制策略,这也是该领域研究热点和难点问题。在振动噪声控制领域,最小均方LMS自适应算法因运算效率高等优点而备受关注[10-13]。然而,由于次级通道存在,LMS算法直接用于振动控制还存在参考和误差信号时域一致性问题。为此,Morgan[14]引入次级通道估计值对参考信号时延,并提出FxLMS算法,该算法及其改进算法工程应用前景十分广泛。但目前这些算法或程序主要通过解释性语言(如C语言)进行编程开发DSP,FPGA等硬件,往往将理论研究和工程实践分割开来,不利于两者有效衔接,开发周期较长、开发难度相对较大。
近年来,随着控制技术快速发展,为有效解决这一问题奠定了良好的基础和思路。特别是随着快速原型控制技术发展,已实现软硬件高效无缝衔接,为开展振动噪声控制研究提供了极大便利。该技术能有效地将理仿真与工程实践结合起来,在样机实验阶段具有重要的开发和验证价值。王婷[15]、陈亮[16]、沈佳明[17]、庞齐齐[18]等基于快速原型控制技术,在Matlab/Simulink环境下开展伺服系统全数字原型验证、整车动力学模型原型试验、无人机快速原型验证等研究,结果表明该方法可方便快捷且高效地进行开发调试及样机实验,能快速打通理论与工程壁垒,有效节省开发周期。
因此,针对振动主动控制过程中次级通道辨识精度要求高、控制策略用传统编程手段开发周期长、编程困难大等问题,本文以双层隔振系统单通道控制为研究对象,以离线辨识FxLMS滤波自适应控制算法为基础,基于Speedgoat快速原型控制技术开展振动主动控制实验验证研究,为后期开展大规模、多通道、在线辨识等条件下浮筏隔振系统振动控制验证奠定良好基础。
1 隔振系统建模双层隔振台架原理图如图1所示。该系统为多输入/多输出(MIMO)控制系统,上层为含有复杂激励振源设备和隔振平台,上层和中层台架之间有4个主被动一体化隔振器。中层隔振平台为具有一定结构和尺寸刚性阀架,通过4个橡胶隔振器固结于基础上。参考传感器位于振源设备机脚位置,拾取参考信号
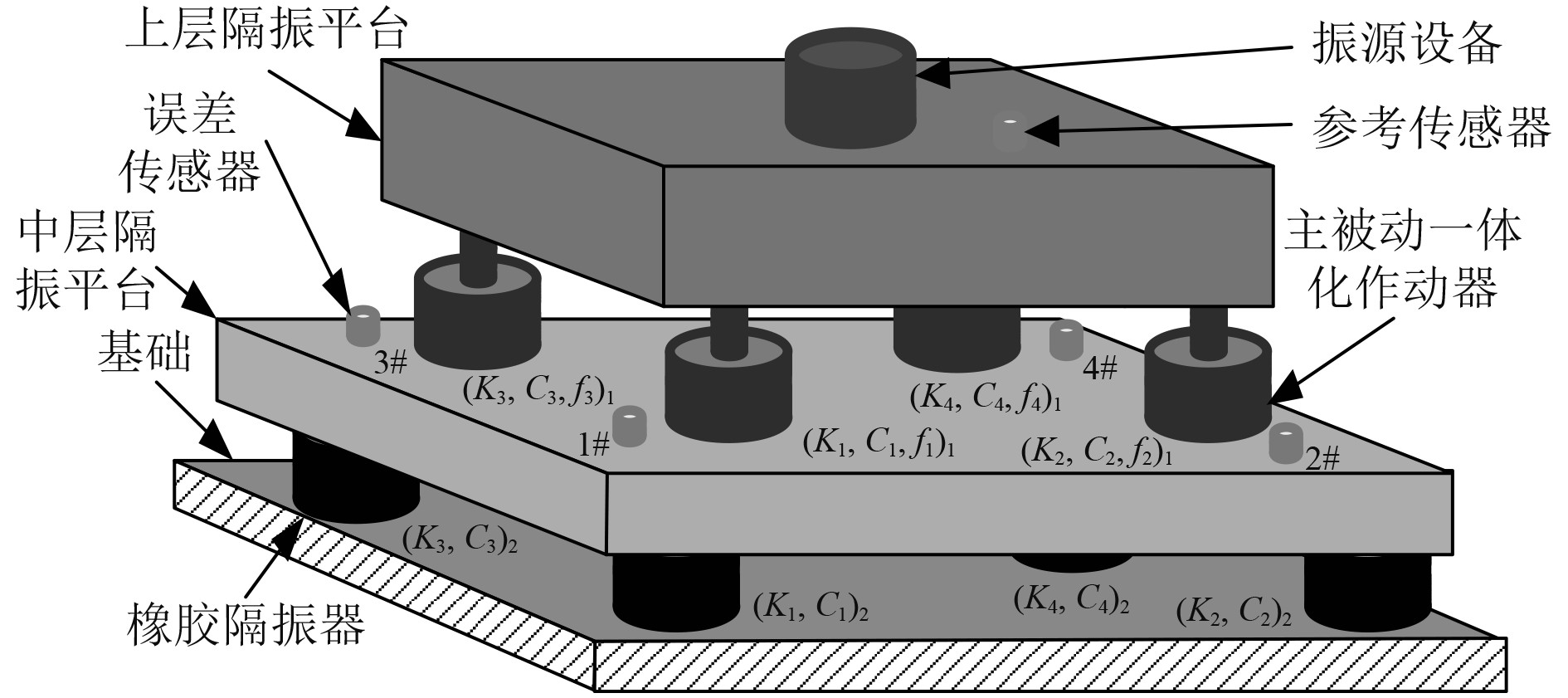
|
图 1 双层隔振系统结构图 Fig. 1 Active vibration control system |
为应用快速原型控制方法,实验过程中仅选隔振系统1#通道作为控制对象,开展次级通道辨识和主动控制验证性研究。此时,图1可简化为图2所示单通道隔振系统。
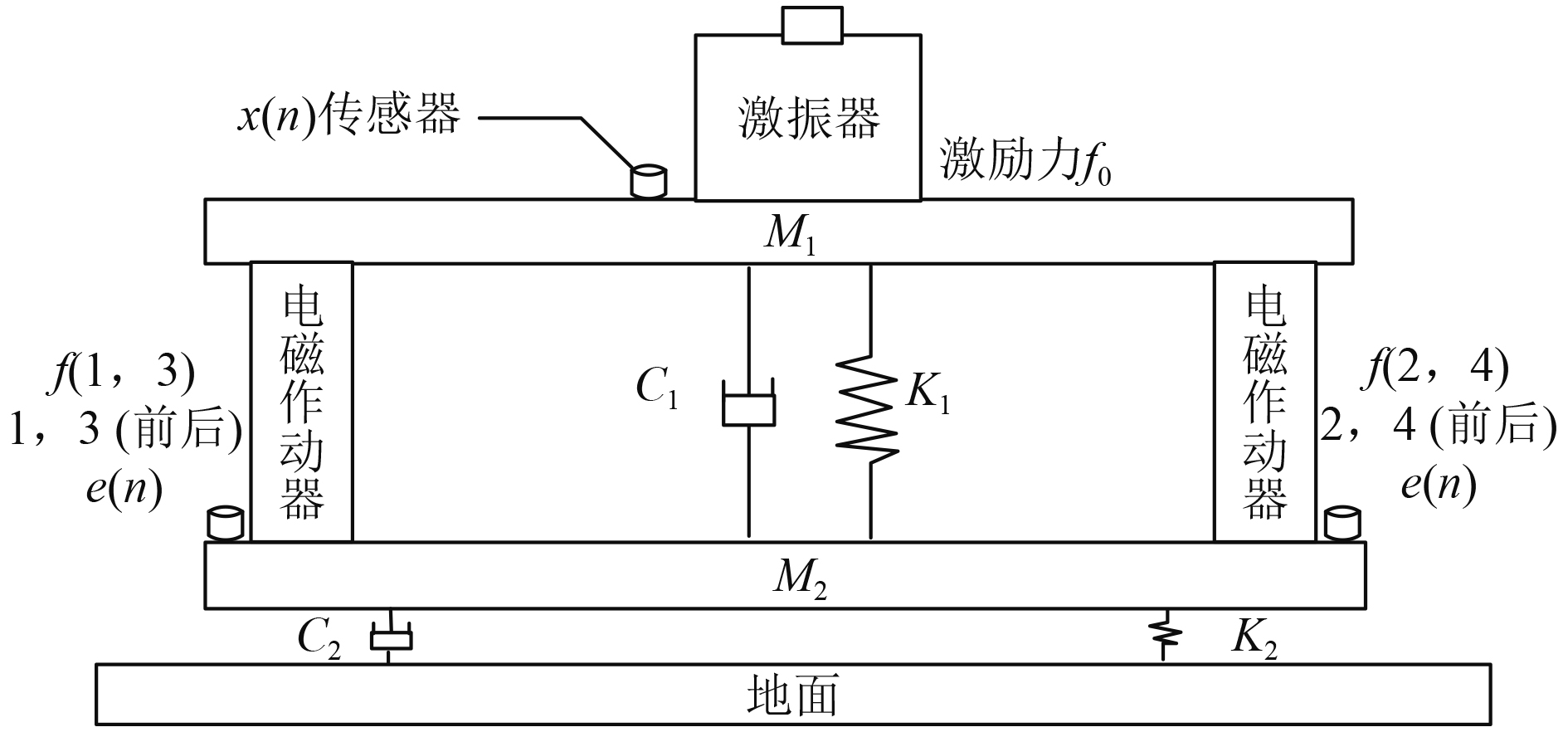
|
图 2 隔振平台简化图 Fig. 2 Simplified diagram of vibration isolation platform |
20世纪60年代,Hoff[19]提出LMS最小均方算法,以实现简单及信道稳健等优点在噪声对消、系统辨识等领域广泛应用[20]。含次级通道的单输入单输出自适应算法如图3所示,其原理为滤波器
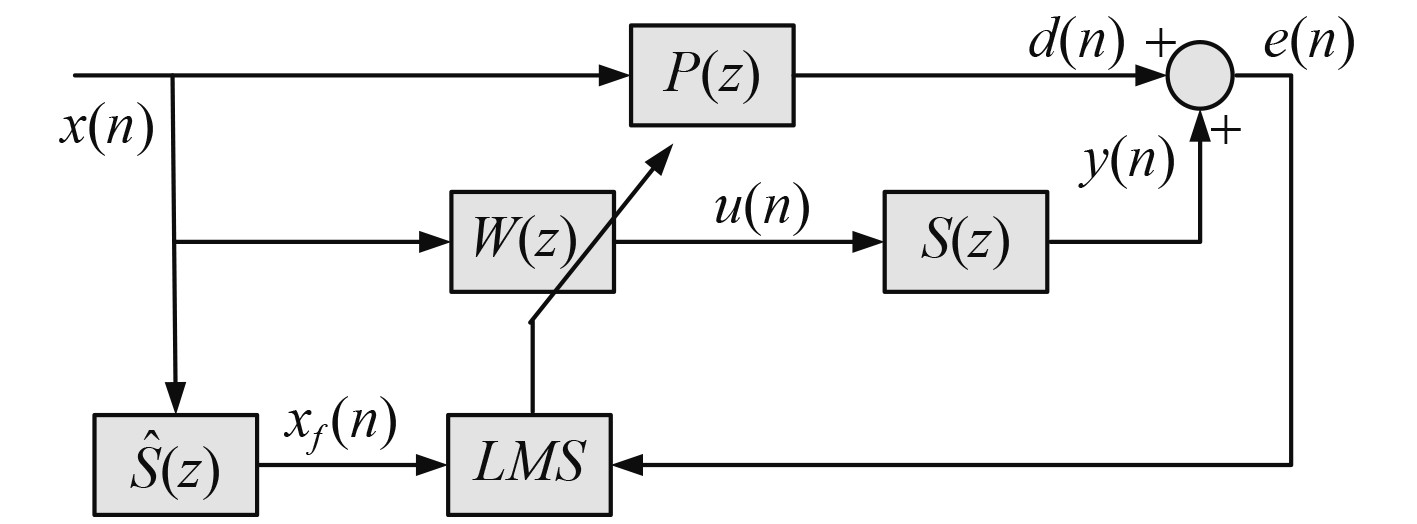
|
图 3 滤波自适应算法结构图 Fig. 3 The structure diagram of FxLMS adaptive algorithm |
图中,
| $e(n) = d(n) + y(n)\text{。}$ | (1) |
其中:
| $u(n) \!=\! \sum\limits_{i = 0}^{N - 1} {{w_i}(n)x(n \!-\! i) \!=\! {W^{\rm T}}\left( n \right)X\left( n \right) \!=\! {X^{\rm T}}\left( n \right)W\left( n \right)}\text{,} $ | (2) |
其中:
| $\begin{split} y(n) = &{[{X^{\rm T}}(n)W(n)]^{\rm T}}S(n) = {W^{\rm T}}(n)X(n)S(n) = \\ & {W^{\rm T}}(n){X_f}(n) = {X^{\rm T}}_f(n)W(n)\text{。} \end{split} $ | (3) |
式中:
| $J\left( n \right){\rm{ = }}E\left[ {{e^2}\left( n \right)} \right]\text{。}$ | (4) |
实际上,往往可用瞬时误差
| $\begin{split} J\left( n \right) \approx &{e^2}\left( n \right) = {\left( {d\left( n \right) + \sum\limits_{i = 0}^{M - 1} {{S_i}\left( n \right)u\left( {n - i} \right)} } \right)^2} = \\ & {\left( {d\left( n \right) + \sum\limits_{i = 0}^{M - 1} {{S_i}\left( n \right)\sum\limits_{i = 0}^{N - 1} {{w_j}} \left( {n - i} \right)} x\left( {n - i - j} \right)} \right)^2} \text{。} \end{split} $ | (5) |
此时,若次级通道不随时间变化,目标函数
| $\frac{{\partial J\left( n \right)}}{{\partial W\left( n \right)}} = 2e\left( n \right){X_f}\left( n \right)\text{,}$ | (6) |
那么,权值迭代系数更新可表示为:
| $W\left( {n + 1} \right) = W\left( n \right) - \mu e\left( n \right){X_f}\left( n \right)\text{。}$ | (7) |
式中:μ为迭代步长,其值对控制算法收敛速度有较大影响,应选择合适的参数。
3 隔振平台实验研究 3.1 系统实验原理简介双层隔振系统实验原理如图4所示,结合隔振系统建模和算法分析可知,系统工作时上层加速度传感器拾取参考信号
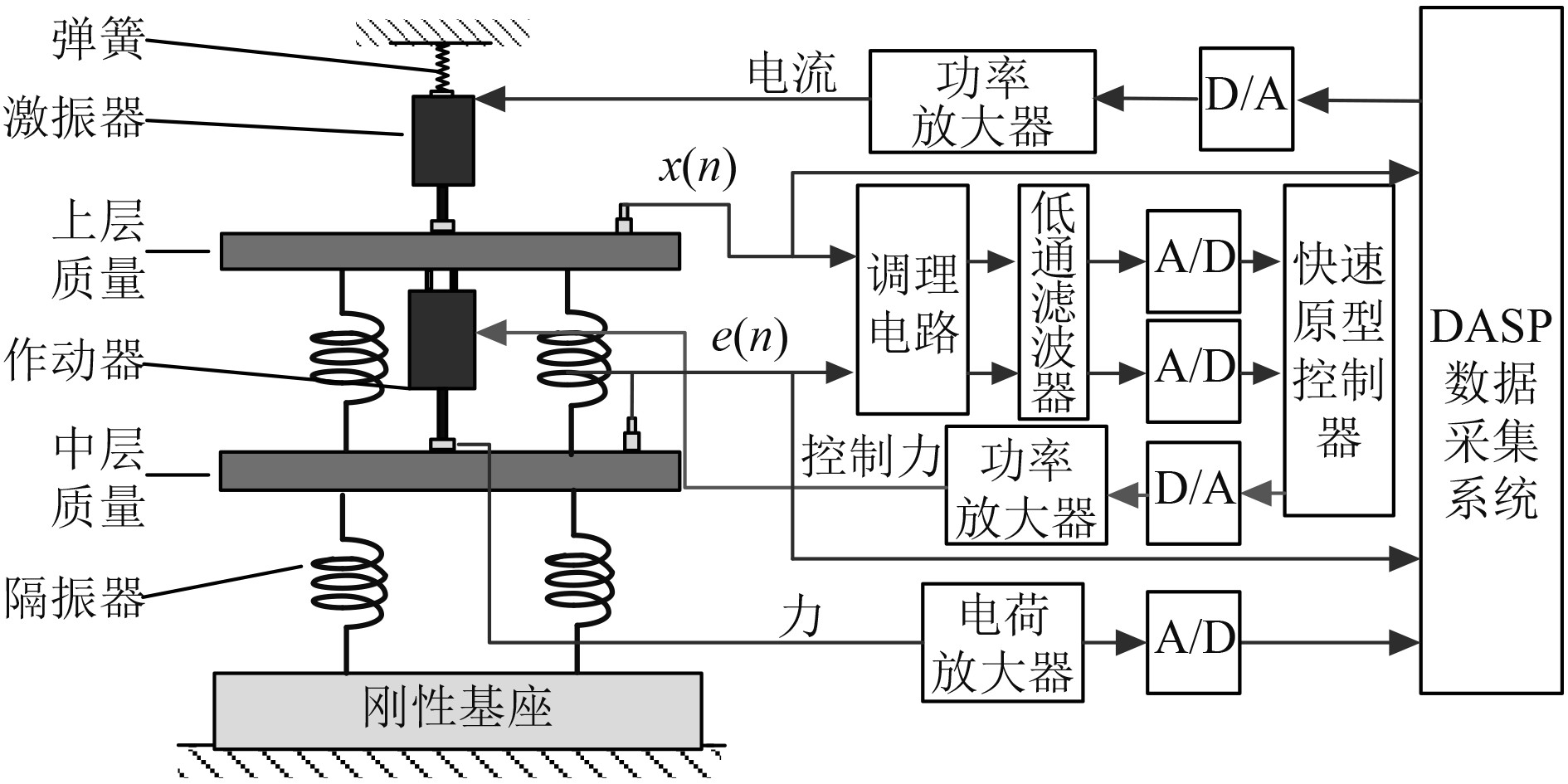
|
图 4 主动控制实验原理图 Fig. 4 Schematic diagram of active control experiment |
由图4可知,主通道和次级通道为实际物理系统,但要实现算法就需对次级通道进行离线辨识,获得较为准确的估计次级通道,并将其装载至控制算法后才能执行运算。次级通道离线辨识时,需采集控制器输出信号和中层平台误差信号,可以白噪声作为激励信号进行次级通道离线辨识,尽量获取模态信息较为全面的次级通道。
3.2 试验系统组成隔振平台上层以置于平板中心的惯性激振器为振源,中层隔振板四角各有电磁主被动一体作动器,其底部橡胶为被动隔振器件,下层还有BE85橡胶隔振器固结于地面,该平台可简化为双层隔振弹簧-阻尼系统。
试验系统由硬件和软件两部分组成,硬件主要包括激振器、双层隔振平台、信号发生器、电磁作动器、DASP数据采集仪、Speedgoat快速原型控制器、功率放大器及加速度传感器等设备器件。其中Speedgoat作为FxLMS算法部署载体,是一款高性能实时控制器。功率放大器是将弱电信号放大驱动作动器和激振器,而DASP硬件及传感器用于信号采集和数据分析。软件主要含DASP工程版软件及快速原型控制程序,DASP上位机分析软件用于加速度、电流等信号实时显示、数据存储及分析处理。
此外,快速原型控制软件包括两部分(上位机和下位机),均需在Matlab/Simulink环境下完成编译。其中下位机程序主要实现指令接受、信号采集、数据上传、FxLMS自适应算法运算及信号输出等功能。上位机软件主要是用于指令传输、数据存储、过程观测和后期分析。根据试验功能需求,便于开展次级通道辨识和主动控制试验,在下位机中将两项功能结合起来,通过模式选择实现功能切换。
3.3 试验步骤本试验目的主要是验证自适应算法有效性及控制效果,试验流程主要包括以下步骤:
1)搭建双层隔振系统试验台架,将激振器和上层平台中心位置紧固连接,在上层质量和中层之间安装一体化电磁作动器,检查各机脚限位装置,防止过载损害作动器。用带有屏蔽功能动力电缆连接激振器和功率放大器、作动器和数控电源,将传感器加速度信号用三通接头连接测试监控仪器和快速原型控制器,将功率放大器信号连接值数据采集系统通道。
2)设置信号发生器激励电流幅值和频率,调节功率放大器通过上位机监控软件观测上层质量振动情况,依次确保主通道和次级通道工作正常,然后将信号端口连接至快速原型控制器。用快速原型控制器上位机输出零均值随机信号激励作动器,并采集残差信号完成次级通道离线辨识工作,获取次级通道估计值,并将其装载至算法估计次级通道环节。
3)完成次级通道离线辨识后,设置激励信号幅值和频率,通过信号发生器或控制器激励振动台架,即可开展主动控制试验。单次试验为10 s,系统激励稳定后可切换快速原型控制器进入主动控制状态,使用上位机软件可进行参数在线调整和过程检测,使用DASP数据采集系统可记录上层、中层平台加速度等信号,该过程主要验证自适应控制算法效果。
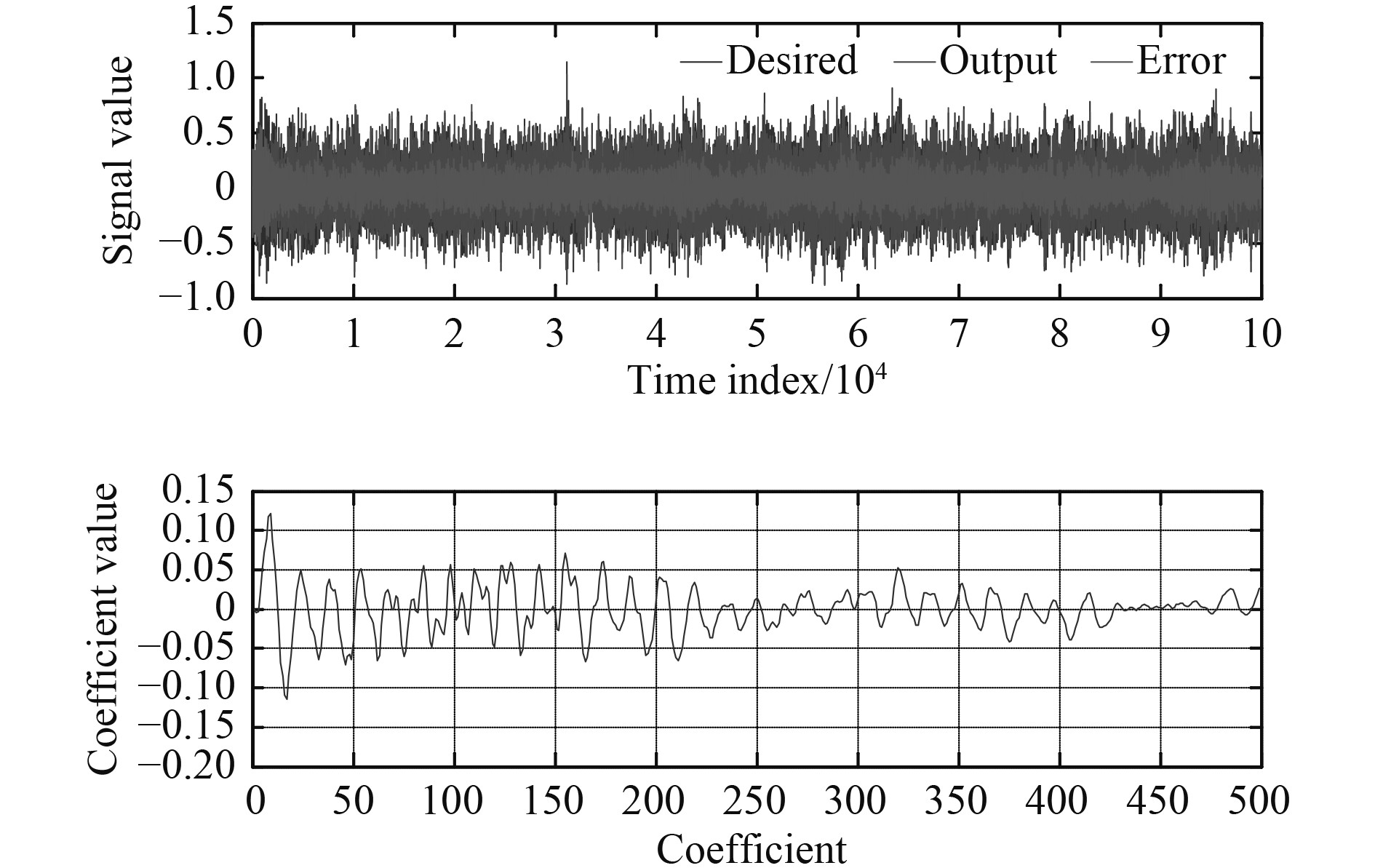
3.4 结果与分析根据滤波自适应算法,需获取台架1#机脚次级通道估计模型,利用退化FxLMS算法进行参数辨识。在辨识状态下利用Speedgoat控制器产生白噪声,并经D/A输出驱动电磁作动器,由A/D模块采集中层加速度信号即可完成一次数据采集。其中,白噪声为辨识输入,中层加速度为理想输出,辨识采用500阶FIR滤波器,步长5E-4,采样时间为0.1 ms,采样周期为10 s,辨识效果如图5所示。
|
图 5 次级通道辨识 Fig. 5 Identification of secondary path |
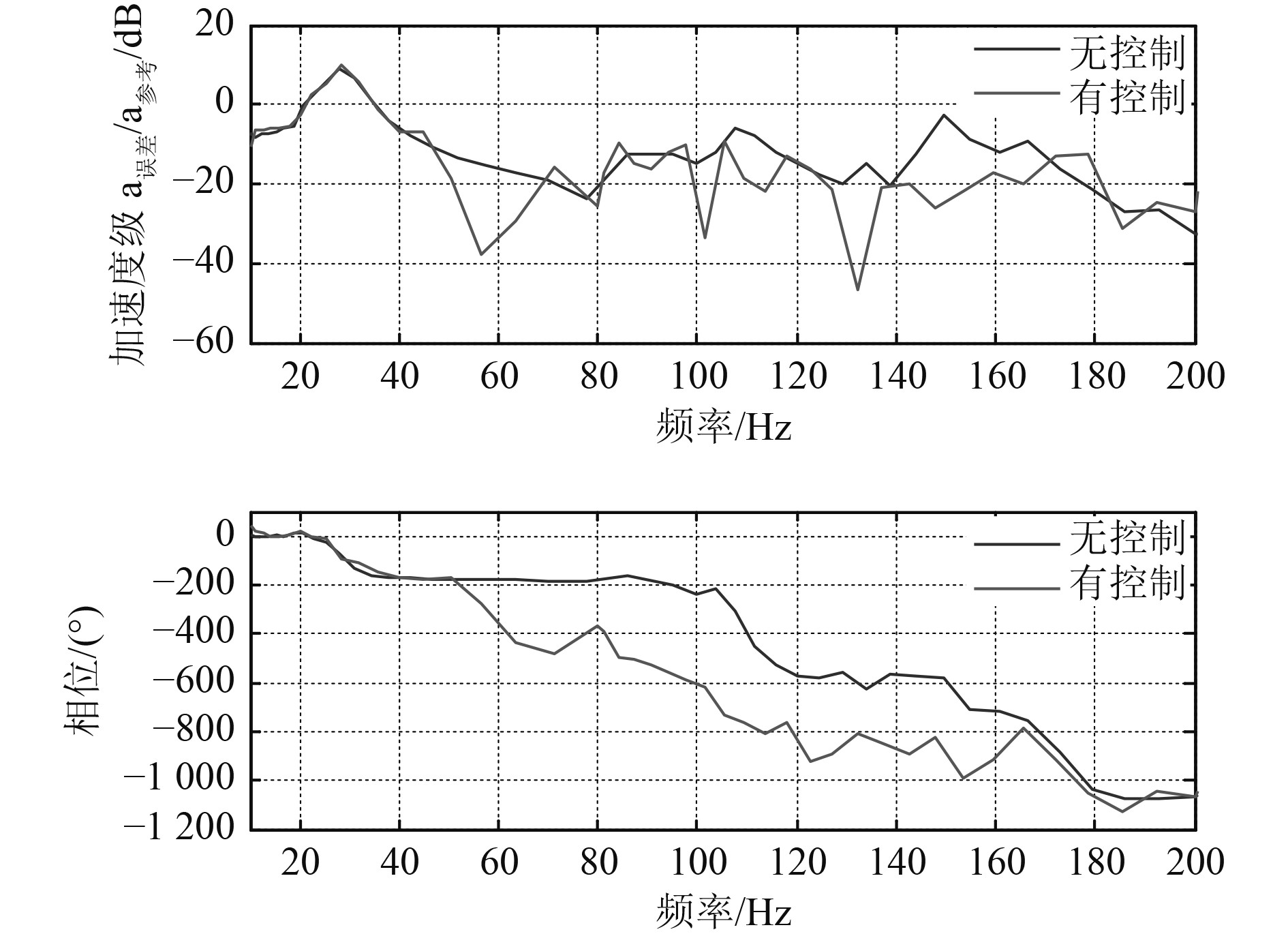
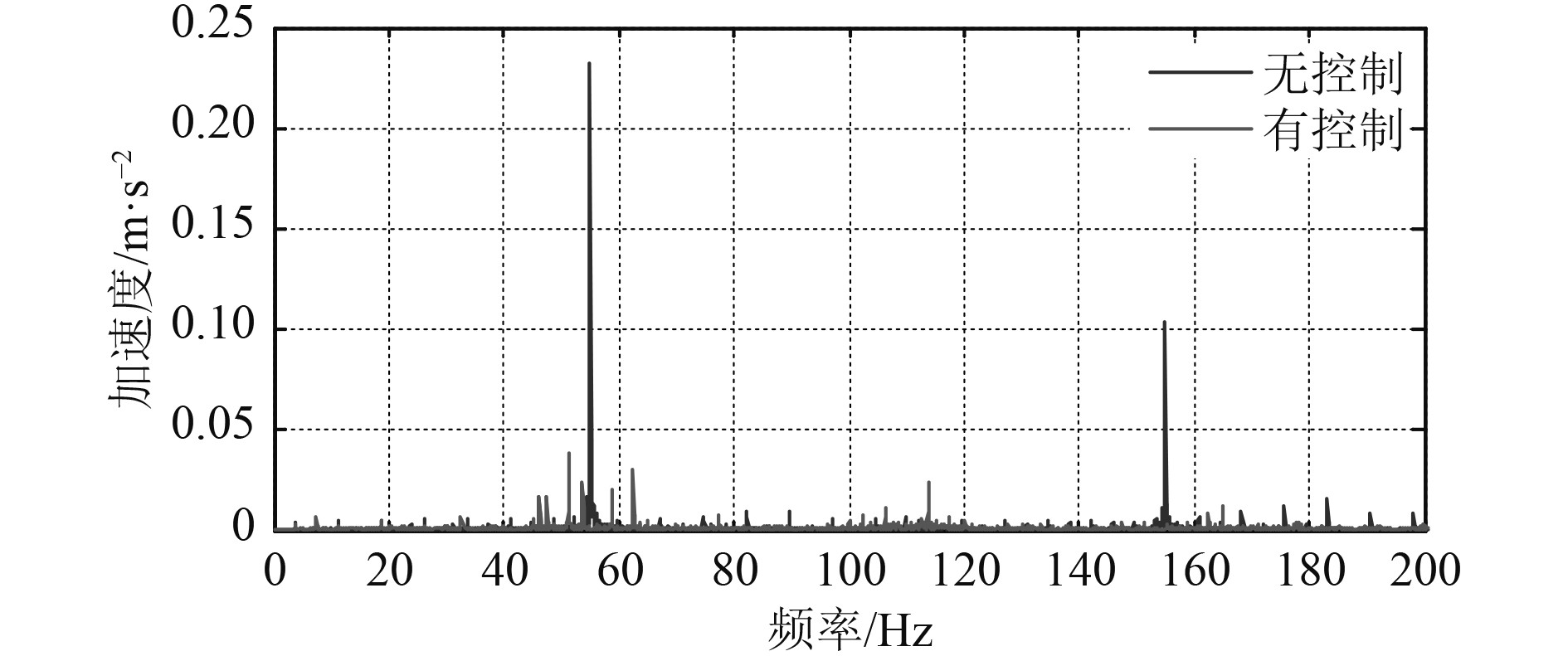
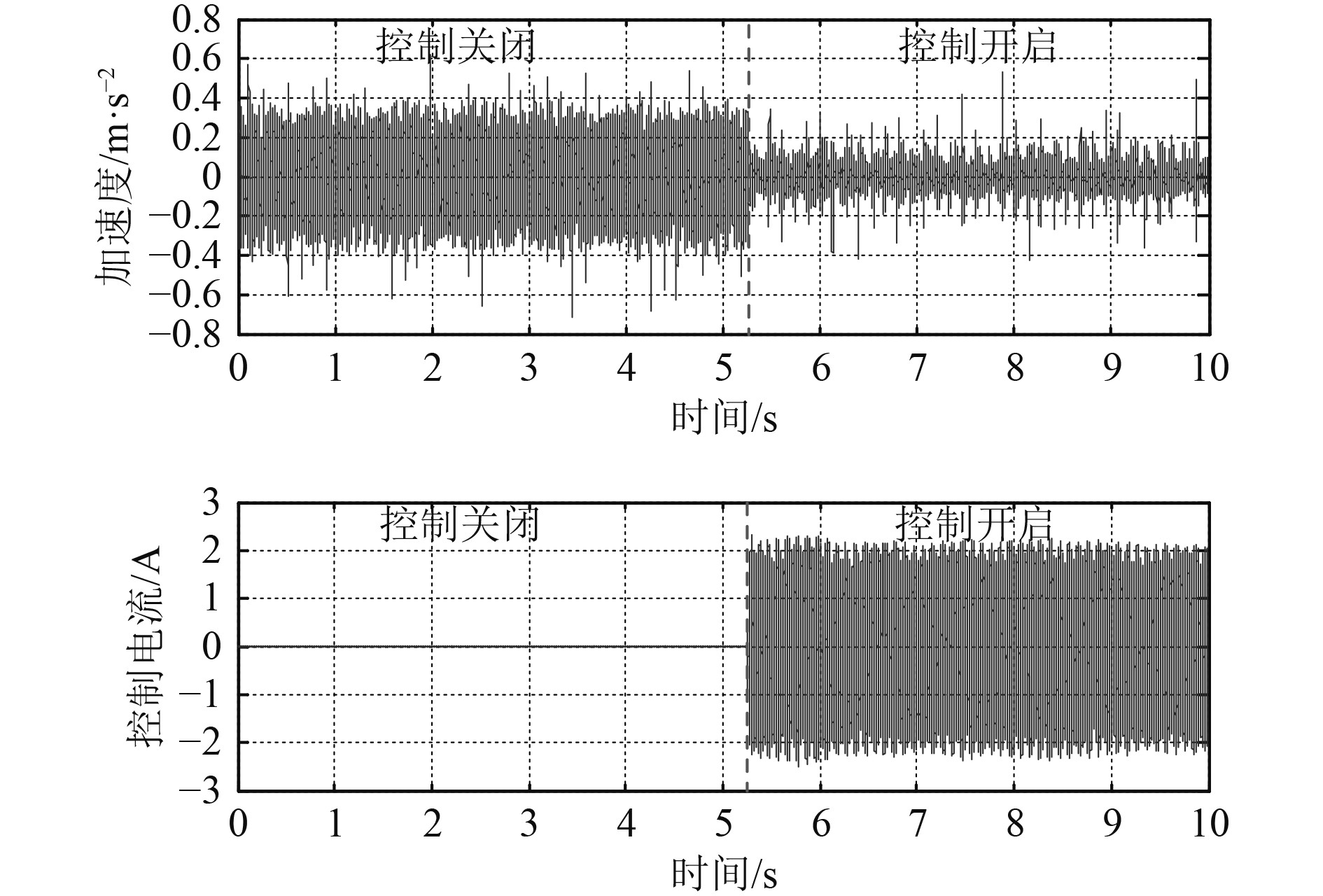
根据次级通道辨识参数可知,500阶滤波器基本趋近于零,能够有效描述其通道特性,故可将估计次级通道模型装载至算法中,利用图3所示模型在控制状态下开展控制算法验证研究。试验过程中,台架控制试验输入分别为单频激励和双频激励。其中,单频振动控制用扫频法对振动控制前后参考信号到误差信号传递函数幅频和相频特性进行分析,扫频范围10~200 Hz,涵盖一体化电磁作动器有效频段,控制效果如图6所示。双频振动输入以55 Hz和155 Hz作为激励信号,残差信号频域、时域及驱动电流时域信号如图7和图8所示。
|
图 6 单频激励传递函数幅频特性 Fig. 6 Amplitude-frequency characteristics of transfer function with one signal |
|
图 7 双频激励残差信号的FFT频谱图 Fig. 7 FFT spectrogram of error signal for double-frequency stimulate |
|
图 8 残差信号和控制器输出信号 Fig. 8 Error signal and controller output with/without control |
由图6可知,开启主动控制后在55 Hz,105 Hz,133 Hz,155 Hz,165 Hz等多个频点附近,加速度级能够迅速下降,隔振效果非常明显,隔振幅度可达到22 dB,这初步验证了自适应控制算法有效性和通道辨识准确性。但是在30 Hz附近峰值没有明显减弱,主要是作动器到残差信号之间频响特性在30 Hz附近幅值较弱所致。如需抑制30 Hz附近峰值,需要在控制器设计中针对30 Hz进行窄带滤波控制设计,从而确保系统稳定条件下,作动器线谱能量有效减弱该线谱振动。
此外,针对激振器输出55 Hz和155 Hz线谱振动。图7为主动控制开启与未开启时,一体化隔振器机脚附近加速度残差信号频谱对比图。未开启主动控制时,55 Hz与155 Hz处两根线谱十分明显,而开启后2根线谱振动基本完全倍抑制,其频谱幅值下降10倍以上。图8为与图7对应的时域信号,主动控制关闭时控制电流输出为0,残差加速度信号幅值较大,而当主动控制开启后,控制电流幅值增至2A左右,残差信号幅值明显下降,主动隔振效果十分明显。
4 结 语本文构建了双层隔振试验平台及其模型,结合Speedgoat快速原型控制器,设计了基于FIR滤波器的FxLMS自适应主动控制策略,并在Matlab/Simulink环境下构建上位机和下位控制程序,开展了次级通道离线辨识和主动控制实验,验证辨识精度和自适应控制算法的有效性。经过分析可以得到如下结论:
1)作为误差通道辨识估计模型,横向滤波器的阶数不宜过小,否则无法逼近实际通道。实际工程中,电磁干扰和通道非线性等因素常会引起辨识精度,并且无法完全消除。
2)从控制前后参考信号到误差信号传递函数频谱来看,在55 Hz,105 Hz,133 Hz,155 Hz,165 Hz等多个频率附近,加速度级都有明显下降,隔振效果非常明显。隔振效果可达22 dB,说明主被动一体化隔振器的线谱控制效果较好。
3)对于双频激励,线谱振动基本被完全抑制,频谱下降10倍以上,隔振效果十分明显,验证了辨识精度和控制算法的有效性。
4)利用快速原型控制控制技术,能够高效开展理论研究和实验验证,实现理论设计和样机验证无缝衔接,该方法可为后期工程应用和复杂的多通道控制提供有效的开发手段。
| [1] |
束立红, 胡宗成, 吕志强. 国外舰船隔振器研究进展[J]. 舰船科学技术, 2006(3): 109-112. |
| [2] |
张洪田, 李玩幽, 刘志刚. 电动式主动吸振技术研究[J]. 振动工程学报, 2001(1): 117-121. |
| [3] |
HANSEN C H, SNYDER S D. Active control of noise and vibration[M]. 2012.
|
| [4] |
WALROD JOHN. Sensor and actuator networks for acoustic signature monitoring and control[A]. Undersea Defence Technology 1999, France.
|
| [5] |
DALEY S, JOHNSON F. A, et al. A, et al. Active vibration control for marine applications[J]. Control Engineering Practice, 2004, 12(4): 465-474. DOI:10.1016/S0967-0661(03)00135-7 |
| [6] |
WINBERG M, JOHANSSON S, LAG T L. Active control of engine induced noise in a naval application[M]. Hong Kong, China, 2001.
|
| [7] |
何琳, 李彦, 杨军. 磁悬浮-气囊主被动混合隔振装置理论和实验[J]. 声学学报, 2013, 38(2): 242-249. |
| [8] |
杨铁军, 石慧, 李新辉, 等. 一种基于智能减振器的舰船机械设备主动减振系统研究[J]. 振动工程学报, 2017, 30(2): 167-176. |
| [9] |
张志谊, 王俊芳, 周建鹏, 等. 基于跟踪滤波的自适应振动控制[J]. 振动与冲击, 2009, 28(2): 64-67. DOI:10.3969/j.issn.1000-3835.2009.02.016 |
| [10] |
HANSEN C H, SCOTT D S, QIU XIAOJUN, et al. Active control of noise and vibration and vibration[M]. Boca Raton: Taylor&Francis 2013.
|
| [11] |
ELLIOTT SJ, STOTHERS IM, NELSON PA. A Multiple error LMS algorithm and its application to the active control of sound and vibration[J]. IEEE Trans. ASSP, 1987, 35 (10): 1423−1434.
|
| [12] |
BURDISSO R. A, FULLER C. R, SUAREZ L. E. Adaptive feedforward control of structures subjected to seismic excitation[C]//. In Proceedings of the 1993 American Control Conference, San Francisco, USA, 1993, 28: 2104−2108.
|
| [13] |
TUY, FULLER C. R. Multiple reference feedforward active noise control part II: preprocessing and experimental results[J]. Journal of Sound and Vibration, 2000, 233(5): 761−774.
|
| [14] |
MORGAN D R. History, applications and subsequent development of the FXLMS algorithm[J]. Signal Processing Magazine, IEEE, 2013, 30(3): 172-176. DOI:10.1109/MSP.2013.2242394 |
| [15] |
王婷, 牛振, 武飞. 基于Labview-RT系统的伺服系统快速原型平台设计[J]. 信息与电脑(理论版), 2020, 32(10): 60-62. |
| [16] |
陈亮, 郝洪涛, 倪凡凡, 等. 基于dSPACE湿式双离合变速器系统建模与仿真研究[J]. 传动技术, 2018, 32(1): 8-18. DOI:10.3969/j.issn.1006-8244.2018.01.002 |
| [17] |
沈佳明. 基于快速原型的无人机仿真系统设计与开发[D]. 南京: 南京航空航天大学, 2019.
|
| [18] |
庞齐齐, 张丽霞, 何一超, 等. 磁流变半主动悬架控制算法验证平台[J]. 清华大学学报(自然科学版), 2019, 59(7): 567-574. |
| [19] |
PAULOSRDINIZ著, 刘郁林译. 自适应滤波算法与实现[M]. 北京: 电子工业出版社, 2004.
|
| [20] |
BAGESHREE PATHAK, PADMA P HIRAVE. FXLMS Algorithm for feed forward active noise cancellation[C]//. Conference Advances in Computer, Electronics and Electrical Engineering, 2012: 18−22.
|
 2021, Vol. 43
2021, Vol. 43
