2. 中国船舶及海洋工程设计研究院,上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China
船体有限元参数化网格划分方案主要有2种:1)使用通用软件在进行必要的约束设置后直接对几何进行网格划分,然后手动进行修改以满足有限元计算的精度需要,如Catia,Napa等;2)使用通用软件的二次开发功能,设置硬点和硬线,或者将几何目标域离散化为细小的、形状尽可能规则的零件(如肘板的趾端,开孔或者角隅的边缘),分别对其进行网格划分,然后拼装在一起,如在Patran中使用PCL程序。
若使用第1种方法进行参数化网格划分,可能无法直接满足有限元计算精度的要求(如开孔边缘出现三角形等);如果使用第2种方法,则需要考虑根据不同的情况(如几何边界,内部有无开孔等)制作参数化几何模型后再划分单元,稍显缺乏灵活性。
所以,一个较为折衷的方案是几何形状较为规整的位置使用通用软件进行网格划分,而在有限元计算较为关注网格质量及需要形状参数优化的特殊区域,使用自定义网格划分方法。不失一般性,本文主要研究二维平面多连通域的网格划分方法,坐标变换后可适用于三维空间平面的情况。
对于目标域的四边形网格划分,目前商业软件主要使用映射法和铺砌法。映射法算法效率高,网格质量好,但是仅适用于简单的规则区域。而铺砌法的适用范围较广,可用于划分复杂不规则区域或多连通区域,网格质量一般较好,边界网格形态规则,不规则节点较少,但是交叉判断和实现算法较为复杂[4]。
为实现多连通域的网格划分,同时避免算法的复杂性,本文使用分子动力学的方法控制目标域内节点之间的相互距离和相互位置关系,并由此尝试控制目标域内的网格形状和网格质量。
1 带电粒子的分子动力学模拟分子动力学(MD)是研究复杂物理和化学系统的常规建模工具,其核心类似于计算机图形学中的粒子系统[5]。“粒子”是分子动力学的基本模拟单元,可以表示物理世界中的原子、分子、离子等。在实践中,它被编码为具有位置、速度、加速度和其他物理属性(如电荷)的质量点。
1.1 理论模型在粒子系统中,若假设粒子的质量为单位质量1,则任意粒子i的动力学方程为:
| $ a_{i}=\sum_{i \in N j \neq i} F_{i j}\left(r_{i}, r_{j}\right)+D_{i}\left(v_{i}\right)\text{。} $ | (1) |
式中:ai,vi,ri分别为粒子i的加速度、速度和位移;粒子j为粒子i的相邻粒子;Fij为粒子i与粒子j之间作用于粒子i的相互间作用力;Di为粒子i在运动过程中受到的阻力。
如用分子间相互作用势函数表示分子间的相互作用,则势函数V与分子间相互作用力函数Fij间的关系为:
| $ F_{i j}=-\nabla V(r)\text{。} $ | (2) |
式中:势函数V可表示为
| $ V(r)=\lambda\left(\frac{1}{r^{12}}-\frac{1}{r^{6}}\right)-(1-\lambda) \frac{q_{i} q_{j}}{n r^{n}}\text{。} $ | (3) |
其中:
| $ r=\left|r_{i}-r_{j}\right| / \sigma\text{。} $ | (4) |
式中:r为粒子间的相对距离;σ为网格划分大小;qi为粒子的电量,大于0带正电荷,小于0则带负电荷。
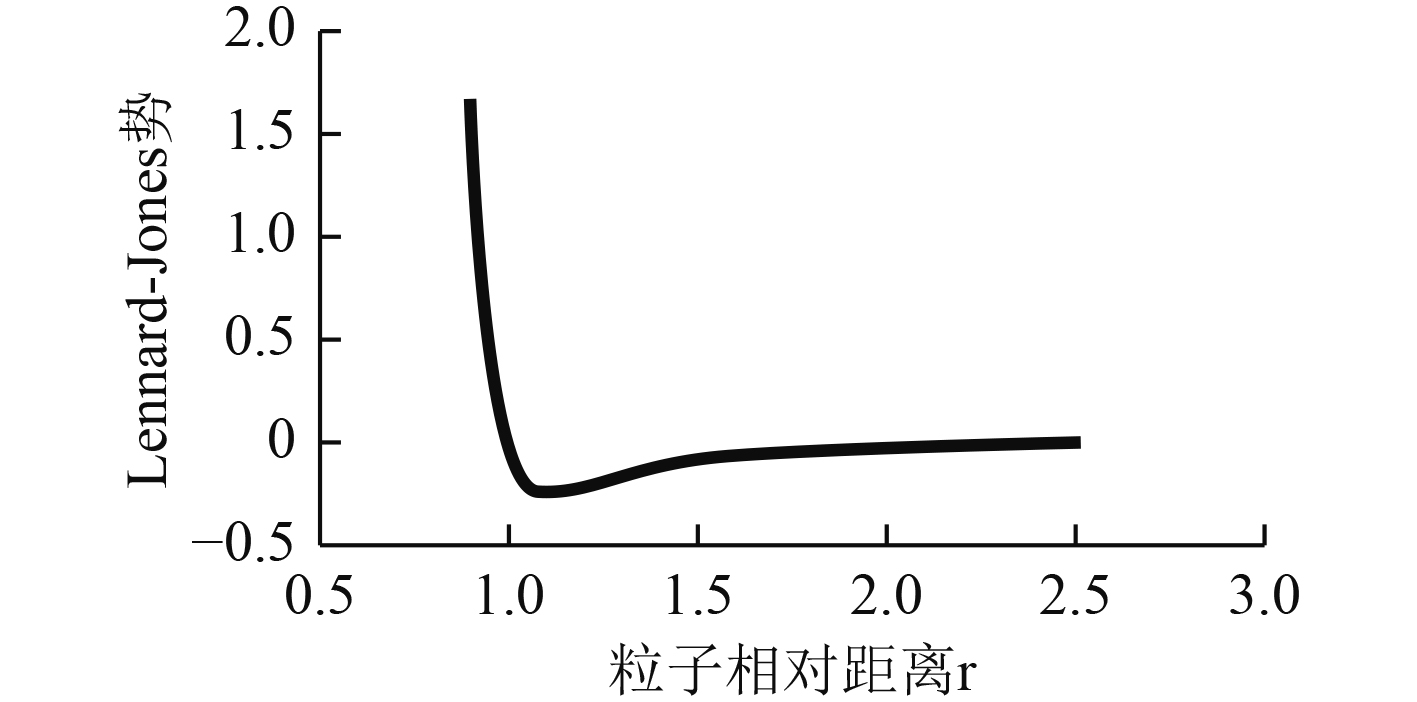
式(3)中的第一项为Lennard-Jones势函数。Lennard-Jones势函数随粒子间距的变化如图1所示。
|
图 1 Lennard-Jones势函数随粒子间距变化 Fig. 1 Trend of the Lennard-Jones potential function varies with spacing of the particles |
由势函数表达式及图1可见,当粒子间距无穷远时,粒子间产生的相互吸引作用非常微弱,无限接近于0;当它们相互靠近时,粒子间产生相互吸引力逐渐增加;当粒子间的相对位置r=1时,Lennard-Jones势为0,吸引力消失。这时,如果2个粒子继续靠近,它们之间将相互排斥,且粒子间的排斥力随粒子间距离的减小而迅速增大。Lennard-Jones势与带电粒子的正负号无关。
式(3)中的第二项为库伦势函数。带电粒子间的库伦力作用与带电粒子的正负号相关,符号相同的电荷相互排斥,符号相反的电荷相互吸引。自然界中式(3)中的n取值为1,当n取值不为1时,将会影响库伦力的作用范围,从而对数值计算产生影响。
1.2 短程库伦力当式(3)中的库伦势函数参数n取1时,库伦势与粒子间距离的一次方成正比,是一种长程相互作用,不能使用计算近程相互作用时常用的截断近似。这使得计算次数是O(N2)的数量级,其中N是粒子的数量。而式(3)中的Lennard-Jones势函数随距离的增加衰减的很快,是一种短程作用,计算次数是O(N)的数量级。
为了减少计算量,令式(3)中n=5,此时当r=2.5时,即粒子间的距离在网格划分大小的2.5倍左右时,库伦势衰减为r=1时的1%左右。当粒子间的距离大于2.5倍网格划分大小时,库伦势的作用可以忽略不计。
另一方面,电荷符号相反的粒子在距离很小时会产生很大的吸引力,而距离很接近的粒子之间也会由于Lennard-Jones势产生较大的斥力,为了避免粒子产生较大的加速度从而飞出网格划分区域,所以当粒子间的距离小于0.2σ时,仍然取r=0.2。
1.3 势函数权重因子Lennard-Jones势和库伦势在粒子运动过程中的作用有所不同。Lennard-Jones势用于控制粒子间的相对距离在预定的网格划分距离σ附近,而库伦势由于粒子的正负电荷不同,使得粒子在电场作用下位置发生偏移。
为了说明Lennard-Jones势和库伦势在分子运动过程中起到的作用,在一个正方形区域内设置若干等量正负电荷的粒子,正方形区域边界也由正负电荷粒子交替围成防止内部粒子逃逸出区域。粒子的初始状态如图2所示。

|
图 2 粒子间分布初始状态 Fig. 2 Initial state of the particle distribution |
调整式(3)中的λ值分别为:0,即仅有库伦势作用;1,即仅有Lennard-Jones势作用;0.5,即在Lennard-Jones势和库伦势的共同作用下。3种情况下区域内粒子的分布如图3~图5所示。不难发现,当仅有库伦势作用时,粒子分布无规则,甚至有一部分粒子逃逸出矩形区域;仅有Lennard-Jones势作用时,粒子之间保持一定的相对距离,却无法维持初始的四边形分布状态;当Lennard-Jones势和库伦势的共同作用时,粒子维持了初始的四边形分布状态。

|
图 3 λ=0,仅有库伦势作用粒子间分布 Fig. 3 Distribution of particles under coulomb interactions only |

|
图 4 λ=1,仅有Lennard-Jones势作用粒子间分布 Fig. 4 Distribution of particles under Lennard-Jones potentials only |

|
图 5 λ=0.5,Lennard-Jones势和库伦势的共同作用下粒子间分布 Fig. 5 Distribution of particles under coulomb interactions and Lennard-Jones potentials |
由于粒子在运动到平衡位置后会开始作往复振动,若不设置阻尼,粒子将一直运动下去,所以使用下式模拟式(1)中的阻尼项
| $ D_{i}=-\mu v_{i}\text{。} $ | (5) |
式(5)中阻尼系数μ取值大则加快粒子运动的收敛,但是取值过大可能妨碍粒子的正常运动。当粒子运动轨迹相似时,可以考虑使用较大的阻尼加快收敛速度。
1.5 数值积分常见的数值积分方法包括Velocity-Verlet法[1],龙格-库塔(Runge-Kutta)法[6]以及欧拉法。
Velocity-Verlet法更新粒子的位置和速度到下一个时间步长只需要进行一次评估,截断误差为O(h4)(h是步长)。相较而言,四阶龙格-库塔(Runge-Kutta)法虽然截断误差是O(h5)(h是步长),可是其计算量却大于Velocity-Verlet法。而欧拉法虽然简单,但是其精度相对较差。
所以,综合计算精度和计算速度,本文采用Velocity-Verlet法进行数值积分。Velocity-Verlet法计算粒子的位置和速度可以用下式表示:
| $ r_{n+1}=r_{n}+{\rm{d}} t \cdot v_{n}+{\rm{d}} t^{2} \cdot a_{n} / 2\text{,} $ | (6) |
| $ v_{n+1}=v_{n}+{\rm{d}} t \cdot\left(a_{n}+a_{n+1}\right) / 2\text{。} $ | (7) |
式中:r,v,a分别为粒子运动的位移、速度和加速度;dt为时间步长;n为迭代轮次。
1.6 初始化粒子系统的初始化包括区域边界初始化和区域内部初始化,主要任务是确定初始状态下的粒子分布和电荷属性。
粒子系统区域边界的初始化,根据输入的几何形状和网格大小σ要求,将带电粒子均匀分布在边界上,并保证带电粒子正负相间。区域边界上的粒子可以设置成固定在位置上不可移动的,也可以设置为在不破坏粒子间距的情况下(通过Lennard-Jones势)能够沿着输入几何移动,本文使用了前一种定义方式。
粒子系统区域内部的初始化有2种方法:
1)根据输入几何求出最小的外接矩形,在外接矩形中以网格大小σ为间隔均匀布置带电粒子,然后将落在输入几何区域边界外的带电粒子以及距离区域边界较近的粒子删除;
2)与铺砌法类似,沿着输入几何边界作为初始铺砌前沿,根据前沿节点类型,在区域内逐步添加新的带电粒子,并且铺砌前沿不断更新且向区域内部推进,直到继续添加节点会导致与任意前沿节点距离过近为止。
使用第1种方法布置带电粒子效率很高,但是对边界不敏感,即在旋转图形后,区域内的带电粒子相对位置发生改变。使用第2种方法对边界敏感,但是算法复杂,效率较低。本文结合2种方法,在区域内边界附近位置采用第2种方法,而在区域内且离边界较远的位置采用第1种方法,兼顾效率和边界附近带电粒子分布的边界敏感性。
1.7 边界协调如上所述,若采用边界前沿推进法布置区域内带电粒子,通常边界附近的带电粒子分布最终能得到较好的四边形网格。但是若完全使用几何外接矩形法布置区域内的带电粒子,可能最终边界上的网格质量就会较差。由于边界上的固定带电粒子对带相同电荷的带电粒子有排斥,而对带不同电荷的带电粒子有吸引,边界上的带电粒子电荷库伦势对于区域内的节点也有一定的场对齐作用。
为表述库伦势的场对齐作用,设置一个矩形区域。区域内开设两相同方孔,在边界上和区域内部均匀间隔布置不同电荷属性带电粒子,且距离边界上带电粒子最近的区域内部带电粒子的电荷符号相同,如图6所示。

|
图 6 开设两方孔的矩形区域初始粒子分布 Fig. 6 Initial particle distribution of rectangular region with two square holes |
依靠库伦力调整带电粒子位置的方法,可以通过增加边界上固定位置带电粒子的带电量,增加其作用于附近(2.5σ)自由带电粒子的库伦力,从而加强吸引异号电荷,排斥同号电荷的能力,粒子运动模拟结果如图7所示。需要说明的是,如果边界上带电粒子的带电量并不明显大于区域内其他带电粒子的带电量,或者作用粒子与边界上粒子的距离较远,位置调整的作用则不是很明显。

|
图 7 增加边界上带粒子电量后矩形区域最终粒子分布 Fig. 7 Final particle distribution of rectangular region after increasing the charge of the particle on the boundary |
调整带电粒子的带电量,本质上是调整Lennard-Jones势和库伦势之间的比例关系。由上文所述,并不能通过无限增加库伦势的比重达到场对齐的目的,这可能导致带电粒子之间的间距不稳定(异号粒子间距偏小,同号粒子间距偏大),所以本文仅在边界上增加了带电粒子的电量为区域内粒子电量的10倍,并未增加区域内的自由粒子的电量。图7中粒子数量的减少是由于粒子运动时方向的不确定可能向同一个方向聚集,通过算法删除局部多余粒子,增加空隙处粒子的原因造成的。而图中仍缺少的粒子可由后文提及的异常处理方法处理。
2 网格划分在粒子运动模拟完成之后,即可根据区域内的粒子分布进行网格划分。最简单的方法是先将区域内网格进行三角网格划分,然后合并相邻三角形单元获得四边形单元。
2.1 Delaunay三角网格划分Delaunay三角剖分算法具备许多优异特性:1)最接近的三点形成三角形,且各三角形的边皆不相交;2)不论从区域何处开始构建,最终都将得到一致的结果;3)任意2个相邻三角形形成的凸四边形的对角线如果可以互换的话,那么2个三角形6个内角中最小的角度不会变大;4)如果将三角网中的每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大;5)新增、删除、移动某一个顶点时只会影响临近的三角形,等等。
Delaunay三角剖分算法默认划分区域的边界是一个凸多边形的外壳,所以在处理非凸区域的时候需要进行一些额外的处理,将位于网格划分区域外的网格予以删除。
2.2 三角形网格合并在初始化阶段,正负粒子在网格划分区域边界上交替分布,除了上文所述的场对齐作用外,还为区域内的全四边形网格提供了必要条件,即边界上的节点个数为偶数。所以,为了尽可能使得三角形网格合并后依然能获得四边形网格,合并后的单元边界也应该是正负电荷交替分布的。
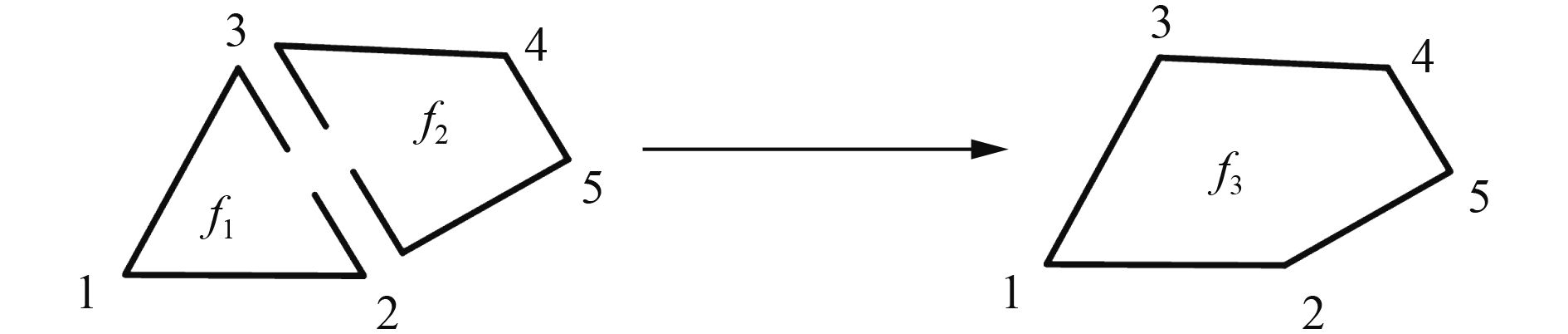
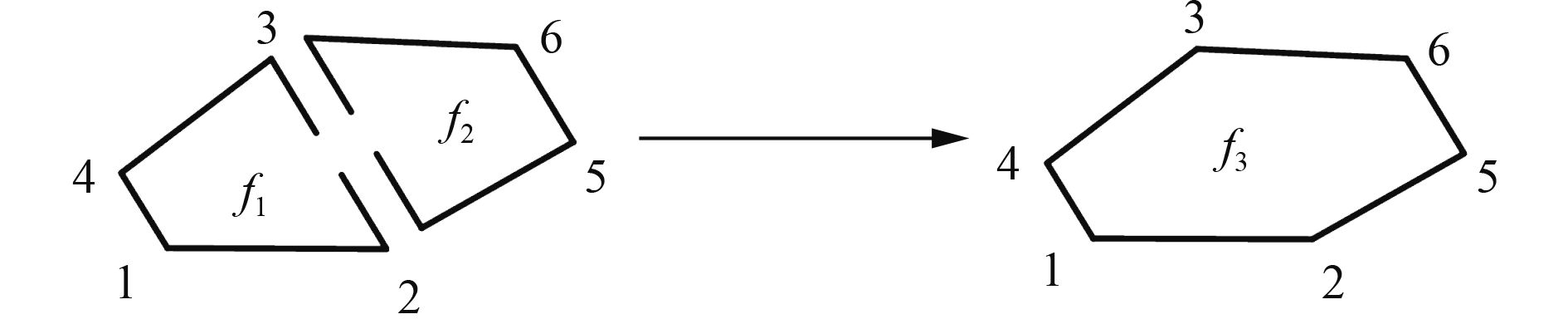
为此,在Delaunay三角剖分的基础上,删除所有连接同号粒子的边,并由此形成一系列偶数边形网格,如图8~图10所示。在图9中,若四边形有一条边上2个端点的粒子电荷符号相同,则一定还存在另一条边,其端点的粒子电荷符号也是相同的,即至少还有一条边会被取消,从而生成偶数变形网格。

|
图 8 三角形网格与三角形网格合并 Fig. 8 Triangular mesh merges with triangular mesh |
|
图 9 三角形网格与多边形网格合并 Fig. 9 Triangular mesh merges with polygonal mesh |
|
图 10 多边形网格与多边形网格合并 Fig. 10 Polygonal mesh merges with polygonal mesh |
如果三角形合并后得到的是四边形网格,且该四边形网格的4个顶点电荷正负交替排列,则可以认为是一个最终的四边形单元。
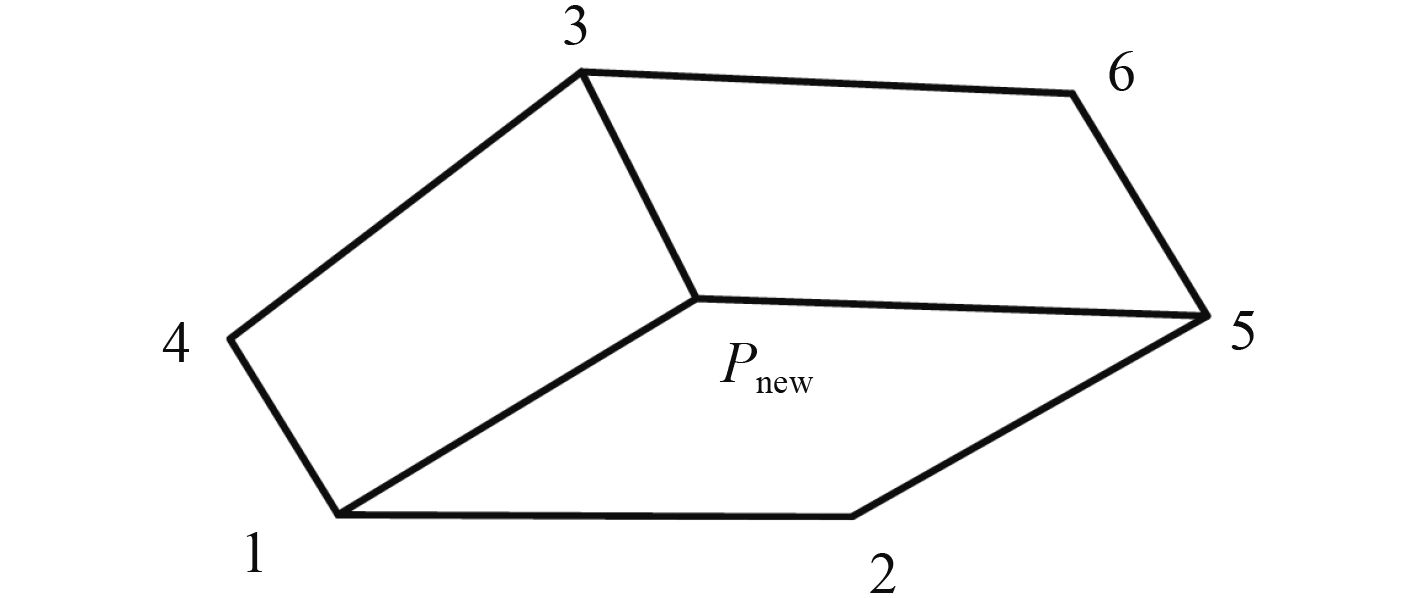
也有可能三角形网格合并后会得到六边形、八边形等一系列偶数边形单元。为了将这些非四边形的偶数边形单元分解为四边形单元,可以按如下步骤进行:
1)在多边形中插入一个中心点,此处可取为多边形的形心点,也可以是多边形各顶点坐标的算数平均;
2)在多边形边界点上寻找与所插入点最接近的点,此时判定所插入点的电荷符号与该点的电荷符号异号;
3)在多边形中从最近点开始,依次取出3个顶点,与多边形中心点一起组合成四边形;
4)重复此过程,直到多边形顶点全部使用完。
上述过程具体如图11所示。
|
图 11 多边形网格分解 Fig. 11 Polygonal mesh decomposition |
一类问题是网格尺寸较大,网格划分区域中的节点数量极少,甚至只使用边界上的节点参与网格划分,此时实际上为粗网格划分。使用上述流程可能无法获得较好的结果,此时,在Delaunay三角剖分后不考虑粒子电荷,仅使用最优三角形合并(即合并得到的四边形质量和与其他三角形合并得到的四边形质量相比是最高的)得到的结果可能更为理想,但是结果可能会出现三角形网格。
还有一类问题是网格尺寸较小,但是由于粒子的运动,在网格划分区域中出现了一些交大的空隙,使用上述插入点获得的四边形网格尺寸远大于要求网格尺寸。此时可以以该多边形网格为新边界,迭代本文所述网格划分的整个过程。由于多边形网格的边界是由正负电荷粒子交替布置,与上文所述区域边界初始化过程要求一致。
2.5 光顺由三角形合并得到的四边形网格,以及通过多边形网格降解生成的四边形网格质量可能较差,可以按下式进行光顺处理[7]:
| $ \left\{\begin{array}{l} x_{i}=\dfrac{1}{N_{i}} \displaystyle\sum_{j=1, j \neq i}^{N_{i}} x_{j} \text{,}\\ y_{i}=\dfrac{1}{N_{i}} \displaystyle\sum_{j=1, j \neq i}^{N_{i}} y_{j}\text{。} \end{array}\right. $ | (8) |
式中:Ni为与节点i所连接的节点总数;j为与i连接的节点;xi,yi分别为节点i的横坐标与纵坐标。
3 实 例 3.1 开孔矩形板开孔矩形板长2000 mm,宽800 mm,正中心开一个腰圆孔,开孔大小为400×600。过程中使用的粒子,连接拆解的网格边线,以及最终的网格单元如图12所示。为显示网格划分结果,仅显示板格的左半边,右半边与左半边对称。

|
图 12 腰圆开孔板网格划分实例 Fig. 12 Mesh of plate with opening |
圆弧肘板臂长800 mm,圆弧大小1000 mm。过程中使用的粒子,连接拆解的网格边线,以及最终的网格单元如图13所示。在肘板趾端狭窄处出现了四边形有三点共线的情况,导致出现了畸形四边形单元。可以通过与圆弧边上四边形合成为偶数边多边形再拆解的方式解决,但是本例较注重圆弧边缘的网格质量,所以仅将非圆弧边缘的四边形网格拆解成2个三角形处理。

|
图 13 圆弧肘板网格划分实例 Fig. 13 Mesh of arc bracket |
图14为型号HP200×10的球扁钢纵骨穿越孔,为清楚描述开孔形状,网格大小设置为10 mm×10 mm。

|
图 14 纵骨穿越孔网格划分实例 Fig. 14 Mesh of longitudinal cut-out |
为了灵活处理船体结构参数化建模,本文提出了一种基于分子动力学的网格划分方法。该方法具有以下优点:1)避免了许多算法上的复杂性,易于编程实现;2)理论上能适应各种不同的边界条件,较为灵活;3)最好情况下能实现全四边形网格划分。
但是在实践过程中,该方法仍存在如下不足:1)由于是基于分子动力学,如果仅使用中央处理器单核运算计算速度较慢。但是该算法的每个粒子在某一时刻的运动是可以并行计算的,利用图形处理器可大大节省时间;2)目前网格划分密度是全局一致的,但是想要在粗网格中嵌入细网格,需要进一步考虑网格过渡问题。
| [1] |
严六明等. 分子动力学模拟的理论与实践[M]. 北京: 科学出版社, 2013.
|
| [2] |
MARK DE BERG等著. 计算几何. 邓俊辉译[M]. 北京: 清华大学出版社, 2009.
|
| [3] |
MARIO BOTSCH. Polygon mesh processing[M]. Natick: A K Peters, 2010.
|
| [4] |
臧文娟. 基于铺砌法的约束四边形网格生成方法研究[D]. 济南: 山东大学, 2018.
|
| [5] |
GRAHAM SELLERS. OpenGL super bible[M]. Crawfordsville: Pearson Education, 2016.
|
| [6] |
TIMOTHY SAUER著. 数值分析. 吴兆金等译[M]. 北京: 人民邮电出版社, 2010.
|
| [7] |
张娟娟. 一种四边形有限元网格生成方法的研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.
|
 2021, Vol. 43
2021, Vol. 43
