随着我国科学技术实力的综合提升,为适应我国海洋权益发展的需求,舰载机在多种海上平台上的应用得到越来越多的关注,相关领域装置的研发和关键技术的攻关获得了长足的发展[1]。其中,舰载机阻拦着舰技术是海上平台发挥其优势作用的关键技术之一。先进且可靠的阻拦系统对提升舰载机的综合应用性能具有重大的实际意义[2]。
最初的飞机阻拦系统仅用来防止飞机在起飞和着舰时发生飞行事故。目前,阻拦设备已从单一的应急安全防护装置向着舰的常规设施方向发展。国外的飞机阻拦设备发展较快,尤其美国的应用起步较早。根据各型飞机的飞行任务要求,竞相研制了多种形式的机械式飞机阻拦系统[3]。为了弥补传统机械式阻拦装置的不足,美国在20世纪90年代率先提出了机电混合的先进阻拦装置(Advanced Arresting Gear,AAG)的研究计划[4]。由于先进阻拦装置采用的是电机及水涡轮为吸能元件的混合型方案,在阻拦调节过程中仍存在调节不够灵活的不足。因此,近年来有关电磁式先进阻拦装置的研究得到更为广泛的关注。
目前,我国对电磁式先进阻拦装置的相关研究尚处于初级阶段。对于先进阻拦装置的设计、评估和分析方法并不完备,对于全系统关键性能的评价指标与评价方法还需要进一步深入研究[5]。
本文以电磁式先进阻拦装置为研究对象,首先阐述该型阻拦装置的系统组成,分析影响装置可靠性分析的关键环节。最后研究并总结适用于先进阻拦装置负载系统的可靠性分析方法。本研究可在系统可靠性方面为电磁式先进阻拦装置的设计、应用与评估等过程提供一定的参考。
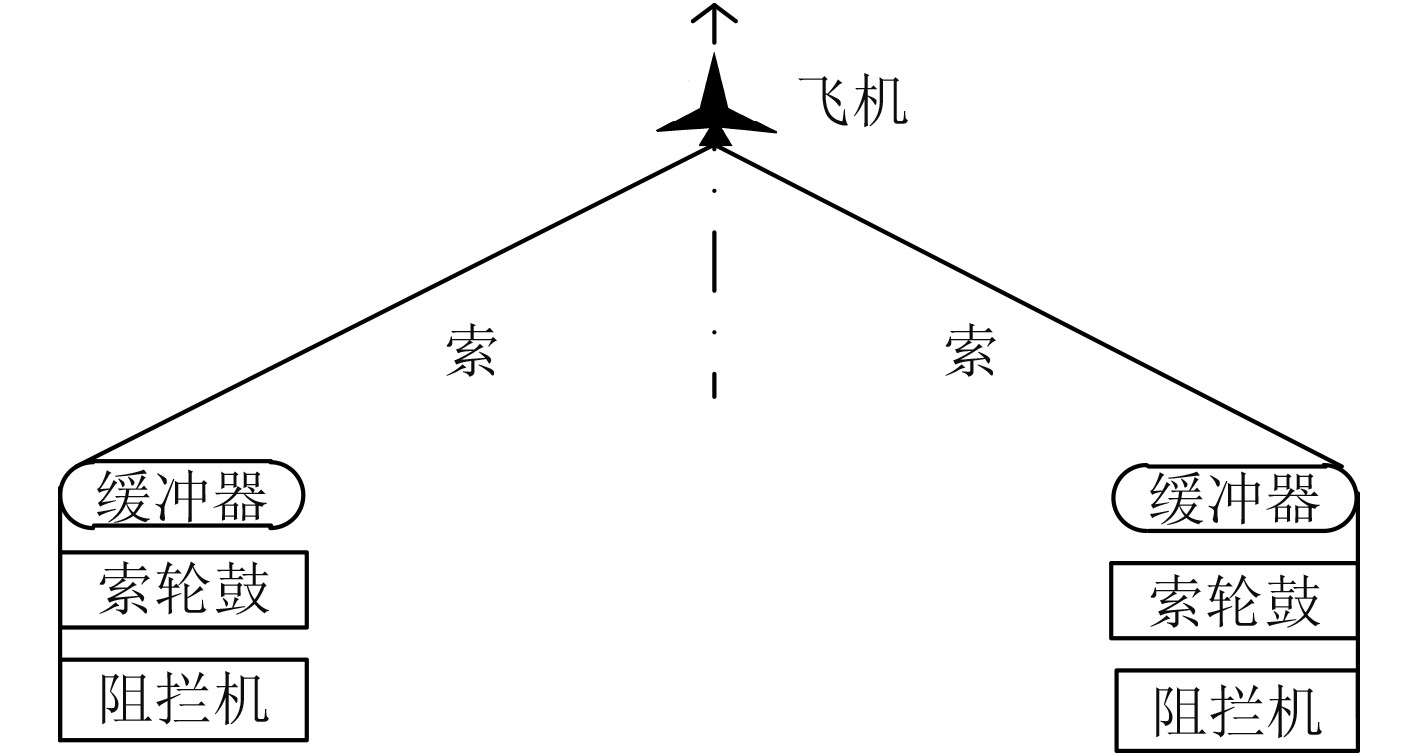
1 电磁式先进阻拦装置组成相比于传统机械式的阻拦装置,电磁式先进阻拦装置(简称电磁阻拦装置)阻拦范围更广,且在阻拦过程中可采用闭环控制策略,能够显著降低阻拦过程中的峰均力比。电磁阻拦装置的构成如图1所示。其特点为完全采用电机作为阻拦过程的调节及吸能元件,以便充分利用电机完全精确可控的优点,实现在飞机阻拦过程中对其阻拦轨迹进行实时闭环调节的目的[6]。
|
图 1 电磁阻拦装置构成图 Fig. 1 Electromagnetic arresting device principle |
如图1所示,该装置由阻拦索、缓冲器、索轮鼓、阻拦机及其调节控制系统等组成。其基本工作原理是:在飞机冲索后,继续拉动阻拦索向前运动,进而通过阻拦索和滑轮索带动索轮鼓旋转放绳。上述过程将飞机的直线运动转换成索轮鼓、阻拦电机的同轴旋转运动。期间通过对阻拦电机施加反向的阻力转矩以吸收飞机的动能,使得飞机在给定的距离内制动下来。电磁阻拦装置可以在阻拦之前先设定飞机的阻拦轨迹,在阻拦过程中,实时检测飞机的阻拦轨迹,并通过对阻拦电机转矩的精确调节使得飞机的实际阻拦轨迹能够良好地跟踪设定轨迹,从而达到对飞机的阻拦过程进行精确闭环控制的目的。与传统的机械阻拦装置相比,该装置具有阻拦范围宽、阻拦过程精确可控等优点。在阻拦过程中通过灵活地改变阻拦电机输出转矩使阻拦索上的张力始终保持在安全范围内,大幅度提高了阻拦性能,从而可以阻拦更高能级的飞机[6]。
电磁阻拦装置的精确控制与灵活调节等优势特性,是基于系统安全稳定运行的条件下实现的。因此,电磁阻拦装置的可靠性是系统设计与使用过程中需要重点考核的。而在评估该装置可靠性的过程中涉及多个关键环节。
2 电磁阻拦装置可靠性分析关键环节在对电磁阻拦装置进行可靠性分析过程中,涉及的关键环节主要包括:确定装置的可靠性指标、梳理装置可靠性分析流程以及明确装置的故障判定、分类与统计原则。
2.1 装置可靠性的指标针对电磁阻拦装置这一复杂系统的可靠性分析问题,结合系统主要特性可将其可靠性指标分为2部分:系统级和设备级。不同级别的可靠性分析指标和流程不尽相同。
一部分是系统级的阻拦装置总体层面的可靠性指标,主要包含飞机过载、阻拦距离和阻拦次数等。其中,阻拦次数是电磁阻拦系统的核心特性,是系统级可靠性分析中的核心对象。
另一部分是设备级的针对阻拦系统的关键组成部分阻拦索的可靠性指标,主要包含索径、股数和使用寿命等。其中,阻拦索的使用寿命是直接关系到阻拦系统性能的关键参数,也是设备级可靠性分析中的重点分析对象。
2.2 装置可靠性的分析流程不同的系统级与设备级的可靠性分析指标对应不同的可靠性分析重点,因而存在不同的可靠性分析流程。
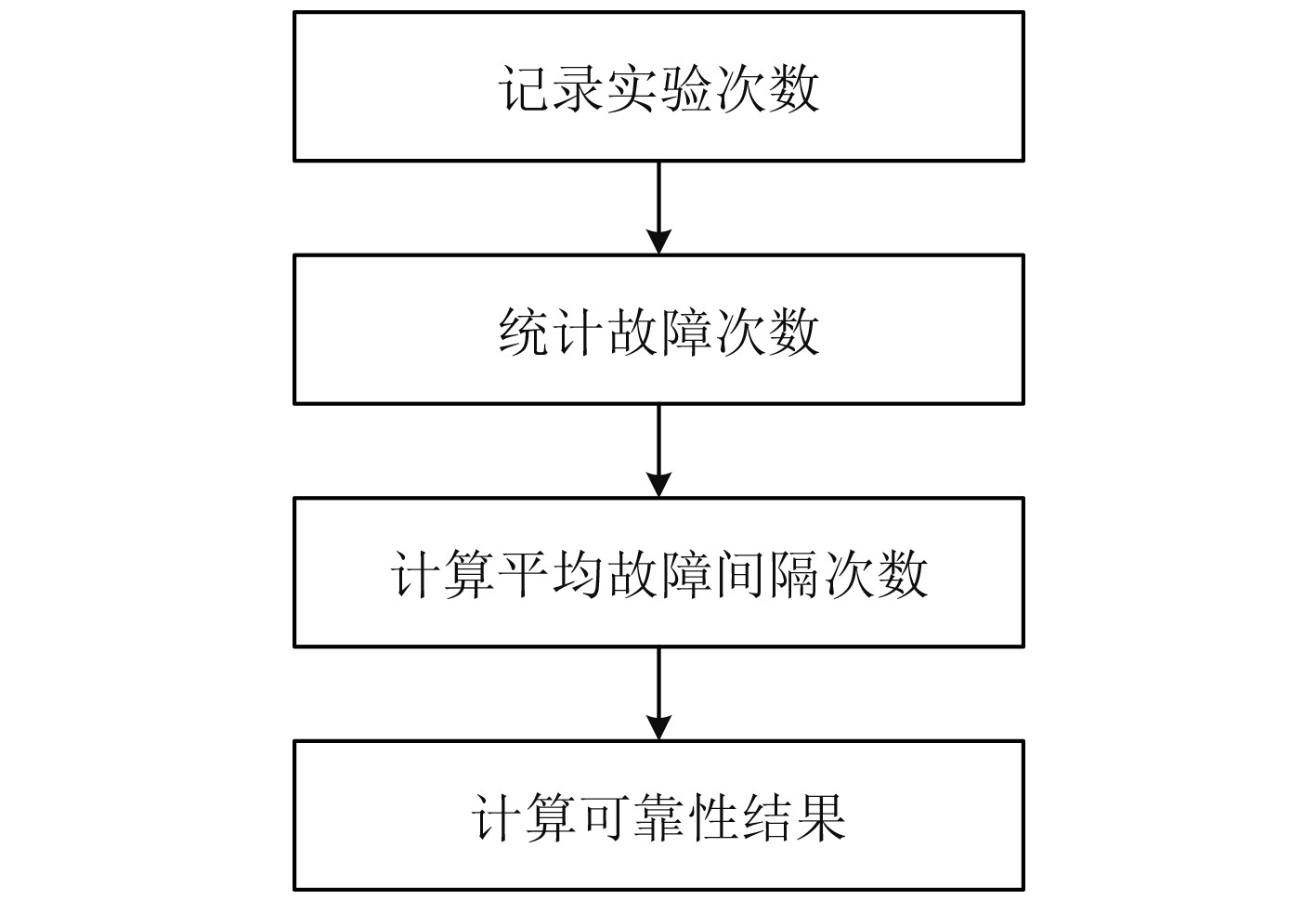
1)对于电磁阻拦装置系统级可靠性的分析流程,主要围绕着其核心指标−阻拦次数进行,包含如下步骤:记录实验次数、统计故障次数、计算平均故障间隔次数和评估可靠性结果。对应的可靠性分析流程,如图2所示。
|
图 2 系统级可靠性分析流程 Fig. 2 System level reliability analysis process |
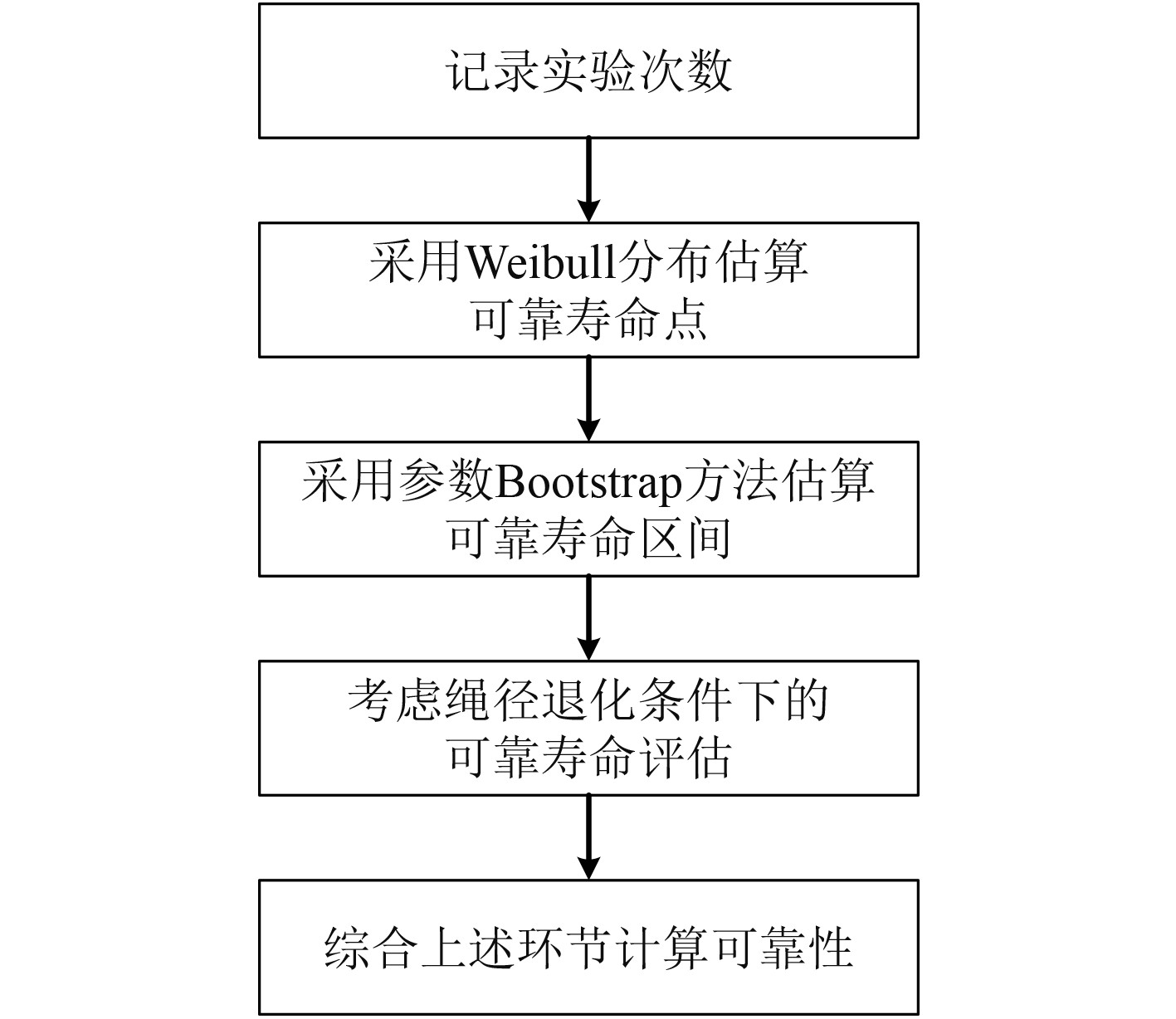
2)对于阻拦索的设备级可靠性分析过程相对复杂,因为阻拦索的疲劳失效存在一个过程。而且相比于其他机械及电气设备,阻拦索的失效对系统带来的负面影响最大,且修护难度和工作量也是最大的。综合考虑上述因素,将阻拦索的使用寿命评估作为电磁阻拦系统可靠性分析的关键组成部分。阻拦索寿命评估流程,如图3所示。
|
图 3 阻拦索寿命可靠性估算流程 Fig. 3 Reliability life estimation process of arresting gear |
在上述流程中,可靠寿命点估算、可靠寿命区间估算和考虑绳径退化的可靠寿命评估是完成阻拦索寿命可靠性评估的关键理论环节。而在基于实验次数与故障次数的采用数理统计原理的可靠性分析中,有一个关键问题需要确定,便是故障次数的计数值。该数值的计算涉及阻拦装置的故障分类、判定和统计原则等相关内容。
2.3 装置的故障分类、判定与统计原则在电磁阻拦装置的故障判定、分类和统计原则方面的研究中,充分借鉴文献[7]中的相关标准进行对应的设计。
可将故障类型分为2类:责任故障和非责任故障。其中,非责任故障的判定依据包含如下几项:误操作、实验装置及仪表故障、不满足额定工作条件、修复引起故障等;相应的,责任故障的判定依据包含如下几项:设计与制造缺陷、元件失效、额定工况下的设备更换以及其他异常情况。
结合上述内容可以设定故障统计原则为:在实验过程中,只有责任故障作为判定受试装置合格与否的依据,并记录其发生次数作为故障次数,其他情况不计入统计。
在明确电磁阻拦装置可靠性分析过程中涉及的指标、流程及故障统计原则等关键环节后,即可研究总结适用于本装置的可靠性分析方法。
3 电磁阻拦装置可靠性分析方法针对电磁阻拦装置的系统组成特点,依据研究内容对系统级可靠性分析过程采用基于数理统计的分析策略,对阻拦索的可靠性寿命评估则结合了Weibull分布法、参数Bootstrap计算和考虑绳径退化因素的等综合评估策略。
3.1 基于数理统计的可靠性分析在基于数理统计的可靠性分析中,首先需确定实验次数。设覆盖装置全部工况的可靠性试验共开展N次。
接着,确定可靠性试验中的故障次数。根据实验结果,在可靠性考核过程中,共出现M次故障。其中,并未出现可导致系统不能完成任务的重大故障,或修护时间超出设定的最长修护时间的故障。责任故障次数统计为R次。
最后,根据设定的置信度计算平均故障间隔次数。设选取的置信度为Q,采用定时截尾置信下限的计算方法[8],结合实验结果,在置信度Q条件下装置平均故障间隔次数MCBF的计算公式为:
| $MCB{F_Q} = \frac{{2N}}{{\chi _{1 - Q}^2\left( {2R + 2} \right)}}\text{。}$ | (1) |
其中,等式右侧分式的分母含义为自由度是(2R+2)的卡方分布函数的(1-Q)的上侧分位数。
根据文献[8]中列举的故障判据和置信度选取有效条件,采用定时截尾的评估方法对MCBF进行评估。若计算结果高于置信度Q下的目标值,则系统可靠性满足合格判定要求。
3.2 基于Weibull分布定时截尾的可靠寿命点估算在分析可靠性过程中,针对具有疲劳特性的设备,且在具备一定数量的实验样本条件下,可采用Weibull分布定时截尾方式对可靠性试验对象进行建模分析[9-10]。
由相关文献可知,Weibull分布的分布函数F(t)和密度函数P(t)分别为:
| $\begin{split} & {F(t) = 1 - {e^{ - {t^m}/\beta }}}, \qquad {t \geqslant 0}\text{,} \\ & {P(t) = \dfrac{{m{t^{m - 1}}}}{\beta }{e^{ - {t^m}/\beta }}} , \quad {t \geqslant 0} \text{。} \end{split}$ | (2) |
其中,m为形状参数,
假设
| $L\left( {m,\beta } \right) = \frac{{{m^r}}}{{{\beta ^r}}}\prod\limits_{i = 1}^r {t_i^{m - 1}} \exp \left\{ { - \frac{1}{\beta }\left[ {\sum\limits_{i = 1}^r {t_i^m + (n - r)t_r^m} } \right]} \right\}\text{。}$ | (3) |
为了简化表达式形式,可设定关系式:
| $\sum {^*} t_i^m = \sum\limits_{i = 1}^r {t_i^m + (n - r) \cdot } t_r^m\text{,}$ | (4) |
则式(4)对m的一阶、二阶偏导数可表示为:
| $\begin{split} & \dfrac{\partial }{{\partial m}}\left( {\displaystyle\sum {^*t_i^m} } \right) \!\!=\!\! \displaystyle\sum\limits_{i = 1}^r {t_i^m\ln {t_i}} \! +\! (n - r)t_r^m\ln {t_r}\!\! = \!\!\displaystyle\sum {^*t_i^m} \ln {t_i} \text{,} \\ & \dfrac{{{\partial ^2}}}{{\partial {m^2}}}\left( {\displaystyle\sum {^*t_i^m} } \right) = \displaystyle\sum {^*t_i^m} {(\ln {t_i})^2}\text{。} \end{split} $ | (5) |
由式(3)推导可得,似然函数的对数形式为:
| $\ln L = r\ln m - r\ln \beta + (m - 1)\sum\limits_{i = 1}^r {\ln {t_i}} - \frac{1}{\beta }\sum {^*t_i^m}\text{,} $ | (6) |
由式(6)可求解对数似然函数的2个偏导数可表示为:
| $\begin{split} & \frac{{\partial \ln L}}{{\partial m}} = \frac{r}{m} + \sum\limits_{i = 1}^r {\ln {t_i}} - \frac{1}{\beta }\sum {^{\rm{*}}t_i^m\ln {t_i}}\text{,} \\ & \frac{{\partial \ln L}}{{\partial \beta }} = - \frac{r}{\beta } + \frac{1}{{{\beta ^2}}}\sum {^*t_i^m} \text{,} \end{split} $ | (7) |
令式(7)为零,则可得到2个似然方程如下:
| $\begin{split} &{\beta = \frac{1}{r}\sum {^*t_i^m} }\text{,} \\ & {\frac{{\displaystyle\sum {^*t_i^m\ln {t_i}} }}{{\displaystyle\sum {^*t_i^m} }} - \frac{1}{m} = \frac{1}{r}\sum {\ln {t_i}} } \text{,} \end{split}$ | (8) |
联立方程组,即可求解参数m和β的极大似然估计值。那么,基于Weibull分布的阻拦索平均寿命E(T)的表达式为:
| $E\left( T \right) = \eta \Gamma \left(1 + \frac{1}{m}\right)\text{,}$ | (9) |
对于给定的可靠性水平r,其可靠寿命tr满足关系:
| $R\left( {{t_r}} \right) = {e^{ - \frac{{t_r^m}}{\beta }}} = r\text{,}$ | (10) |
对式(10)两边取对数可得:
| $ - \frac{{t_r^m}}{\beta } = \ln r\text{,}$ | (11) |
由式(11)计算可得,在上述约束条件下的可靠寿命tr为:
| ${t_r} = \sqrt[m]{{\beta \ln \frac{1}{r}}} = \eta \sqrt[m]{{\ln \frac{1}{r}}}\text{。}$ | (12) |
此时,将Weibull分布参数估计结果m和η代入上式,即可得到可靠寿命点的估计值。
3.3 采用参数Bootstrap方法的可靠寿命区间估算在获得可靠寿命点估计值的条件下,可通过采用参数Bootstrap方法计算得到平均寿命和可靠寿命区间[11-12],具体计算步骤如下:
1)采用极大似然估计法对定时截尾实验数据中的5个数据样本进行计算,得到Weibull分布参数估计值
2)再由Weibull分布
3)将
4)重复上述过程步骤1~步骤3B次,即可得到B个平均寿命和可靠寿命估计值:
| $\left\{ {\tilde E{{(T)}^{(i)}},{{\tilde t}_r}^{(i)},i = 1,2, \cdots ,B} \right\}{\text;}$ | (13) |
5)将B个
6)将B个
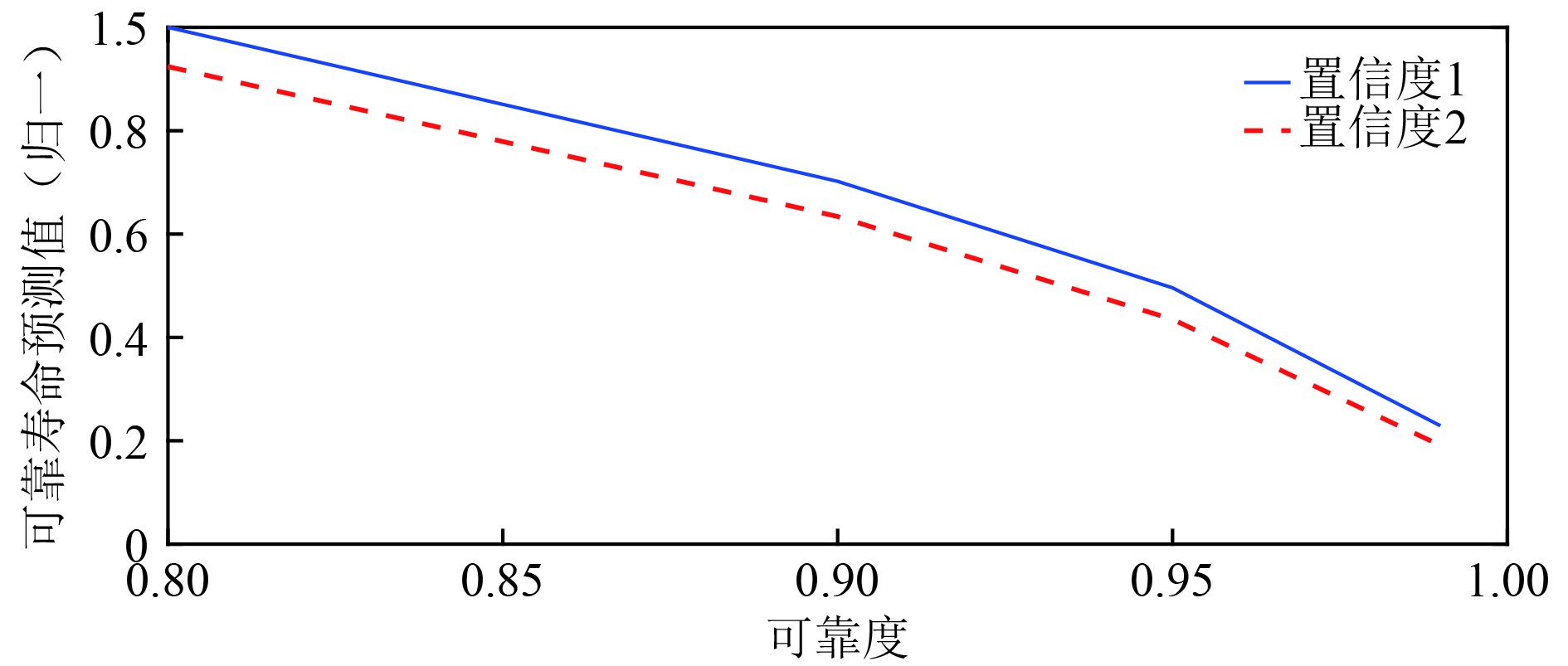
通过实验数据,得到基于Weibull分布不同置信度下的可靠度与寿命预测归一化关系图,如图4所示。
|
图 4 Weibull寿命预测与可靠度归一化曲线 Fig. 4 Weibull life prediction and reliability normalization curve |
除了上述分析过程外,针对阻拦索此类的疲劳损耗设备,在可靠寿命分析中还有一个关键特性需要评估−阻拦索的绳径退化特性。
3.4 基于绳径退化数据的寿命评估随着试验次数的增加,阻拦索在实验过程中不断被消耗。相对于电磁阻拦装置的其他分系统设备,阻拦索的消耗损伤速度最快,对系统整体性能影响最大。其具体表现为,随着试验次数的增加,阻拦索的直径会逐渐减小[13]。这部分影响因素可称为绳径退化。可根据实际应用情况,设定阻拦索失效的绳径阈值为Z(mm),而考虑了绳径退化因素的可靠寿命估算过程如下:
1)间隔一定时间测量阻拦索绳径数据,对其中有效样本阻拦索绳径数据虽试验次数增加的退化规律进行数学拟合,得到拟合斜率、拟合截距和拟合优度,建立阻拦索绳径退化数学模型;
2)根据上述模型对阻拦索的使用寿命进行预测。当阻拦索的绳径下降到阈值Z需要更换时,可得到个样本的预测寿命值;
3)根据上一步骤得到的预测寿命值,再采用Weibull寿命分布极大似然估计法,得到分布参数估计值为
在上述过程中,一个重要环节是确定有效样本的筛选方法,即使用有效使用次数的统计原则。而在使用过程中阻拦索需要更换的判据为:出现断丝或者绳径值低于Z。这里可以采用如下3个统计原则作为可靠寿命评估的输入条件:
1)同一阻拦索使用次数为故障结尾且小于绳径退化预测次数的,在可靠寿命评估过程中采信使用次数;
2)同一阻拦索使用次数为故障结尾且大于绳径退化预测次数的,在可靠寿命评估过程中采信绳径退化预测次数;
3)同一阻拦索使用次数为定时结尾的,在可靠寿命评估过程中采信绳径退化预测次数。
通过实验数据,得到基于绳径退化不同置信度下的可靠度与寿命预测归一化关系图,如图5所示。
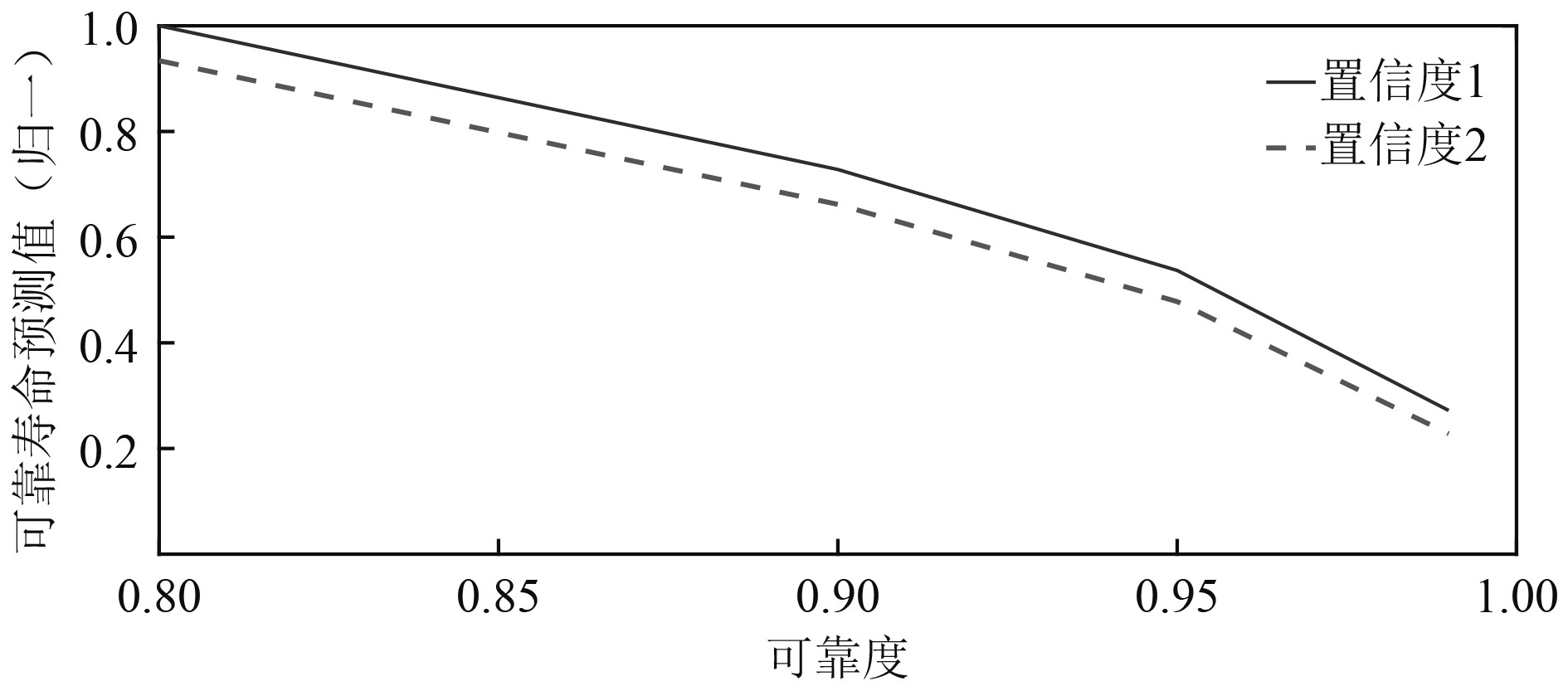
|
图 5 绳径退化寿命预测与可靠度归一化曲线 Fig. 5 Life prediction of rope path and reliability normalization curve |
本文对电磁式先进阻拦装置的可靠性分析方法进行研究。首先阐述了电磁式先进阻拦装置的系统组成与工作原理,对该装置可靠性分析过程中的可靠性指标、分析流程和故障判定统计原则等关键环节进行了分析。最后,结合电磁阻拦装置的系统特点,分析总结了基于数理统计的系统级可靠性分析方法和联合了基于Weibull分布定时截尾方式、采用参数Bootstrap方法以及考虑阻拦索绳径退化的阻拦索设备级可靠性分析方法。上述研究内容可为电磁式先进阻拦装置的可靠性设计、应用于评估过程提供一定的理论参考依据,具有一定的理论研究与实际应用价值。
| [1] |
王鹏, 焦晓辉. 舰载机着舰指挥引导技术[J]. 中国科技信息, 2019(Z1): 35-36. WANG Peng, JIAO Xiao-hui. Shipborne aircraft landing command and guidance technology[J]. China Science and Technology Information, 2019(Z1): 35-36. |
| [2] |
陈裕芹, 程秀全, 戴沅均. 舰载飞机的阻拦着舰动力学建模[J]. 舰船科学技术, 2017, 39(20): 186-188. CHEN Yu-qin, CHENG Xiu-quan, DAI Yuan-jun. Dynamic modeling of ship arresting landing with carrier aircraft[J]. Ship Science and Technology, 2017, 39(20): 186-188. |
| [3] |
黄胜, 郑茂, 王超. 液压阻拦机定长冲跑控制规律优化研究[J]. 北京理工大学学报, 2014(6): 607-612. HUANG Sheng, ZHENG Mao, WANG Chao. Optimization for the constant runout control system of arresting gear[J]. Transaction of Beijing Institute of Technology, 2014(6): 607-612. |
| [4] |
PATTON J. Arresting gear program completes reliability testing[Z]. General Atomics and Affiliated Companies, San Diego, California, 2009.
|
| [5] |
蒋辉虎. 舰载机着舰阻拦规律研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. JIANG Hui-hu. Research on the arresting law of carrier-based aircraft landing[D]. Harbin Engineering University, 2019. |
| [6] |
张晓谞, 张育兴, 刘勇, 等. 阻拦索张力控制方法[J]. 国防科技大学学报, 2016, 38(6): 49-53. ZHANG Xiao-xu, ZHANG Yu-xing, LIU Yong, et al. Method of arresting cable tension control[J]. Journal of National University of Defense Technology, 2016, 38(6): 49-53. |
| [7] |
GJB 841-1990 故障报告、分析和纠正措施系统[S]. GJB 841-1990 Fault reporting, analysis and corrective action system[S]. |
| [8] |
GJB 899A-2009 可靠性鉴定和验收试验[S]. GJB 899A-2009 Reliability appraisal and acceptance test[S]. |
| [9] |
张凯延. Weibull分布下定时截尾试验技术及其无失效数据Bayes可靠性分析[D]. 成都: 电子科技大学, 2018. ZHANG Kai-yan. Timing truncation test technique and Bayes reliability Analysis of non-failure data under Weibull distribution[D]. Chengdu: University of Electronic Science and Technology, 2018. |
| [10] |
姜万民. 关于Weibull分布的加速寿命试验的统计分析[D]. 昆明: 云南大学, 2017. JIANG Wan-min. Statistical analysis of an accelerated life test for the Weibull distribution[D]. Kunming: Yunnan university, 2017. |
| [11] |
SPOKOINY V, WILLRICH N. Bootstrap tuning in Gaussian ordered model selection[J]. The Annals of Statistics, 2019, 47(3): 1351-1380. |
| [12] |
JANSON S, KOZMA R, RUSZINKÓ, et al. A modified bootstrap percolation on a random graph coupled with a lattice[J]. Discrete Applied Mathematics, 2019, 258: 152-165. DOI:10.1016/j.dam.2018.11.006 |
| [13] |
邓文力, 王悦民, 耿海泉. 钢制阻拦索与合成纤维制阻拦索性能分析[J]. 舰船科学技术, 2019, 41(3): 140-144, 149. DENG Wen-li, WANG Yue-min, GENG Hai-quan. Performance analysis of steel arresting gear cable and synthetic material arresting gear cable[J]. Ship Science and Technology, 2019, 41(3): 140-144, 149. |
 2021, Vol. 43
2021, Vol. 43
