0 引　言

水下自主航行器（AUV）可用于海底资源勘探、目标侦察等，是开发海洋的重要工具。小型AUV具有成本低、作业方便等优点，随着海洋开发与商业化的深入，逐渐成为AUV的重要发展方向^[1]。小型AUV执行任务多样，作业水况复杂，对于自主定位导航能力要求较高。低功耗、高可靠的导航定位方案成为小型AUV开发亟待解决的研究热点。

大量的AUV导航系统，依赖多普勒测速仪、深度计、磁力计等传感器测得数据进行导航，而小型AUV限于成本、功耗与体积，往往不能装备足够多的传感器。同时由于小型AUV作业工况复杂，多普勒测速仪等在某些情况下不能正常工作，导航系统的可靠性低。基于微机电系统（MEMS）的惯性导航系统（INS），成本低、体积小、不依赖外界信号、反应迅速，是AUV重要的导航方案。本文基于平方根无迹卡尔曼滤波算法，设计了非线性滤波器，并使用模型辅助提高算法精度。同时经过半实物与仿真实验，验证了算法的有效性。

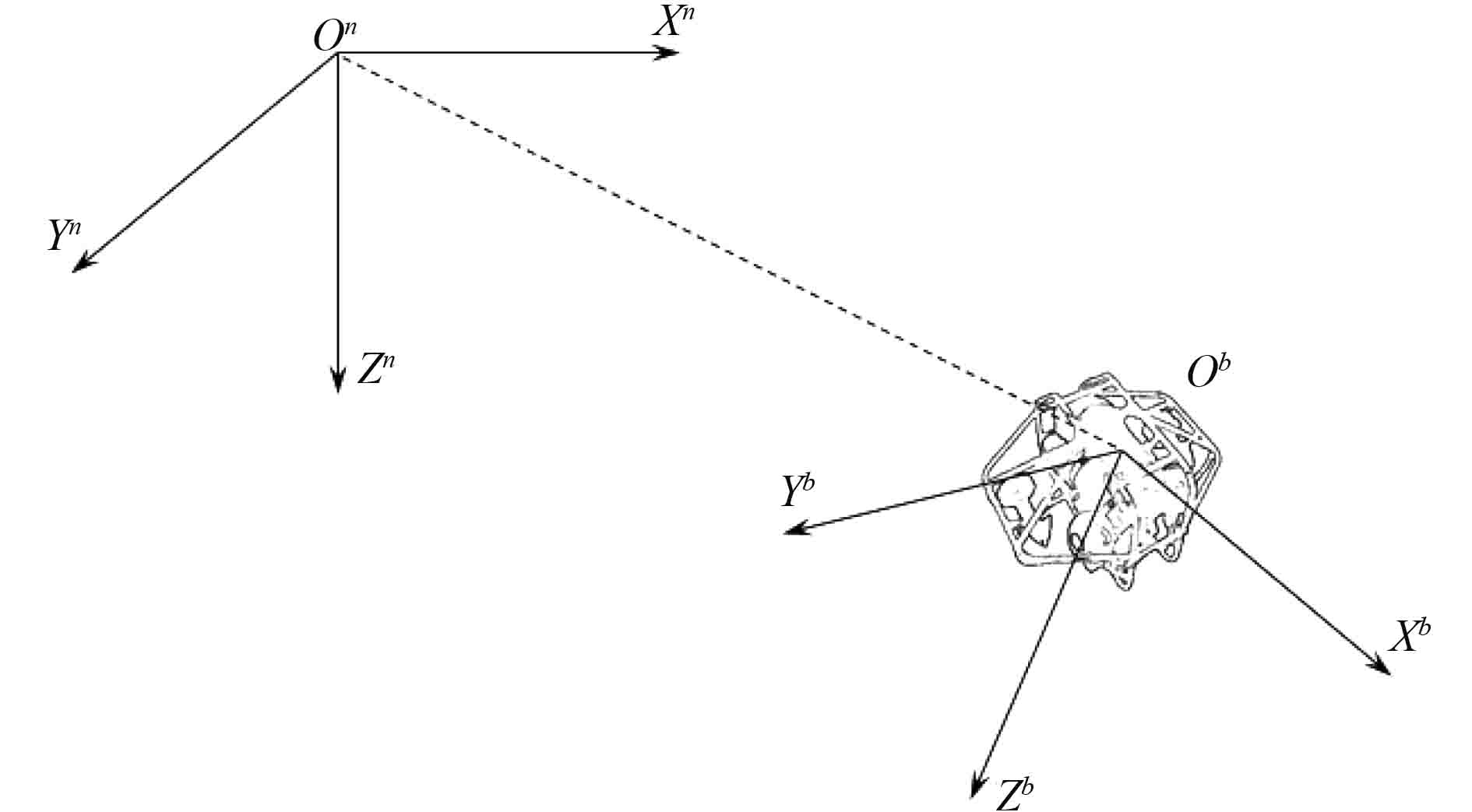
1 AUV建模 1.1 坐标系定义

在导航中使用2种坐标系。一种是惯性坐标系Oⁿ-XⁿYⁿZⁿ，固结在地球上。另一种是载体坐标系O^b-X^bY^bZ^b，固结在AUV重心上。为直观起见，采用欧拉角表示载体坐标系相对惯性坐标系的旋转。定义载体坐标系相对惯性系按X-Y-Z轴依次旋转，其欧拉角为 ${[\phi ,\theta ,\psi ]^{\rm T}}$ ，则 $\phi $ ， $\theta $ ， $\psi $ 分别为AUV的横滚角、纵倾角、首向角，如图1所示。

1.2 运动学与动力学建模

设AUV在惯性坐标系下的坐标为 ${{{\eta }}_{{1}}} = {[x,y,z]^{\rm T}}$ ，令 ${{{\eta }}_{{2}}} = {[\phi ,\theta ,\psi ]^{\rm T}}$ ，AUV在载体坐标系下的速度为 ${{{\nu }}_{{1}}} = $ $ {[u,v,w]^{\rm T}}$ ，角速度为 ${{{\nu }}_{{2}}} = {[p,q,r]^{\rm T}}$ ，令 ${{\eta }} = {[{\eta _1},{\eta _2}]^{\rm T}}$ ， ${{\nu }} = $ $ {[{\nu _1},{\nu _2}]^{\rm T}}$ ，则可建立AUV的运动学模型如下：

$\left\{ {\begin{array}{*{20}{c}} {{{{{\dot \eta }}}_1} = {{{J}}_1}\left( {{{{\eta }}_2}} \right){{{\nu }}_1}}\text{，} \\ {{{{{\dot \eta }}}_2} = {{{J}}_2}\left( {{{{\eta }}_2}} \right){{{\nu }}_2}} \text{。} \end{array}} \right.$

(1)

其中：J₁，J₂为转换矩阵，将正弦函数记作s，余弦函数记作c，正切函数记作t，则

${{{J}}_1} \!\!=\!\! \left[\!\!\!\! {\begin{array}{*{20}{c}} {c\theta c\psi }&{ - s\psi c\phi + c\psi s\theta s\phi }&{s\psi s\phi + c\psi s\theta c\phi } \\ {s\psi c\theta }&{c\psi c\phi + s\psi s\theta s\phi }&{ - c\psi s\phi + s\psi s\theta c\phi } \\ { - s\theta }&{c\theta s\phi }&{c\theta c\phi } \end{array}} \!\!\!\!\right]\text{，}$

(2)

${{{J}}_2} = \left[ {\begin{array}{*{20}{c}} 1&{s\phi t\theta }&{c\phi t\theta } \\ 0&{c\phi }&{ - s\phi } \\ 0&{s\phi /c\theta }&{c\phi /c\theta } \end{array}} \right]\text{。}$

(3)

水动力外形对于AUV的影响十分显著，本文基于Kambara ROV水动力外形参数建立AUV六自由度动力学模型^[2]为：

${{M\dot \nu }} + {{C}}\left( \nu \right){{\nu }} + {{D}}\left( \nu \right){{\nu }} + {{g}}\left( \eta \right) = {{\tau }}\text{。}$

(4)

其中： ${{M}} = {{{M}}_A} + {{{M}}_{RB}}$ 为质量矩阵， ${{C}} = {{{C}}_A} + {{{C}}_{RB}}$ 为科氏矩阵， ${ D}$ 为水动力阻尼矩阵， $g(*)$ 为回复力， ${{\tau }}$ 为AUV所受合外力，则

${{{M}}_A} = \left[ {\begin{array}{*{20}{c}} {{{{A}}_{11}}}&{{{{A}}_{12}}} \\ {{{{A}}_{21}}}&{{{{A}}_{22}}} \end{array}} \right]\text{，}$

(5)

${{{M}}_{RB}} = \left[ {\begin{array}{*{20}{c}} {m{{{I}}_{3 \times 3}}}&{{{{0}}_{3 \times 3}}} \\ {{{{0}}_{3 \times 3}}}&{{{{I}}_0}} \end{array}} \right]\text{，}$

(6)

${{{C}}_A}\left( {{\nu }} \right)\!\! = \!\!\left[ \!\!\!\!{\begin{array}{*{20}{c}} {{{{0}}_{3 \times 3}}}&\!\!{ - {{S}}\left( {{{{A}}_{11}}{{{\nu }}_1} + {{{A}}_{12}}{{{\nu }}_2}} \right)} \\ { - {{S}}\left( {{{{A}}_{11}}{{{\nu }}_1} + {{{A}}_{12}}{{{\nu }}_2}} \right)}&\!\!{ - {{S}}\left( {{{{A}}_{21}}{{{\nu }}_1} + {{{A}}_{22}}{{{\nu }}_2}} \right)} \end{array}} \!\!\!\!\right]\text{，}$

(7)

$\begin{split} &{C}_{RB}(\nu )=\\ &\left[\begin{array}{cc}{0}_{3\times 3}& -mS({\nu }_{1})-mS(S({\nu }_{2})){r}_{G})\\ -mS({\nu }_{1})-mS(S({\nu }_{2})){r}_{G})& mS(S({\nu }_{1})){r}_{G})-S({I}_{0}{\nu }_{2})\end{array}\right]\end{split}\text{。}$

(8)

其中： ${{{A}}_{{{11}}}}$ ， ${{{A}}_{{{12}}}}$ ， ${{{A}}_{{{21}}}}$ ， ${{{A}}_{{{22}}}}$ ，为AUV运动引起水流震荡产生的附加质量； $m$ 为AUV质量； ${{{I}}_{3 \times 3}}$ 为单位矩阵； ${{{I}}_0}$ 为刚体惯性张量； ${{S}}({{a}}) = \left[ {\begin{array}{*{20}{c}} 0&{ - {a_3}}&{{a_2}} \\ {{a_3}}&0&{ - {a_1}} \\ { - {a_2}}&{{a_1}}&0 \end{array}} \right]$ 。

设AUV所受重力为W，浮力为B，载体坐标系下重心坐标为 ${[0,0,0]^{\rm T}}$ ，浮心坐标为 ${[{x_B},{y_B},{z_B}]^{\rm T}}$ ，则

${{g}}\left( {{\eta }} \right)\!\! =\!\! \left[ \!\!\!\!{\begin{array}{*{20}{c}} {\left( {W - B} \right)s\theta } \\ { - \left( {W - B} \right)s\phi c\theta } \\ { - \left( {W - B} \right)c\phi c\theta } \\ { - \left( {{y_G}W - {y_B}B} \right)c\phi c\theta + \left( {{z_G}W - {z_B}B} \right)s\phi c\theta } \\ {\left( {{z_G}W - {z_B}B} \right)s\theta + \left( {{x_G}W - {x_B}B} \right)c\phi c\theta } \\ {\left( {{x_G}W - {x_B}B} \right)s\phi c\theta + \left( {{y_G}W - {y_B}B} \right)s\theta } \end{array}}\!\! \right]\text{。}$

(9)

2 惯性导航算法设计

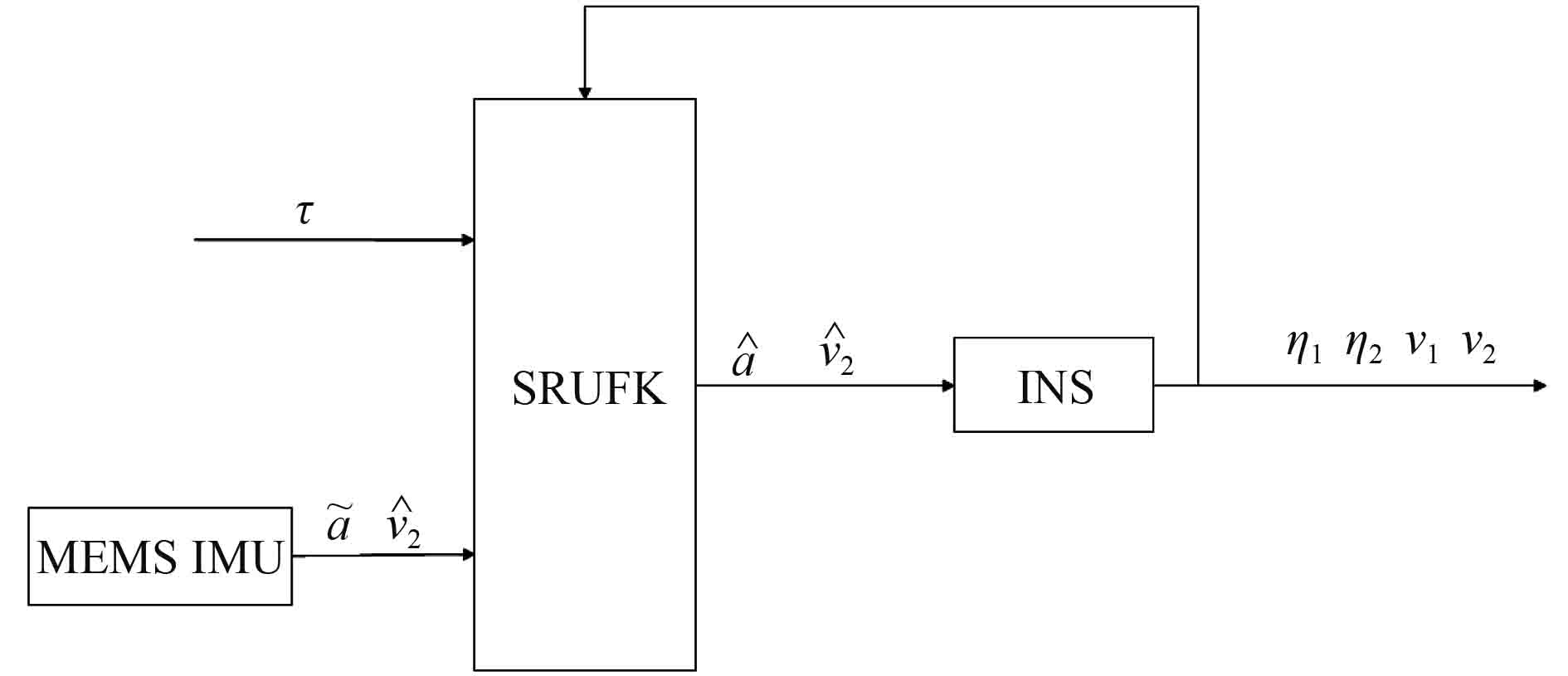
传统的模型辅助AUV导航定位^[3]，在AUV速度计算中引入模型辅助作为参考，忽略了AUV模型在姿态解算中的潜在应用^[4]。为了综合利用AUV传感器测得信息和模型解算得到的加速度与角速度信息，本文设计了基于平方根无迹卡尔曼滤波的惯性导航算法。本文采用的惯性导航系统结构框图如图2所示。

2.1 位姿解算算法设计

在惯性导航算法中，为降低运算量，并避免奇异角等问题，使用单位四元数q实时解算AUV姿态。载体坐标系与惯性坐标系重合时，四元数 ${{q}} = {[1,0,0,0]^{\rm T}}$ 。

设k时刻AUV角度变化量为 $\Delta {{\theta }} = {[{\theta _x},{\theta _y},{\theta _z}]^{\rm T}}$ ，加速度值为 ${{{a}}_k} = {[{a_x},{a_y},{a_z}]^{\rm T}}$ 。采用角度变化量形式的毕卡算法求解四元数^[5]。本文采用4阶近似形式以保证精度，则

$\Delta {{\theta }} = {{{\nu }}_2}\left( {{t_k} - {t_{k - 1}}} \right)\text{，}$

(10)

$\begin{split}{{{q}}_{new}} =& {{{I}}_{4 \times 4}}\left( 1 - 0.125\Delta {{{\theta }}^{\rm T}}\Delta {{\theta }} + 0.0026{{\left( {\Delta {{{\theta }}^{\rm T}}\Delta {{\theta }}} \right)}^2} +\right.\\ &\left.\left( {0.5 - 0.0208\Delta {{{\theta }}^{\rm T}}\Delta {{\theta }}} \right)\Delta {{\Theta }} \right){{q}}\text{，}\end{split}$

(11)

其中 $\Delta {{\Theta }} = \left[ {\begin{array}{*{20}{c}} 0&{ - {\theta _x}}&{ - {\theta _y}}&{ - {\theta _z}} \\ {{\theta _x}}&0&{{\theta _z}}&{ - {\theta _y}} \\ {{\theta _y}}&{ - {\theta _z}}&0&{{\theta _x}} \\ {{\theta _z}}&{{\theta _y}}&{ - {\theta _x}}&0 \end{array}} \right]$ 。

为直观表示滤波效果，将四元数姿态表示转换成欧拉角表示。四元数q与欧拉角 ${[\phi ,\theta ,\psi ]^{\rm T}}$ 有以下转换关系：

$\left\{ {\begin{array}{*{20}{l}} {\phi {{ }} = arctan\left( {{{C}}_b^n\left( {3,2} \right),{{C}}_b^n\left( {3,3} \right)} \right)}\text{，} \\ {\theta {{ }} = - arcsin\left( {{{C}}_b^n\left( {3,1} \right)} \right)}\text{，} \\ {\psi {{ }} = arctan\left( {{{C}}_b^n\left( {2,1} \right),{{C}}_b^n\left( {1,1} \right)} \right)} \text{。} \end{array}} \right.$

(12)

其中 $C_b^n$ 由 $q$ 计算得到：

$\begin{split} C_{{b}}^n =& \left[ {\begin{array}{*{20}{c}} {1 - 2(q{{(2)}^2} + q{{(3)}^2})}&{2(q(1)q(2) - q(0)q(3))} \\ {2(q(1)q(2) - q(0)q(3))}&{1 - 2(q{{(1)}^2} + q{{(3)}^2})}\\ {2(q(1)q(3) - q(0)q(2))}&{2(q(2)q(3) - q(0)q(1))} \end{array}} \right.\\ &\left.\begin{array}{*{20}{c}} {2(q(1)q(3) - q(0)q(2))}\\ {2(q(2)q(3) - q(0)q(1))} \\ {1 - 2(q{{(1)}^2} + q{{(2)}^2})} \end{array}\right]\text{。}\\[-30pt]\end{split}$

(13)

小型AUV由于体积、功率限制，其加速度变化率有限，因此采用 ${t_k}$ 时刻与 ${t_{k - 1}}$ 时刻的加速度平均值作为 ${t_k} - {t_{k - 1}}$ 时间段的加速度值近似平均值，并计算得到 ${t_k}$ 时刻速度值。同理，采用惯性坐标系下 ${t_k}$ 时刻与 ${t_{k - 1}}$ 时刻的速度平均值作为 ${t_k} - {t_{k - 1}}$ 时间段的速度值，并与AUV运动学方程联立，计算得到 ${t_k}$ 时刻AUV坐标。

${{{\nu }}_{{1_k}}} = \int_{{t_{k - 1}}}^{{t_k}} {{a}} {\rm d}t \doteq \frac{1}{2}\left( {{{{a}}_{k - 1}} + {{{a}}_k}} \right)\left( {{t_k} - {t_{k - 1}}} \right) + {{{\nu }}_{{1_{k - 1}}}}\text{，}$

(14)

${{{\dot \eta }}_{{1_k}}} = {{{J}}_1}\left( {{{{\eta }}_{{2_k}}}} \right)\text{，}$

(15)

${{{\eta }}_{{1_k}}} = \int_{{t_{k - 1}}}^{{t_k}} {{{{{\dot \eta }}}_1}} {\rm d}t \doteq \frac{1}{2}\left( {{{{{\dot \eta }}}_{{1_{k - 1}}}} + {{{{\dot \eta }}}_{{1_k}}}} \right)\left( {{t_k} - {t_{k - 1}}} \right) + {{{\eta }}_{{1_{k - 1}}}}\text{。}$

(16)

2.2 平方根无迹卡尔曼滤波算法设计

由式（4）可知，AUV的6个自由度间的运动互相交叉耦合，运动方程高度非线性化。扩展卡尔曼滤波（EKF）在计算时使用一阶泰勒展开线性化状态方程，性能不稳定，结果易发散。本文采用平方根无迹卡尔曼滤波算法对传感器数据与AUV模型计算得到数据进行滤波融合处理，通过选取sigma点进行无迹变换，匹配AUV运动数据的统计特性，从而保障了估计精度^[6-7]。同时，在滤波中使用协方差平方根代替协方差进行运算，保障了协方差的对称正定性，避免滤波算法因舍入误差积累而发散，提高了算法稳定性。

选取AUV运行时的加速度 ${{a}}$ 与角速度 ${{{\nu }}_2}$ 作为系统状态量，则 ${{X}} = {[{{a}},{{{\nu }}_2}]^{\rm T}}$ 。选取MEMS 惯性测量单元（IMU）测量得到的加速度 ${{\tilde a}}$ 与角速度 ${{{\tilde \nu }}_{{2}}}$ 作为系统观测量，则 $\widehat {{Z}} = {[{{\tilde a}},{{{\tilde \nu }}_2}]^{\rm T}}$ 。

设计平方根无迹卡尔曼滤波算法：

1）参数设置及初始化

根据AUV的初始状态 ${{{X}}_0}$ ，初始化滤波系统的状态向量 $\widehat {{{{X}}_0}}$ 和状态误差协方差矩阵平方根 ${{{S}}_{0|0}}$ 如下：

${{{\hat X}}_0} = E\left[ {{{{X}}_0}} \right]\text{，}$

(17)

${{{S}}_{0|0}} = chol\left( {E\left[ {\left( {{{{X}}_0} - {{{{\hat X}}}_0}} \right){{\left( {{{{X}}_0} - {{{{\hat X}}}_0}} \right)}^{\rm T}}} \right]} \right)\text{。}$

(18)

其中 $chol({{A}})$ 为矩阵 ${{A}}$ 的Cholesky分解的上三角矩阵。

2）计算sigma点

采用对称选点的方式，选取sigma点近似非线性系统的统计特性。根据噪声的分布特性确定sigma的点数。

${{\bar X}} = {{{\hat X}}_{k - 1}}\text{，}$

(19)

${{S}} = {{{S}}_{k - 1|k - 1}}\text{，}$

(20)

${{\xi }} = \left[ {{{\bar X}},{{\bar X}} + \sqrt {n + \lambda } {{S}},{{\bar X}} - \sqrt {n + \lambda } {{S}}} \right]\text{。}$

(21)

其中 $n$ 为系统状态量的维度，此处 $n = 6$ 。 $\lambda = {\alpha ^2}(n + \kappa ) - n$ ， $\alpha $ ， $\kappa $ 为第一、第三刻度因数，决定sigma点距离平均值点的离散程度。

3）计算时间更新方程

${{X}}_{k|k - 1}^{\left( i \right)} = f\left( {{{{\xi }}^{\left( i \right)}},{{u}}} \right)\text{，}$

(22)

式中：f(*)为滤波系统的状态方程，这里为AUV动力学方程式（4）， ${{u}}$ 为上一步滤波后INS系统解算得到的AUV姿态、速度数据以及AUV受到的推进力。

${{{\hat X}}_{k|k - 1}} = {\omega _{m0}}{{X}}_{k|k - 1}^{\left( 1 \right)} + \sum\limits_{i = 2}^{2n + 1} {{\omega _m}} {{X}}_{k|k - 1}^{\left( i \right)}\text{，}$

(23)

$\begin{split} {{S}}_{k|k - 1}^ - =& qr\left( \left[ \sqrt {{\omega _c}} \left( {{{X}}_{k|k - 1}^{\left( 2 \right)} - {{{{\hat X}}}_{k|k - 1}}} \right)\quad \sqrt {{\omega _c}} \left( {{{X}}_{k|k - 1}^{\left( 3 \right)} - {{{{\hat X}}}_{k|k - 1}}} \right)\right.\right.\\ & \left.\left. \cdots \quad \sqrt {{\omega _c}} \left( {{{X}}_{k|k - 1}^{\left( {2n + 1} \right)} - {{{{\hat X}}}_{k|k - 1}}} \right),\sqrt {{Q}} \right] \right)\text{，}\\[-10pt]\end{split}$

(24)

${{{S}}_{k|k - 1}} = {\rm{cholupdate}}\left[ {{{S}}_{k|k - 1}^ - ,{{X}}_{k|k - 1}^{\left( 1 \right)} - {{{{\hat X}}}_{k|k - 1}},{\omega _{c0}}} \right]\text{。}$

(25)

其中： $qr({{A}})$ 计算矩阵 ${{A}}$ 的QR分解的上三角矩阵； ${\rm{cholupdate}}({{R}},{{x}})$ 计算矩阵 ${{A}} + {{{x}}^*}{{{x}}^{ - 1}}$ 的Cholesky分解的上三角矩阵，其中 ${{R}} = chol({{A}})$ ； ${\omega _m}$ ， ${\omega _c}$ ， ${\omega _{m0}}$ ， ${\omega _{c0}}$ 按照以下公式计算得到：

$\left\{ {\begin{array}{*{20}{l}} {{\omega _{m0}} = \dfrac{\lambda }{{n + \lambda }}}\text{，} \\ {{\omega _{c0}} = {\omega _{m0}} + \left( {1 - {\alpha ^2} + \beta } \right)}\text{，} \\ {{\omega _m} = {\omega _c} = \dfrac{1}{{2\left( {n + \lambda } \right)}}} \text{。} \end{array}} \right.$

(26)

式中， $\ \beta $ 为第二刻度因数。

4）计算观测更新方程

${{Z}}_{k|k - 1}^{\left( i \right)} = h\left( {{{X}}_{k|k - 1}^{\left( i \right)}} \right)\text{，}$

(27)

式中 $h(*)$ 为观测函数， $h(a) = a$ 。

${{{\hat Z}}_{k|k - 1}} = {\omega _{c0}}{{Z}}_{k|k - 1}^{\left( 1 \right)} + \sum\limits_{i = 2}^{2n + 1} {{\omega _c}} {{Z}}_{k|k - 1}^{\left( i \right)}\text{，}$

(28)

$\begin{split}{{S}}_Z^ - =& qr\left( \left[ \sqrt {{\omega _c}} \left( {{{Z}}_{k|k - 1}^{\left( 2 \right)} - {{{{\hat Z}}}_{k|k - 1}}} \right)\quad \sqrt {{\omega _c}} \left( {{{Z}}_{k|k - 1}^{\left( 3 \right)} - {{{{\hat Z}}}_{k|k - 1}}} \right)\right.\right.\\ &\left.\left.\cdots \quad \sqrt {{\omega _c}} \left( {{{Z}}_{k|k - 1}^{\left( {2n + 1} \right)} - {{{{\hat Z}}}_{k|k - 1}}} \right),\sqrt {{R}} \right] \right)\text{，}\\[-10pt]\end{split}$

(29)

${{{S}}_Z} = {\rm{cholupdate}}\left[ {{{S}}_Z^ - ,{{Z}}_{k|k - 1}^{\left( 1 \right)} - {{{{\hat Z}}}_{k|k - 1}},{\omega _{c0}}} \right]$

(30)

$\begin{split}{{{P}}_{XZ}} =& {\omega _{c0}}\left( {{{X}}_{k|k - 1}^{\left( 1 \right)} - {{{{\hat X}}}_{k|k - 1}}} \right){\left( {{{Z}}_{k|k - 1}^{\left( 1 \right)} - {{{{\hat Z}}}_{k|k - 1}}} \right)^T} +\\ &\sum\limits_{i = 2}^{2n + 1} {{\omega _c}} \left( {{{X}}_{k|k - 1}^{\left( i \right)} - {{{{\hat X}}}_{k|k - 1}}} \right){\left( {{{Z}}_{k|k - 1}^{\left( i \right)} - {{{{\hat Z}}}_{k|k - 1}}} \right)^T}\text{。}\end{split}$

(31)

5）结果更新

${{{K}}_k} = {{{P}}_{XZ}}{\left( {{{{S}}_Z}{{S}}_Z^T} \right)^{ - 1}}\text{，}$

(32)

${{{\hat X}}_{k|k}} = {{{\hat X}}_{k|k - 1}} + {{{K}}_k}\left( {{{{Z}}_k} - {{{{\hat Z}}}_{k|k - 1}}} \right)\text{，}$

(33)

${{U}} = {{{K}}_k}{{{S}}_Z}\text{，}$

(34)

${{{S}}_{k|k}} = {\rm{cholupdate}}\left[ {{{{S}}_{k|k - 1}},{{U}}, - 1} \right]\text{。}$

(35)

3 仿真、实验与结果分析

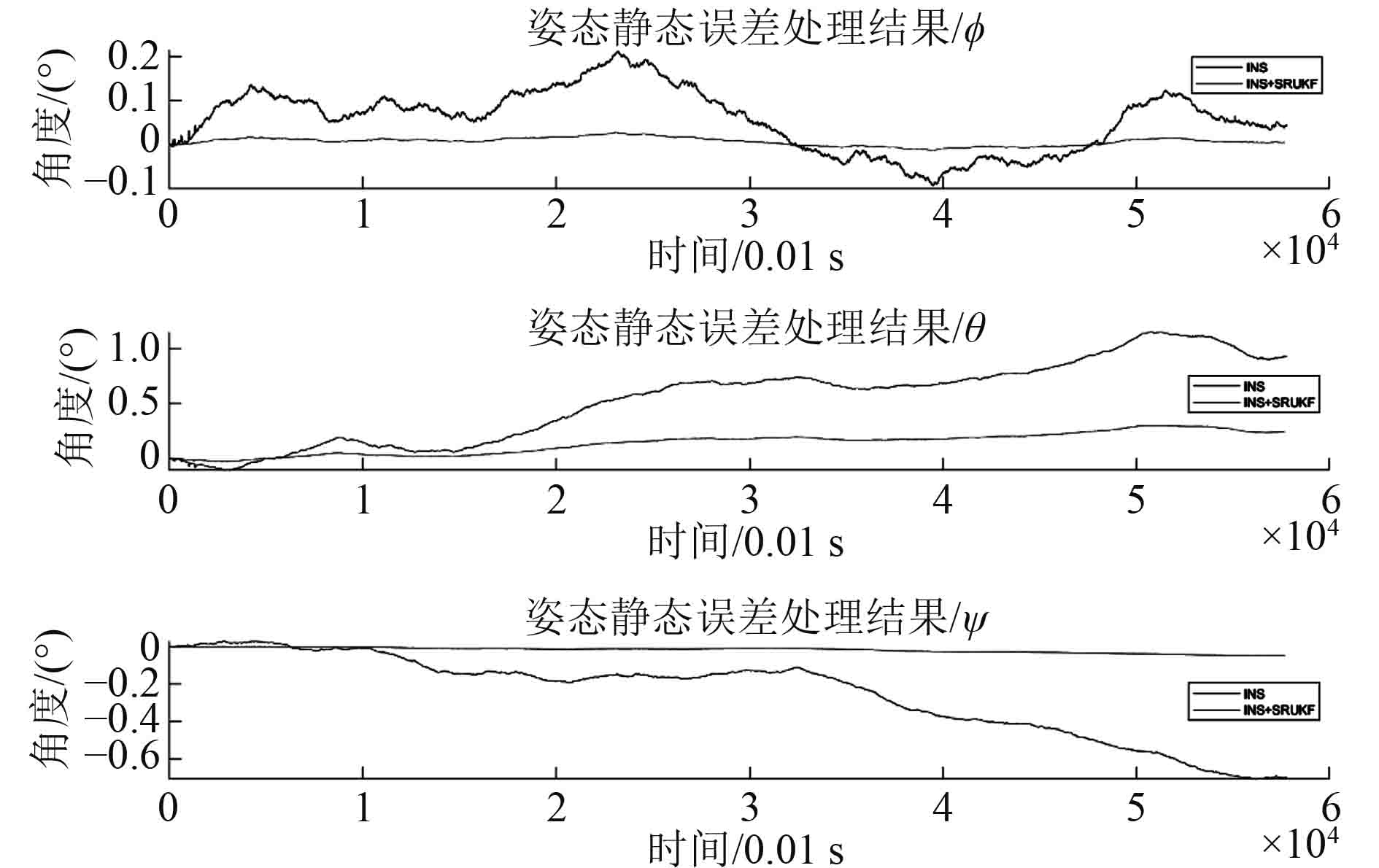
使用手机模拟AUV进行算法的静态测试。将手机静置，基于手机内置MEMS IMU得到加速度与角速度测量数据，并输入导航算法中进行测试。滤波、解算得到AUV静态时姿态如图3所示。由图可知，基于SRUKF的惯性导航算法能够较好补偿静态误差，角度误差在0.3°以内，且误差增长缓慢。

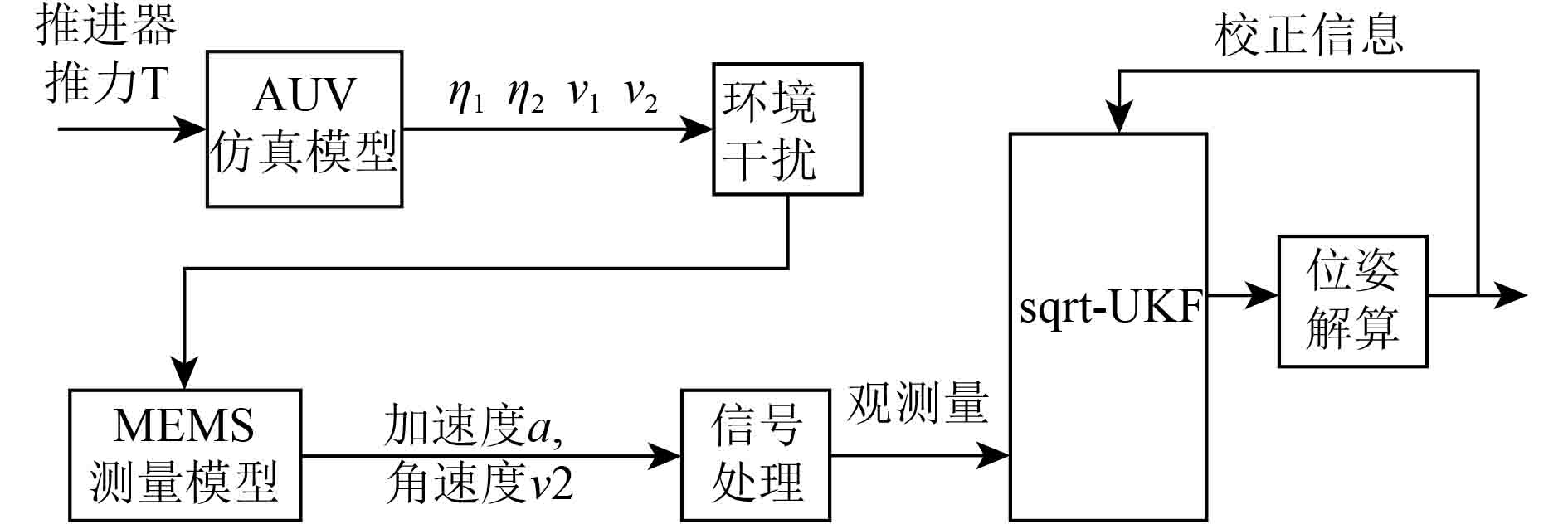
使用Matlab搭建仿真模型，测试AUV动态运行时惯性导航算法的性能。仿真程序的仿真流程图如图4所示。

考虑MEMS传感器的刻度因子误差、非正交安装误差、系统误差等，建立加速度传感器的误差模型：

$\begin{split}\left[ {\begin{array}{*{20}{c}} {{{\bar a}_x}} \\ {{{\bar a}_y}} \\ {{{\bar a}_z}} \end{array}} \right] =& \left[ {\begin{array}{*{20}{c}} {1.0021}&{ - 0.0063}&{ - 0.0041} \\ {0.0003}&{1.0027}&{0.0020} \\ { - 0.0128}&{0.0011}&{1.0003} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_x}} \\ {{a_y}} \\ {{a_z}} \end{array}} \right] +\\ &\left[ {\begin{array}{*{20}{c}} { - 0.0055} \\ {0.0790} \\ {0.0105} \end{array}} \right] + {{\tilde a}}\text{。}\end{split}$

(36)

其中： ${{\tilde a}} = {[{\tilde a_x},{\tilde a_y},{\tilde a_z}]^{\rm T}}$ 为传感器随机误差。基于手机MEMS IMU单元实测，使用自回归模型（Autoregressive model，AR模型）并基于赤池信息量准则建立MEMS IMU的随机误差模型：

${{{\tilde a}}_k} = - 0.3387{{{\tilde a}}_{k - 1}} + {{{\alpha }}_t}\text{，}$

(37)

其中 ${{{\alpha }}_t}$ 是 ${{t}}$ 时刻加速度计的白噪声。

同理，建立MEMS角速度传感器误差模型：

$\bar \Delta {{\theta }} = \Delta {{\theta }} - 0.2373\tilde \Delta {{\theta }} + {{{\beta }}_t}\text{。}$

(38)

其中 ${{{\beta }}_t}$ 是 ${{t}}$ 时刻角速度计的白噪声。

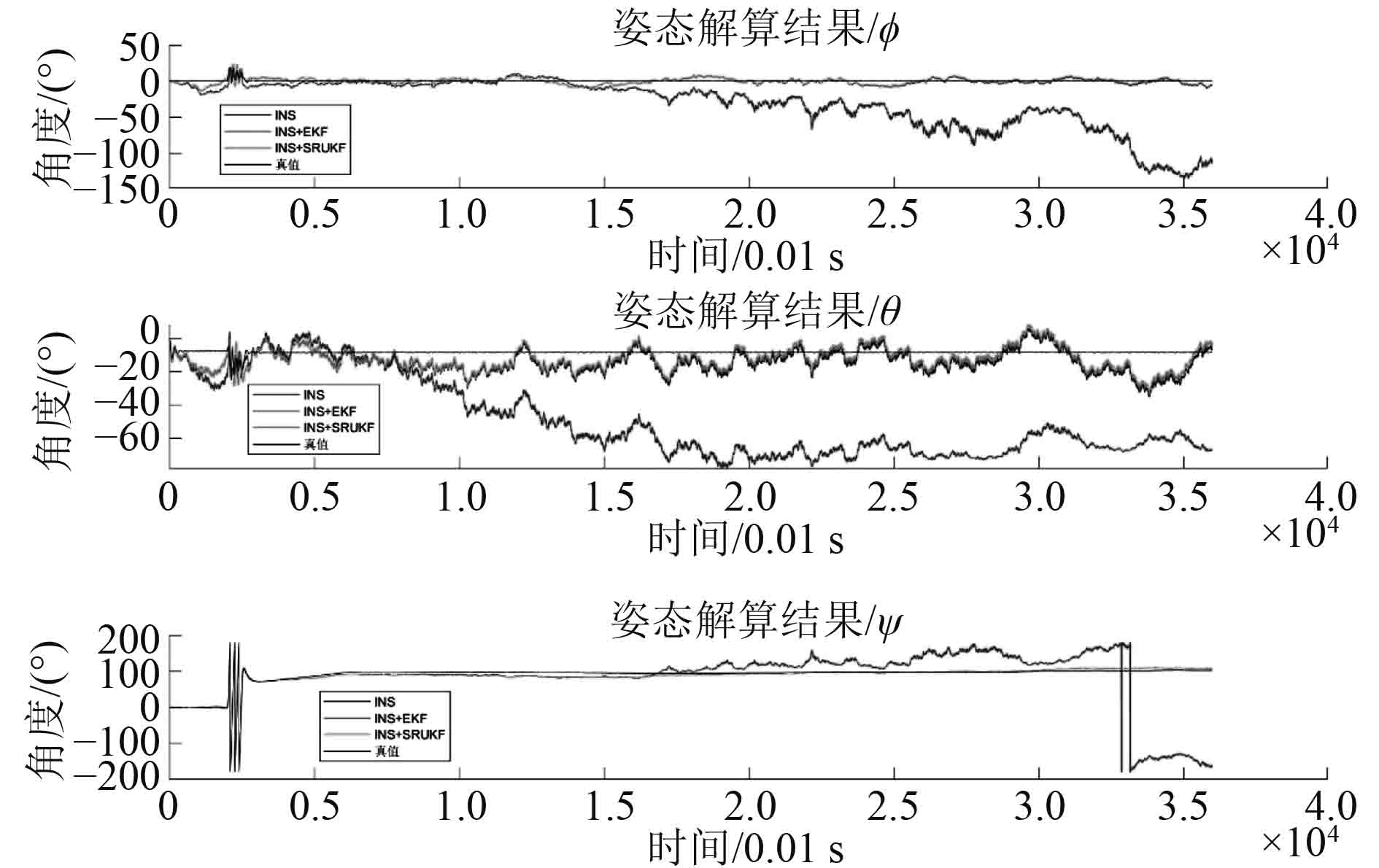
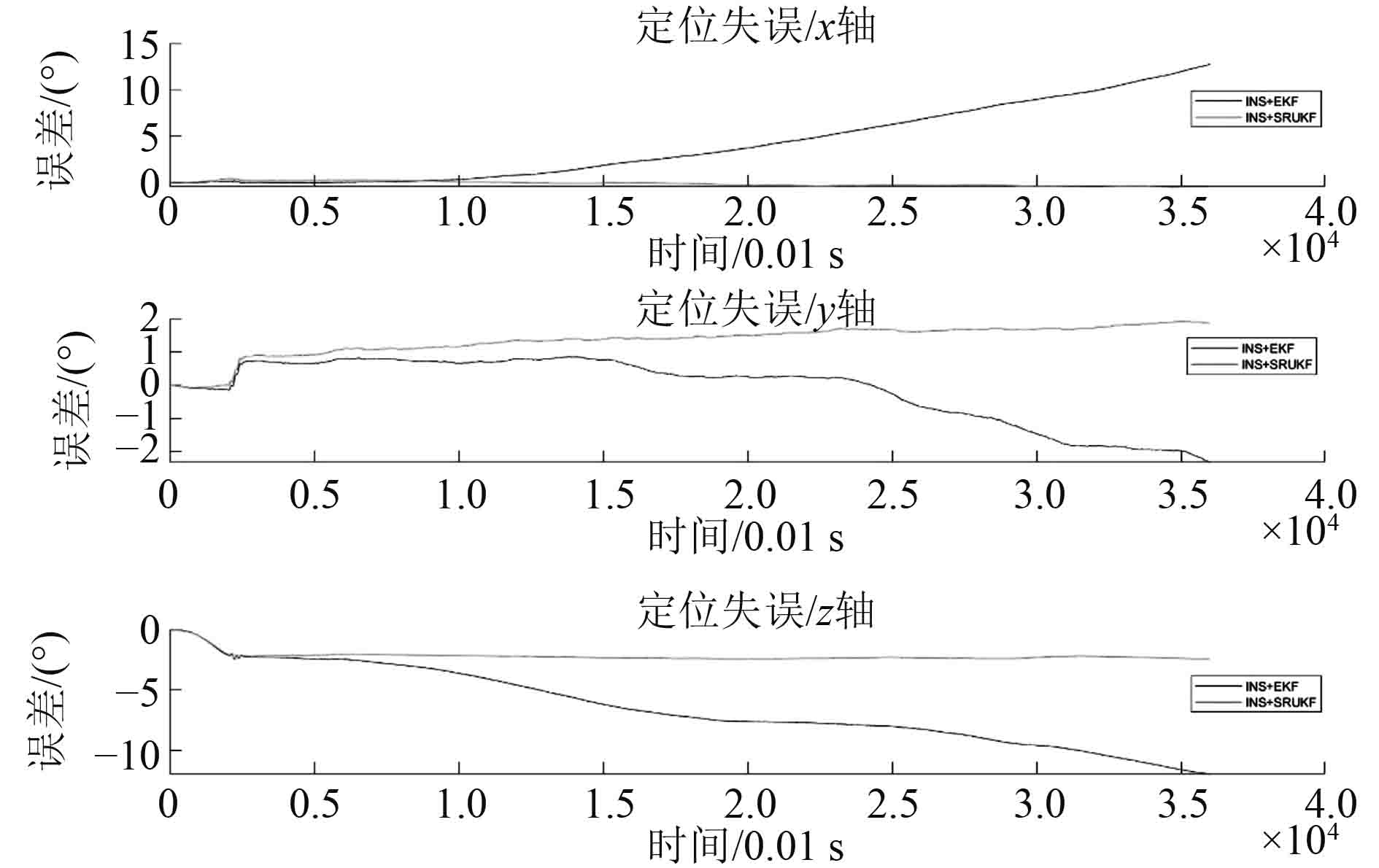
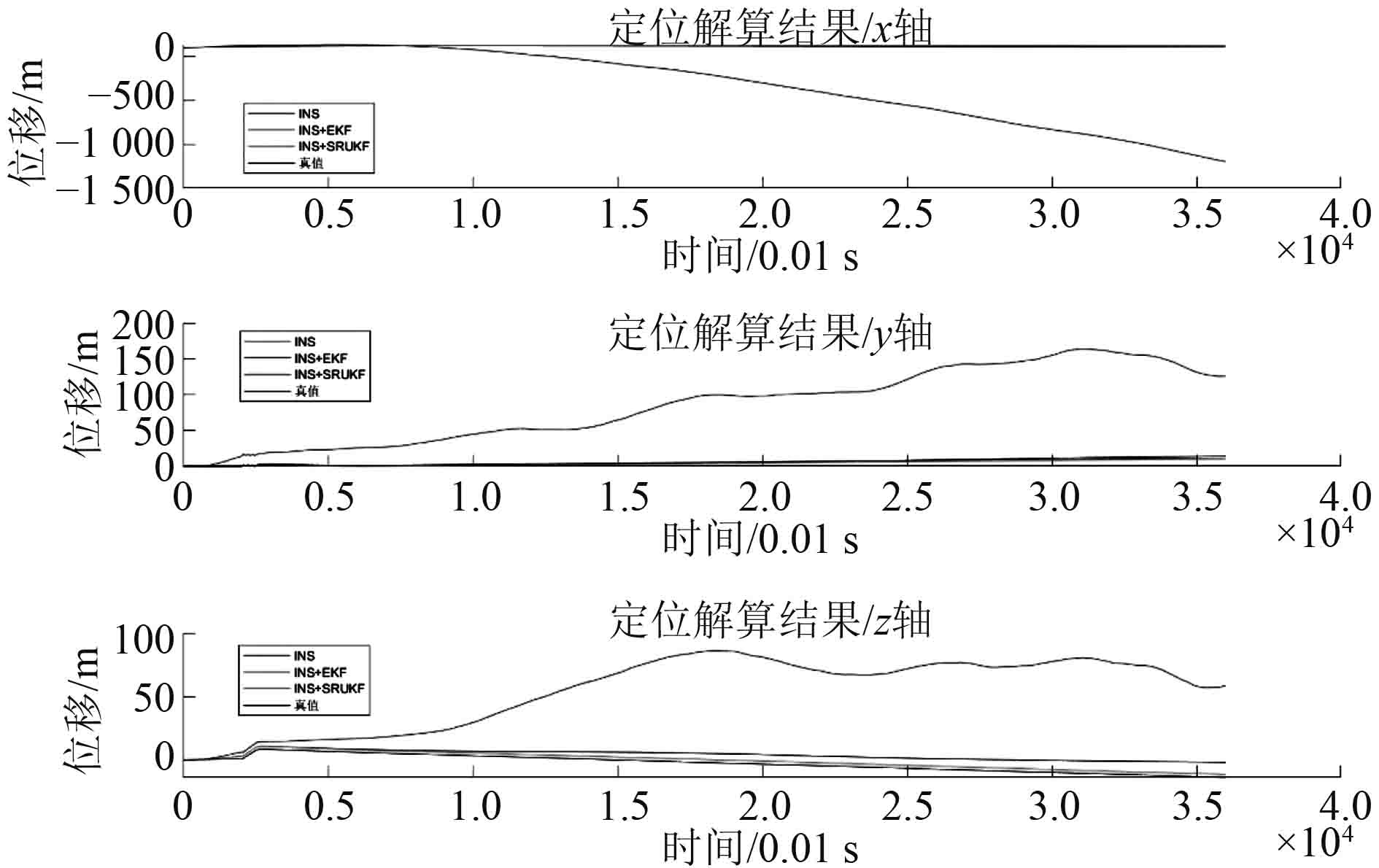
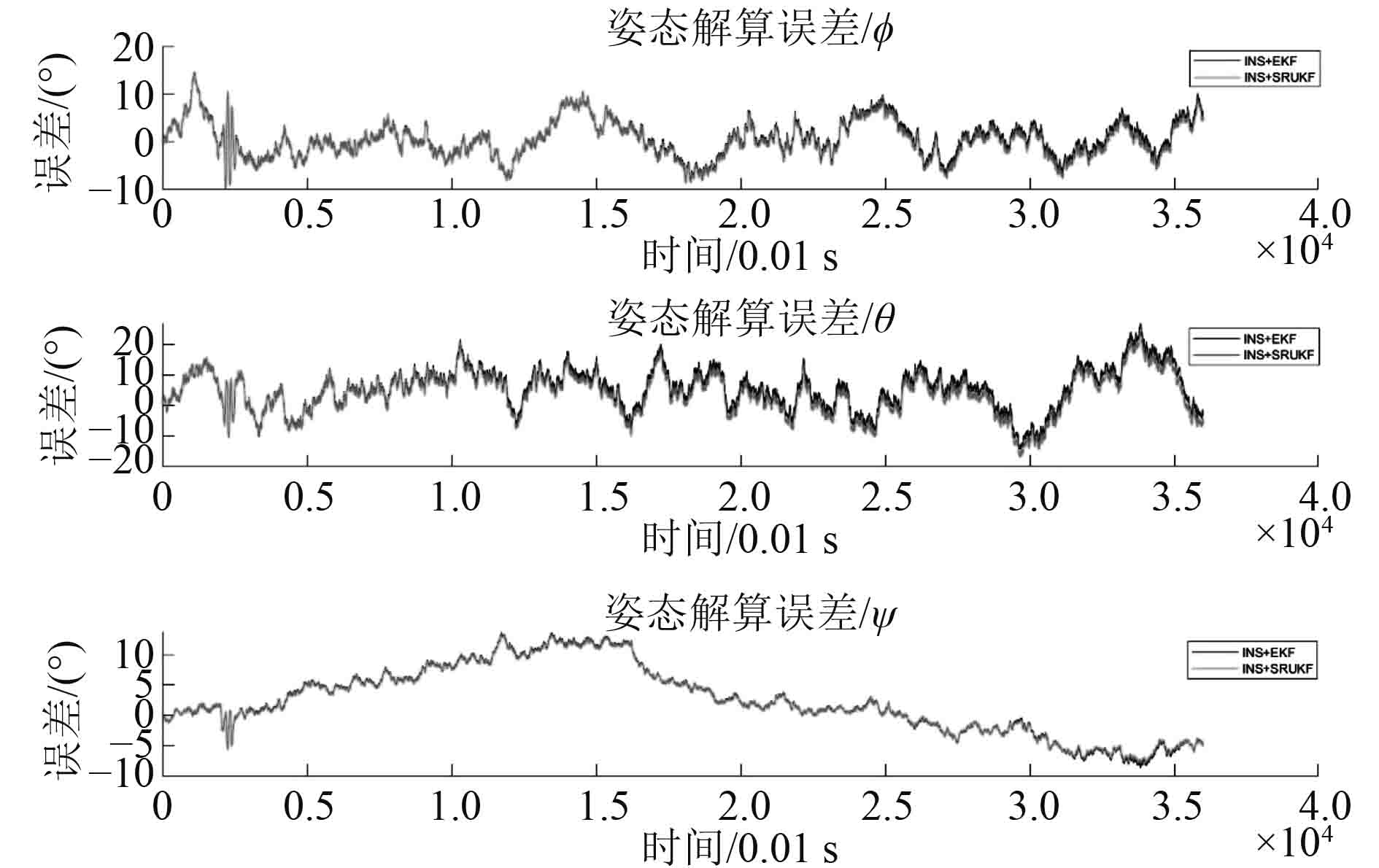
基于上述仿真模型，进行动态误差测试。计算AUV在纯惯性导航（INS）、使用EKF滤波（INS+EKF）、使用SRUKF滤波（INS+SRUKF）3种情况下的导航效果。解算得到AUV姿态、速度、位置数据和误差如图5～图10所示。

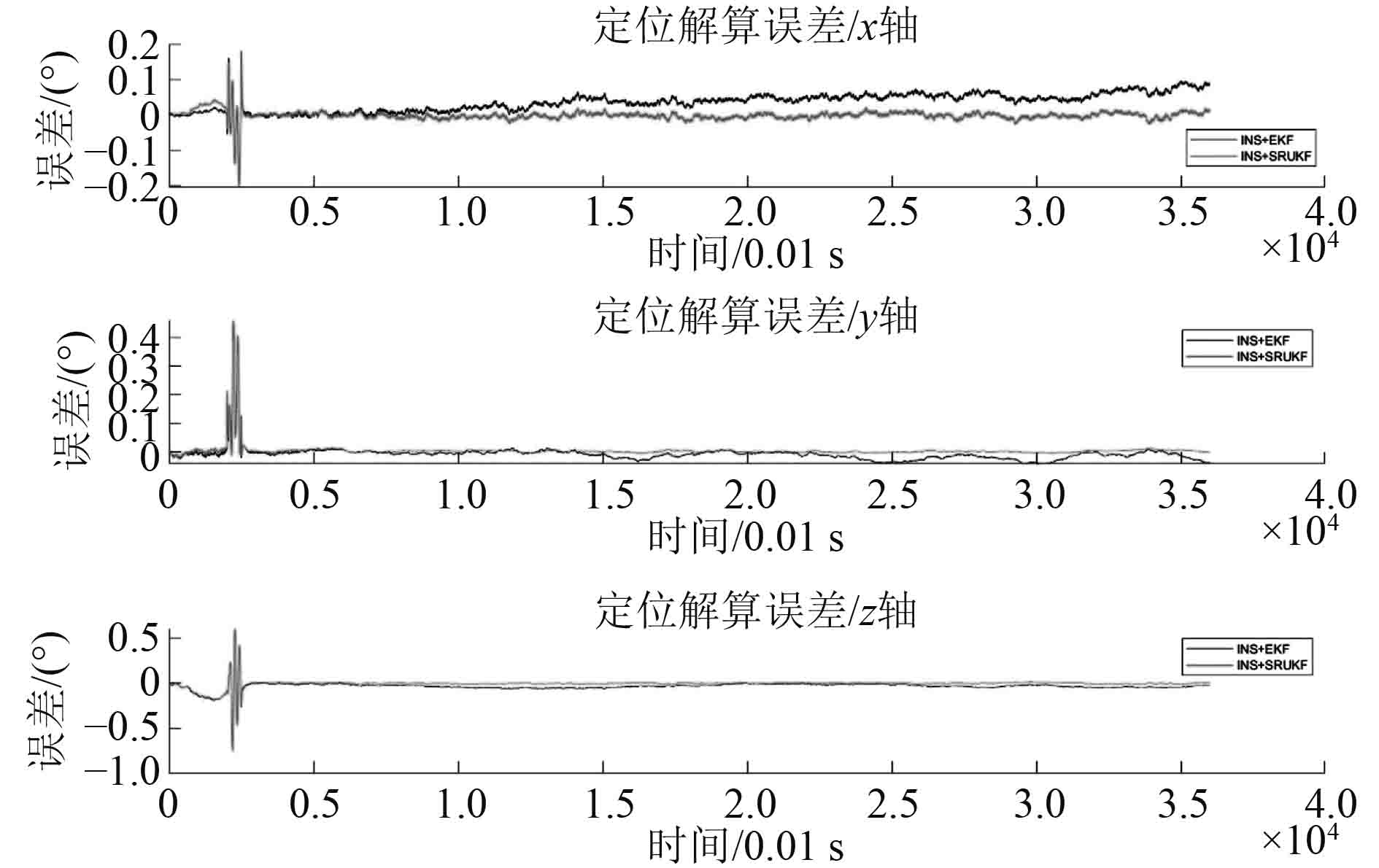
由图5和图6可知，INS解算的姿态和速度误差积累迅速。由图7可知，INS解算位置误差迅速达到百米量级，x轴误差已大于1000 m，使得解算结果完全不可用。

由图8和图9可知，INS+EKF解算出的姿态和速度误差均大于INS+SRUKF解算结果，且由图10可知，由于位置由速度和姿态积分得到，速度和姿态的误差经积分运算迅速扩大，使得INS+EKF导航的结果更加不可靠。分析可知，AUV受力简单、工作平稳时工作点的1阶泰勒展开能较好反应AUV运动状态，此时INS+EKF解算效果较好。当AUV突然改变工况、六自由度运动相互影响加剧时，INS+EKF出现发散现象。

使用INS+SRUKF进行解算，AUV工作平稳时解算结果与INS+EKF基本一致，当AUV突然改变工况时，仍能较好解算AUV位置。速度、姿态误差的增加主要出现在AUV工作状态突然改变时。定位误差随时间增长，但增长缓慢。其最大定位误差小于2 m。

4 结　语

通过建立小型AUV的运动学和动力学模型，解算得到AUV的运动状态和位置信息，可以为限于功耗、体积而不能装备足够传感器的小型AUV提供定位导航参考。设计平方根无迹卡尔曼滤波算法，综合利用AUV模型解算数据和MEMS IMU测量数据，并能够克服AUV运动方程高度非线性的困难，提高惯性导航精度。同时经过半实物实验和Matlab仿真实验，验证了算法的可行性。结果表明，基于模型辅助的平方根无迹卡尔曼滤波算法，性能优于扩展卡尔曼滤波算法，能够显著提高惯性导航的精度，满足小型AUV的导航定位需求。