虽然甚低频通信不如卫星通信等信息传输率高,但由于海上降雨频繁,卫星通信的高频段信号波长与雨滴直径较为接近,雨水会对信号造成严重衰减[1]。而甚低频具有传播距离远,在一定程度上能穿透海水及地表,传输信息稳定的能力等特点,是恶劣天气条件下卫星通信失效时,一种陆地对远洋航行中船舶传递信息的备用手段。因此,开展甚低频信号高速传输的研究,对用于对潜通信的甚低频通信技术未来发展具有一定指导意义[2]。
甚低频的通信频率为3~30 kHz,其实现传输过程中的不足为噪声干扰。超低频远洋通信成功的关键是进行有效的干扰抵消。远洋通信在接收端受到的干扰主要包括:通信信道内的非合作人工干扰(广播信号、工业干扰、大气噪声等)[3]。另外,船舶周围也存在强烈的低频干扰噪声,主要与船舶轴频电场、防腐系统、大电流设备等电流脉动有关。由于噪声形态在频域、时域和空域呈现随机变化的非平稳状态,要实现船舶电磁噪声抵消,特别是要实现很大的噪声抑制比,技术难度大,需要在多个学术领域开展多基础理论与相关技术创新研究[4]。
关于电磁噪声特征及其抵消技术,美国和俄罗斯都曾开展过较为深入的研究。然而仅从国外文献获悉有关电磁噪声较多的描述,无具体数据和技术可借鉴[5]。本文首先将信号通过带通滤波器有效滤除带外噪声。其次,对于带内噪声,采用改进的间接滤波算法进行降噪技术抑制带内噪声,传统的自适应滤波算法。
本文搭建接收信号所用到的天线模型,即一种垂直双通道的天线接收模型,对信道接收的信号进行了简单的建模;针对传统的滤波算法无法直接恢复期望信号的问题,介绍间接滤波算法的基本原理,以及结合小波变换进一步改进了间接滤波算法;针对本文提出的2种算法进行仿真和实验验证。
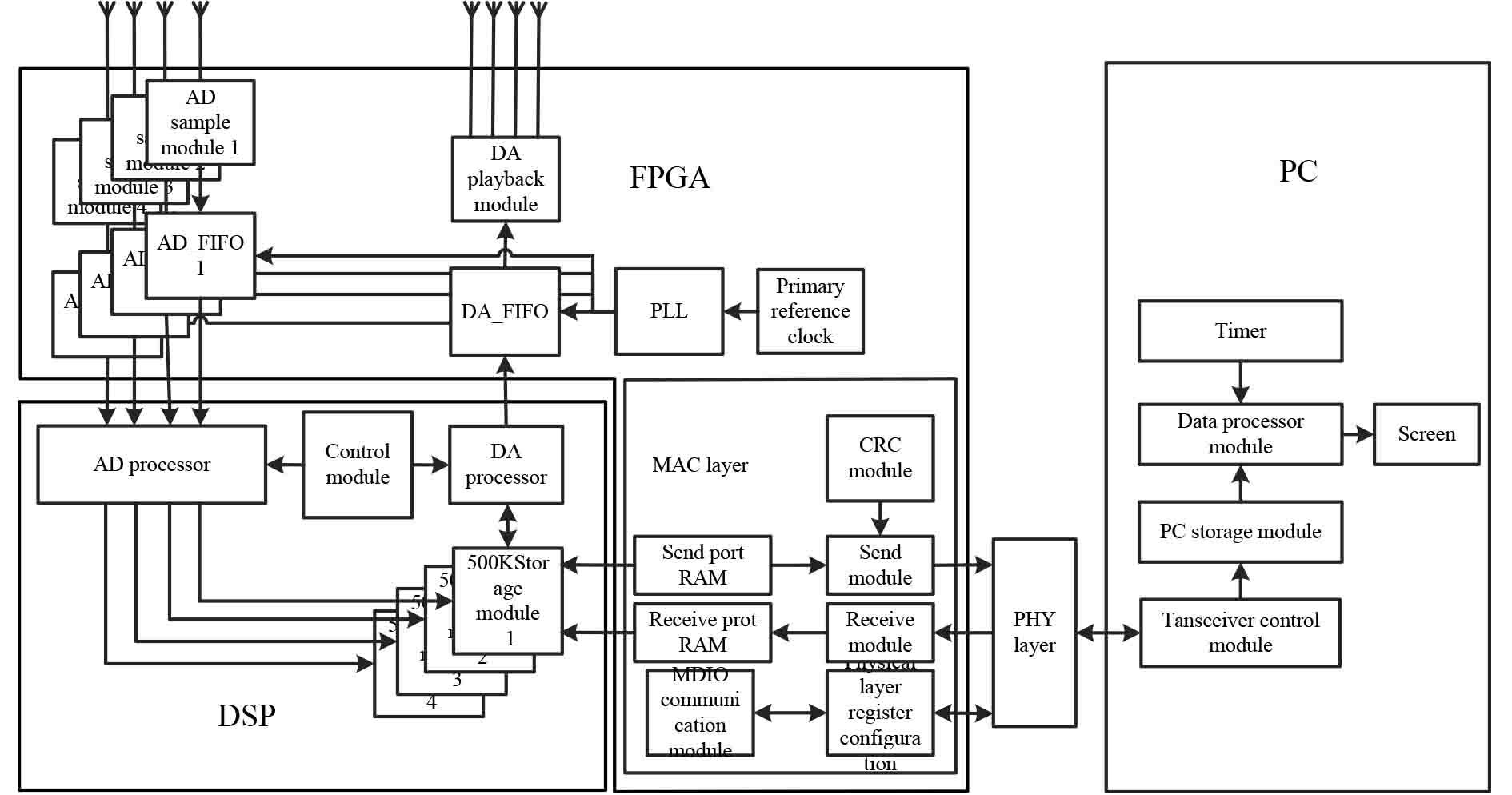
1 信号与天线模型 1.1 天线模型本文提出一种垂直双通道的天线接收模型布设方法。如图1所示,主接收天线m与参考天线n在空间中正交放置。采用两互相垂直的天线接收信号,主天线正对信号源,参考天线平行于信号源。由于磁性天线增益最大的地方在磁芯方向,而正交于磁芯方向增益最小。主天线m直接接收到信号,参考天线n中期望信号的成分最少,理论上能接收到除了主天线方向以外空间中的所有干扰信号,但信号受到教研室有限环境影响发生反射,所以参考天线n也会收到期望信号,但十分微弱可忽略。
|
图 1 数据传输硬件系统结构图 Fig. 1 Structure diagram of data transmission hardware system |
由图1 得出,主天线在i时刻接收到信号
| $x(i) = e(i) + n(i){\text。}$ | (1) |
其中:
参考天线与主天线互相垂直,接收到的信号几乎不包含期望信号成分。且由于磁性天线间相距较近,远小于甚低频电磁波信号的波长,在此忽略两天线之间接收信号的延时带来的影响。则参考天线在i时刻接收到信号
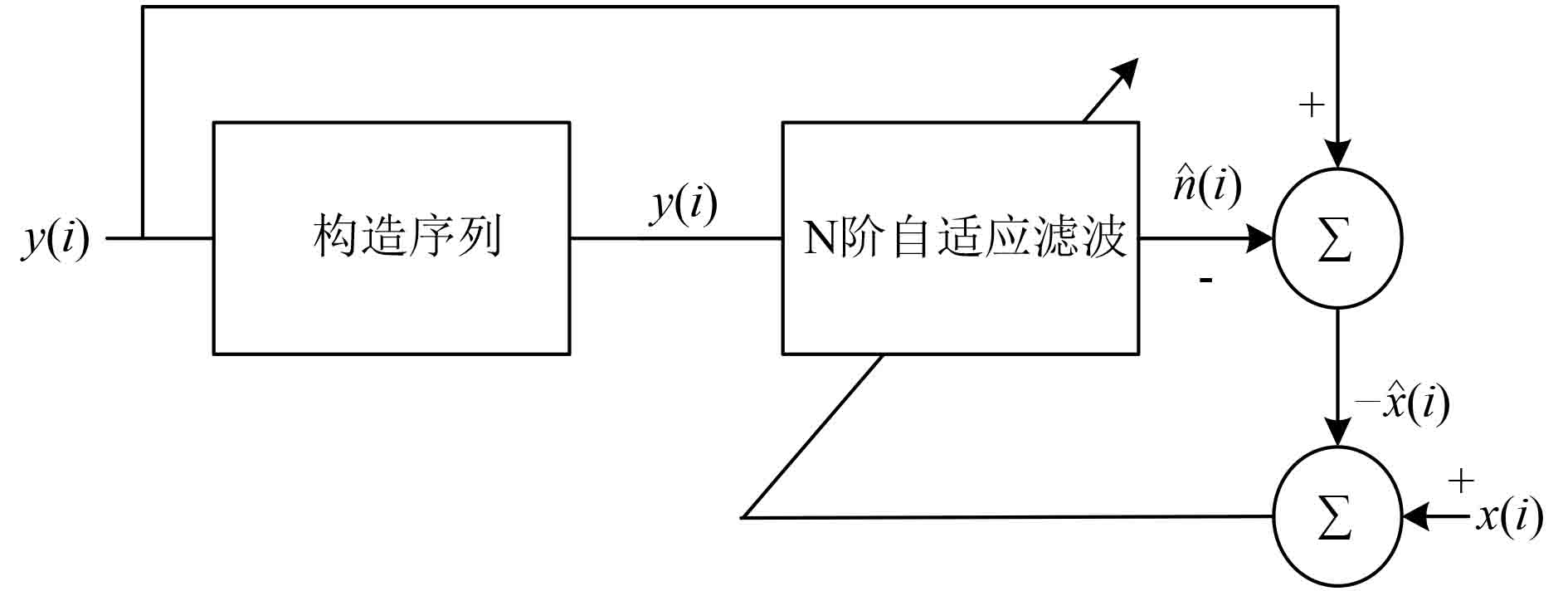
一般地,自适应滤波算法以期望信号作为滤波器输出,当信噪比极小时,往往因为期望信号微弱而导致滤波器系数偏差较大,很难恢复出理想的期望信号。与以往滤波算法不同的是间接滤波算法以噪声作为自适应滤波器输出信号。假设信号与噪声之间互不相关,由于接收机接收到的序列中信号功率小于噪声的功率,传统的自适应滤波算法很难将信号从噪声中恢复出来。本文分别在传统的最小均方自适应滤波算法(MLSA)的基础上,提出一种间接最小均方自适应滤波算法,并对处理后的结果运用小波变换分解,进一步抑制噪声提高通信信噪比(SNR),解决双通道下的低信噪比的滤波问题。间接自适应滤波器的原理框图如图2所示。
|
图 2 间接自适应滤波器原理图 Fig. 2 Schematic diagram of indirect adaptive filter |
将主通道接收的离散信号构造信号接收序列
| ${{y}}(i) = {{x}}(i) + {{n}}(i){\text{。}}$ | (2) |
首先,利用信号接收序列
| $\hat n(i)= {{{w}}^{\rm H}}{{y}}(i) = {{{w}}^{\rm H}}{{x}}(i) + {{{w}}^{\rm H}}{{n}}(i){\text,}$ | (3) |
式中:
| $\begin{split}\hat x(i) =& y(i) - \hat n(i) = y(i) - {{{w}}^{\rm H}}{{y}}(i) =\\& \left({{{I}}_1} - {{{w}}^{\rm H}}\right){{x}}(i) + \left({{{I}}_1} - {{{w}}^{\rm H}}\right){{n}}(i)\text{。}\end{split}$ | (4) |
其中
| $\begin{split}n(i) = &x(i) - \hat x(i) =\\ &{{{I}}_1}{{x}}(i) - \left({{{I}}_1} - {{{w}}^{\rm H}}\right){{x}}(i) - \left({{{I}}_1} - {{{w}}^{\rm H}}\right){{n}}(i) = \\ &{{{w}}^{\rm H}}{{x}}(i) - \left({{{I}}_1} - {{{w}}^{\rm H}}\right){{n}}(i)\text{。}\end{split}$ | (5) |
其中,
梯度向量
| $\nabla J = \frac{{\partial J}}{{\partial {{w}}}}{\rm{ = }}\frac{{\partial [{n^2}(i)]}}{{\partial {{w}}}}{\rm{ = 2}}\left( {{{{w}}^{\rm H}}{{{R}}_{{{xx}}}} - {{{R}}_{{{nn}}}}{{{I}}_1} + {{{w}}^{\rm H}}{{{R}}_{{{nn}}}}} \right){\rm{ = }}0$ | (6) |
通过求解式(6)最终得到间接最小均方自适应滤波器的系数向量为:
| ${{w}} = ({{{R}}_{{{xx}}}} + {{{R}}_{{{nn}}}}{)^{ - 1}}{{{R}}_{{{nn}}}}{{{I}}_1} = {{R}}_{{{yy}}}^{ - 1}{{{R}}_{{{nn}}}}{{{I}}_1}\text{。}$ | (7) |
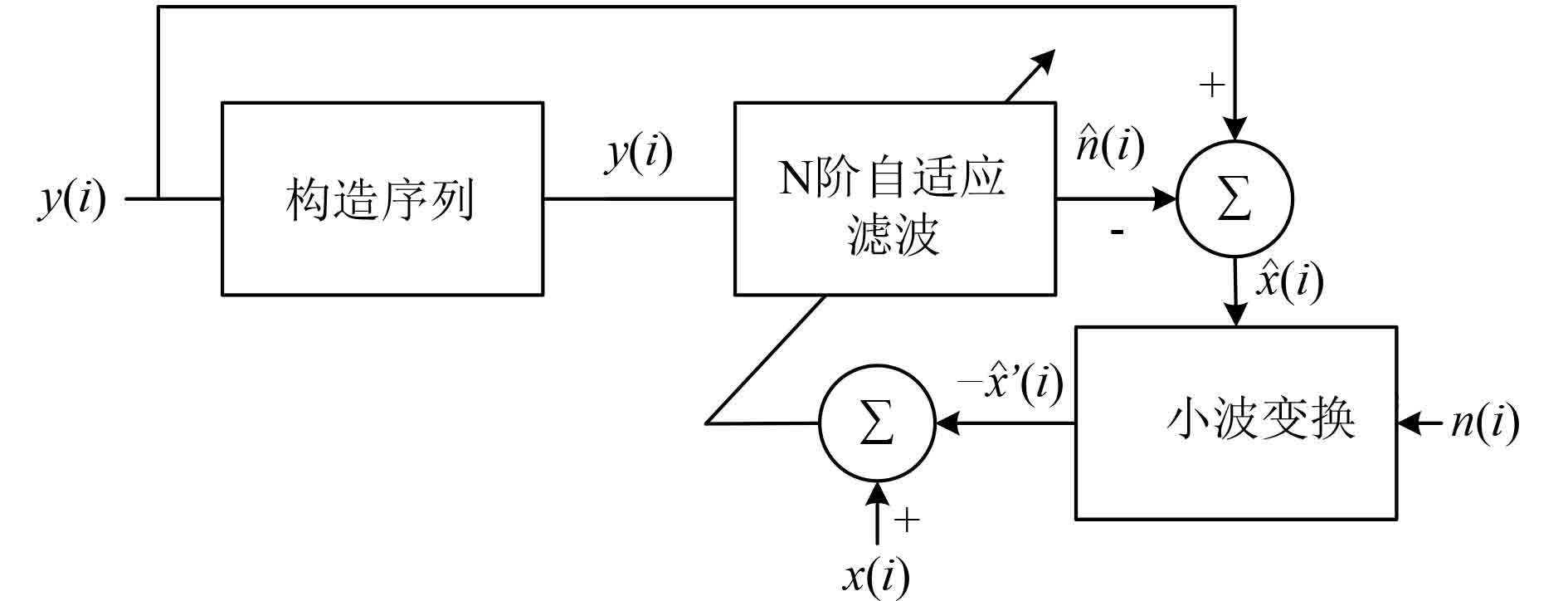
改进后的间接滤波算法如图3 所示。算法改进主要有两方面:为减少求解滤波系数向量计算量,将厄米特矩阵二次型应用到间接滤波算法中;同时,引入小波变换分别对自适应滤波器后的期望信号
|
图 3 改进的间接滤波算法原理图 Fig. 3 Schematic diagram of improved indirect filtering algorithm |
假设期望信号协方差矩阵
| $\begin{split} {{w = U}}{{{w}}_{{0}}} =& [{u_1},{u_2} \cdots \cdots {u_{{r_x}}}] \cdot [{w_1},{w_2} \cdots \cdots {w_{{r_x}}}] +\\ &[{u_{{r_x} + 1}},{u_{{r_x} + 2}} \ldots \cdots {u_{rn}}] \cdot [{w_{{r_x} + 1}},{w_{{r_x} + 2}} \cdots \cdots {w_{{r_n}}}]= \\ &{{{U}}_{{r_x}}}{{{w}}_{0{r_x}}}{{ + }}{{{U}}_{{r_n} - {r_x}}}{{{w}}_{0{r_n} - {r_x}}}\text{。} \end{split}$ | (8) |
为了使自适应滤波算法的输出
| $\begin{split} J =& \min \left\{ E[n_{{r_n} - {r_x}}^2(n)]\right\}= \\ & {\rm min}\Big\{ ({{I}}_{{1}}^{} - {{U}}_{{r_n} - {r_x}}^{}{{w}}_{0{r_n} - {r_x}}^{}{)^{\rm H}}{{{R}}_{{{vv}}}}({{{I}}_{{1}}} - {{{U}}_{{r_n} - {r_x}}}{{{w}}_{0{r_n} - {r_x}}}{\rm{\Big\} }}=\\ &{\rm min}\Big\{ {{I}}_{{1}}^{\rm H}{{{R}}_{{{vv}}}}{{{I}}_{{1}}} \!-\! {{I}}_{{1}}^{\rm H}{{{R}}_{{{vv}}}}{{{U}}_{{r_n} \!-\! {r_x}}}{{{w}}_{0{r_n} \!-\! {r_x}}} \!-\! {{w}}_{0{r_n} \!-\! {r_x}}^{\rm H}{{U}}_{{r_n} \!-\! {r_x}}^{\rm H}{{{R}}_{{{vv}}}}{{{I}}_{{1}}}\!+ \\ & {{w}}_{0{r_n} - {r_x}}^{\rm H}{{U}}_{{r_n} - {r_x}}^{\rm H}{{{R}}_{{{vv}}}}{{{U}}_{{r_n} - {r_x}}}{{{w}}_{0{r_n} - {r_x}}}{\rm{\Big\} }}=\\ &{\rm min}\Bigg\{ {{I}}_{{1}}^{\rm H}{{{R}}_{{{vv}}}}{{{I}}_{{1}}} - {{I}}_{{1}}^{}{{{R}}_{{{vv}}}}\left( {{{{U}}_{{r_n} - {r_x}}}{{{w}}_{0{r_n} - {r_x}}}+ {{w}}_{0{r_n} - {r_x}}^{\rm H}{{U}}_{{r_n} - {r_x}}^{\rm H}} \right)+\\ & {{w}}_{0{r_n} - {r_x}}^{\rm H}{{U}}_{{r_n} - {r_x}}^{\rm H}{{{R}}_{{{vv}}}}{{{U}}_{{r_n} - {r_x}}}{{{w}}_{0{r_n} - {r_x}}}{\rm{\Bigg\} }}\text{。} \end{split}$ | (9) |
利用式(9)对
| $ \frac{{\partial J}}{{\partial {{w}}}} \!=\! - \!\left( {{{U}}_{{r_n} \!-\! {r_x}}^{} \!+\! {{U}}_{{r_n} \!-\! {r_x}}^{\rm H}} \right){{{R}}_{{{vv}}}}{{{I}}_{{1}}}\!{\rm{ + }}\!2{{U}}_{{r_n} \!-\! {r_x}}^{\rm H}{{{R}}_{{{vv}}}}{{{U}}_{{r_n} \!-\! {r_x}}}{{{w}}_{0{r_n} \!-\! {r_x}}}{\rm{ = }}0,$ | (10) |
解得滤波算法基底向量为:
| $ {{{w}}_{0{r_n} - {r_x}}}= \frac{1}{2}{\left( {{{U}}_{{r_n} - {r_x}}^{\rm H}{{{R}}_{{{vv}}}}{{{U}}_{{r_n} - {r_x}}}} \right)^{ - 1}}\left( {{{U}}_{{r_n} - {r_x}}^{} + {{U}}_{{r_n} - {r_x}}^{\rm H}} \right){{{R}}_{{{vv}}}}{{{I}}_1},$ | (11) |
从而求得滤波系数向量为:
| $ \begin{split} {{{w}}_{{r_n} - {r_x}}} =& {{{I}}_1} - {{{U}}_{{r_n} - {r_x}}}{{{w}}_{0{r_n} - {r_x}}}=\\ & {{{I}}_1} - {{{U}}_{{r_n} - {r_x}}} \cdot \frac{1}{2}{\left( {{{U}}_{{r_n} - {r_x}}^{\rm H}{{{R}}_{{{vv}}}}{{{U}}_{{r_n} - {r_x}}}} \right)^{ - 1}}\cdot\\ &\left( {{{U}}_{{r_n} - {r_x}}^{} + {{U}}_{{r_n} - {r_x}}^{\rm H}} \right){{{R}}_{{{vv}}}}{{{I}}_1}=\\ & {{{I}}_1} \!-\! \frac{1}{2}{{{U}}_{{r_n} \!-\! {r_x}}}{\rm{D}}_{2,{r_n} \!-\! {r_x}}^{ - 1}\left( {{{U}}_{{r_n} \!-\! {r_x}}^{} \!+\! {{U}}_{{r_n} \!-\! {r_x}}^{\rm H}} \right){{{R}}_{{{vv}}}}{{{I}}_1}\text{。} \end{split}$ | (12) |
其中:
| ${{D}}_2^{}{{ = D}}_{2,{r_x}}^{} + {{D}}_{2,{r_n} - {r_x}}^{}\text{。}$ | (13) |
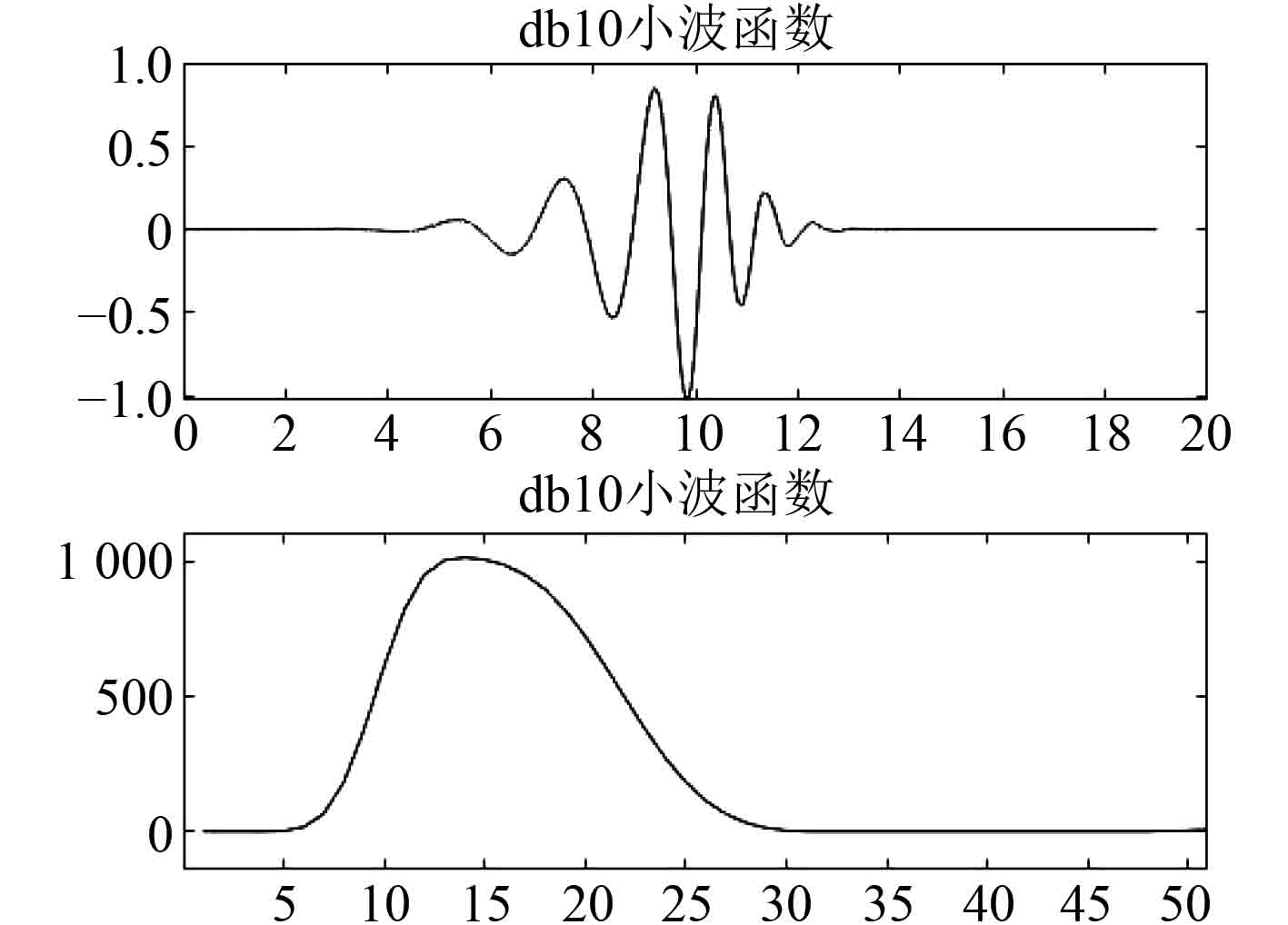
小波变换算法可以很好地对信号的细节进行分析,其在降噪应用领域十分广泛。小波基的选取对降噪效果影响很大,但目前只是往往采用经验和不断试验的方法选取[8]。本文小波基的选取采用Daubechies小波,简称db小波,记为
|
图 4 Db10小波基函数与频谱 Fig. 4 Db10 wavelet basis function and spectrum |
| ${\varphi _{a,b}}\left( i \right) = \frac{1}{{\sqrt {\left| a \right|} }}\varphi \left( {\frac{{i - b}}{a}} \right),\begin{array}{*{20}{c}} {}&{a,b \in R;a \ne 0} {\text,} \end{array}$ | (14) |
其中:a为伸缩因子,b为平移因子。任意函数的连续小波变换为该函数与某小波序列的卷积。
本文引入小波变换分别对自适应滤波器后的期望信号
1)期望信号
2)噪声信号
3)找出不同层分解信号并重构期望信号
改进的间接滤波算法输出信噪比定义为经过自适应滤波算法处理后的期望信号
| $\begin{split} SNR({{W}})=&\frac{E\left\{{\left|{x}_{r}\left(i\right)\right|}^{2}\right\}}{E\left\{{\left|{n}_{r}\left(i\right)\right|}^{2}\right\}}=\frac{{{{W}}}^{\rm H}{{{R}}}_{xx}{{W}}}{{{{W}}}^{\rm H}{{{R}}}_{vv}{{W}}}=\\ &\frac{{{{w}}}_{0,{r}_{n}-{r}_{x}}^{\rm H}{{{U}}}_{{r}_{n}-{r}_{x}}^{\rm H}{{{R}}}_{xx}{{{U}}}_{{r}_{n}-{r}_{x}}{{{W}}}_{0,{r}_{n}-{r}_{x}}}{{{{W}}}_{0,{r}_{n}-{r}_{x}}^{\rm H}{{{U}}}_{{r}_{n}-{r}_{x}}^{\rm H}{{{R}}}_{vv}{{{U}}}_{{r}_{n}-{r}_{x}}{{{W}}}_{0,{r}_{n}-{r}_{x}}}=\\ &\frac{{\displaystyle \sum _{i=1}^{{r}_{n}-{r}_{x}}{\left|{w}_{r+i}\right|}^{2}{\lambda }_{r+i}}}{{\displaystyle \sum _{i=1}^{{r}_{n}-{r}_{x}}{\left|{w}_{r+i}\right|}^{2}}}{\text。}\end{split}$ | (15) |
为测试算法的效果,本文分别用模拟仿真和实验室测量2种方法进行验证,并与原始滤波算法分别进行比较分析。
3.1 仿真本文仿真数据实现的具体过程为:分别生成幅度为0.1 V、频率为20 kHz的期望信号,信号的采样频率为1 MHz。噪声信号服从标准正态分布,为使信号完全淹没于噪声之中,设定信噪比
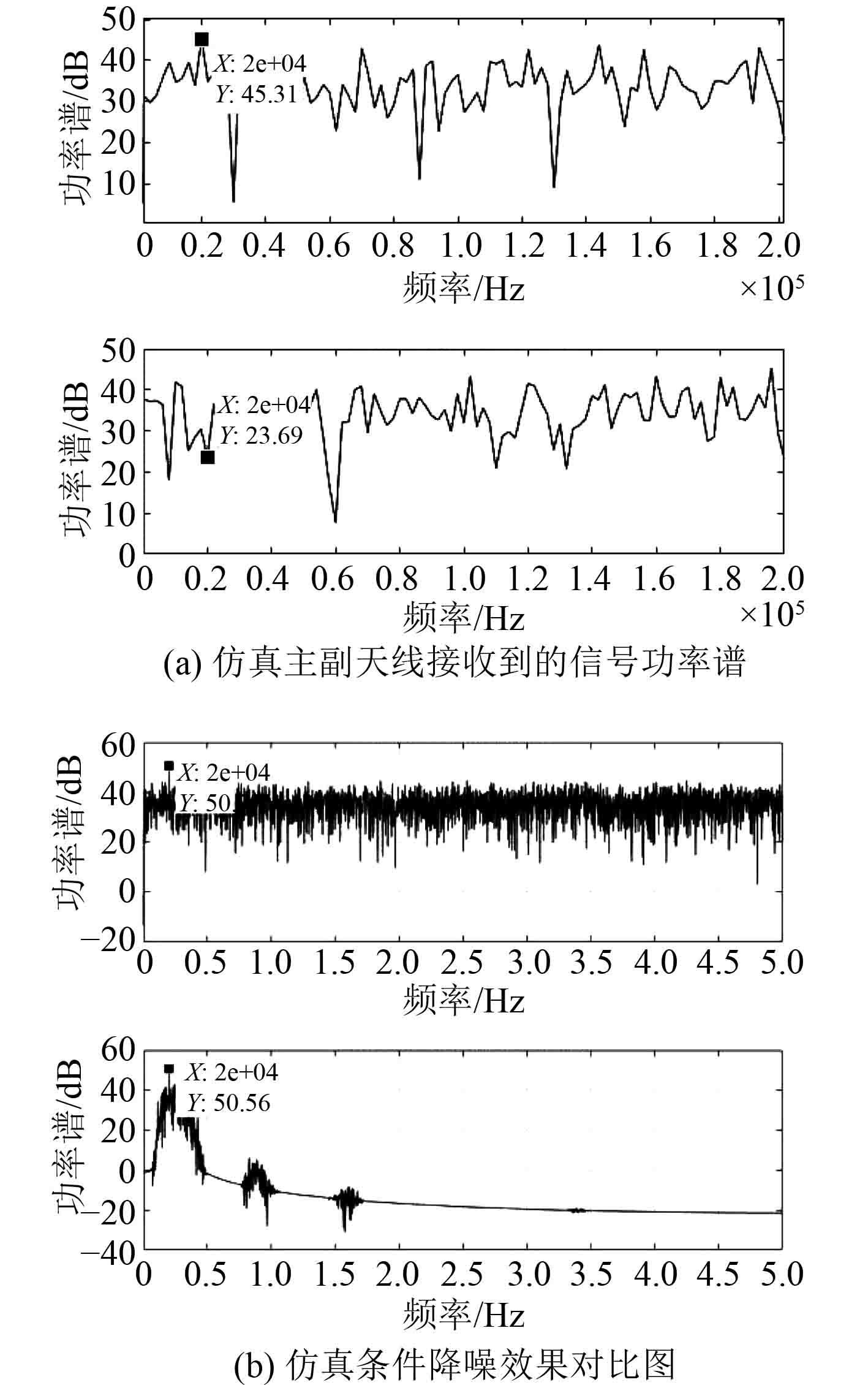
|
图 5 仿真信号功率谱 Fig. 5 Power spectrum of simulation signa |
通过观察图5(b)发现,在以上2种仿真算法实验中期望信号的功率基本相同,而在第2种方法中噪声功率得到了明显的抑制,可见小波变换在一定程度上抑制了信噪的高频信号,提高了SNR。
3.2 实验为进一步验证提出算法的效果,在实验室环境中搭建发射信号装置以及接收信号摆放天线结构。
信号源有信号发生器产生,频率与仿真信号频率相同,幅度为100 mV。主副天线分别与FPGA搭建的信号接收设备相连,其采样频率与信号模拟频率相同,能将接收到的数据存入电脑以分析处理。信号源的发射线圈距离主天线中心为5 m。
图6(a)为实测主天线和副天线接收到的信号功率谱。图6(a)中,通过与仿真信道的对比发现信号的频率为2.016 kHz,并非理想的2 kHz,原因可能是FPGA作为接收设备的晶振频率存在一定的偏差导致分频的采样频率不精确。
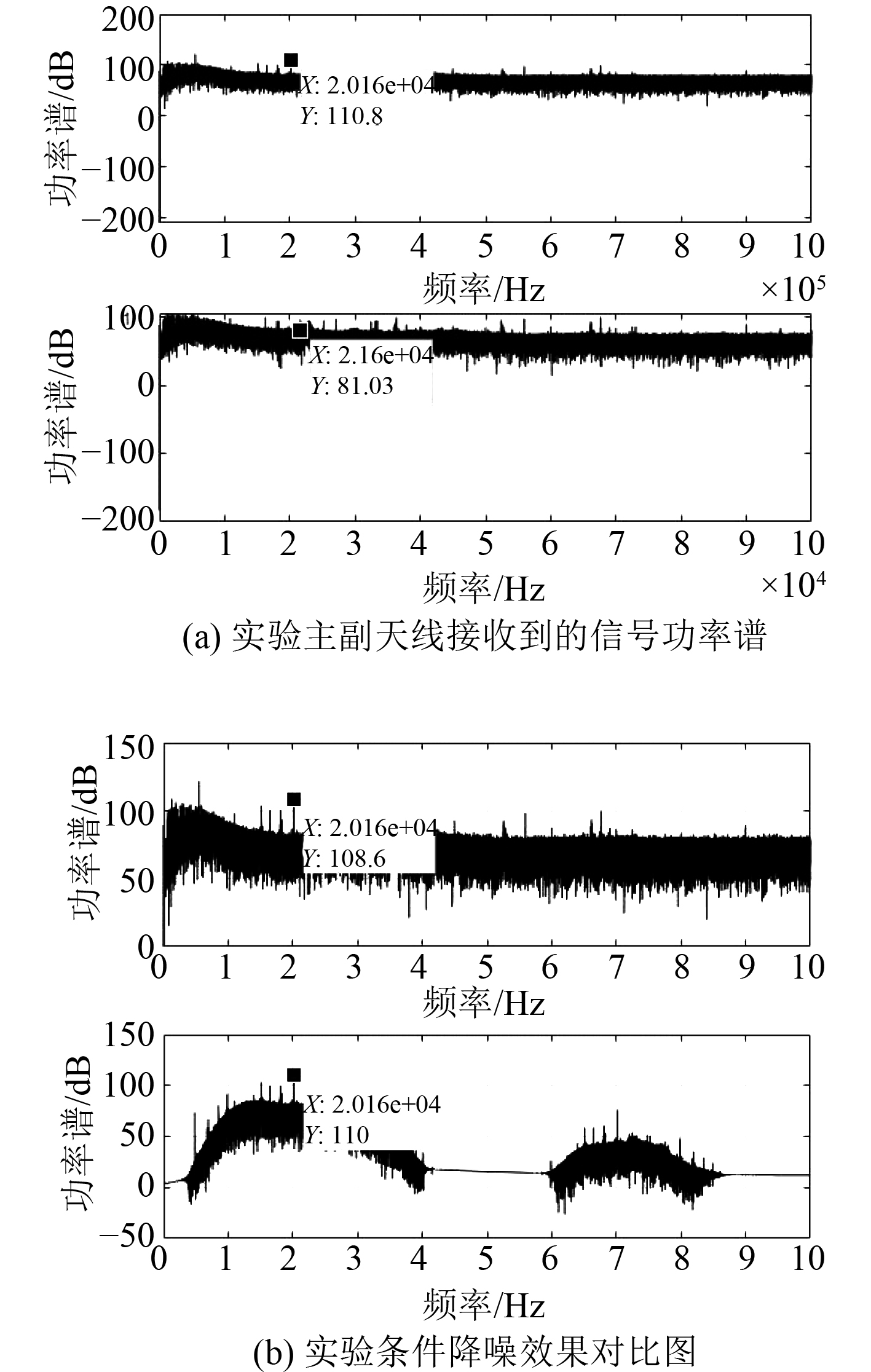
|
图 6 实验信号功率谱 Fig. 6 Power spectrum of experimental signal |
由图6(b)可知,两类滤波算法对于实验室环境下噪声信号干扰均存在抑制效果,但改进的间接滤波算法能够更好地将低频中高于信号的部分降低,能够在信噪比较低的情况下抵消更多的干扰信号,突出信号的功率。
将2种算法的仿真与实验信噪比计算测量各10次后取平均结果列入表1。模拟数据中理论计算与测量结果偏差较大,可能是小波重构的信号功率不及原信号的功率大引起的;其次可能是仿真噪声采用高斯白噪声没有现实噪声复杂真实;再次是受统计次数不足,测量结果有误差以及保留有效数位影响。实验测量数据与理论计算值较为接近,验证算法可行性。虽然改进的算法性能提升效果不明显,但是从功率谱不难看出,改进的算法能更好地抑制部分噪声功率。
|
|
表 1 两种算法的信噪比10次试验结果平均值 |
本文描述了甚低频通信时存在的问题,结合小波变换算法提出改进的间接滤波算法来解决问题。首先搭建垂直双通道的天线接收模型,简单介绍了间接滤波器算法和小波变换算法并结合对算法提出了改进。提出的改进的间接滤波算法算法结合了小波变换,仿真和实验结果表明,改进后的算法相比于传统算法,能够在信噪比较低的情况下抵消更多的干扰信号,比普通间接滤波算法信噪比更高。2种算法计算与实验数据基本吻合,验证了算法的可行性。本文存在的主要问题是只在实验室进行测量验证,未在远距离通信、更复杂的干扰环境下对算法进行实验,下一步将对此进行改进完善。
| [1] |
高化猛, 李智. 一种 Ka 频段海上卫星通信抗雨衰编码方案[J]. 舰船科学技术, 2011, 33(12): 76-78. DOI:10.3404/j.issn.1672-7649.2011.12.017 |
| [2] |
贾琦, 王奎. 甚低频窄带网络下的高速信号传输方法研究[J]. 舰船电子工程, 2020, 40(1): 60-62. DOI:10.3969/j.issn.1672-9730.2020.01.015 |
| [3] |
郭锐. “短波自适应选频”的研究[D]. 西安:西北工业大学, 2006: 14.
|
| [4] |
朱开波. 自适应抵消技术船舶综合声呐系统[J]. 舰船科学技术, 2019, 41(6): 115-117. DOI:10.3404/j.issn.1672-7649.2019.06.024 |
| [5] |
LI Chun-teng, JIANG Yu-zhong, LIU Fang-jun. New insights about interference suppression algorithm based on analog circuits and linear filtering method in elf communication[J]. AEU- International Journal of Electronics and Communications, 2018, 93: 154-162. DOI:10.1016/j.aeue.2018.06.015 |
| [6] |
刘明, 徐洪波, 宁国勤. 数字信号处理, 原理与算法实现[M]. 北京:清华大学出版社, 2006: 1−7.
|
| [7] |
B. WIDROW and M. E. HOFF, “Adaptive switching circuits, ” WES COM Conv. Rec, pt. 4, 1960: pp. 96–140.
|
| [8] |
沈再阳. 精通MATLAB信号处理[M]. 北京:清华大学出版社, 2015: 34−40.
|
| [9] |
吕泽承, 杨健, 邬蓉蓉, 等. 基于自适应阀值的小波全频降噪方法研究及实现[J]. 广西电力, 2019, 42(6): 13-16+21. DOI:10.3969/j.issn.1671-8380.2019.06.003 |
| [10] |
Yansun XU, J. B. WEAVER, D. M. HEALY, et al. Wavelet transform domain filters: a spatially selective noise filtration technique[J]. IEEE Transactions on Image Processing.3(6): 747−758
|
 2021, Vol. 43
2021, Vol. 43
