2. 中国舰船研究院,北京 100101;
3. 中国人民解放军91001部队,北京 100841
2. China Ship Research Academy, Beijing 100101, China;
3. No 91001 Unit of PLA, Beijing 100841, China
20世纪80年代,中国工程院陆建勋院士提出了利用短波信道背景噪声频谱的“多孔性”提升通信质量的短波自适应通信新思想[1]。随着认知无线电概念的提出与相关研究工作的不断深入[2-3],该短波通信新思想也逐渐成熟完善,形成了短波动态频谱抗干扰(Dynamic Spectrum Anti-Jamming, DSAJ)通信新体制[4]。DSAJ通信体制实时感知工作频段内的频谱空洞,根据频谱空洞的位置确定发射频率,使信息在频谱空洞内传输,实现通信与干扰的分离。
当前对DSAJ体制的理论研究主要集中于体制的总体抗干扰增益以及实际抗干扰性能两方面。文献[5-7]分别在短波干扰信道以及部分频带噪声干扰信道下,对DSAJ系统的容量、比特误码率以及处理增益等性能参数进行了理论分析,定量给出了DSAJ体制的总体抗干扰增益,以及相对于常规抗干扰体制的性能提升。文献[8-9]则分析了DSAJ系统在多音干扰及多址干扰下的通信性能,文献[10]则介绍了一种基于DSAJ体制的原理样机设计方法。
对抗干扰通信系统而言,纠错编码对提升系统的抗干扰能力至关重要[11]。在精确干扰状态信息无法获取的情况下,系统必须采用抗干扰译码度量来保证纠错编码的抗干扰分集效果。针对编码DSAJ系统,文献[6]分析了乘积译码度量在短波干扰信道下的性能。文献[7]则分析了噪声归一化译码度量在部分频带干扰信道下的性能。为进一步深化对DSAJ通信体制的研究工作,寻求对应于不同干扰类型的最优译码方案,本文考虑一种新的译码度量——限幅度量,研究基于该度量的编码DSAJ系统,在短波干扰信道下的抗干扰性能,并与文献[6]给出的相关结果进行比较,对限幅度量的抗干扰能力进行分析与评估。
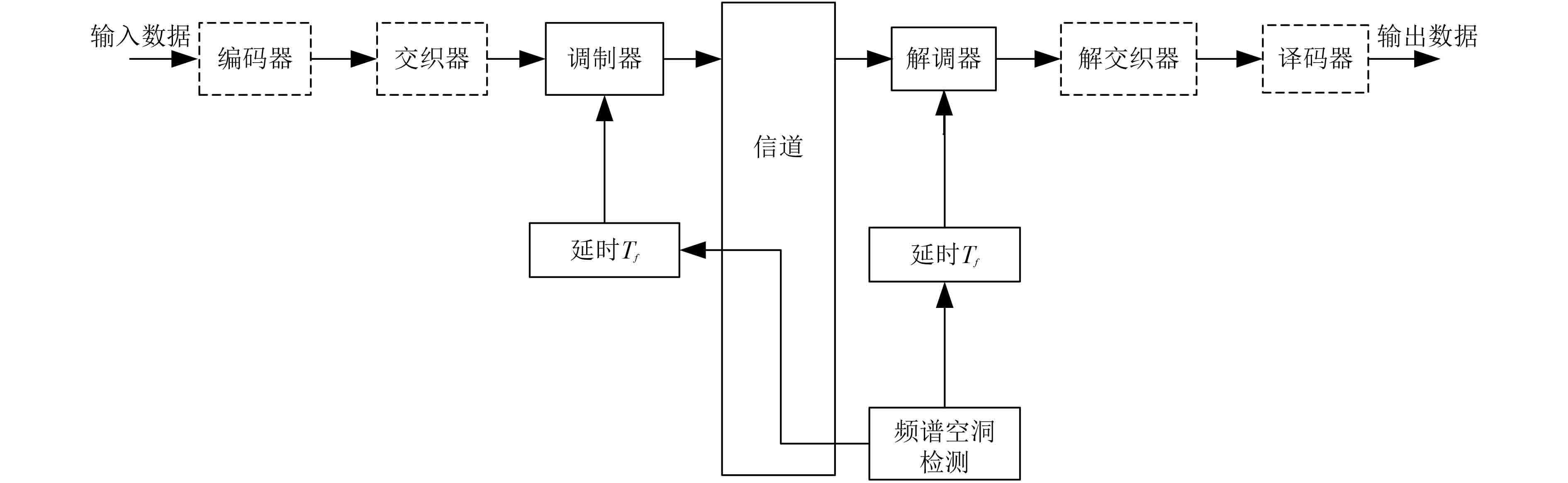
1 DSAJ系统一种简化的DSAJ通信系统框图如图1所示。输入数据经编码及交织后送入调制器。接收端频谱空洞检测单元对通信频段内的频谱空洞进行检测,根据频谱空洞的分布状况确定下一帧所用的发射频率号(个数不确定),并将该信息反馈回发射端(假设信息的反馈过程是无差错的)。调制器则根据反馈回的频率号生成相应的发射载波,并在下一帧持续时间内循环使用,由编码数据对其进行调制。调制波形经信道传输后在接收端进行解调、解交织及译码,从而恢复出发送信息。图中,Tf为每帧持续时间。
|
图 1 DSAJ通信系统简化框图 Fig. 1 Simplified block diagram of a DSAJ communication system |
DSAJ系统采用MFSK调制与非相干解调,其频率结构如下:将系统工作频段划分为Nt个相邻且互不重叠的可用信道,每个信道的带宽等于传输符号的带宽,各信道的中心频率为系统的可用频率集。为了实现MFSK调制,将每M(MFSK调制符号集大小)个相邻的可用信道合并为一个M进制信道。假设系统总带宽中包含K(>1)个M进制信道,则
20世纪80年代,Laycock与Gott等学者提出了短波信道的拥塞度模型[12-13]。该模型将短波信道的背景干扰建模为一个平均功率随机变化的高斯噪声,其干扰平均功率的概率密度函数(Probability Density Function, PDF)为[13]:
| ${p_I}\left( x \right)\; = \frac{{ - B\exp \left( {\alpha + Bx} \right)}}{{{{\left[ {1 + \exp \left( {\alpha + Bx} \right)} \right]}^2}}}\text{。}$ | (1) |
式中:干扰功率x的单位为dBm,α与B为由干扰观测值拟合得到的参数,干扰平均功率的均值
本文的理论分析假设DSAJ系统在频谱空洞检测过程中,实时测量工作频段中K个M进制信道内的干扰平均功率,并将其中干扰平均功率最小的M进制信道作为下一帧使用的频谱空洞。
3 频谱空洞内干扰平均功率的PDF由于频谱空洞是工作频段内干扰平均功率最小的M进制信道,因此空洞内部干扰平均功率的PDF与工作频段内的干扰平均功率PDF(即式(1))并不一致。令K个M进制信道内所测得的干扰平均功率为
| $ {F_Y}\left( y \right) \!=\!1 \!-\! \prod\limits_{i = 1}^K {P\left( {{I_i} \geqslant y} \right)} \!=\! 1 \!-\! \prod\limits_{i = 1}^K {\left[ {1 \!-\! \int_{ - \infty }^y {{p_{{I_i}}}\left( x \right){\rm d}x} } \right]} \text{。} $ | (2) |
为了便于计算,对式(2)进行一些简化。假设所有K个M进制信道内的干扰PDF具有相同的α值,则将式(1)代入式(2),得
| ${F_Y}\left( y \right) = 1 - \frac{1}{{{{\left\{ {1 + \exp \left[ { - \left( {\alpha + By} \right)} \right]} \right\}}^K}}}\text{,}$ | (3) |
将式(3)对y求导,得到Y的PDF为:
| ${p_Y}\left( y \right) = - \frac{{BK\exp \left[ { - \left( {\alpha + By} \right)} \right]}}{{{{\left\{ {1 + \exp \left[ { - \left( {\alpha + By} \right)} \right]} \right\}}^{K + 1}}}}\text{。}$ | (4) |
然而,与式(1)一致,Y的单位依然为dBm。令X为对应于Y的普通形式,则根据dBm的定义,
| ${p_X}\left( x \right) \!=\! \frac{{ - 10BK\exp \left\{ { - \left[ {\alpha \!+\! 10B\left( {3 \!+\! {{\log }_{10}}x} \right)} \right]} \right\}}}{{x\ln 10{{\left\{ {1 \!+\! \exp \left[ { -\! \left( {\alpha \!+\! 10B\left( {3 \!+\! {{\log }_{10}}x} \right)} \right)} \right]} \right\}}^{K + 1}}}}\text{。}$ | (5) |
对编码通信系统而言,分析其精确的BER性能难度很大,实用的分析方法是采用联合界给出系统译码性能的BER上界[14]。联合界是一种渐近上界,随着信噪比的增大,实际BER值以指数率接近联合界。联合界以成对错误概率(Pairwise Error Probability)的计算为基础。成对错误概率
| ${P_s} \leqslant \sum\limits_{d = {d_{free}}}^\infty {{a_d}{P_2}\left( d \right)} \text{。}$ | (6) |
式中:
| ${P_2}\left( d \right) \leqslant \frac{1}{2}{D^d}\text{,}$ | (7) |
式中:D为切尔诺夫参数,它可计算为:
| $\begin{split} D = &\mathop {\min }\limits_{\lambda \geqslant 0} D\left( \lambda \right) = \\ &\mathop {\min }\limits_{\lambda \geqslant 0} E\left\{ {\exp (\lambda \left[ {m\left( {{y_n},{{\hat x}_n};{z_n}} \right) - m\left( {{y_n},{x_n};{z_n}} \right)} \right])\left| x \right.} \right\} \text{。} \end{split} $ | (8) |
式中:xn为发送码字中的一个码元,
限幅度量是当通信系统无法获取精确干扰状态信息时所采用的一种次优译码度量。与文献[6]中的乘积度量以及文献[7]中的噪声归一化度量类似,采用次优译码度量的主要目的是对非相干解调器的输出能量进行限制,从而减小当前通信频率被干扰时的非相干解调器输出能量,降低干扰对译码过程的影响。限幅度量可以表示为[15]:
| $m\left( {r,{f_i}} \right) = \min \left( {{r_i},c{A^2}} \right) \left( {1 \leqslant i \leqslant M} \right)\text{。}$ | (9) |
式中:r为对应于某个码元的非相干解调器输出能量序列,fi为由该码元所确定的发送频率,ri为该频率上的非相干解调器输出能量,
不失一般性,假设实际发送频率为
| $D\left( {\lambda \left| x \right.} \right) = \exp \left\{ {\lambda \left[ {\min \left( {{r_2},c{A^2}} \right) - \min \left( {{r_1},c{A^2}} \right)} \right]\left| x \right.} \right\}\text{,}$ | (10) |
根据
| $\begin{split} D\left( {\lambda \left| x \right.} \right) =& E\left\{ {1\left| {{r_1} \geqslant c{A^2},{r_2} \geqslant c{A^2};x} \right.} \right\} +\\ &E\left\{ {\exp \left[ {\lambda \left( {{r_2} - c{A^2}} \right)} \right]\left| {{r_1} \geqslant c{A^2},{r_2} < c{A^2};x} \right.} \right\} +\\ &E\left\{ {\exp \left[ {\lambda \left( {c{A^2} - {r_1}} \right)} \right]\left| {{r_1} < c{A^2},{r_2} \geqslant c{A^2};x} \right.} \right\} +\\ &E\left\{ {\exp \left[ {\lambda \left( {{r_2} - {r_1}} \right)} \right]\left| {{r_1} < c{A^2},{r_2} < c{A^2};x} \right.} \right\} \text{。}\\[-10pt] \end{split} $ | (11) |
由于短波干扰为高斯噪声,因此给定干扰功率
| ${p_{{R_1}}}\left( {{r_1}\left| x \right.} \right) = \frac{1}{{2x}}{e^{ - \frac{{{r_1} + {A^2}}}{{2x}}}}{I_0}\left( {\frac{{A\sqrt {{r_1}} }}{x}} \right)\text{,}$ | (12) |
及
| ${p_{{R_2}}}\left( {{r_2}\left| x \right.} \right) = \frac{1}{{2x}}{e^{ - \frac{{{r_2}}}{{2x}}}}\text{。}$ | (13) |
式(12)中,
用
| $\begin{split} {D_1}\left( {\lambda \left| x \right.} \right) =& \int_{c{A^2}}^\infty {\frac{1}{{2x}}{e^{ - \frac{{{r_2}}}{{2x}}}}{\rm d}{r_2}} \int_{c{A^2}}^\infty {\frac{1}{{2x}}} {e^{ - \frac{{{r_1} + {A^2}}}{{2x}}}}{I_0}\left( {\frac{{A\sqrt {{r_1}} }}{x}} \right){\rm d}{r_1} =\\ &{e^{ - \frac{{c{A^2}}}{{2x}}}}{Q_1}\left( {\frac{A}{{\sqrt x }},\frac{{\sqrt c A}}{{\sqrt x }}} \right) \text{,} \\[-15pt] \end{split} $ | (14) |
| $\begin{split} {D_2}\left( {\lambda \left| x \right.} \right) =& {e^{ - \lambda c{A^2}}}\int_{c{A^2}}^\infty {\frac{1}{{2x}}} {e^{ - \frac{{{r_1} + {A^2}}}{{2x}}}}{I_0}\left( {\frac{{A\sqrt {{r_1}} }}{x}} \right){\rm d}{r_1}\times\\ &\int_0^{c{A^2}} {{e^{\lambda {r_1}}}} \frac{1}{{2x}}{e^{ - \frac{{{r_2}}}{{2x}}}}{\rm d}{r_2} = {e^{ - \lambda c{A^2}}}{Q_1}\times\\ &\left( {\frac{A}{{\sqrt x }},\frac{{\sqrt c A}}{{\sqrt x }}} \right)\frac{1}{{1 - 2\lambda x}}\left( {1 - {e^{ - \frac{{1 - 2\lambda x}}{{2x}}c{A^2}}}} \right) \text{,} \end{split} $ | (15) |
| $\begin{split} {D_3}\left( {\lambda \left| x \right.} \right) = &{e^{\lambda c{A^2}}}\int_{c{A^2}}^\infty {\frac{1}{{2x}}{e^{ - \frac{{{r_2}}}{{2x}}}}{\rm d}{r_2}} \int_0^{c{A^2}} {{e^{ - \lambda {r_1}}}} \frac{1}{{2x}}\times\\ & {e^{ - \frac{{{r_1} + {A^2}}}{{2x}}}}{I_0}\left( {\frac{{A\sqrt {{r_1}} }}{x}} \right){\rm d}{r_1} \!=\! {e^{ - \frac{{1 - 2\lambda x}}{{2x}}c{A^2}}}\frac{1}{{1 \!+\! 2\lambda x}}{e^{ - \frac{{\lambda {A^2}}}{{1 + 2\lambda x}}}}\!\times\\ &\left[ {1 - {Q_1}\left( {\frac{A}{{\sqrt {x\left( {1 + 2\lambda x} \right)} }},\frac{{A\sqrt {c\left( {1 + 2\lambda x} \right)} }}{{\sqrt x }}} \right)} \right] \text{,} \\[-15pt] \end{split} $ | (16) |
| $\begin{split} {D_4}\left( {\lambda \left| x \right.} \right) =& \int_0^{c{A^2}} {{e^{\lambda {r_2}}}} \frac{1}{{2x}}{e^{ - \frac{{{r_2}}}{{2x}}}}{\rm d}{r_2}\int_0^{c{A^2}} {{e^{ - \lambda {r_1}}}} \frac{1}{{2x}}{e^{ - \frac{{{r_1} + {A^2}}}{{2x}}}}{I_0}\times\\ &\left( {\frac{{A\sqrt {{r_1}} }}{x}} \right){\rm d}{r_1} \!=\! \frac{1}{{1 \!-\! 4{\lambda ^2}{x^2}}}{e^{ - \frac{{\lambda {A^2}}}{{1 \!+\! 2\lambda x}}}}\left( {1 \!-\! {e^{ - \frac{{1 - 2\lambda x}}{{2x}}c{A^2}}}} \right)\!\times\\ & \left[ {1 - {Q_1}\left( {\frac{A}{{\sqrt {x\left( {1 + 2\lambda x} \right)} }},\frac{{A\sqrt {c\left( {1 + 2\lambda x} \right)} }}{{\sqrt x }}} \right)} \right] \text{。} \\[-15pt] \end{split} $ | (17) |
式(14)~(17)中:
| ${Q_1}\left( {a,b} \right) = \int_b^\infty {x{e^{ - \frac{{{x^2} + {a^2}}}{2}}}{I_0}\left( {ax} \right){\rm d}x}\text{。} $ |
根据式(14)~(17)及式(8),切尔诺夫参数
| $D = \mathop {\min }\limits_{\lambda \geqslant 0} \sum\limits_{i = 1}^4 {\int_0^\infty {{D_i}\left( {\lambda \left| x \right.} \right){p_X}\left( x \right){\rm d}x} }\text{,} $ | (18) |
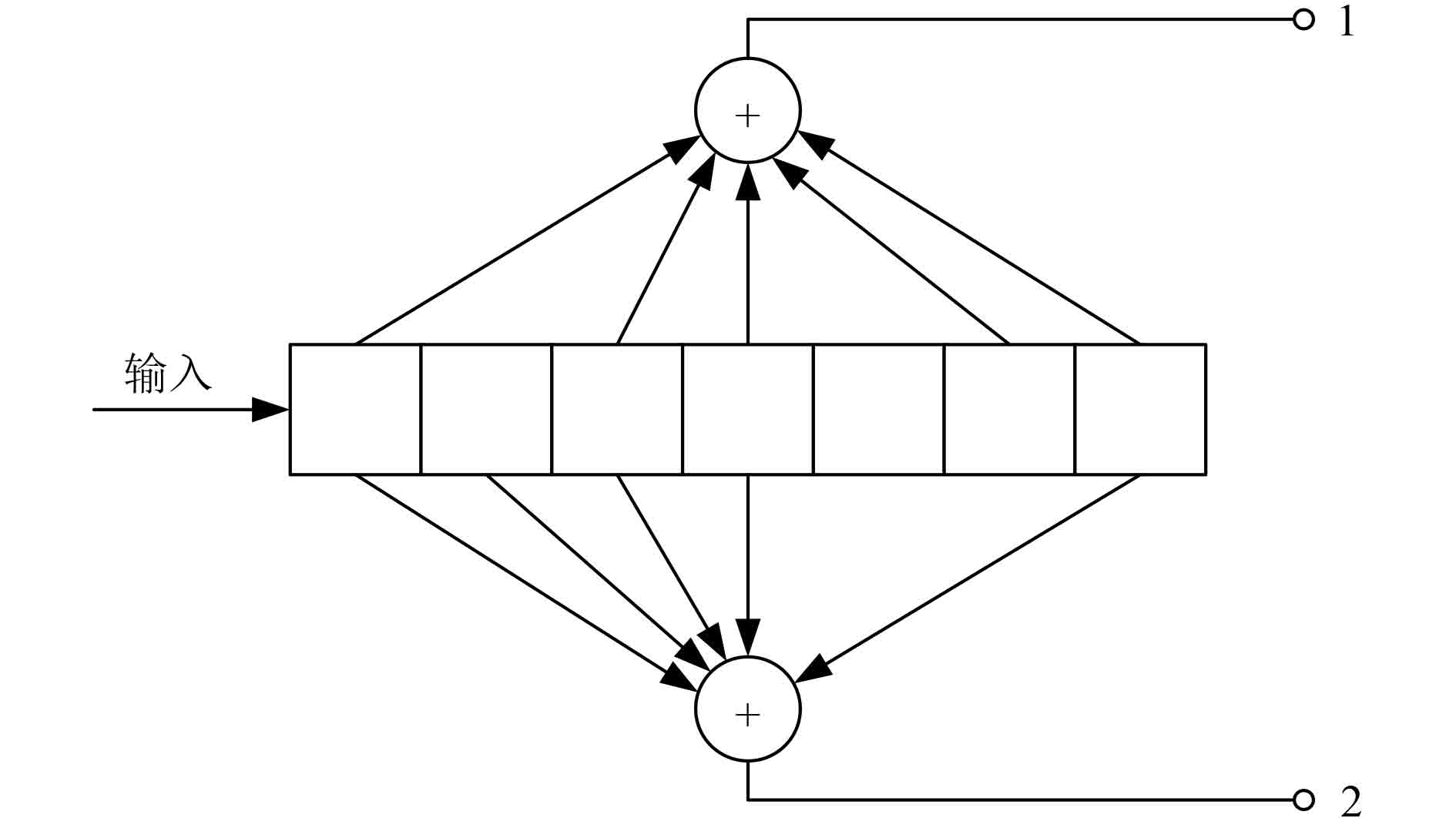
假设DSAJ系统将Odenwalder
| $\begin{split} G\left( D \right) =& \sum\limits_{d = {d_{free}}}^\infty {{a_d}{D^d}} = 36{D^{10}} + 211{D^{12}} + 1404{D^{14}} +\\ & 11633{D^{16}} \!+\! 77433{D^{18}} \!+\! 502690{D^{20}} \!+\!3322763{D^{22}} \!+\\ & 21292910{D^{24}} + 134365911{D^{26}} + \cdots \text{。} \\[-10pt] \end{split} $ | (19) |
其编码器示意图如图2所示。
|
图 2
Odenwalder
|
将式(18)代入式(19),再乘以系数1/2,即可得到短波干扰信道下,采用限幅度量的编码DSAJ系统BER上界。
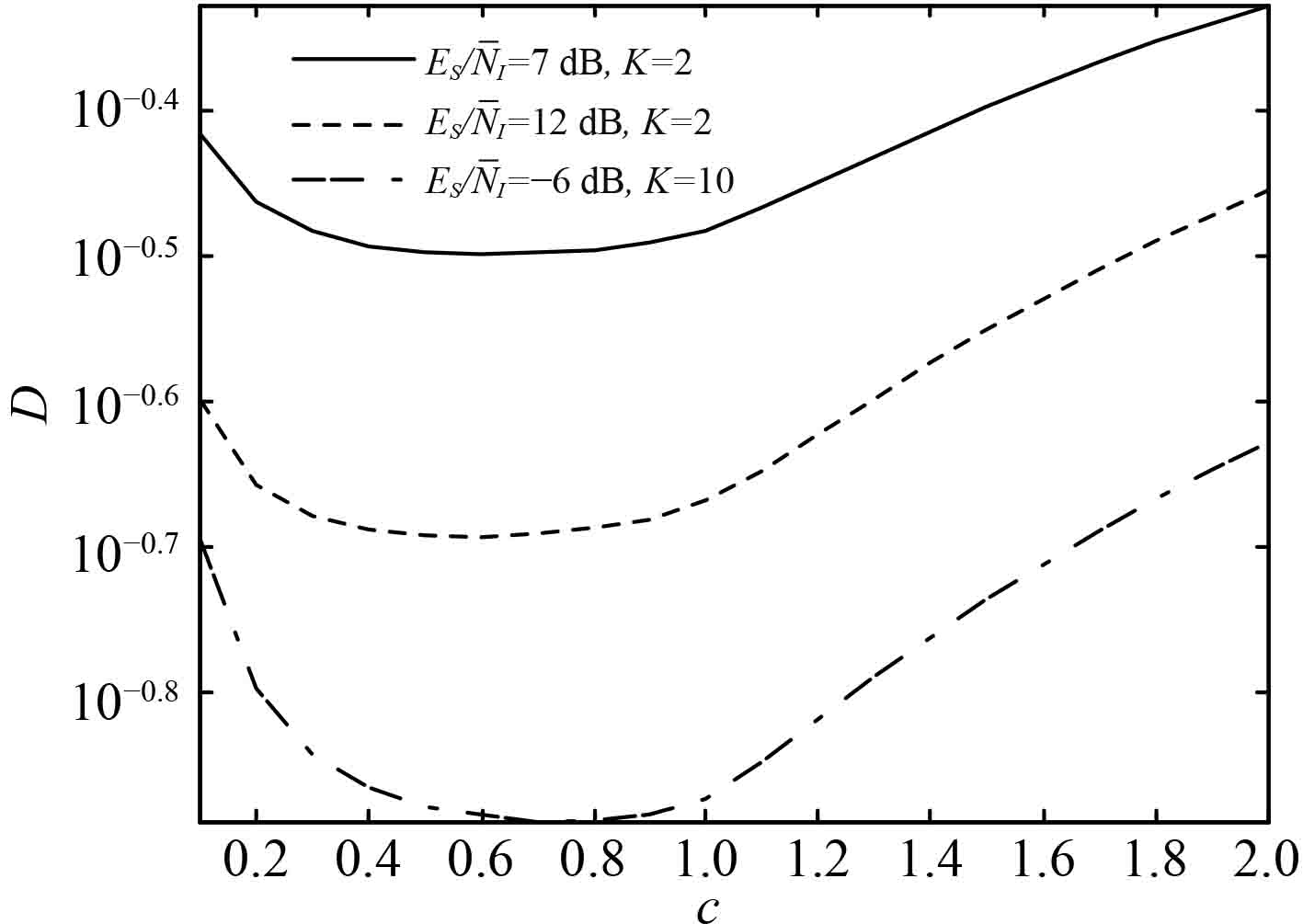
6 数值与仿真结果由式(14)~(17)可见,切尔诺夫参数
|
图 3
对不同的
|
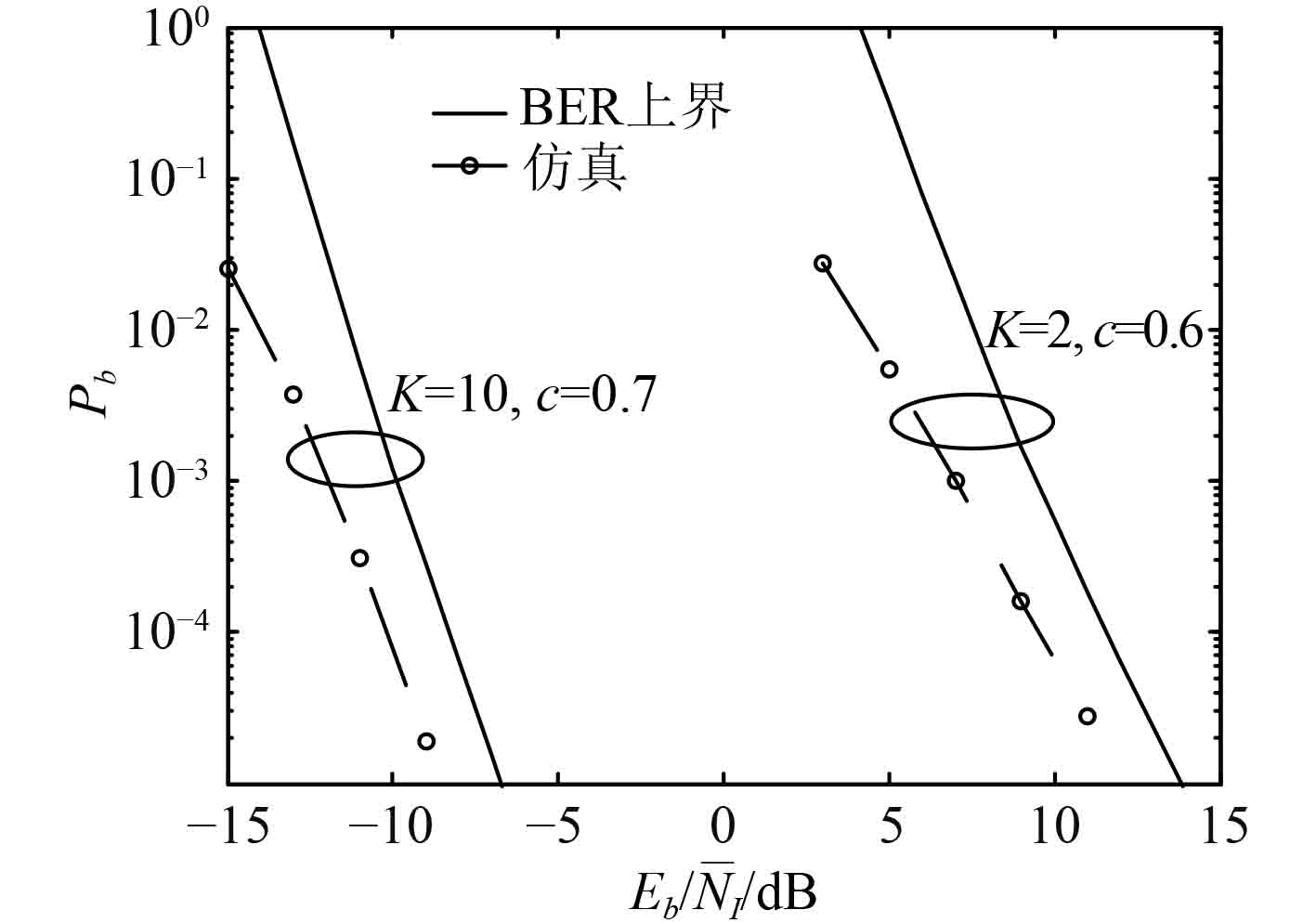
当
|
图 4 采用限幅度量的编码DSAJ系统,在短波干扰信道下的BER性能 Fig. 4 BER performance of a coded DSAJ system using clipped decoding metric, under the HF interference channel |
本文研究基于限幅度量的编码DSAJ系统,在短波干扰信道下的抗干扰性能,并与文献[6]中采用乘积度量的编码DSAJ系统抗干扰性能进行了比较与评估。结果表明,在无精确干扰状态信息的情况下,采用频谱空洞检测与上述两种译码度量相结合的抗干扰策略,可有效筛选出干扰平均功率较低的好信道,同时抑制空洞内随机强干扰对译码过程的影响,实现良好的抗干扰能力。DSAJ是一种智能化的抗干扰通信新体制,具有广阔的应用前景。
| [1] |
陆建勋. 短波自适应通信新体制原理探讨[J]. 舰船无线电通信, 1982(3): 1-8. |
| [2] |
GOLDSMITH A, JAFAR S A, MARIC I, et al. Breaking spectrum gridlock with cognitive radios: an information theoretic Per- spective[J]. IEEE Proceedings, 2009, 97(5): 894-914. DOI:10.1109/JPROC.2009.2015717 |
| [3] |
HAYKIN S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journals on Selected Areas in Communications, 2005, 23(2): 201-220. DOI:10.1109/JSAC.2004.839380 |
| [4] |
陆建勋. 信息对抗与智能无线通信[J]. 现代军事通信, 2012, 20(2): 1-6. |
| [5] |
Y. ZHU. Processing gain of dynamic spectrum anti-jamming systems[C]//Proc. of 7th International Conference on Wireless Communications, Networking and Mobile Computing. Wuhan, China, 2011: 1−4.
|
| [6] |
朱毅超. 动态频谱抗干扰系统的比特误码率分析[C]//军事通信抗干扰研讨会, 2011, 519−524.
|
| [7] |
朱毅超, 陆建勋. 动态频谱抗干扰系统在部分频带干扰下的性能[J]. 电子学报, 2011, 39(10): 2331-2337. |
| [8] |
朱毅超, 王平, 张鑫明, 等. 动态频谱抗干扰系统在多音干扰下的比特误码率[J]. 现代军事通信, 2016, 24(1): 6-10. |
| [9] |
ZHU Yi-chao, GUO Chao, WANG Xiao-xue. Throughput analysis of dynamic spectrum anti-jamming multiple-access in HF communication systems[J]. China Communications, 2018, 15(9): 85-94. DOI:10.1109/CC.2018.8456454 |
| [10] |
ZHU Yi-chao, WANG Ping, LU Jian-xun. A new HF radio prototype based on dynamic spectrum anti-jamming concept[C]//Proc. of CHINACOM’11, Harbin, China, 2011: 1−4.
|
| [11] |
SIMON M K, OMURA J K, SCHOLTZ R A, et al. Spread spectrum communications handbook[M]. 北京: 人民邮电出版社, 2002.
|
| [12] |
GOTT G F, CHAN S K, PANTJIAROS C A, et al. High frequency spectral occupancy at the solstices[J]. IEEE Proceedings on Communications, 1997, 144(1): 24-32. DOI:10.1049/ip-com:19970983 |
| [13] |
BARK G. Performance comparison of spread-spectrum methods on an interference-limited HF channel[J]. IEEE Proceedings on Communications, 1999, 146(1): 23-28. DOI:10.1049/ip-com:19990283 |
| [14] |
PROAKIS J G. Digital communications (4th ed)[M]. 北京: 电子工业出版社, 2001.
|
| [15] |
C. M. KELLER, M. B.. Pursley clipped diversity combining for channels with partial-band interference-Part II: Ratio-statistic combining[J]. IEEE Transactions on Communications, 1989, 37(2): 145-151. DOI:10.1109/26.20082 |
 2021, Vol. 43
2021, Vol. 43
