超短基线(ultra short baseline,USBL)系统是一类基于水声测量技术的定位系统,该类系统由于基阵尺寸小、操作简单、安装使用及维修方便,十分适用于母船对水下目标定位。目前,该类系统已在深水潜堤施工、潜水员作业、港湾水下目标探测、海峡电缆管道铺设、海洋勘探、海洋科学等领域广泛应用[1-4]。
USBL定位系统,一般由应答器、声基阵、母船航姿及定位系统组成。其中,应答器固定安装在水下目标上,其余设备固定安装在母船上。超短基线定位系统通过实时测量水下目标相对于母船的相对位置矢量,再结合母船的实时位置信息,实现对水下目标的精确定位。在实际应用时,声基阵相对于母船的安装偏差是影响该类系统定位精度的一个重要因素[5-6]。一般来说,1°的首向安装偏角将会产生1.7%斜距的定位误差[7],因此,在使用该类系统进行定位之前,必须先对声基阵安装偏差进行校准。
解决超短基线定位系统安装偏差校准问题的基本方法是最小二乘法[8],即通过两组一一对应的观测数据来拟合参数。由于该校准问题的模型是非线性的,因此通常运用循环迭代的思想来求解[9-12]。唐秋华等[9]提出了基于高斯-牛顿法的安装偏差校准算法,该方法的有效性在实际工程应用中不断得到验证[10-11]。杨保国等[12]比较了高斯-牛顿法、牛顿法、最速下降法等各类循环算法的性能,提出了将循环算法与非循环算法相结合的安装偏差求解算法。少数学者还根据一些特定应用背景提出了相应的校准方法,江林等[13]根据工程船施工作业特殊性提出了基于太阳时角法的静态校准方法,Zheng等[14]针对深海长程超短基线系统提出了基于声线跟踪理论的校准方法。
当声速测量值存在固定测量误差时,一般需要通过规划特定的测线轨迹来消除该测量误差的影响[15-16]。这种处理方式相对费时费力,并且还需要母船循迹航行。针对上述应用背景条件,本文引入带约束的最小二乘法进行安装偏差校准,通过在模型上添加适当的系数矩阵,提出一种在声速测量误差条件下的校准方法,并通过仿真验证了本文方法的有效性。
1 超短基线的基本测量原理设

|
图 1 相对位置矢量示意图 Fig. 1 Schematic diagram of relative position vector |
| $\left\{ {\begin{array}{*{20}{c}} {{x_a} = \dfrac{c}{{2{\text{π}} df}}l{\phi _x},}\\ {{y_a} = \dfrac{c}{{2{\text{π}} df}}l{\phi _y},}\\ {{z_a} = \sqrt {{l^2} - {{\left(\dfrac{{cl{\phi _x}}}{{2{\text{π}} df}}\right)}^2} - {{\left(\dfrac{{cl{\phi _y}}}{{2{\text{π}} df}}\right)}^2}} } {\text。}\end{array}} \right. $ | (1) |
其中,坐标
超短基线定位系统的校准工作主要是完成对声基阵安装偏差的估计,其待估计的参数包括声基阵相对于母船基准位置的安装角度偏差和声基阵相对于母船基准位置的安装距离偏差。
超短基线声基阵安装偏差一般采用高斯-牛顿法进行校准。该方法需要2组测量数据,一组是参考基准值,另一组为测量值,这2组数据一般会拟定存在某种对应关系(即数学模型),将这2组数据按照最小二乘准则,完成对模型参数的最优估计。
就超短基线校准问题来说,参考基准值为母船基准位置至应答器的位置矢量
| $p_{OB}^b = p_{OA}^b + {{C}}_u^bp_{AB}^u{\text{。}}$ | (2) |
其中,
这里,参考基准值一般由下式求得:
| $p_{OB}^b = C_n^b(p_{NB}^n - p_{NO}^n){\text{。}}$ | (3) |
其中:
另一方面,参考基准值可根据测量值通过下式进行估计:
| $\hat p_{OB}^b = \hat p_{OA}^b + \hat {{C}}_u^bp_{AB}^u {\text。}$ | (4) |
设估计偏差为
1)带旋转矩阵约束的最小二乘估计法
由参考文献[18]可知,关于带旋转矩阵约束的最小二乘估计法存在如下结论:
引理1
假设m维空间的两组矢量集
| $\left\{ {\begin{array}{*{20}{l}} {{\mu _x} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{x_i}} } {\text,}\\ {{\mu _y} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{y_i}} } {\text,}\\ {\sigma _x^2 = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{\left\| {{x_i} - {\mu _x}} \right\|}^2}} } {\text,}\\ {\sigma _y^2 = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{\left\| {{y_i} - {\mu _y}} \right\|}^2}} }{\text,}\\ {{\displaystyle\sum _{xy}} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {({y_i} - {\mu _y})} {{({x_i} - {\mu _x})}^{\rm{T}}}} {\text,} \end{array}} \right.$ | (5) |
并且设
| $\left\{ {\begin{array}{*{20}{l}} {{\displaystyle\sum _{xy}} = UD{V^{\rm{T}}}{\text,}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ {D\; = {\rm{diag}}({d_i}),\;\;\;{d_1} \geqslant \cdots \geqslant {d_m} \geqslant 0} {\text,} \end{array}} \right.$ | (6) |
则关于变量R,t,c的均方误差函数为:
| ${e^2}({{R}},t,c) = \dfrac{1}{N}\sum\limits_{i = 1}^N {{{\left\| {{y_i} - (c{{R}}{x_i} + t)} \right\|}^2}}{\text,} $ | (7) |
最小值为:
| ${\varepsilon ^2} = \sigma _y^2 - {{tr{{(DS)}^2}} / {\sigma _x^2}}{\text,}$ | (8) |
并且当
| $\left\{ {\begin{array}{*{20}{c}} {{{R}} = US{V^{\rm{T}}}{\text,}\;\;\;\;\;\;\;\;\;} \\ {t = {\mu _y} - c{{R}}{\mu _x}{\text,}\;\;} \\ {c = {{tr{{(DS)}^2}} / {\sigma _x^2}}} {\text{。}} \end{array}} \right.$ | (9) |
其中:
| $S = \left\{ {\begin{array}{*{20}{c}} {I\;,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\det \left({\displaystyle\sum _{xy}}\right) \geqslant 0} {\text,}\\ {{\rm{diag}}(1,1, \cdots ,1, - 1)\;,\;\;\det \left({\displaystyle\sum _{xy}}\right) < 0}{\text。} \end{array}} \right.$ | (10) |
为方便起见,以下将该方法简称为带约束的最小二乘法。事实上,该方法已在水下航行器声学多普勒计程仪安装偏差的在线校准问题上得到了实际应用[19-20]。
2)安装偏差的校准思路
根据引理1可知,要估计2组矢量之间的变换参数,先要知道2组矢量的观测值以及矢量之间的对应关系或者模型,然后才能应用该引理求解。
在超短基线系统校准问题中,具体求解思路可总结为:
首先,超短基线量测矢量组
其次,参考基准矢量组
然后,将2组观测矢量之间的对应关系设定为
最后,定义
当声速测量存在固定测量偏差(以下简称固定声速误差)时,2组观测值
下面通过分析固定声速误差对超短基线相对位置矢量测量值的影响,给出在该条件下的校准方法。
1)固定声速误差的影响分析
设
| $ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{x^*}}}{{\tilde x}} = \dfrac{{\tilde x - \left( {{{\left. {\dfrac{{\partial p_{AB}^u}}{{\partial c}}(1)} \right|}_{c = \tilde c}}} \right)\Delta c}}{{\tilde x}} = 1 - \dfrac{{2 \cdot \Delta c}}{{\tilde c}}} {\text,}\\ {\dfrac{{{y^*}}}{{\tilde y}} = \dfrac{{\tilde y - \left( {{{\left. {\dfrac{{\partial p_{AB}^u}}{{\partial c}}(2)} \right|}_{c = \tilde c}}} \right)\Delta c}}{{\tilde y}} = 1 - \dfrac{{2 \cdot \Delta c}}{{\tilde c}}} {\text,}\\ {\dfrac{{{z^*}}}{{\tilde z}} = \dfrac{{\tilde z - \left( {{{\left. {\dfrac{{\partial p_{AB}^u}}{{\partial c}}(3)} \right|}_{c = \tilde c}}} \right)\Delta c}}{{\tilde z}} = 1 - \left( {1 - \dfrac{1}{{2{{\cos }^2}{\theta _z}}}} \right)\dfrac{{2 \cdot \Delta c}}{{\tilde c}}} {\text{。}} \end{array} } \right.$ | (11) |
其中,
若将
2)处理方法及校准思路
由于固定声速误差对相对位置矢量测量值的x轴和y轴分量的影响是一致的,故考虑将z轴分量的测量值乘以系数
设
| $m = \dfrac{{1 - \left( {1 - \dfrac{1}{{2{{\cos }^2}{\theta _z}}}} \right)\dfrac{{2 \cdot \Delta c}}{{\tilde c}}}}{{1 - \dfrac{{2 \cdot \Delta c}}{{\tilde c}}}}{\text,}$ | (12) |
显然该系数是时变的,其实时估计值为:
| $\hat m = \dfrac{{1 - \left( {1 - \dfrac{1}{{2{{\cos }^2}{\theta _z}}}} \right)\dfrac{{2 \cdot \Delta \hat c}}{{\tilde c}}}}{{1 - \dfrac{{2 \cdot \Delta \hat c}}{{\tilde c}}}}{\text。}$ | (13) |
其中,
从而,当声速测定存在固定偏差时,可以将两组观测值
在实际求解时,令
因此,声速测量误差条件下的超短基线安装偏差校准步骤可归纳为:
1)获取2组观测值
2)根据尺度因子
3)将
4)根据
5)针对矢量集
设母船在水面航行,初始点位置为n系的坐标原点,应答器三维坐标位置为(0 m,20 m,20 m),母船绕应答器航行的轨迹如图2所示。假设DGPS和USBL的数据采样频率均为1 Hz,数据采样总数为400对。
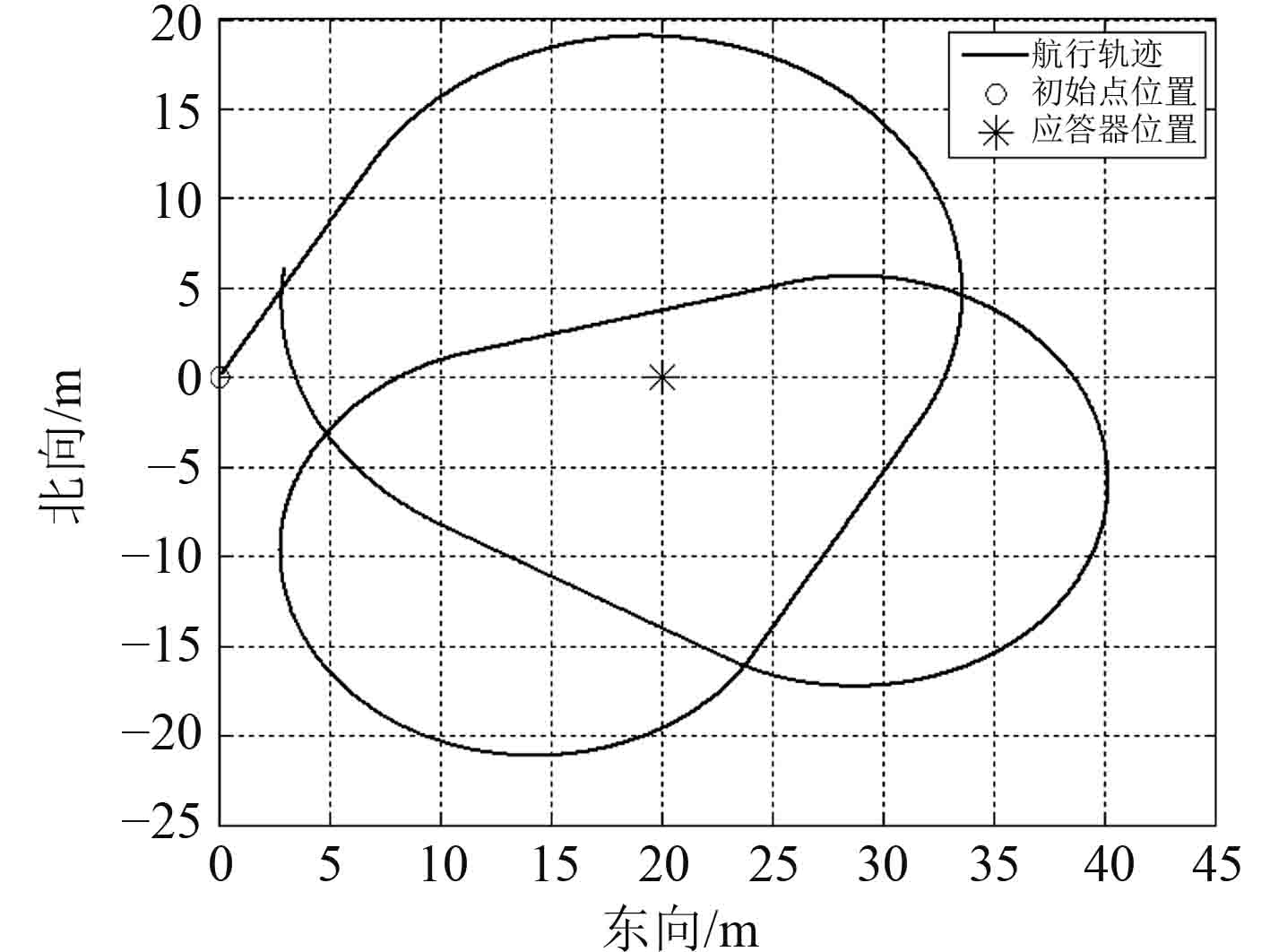
|
图 2 航行轨迹图 Fig. 2 Navigation trajectory |
假设安装角度偏差为(3°,2°,5°),安装位置偏差为(–1 m,0 m,1 m);设DGPS的随机测量误差服从高斯分布N(0,0.12),USBL相对位置矢量的随机测量误差服从N(0,0.12)和N(0,r2)的高斯混合分布,其中后者以0.05的概率出现,这里误差标准差的单位为m;设定声速真值为1500 m/s。若将r≥0.3作为存在测量粗差的判据(即认为在r=0.1时无测量粗差),则可以通过调节r来改变测量粗差的大小。
假设高斯-牛顿法的角度偏差、角度修正量、距离偏差、距离修正量的迭代初值均置零,设定迭代次数为8次,设4对样本点分别为第100对、第150对、第250对和第300对。
为方便起见,下面将存在固定声速误差情形下的校准方法称为抗固定声速误差法。
1)仿真实验1
本实验为抗粗差能力测试,假设不存在固定声速测量误差。
在抗粗差能力方面,经过多次仿真后发现,当相对位置矢量无测量粗差(对应r=0.1)时,高斯-牛顿法、带约束最小二乘法和抗固定声速误差法的校准精度相当;当相对位置矢量存在测量粗差(对应r=1),特别是在上述4对样本点中含有粗差时,高斯-牛顿法的校准结果将出现较大偏差,如表1所示。然而,粗差的出现对带约束最小二乘法和抗固定声速误差法的校准结果的影响相对较小。可见,带约束最小二乘法和抗固定声速误差法都具有一定的抗粗差能力。
|
|
表 1 在不同相对位置矢量测量误差情形下,不同方法的校准结果 Tab.1 Calibration results of different methods under different relative position vector measurement errors |
2)仿真实验2
本实验为抗固定声速测量误差能力测试,假设USBL相对位置矢量无测量粗差。
在抗固定声速测量误差能力方面,考虑到固定声速误差会使校准结果产生系统误差,为研究这种系统误差,特意针对不同的声速误差,分别进行100次仿真模拟,然后将校准结果求平均,得到不同声速测量误差条件下的校准结果。
首先,根据仿真结果可知,在不存在固定声速测量误差的条件下,3种校准方法的校准精度相当;当出现10 m/s(或–10 m/s)的固定声速误差时,高斯-牛顿法和带约束最小二乘法的校准结果均受到一定的影响,然而抗固定声速误差法的校准结果基本不受声速测量误差的影响,如表2所示。
|
|
表 2 在不同固定声速测量误差条件下,不同方法的校准结果 Tab.2 Calibration results of different methods under different fixed sound velocity measurement errors |
其次,若将角度校准的误差定义为角度校准结果向量与安装角度偏差向量的矢量差向量的模,将距离校准的误差定义为距离校准结果向量与安装距离偏差向量的矢量差向量的模,将角度校准的误差和距离校准的误差统称为校准误差,则根据仿真结果可知,当出现一定的固定声速误差时(见图3),固定声速误差对高斯-牛顿法和带约束最小二乘法的影响相对较大,校准误差随着声速测量误差的增大而逐渐增大,而固定声速误差对抗固定声速误差法的影响相对较小。
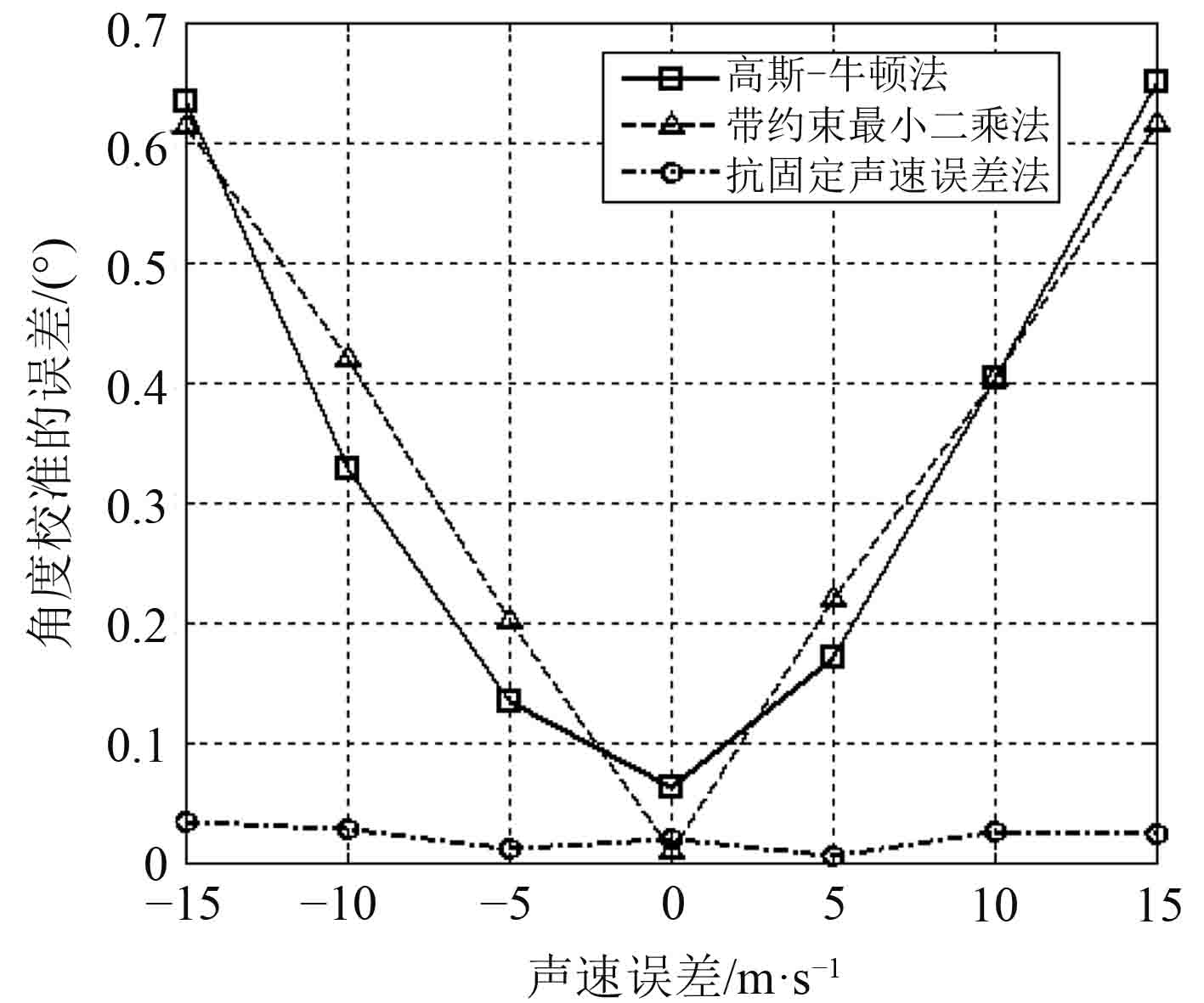
|
图 3 校准误差随声速误差的变化曲线 Fig. 3 Curve of calibration error versus sound velocity error |
由此可见,抗固定声速误差法具有一定的抗固定声速测量误差的能力。
4 结 语1)针对超短基线安装偏差的校准问题,提出应用带约束的最小二乘法来进行校准。仿真结果表明,该校准方法适用于求解超短基线安装偏差校准问题,并且具有一定的抗粗差能力。
2)在上述校准方法的基础上。仿真结果表明,该方法具有一定的抗粗差能力和抗固定声速测量误差能力,因此,该方法适用于存在固定声速测量误差的情况。
本文的校准方法是以声线为直线传播为前提的,适用于声速变化范围较小的应用场景(比如浅水区)。若用于声速变化范围较大的应用场景(如深水区甚至深海),且声线的初始掠射角偏小,则会导致声线严重弯曲,本文方法不再适用。这里有一种应对思路可供参考:尽量缩小母船的绕行半径,进而缩小与应答器的水平距离,以增大初始掠射角,降低声线弯曲程度,使声线接近直线,以便运用本文方法求解。
| [1] |
石峰. 深水潜堤施工的水下定位与检测技术探讨[J]. 中国港湾建设, 2015, 35(12): 62-65. |
| [2] |
吴军华. 潜水员水下作业安全监测系统[D]. 厦门:厦门大学, 2018.
|
| [3] |
杨立文, 焦永强, 徐健. 基于超短基线的侧扫声呐水下目标定位技术[J]. 中国港湾建设, 2017, 37(3): 6-9. |
| [4] |
金博楠, 徐晓苏, 张涛, 等. 超短基线定位技术及在海洋工程中的应用[J]. 导航定位与授时, 2018, 5(4): 8-20. |
| [5] |
刘文勇, 江林, 钱立兵, 等. 超短基线水下定位校准方法的探讨与分析[J]. 测绘通报, 2011(1): 82-84+93. |
| [6] |
汪志明, 田春和. 超短基线系统水下定位误差分析[J]. 测绘信息与工程, 2010, 35(6): 30-31. |
| [7] |
郑翠娥, 孙大军, 张殿伦, 等. 超短基线声学定位系统安装误差精确校准[J]. 哈尔滨工程大学学报, 2007, 28(8): 894-898. DOI:10.3969/j.issn.1006-7043.2007.08.012 |
| [8] |
OPDERBECKE J. At-sea calibration of a USBL underwater vehicle positioning system[C]// OCEANS '97. MTS/IEEE Conference Proceedings. IEEE, 1997.
|
| [9] |
唐秋华, 吴永亭, 丁继胜, 等. 超短基线定位系统的校准技术研究[J]. 声学技术, 2006, 25(4): 281-287. DOI:10.3969/j.issn.1000-3630.2006.04.003 |
| [10] |
YU Min. In-situ calibration of transceiver alignment for a high-precision USBL system[C]// 2010 International Conference on Computer Application and System Modeling. Taiyuan, China: IEEE, 2010.
|
| [11] |
王德刚, 韩富江, 来向华, 等. 超短基线定位原理及校正方法研究[J]. 海洋科学, 2011, 35(2): 77-81. |
| [12] |
杨保国, 郑翠娥, 张殿伦, 等. 非线性参数估计在超短基线安装校准中的应用[J]. 哈尔滨工程大学学报, 2010, 31(7): 915-919. DOI:10.3969/j.issn.1006-7043.2010.07.016 |
| [13] |
江林, 刘文勇, 陈俊明, 等. 太阳时角法在超短基线静态校准中的应用[J]. 测绘科学, 2016, 41(2): 154-157. |
| [14] |
ZHENG C, LI Z, SUN D. Study on the calibration method of USBL system based on ray tracing[C]//2013 OCEANS-San Diego. IEEE, 2013: 1-4.
|
| [15] |
李昭, 郑翠娥, 孙大军. 超短基线声传感器安装偏差标定测线规划[J]. 系统工程与电子技术, 2016, 38(5): 1010-1016. DOI:10.3969/j.issn.1001-506X.2016.05.07 |
| [16] |
LI Z, ZHENG C, SUN D. Track analysis and design for ultra short baseline installation error calibration[C]//2013 OCEANS-San Diego. IEEE, 2013: 1−5.
|
| [17] |
赵琳, 杨晓东, 程建华, 等. 现代舰船导航系统[M]. 北京: 国防工业出版社, 2015.
|
| [18] |
Shinji Umeyama. Least-squares estimation of transformation parameters between two point patterns[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1991, 13(4): 376-380. DOI:10.1109/34.88573 |
| [19] |
KINSEY J C, WHITCOMB L L. In situ alignment calibration of attitude and Doppler sensors for precision underwater vehicle navigation: theory and experiment[J]. IEEE Journal of Oceanic Engineering, 2007, 32(2): 286-299. DOI:10.1109/JOE.2007.893686 |
| [20] |
TRONI G, WHITCOMB L L. Advances in in situ alignment calibration of Doppler and high/low-end attitude sensors for underwater vehicle navigation: theory and experimental evaluation[J]. Journal of Field Robotics, 2015, 32(5): 655-674. DOI:10.1002/rob.21551 |
 2021, Vol. 43
2021, Vol. 43
