0 引　言

波束形成技术是阵列信号处理的关键技术之一，在雷达、声呐信号处理领域有着广泛的应用。在主动声呐阵列信号处理中，常规波束形成方法（CBF）主瓣较宽、旁瓣较高，空间分辨力的不足导致CBF对多目标、弱目标的检测性能不足。自适应波束形成方法拥有较高的空间分辨力，在多目标和弱目标检测上体现了良好的性能，因此研究自适应检测方法具有重要的意义^[1]。

MVDR^[2]是已经较为成熟的一种自适应波束形成方法，传统MVDR方法为频域MVDR，其缺陷是需要较长的数据长度进行累积来保证最优权向量^[2]的稳定估计。文献[3]提到时域MVDR方法TMVDR，该方法在构造时域解析信号的基础上，对每一路时域解析信号引入复权，提高了MVDR最优权向量估计的稳定性。但在大孔径主动声呐信号处理的应用环境中，回波信号脉宽较短、有效快拍次数较少以及阵列可能存在的阵型失配等问题，必然会使MVDR滤波器的最优权向量估计存在误差，最终导致其输出功率失真，降低了MVDR的工程实用价值。本文在TMVDR的基础上加入了误差恒定和功率恒定2个约束条件^[4-5]，实现了一种双约束条件的时域MVDR自适应波束形成方法DCTMVDR（Double constraint Time-domain MVDR），本方法对原本MVDR无约束的最优权输出进行了误差恒定和功率恒定的约束补偿，在保证较高空间分辨率的同时有效解决了MVDR在恶劣环境下性能下降的问题，提高了算法鲁棒性。同时本方法的协方差矩阵估计采用对角加载法^[6]，增加了协方差矩阵的稳定性，进一步减少误差。本方法可以在单个快拍下实现最优权向量的稳定估计，在实际工程中也能体现出较好的性能。

1 TMVDR原理及主动处理的应用

假设主动声呐M个阵元接受到的时域数据为：

$X(n) = {[{x_1}(n),{x_2}(n), \cdots ,{x_M}(n)]^{\rm{T}}}{\text，}$

(1)

其中， $n = 1,2, \cdots ,N$ 表示时间采样点， $N$ 表示一个处理拍快的数据长度。

假设 $m = 1,2, \cdots ,M$ 为阵元序号，第m路阵元时域数据可以表示为：

${x_m}(n) = {s_m}(n) + {v_m}(n){\text，}$

(2)

其中， ${v_m}(n)$ 表示噪声， ${s_m}(n)$ 表示期望信号：

${s_m}(n) = \left\{ {\begin{split} & {Aa \text{，}}{{n_0} \leqslant n \leqslant {n_0} + {N_a}} {\text{，}} \\ & 0 {\text{，}}{n < {n_0},n > {n_0} + {N_a}} {\text{，}} \end{split}} \right.$

(3)

其中，A表示信号幅值， ${n_0}$ 表示回波信号到达时间点， ${N_a}$ 表示发射信号脉宽长度， $a$ 表示发射信号：

$a = {[a(1),a(2), \cdots ,a({N_a})]^{\rm{T}}}{\text，}$

(4)

对 ${x_m}(n)$ 做Hilbert变换，得到：

${\bar x_m}(n) = {\bar s_m}(n) + {\bar v_m}(n){\text，}$

(5)

其中， ${\bar x_m}(n) = H({x_m}(n))$ ， ${\bar s_m}(n) = H({s_m}(n))$ ， ${\bar v_m}(n) = $ $ H({v_m}(n))$ 。

第m阵元信号的时域数据构造时域解析信号如下：

$ {f}_{m}(n)={x}_{m}(n)+j \cdot {\overline{x}}_{m}(n){\text，}$

(6)

以 $a$ 作为匹配信号对 ${f_m}(n)$ 进行相关估计得到：

${y_m} = {f_m}^ * \odot a{\text，}$

(7)

其中，*表示共轭， $ \odot $ 表示Hadamard积。

则可得到阵列相关检测输出：

$Y(n) = {[{y_1}(n),{y_2}(n), \cdots ,{y_M}(n)]^{\rm{T}}}{\text，}$

(8)

计算本次快拍下相关检测输出的协方差矩阵：

${{R}} = \frac{1}{N}\sum\limits_{n = 1}^N {Y(n)Y_{}^H(n)} {\text，}$

(9)

其中，R为M×M矩阵。

假设TMVDR滤波器的权矢量为 $w$ ，则其输出可表示为：

$Z = w_{}^{\rm{H}}Y(n){\text，}$

(10)

其中，H表示共轭转置。

TMVDR的约束问题表达式^[3]如下：

$\min \{ {w^H}Rw\} \;\;\;s.t.\;\;\;{w^H}I = 1 {\text，}$

(11)

其中，I表示 $M \times 1$ 维单位向量。

用拉格朗日乘数法求解式（11）可解得TMVDR滤波器的最优权矢量：

${w_{opt}} = \frac{{{I^T}R_{}^{ - 1}}}{{{I^T}R_{}^{ - 1}I}}{\text，}$

(12)

代入式（10）则可得到TMVDR滤波器的最优权向量：

${{{Z}}_{opt}} = w_{opt}^HY(n){\text。}$

(13)

需要注意的是由于协方差矩阵的估计很难得到满秩且稳定的 $M \times M$ 维矩阵，采用对角加载方法可以缓解这一问题。

2 DCTMVDR原理

假设式（12）中的期望值为单位向量I，当协防差矩阵 ${{R}}$ 的估计产生误差时则必然使得输出的权矢量不是最优值，导致性能下降。

假设存在一个补偿权向量 $b$ ，对 $R$ 进行误差补偿后可以使 ${w_{opt}}$ 的输出达到最优。以 $\bar b = I$ 作为期望值，则以 ${\left\| {b - I} \right\|^2} \leqslant \varepsilon $ 视为误差上限为 $\varepsilon $ 的误差恒定约束条件，以 ${\left\| b \right\|^2} = M$ 视为能量恒定约束条件，因此DCTMVDR的优化问题可归纳为如下表达式：

$\begin{split} \min \{ {b^H}R_m^{ - 1}b\} &,{\rm{s.t.}}{\left\| {b - I} \right\|^2} \leqslant \varepsilon , \\ &{\left\| b \right\|^2} = M {\text。} \end{split} $

(14)

其中： $\varepsilon $ 代表 $b$ 与I之间误差范围。我们将给定误差范围的 $b$ 的值域视为一个以I为圆心、半径为 $\sqrt \varepsilon $ 的球体，DCTMVDR的原理可以表示为搜索该球体以寻找一个同时满足2个约束条件的理想值 $\hat b$ 使得算法输出权向量 ${w_{opt}}$ 的值为最优。

在不考虑第二约束条件 ${\left\| b \right\|^2} = M$ 的前提下，利用拉格朗日算法求解式（14），可以得到单约束条件下的解：

${\hat b_0} = {{I}} - {({{{I}}_{M \times M}} + \lambda R_{}^{ - 1})^{ - 1}}{{I}}{\text，}$

(15)

其中： ${I_{M \times M}}$ 为单位对角阵。则结合约束条件一 ${\left\| {b - I} \right\|^2} \leqslant $ $ \varepsilon $ ，可得到 $\lambda $ 的函数 $g(\lambda )$ ：

$g(\lambda ) = {\left\| {{{({{{I}}_{M \times M}} + \lambda R)}^{ - 1}}{{I}}} \right\|^2} = \varepsilon {\text，}$

(16)

对 ${{R}}$ 进行特征值分解，可以得到：

${{R}} ={{ U}}\varLambda {{{U}}^H}{\text{。}}$

(17)

其中 $\Lambda $ 表示由特征值构建的对角矩阵，其中特征值按从大到小排序，即 ${\gamma _1} > {\gamma _2}\cdots > {\gamma _M}$ ， ${{U}}$ 表示对应各个特征值的特征向量矩阵。令 $z = {{{U}}^H}{{I}}$ ，则式（16）可化简为：

$g(\lambda ) = \sum\limits_{m = 1}^M {\frac{{{{\left| {{z_m}} \right|}^2}}}{{{{(1 + \lambda {\gamma _m})}^2}}} = \varepsilon } {\text，}$

(18)

利用式（18）可求得 $\lambda $ 。需要注意的是，因为 ${\left\| I \right\|^2} > \varepsilon $ ，所以由式（16）可得到 $g(\lambda )$ 是 $\lambda $ 的单调递减函数，且 $g(0) > \varepsilon $ ，故 $\lambda \ne 0$ 。由式（18）得到 $\mathop {\lim }\limits_{\lambda \to \infty } g(\lambda ) = $ $ 0 < \varepsilon $ ，可知对于式（18）存在 $\lambda $ 的唯一解（ $\lambda > 0$ ）。由排列方式可知 ${\gamma _M}$ ， ${\gamma _1}$ 分别为特征值 $\gamma $ 的最小值和最大值，由式（18）可解得 $\lambda $ 取值范围的上下界。去掉式（18）分母中的1，可以得到 $\lambda $ 的另一个上界，故 $\lambda $ 取值范围为：

$\frac{{\left\| I \right\| - \sqrt \varepsilon }}{{{\gamma _1}\sqrt \varepsilon }} \leqslant \lambda \leqslant \min \left\{ {{{\left( {\frac{1}{\varepsilon }\sum\limits_{m = 1}^M {\frac{{{{\left| {{z_m}} \right|}^2}}}{{\gamma _M^2}}} } \right)}^{\frac{1}{2}}},\frac{{\left\| I \right\| - \sqrt \varepsilon }}{{{\gamma _M}\sqrt \varepsilon }}} \right\}{\text，}$

(19)

利用拉格朗日算法求解式（14），可以得到双约束条件下的最优解：

$\hat b = \left(M - \frac{\varepsilon }{2}\right)\frac{{{{\left(\dfrac{{R_{}^{ - 1}}}{\lambda } + {I_{M \times M}}\right)}^{ - 1}}I}}{{{I^T}{{\left(\dfrac{{R_{}^{ - 1}}}{\lambda } + {I_{M \times M}}\right)}^{ - 1}}I}}{\text，}$

(20)

将式（18）得到的 $\lambda $ 代入得到DCTMVDR的理想补偿值 $\hat b$ 。

则DCTMVDR滤波器的最优权矢量可以表示为：

${w_{DCTMVDR}} = \frac{{\hat b_{}^HR_{}^{ - 1}}}{{\hat b_{}^HR_{}^{ - 1}{{\hat b}_{}}}}{\text，}$

(21)

DCTMVDR滤波器的最优输出可以表示为：

${Z_{DCTMVDR}} = w_{DCTMVDR}^HY(n){\text{。}}$

(22)

3 数值仿真验证

通过数值仿真进行阵列输出数据模拟，分别在理想条件和阵型失配条件下，对CBF，TMVDR和DCTMVDR三种方法进行比较，验证DCTMVDR的有效性。

1）理想条件下的波束响应

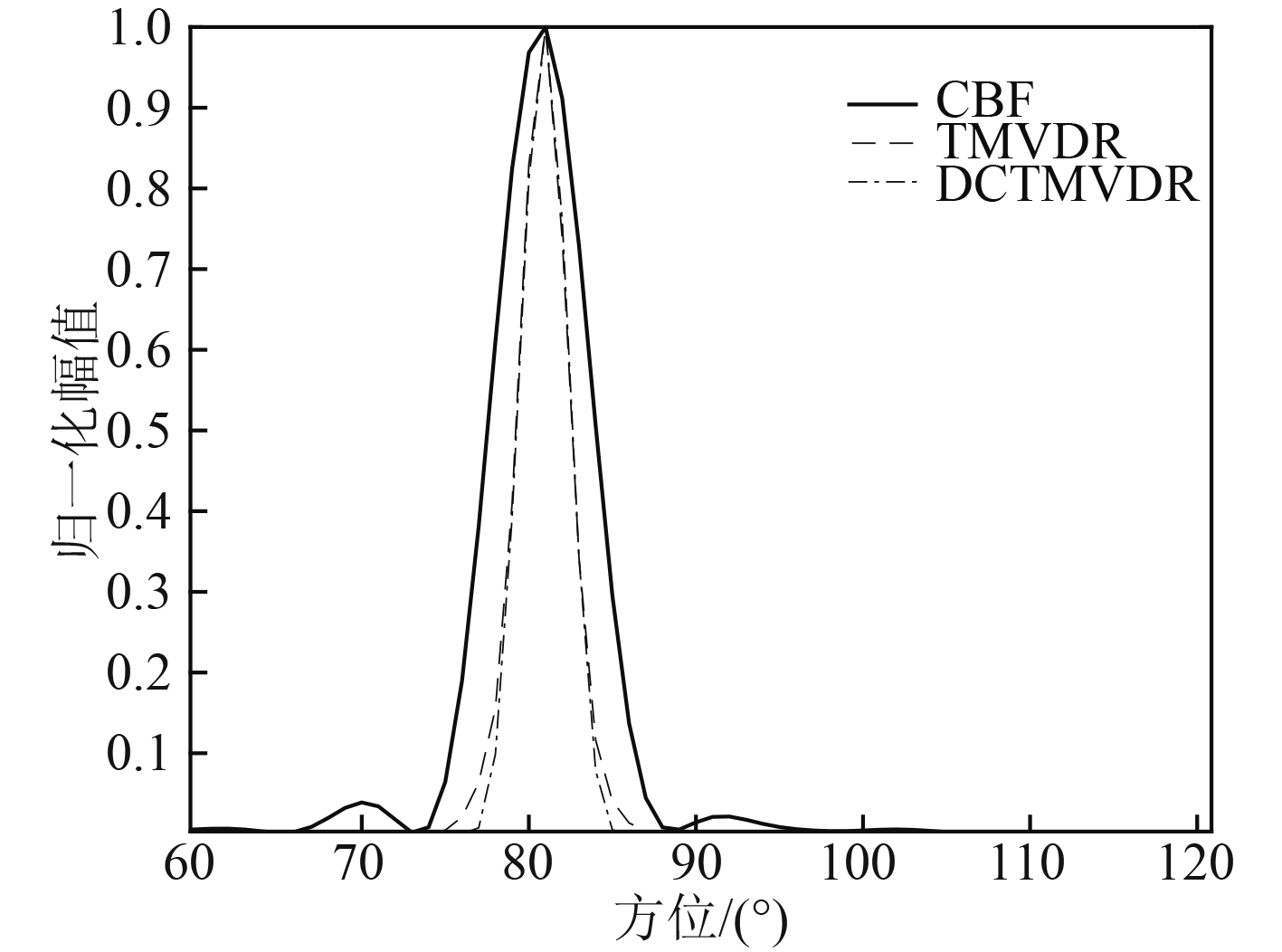
仿真条件：进行32元等间距线阵数据模拟，发射信号模拟频率为1.2 kHz的调频信号，带宽为500 Hz，脉宽为0.2 s，采样率为15 kHz，仿真单个目标回波，目标方位81°，输入信噪比30 dB。

图1仿真结果表明，在理想条件下，相比较与CBF，TMVDR和DCTMVDR拥有更好的空间分辨力和较低的旁瓣级。而TMVDR和DCTMVDR体现的性能基本相同，其中DCTMVDR的旁瓣级略低于TMVDR。

2）阵型失配条件下的波束响应

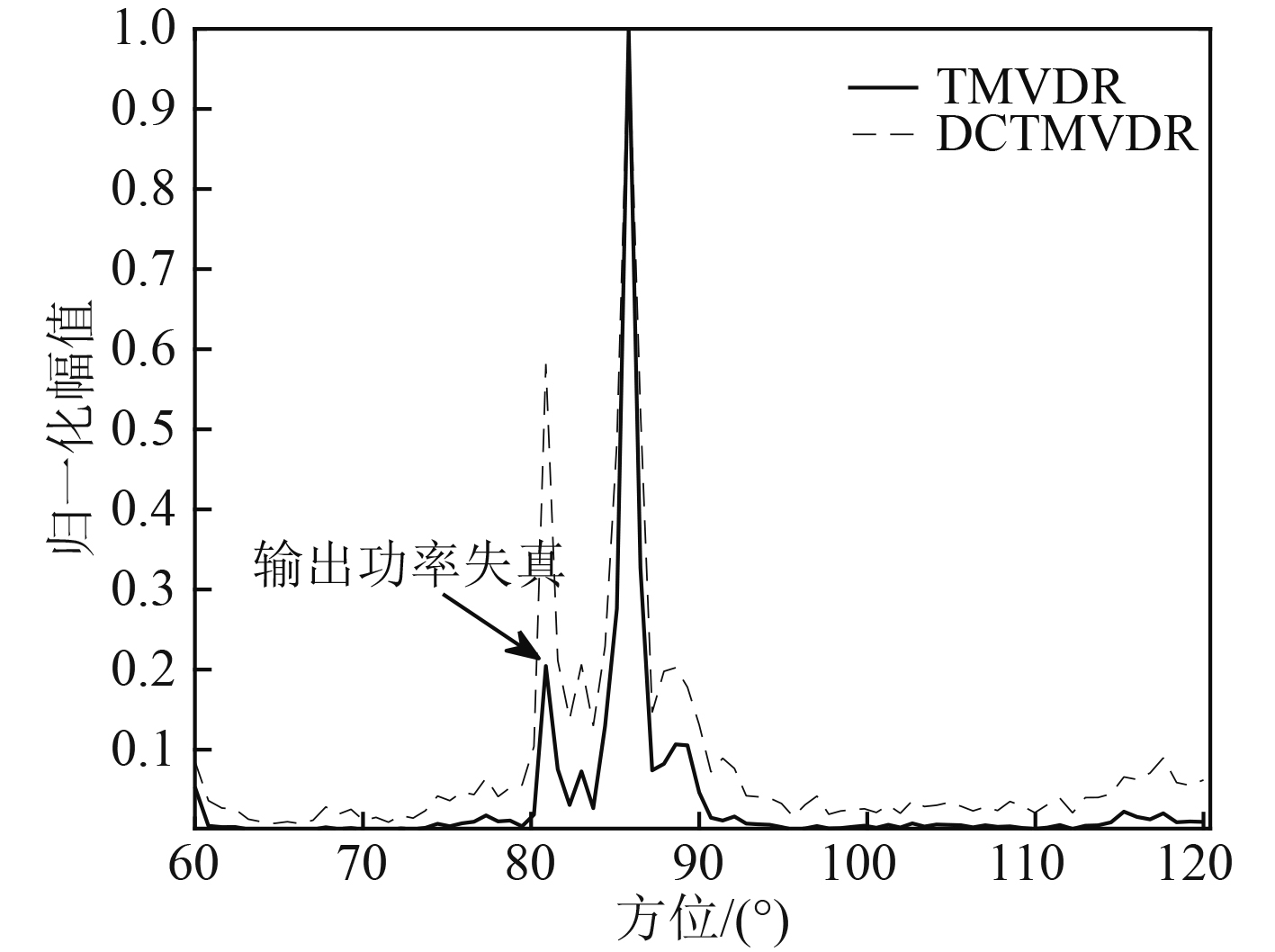
仿真条件：进行80元等间距线阵数据模拟，发射信号模拟频率为2.5 kHz的调频信号，带宽为500 Hz，脉宽为0.2 s，采样率为15 kHz，仿真2个目标回波，目标1方位81°，输入信噪比10 dB，目标2方位86°，输入信噪比15 dB。进行阵型失配模拟，在每个通道加入随机的相位扰动。

图2仿真结果表明，在条件恶劣的情况下，TMVDR会发生输出功率失真的现象，相比之下DCTMVDR输出功率稳定，在保证输出能量不失真的前提下提高了时间分辨率，体现了最优的性能。

4 实验数据分析

选取某型号大型拖线阵声呐实验数据中的1个数据段作为数据分析样本。通过对CBF，TMVDR和DCTMVDR三种方法进行性能比较，验证DCTMVDR的有效性。

实验数据说明，选用实验数据中某一周期数据，该段数据处于阵型轻微失配环境，截取包括宽带信号目标回波在内的数据段，数据段长度为2 s，发射信号为宽带调频信号。

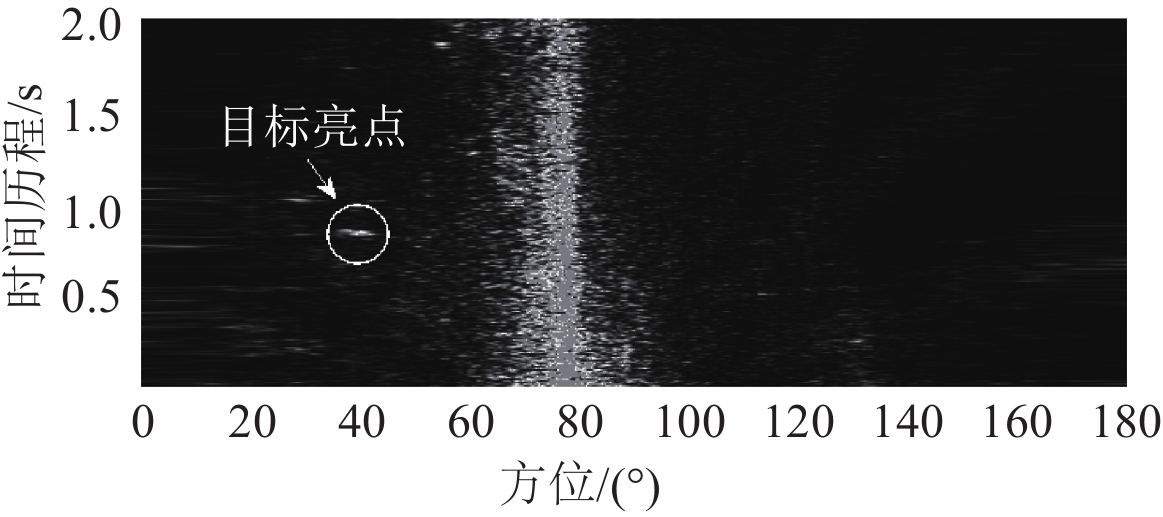
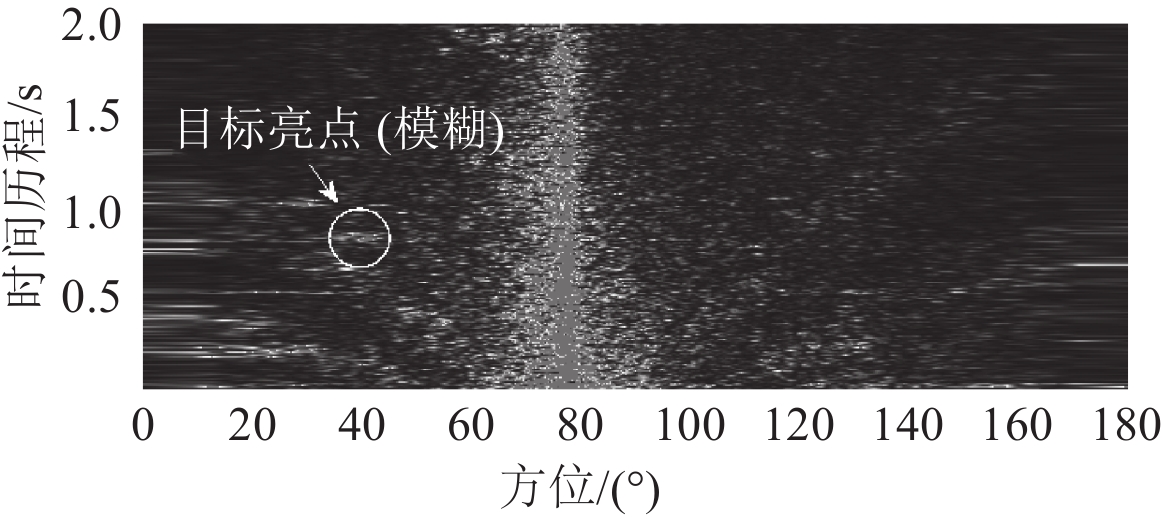
图3～图5为3种方法的方位历程图。由图可见，回波目标位于方位39°、距离0.85 s的位置（图中已标注），位于80°左右有1个强干扰目标。CBF检测目标较为模糊，TMVDR检测目标失败，DCTMVDR检测目标清晰可见。

分析结果可以表明，CBF的空间分辨率较低，受到强干扰影响，检测出的目标较为模糊。由于环境恶劣，TMVDR性能下降，没有能够检测出目标。相比较之下，DCTMVDR不仅拥有更好的空间分辨率，有效地抑制了强干扰的旁瓣，也体现了稳健良好的目标检测性能。

5 结　语

TMVDR方法可以有效地提高声呐波束输出的空间分辨率、降低旁瓣级，在大孔径主动声呐的应用环境下，由于单次快拍协方差矩阵估计的不稳定性以及可能存在的阵型失配等不确定因素，其存在输出功率失真的问题，导致其性能下降。相对于TMVDR，DCTMVDR在一定程度上能够有效地避免由于最优权向量估计误差导致的性能下降问题，在估计最优输出的同时拥有更好的鲁棒性。数值仿真和实验数据验证了DCTMVDR方法的有效性。