0 引　言

在水下声呐系统中，对传感器接收的来波信号处理（一般是指声信号）是从传感器基阵开始的^[1]。传感器基阵除了需要将处理后的来波信号转换为电信号，通常还需要实现对多个方向的信号源来波进行独立的检测与分辨，并准确估计出信号的来波方向。

波达方向估计^[2]就是对传感器接收信号的入射方向的估计，目前针对波达方向估计算法的研究通常有2个方向：一种是通过传统的数学建模方式，如20世纪60年代以来，一些经典的谱估计方法如Burg的最大熵谱估计算法^[3]（Maximum Entropy Method，MEM）和Capon J.的最小方差谱估计算法^[4]（Minimum Variance Method，MVM）等被众多学者们陆续提出，在一定程度上对高分辨率DOA估计打下了基础。随后基于子空间原理的多重信号分类（MUSIC）算法和旋转不变子空间（ESPRIT）算法为代表的波达方向估计算法在20世纪80年代后成为研究的主要方向。MUSIC算法利用阵列导向矢量与子空间存在的正交性来提高信号方位估计精度和高分辨率^[5]，Paulraj等^[6]则针对该算法谱峰搜索会带来的巨大运算量缺陷提出了ESPRIT算法，利用2个完全相同子空间的旋转不变性进行空间谱估计。然而这些算法普遍存在着以下2个缺点：算法步骤复杂，计算量过大，满足不了实时性要求；在实际海洋低信噪比环境下适用性较差，其性能也达不到更好的要求。第2种是在当今社会技术革新的浪潮下，越来越多的学者提出通过神经网络算法进行DOA估计。神经网络算法最大的优势可以在原始目标回波信息的基础上自动学习回波特征。20世纪初，Zooghby等^[7]率先将径向基函数神经网络运用到DOA估计中去。陈荆花等^[8]基于特征矢量的采集输入数据方法结合径向基函数神经网络，计算量大幅减少，精度得到提高。李鹏飞等^[9]为降低特征种类，将互相关函数的相位信息作为RBF神经网络的输入特征，缩短了算法的训练时间。因此本文主要研究神经网络在DOA估计领域中的应用，并旨在解决水下目标回波信号的波动性和复杂性及低信噪比下DOA估计精度不高的问题。

2014年，Dragomiretskiy等^[10]率先通过将非线性、非对称、且结构复杂的多重信息序列依次分解为多个频率依次变化的、幅值相对平稳的固有模态分量（band-limited intrinsic mode functions，BLIMF），即著名的变分模态分解（Variational Mode Decomposition，VMD）算法。VMD算法作为一种新型的信号解析方法，常被用于处理水下数据的复杂性和波动性特征，且能够很好的解决传统的经验模态分解（Experience Mode Decomposition，EMD）算法、部分域均值分解算法、经验小波变换算法等算法中存在的固有模态信息混叠、无法很好地去除附加噪声和确定本征模态函数总体数目的问题。

考虑到在实际海洋水下环境中阵列接收到的目标回波数据存在较多的散射波和人为及生物噪声干扰，且由于传统DOA估计算法的公式推导复杂、计算量巨大等问题，充分结合近些年一些深度学习算法在DOA估计中的成功应用，本文利用VMD模型，将阵元接收到的声源信号通过变分模态分解得到的时频谱图直接作为神经网络的输入，通过BP神经网络优良的非线性拟合能力，构建基于VMD-PSO-BP模型的波达方向估计方法。仿真结果表明，VMD模型降低了水下复杂环境声源数据的非线性和复杂性，再通过PSO-BP神经网络处理，有效提高了波达方向角的估计精度。

1 基于变分模态分解的阵元信号处理

WVD时频分析方法在满足二次型（双线性）的同时，又有着良好的能量聚集性、时频域分辨率和聚集性等优点，因而在目标信号的解析领域得到了普遍的使用^[11]。但如何抑制交叉项干扰是Wigner-Ville分析需要解决的首要问题。信号 $x(t)$ 的WVD分布定义为：

$ {W_x}(t,f) = \int_{ - \infty }^\infty {x(t + \tau /2)x(t - \tau /2){e^{ - j2\text{π} f\tau }}} {\rm{d}}\tau {\text{。}} $

(1)

通过上式可以发现积分项中包含两次 $x(t)$ 信号，所以在满足了双线性的同时出现了WVD的干扰项。令 $x(t) = {x_1}(t) + {x_2}(t)$ ，通过WVD算法的具体计算过程如下：

${W_x}(t,f) = {W_{{x_1}}}(t,f) + {W_{{x_2}}}(t,f) + {W_{{x_1}{x_2}}}(t,f){\text，}$

(2)

${W_{{x_1}{x_2}}}(t,f) \!=\! \frac{1}{{2\text{π} }}\int_{ - \infty }^\infty {{x_1}(t \!+\! \tau /2){x_2}(t \!-\! \tau /2){e^{ - j2\text{π} f\tau }}{\rm{d}}\tau } {\text{，}}$

(3)

${W_{{x_1}{x_2}}}(t,f) = {W_{{x_2}{x_1}}}(t,f){\text{。}}$

(4)

经过式（2）～式（4），可以得到Wigner-Ville分布：

${W_x}(t,f) = {W_{{x_1}}}(t,f) + {W_{{x_2}}}(t,f) + 2{\rm{Re} {W_{{x_1}{x_2}}}}(t,f){\text，}$

(5)

式中： $ {W}_{{x}_{1}}(t,f){\text{，}}{W}_{{x}_{2}}(t,f)$ 为信号的自项； ${\rm{Re} {W_{{x_1}{x_2}}}}(t,f)$ 称为两信号的交叉干扰项。

作为具有准正交、自适应、非递归等特性的信号解析算法，VMD算法能够将多分量调幅调频信号分解成多个只含有有限带宽的BLIMF分量。通过对变分结构内的调幅调频信号完成分解处理，随后搜索约束变分结构内的约束和最优化来完成信号的自适应解析，进而达到获取单分调幅调频信号及其所属的中心频率的目的。

考虑到VMD算法的各BLIMF各自不存在关联，而且都处于目标信号对应的中心频率附近。根据这一特性，本文将结合VMD算法来改善WVD时频分布中固有的交叉项干扰缺陷。首先将经VMD分解后的各BLIMF依次完成WVD处理，再对所有处理后的BLIMF线性叠加，从而得到原始信号的VMD-WVD分布结果。该算法的思路可表示为：

步骤1　将阵元收集的目标回波信号 $x(t)$ 进行VMD分解；

步骤2　通过中心频率观察法选取含有目标亮点信息的有效信息分量，由分量瞬时频率的均值来得到分量模态个数 $K$ ，在满足 $K = n$ 时，即得到了 $n$ 个具有不同中心频率的BLIMF，记为 ${x_i}(t)(i = 1,2, \cdots ,n)$ ；

步骤3　对每个BLIMF分量 ${x_i}(t)(i = 1,2 ,\cdots ,n)$ 进行时频分析，得到相应的WVD分布 ${w_i}(t)(i = 1,2, \cdots ,n)$ ；

步骤4　将 ${w_i}(t)$ 依次完成线性叠加，即得到了结合VMD算法的目标回波信号 $x(t)$ 的Wigner-Ville分布结果，即

${W_{{\rm{VMD}}}}(t,f) = \int_{ - \infty }^{ + \infty } {x\left(t + \frac{\tau }{2}\right)} {x^*}\left(t + \frac{\tau }{2}\right){e^{ - j2\text{π} f\tau }}{\rm{d}}\tau{\text。} $

(6)

2 基于PSO-BP神经网络的识别方法

BP神经网络是一种前馈型误差修正网络，其网络结构为输入-隐藏-输出3层结构，将输出与期望值间的误差作为调整信号逐层反向传播来修正权值和阈值使得误差最小化。然而在BP神经网络的训练过程中会出现过拟合的问题，导致对训练集以外的新鲜样本不能得到适当的输出，降低泛化能力。

1995年，Eberhart和Kennedy在通过观察和总结自然界中鸟类搜寻食物的协同过程后提出了一种随机优化算法，将之形象的称作粒子群（particle swarm optimization，PSO）算法^[12]。经粒子群优化的反向传播算法的目的是依据PSO算法的搜索特性来优化BP神经网络每层结构之间的权值和阈值，按照将BP神经网络的训练输出与真实值之间的误差作为PSO算法的适应度函数的原理，将BP神经网络的权值、阈值分别对应于PSO算法中每个粒子在可行解空间中的一个解，BP神经网络的正向传递过程即为每个粒子每次飞行迭代位置的过程。在BP神经网络的训练过程中，粒子不断调整自身飞行速度和所在最佳位置的具体表达式：

$\begin{split} {v^{k + 1}}_{id} =& w*{v^k}_{id} + {c_1}*ran{d_1}()(pbes{t^k}_{id} - {x^k}_{id})+\\ &{c_2}{\rm{*}}ran{d_2}()(gbes{t^k}_{id} - {x^k}_{id}) {\text，} \end{split} $

(7)

${x^{k + 1}}_{id} = {x^k}_{id} + {v^{k + 1}}_{id}{\text。}$

(8)

其中： $w$ 是惯性权重，代表粒子历史飞行结束后的速度在本次飞行中对飞行速度的影响程度，合理选取 $w$ 值可以避免过多的训练迭代次数； $k$ 是当前迭代次数； $ {c}_{1}{\text{，}}{c}_{2}$ 为学习因子，分别表示粒子朝个体极值和全局极值加速运动的权重， $ ran{d}_{1}(){\text{，}}ran{d}_{2}()$ 均为介于[0，1]之间的随机数。 ${x^k}_{id}$ 及 ${v^{k + 1}}_{id}$ 都为被限制在一定范围内的第k次迭代时粒子i在第d维的速度和位置。 $pbes{t^k}_{id}$ 是第d维下粒子i的个体极值位置， $gbes{t^k}_{id}$ 是第d维下种群的全局最优解位置。

本文算法具体实现步骤如图1所示。

3 数据仿真与分析

为验证经变分模态分解结合粒子群算法后的神经网络对目标DOA估计的效果，利用主动声呐发射LFM信号，假设采用5元均匀阵列阵接收，信噪比SNR设定为10 dB，快拍数为1000，阵元间距取半长波。仿真环境为：Intel（R）Core（TM）i7-4790 CPU@3.6 GHz，16 GB RAM，Matlab 2018 a，Dell。接收信号源空间角度之间的划分取15°，从0°～90°间隔 0.5°来依次获取1个样本，总共得到181个样本，作为神经网络的训练样本。同样的，将接收信号源空间角度之间的划分取5°，从0°～90°间隔1°依次获取一个样本，共得到91个样本，作为神经网络的测试样本。以间隔取15°为例，当第1个信号源为0°时，第2个信号源为15°；第1个信号源为0.5°时，第2个信号源为15.5°，依据上述空间角度的划分步骤，完成整个 $[0,{90^ \circ }]$ 方向的取值，并展开200次Monte-Carlo仿真实验。

3.1 源信号的时频预处理

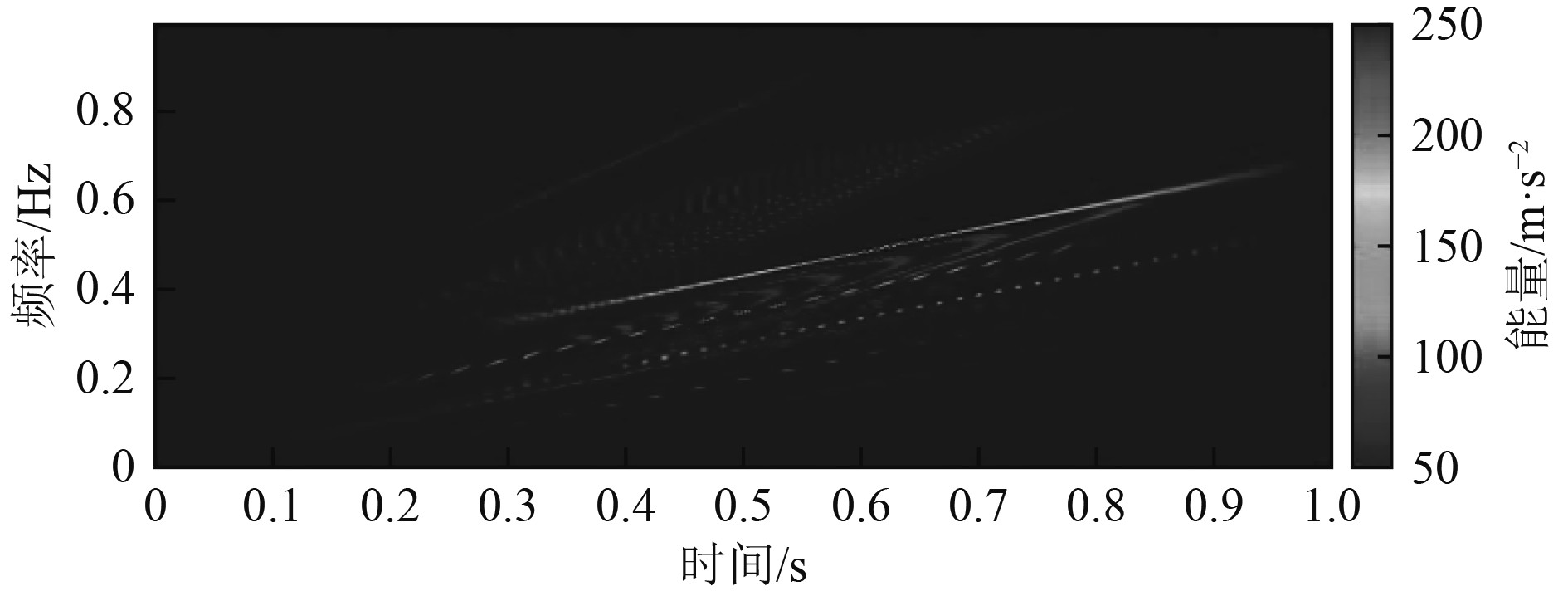
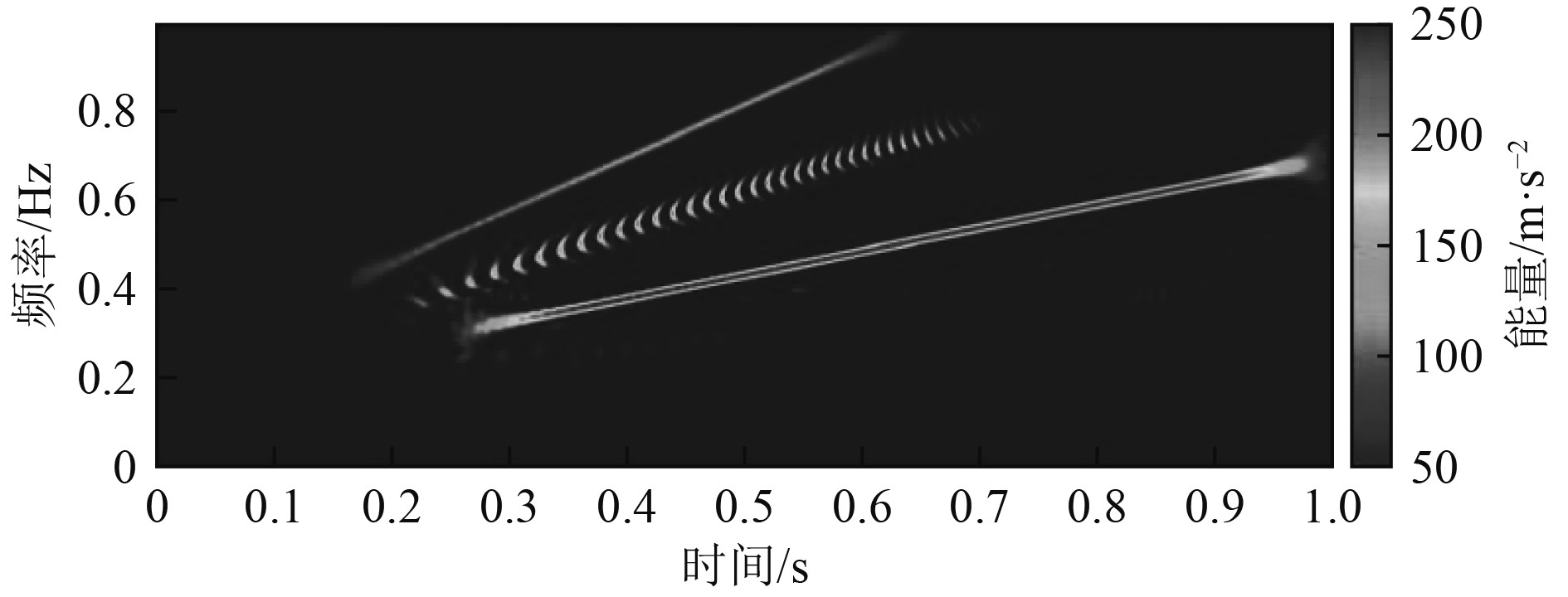
对实验采集到的信号源回波信号分别进行EMD-WVD和VMD-WVD时频分析，相同信号源接收到的回波信号对应的时频分析谱图如图2和图3所示。

由于海底回波信号是由不同中心频率的多个分量信号叠加的复杂信号，从信号源回波信号的EMD-WVD谱图中可以大致观测出亮点信号的存在，但是无法确定目标信号的有效频率成分，交叉项干扰严重。并且由于EMD算法在信号分解的过程中出现了伪模态分量，导致了EMD-WVD的时频分布中产生了非目标回波信号的低频率成分。而通过VMD-WVD算法的谱图中，不同回波信号中包含的目标亮点主频所处位置都可以清楚的看出。这是因为经VMD算法分解后的各个BLIMF不存在关联性、中心频率唯一、频率不会混叠而且避免了EMD算法易出现的伪模态分量问题。由此可见，可以将目标回波信号的VMD-WVD分布特征应用于阵元信号DOA估计中去。

为了体现VMD-WVD时频分析的优势所在和其在DOA估计上的可行性，本文对EMD-WVD方法和VMD-WVD方法获取的时频分析谱图完成灰度化处理。通过提取谱图中灰度熵的特征信息，将得到的纹理特征作为BP神经网络中的输入来训练网络。通过将算法的网络结构模型设置为1-9-1的3层结构，激励函数选择双曲正切S型函数，最大迭代次数设定为1000次，误差mse设定为1E-3，所得结果如表1所示。

由表1可知，基于VMD-WVD的识别结果有着更高的识别率。但是考虑到传统BP神经网络的特征选择存在一定的局限性，无法全面的表征分布特征，表1中所得正确识别率仍然偏低。基于此，采用PSO-BP网络通过获取的时频分布谱图作为网络的输入特征，以此来达到提升识别精度的目的。

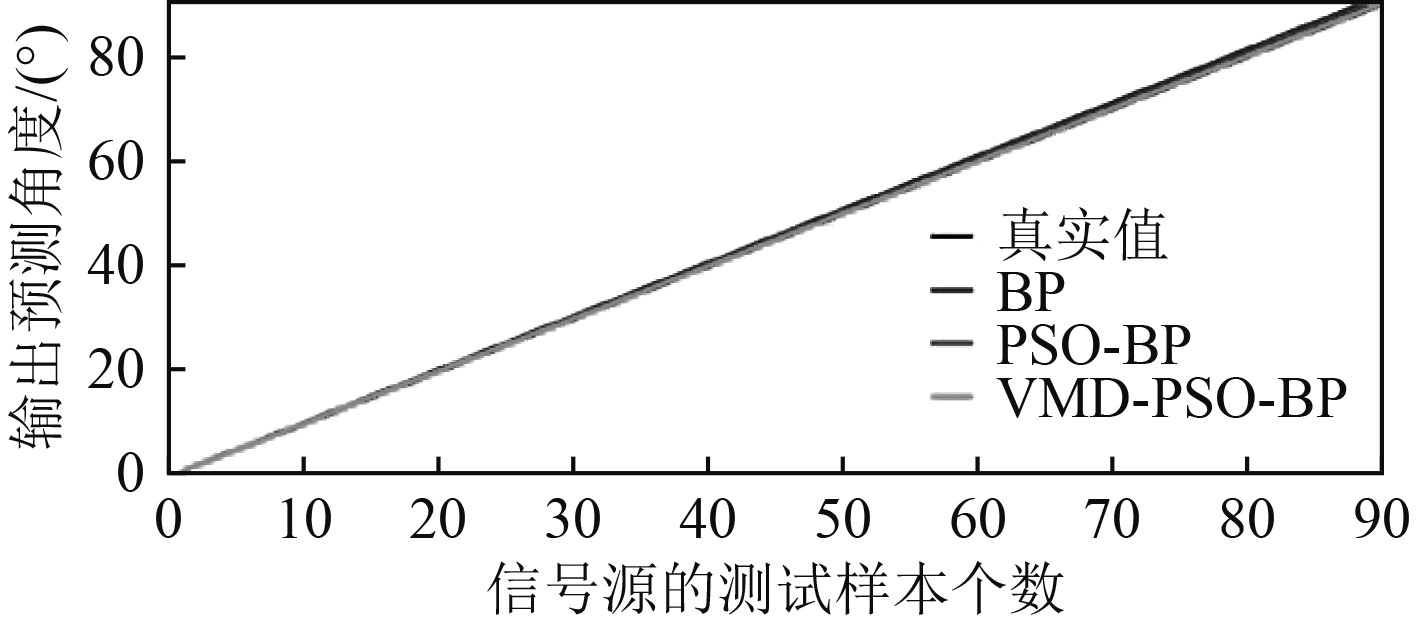
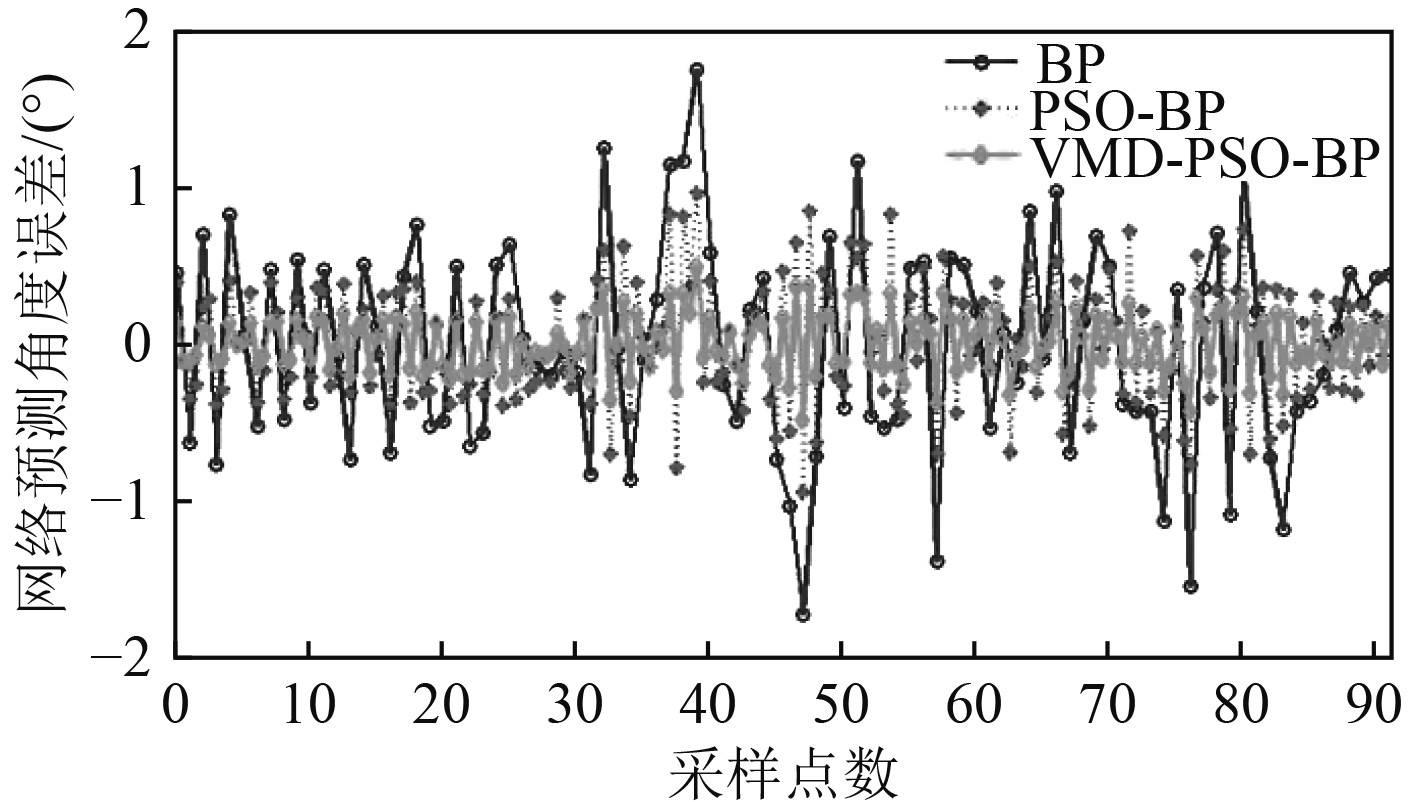
3.2 多信号目标来波方向估计 3.2.1 多信号源DOA估计精度对比分析

分别利用BP神经网络、基于上三角特征作为输入的PSO-BP网络和本文中直接利用变分模态分解后的时频分析谱图作为输入的PSO-BP网络对两信号源的DOA方向进行估计，得到阵元接收信号的DOA估计和估计误差如图4和图5所示。

图4为3种不同神经网络方法下的DOA估计输出预测值和真实值的对比。可以看出，通过VMD-PSO-BP神经网络算法下的预测值与真实值最为接近，基于上三角特征的PSO-BP网络的预测值与真实值仍有较明显差别，BP神经网络的预测值与真实值相差最大。图5为3种不同神经网络方法下的DOA估计的误差曲线。可以看出，VMD-PSO-BP神经网络算法下的DOA估计精度误差相较PSO-BP网络有着明显的减小，而BP神经网络作为早期的神经网络算法，其DOA估计精度误差最大，性能最差。从DOA估计输出预测曲线图和误差曲线图可以明显得出，本文采用的VMD-PSO-BP算法相比于其他2种算法在DOA估计精度上有着更好的性能。

表2为3种模型下的平均绝对误差、均方误差及均方根误差值，可以更好地反映预测值误差的实际情况。

从表中数据可以明显看出：传统BP神经网络训练的各项指标是最大的，而经VMD-PSO-BP神经网络训练后的MAE，MSE，RMSE都是最小的，同时对比PSO-BP网络的各项参数，采用VMD-PSO-BP对DOA进行估计有着更好的优势。

3.2.2 不同信噪比下的性能分析

仿真条件与上述情况一致，本文依次对信噪比位于−10 dB～10 dB之间的输入通过3种神经网络算法，并计算了3种算法的均方根误差RMSE，其具体表达式如下：

$RMSE = \frac{1}{N}\sum\limits_{n - 1}^N \left(\frac{{{y_n} - {{\hat y}_n}}}{{{{\hat y}_n}}} \right)^2{\text。}$

(9)

其中： ${y_n}$ 为第 $n$ 次实际输出值； ${\hat y_n}$ 为第 $n$ 次的网络输出值。实际结果如图6所示。

从图6可以看出，目标回波信号DOA估计精度的均方根误差在信噪比SNR不断变好的情况下也越来越小。其中，BP神经网络的均方根误差要比其他两种方法差很多，算法性能最差。而通过对比PSO-BP神经网络算法和VMD-PSO-BP神经网络算法的误差曲线，VMD-PSO-BP神经网络算法要比PSO-BP神经网络算法的均方根误差要低，尤其在信噪比状况理想的情况下效果更好。因此，本文提出的VMD-PSO-BP神经网络算法具有更好的抗干扰性能，DOA估计精度更高。

4 结　语

本文针对水下声源信号的复杂性、噪声干扰严重以及传统的BP神经网络容易陷入局部最优的问题，通过粒子群算法优异的全局搜索能力，结合VMD算法下可以有效减小数据的波动性和复杂性影响的特点，提出结合变分模态分解的粒子群算法优化BP神经网络（VMD-PSO-BP），实现了阵列接收信号的DOA估计和在不同信噪比下的误差估计。仿真结果表明，本文提出的VMD-PSO-BP神经网络算法在DOA估计精度和不同信噪比下的均方误差均优于传统BP神经网络和经粒子群算法优化后的BP神经网络，具有更好的估计精度和泛化能力，对于相关研究的进一步展开有一定的借鉴意义。