0 引　言

拖曳线列阵声呐是现代声呐的重要发展方向之一，其具有孔径大、工作频率低、探测距离远等特点，广泛应用在各类舰艇上，成为水下远距离探测的重要有效手段。常规的单线阵由一系列无指向性的水听器组成，由于水听器没有指向性，其对整个圆锥面上所有入射信号的响应完全一致，如果考虑水平面一个平面，则单线阵将出现左右舷模糊问题，无法区分信号来源于左舷还是右舷。常规的单线阵通常采用平台机动的方式，根据声呐时间-方位历程图中目标舷角的变换趋势来判断左右舷或者是利用平台机动时阵型估计的信号处理方法来区分左右舷^[1-7]。舷角的变化通常需要人工来完成，无法进行自动判决。另外，平台的大角度机动势必会导致阵型严重畸变，增加目标丢失的可能性，因此，急需一种小角度机动就能完成左右舷分辨的方法。

本文在深入研究平台机动时左右舷分辨的基础上，创新提出了一种以目标跟踪为基础的单线阵左右舷分辨方法，通过仿真分析，验证了该方法的可行性与有效性，可望应用于工程实践中。

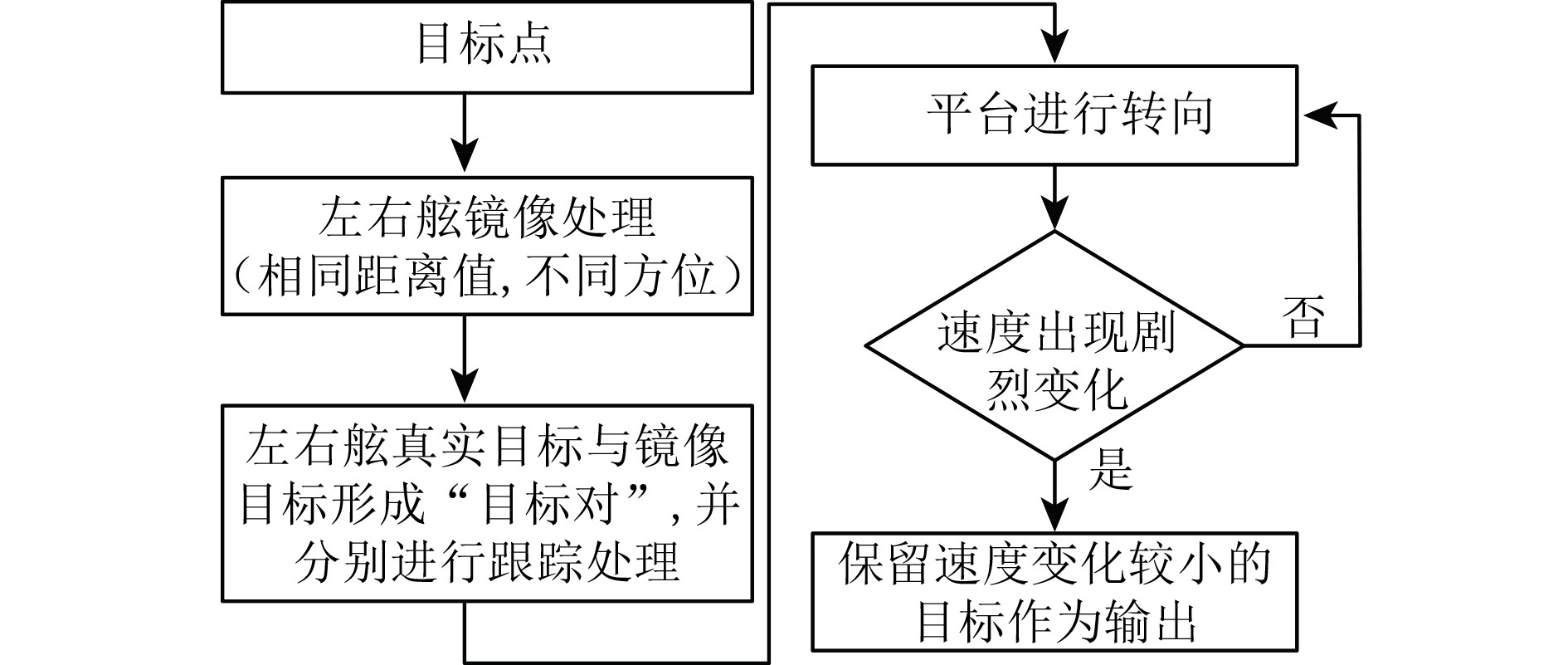
1 单线阵左右舷分辨基本原理

本文采用平台机动与目标跟踪相结合的方法，具体流程如图1所示。拖曳线列阵声呐在开机使用过程中发现过门限的目标，利用过门限的目标数据，进行左右舷镜像处理，两者组成一个左右舷“目标对”，两者具有相同的幅值和距离值，但是方位不同（例如，平台航向为0°时，右舷80°方位镜像到左舷为280°方位），就如同从左右舷两边都收到数据一样，然后将“目标对”中的2个目标分别进行跟踪处理。平台按照规定进行转向机动，根据“目标对”中2个目标速度变化趋势来判断左右舷。假设平台机动过程中能够检测到目标并且稳定跟踪，通过一系列周期，真实目标的速度变化不明显，但镜像目标的速度将发生剧烈变化，保留速度变化较小的跟踪器，从而可以确定目标真实方位，无需人工干预即可实现目标左右舷自动判决。

2 目标跟踪算法

为了提高对机动目标的跟踪能力，本文采用IMM-Kalman滤波跟踪算法。交互多模型（Interactive Multiple Models，IMM）跟踪算法采用多个运动模型，每个模型都有一个相应的模型概率，通过马尔科夫转移矩阵完成不同模型之间的转换，在运算过程中，系统实时为每个模型计算概率，最终输出结果为各个模型的加权平均^[8-9]。

设有n个模型，目标运动方程为：

$ {{{x}}^j}\left( k \right) = \mathop {{\varPhi}} \nolimits^j {{{x}}^j}\left( {k - 1} \right) + \mathop {{G}}\nolimits^j \mathop {{W}}\nolimits^j \left( {k - 1} \right), $

(1)

其中， $j = 1,2, \cdots ,n$ ； ${{{x}}^j}\left( k \right)$ 为k时刻状态向量； $\mathop {{\varPhi}} \nolimits^j$ 为状态转移矩阵； $\mathop {{W}}\nolimits^j \left( {k - 1} \right)$ 为k-1时刻过程噪声； $\mathop {{G}}\nolimits^j $ 为过程噪声分布矩阵。

测量方程为：

$ {{Z}}\left( k \right) = {{{H}}^j}\left( k \right){{x}}\left( k \right) + {{{V}}^j}\left( k \right)\text{。} $

(2)

其中： ${{{H}}^j}\left( k \right)$ 为测量矩阵； ${{{V}}^j}\left( k \right)$ 为测量噪声。

IMM算法滤波可分为几步：

1）模型交互作用

$ {\mu ^{i/j}}(k - 1|k - 1) = \frac{{\mathop p\nolimits_{ij} \mathop \mu \nolimits^i \left( {k - 1} \right)}}{{{{\overline C }_j}}}, $

(3)

$ {\overline C _j} = \sum\limits_{i = 1}^n {\mathop p\nolimits_{ij} \mathop \mu \nolimits^i \left( {k - 1|k - 1} \right)} , $

(4)

$ \mathop {\hat {{x}}}\nolimits^{0j} (k - 1|k - 1) = \sum\limits_{i = 1}^n {\mathop \mu \nolimits^{{i / j}} (k - 1|k - 1)} \mathop {\hat {{x}}}\nolimits^i (k - 1|k - 1), $

(5)

$ \begin{split} {{{P}}^{0j}}\left( {k \!-\! 1|k \!-\! 1} \right) \!=\! & \sum\limits_{i = 1}^n {\mathop \mu \nolimits^{{i / j}} } \left( {k \!-\! 1|k \!-\! 1} \right)\left[ {\mathop {{P}}\nolimits^i \left( {k \!-\! 1|k \!-\! 1} \right)} \right. +\\ &\left( {\mathop {\hat {{x}}}\nolimits^i \left( {k - 1|k - 1} \right) - \mathop {\hat {{x}}}\nolimits^{0j} \left( {k - 1|k - 1} \right)} \right) \cdot\\ &\left. {{{\left( {\mathop {\hat {{x}}}\nolimits^i \left( {k \!-\! 1|k \!-\! 1} \right) \!-\! \mathop {\hat {{x}}}\nolimits^{0j} \left( {k \!-\! 1|k \!-\! 1} \right)} \right)}^T}} \right] \text{。} \end{split} $

(6)

其中： ${p_{ij}}$ 为第i个模型到第j个模型的转移概率； ${\ \mu ^i}(k - 1)$ 为第i个模型的概率； ${\overline C _j}$ 为预测的第j个模型k时刻的概率； $\ \mathop \mu \nolimits^{{i / j}} (k - 1|k - 1)$ 为在第j个模型条件下第i个模型k-1时刻的概率； ${\hat {{x}}^i}(k - 1|k - 1)$ 为第i个模型k-1时刻的状态估计； ${{{P}}^i}(k - 1|k - 1)$ 为相应的协方差； $\mathop {\hat {{x}}}\nolimits^{0j} (k - 1| $ $ k - 1)$ 为交互作用下第j个模型k-1时刻的状态估计； ${{{P}}^{0j}} $ $ \left( {k - 1|k - 1} \right)$ 为交互作用下第j个模型k-1时刻的协方差。

2）模型条件滤波

计算模型的预测滤波状态及协方差：

$ \mathop {{{\hat x}}}\nolimits^j \left( {k|k - 1} \right) = \mathop {{\Phi }}\nolimits^j \mathop {{{\hat x}}}\nolimits^{0j} \left( {k - 1|k - 1} \right),$

(7)

$ \mathop {{P}}\nolimits ^j \left( {k|k - 1} \right) = \mathop {{\Phi }}\nolimits ^j \mathop {{P}}\nolimits ^{0j} \left( {k|k - 1} \right){{\mathop {{\Phi }}\nolimits ^j} ^{\rm T}} + \mathop {{G}}\nolimits ^j \mathop {{Q}}\nolimits ^j {{\mathop {{G}}\nolimits ^j} ^{\rm T}}\text{。}$

(8)

其中： $\mathop {\hat {{x}}}\nolimits^j \left( {k|k - 1} \right)$ 为第j个模型k-1时刻预测的状态估计； $\mathop {{P}}\nolimits^j \left( {k|k - 1} \right)$ 为第j个模型k-1时刻预测的协方差。

计算模型的滤波状态及协方差：

$ \mathop {{S}}\nolimits^j \left( k \right) = \mathop {{H}}\nolimits^j \left( k \right)\mathop {{P}}\nolimits^j \left( {k|k - 1} \right)\mathop {{H}}\nolimits^j {\left( k \right)^{\rm T}} + \mathop {{R}}\nolimits^j \left( k \right), $

(9)

$ \mathop {{K}}\nolimits^j \left( k \right) = \mathop {{P}}\nolimits^j \left( {k|k - 1} \right)\mathop {{H}}\nolimits^j {\left( k \right)^{\rm T}}\mathop {{S}}\nolimits^j {\left( k \right)^{ - 1}}, $

(10)

$ \mathop {{\nu }}\nolimits^j \left( k \right) = {{Z}}\left( k \right) - \mathop {{H}}\nolimits^j \left( k \right)\mathop {{{\hat x}}}\nolimits^j \left( {k|k - 1} \right), $

(11)

$ \mathop {{{\hat x}}}\nolimits^j \left( {k|k} \right) = \mathop {{{\hat x}}}\nolimits^j \left( {k|k - 1} \right) + \mathop {{K}}\nolimits^j \left( k \right)\mathop {{\nu }}\nolimits^j \left( k \right), $

(12)

$ \mathop {{P}}\nolimits^j \left( {k|k} \right) = \left[ {{{I}} - \mathop {{K}}\nolimits^j \left( k \right)\mathop {{H}}\nolimits^j \left( k \right)} \right]\mathop {{P}}\nolimits^j \left( {k|k - 1} \right)\text{。} $

(13)

其中： $\mathop {{\nu}} \nolimits^j \left( k \right)$ 为第j个模型k时刻的新息（残差）； $\mathop {{S}}\nolimits^j \left( k \right)$ 为第j个模型k时刻残差的协方差； $\mathop {{K}}\nolimits^j \left( k \right)$ 为第j个模型k时刻的滤波增益； ${{I}}$ 为单位矩阵。

3）模型概率更新

计算模型的似然概率：

$ \mathop {{\Lambda }}\nolimits^j \left( k \right) = \frac{1}{{\sqrt {\left| {\mathop {2\text{π} {{S}}}\nolimits^j \left( k \right)} \right|} }}\exp \left\{ { - \frac{1}{2}\mathop {{\nu }}\nolimits^j {{\left( k \right)}^T}\mathop {{S}}\nolimits^j {{\left( k \right)}^{ - 1}}\mathop {{\nu }}\nolimits^j \left( k \right)} \right\}, $

(14)

计算模型的更新概率：

$\mathop \mu \nolimits^j \left( {k|k} \right) = \frac{1}{C}\mathop {{\Lambda }} \nolimits^j \left( k \right){\overline C _j},$

(15)

$C = \sum\limits_{i = 1}^n {\mathop {{\Lambda }}\nolimits^{\bf{i}} \left( k \right)} {\overline C _j}\text{。}$

(16)

4）交互模型输出

$\hat {{x}}\left( {k|k} \right) = \sum\limits_{j = 1}^n {\mathop \mu \nolimits^j \left( {k|k} \right)\mathop {\hat {{x}}}\nolimits^j \left( {k|k} \right)}, $

(17)

$\begin{split} \hat {{P}}\left( {k|k} \right) =& \sum\limits_{i = 1}^n {\mathop \mu \nolimits^{{i / j}} } \left( {k|k} \right)\left[ {\mathop {{P}}\nolimits^i \left( {k|k} \right)} \right. +\\ &\left( {\hat {{x}}\left( {k|k} \right) - \mathop {\hat {{x}}}\nolimits^i \left( {k|k} \right)} \right) \cdot \left. {{{\left( {\hat {{x}}\left( {k|k} \right) - \mathop {\hat {{x}}}\nolimits^i \left( {k|k} \right)} \right)}^{\rm T}}} \right] \text{。}\end{split}$

(18)

3 仿真与结果分析

选取匀速CV模型和匀加速CA模型，取状态向量 ${{x}} = {\left[ {x,\dot x,y,\dot y} \right]^{\rm T}}$ ，其中x和y分别为目标在x轴和y轴的位置分量， $\dot x$ 和 $\dot y$ 分别为目标在x轴和y轴的速度分量。初始状态和初始协方差矩阵分别为：

${{x}}(1|1) = \left[ {\begin{array}{*{20}{c}} {{Z_x}(1)} \\ {\dfrac{{{Z_x}(1) - {Z_x}(0)}}{T}} \\ {{Z_y}(1)} \\ {\dfrac{{{Z_y}(1) - {Z_y}(0)}}{T}} \end{array}} \right],$

(19)

${{P}}(1|1) = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{\dfrac{{{r_{11}}}}{T}}&0&0 \\ {\dfrac{{{r_{11}}}}{T}}&{\dfrac{{2{r_{11}}}}{{{T^2}}}}&0&0 \\ 0&0&{{r_{22}}}&{\dfrac{{{r_{22}}}}{T}} \\ 0&0&{\dfrac{{{r_{22}}}}{T}}&{\dfrac{{2{r_{22}}}}{{{T^2}}}} \end{array}} \right],$

(20)

状态转移矩阵：

${{{\Phi}} ^1} = {{{\Phi}} ^2} = \left[ {\begin{array}{*{20}{c}} 1&0&T&0 \\ 0&1&0&T \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right],$

(21)

过程噪声分布矩阵：

${{{G}}^1} = 0,$

(22)

${{{G}}^2} = \left[ {\begin{array}{*{20}{c}} {{T^2}/2}&0 \\ 0&{{T^2}/2} \\ T&0 \\ 0&T \end{array}} \right]\text{。}$

(23)

其中，T为周期， ${r_{11}} = {r_{22}} = {\sigma ^2}$ ， ${Z_x}$ 和 ${Z_y}$ 为测量值在x轴和y轴上的投影。

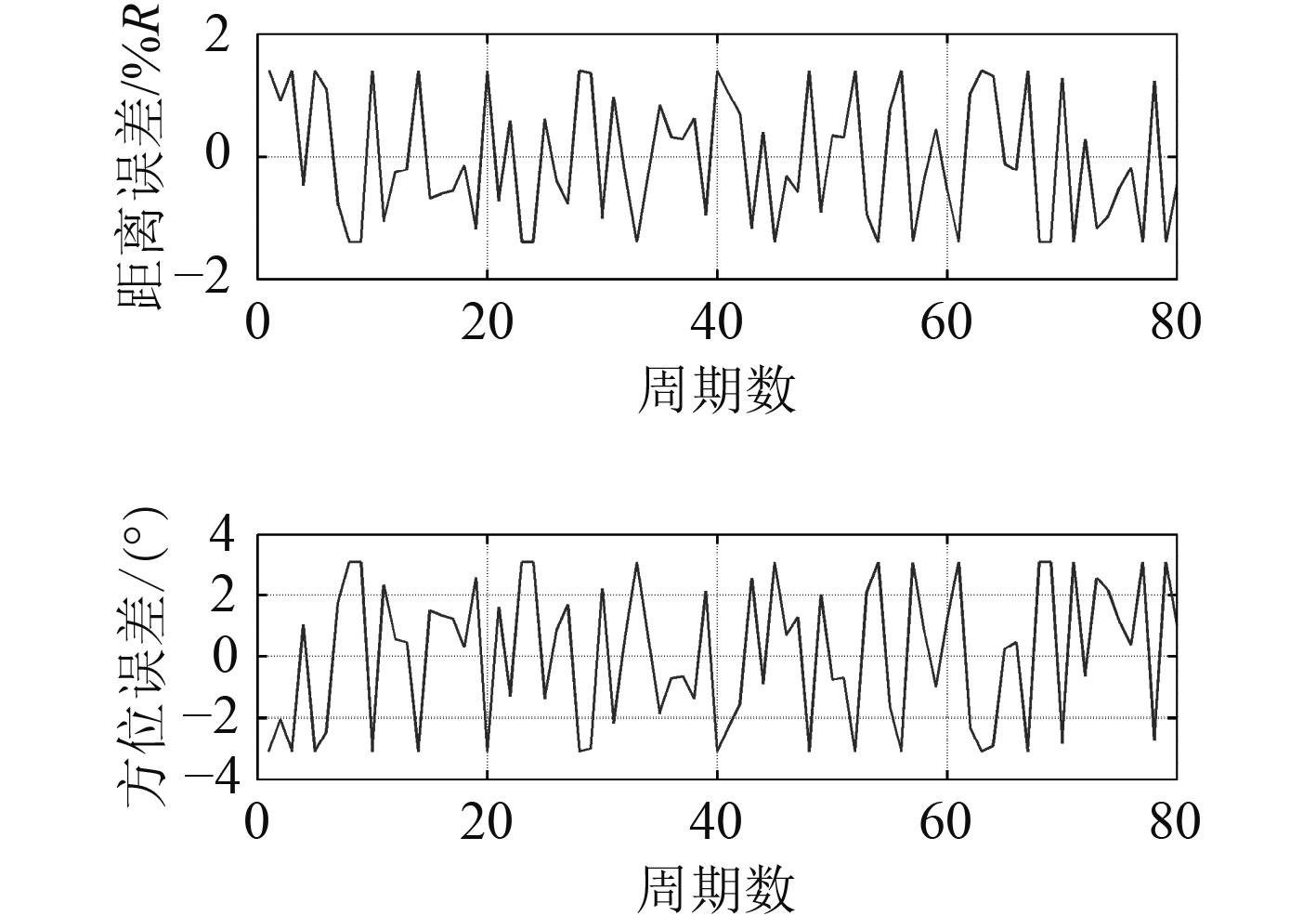
在实际情况中，测距与测向都会存在一定测量误差。为模拟实际情况，在仿真中添加了均方根为1.02%的测距误差和2.26°的测向误差，如图2所示。总共运动80个周期，从目标位于左舷与右舷2种情况进行分析，忽略了平台小角度机动时阵型畸变的影响，认为阵型畸变不大，依然能够持续检测到目标，保证跟踪器能进行稳定跟踪。

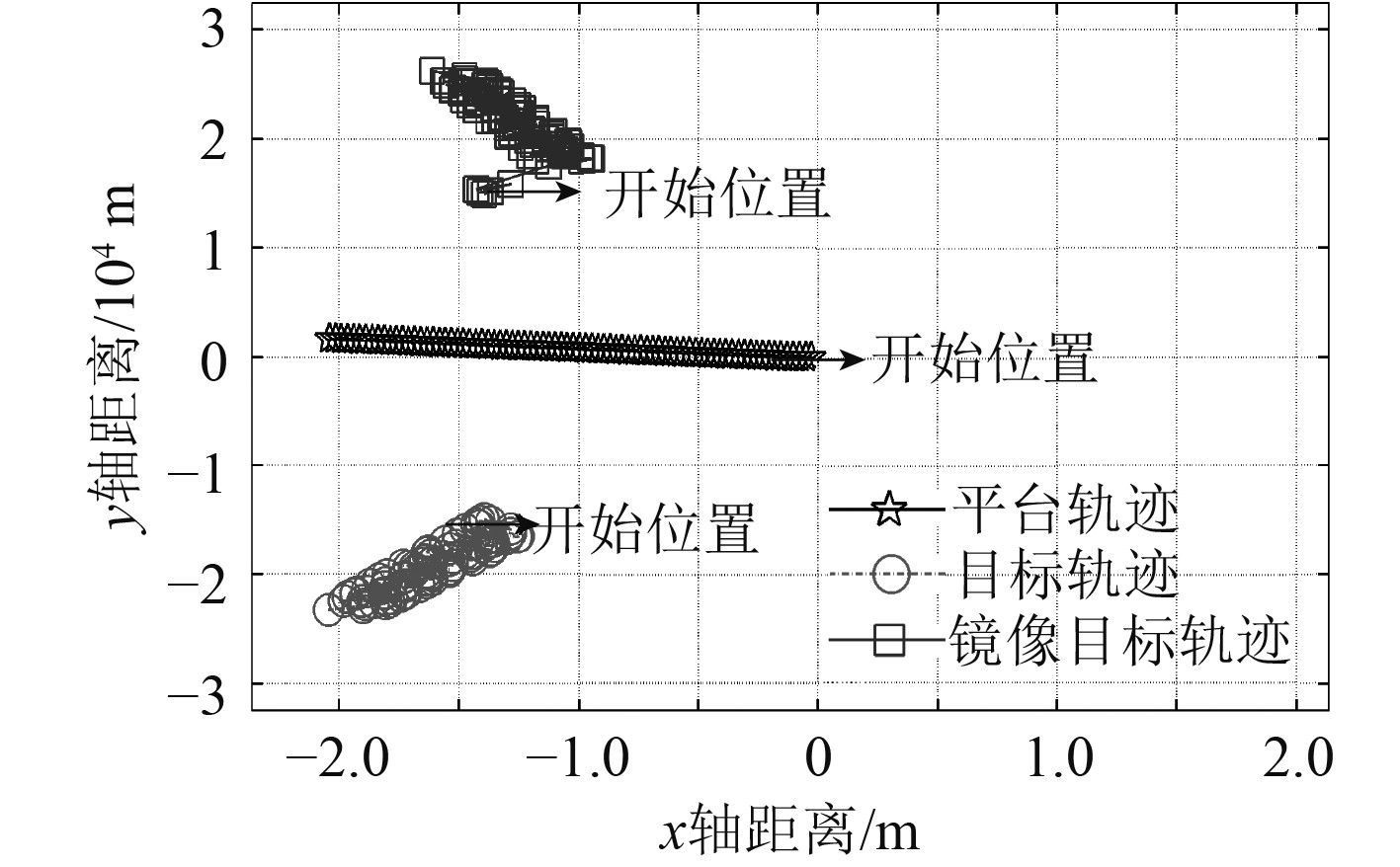
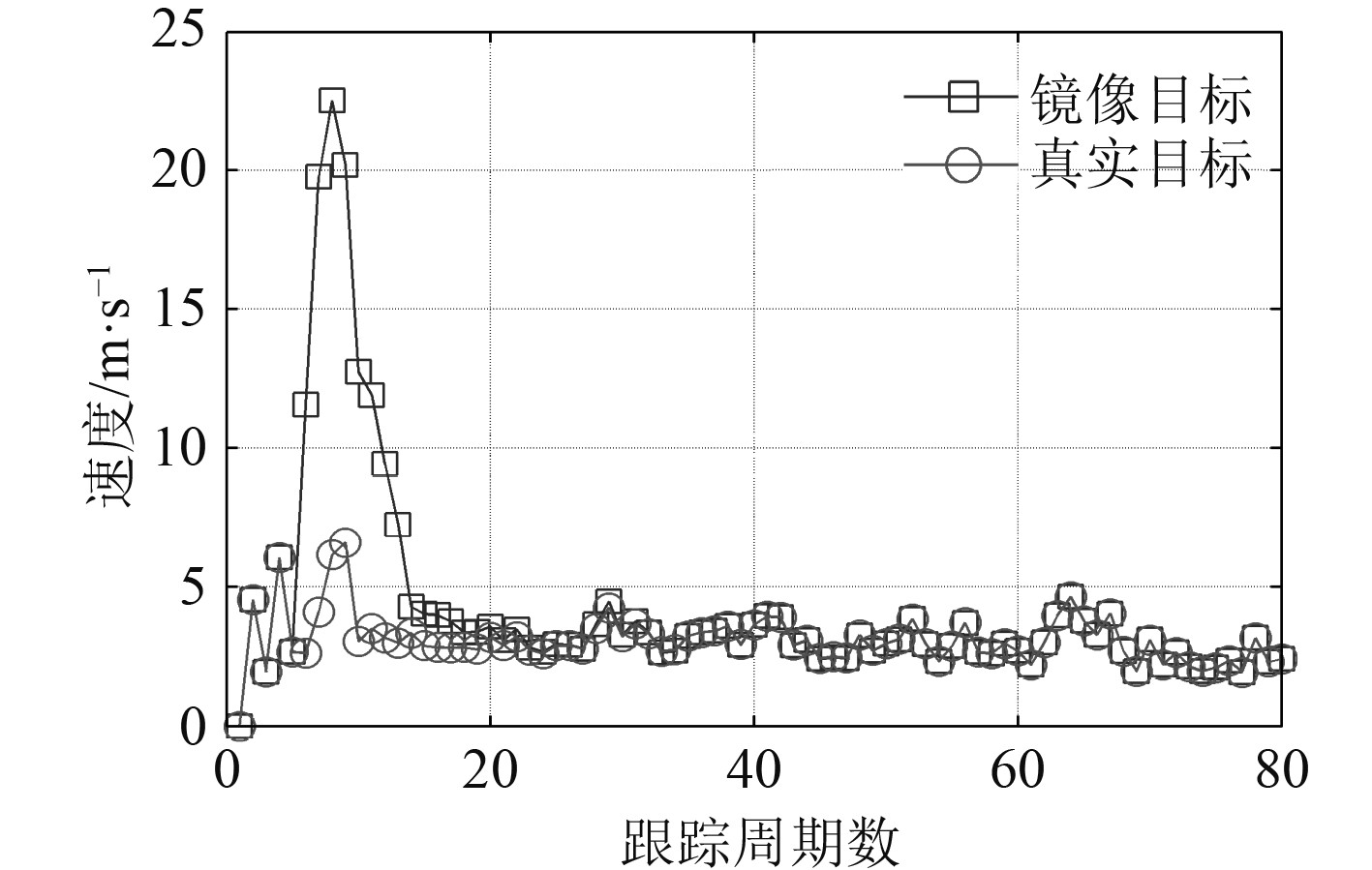
当目标位于左舷的情况，设置平台的航向为270°，航速6 m/s，目标方位220°，初始距离20 km，航向220°，航速3 m/s。从6个周期（T=R/C根据量程32 km确定）开始转向5°，然后保持航向不变，真实目标、镜像目标与平台位置关系如图3所示，两跟踪器的速度值输出如图4所示。可见，当目标位于左舷，在平台机动未进行转向的时候，两跟踪器的速度输出值完全一样，速度差为0 m/s，无法区分左右舷。在平台机动转向之后，两跟踪器的速度值开始出现差异，真实目标的速度变化不明显，真实目标速度为3 m/s左右上下波动，但镜像目标的速度将发生剧烈变化，在转向后的第1个周期，其目标速度就大于10 m/s，两者速度的差值已经超过测速误差，根据两跟踪器的速度差异信息，保留速度变化较小的目标，完成左右舷分辨。

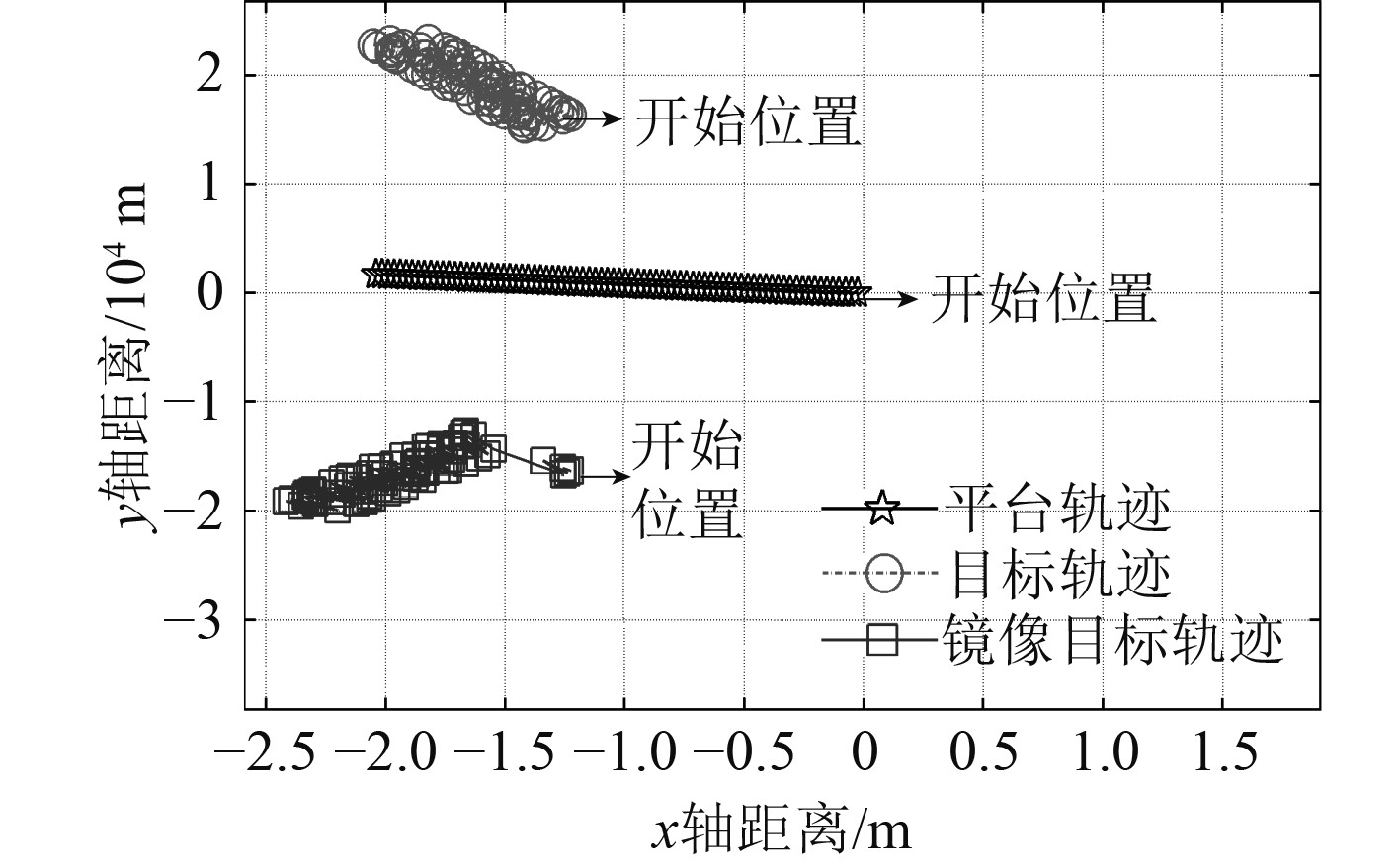
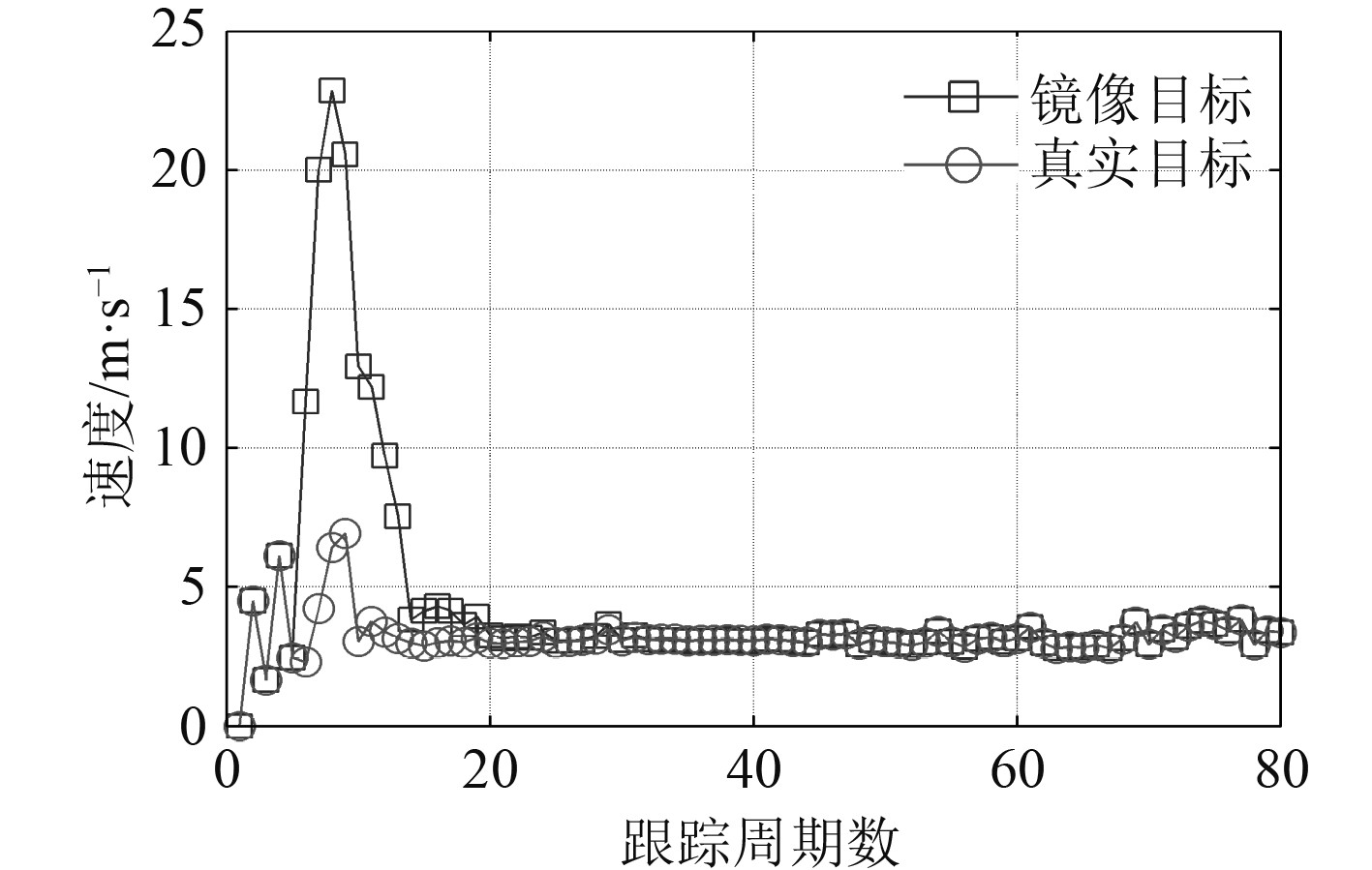
当目标位于右舷的情况，平台的航向为270°，航速6 m/s，目标方位320°，初始距离20 km，航向320°，航速3 m/s。从6个周期开始转向5°，然后保持航向不变，真实目标、镜像目标与平台位置关系如图5所示，两跟踪器的速度值输出如图6所示。可见，当目标位于右舷，与目标位于左舷的情况类似，在平台机动未进行转向的时候，两跟踪器的速度输出值一模一样，速度差为0 m/s，在平台机动转向之后，真实目标速度为3 m/s左右波动，速度改变不明显，但镜像目标在转向后的第1个周期，其目标速度就大于10 m/s，其速度变化较大，根据两跟踪器的速度差异信息，保留速度变化较小的目标，同样可以确定目标真实方位，完成左右舷分辨。

4 结　语

对于单线阵而言，左右舷分辨是一个重点，也是一个难点。为解决单线阵左右舷模糊问题，本文提出了一种基于目标跟踪的单线阵左右舷分辨方法，将平台机动与目标跟踪相结合，利用跟踪目标速度差异来分辨左右舷。由仿真结果可知，当目标位于左舷或者右舷，在平台进行小角度转向后，比如5°，经过2个扫描周期就可以区分目标左右舷，验证了本方法的可行性与有效性，在工程实践中，具有一定的应用前景与指导意义。