随着船舶电力系统容量的不断增大,船用电力需求日趋复杂,传统的电力系统已不能满足需求,越来越多的船舶开始采用综合电力系统。与船舶交流综合电力系统相比,基于中压直流的综合电力系统具有一系列优势,如解决了交流发电机组并网所需的电压频率、相位和复制相同的苛刻条件,降低了对原动机调速性能的要求;系统更紧凑,功率密度更高,可发电、变电、配电和负载等集成化设计,便于全船能量的统一调度等[1-2],具有广泛的应用前景。而船用直流电缆作为船舶综合电力系统实现电能从源到负载传输的重要通道,是构成综合电力系统的核心环节,直流电缆运行状态是否良好直接影响舰船综合电力系统能否可靠工作,而电缆温度是直接反应电缆运行状态的重要指标。目前对于交流电缆的温度场特性研究较多,而对于直流电缆的温度场特性研究的并不是很多,因此对直流电缆温场特性进行分析,为充分发挥直流电缆载流能力和运行安全提供参考。
目前,对于电缆温度场的分析计算一般基于解析算法[3]和数值计算法,解析算法作为一种方便快捷的计算手段,在早期的电缆温度场问题求解中被普遍应用。诸多解析计算基本以IEC标准为基础,结合实际的物理情况对计算参数进行局部修正来完成,解析计算基于 Kennelly假设[3]的基础上把电缆的计算模型简化为一维,并将该一维热场以热路的方式进行等值,通过计算热流在热路中传导及产生的温度差得到缆芯温度和电缆载流量。数值计算方法包括模拟热荷法、有限容积法、有限差分法及有限元法。
IEC60287《电缆载流量计算》中给出了基于热路模型求解均匀介质中敷设电缆的载流量计算方法[4];杨宁[5]对IEC解析计算法的适用范围进行研究,分析高回填土热阻下IEC计算法的误差原因,对IEC公式进一步完善改进,并进行了工程实例验证;郝艳捧[6]、刘云鹏[7]等在考虑线芯导体最高长期允许温度和绝缘层最大允许温差的基础上提出了高压直流电缆稳态载流量解析计算方法;梁永春等[8]根据温度场与电场的相似性,提出了用于计算地下电缆群稳态温度场的模拟热荷法,利用热路的方法将电缆金属套损耗和铠装层损耗归算到电缆导体,在满足精度的基础上,简化了建模过程;周晓虎[9]、于建立[10]等使用基于坐标组合的有限容积法来处理土壤区域和电缆区域边界形状不一致的问题,加快了求解速度;阮羚等[11]采用有限元法针对三相电流不平衡情况下电缆的温度场特性进行了分析;鲁志伟等[12]提出采用阶梯直线代替电缆圆形边界,在直角坐标系中直接求解电缆暂态温度场的方法,有效地解决了应用有限差分法计算电缆温度场时难以处理电缆圆形边界和周围土壤矩形边界的问题,崔明等[13]采用有限差分法对周期变化的负荷下电力电缆温度场特性进行了分析,提出了计算更加简便精确的周期性负荷载流量解析计算公式;梁永春等[14]在考虑趋肤效应和邻近效应的基础上,利用有限元法对电缆群不同排列方式和接地方式下的导体交流损耗和金属屏蔽层涡流损耗进行了计算;张华富等[15]构造出载流量和热流密度间的换算关系和边界条件,建立直埋三芯电力电缆的温度场模型,采用有限元方法对电缆温度场和载流量进行计算。由此可知,目前的研究大都针对交流电缆的温度场特性进行,而针对船用交流电缆与直流电缆之间的温度场特性的差异分析并不是很深入。
为此本文以架空敷设条件下的标称截面积为120 mm2船用直流电缆JDEPJ/SC和船用交流电缆JEZ85/SC为研究对象,分别采用热路解析计算和有限元仿真的方法对比分析二者温度场之间的区别与联系。
1 温度场理论分析电缆稳态温度场分析的是电缆在缆芯发热情况下的热传导问题,即温度在空间的分布,可以用热传导定律[16]来描述,如下式:
| $Q = - \lambda A\frac{{\partial T}}{{\partial n}}\text{。}$ | (1) |
式中:Q表示单位时间内传导的热量;λ表示材料的传热系数;A表示传热截面面积;
在电缆运行过程中,当通入电流I时,根据焦耳定律,电缆线芯发热,其产生的热量为
表1为标称截面积为120 mm2船用直流电缆JDEPJ/SC和船用交流电缆JEZ85/SC电缆参数,表2为电缆各层材料具体属性。
|
|
表 1 交直流电缆参数对比 Tab.1 Comparison of ac and dc cable parameters |
|
|
表 2 电缆材料属性 Tab.2 Cable material properties |
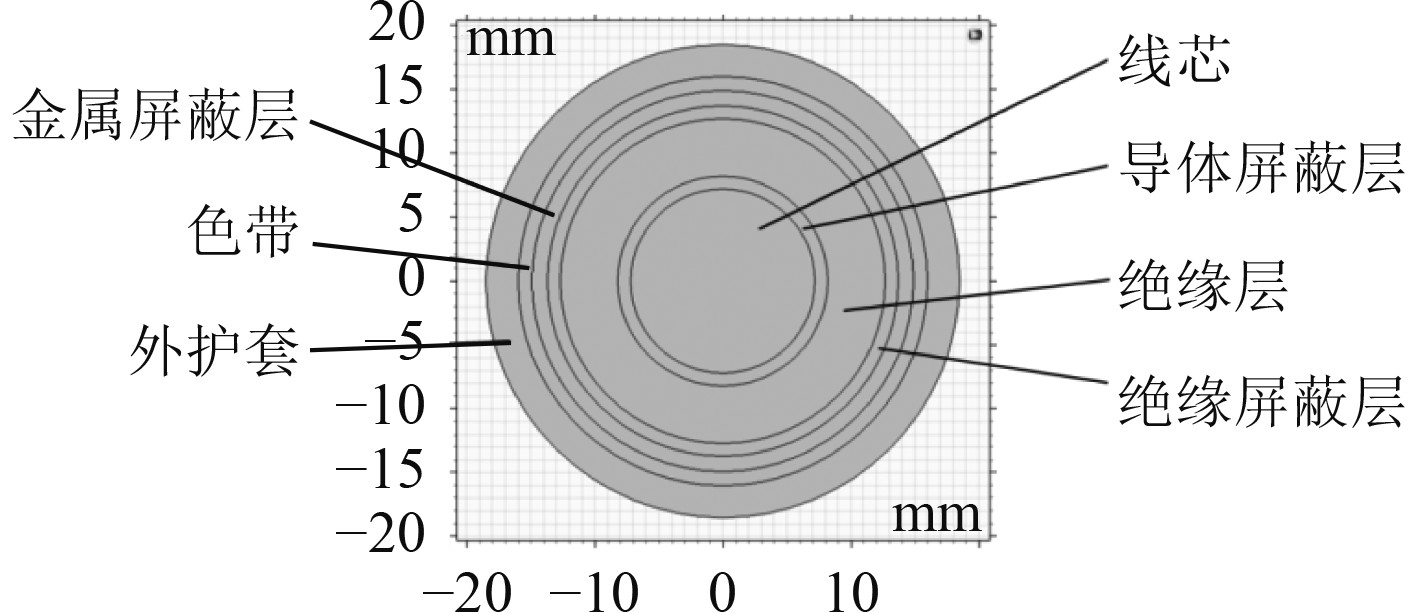
直流电缆JDEPJ/SC绝缘层采用乙丙橡胶材料、金属屏蔽层为铜带加铜丝编织、外护套交采用联聚烯烃材料,电缆由缆芯导体、导体屏蔽层、绝缘层、绝缘屏蔽层、金属屏蔽层、包带及外护套组成,图1为该电缆的几何模型,表3为其几何结构。
|
图 1 JDEPJ/SC电缆几何模型 Fig. 1 Geometry model of JDEPJ/SC cable |
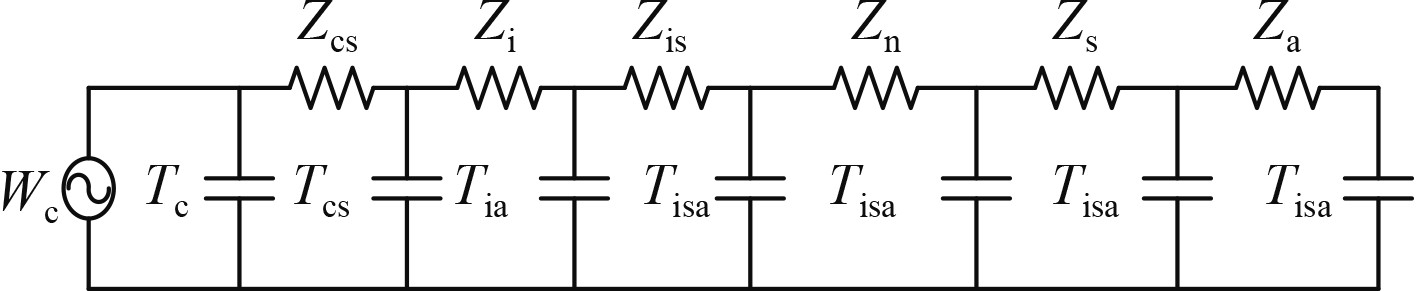
建立电缆的等效热路模型如图2所示。
|
图 2 直流电缆等效热路图 Fig. 2 Equivalent heat circuit diagram of dc cable |
图中,Wc表示电缆线芯热源,Ws表示电缆三相芯线金属屏蔽层感应发热热源,Zcs表示导体屏蔽层的热阻,Zi表示绝缘层的热阻,Zis表示绝缘屏蔽层的热阻,Zn表示电缆包带层的热阻,Zs表示电缆外护套的热阻,Za表示电缆外表面与环境之间的等效热阻;Tc表示线芯温度,Tcs表示导体屏蔽层外表面的温度,Ti表示绝缘层外表面的温度,Tis表示绝缘屏蔽层外表面的温度,Tn表示电缆包带层外表面的温度,Ts表示电缆外护套外表面的温度,Ta表示环境温度;金属屏蔽层由于材料为铜,其热阻相比其他结构可忽略不计,可以认为其内外表面的温度相等。
1.2 直流电缆温度理论计算电缆各层热阻计算公式[16]为:
| $Z{\rm{ = }}\frac{{{\rho _T}}}{{2\text{π} }}\ln \left( {\frac{{{D_o}}}{{{D_i}}}} \right){\text{。}}$ | (2) |
式中:ρT为材料热阻系数,可通过查表2获知;Do为该层外径;Di为该层内径,将JDEPJ/SC电缆相关数据代入式(2)可求得其各层热阻,如表4所示。
|
|
表 4 JDEPJ/SC电缆各层热阻值 Tab.4 Thermal resistance values of each layer of JDEPJ/SC cable |
电缆表面与环境进行传导-自然对流换热,其等效热阻取为1.491 m2K/W。
单位长度直流电缆线芯损耗计算公式[17]为:
| ${W_c} = {I^{^{_2}}}{R_{DC}}{\text{。}}$ | (3) |
式中:I为电缆流过电流值;RDC为线芯单位长度直流电阻。
直流电阻计算公式为:
| ${R_{DC}} = {R_{20}}\left[ {1 + 0.003\;93\left( {T - 20} \right)} \right]{\text{。}}$ | (4) |
将式(4)代入式(3)可得单位长度电缆单芯线损耗如下式:
| ${W_c} = {I^2}R{}_{DC} = {I^2}{R_{20}}\left[ {1 + 0.003\;93(T - 20)} \right]{\text{。}}$ | (5) |
在正常运行状态下,电缆铜线芯温度最高,并沿径向递减,因此直流电缆中只存在由电缆线芯向外传热的传热过程。按照图2所示的等效热路模型,在已知环境温度Ta的条件下,线芯温度为:
| ${T_c} = {T_a} + \Delta {T_{ac}},$ | (6) |
| $\Delta {T_a}_c = {W_c}{Z_1},$ | (7) |
| ${Z_1} = {Z_{cs}} + {Z_i} + {Z_{is}} + {Z_n} + {Z_s} + {Z_a}\text{。}$ | (8) |
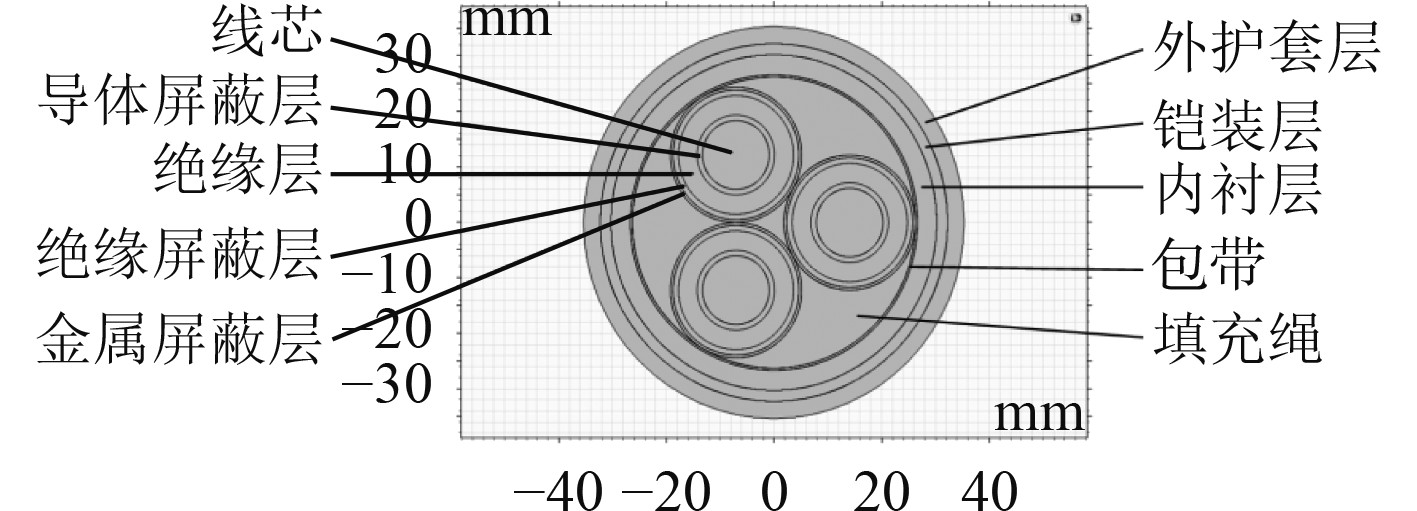
交流电缆JEZ85/SC采用乙丙橡胶绝缘,该电缆采用铜丝编织铠装,交联聚烯烃外护套,电缆由缆芯导体、导体屏蔽层、绝缘层、绝缘屏蔽层、金属屏蔽层、填充物、包带、内衬层、铠装层及外护套组成,图3为该电缆的几何模型,表5为其几何结构参数。
|
图 3 JEZ85/SC电缆几何模型 Fig. 3 Geometric model of JEZ85/SC cable |
|
|
表 5 JEZ85/SC电缆几何结构参数及材料 Tab.5 Geometric structure parameters and materials of JEZ85/SC cable |
当电缆通入交流电时,交变的电流产生交变的磁场,由电磁感应定律可知在金属屏蔽层和铠装层中会产生感应电流[17],进而产生涡流损耗;因此交流电缆运行过程中存在导体线芯,金属屏蔽层和铠装层3个热源。
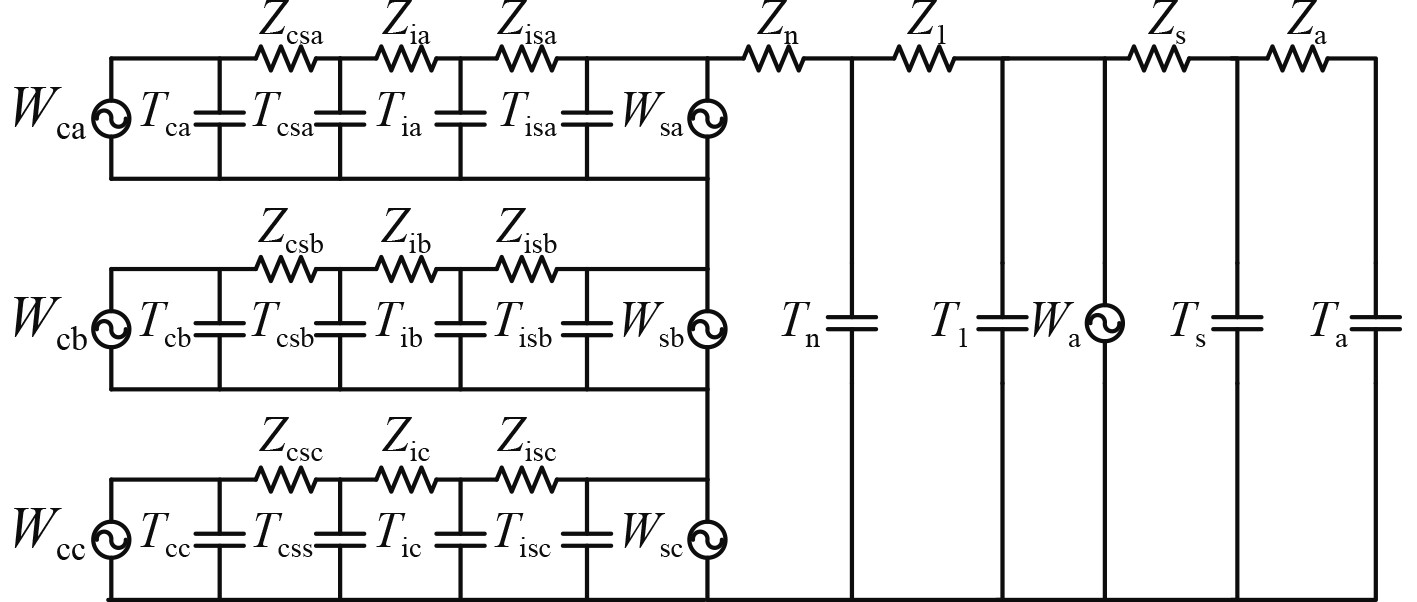
建立交流电缆的等效热路模型,如图4所示。
|
图 4 交流电缆等效热路图 Fig. 4 Equivalent heat circuit diagram of ac cable |
图中,Wca,Wcb,Wcc分别表示电缆A,B,C三相线芯热源,Wsa,Wsb,Wsc分别表示电缆A,B,C三相芯线金属屏蔽层感应发热热源,Wa表示电缆铠装层感应发热热源;Zcsa,Zcsb,Zcsc分别表示A,B,C三相芯线导体屏蔽层的热阻,Zia,Zib,Zic分别表示A,B,C三相芯线绝缘层的热阻,Zisa,Zisb,Zisc分别表示A,B,C三相芯线绝缘屏蔽层的热阻,Zn表示电缆包带层的热阻,Zl表示电缆内衬层的热阻,Zs表示电缆外护套的热阻,Za表示电缆外表面与环境之间的等效热阻;Tca,Tcb,Tcc分别表示A,B,C三相芯线温度,Tcsa,Tcsb,Tcsc分别表示A,B,C三相芯线导体屏蔽层外表面的温度,Tia,Tib,Tic分别表示A,B,C三相芯线绝缘层外表面的温度,Tisa,Tisb,Tisc分别表示A,B,C三相芯线绝缘屏蔽层外表面的温度,Tn表示电缆包带层外表面的温度,Tl表示电缆内衬层外表面的温度,Ts表示电缆外护套外表面的温度,Ta表示环境温度;金属屏蔽层及铠装层由于材料为铜,其热阻相比其他结构可忽略不计,认为其内外表面的温度相等。
1.4 交流电缆温度理论计算将JEZ85/SC电缆相关数据代入式(2)可求得其各层热阻,如表6所示。
|
|
表 6 JEZ85/SC电缆各层热阻值 Tab.6 Thermal resistance values of each layer of JEZ85/SC cable |
电缆表面与环境进行传导-自然对流换热,其等效热阻取为0.731 m2K/W。
单位长度交流电缆的线芯损耗计算公式[17]为:
| ${W_c} = {I^{^{_2}}}{R_{AC}}{\text{。}}$ | (9) |
式中:I为电缆流过电流有效值;RAC为线芯单位长度交流电阻。
交流电阻RAC计算公式[18]为:
| ${R_{AC}} = {R_{DC}}\left( {1 + {Y_s} + {Y_p}} \right){\text{。}}$ | (10) |
式中:YS为集肤效应因数;YP为邻近效应因数。
一般情况下:
| $\left\{ \begin{array}{l} {Y_s} = \dfrac{{{X_s}^4}}{{192 + 0.8{X_s}^4}} ,\\ {X_s}^2 = \dfrac{{8\text{π} f}}{{{R_{DC}}}} \times {10^{ - 7}}{k_s,} \\ {Y_p} = \dfrac{{{X_p}^4}}{{192 + 0.8{X_p}^4}}\left( {\dfrac{{{d_c}}}{s}} \right)\times 2.9 ,\\ {X_p}^2 = \dfrac{{8\text{π} f}}{{{R_{DC}}}} \times {10^{ - 7}}{k_p} {\text{。}} \end{array} \right.$ | (11) |
式中:dc表示导体外直径,为0.4 mm;s表示导体中心轴之间的距离,为0.4 mm;R20为20 ℃时电缆直流电阻;T为导体温度;电缆导体为紧压圆形导体,故ks,kp均取1。
在工频50 Hz的条件下:
| ${X_s}^2 = {X_p}^2 = \frac{{0.4\text{π} }}{{1.49 + 0.006\;4T}}{\text{。}}$ | (12) |
由式(12)可知,Xs2和Xp2为温度T的函数,但T的系数很小,在温度变化范围(0~95 ℃)的情况下可以忽略温度影响,认为临近效应系数和集肤效应系数为恒值,取T为20 ℃时,Ys=0.0031,Yp=0.009,由此可以得到单位长度电缆交流电阻如下式:
| $ \begin{split}&{R}_{AC}=1.012\;1{R}_{20}\left[1+0.003\;93\left(T-20\right)\right]\\ &\left(0 {\text{℃}}\leqslant T\leqslant 95 {\text{℃}}\right),\end{split}$ | (13) |
单位长度交流电缆单芯线损耗如下式:
| $ \begin{split}&{W}_{ac}={W}_{bc}={W}_{cc}={I}^{2}{R}_{AC}=1.012\;1{I}^{2}{\rm{R}}_{\rm{20}}\times \\ &\qquad\;\;\left[1+0.003\;93\left(T-20\right)\right]\\ &\left(0 {\text{℃}}\leqslant T\leqslant 95 {\text{℃}}\right){\text{。}}\end{split}$ | (14) |
金属屏蔽层及铠装层涡流损耗计算困难,一般采用有限元方法进行计算,经COMSOL有限元仿真软件计算得到20 ℃下金属屏蔽层涡流损耗为59.017 W/km,铠装层涡流损耗为9.17 W/km,涡流损耗的值随温度变化较小,在正常工况下可看作恒定值。
在正常运行状态下,电缆铜线芯温度最高,并沿径向递减,因此在金属屏蔽层内只存在由电缆线芯向外传热的传热过程。
因此,按照图4所示的等效热路模型,在已知环境温度Ta的条件下,线芯温度为:
| ${T_{ca}} = {T_{cb}} = {T_{cc}} = {T_a} + \Delta {T_{ac}},$ | (15) |
| $\Delta {T_{ac}} = 3{W_{ca}}{Z_1} + 3{W_{sa}}{Z_2} + {W_s}{Z_3},$ | (16) |
| ${Z_1} = Z{}_{ca} + {Z_{csa}} + {Z_{ia}} + {Z_{isa}} + Z_n^{} + {Z_l} + {Z_s} + {Z_a},$ | (17) |
| ${Z_2} = {Z_n} + {Z_l} + {Z_s} + {Z_a},$ | (18) |
| ${Z_3} = {Z_s} + {Z_a}\text{。}$ | (19) |
经理论计算得到JEZ85/SC电缆与JDEPJ/SC电缆在不同环境温度下表皮与缆芯温升数据,如表7所示。
|
|
表 7 理论计算电缆温升数据 Tab.7 Theoretical calculation of cable temperature rise data |
利用多物理场耦合仿真软件COMSOL Multiphysics对不同环境温度下额定通流的直流电缆与交流电缆的温度场进行仿真。由于本文研究的重点在于电缆径向温度场分布,因此在COMSOL软件中建立直流电缆二维模型见图1,交流电缆二维模型见图3,并在此基础上进行仿真研究。电缆几何结构尺寸见表3和表5,仿真所需的其他参数设置见表2。
|
|
表 3 JDEPJ/SC电缆几何结构参数及材料 Tab.3 Geometric structure parameters and materials of JDEPJ/SC cable |
在COMSOL软件中选择稳态仿真模式,结合电流与固体传热仿真模块,设定电缆电流为额定电流,即直流电缆通过电流为239A,交流电缆三相分别通入有效值为224A,相角相差120°的交流电流。改变固体传热的环境温度即可得到不同环境温度下电缆的温度场仿真结果,分别对直流电缆和交流电缆在0 ℃,10 ℃,20 ℃,30 ℃,40 ℃,50 ℃六种运行工况下进行温度场仿真计算,直流电缆温度场仿真结果如图5所示,交流电缆温度场仿真结果如图6所示。表8为交、直流电缆均流过额定电流时,其在6种不同运行工况下的仿真计算温升结果。

|
图 5 额定通流情况下直流电缆温度分布 Fig. 5 Temperature distribution of DC cable under rated current condition |
|
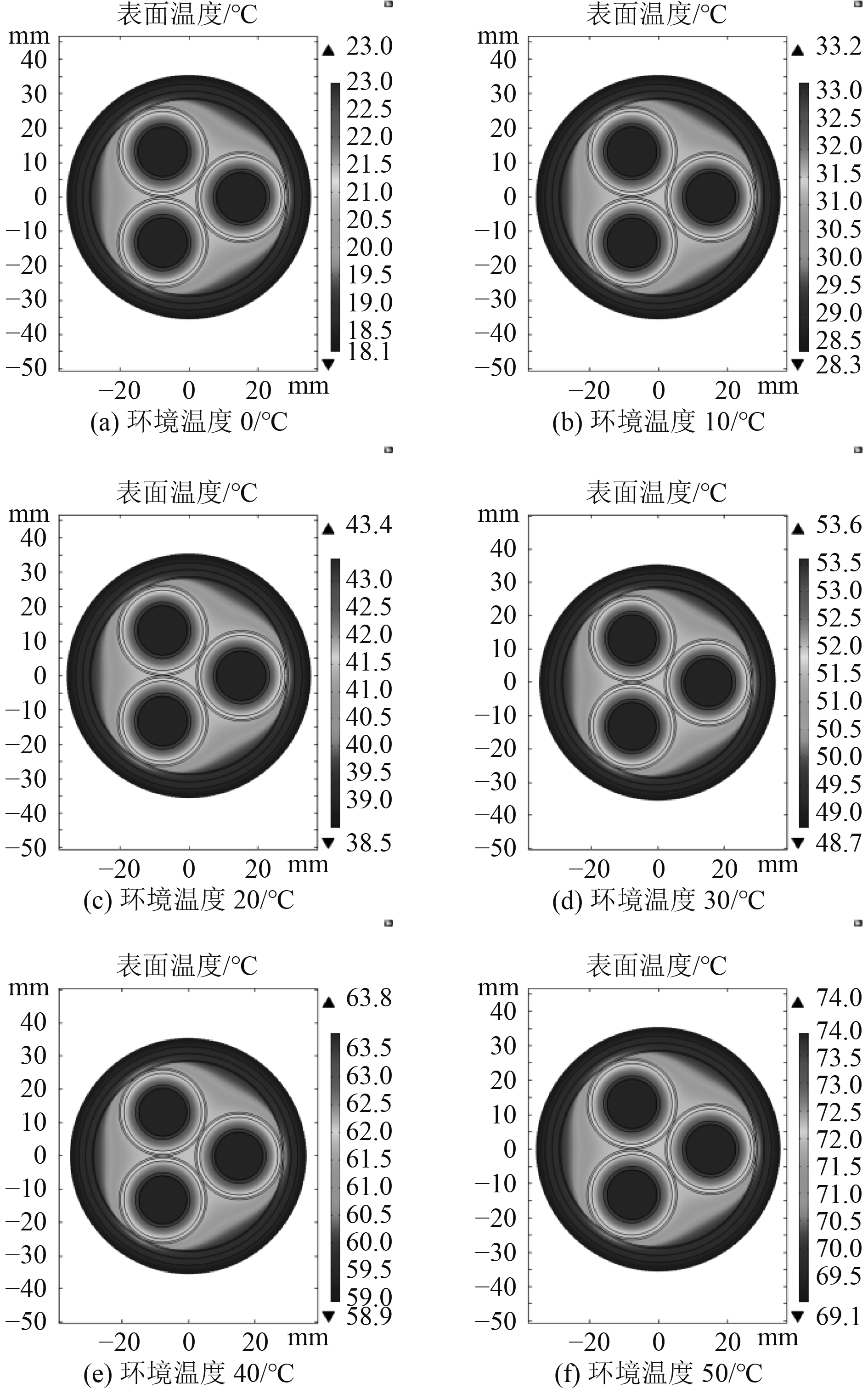
图 6 额定通流情况下交流电缆温度分布 Fig. 6 Temperature distribution of AC cable under rated current condition |
|
|
表 8 仿真计算电缆温升数据 Tab.8 Simulation calculation of cable temperature rise data |
从表8可知,当环境温度为0 ℃时,直流电缆的表皮温度为13.6 ℃,线芯温度为16.9 ℃,交流电缆的表皮温度为18.1 ℃,线芯温度为23 ℃,随着环境温度升高,交直流电缆表皮和线芯的温升都随之增大,与理论分析结果相同,随着温度上升,电缆线芯导体电阻增大,热功率随之增大;通过对比直流电缆与交流电缆温升数据可以看出,在相同环境温度下,直流电缆的温升小于交流电缆,且直流电缆线芯与电缆外表皮的温差也小于交流电缆,此外在通过额定载流量时,直流JDEPJ/SC电缆和交流JEZ85/SC电缆的表皮和线芯温升随着环境温度的升高而增大。仿真计算结果与按照热路模型解析计算的结果相符,表明本文所进行的解析计算是正确可行的。
3 结 语本文通过解析计算与仿真研究相结合的方式,对交、直流电缆的温度场特性进行对比分析与研究。研究结果表明,直流电缆温度场分布简单,在电缆中仅存在一个线芯导体为热源,热源产生的热量沿径向向外扩散,而三芯交流电缆不仅有3个线芯导体热源,且在导体外围存在金属屏蔽层和铠装层涡流损耗热源,使得三芯交流电缆的温度场分布更加复杂。通常船用电缆工作的环境温度在50 ℃以下,当环境温度设置为50 ℃时,交流电缆额定工况下的线芯温度为74 ℃,基本达到了乙丙橡胶的长期允许工作温度,而直流电缆额定工况下的线芯温度为67.5 ℃,尚未达到乙丙橡胶的温度限制,这表明直流电缆的参考载流量设置较为保守,未能完全发挥其载流能力,后续研究将通过提高解析计算模型精度、进行实验等方式对该结论进行将进一步验证。
此外,直流电缆温度场分布简单,易于计算和监测,因此对直流电缆进行实时温度监测的技术实施难度较小,且测得数据具有更高的准确性。
| [1] |
马伟明. 舰船综合电力系统中的机电能量转换技术[J]. 电气工程学报, 2015, 10(4): 3-10. |
| [2] |
马伟明. 舰船动力发展的方向——综合电力系统[J]. 上海海运学院学报, 2004(1): 1-11. DOI:10.3969/j.issn.1672-9498.2004.01.001 |
| [3] |
KELLOW M A. A numerical procedure for the calculation of the temperature rise and ampacity of underground cables[J]. IEEE Transactions on Power Apparatus Systems, 1981, PER-1(7): 3322-3330. |
| [4] |
S IEC 602872321—1995 Calculation of the current rating of electric cables, part 3: Sections on operating conditions, section 1: Reference operating conditions and selection of cable type[S]. 1995.
|
| [5] |
杨宁. 高压电力电缆输送能力的计算研究[D]. 吉林: 东北电力大学, 2019.
|
| [6] |
郝艳捧, 黄吉超, 阳林, 等. 高压直流电缆稳态载流量解析计算方法[J]. 电网技术, 2016, 40(4): 1283-1288. |
| [7] |
刘云鹏, 许自强, 陈铮铮, 等. ±160 kV直流XLPE海底电缆载流特性仿真及试验[J]. 电力自动化设备, 2018, 38(2): 130-136. |
| [8] |
梁永春, 李延沐, 李彦明, 等. 利用模拟热荷法计算地下电缆稳态温度场[J]. 中国电机工程学报, 2008(16): 129-134. DOI:10.3321/j.issn:0258-8013.2008.16.021 |
| [9] |
周晓虎. 地下高压电力电缆温度场数值计算[D]. 吉林: 东北电力大学, 2008.
|
| [10] |
于建立, 隋琳琳, 田际平, 等. 预埋管电缆载流量的有限容积法计算和分析[J]. 东北电力大学学报, 2013, 33(3): 43-46. |
| [11] |
阮羚, 赵艾萱, 邓丹, 等. 三芯电缆不平衡电流对温度分布的影响[J]. 高电压技术, 2018, 44(8): 2704-2709. |
| [12] |
鲁志伟, 张航, 敖明, 等. 电缆载流量试验热稳定判据及试验误差的研究[J]. 东北电力大学学报, 2016, 36(5): 25-31. DOI:10.3969/j.issn.1005-2992.2016.05.005 |
| [13] |
崔明, 杨宁, 敖明, 等. 直埋电缆周期性负荷载流量的计算分析[J]. 电测与仪表, 2019, 56(20): 91-96. |
| [14] |
梁永春, 柴进爱, 李彦明, 等. 有限元法计算交联电缆涡流损耗[J]. 高电压技术, 2007(9): 196-199. DOI:10.3969/j.issn.1003-6520.2007.09.044 |
| [15] |
张华富, 秦波. 10 kV配网电缆温度场和载流量计算分析[J]. 电工技术, 2019(13): 13-15. DOI:10.3969/j.issn.1002-1388.2019.13.005 |
| [16] |
赵镇南. 传热学[M]. 北京: 高等教育出版社, 2008.
|
| [17] |
刘建科. 大学物理[M]. 北京: 科学出版社, 2011.
|
| [18] |
张瑞永, 赵新宇, 陶礼学. 架空导线的交流电阻计算方法对比[J]. 电线电缆, 2014(4): 1-3. DOI:10.3969/j.issn.1672-6901.2014.04.001 |
 2021, Vol. 43
2021, Vol. 43
