0 引　言

自然循环是指依靠密度差和高度差形成的驱动力驱动流体循环流动的现象。自然循环在核动力系统中非常常见，其对反应堆安全有重要影响，因此准确模拟自然循环现象是当前反应堆热工水力分析中最重要研究内容之一。

目前主流热工水力系统分析程序如RELAP5，CATHARE，TRACE等普遍采用低阶差分法来求解基本守恒方程，其在模拟自然循环不稳定性问题时存在预测误差。为提高自然循环不稳定性问题的计算精度，本文采用基于两流体双压力两相流模型的高精度数值解法对Welander自然循环进行计算分析。

1 两流体双压力模型

两流体双压力模型基本守恒方程：

体积份额输运方程

$A\frac{{\partial {\alpha _g}}}{{\partial t}} + A{v_{\rm{int} }}\frac{{\partial {\alpha _g}}}{{\partial x}} = A\mu \left( {{P_g} - {P_f}} \right) + A\frac{{{\varGamma _g}}}{{{\rho _{\rm{int} }}}}{\text{。}}$

(1)

式中： ${\alpha _g}$ 表示汽相体积份额； ${P_g}$ 和 ${P_f}$ 分别代表汽相和液相压力，Pa； ${v_{\rm{int} }}$ 为相间界面速度，m·s⁻¹； $\mu $ 为压力松弛因子，Pa⁻¹·s⁻¹，表示汽液两相压力达到平衡的松弛速率； $A$ 为管道截面积，m²； ${\rho _{\rm{int} }}$ 为相间界面密度，kg·m⁻³； ${\varGamma _g}$ 为单位体积液-汽相间质量交换率，kg·m⁻³·s⁻¹。汽、液两相体积份额关系应满足：

${\alpha _g} + {\alpha _f} = 1,$

(2)

压力松弛系数为：

$\mu = \frac{1}{{{\tau _P}}}\frac{{{\alpha _f}{\alpha _g}}}{{{P_f} + {P_g}}}\text{。}$

(3)

其中 ${\tau _P}$ 为压力松弛时间，s。

质量守恒方程

$\frac{\partial }{{\partial t}}\left( {{\alpha _g}{\rho _g}} \right) + \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _g}{\rho _g}{v_g}A} \right) = {\varGamma _g},$

(4)

$\frac{\partial }{{\partial t}}\left( {{\alpha _f}{\rho _f}} \right) + \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _f}{\rho _f}{v_f}A} \right) = - {\varGamma _g}\text{。}$

(5)

式中： ${\varGamma _f} = - {\varGamma _g}$ 为单位体积汽-液相间质量交换率，kg·m⁻³·s⁻¹； $\rho $ 为相密度，kg·m⁻³； $v$ 为相速度，m·s⁻¹；f为液相标识；g为汽相标识。

动量守恒方程：

$\begin{split} \frac{\partial }{{\partial t}}\left( {{\alpha _g}{\rho _g}{v_g}A} \right) +\;& \frac{\partial }{{\partial x}}\left( {{\alpha _g}{\rho _g}v_g^2A} \right) = - {\alpha _g}A\frac{{\partial {P_g}}}{{\partial x}} + \\ & ({P_{\rm{int} }}\; \; - {P_g})A\frac{{\partial {\alpha _g}}}{{\partial x}} + {\alpha _g}{\rho _g}{{\rm{g}}_{\rm{x}}}A + {\Gamma _g}{v_{\rm{int} }}A - \\ & \frac{1}{8}{\rho _c}{C_{iD}}{A_{\rm{int} }}\left( {{v_g} - {v_f}} \right)\left| {{v_g} - {v_f}} \right|A - \\ & \frac{1}{2}\frac{{{f_{wall,g}}}}{D}{\rho _g}v_g^{}\left| {v_g^{}} \right|{\alpha _g}A,\\[-15pt] \end{split} $

(6)

$\begin{split} \frac{\partial }{{\partial t}}\left( {{\alpha _f}{\rho _f}{v_f}A} \right) +\;& \frac{\partial }{{\partial x}}\left( {{\alpha _f}{\rho _f}v_f^2A} \right) = - {\alpha _f}A\frac{{\partial {P_f}}}{{\partial x}} +\\ & ({P_{\rm{int} }} - {P_f})A\frac{{\partial {\alpha _f}}}{{\partial x}} + {\alpha _f}{\rho _f}{{\rm{g}}_{\rm{x}}}A - {\Gamma _g}{v_{\rm{int} }}A + \\ & \frac{1}{8}{\rho _c}{C_{iD}}{A_{\rm{int} }}\left( {{v_g} - {v_f}} \right)\left| {{v_g} - {v_f}} \right|A - \\ & \frac{1}{2}\frac{{{f_{wall,f}}}}{D}{\rho _f}v_f^{}\left| {v_f^{}} \right|{\alpha _f}A\text{。}\\[-15pt] \end{split} $

(7)

式中： ${P_{\rm{int} }}$ 为相间界面压力，Pa； ${f_{wall,k}}$ 为阻力系数; ${\rho _c}$ 为连续相密度，kg·m⁻³； ${C_{iD}}$ 为相间阻力系数； ${A_{\rm{int} }}$ 为单位体积相间界面面积，m⁻¹； ${g_x}$ 为重力加速度在流动方向的投影，m·s⁻²。

能量守恒方程

$\begin{split} \frac{\partial }{{\partial t}}\left( {{\alpha _g}{\rho _g}{e_g}} \right) +& \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _g}{\rho _g}{e_g}{v_g}A} \right) +\\ &\frac{1}{A}{P_g}\frac{\partial }{{\partial x}}\left( {{\alpha _g}{v_g}A} \right) = - {P_{\rm{int} }}\frac{{\partial {\alpha _g}}}{{\partial t}} +\\ &({P_g} - {P_{\rm{int} }}){v_g}\frac{{\partial {\alpha _g}}}{{\partial x}} + {\varGamma _g}\frac{{{{({v_g} - {v_{\rm{int} }})}^2}}}{2} + {Q_{wg}} +\\ &{H_{ig}}({T^s} - {T_g}) + {\varGamma _g}h_g^* + \frac{1}{2}\frac{{{f_{wall,g}}}}{D}{\rho _g}v_g^2\left| {v_g^{}} \right|{\alpha _g} \end{split}, $

(8)

$\begin{split} \frac{\partial }{{\partial t}}\left( {{\alpha _f}{\rho _f}{e_f}} \right) +& \frac{1}{A}\frac{\partial }{{\partial x}}\left( {{\alpha _f}{\rho _f}{e_f}{v_f}A} \right) +\frac{1}{A}{P_f}\frac{\partial }{{\partial x}}\left( {{\alpha _f}{v_f}A} \right) = \\ & - {P_{\rm{int} }}\frac{{\partial {\alpha _f}}}{{\partial {\rm{t}}}} +({P_f} - {P_{\rm{int} }}){v_f}\frac{{\partial {\alpha _f}}}{{\partial x}} - \\ &{\varGamma _g}\frac{{{{({v_f} - {v_{\rm{int} }})}^2}}}{2} + {Q_{wf}} {H_{if}}({T^s} - {T_f}) - \\ &{\varGamma _g}h_f^* + \frac{1}{2}\frac{{{f_{wall,k}}}}{D}{\rho _f}v_f^2\left| {v_f^{}} \right|{\alpha _f}\text{。}\\[-15pt] \end{split} $

(9)

式中： ${e_k}$ 为k相比内能/J·kg⁻¹； ${Q_{wg}}$ 为汽相单位体积壁面换热量，W·m⁻³； ${Q_{wf}}$ 为液相单位体积壁面换热量，W·m⁻³； ${H_{ig}}$ 为单位体积相间界面到汽相的换热系数，W·m⁻³·K⁻¹； ${H_{if}}$ 为单位体积相间界面到液相换热系数，W·m⁻³·K⁻¹； ${T^s}$ 为相间界面温度， ${T_k}$ 为k相温度，K； $h_g^*$ 为相间界面汽相比焓，J·kg⁻¹； $h_f^*$ 为相间界面液相比焓，J·kg⁻¹。

2 高精度数值算法 2.1 半隐式数值解法

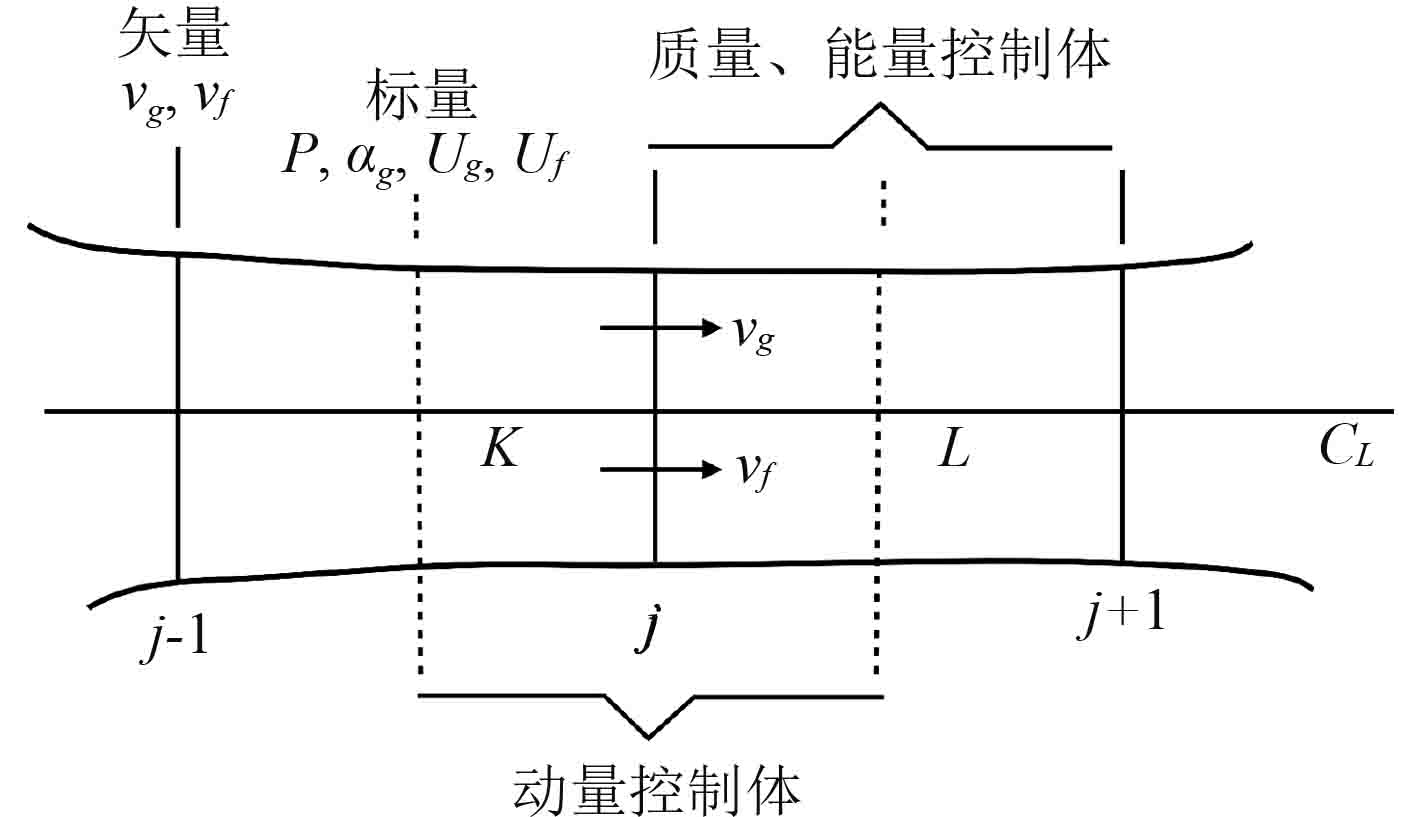
采用参考文献[1]作者提出的半隐数值算法求解两流体双压力模型。为达到快速计算的效果，半隐算法只对时间常数小、传播速度快的量隐式处理，如两相速度、压力梯度、相间界面质量和动量交换项，其他量显式处理。为了解决两相和单相之间转变带来的数值不稳定性问题，动量守恒方程和质量守恒方程处理成和与差的微分方程，所有守恒方程瞬态项采用展开的形式，再进行数值差分。采用交错网格划分控制体，如图1所示。K，L等表示求解质量、能量守恒方程的控制体，存储流场中的标量如压力、比内能、空泡份额等；j代表动量控制体（虚线包围），用于求解动量守恒方程，存储流场中速度矢量。

2.2 瞬态项二阶差分格式

目前现有的系统程序普遍采用一阶时间差分（BDF1）离散守恒方程瞬态项。BDF1离散误差大，给守恒方程的差分方程引入了“人工”扩散，宜采用精度更高的二阶时间差分（BDF2）来降低瞬态项的离散误差。二阶时间差分根据Taylor级数展开法得到^[2]：

$\begin{split} {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{{t_{n{\rm{ + }}1}}}} = &\frac{{\left( {\Delta {t_{old}} + 2\Delta {t_{}}} \right)}}{{\Delta {t_{}}\left( {\Delta {t_{old}} + \Delta {t_{}}} \right)}}\varphi _{}^{n{\rm{ + }}1} -\frac{{\left( {\Delta {t_{old}} + \Delta {t_{}}} \right)}}{{\Delta {t_{old}}\Delta {t_{}}}}\varphi _{}^n +\\ & \frac{{\Delta {t_{}}}}{{\Delta {t_{old}}\left( {\Delta {t_{old}} + \Delta {t_{}}} \right)}}\varphi _{}^{n - 1}\; {\text{。}}\end{split} $

(10)

其中： $\partial \varphi /\partial t$ 表示守恒方程中的瞬态项， $\Delta t = {t_{n + 1}} - {t_n}$ ， $\Delta {t_{{\rm{old}}}} = {t_n} - {t_{n - 1}}$ 。该式考虑了时间步长的变化，具有一般性，在系统程序中应用更为方便。BDF1和BDF2可处理成统一形式：

$\begin{split} &{\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{{t_{n + 1}}}} = \frac{{\delta \varphi _{}^{n + 1}}}{{\Delta t}} = \\ &\left\{ \begin{aligned} &{ \dfrac{1}{{\Delta {t_{}}}}\left( {\varphi _{}^{n + 1} - \varphi _{}^n} \right)},\qquad\qquad {\rm{BDF1}}, \\ & \begin{aligned}\dfrac{1}{{\Delta {t_{}}}}\left( \dfrac{{\left( {\Delta {t_{old}} + 2\Delta {t_{}}} \right)}}{{\left( {\Delta {t_{old}} + \Delta {t_{}}} \right)}}\varphi _{}^{n + 1} - \dfrac{{\left( {\Delta {t_{old}} + \Delta {t_{}}} \right)}}{{\Delta {t_{old}}}}\varphi _{}^n +\right.\\ \left.\dfrac{{\left( {\Delta {t_{}}} \right)_{}^2}}{{\Delta {t_{old}}\left( {\Delta {t_{old}} + \Delta {t_{}}} \right)}}\varphi _{}^{n - 1} \right),\;\;\, {\rm{BDF2}}\text{。}\qquad\;\;\end{aligned} \end{aligned} \right. \end{split}$

(11)

2.3 对流项三阶TVD差分格式

目前主流热工水力程序采用一阶施主元法离散对流项。一阶施主元法本质上是一阶迎风，计算精度低，因此宜采用稳定高阶施主元法，以提高对流项的计算精度。双压力模型守恒方程中与速度相关的项均采用施主元法计算。以能量方程对流项为例，其离散形式为：

$\begin{split}&{\left. {\frac{\partial }{{\partial x}}\left( {{\alpha _k}{\rho _k}{e_k}{v_k}A} \right)} \right|_L} =\\ &\quad\frac{{\left( {\dot \alpha _{k,j + 1}^n\dot \rho _{k,j + 1}^n\dot e_{k,j + 1}^n} \right)v_{k,j + 1}^{n + 1}{A_{j + 1}} - \left( {\dot \alpha _{k,j}^n\dot \rho _{k,j}^n\dot e_{k,j}^n} \right)v_{k,j}^{n + 1}{A_j}}}{{\Delta {x_L}}}\end{split},$

(12)

由于速度本身定义在接管上，因此对流项的计算精度很大程度上取决于接管上的标量 $\dot \phi $ （如 $\dot \alpha ,\;\dot \rho , \; \dot \alpha \dot \rho , $ $ \dot \alpha \dot \rho \dot e$ ）的计算方案。接管上标量 $\dot \phi $ 数值计算的统一形式可以写成：

$ {\dot{\phi }}^{n}{}_{j}=\left\{\begin{array}{l}{\phi }_{K}{}^{n}+\dfrac{\Delta {x}_{K}}{2}\psi \left(r\right){\left(\dfrac{\partial \phi }{\partial x}\right)}_{j-1}^{n},{\text{若}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}{v}_{j}>0,\\ {\phi }_{L}{}^{n}-\dfrac{\Delta {x}_{L}}{2}\psi \left(r\right){\left(\dfrac{\partial \phi }{\partial x}\right)}_{j+1}^{n}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}},{\text{若}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}{v}_{j}<0{\text{。}}\end{array}\right.$

(13)

其中： $\Delta x$ 是控制体长度； $\partial \phi /\partial x$ 是控制体边界上的梯度； $\psi \left( r \right)$ 为通量限制函数；r为梯度比，由下式给出：

$ r=\left\{\begin{array}{l}{\left(\dfrac{\partial \phi }{\partial x}\right)}_{j}^{n}\Biggr/{\left(\dfrac{\partial \phi }{\partial x}\right)}_{j-1}^{n},{\text{若}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}{v}_{j}>0,\\ {\left(\dfrac{\partial \phi }{\partial x}\right)}_{j}^{n}\Biggr/{\left(\dfrac{\partial \phi }{\partial x}\right)}_{j+1}^{n},{\text{若}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}\rm{\hspace{0.05em}}{v}_{j}<0{\text{。}}\end{array}\right.$

(14)

空间离散方案统一形式（13）由两部分组成，第一部分为稳定的一阶迎风方案，第二部分为反扩散项。因此，物理量 $\dot \phi $ 计算精度由反扩散项中的通量限制函数 $\psi \left( r \right)\; $ 决定。

稳定三阶TVD差分格式（命名为TOU_TVD_CFL）为^[2]：

$\psi \left( {{r_{}}} \right) = \max \left\{ {0,\min \left[ \begin{gathered} \min \left( {2\frac{{1 - C}}{C}\; \; ,2} \right)\; {r_{}}, \\ \min \left( {2\frac{{1 - C}}{C}\; \; ,2} \right),\frac{{2r + 1}}{3} \end{gathered} \right]} \right\}\text{。}$

(15)

式中C为Courant数。

3 计算分析 3.1 Welander自然循环问题

Welander提出了竖直回路中单相自然循环问题来研究流体的不稳定性行为^[3]。Welander自然循环回路由2个平行的竖直绝热管，顶部冷源和底部热源组成，如图2所示，回路总长为L，截面积为A，热阱和热源长度为 $\Delta s$ 。通过顶部热阱的冷却和底部热源加热，流体在回路顶部和底部产生密度差，从而驱动流体发生自然循环流动。通过选择合适的浮力与摩擦阻力的比值，流动可能会出现稳定、弱不稳定和强不稳定行为。在文献[3]中，Welander推导了实验回路层流下流动不稳定性理论边界，Ambrosini和Ferreri^[4]将不稳定性边界扩展湍流情况，如图3所示。Welander自然循环稳定性边界绘制成无量纲重力系数 $\alpha $ 和无量纲摩擦系数 $\varepsilon $ 的关系式图，无量纲量具体表达式为：

$\left\{ \begin{gathered} \alpha = \frac{{g\; \beta \; \Delta T\; \left( {L - 2\Delta s} \right)}}{{2(k\; \; \Delta s)_{}^2}}, \\ \varepsilon = \frac{a}{{16}}\left( {\frac{{{\rho _f}\; D\; k\; \Delta s}}{{{\mu _f}}}} \right)_{}^{1 - b}\frac{{R\; L}}{{2k\; \; \Delta s}} \text{。}\\ \end{gathered} \right.$

(16)

式中：Welander定义的层流摩擦系数为 $R = 64/{\rm{Re} _f} \cdot $ $ \left| {{v_f}} \right|/\left( {2D} \right) = 32{\mu _f}/\left( {{\rho _f}D_{}^2} \right)$ ；Welander定义的换热系数为 $k = {h_f}/{\rho _f}{C_{Pf}} \cdot \text{π} D\Delta s/ $ $ \left( {\text{π} r_{}^2\Delta s} \right)$ ；温差 $\Delta T = \left( {T_{w,heater}} - \right. $ $ \left. {T_{w,cooler}} \right)/2$ ；当 $a = 0.316\;4/ $ $ 4,b = 0.25$ 时，表示湍流条件；当 $a = 16,b = 1$ 时，表示层流条件。

对于Welander单相振荡自然循环问题，选取Ambrosinia和Ferreri ^[5]设置的几何参数和边界条件。管内径为0.1 m，热源和冷源长度为0.1 m。管道充满压力为0.1 MPa的过冷水。热源温度为30 ℃，与流体换热系数为20000 W·m⁻²·K⁻¹，冷源温度维持20 ℃，与流体换热系数为20000 W·m⁻²·K⁻¹。本文研究Welander单相振荡自然循环问题3个不同的实验工况：强不稳定模式、弱不稳定模式和稳定模式，见表1。

图4给出了Welander自然循环回路数值模拟节点图。在进行模拟计算时，时间步长为0.5 s，热源和冷源分别采用一个节点模拟，两垂直绝热管都均分为N个控制体，因此环路控制体总数为2N+2。

3.2 数值结果

对于强不稳定模式工况，环路长度取L=20.2 m，此时 $(\alpha ,\varepsilon )$ 为 $ (343.79,\rm{ }2.346\;84)$ 。强不稳定模式时，实验回路流量出现流动反转现象，并作平均速度为零的等幅振荡。为便于观测到流动不稳定性行为，实验之初，给定回路一个极小流量的扰动。

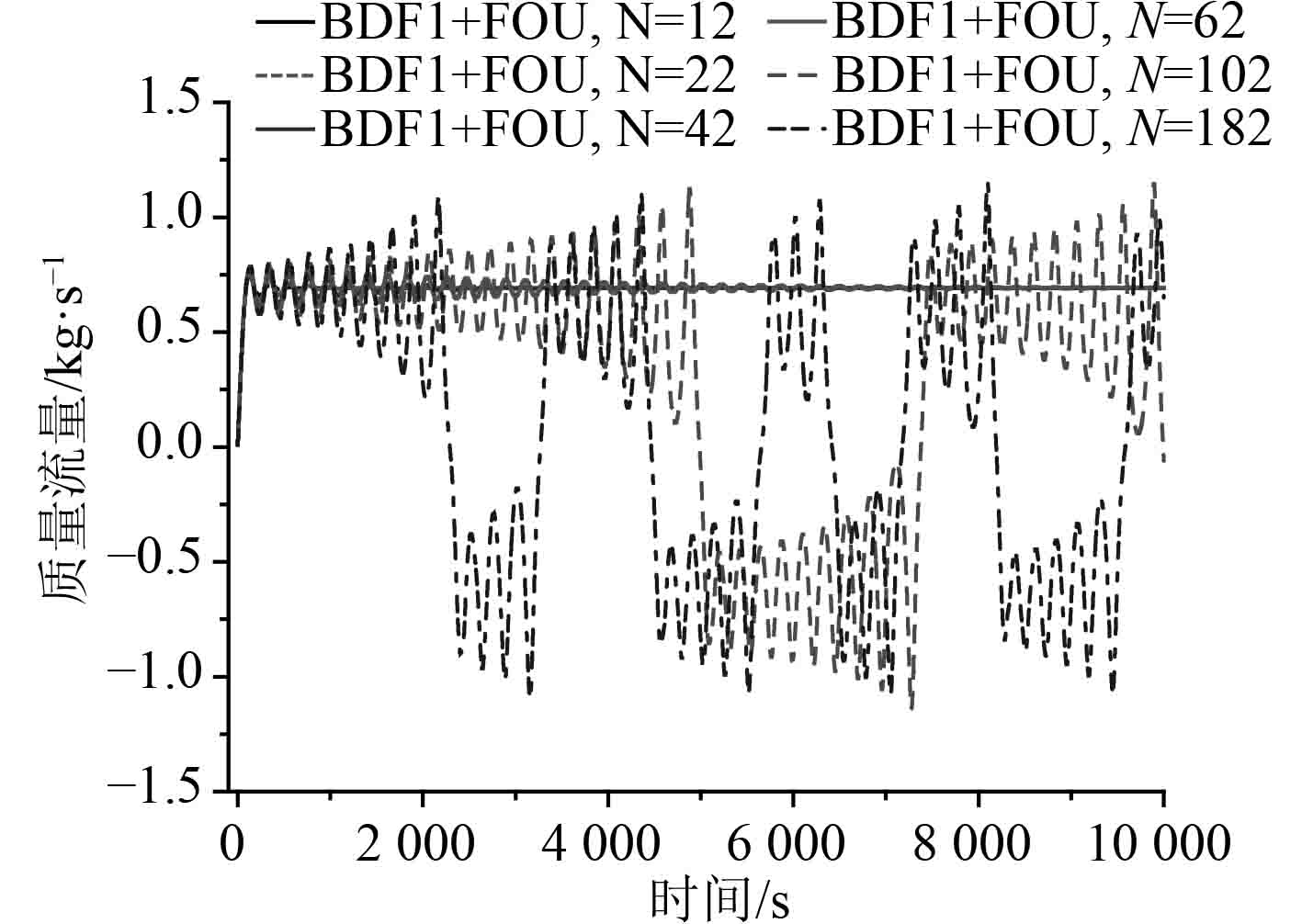
图5给出了使用低阶差分方案BDF1+FOU在不同控制体数下的数值结果。由图可知控制体数低于62时，数值误差过大，无法预测出不稳定行为；控制体数达到102时才预测出不稳定性行为，控制体数越多，数值误差越小，预测的不稳定行为振荡周期越短。由于数值误差的阻尼作用，粗糙网格可以稳定物理上不稳定的系统。采用不同计算节点，低阶差分数值结果会出现系统稳定和不稳定2种相矛盾的情况。因此数值误差对不稳定性行为准确预测有很不利的影响，低阶差分方案BDF1+FOU精度低，不利于研究流动不稳定行为。

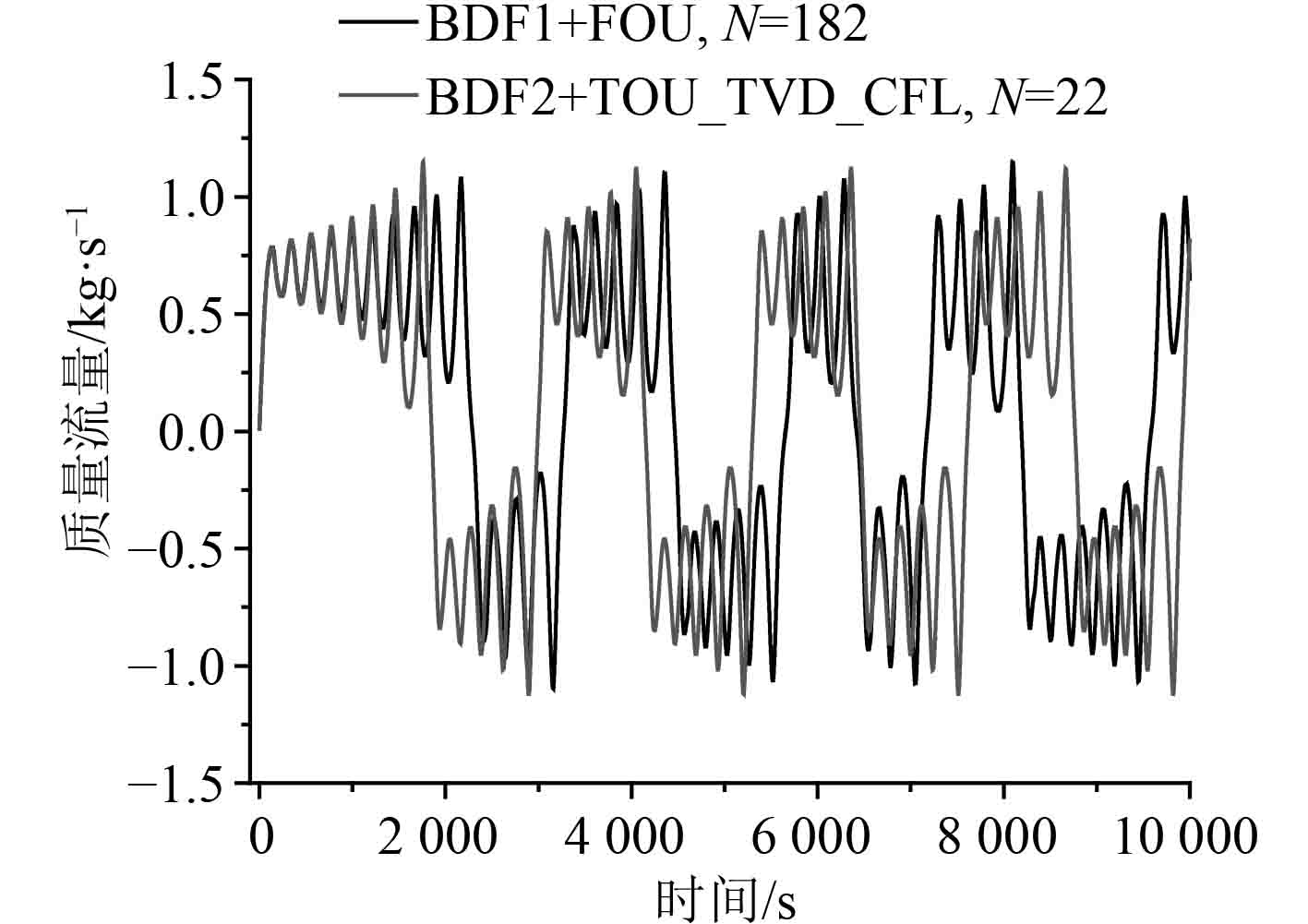
图6给出了高阶差分方案与低阶差分方案结果的对比。高阶差分方案模拟流动不稳定性行为具有相当大的优势。高阶差分方案TOU_TVD_CFL只需22个控制体就可以预测出不稳定行为，因此高阶算法有效减小了数值扩散，提高了计算精度。高阶差分算法采用22个控制体的数值精度可达到低阶差分算法控制体数为182的计算精度，振荡周期相近。

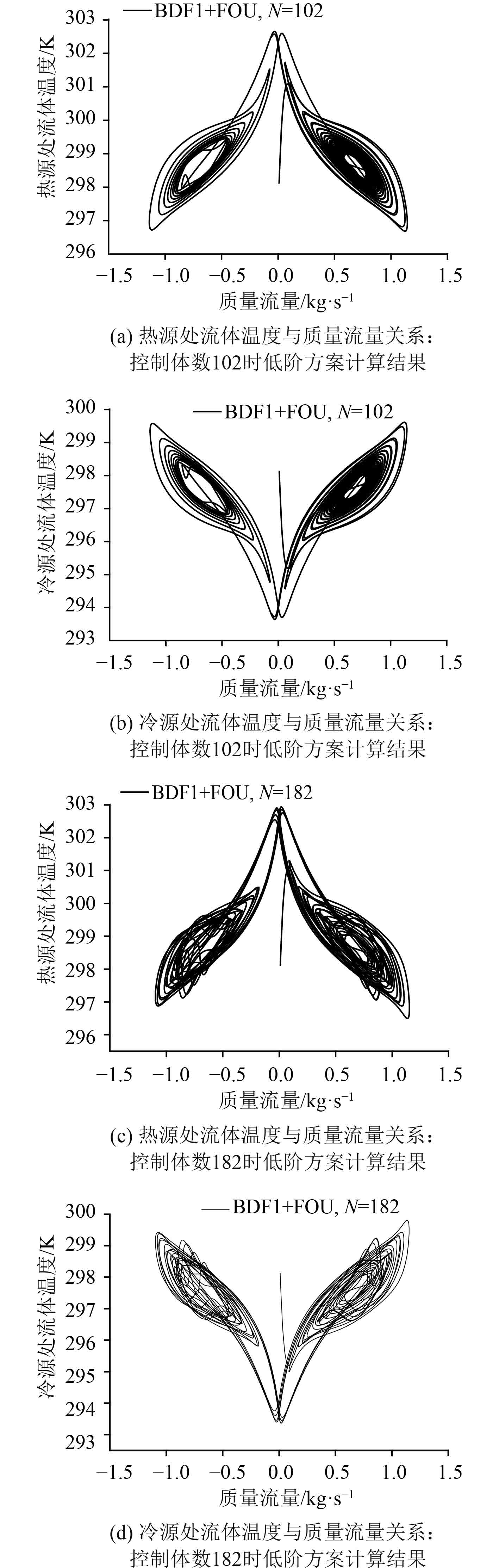
图7给出了低阶差分方案BDF1+FOU计算的流体温度与质量流量关系图，随着控制体数增多，精度越高，混沌行为（Chaotic Behavior）越明显。图8给出了高阶BDF2+TOU_TVD_CFL方案计算的流体温度与质量流量关系图。同样可以看出，随着控制体数增多，可以预测到流动反转的混沌演化过程，流体温度与质量流量关系图类似蝴蝶形状。

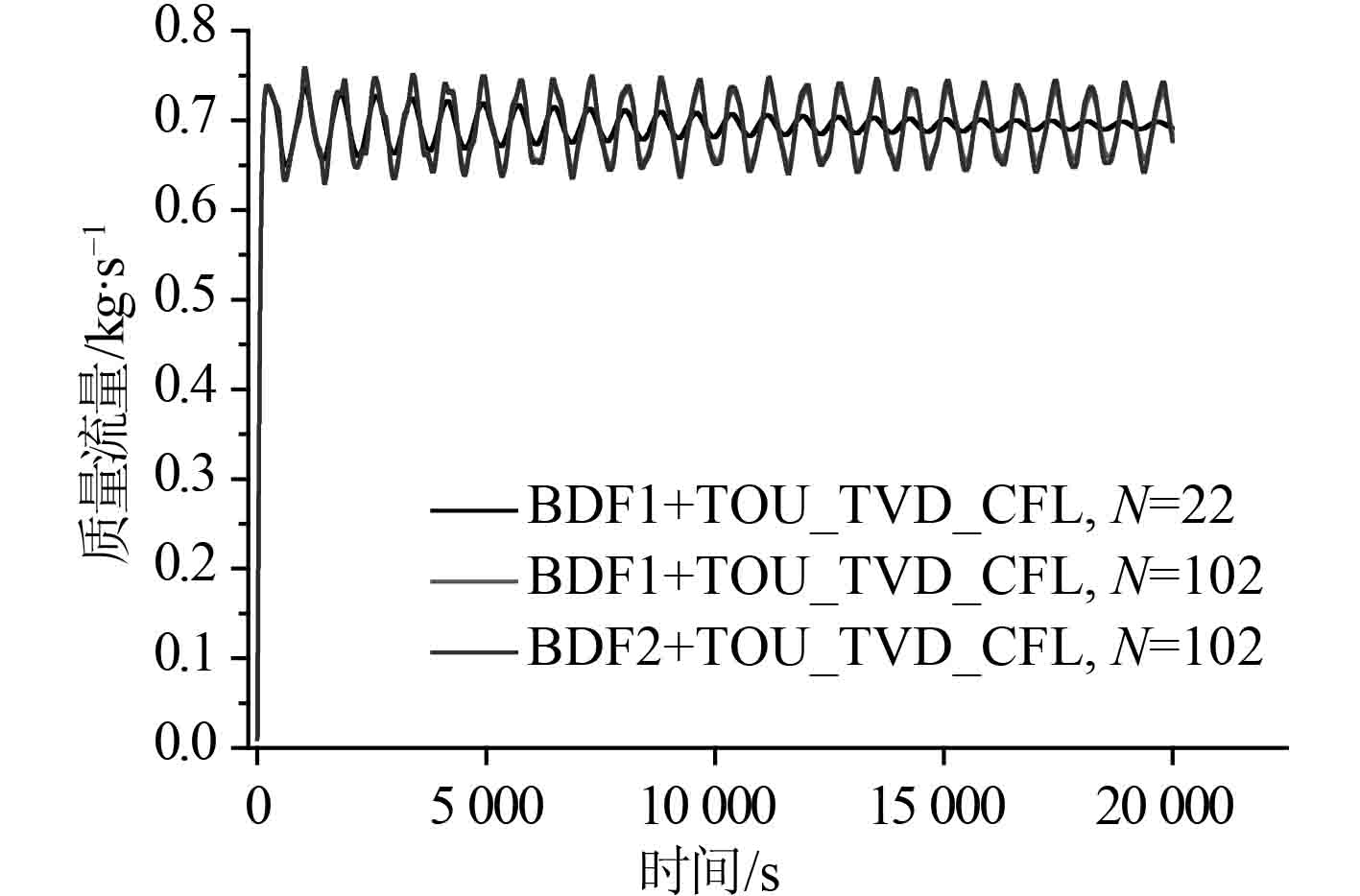
针对弱不稳定工况，回路总长为80.2 m。弱不稳定模式时，回路流量不会出现流动反转现象，其维持一个流动方向上的近似等幅振荡。图9给出了采用低阶方案计算的质量流量随时间变化图。控制体数为722时质量流量的数值结果依旧出现缓慢的衰减，低阶差分结果误差大。图10给出了弱不稳定工况下采用高阶差分方案计算的质量流量随时间变化图。高阶算法的结果有效减小人工粘性，抑制振荡衰减，控制体数为102时就可以模拟出等幅振荡的流动不稳定性行为。

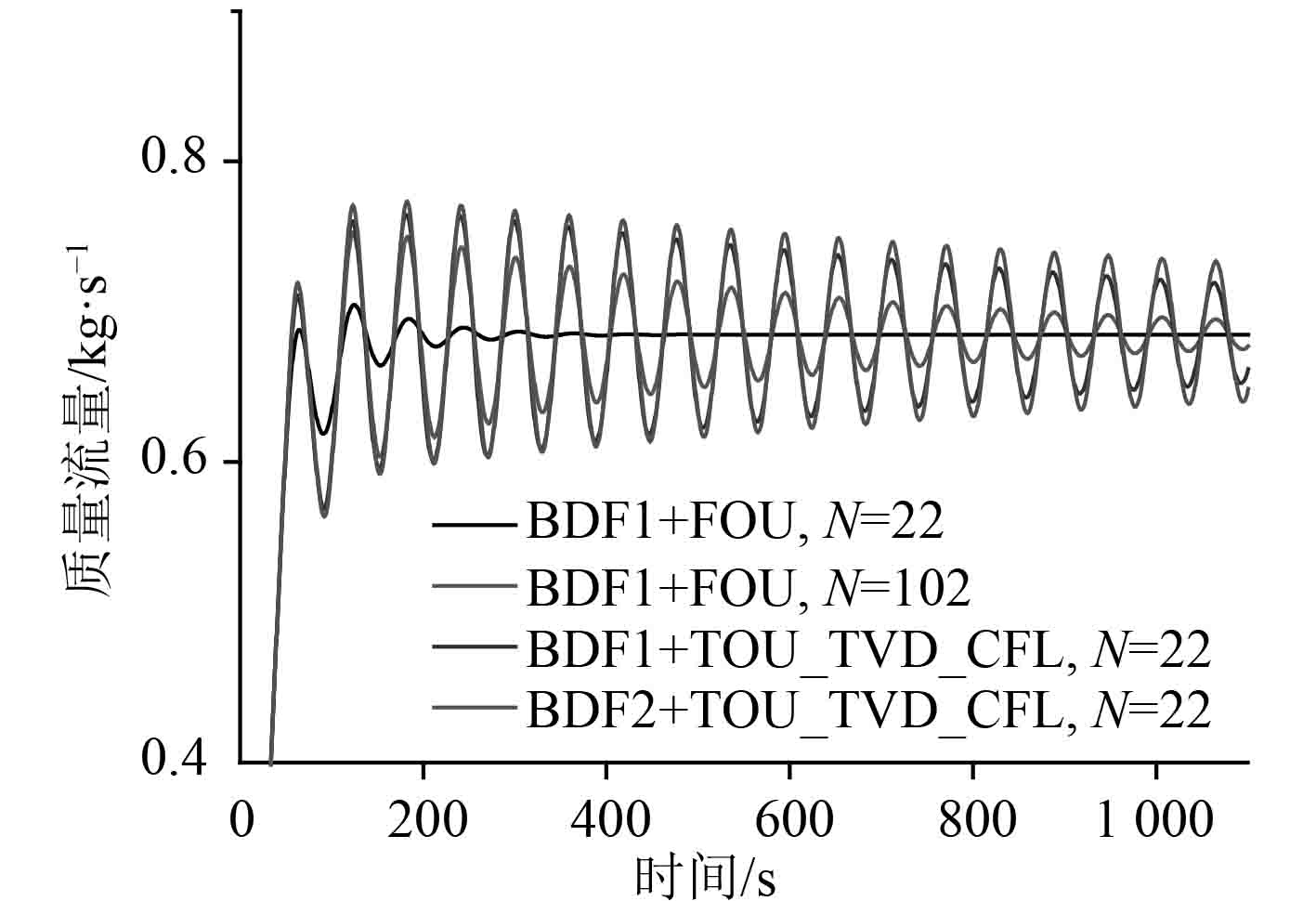
针对L=5.2 m的稳定模式工况，表现为：质量流量初始增加到最大值，然后经过一段时间的衰减型振荡后维持稳定运动。图11和图12给出了稳定模式工况下质量流量的计算结果，高阶方案与低阶方案计算结果对比见图13。因为人工粘性的影响，低阶差分预测更小的振荡振幅，更快达到稳定状态；控制体数为102的低阶结果精度比控制体数为22的高阶结果精度还低，振荡衰减更快。由于高阶差分对稳态没影响，最终高阶差分预测的稳态流量与低阶结果一致。

4 结　语

本文采用两流体双压力两相流模型高精度数值算法对Welander自然循环的流动不稳定性问题进行计算分析，数值结果表明：高阶差分格式可以以较少的网格精确地预测不稳定性边界和混沌行为，而采用低阶差分在网格不够精细的情况下有可能将自然循环不稳定模式预测为稳定模式，得到错误的结果。因此高精度数值解法能有效减小数值扩散，提高自然循环问题的预测精度。