船用燃气轮机运行时,箱装体内温度较高,为了保证各工作部件和运行人员的正常工作,必须对燃气轮机箱装体内进行冷却。冷却的方式一般有2种,一种是利用风机对箱装体进行强制通风来冷却,另一种方式即利用燃气轮机高温高速的排气来引射空气,在箱装体内形成连续的空气流来冷却。第2种方式不需要安装专门的设备,既简单又不消耗能源,被广泛应用于船用燃气轮机箱装体[1]。本文研究的某型船即采用的这种方式。衡量排气引射系统的性能主要有2个指标[2]:1)引射系数n,利用被引射的空气的质量流量与燃气轮机排气流量的比值来定义,n值越大,引射性能越好;2)混合度ε,即引射器出口处气体流速的均匀程度,利用出口处最大速度与平均速度的比值来定义,ε值越接近1,混合越好。在船用排气引射系统中对混合度没有要求,根据相关技术文件要求,为了达到规定的冷却效果,在燃机满工况运行时,某型船的排气引射系数不能低于10%,本文即对某型船的排气引射系统进行分析和优化改进,使其达到设计要求。
1 原装置的数值分析 1.1 排气引射装置结构分析及建模针对引射冷却空气通道及排气引射通道内气体的流动,严格按照原装置的结构布置和尺寸在UG软件中建立几何模型,对排气引射性能影响较小的结构进行适当简化。最终模型结构如图1所示。

|
图 1 燃气轮机排气引射系统模型 Fig. 1 Model of gas turbine exhaust ejector system |
从图中可以看出,排气引射系统主要包括进气室、稳压室、联通通道、箱装体、燃气轮机、排气管、混合段和机外引射装置等。其中引射混合段相对于排气管轴线向后倾斜,高度约5 m,混合段为扩张形,入口直径比出口直径小。为方便进行数据统计,分别定义多个参考截面。各截面分别为:A为压力入口;B为竖井进口面;C为引射空气箱装体入口;D为引射截面1;E为引射截面2;F为排气管入口;G为排气管出口;H为引射混合段入口;I为混合段考察截面;J为燃机排气喷口;K为排气引射系统出口。燃气轮机工作时,高温高速的排气从排气管出口G喷出形成射流,由于气体增速降压,在排气管出口处形成一定的低压区,冷却空气流入之后被主流不断卷吸进入混合段,最终流出系统外。
1.2 网格划分由于排气系统模型尺寸较大,同时包含有小尺寸结构,划分结构网格较为困难且难以保证网格质量,因此采用非结构网格划分。在重点考察部分及结构尺寸较小的区域进行了加密处理,以期达到较高的计算效率和计算精度。本文使用的网格划分工具为ANSYS ICEM CFD,计算域网格总数为700万,质量在0.2以上,网格如图2所示。

|
图 2 排气引射系统计算网格 Fig. 2 Grid of exhaust ejector system |
在对排气引射系统进行数值模拟时,对于可压缩的粘性气体,如忽忽略质量力,则流场的参数控制方程组如下[3-5]:
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho \mathop V\limits^{\rightharpoonup} ) = 0,$ | (1) |
| $\frac{{\partial (\rho \mathop V\limits^{\rightharpoonup} )}}{{\partial t}} + \nabla \cdot (\rho \mathop V\limits^{\rightharpoonup} \mathop V\limits^{\rightharpoonup} ) = - \nabla p + \nabla \cdot \Pi, $ | (2) |
| $\frac{{\partial (\rho E)}}{{\partial t}} + \nabla \cdot (\rho \mathop V\limits^{\rightharpoonup} E) = \nabla \cdot \left[ {( - pI + \Pi ) \cdot \mathop V\limits^{\rightharpoonup} } \right] - \nabla \cdot \mathop q\limits^{\rightharpoonup}, $ | (3) |
| $\frac{p}{\rho } = RT{\text{。}}$ | (4) |
式中:
| $\varPi = - \frac{2}{3}\mu (\nabla \cdot {\mathop V\limits^{\rightharpoonup}} )I + \mu (\nabla {\mathop V\limits^{\rightharpoonup}} + \nabla {{\mathop V\limits^{\rightharpoonup}} ^{\rm{T}}}),$ | (5) |
| $I = \left\{ {{\delta _{ij}}} \right\},$ | (6) |
| $E = e + \frac{1}{2}{\mathop V\limits^{\rightharpoonup}} \cdot {\mathop V\limits^{\rightharpoonup}}, $ | (7) |
| $e = \frac{1}{{(\gamma - 1)}}\frac{p}{\rho },$ | (8) |
| ${\mathop q\limits^{\rightharpoonup}} = - k\nabla T{\text{。}}$ | (9) |
其中:
数值计算使用Ansys Fluent商用软件,其基于有限体积法对控制方程进行离散,湍流模型选用κ-ε模型,在保证网格质量和正确边界条件的情况下计算精度可以达到工程要求[6]。
1.4 计算边界条件综合分析实船排气引射系统的工作条件以及工作环境,对计算模型的边界条件设置如下:
参考压力为101325 Pa;
引射空气进口处于标准大气条件下,设为压力入口,相对参考压力为0 Pa,温度为300 K,法向进气;
排气管进口设为质量流量进口(mass flow-inlet),给定燃气轮机1.0工况运行时的流量和动力涡轮的排气温度,法向进气;
引射系统出口处于标准大气条件下,设为压力出口,相对参考压力为0 Pa,温度为300 K,法向排气;
进气滤清器等效转换为多孔介质,对于简单的均匀多孔介质,
| ${S_i} = - \left( {\frac{\mu }{\alpha }{v_i} + {C_2}\frac{1}{2}\rho \left| v \right|{v_i}} \right)\text{。}$ | (10) |
其中:α为渗透率,C2为惯性阻力因子,按照滤清器阻力特性,利用总压损失与速度的关系拟合成二次曲线的形式,经拟合得到其公式表达式△P=aV2+bV,进而可得到多孔介质的渗透率α及压力阶跃系数C2。
将进气滤清器设置为多孔介质边界,根据提供的参数,最终确定α=1.57E−07,△m=100,C2=95.36。
对于所有的外壁面,全部设成绝热无滑移壁面。
1.5 原型计算结果经过对原型排气引射系统的计算,得到排气引射系数为6.51%,远小于设计要求10%。表1为排气引射系统各截面总压及压力损失值,从表中可以看出,随着高温排气和引射空气的流动,总压不断降低,但是在D到E截面总压增加,阻碍了引射气体的流动,产生回流,导致引射性能下降,箱装体温度过高,因此需要对排气引射系统进行结构改进来提高引射系数。
|
|
表 1 各截面总压及压力损失 Tab.1 Total pressure and pressure loss of each section |
李东明等[7]利用数值计算和试验的方法研究了不同引射器结构对引射性能的影响。结果表明,在进口条件相同时,带有圆柱形混合段的引射器的引射系数大于锥形混合段的引射器。因此本文拟将原型引射器改为圆柱形混合段的引射器。引射器的结构如图3所示,主要部件有:工作喷嘴、接受室、混合段、扩压段,1-1截面是混合段入口截面,2-2截面是混合段出口截面,3-3截面是扩压段出口截面。
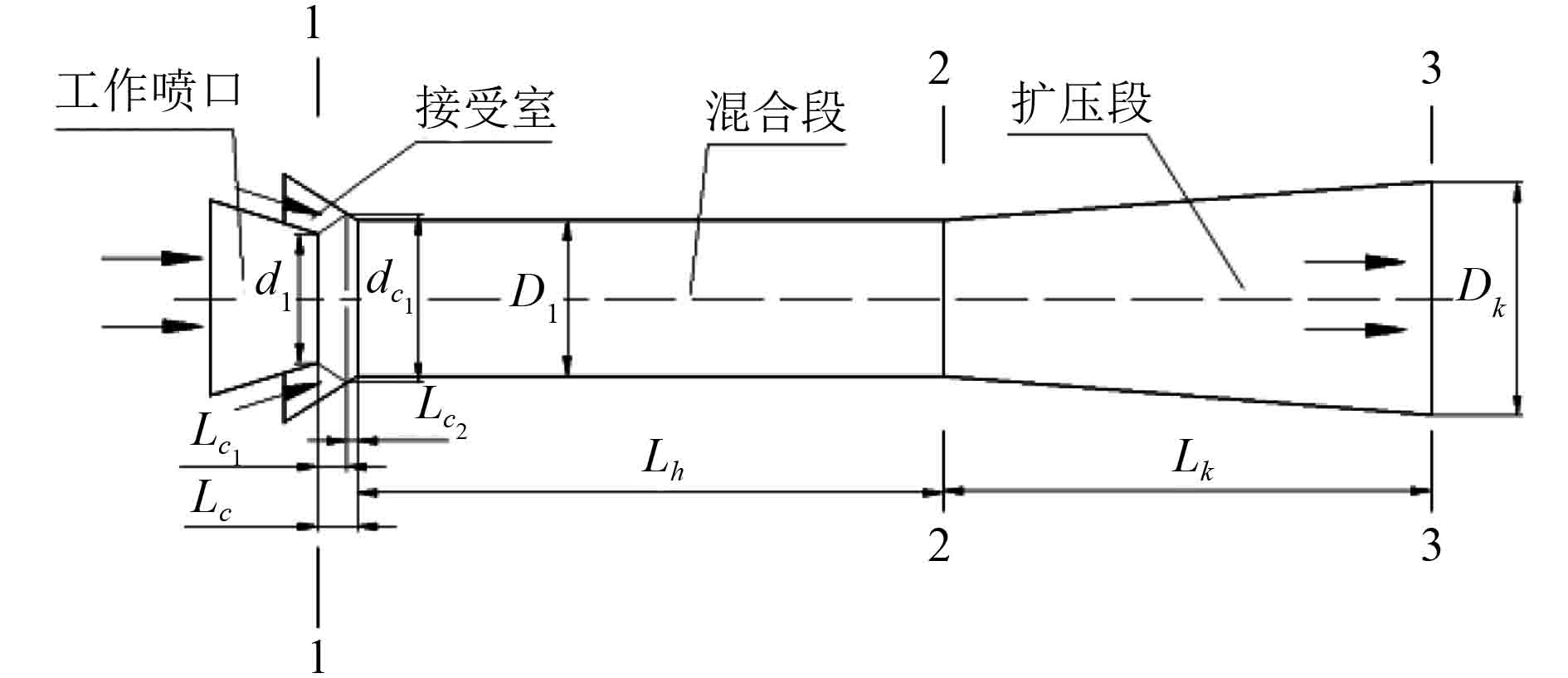
|
图 3 引射器结构示意图 Fig. 3 Structure diagram of ejector |
本文的目标引射系数为n=0.1,根据原型的计算结果初步给定扩压器出口截面的静压P3=2500 Pa。
引射器各处边界条件:
工作流体温度T1、压力P1=0.1068 MPa、比容V1=2.218 m3/kg、密度ρ1=0.451 kg/m3;引射流体温度T2=100 ℃、压力P2=0.109 MPa、比容V2=1.068 m3/kg、密度ρ1=0.936 kg/m3;混合流体温度T3=(T1+nT2)/(1+n)、压力P3=0.104 MPa、比容V3=2.058 m3/kg、密度ρ1=0.451 kg/m3。
根据引射器设计原理[8],对引射能力进行计算如下:
面积比
| $ ({f_2}/{f_{11}})opt = ( - b + \sqrt {{b^2} - 4ac} )/2a, $ | (11) |
其中:
| $a = {\varphi _1}{\varphi _2},$ | (12) |
| $b = - \left\{ {}{\varphi _1}{\varphi _2} + 2{\varepsilon _{12}}\left[ \begin{gathered} \left( {\frac{1}{{{\varphi _3}}} - 0.5} \right)\frac{{{\upsilon _3}}}{{{\upsilon _1}}}{\left( {1 + n} \right)^2} \\ - \left( {{\varphi _2}{\varphi _4} - 0.5} \right)\frac{{{\upsilon _3}}}{{{\upsilon _1}}}{n^2} \\ \end{gathered} \right] {} \right\},$ | (13) |
| $c = 2{\varepsilon _{12}}\left( {\frac{1}{{{\varphi _3}}} - 0.5} \right)\frac{{{\upsilon _3}}}{{{\upsilon _1}}}{\left( {1 + n} \right)^2}{\text{。}}$ | (14) |
式中:
通过计算得到a = 0.92625,b = −2.2367,c = 1.31761。代入可得最佳面积比(f2/f11)opt = 1.39523。
引射流体的压力升高公式为:
| $\frac{{\Delta p}}{{{p_2}}} = {k_p}{\Pi _{1*}}\frac{{{p_1}}}{{{p_2}}}\frac{{{f_{11}}}}{{{f_2}}}q_{12}^2\left[ \begin{split} &{\varphi _1}{\varphi _2}\frac{{{\lambda _{12}}}}{{{q_{12}}}} \\ &+ {\varepsilon _{1*}}\left( {{\varphi _1}{\varphi _2} - 0.5} \right)\frac{{{\upsilon _2}}}{{{\upsilon _1}}}\frac{{{f_{11}}}}{{{f_{12}}}}{n^2} \\ & - {\varepsilon _{1*}}\left( {\frac{1}{{{\varphi _3}}} - 0.5} \right)\frac{{{\upsilon _3}}}{{{\upsilon _1}}}\frac{{{f_{11}}}}{{{f_2}}}{\left( {1 + n} \right)^2} \\ \end{split} \right]{\text{。}}$ | (15) |
式中:kp = 1.4,Π1* = 0.528,ε1* = 0.634,f2 = f11 + f12,将各参数代入可得:
| $\frac{{\Delta p}}{{{p_2}}} = 0.037\;71,$ | (16) |
| $\Delta p = 0.037\;1{p_2} = 3\;804{\rm{Pa}},$ | (17) |
| ${p_3} = {p_2} + \Delta p = 0.104\;68{\rm{MPa}}\text{。}$ | (18) |
从上述结果可以看出,通过计算得到的混合流体压力P3大于假设的P3,所以假设是成立的。
2.2 引射器结构尺寸计算已知工作喷嘴的直径d1,扩压器出口直径Dk。
自由流束的长度:
| ${l_{c1}} = \left[\sqrt {0.083 + 0.76n} - 0.29\right]{d_1}/0.16,$ | (19) |
自由流束直径:
| ${d_{c1}} = 3.4{d_1}\sqrt {0.083 + 0.76n}, $ | (20) |
混合段的直径:
| ${D_1} = {d_1}\sqrt {{{({f_2}/{f_{11}})}_{opt}}} ,$ | (21) |
混合段入口长度:
| ${l_{c2}} = ({d_{c1}} - {D_1})/2,$ | (22) |
工作喷口截面与混合段入口截面的距离:
| ${l_c} = {l_{c1}} + {l_{c2}}\text{。}$ | (23) |
根据上述计算,综合考虑燃气轮机的排气损失及现场安装情况,确定混合段直径D1,
引射系统改进的目的是在尺寸最小的排气装置中建立起足够多的引射空气量,同时要考虑排气系统对燃气轮机性能的影响,考虑到引射器实际安装情况,要保持排气管出口d1、扩压器出口直径Dk、工作喷口截面与混合段入口截面的距离
|
|
表 2 不同长度混合段的计算结果 Tab.2 Results of mixing section with different length |
从表中可以看出,相同进排气条件下,当混合室直径为D1时,长度为1.87 D1,计算的引射系数得到明显提升,考虑实际安装空间和船厂要求,最终确定混合段长度Lh取1.87 D1。
3 排气引射系统改进计算分析原型中混合段与排气管轴线有一定的倾斜角度,这会造成阻力的增加,从而影响引射气体的流动,针对此原因以及前面的计算结果,制定了2种改进方案。方案1:将混合段向后倾斜改为与排气管中心线平行,其他结构尺寸保持不变;方案2:将引射混合段改为与排气管中心线平行的直段,直径D1、长度1.87 D1,保证引射器总体高度和接口尺寸不变来确定扩压器的模型。最终建立的几何模型如图4所示。
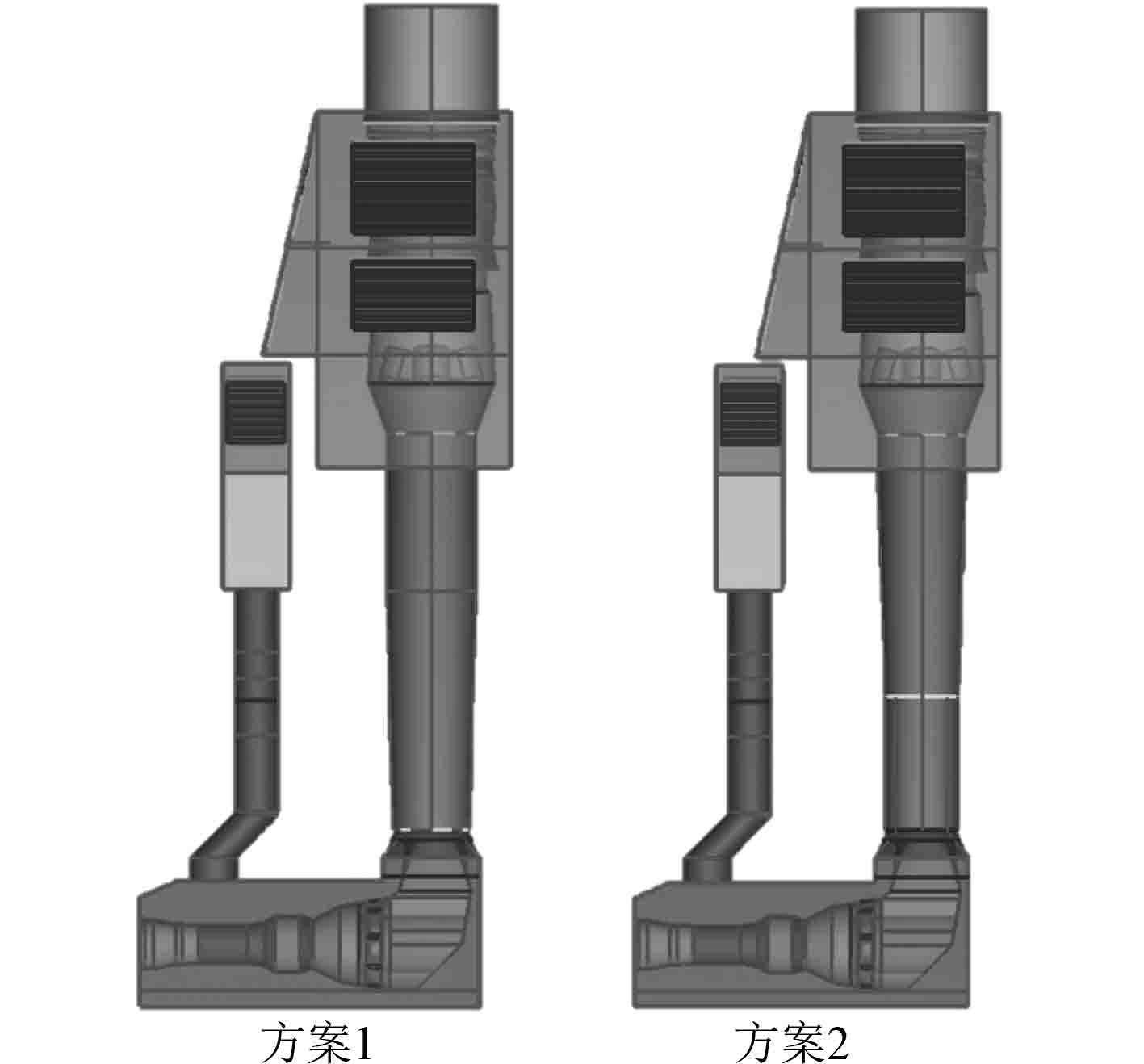
|
图 4 改进后的几何模型 Fig. 4 Improved geometric model |
经过对改进后方案的计算,方案1的引射系数达到8.81%,引射性能相对原模型的6.51%有所提升,这说明引射混合段向后倾斜削弱了引射效果。方案2的引射系数为10.62%,引射能力显著增加,这说明混合段的结构尺寸对于排气引射的性能有重要的影响,将混合段改为圆柱形,增设扩压段能够有效的提高引射系数,因此可根据改进方案2对后舱排气引射系统结构进行改进。
图5和图6给出了燃气轮机中截面上速度矢量及静温分布云图。可以看出,原型的混合段向后倾斜,严重阻碍了引射气体的流动,特别是排气管出口左侧流出的引射气体很少,在引射器直段后部形成了强烈的回流区域,大大降低了排气引射能力。方案1引射器内气体速度并无明显增加,但排气管出口外引射空气流道内的回流减弱,引射性能有所提升。方案2混合段内气体速度明显增大,排气管出口外引射空气流道内的回流基本消失,引射性能得到了有效提升。

|
图 5 中截面速度矢量图 Fig. 5 Velocity vector diagram of middle section |

|
图 6 中截面静温分布图 Fig. 6 Static temperature of medium section |
经过对各截面总压值的测量,发现方案1中D面至E面的总压差变为为正值,这表明箱装体出口部分已形成正压梯度,这将有利于引射冷空气的流动,提高引射系数。但引射器H面至I面引射混合段的压力损失却增加了13 Pa。相比方案1和原模型结果,方案2D面至E面的总压差为正值,并略有提高。另外,H面至I面引射混合段的总压差比原模型减小了216 Pa,可见引射混合段结构和尺寸的变化在改善流动状态的同时也减小了沿程阻力,进一步提升了引射性能。结构改进后,方案2提高了引射系数的同时,相比原模型排气管入口F面压力减小了241 Pa,意味着动力涡轮背压减小,这也将会提高燃机性能。
表3为几个截面的静压值。可以看出,改进后的F,G,H面的静压值较小,在燃机相同功率时,改进模型动压增大,从而使得排气管出口的速度提高,也会带动和抽引更多流体参与到主流流动中,提升了引射流量,从而改善排气引射系统的引射性能。
|
|
表 3 燃气侧导流段总压损失 Tab.3 Total pressure loss of gas side diversion section |
通过对某型船用排气引射装置的计算,发现原装置的引射系数为6.51%,达不到设计要求10%。经过一维计算及优化改进,可以得到以下结论:
1) 将原型混合段改为和排气管轴线重合之后,虽然没有达到设计要求,但排气引射系数有所提高。在进行排气引射系统设计时,应尽量保持引射器管道与燃机轴线垂直,尤其是引射器混合段。
2) 可将排气引射系统按照方案2进行改进,即混合段改为与排气管轴线重合的圆柱管段,直径D1,长度1.87D1,增设扩压管段,此时排气引射系数为10.62%,达到10%以上的设计要求。
3) 根据方案2改进之后,排气管道的压力损失减小,排气管入口面的总压降低,即动力涡轮的背压减小,这有利于提高燃气轮机的性能。
4) 在进行排气系统的设计时,应综合考虑对排气引射性能及排气压力损失的影响,在安装允许的情况下,管道宜直而短,弯头和收缩段要少。
| [1] |
王小玲. 高速舰用燃气轮机超短型排气引射装置的研究与应用[J]. 船舶, 2005(5): 35-40. |
| [2] |
王忠义. 船用燃气轮机排气引射装置性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [3] |
姚朝晖. 计算流体力学入门[M]. 北京: 清华大学出版社, 2002.
|
| [4] |
周绍荣, 陈汉平, 杜朝辉, 等. 燃气轮机排气引射冷却系统的数学模型及其计算[J]. 上海交通大学学报, 2000, 34(9). DOI:10.3321/j.issn:1006-2467.2000.09.001 |
| [5] |
张谋进. 用于粘性可压缩流动数值计算的SIMPLE方法[J]. 航空动力学报, 1997(1): 46-50. |
| [6] |
韩蕴蕾. 船用燃气轮机排气引射器数值模拟及实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2005.
|
| [7] |
李东明, 王林. 船用燃机排气引射器的数值模拟及试验研究[J]. 热能动力工程, 2002, 17(99): 226-230. |
| [8] |
索科洛夫ЁЯ, 津格尔HM. 喷射器[M]. 黄秋云, 译. 北京: 科学出版社, 1977.
|
 2021, Vol. 43
2021, Vol. 43
