2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
受到风、浪、涌的影响核动力船舶会产生倾斜、摇摆、起伏、俯仰等运动[1-3],这些运动都会引起船用核动力装置动力系统的热工水力特性发生变化,而流量的波动特性尤为显著。研究海洋条件下强迫循环回路流量的波动特性,对核动力装置的可靠性、经济性、安全性都有重要意义。Wang[4-5],Xing[6-7],Yan[8]通过实验和计算研究表明,在摇摆工况下强迫循环回路的摩擦阻力系数和换热系数会出现明显的波动,并随着摇摆角度和摇摆频率的增加,摩擦阻力系数和换热系数的波动振幅增加。Murata[9]和Tan[10-11]的研究结果表明,自然循环传热系数的时均值和波动振幅随着摇摆角度和摇摆频率的增加而增加。高璞珍[12]指出在海洋条件下流体会受到附加力的作用,且由向心力引起的附加压降只与流动起始点的位置有关与积分路径无关,而由切向力引起的附加压降与积分路径有关。
综上所述,在海洋环境条件下船体的横摇、纵摇和起伏运动会使流体系统受到附加力的影响,舰船流体环路中的流场和温度场都会发生周期性的波动,且摇摆运动对强迫循环和自然循环的流动传热特性都有影响,很多学者都比较关注摇摆运动对阻力特性和传热特性的影响,而对流量波动特性的影响关注比较少。同时窄矩形通道由于其较高的换热性能是船用紧凑式换热器的主要结构之一,然而对摇摆条件下窄矩形通道内单相水的流量波动特性的研究非常少,因此本文将从理论和实验两部分展开摇摆工况下窄矩形通道内的流体特性研究。
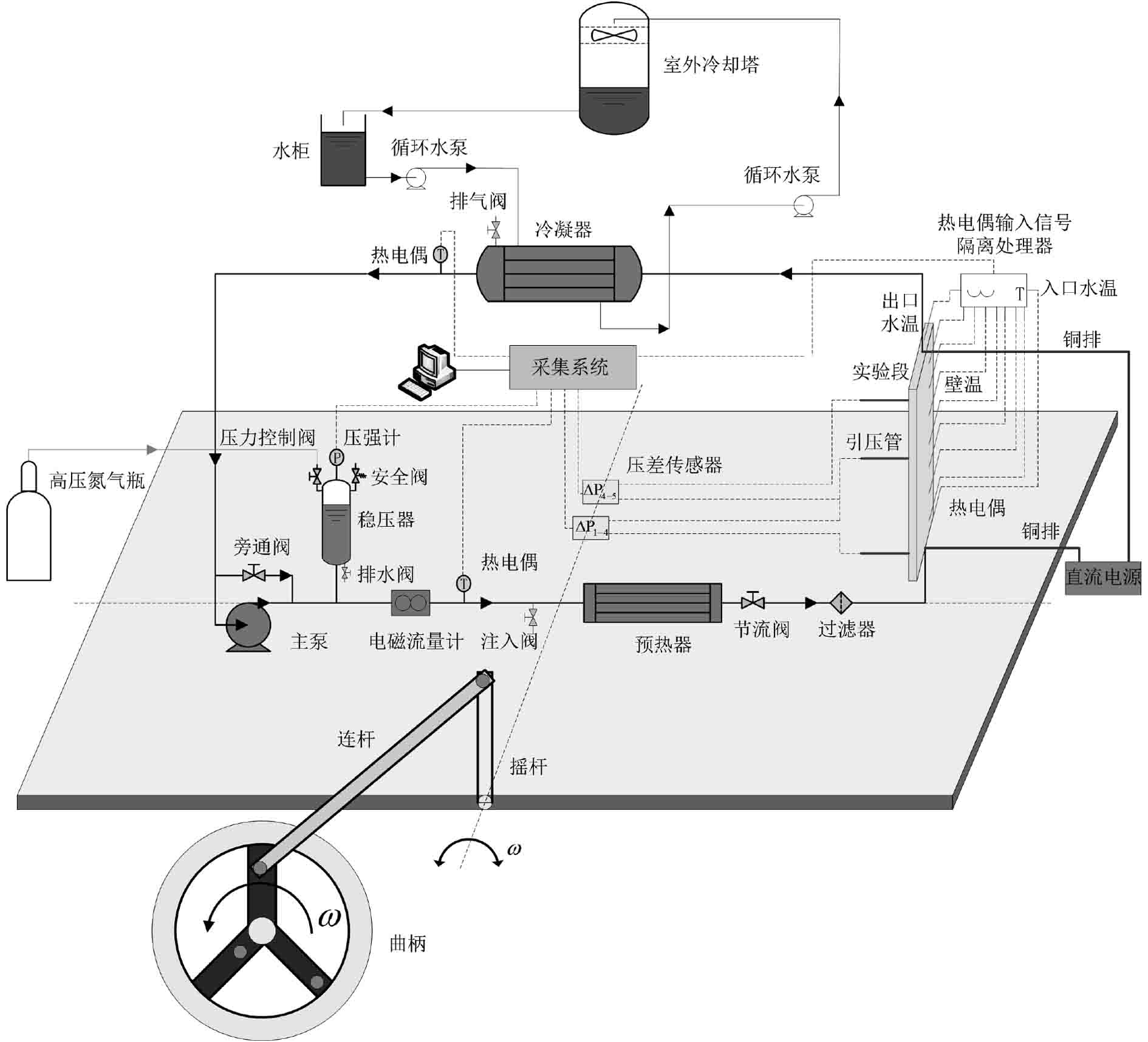
1 实验装置海洋环境模拟实验装置示如图1所示。实验装置的摇摆角度分别为20°,15°,10°,摇摆周期分别为10 s,15 s,20 s,主要用于模拟船舶摇摆运动,同时摇摆周期和摇摆角度可以不同组合以满足不同的工况实验需求。在摇摆平台上搭建闭式的热工水力实验回路用于模拟船舶动力系统流体系统,整个热工实验回路随着摇摆平台的运动而周期性的运行,实验回路主要包括加热回路和冷却回路,加热回路主要用于加热窄矩形通道的流体,以及系统流体的平均温度;冷却回路主要用于冷却窄矩形实验段出口的流体,确保实验过程中流体温度的稳定,其中冷却回路安装在实验室平台,不参与摇摆运行,冷却回路与冷却器的采用软管连接确保摇摆过程中冷却回路不受影响,其中冷却塔放在室外采用风冷的形式。实验过程中采用和换热器1∶1尺寸的窄矩形实验通道,实验通道长宽为2 mm×40 mm,高度为1100 mm,实验通道采用电加热的方式,同时在实验通道外侧包覆绝热层,以减少热量的损失。同时在实验段的一侧安装3个引压管用来测量不同时刻实验通道内的压力和压降,在稳压器和预热器之间安装了高精度的电磁流量计,用来测量回路的流量波动。实验过程中系统的压力由稳压器控制,稳压器连接着高压氮气瓶,可以实现系统压力的持续稳定,实验系统的流量控制主要采用节流阀调节的形式。
|
图 1 机械摇摆热工水力实验装置 Fig. 1 Mechanical rolling thermal-hydraulic experimental facility |
海洋环境模拟实验装置通过变频器和连杆与摇杆的组合,可实现摇摆角度和摇摆周期的准确控制,摇摆角度随时间的变化为:
| ${\theta _t} = {\theta _{\max }}\sin \left( {2\text{π} {\rm{/}}T} \right){\text,}$ | (1) |
摇摆角速度和摇摆角加速度分别为:
| ${\omega _t} = \frac{{2\text{π} }}{T}{\theta _{\max }}\cos \left( {2\text{π} t{\rm{/}}T} \right){\text,}$ | (2) |
| ${\beta _t} = - {\left( {\frac{{2\text{π} }}{T}} \right)^2}{\theta _{\max }}\sin \left( {2\text{π} t/T} \right){\text。}$ | (3) |
式中:θt,ωt,βt,θmax和T分别为海洋环境模拟实验装置的瞬时摇摆角度,角速度,角加速度,最大摇摆角度和摇摆周期。
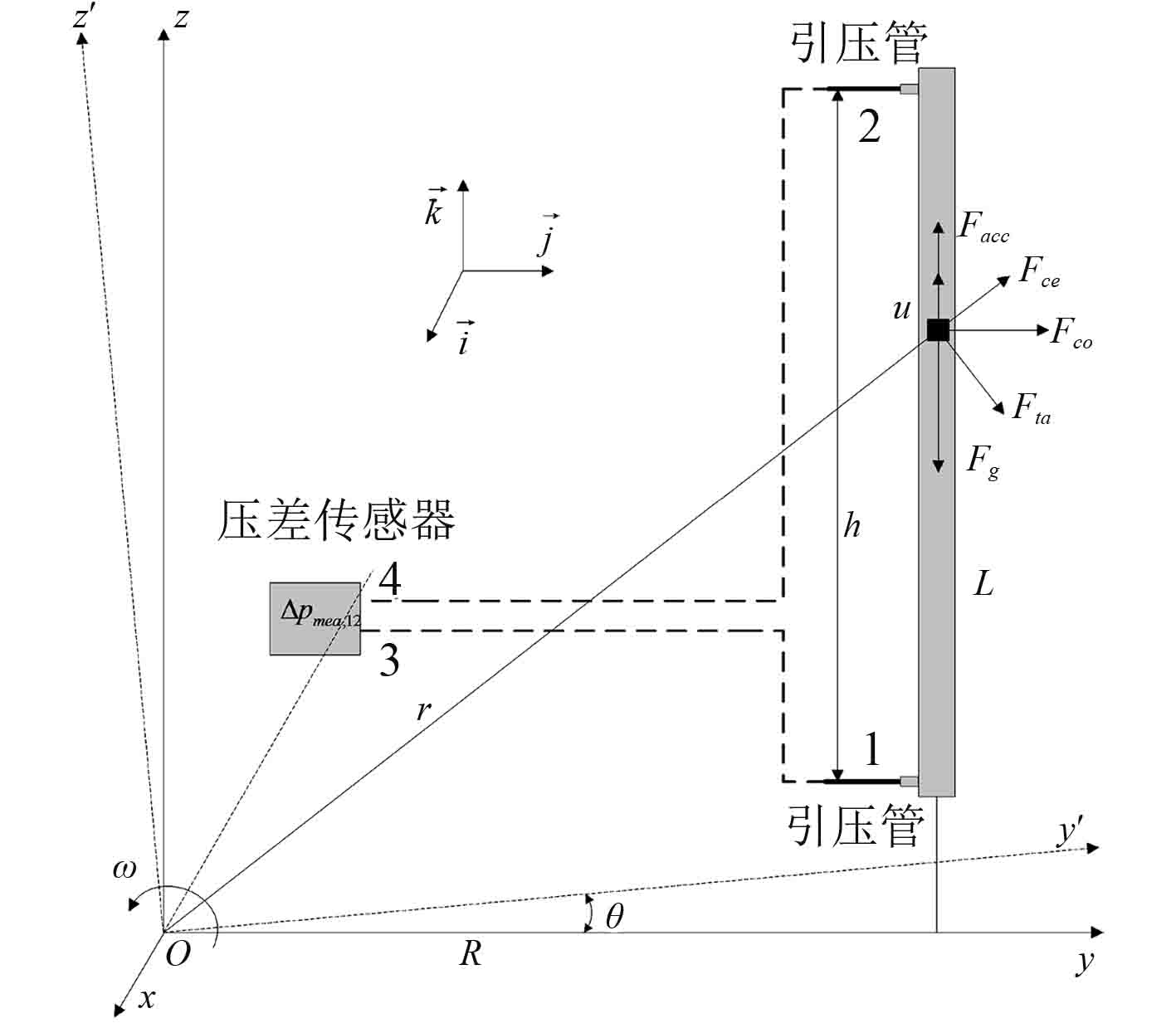
2 窄矩形通道附加压降的理论分析在摇摆工况下船舶流体系统内流体的受力分析如图2所示。与稳态工况相比摇摆工况下由于旋转特性的影响流体会受到向心力、切向力和科氏力的作用,同时作用在流体上的有效重力也会随着摇摆角度的不同而发生变化。流体在附加力的作用下会产生相应的加速度和附加压降从而导致流体的流量会发生周期性的波动。
|
图 2 摇摆工况下流体的受力分析 Fig. 2 Force analysis of fluid element under rolling motion condition |
| ${\vec a_{ce}} = \vec w \times \left( {\vec w \times \vec r} \right) = - {w^2}\left( {y\overrightarrow j + z\overrightarrow k } \right){\text,}$ | (4) |
| ${\vec a_{ta}} = \vec \beta \times \vec r = \beta \left( {y\overrightarrow k - z\overrightarrow j } \right){\text,}$ | (5) |
| ${\vec a_{co}} = 2\vec \omega \times \vec u {\text。}$ | (6) |
式中:ace为向心加速度;ata为切向加速度;aco为科氏加速度;u为流体的速度;r为摇摆轴到流体质点的距离;y和z为流体微元的相对坐标。
如图2所示,对实验回路沿实验通道的流动方向对流体的附加惯性力积分,得到实验通道的附加压降为:
| $\Delta {p_{add,12}} \!=\! \frac{1}{{{A_{cs}}}}\!\int_1^2 \!{\frac{{{\rm{d}}\overrightarrow F \cdot {\rm{d}}\overrightarrow l }}{{{\rm{d}}l}}} \!=\! \rho\! \!\int_1^2 {\left( {\overrightarrow {{a_{ce}}} \!+\! \overrightarrow {{a_{ta}}} \!+\! \overrightarrow {{a_{co}}} } \right)} \cdot {\rm{d}}\overrightarrow l {\text。}$ | (7) |
将式(4)~式(6)代入式(7)得:
| $\Delta {p_{add,12}} = \int_1^2 {\rho {\omega ^2}\left( {y{\rm{d}}y + z{\rm{d}}z} \right)} + \int_1^2 {\rho \beta \left( {z{\rm{d}}y - y{\rm{d}}z} \right)} {\text,}$ | (8) |
施加在流体微元上有效重力压降的变化为:
| $\Delta {p_{g,v}} = \rho hg\left( {\cos {\theta _t} - 1} \right){\text。}$ | (9) |
式中:Acs为窄矩形通道的横截面积;ρ为实验流体的密度;g为重力加速;h为2个引压管之间的距离。
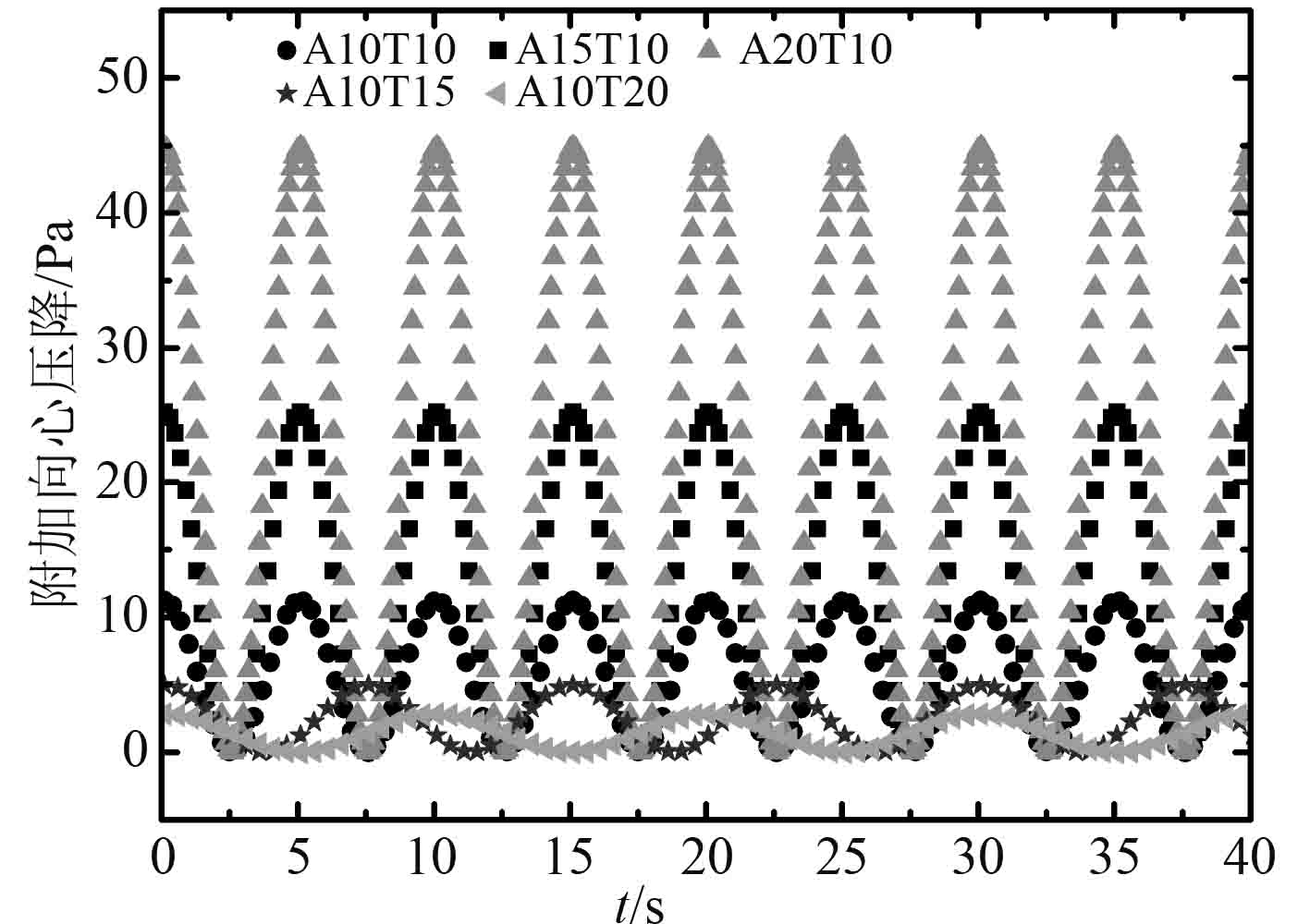
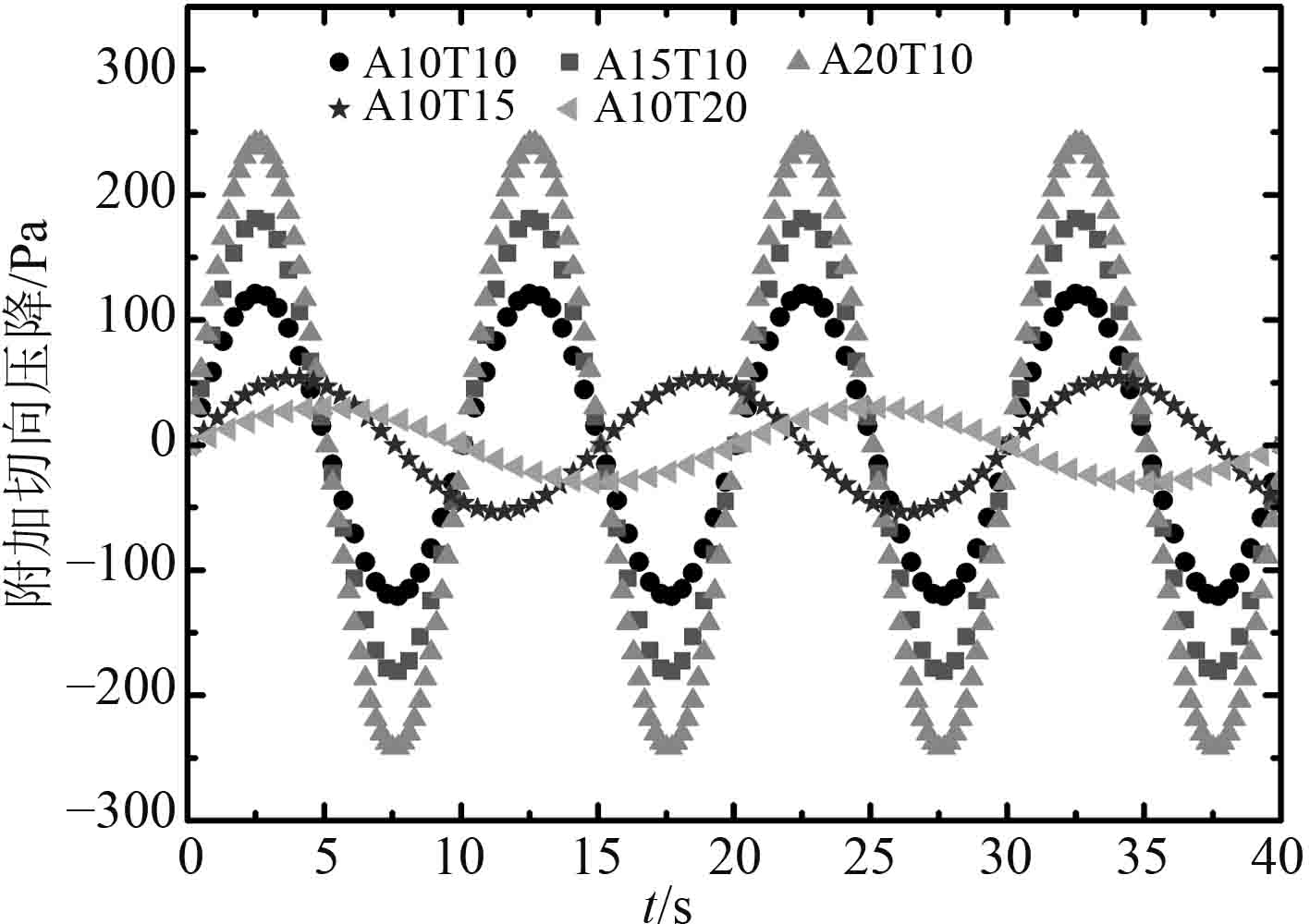
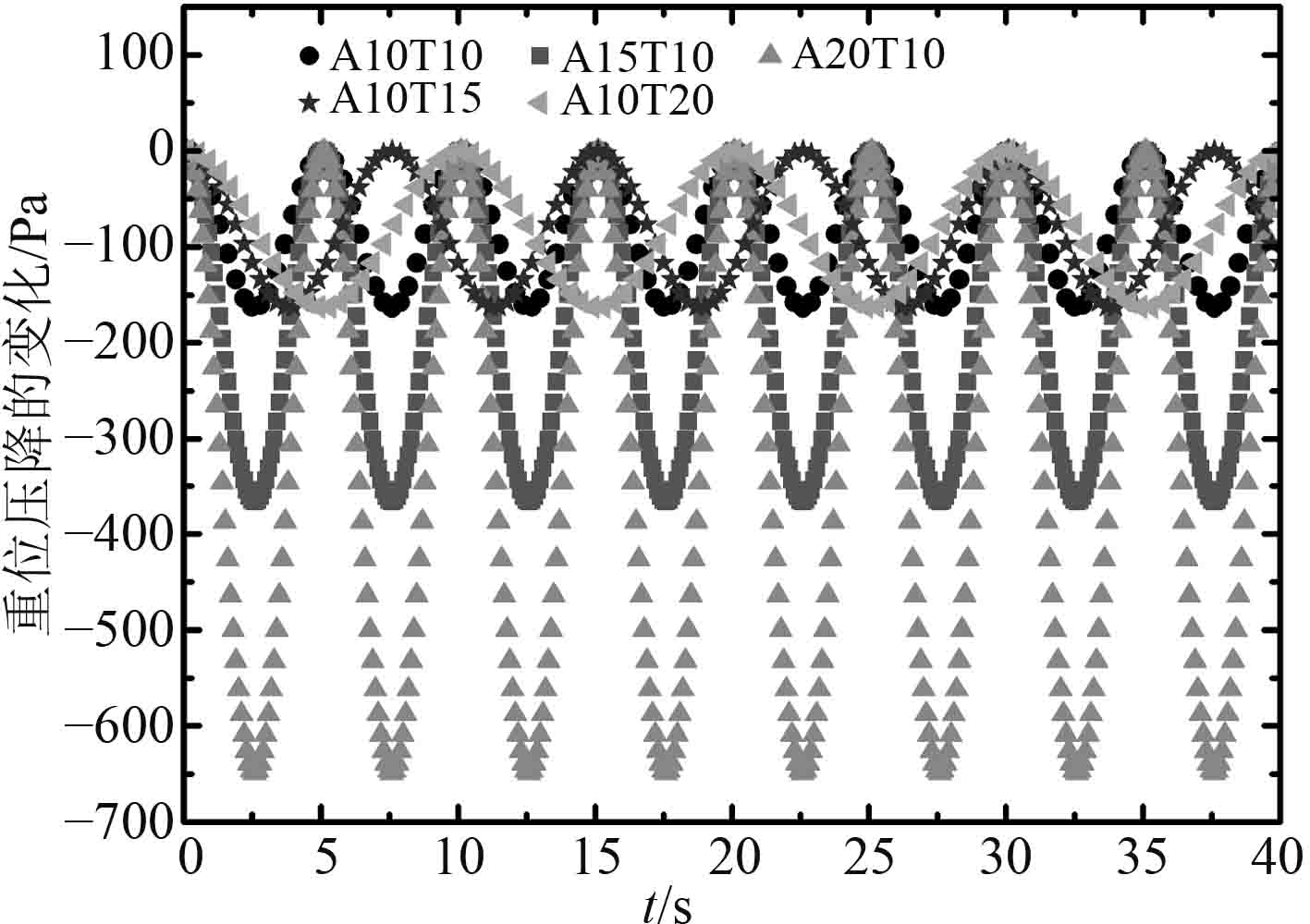
由海洋摇摆运动引起的向心压降、切向压降以及重位压降的变化如图3~图5所示,由于切向压降与流体回路的积分路径有关,其波动周期和摇摆周期一致,而向心压降和重位压降只与流体起始点的位置有关,它们的波动周期为摇摆周期的一半。随着摇摆角度的增加和摇摆周期的减小,向心压降和切向压降的波动振幅明显增加,且切向压降的波动振幅远大于向心压降的波动振幅,也就意味着在摇摆过程中附加切向力对流体的作用要远大于附加向心力的作用。重位压降的波动振幅只与摇摆角度有关而与摇摆周期无关,同时重位压降的波动振幅要大于切向压降的波动振幅。在摇摆运动中,重力和切向力对流体的作用效果比较大,而向心力的作用效果比较小。
|
图 3 附加向心压降 Fig. 3 Additional centripetal pressure drop |
|
图 4 附加切向压降 Fig. 4 Additional tangential pressure drop |
|
图 5 重位压降的变化 Fig. 5 Variation of Gravity pressure drop |
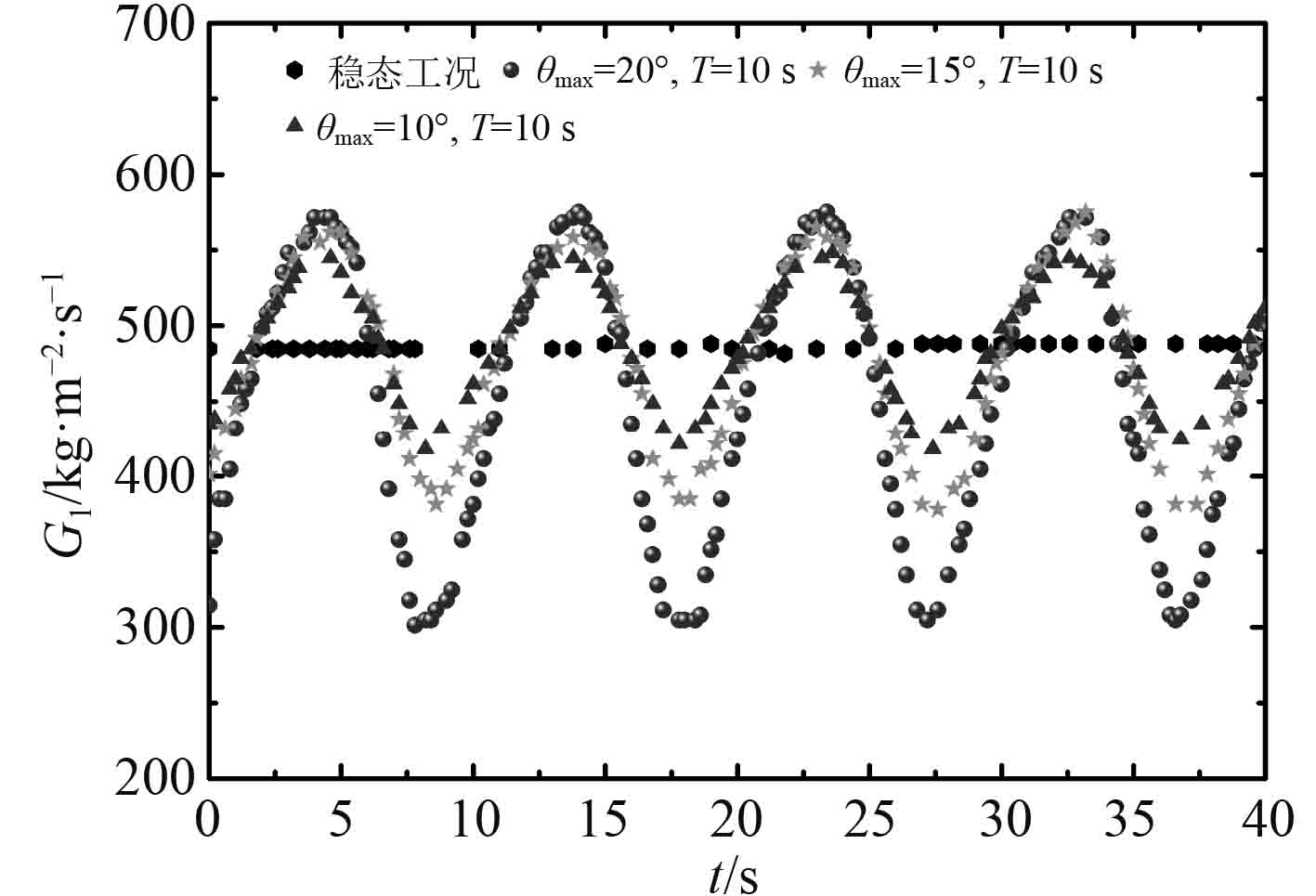
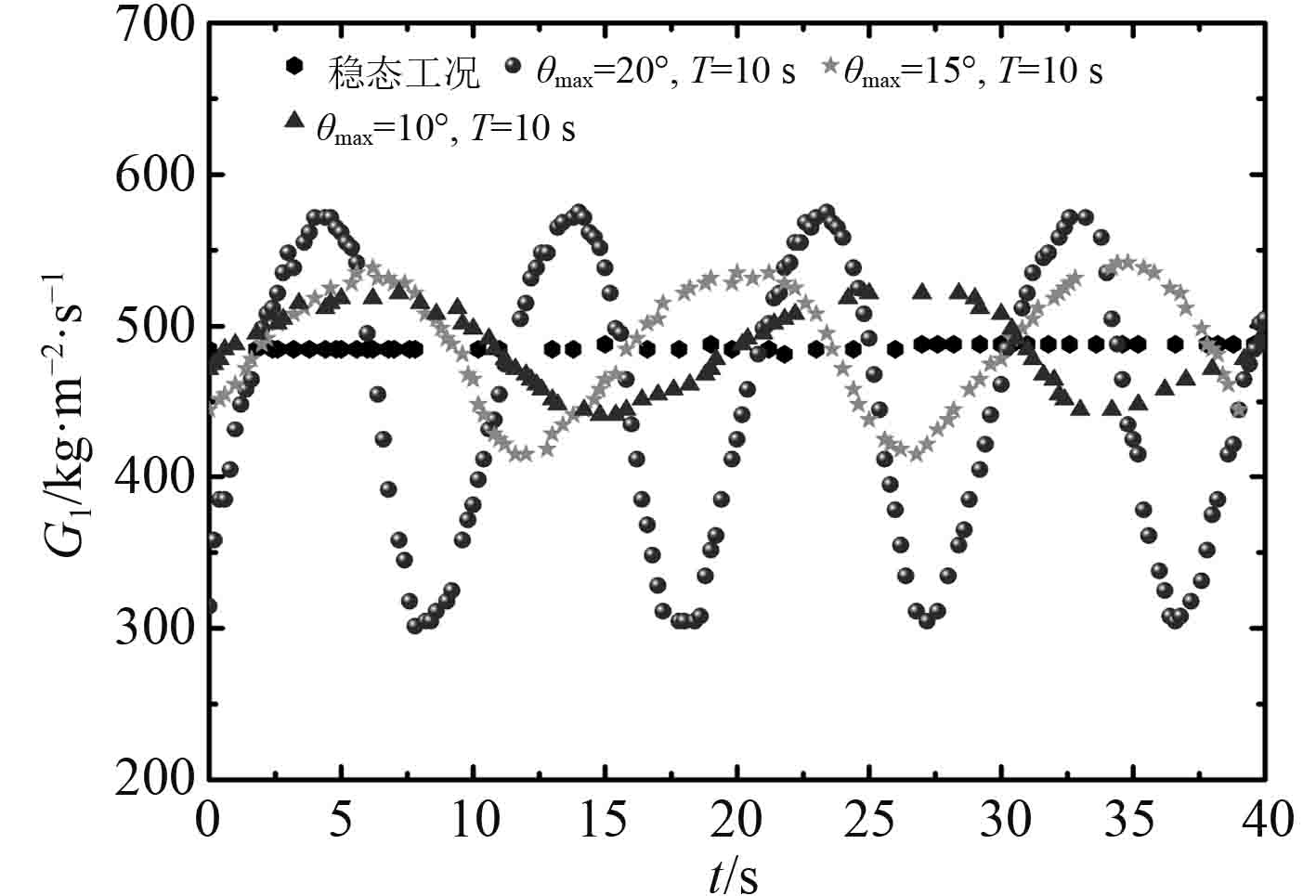
摇摆角度和摇摆周期对质量流速波动特性的影响如图6和图7所示。在摇摆工况下,质量流速的波动周期与摇摆周期一致,且随着摇摆角度和摇摆频率的增加,质量流速的波动振幅增加,这主要是因为在单相区域质量流速的波动主要受到附加压降的影响,且附加压降的波动振幅随着摇摆角度和摇摆频率的增加而增加。从图6和图7还可以看出,摇摆工况下的时均质量流速要小于稳态工况下质量流速,且随着质量流速波动振幅的增加时均质量流速越小。
|
图 6 摇摆角度对质量流速波动的影响 Fig. 6 Effect of rolling angle on mass flux |
|
图 7 摇摆周期对质量流速波动的影响 Fig. 7 Effect of rolling period on mass flux |
质量流速的相对波动振幅能更好地研究摇摆参数对质量流速波动特性的影响,其表达式为:
| ${G_{ampr}} = \frac{{{G_{{\rm{max}}}} - {G_{{\rm{min}}}}}}{{{G_{ta}}}}{\text。}$ | (10) |
式中:Gampr为质量流速的相对波动振幅;Gmax为质量流速波动的最大值;Gmin为质量流速波动的最小值;Gta为质量流速波动的时均值。
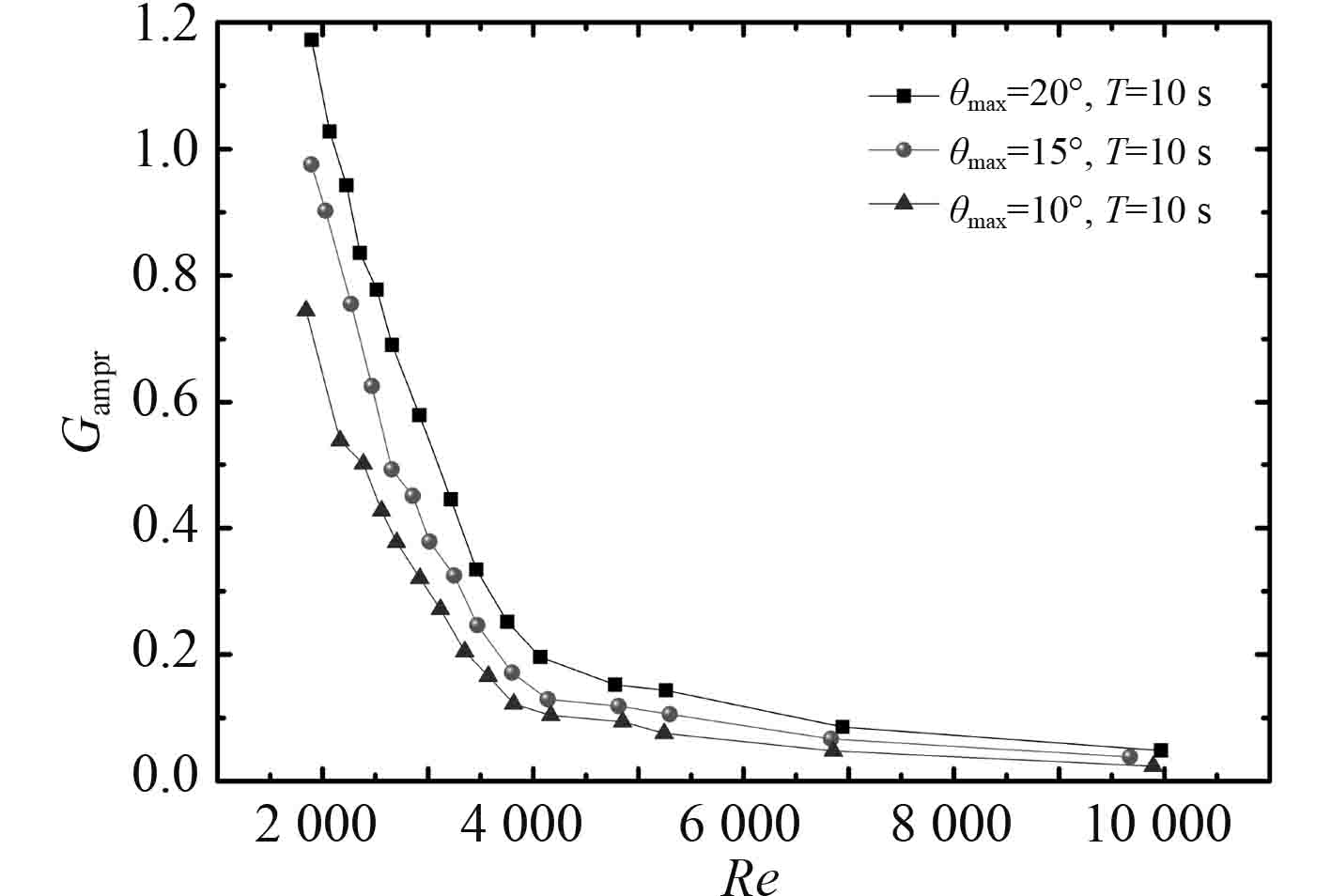
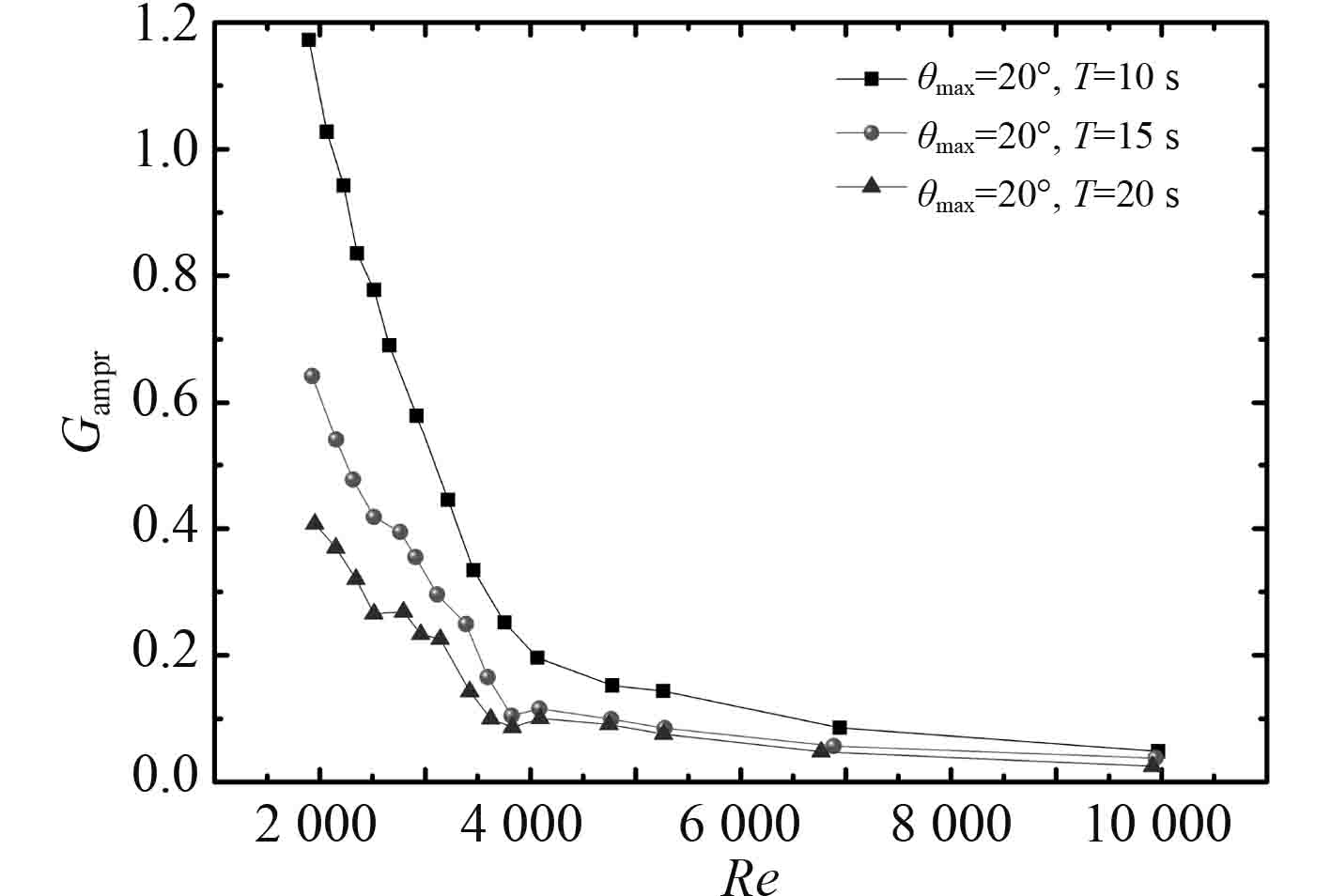
摇摆角度和摇摆周期对质量流速相对波动振幅的影响如图8和图9所示。在同一雷诺数下,随着摇摆角度和摇摆频率的增加质量流速的相对波动振幅增加,主要是因为随着摇摆角度和摇摆周期的增加,通道内的附加压降增加,在同一雷诺数下附加压降占通道总压降的份额增加,质量流速的相对波动振幅增加。在雷诺数小于4500的区域,质量流速的相对波动振幅随着雷诺数的增加而快速减小,这主要是因为在摇摆运动下雷诺数的增加主要依靠泵驱动压头的增加,在雷诺数小于4500的区域,附加压降在通道总压降的份额比较大,随着雷诺数的增加,附加压降的份额快速减小,从而导致质量流速相对波动振幅的快速减小。在雷诺数大于4500的区域,质量流速的相对波动振幅随着雷诺数的增加变化不是很大,且当雷诺数大于10000时,摇摆角度和摇摆频率对质量流速相对波动振幅的影响很小。
|
图 8 摇摆角度对质量流速相对波动振幅的影响 Fig. 8 Effect of rolling angle on relative fluctuation amplitude of mass flux |
|
图 9 摇摆周期对质量流速相对波动振幅的影响 Fig. 9 Effect of rolling period on relative fluctuation amplitude of mass flux |
在海洋条件下对流体的流量波动特性进行实验研究和理论分析,得出如下结论:
1)摇摆运动下流体会受到切向力、法向力、科氏力的影响导致流量的周期性波动,且流量的波动周期与摇摆周期一致。
2)随着摇摆角度和摇摆频率的增加,附加向心压降和附加切向压降的波动振幅明显增加,且重力和附加切向力对流体的作用效果远大于附加向心力的作用效果。
3)通道质量流速的波动振幅随着摇摆角度和摇摆频率的增加而增加,但时均质量流速随着波动振幅的增加而减小。
4)在摇摆运动下,质量流速的相对波动振幅随着雷诺数的增加而减小,在雷诺数小于4500的区域附加压降对质量流速相对波动振幅的影响比较大,在雷诺数大于4500的区域,附加压降对质量流速相对波动振幅的影响比较小。
| [1] |
刘传成, 阎昌琪, 孙立成, 等. 摇摆运动下矩形窄通道内摩擦压降特性研究[J]. 原子能科学技术, 2013(4): 576-581. |
| [2] |
王占伟, 谭思超, 张文超, 等. 摇摆运动下自然循环高含汽率流动特性研究[J]. 原子能科学技术, 2013(3): 371-375. |
| [3] |
幸奠川, 阎昌琪, 曹夏昕, 等. 摇摆条件下单相水强制循环阻力特性实验研究[J]. 原子能科学技术, 2011(6): 672-676. |
| [4] |
WANG Chang, WANG Shao-Wu, WANG Hao, et al. Investigation of flow pulsation characteristic in single-phase forced circulation under rolling motion[J]. Annals of Nuclear Energy, 2014, 64(2014): 50-56. |
| [5] |
WANG Chang, LI Xiaohui, WANG Hao, et al. Experimental study on friction and heat transfer characteristics of pulsating flow in rectangular channel under rolling motion[J]. Progress in Nuclear Energy, 2014, 71(2014): 73-81. |
| [6] |
XING Dianchuan, YAN Changqi, SUN Licheng, et al. Effect of rolling motion on single-phase laminar flow resistance of forced circulation with different pump head[J]. Annals of Nuclear Energy, 2013, 54(2013): 141-148. |
| [7] |
XING Dianchuan, YAN Changqi, SUN Licheng, et al. Frictional resistance of adiabatic two-phase flow in narrow rectangular duct under rolling conditions[J]. Annals of Nuclear Energy, 2013, 53(2013): 109-119. |
| [8] |
YAN B. H., GU H. Y., YANG Y. H., et al. Effect of rolling on the flowing and heat transfer characteristic of turbulent flow in sub-channels[J]. Progress in Nuclear Energy, 2011, 53(1): 59-65. DOI:10.1016/j.pnucene.2010.09.003 |
| [9] |
Murata Hiroyuki, Sawada Ken-Ichi, Kobayashi Michiyuki. Natural circulation characteristics of a marine reactor in rolling motion and heat transfer in the core[J]. Nuclear Engineering and Design, 2002, 215(1-2): 69-85. DOI:10.1016/S0029-5493(02)00042-0 |
| [10] |
TAN Si-Chao, SU Guang-Hui, GAO Pu-Zhen. Heat transfer model of single-phase natural circulation flow under a rolling motion condition[J]. Nuclear Engineering and Design, 2009, 239(10): 2212-2216. DOI:10.1016/j.nucengdes.2009.05.002 |
| [11] |
TAN Si-Chao, SU Guang-Hui, GAO Pu-Zhen. Experimental and theoretical study on single-phase natural circulation flow and heat transfer under rolling motion condition[J]. Applied Thermal Engineering, 2002, 29(14-15): 3160-3168. |
| [12] |
高璞珍, 庞凤阁, 王兆祥. 核动力装置一回路冷却剂受海洋条件影响的数学模型[J]. 哈尔滨工程大学学报, 1997, 18(1): 26-29. |
 2021, Vol. 43
2021, Vol. 43
