2. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003;
3. 招商局重工(江苏)有限公司,江苏 南通 226116
2. School of Ship and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;
3. China Merchants Heavy Industry (Jiangsu) Co., Ltd, Nantong 226116, China
半潜式起重平台是集重型起重、安装、改装、退役和拆除等于一体的大型海上结构物,在吊运过程中一旦发生跌落事故,会危及平台结构及人员安全[1]。重物跌落对平台的影响差异主要体现在不同接触形式以及不同的接触位置和角度上[2],因此,有必要探究跌落场景中各参数对于结构损伤的敏感性,从而对甲板抗冲击性能进行优化。
目前国内外围绕跌落冲击问题开展了多方面研究。B G Jung[3] 对甲板结构进行了冲击试验及数值模拟,分析了结构的抗冲击性能。夏侯命胜等[4]模拟了钻台不同构件下的失效过程,最终得到了坠物载荷作用下相关结构简化评估方法,为类似实际工程问题提供参考。刘伟等[5]通过数值仿真研究钻铤坠落对钻台甲板冲击损伤,通过讨论非线性有限元求解技术,研究适合于坠物与钻台甲板碰撞分析的数值仿真方法。Gong Xiang等[6-7]研究发现跌落角度、法向阻力系数和滚动频率是决定运动轨迹的三大关键因素。孙晓东等[8]通过梳理跌落事故数据和分析方法、边界条件,同时验证了方法的适用性和合理性。王醍等[9]研究甲板板架在钻铤撞击下的动态损伤行为,总结了计算板架被穿透时的临界变形能公式。周世博[10]对立管跌落到平台甲板进行了数值仿真,运用优化算法SAPSO与BP神经网络结合,对海洋平台进行了坠物冲击损伤分析。余峙伟等[11]对水下管汇受锚机跌落的影响进行研究,得到不同防护板厚下吸能比率和变形抗性,研究发现5~8mm的防护板厚较为合理。
本文基于非线性动力学理论以某半潜式平台为对象,选取典型的跌落模块,采用Ls-dyna软件对平台甲板损伤开展研究,分析坠物不同参数对结构的影响,提出了安全作业建议。
1 模型及相关参数在接触形式上,坠物主要分扁长型和方圆型;在跌落位置上,主要分以冲击点位置(纵骨及横梁等)进行划分。本文采用4种坠物模型,选取导管架结构作为典型的大型细长型结构物,导管架平台上甲板局部结构为典型的大型方形结构物。如表1所示,导管架结构长宽高尺寸为25 m×25 m×90 m,导管架上甲板结构共3层,长宽高尺寸为40 m×22 m×16 m,包含甲板、纵骨、横梁和支柱等主要结构。针对坠物不同位置的损伤影响时细长型坠物的选取为长10 m,直径250 mm,重量3 t的细杆;方形坠物为20 GP标准集装箱,尺寸为6.058 m×2.438 m×2.591 m,考虑其配货后整体重量为20 t。进行敏感性分析时,所有坠物均为普通结构钢,对导管架、甲板板及集装箱坠物采用弹塑性材料,而细杆属于扁长型坠物由于其危险性需按规范要求用刚体进行计算。
|
|
表 1 坠物主要参数 Tab.1 Main parameters of falling objects |
本文半潜式起重平台上船体高11.30 m,主甲板长81.00 m,宽81.00 m,模型范围为主甲板向下的整个甲板室结构,整体采用高强度钢,并根据分析要求对结构进行次要性简化和板厚平铺,其中甲板结构非跌落区域平均网格尺寸为375 mm,跌落细化区域平均网格尺寸为75 mm,导管架平均网格尺寸为200 mm。在进行位置敏感性分析中的主甲板尺寸为18 m×22.5 m,甲板板厚16 mm,纵骨尺寸为HB220 mm×10 mm,纵桁尺寸为750 mm×15 mm /350 mm×30 mm,横梁尺寸为1000 mm×20 mm /400 mm×35 mm。通过刚性固定远离平台的跌落区域的节点,作为跌落模拟的边界条件[12]。
|
|
表 2 弹塑性材料(C-S DYMAT24)参数 Tab.2 Elastic-plastic materials(C-S DYMAT24)parameters |
真实跌落事故大概率发生在移动过程中,坠物在与平台接触时并非竖直向下,而是具有一定的偏移角。半潜式起重平台属于漂浮于海面上的结构物,自身存在运动,同时环境载荷也会作用到坠物之上,有必要研究跌落角度对跌落损伤的影响。DNV规定在研究浮体上的坠物影响时必须考虑5°~10°的倾斜,本文考虑0°,2°,4°,6°,8°,10°六个不同角度,并定义竖直跌落时为0°。
|
|
表 3 跌落角度敏感性分析工况 Tab.3 Sensitive analysis conditions for drop angles |
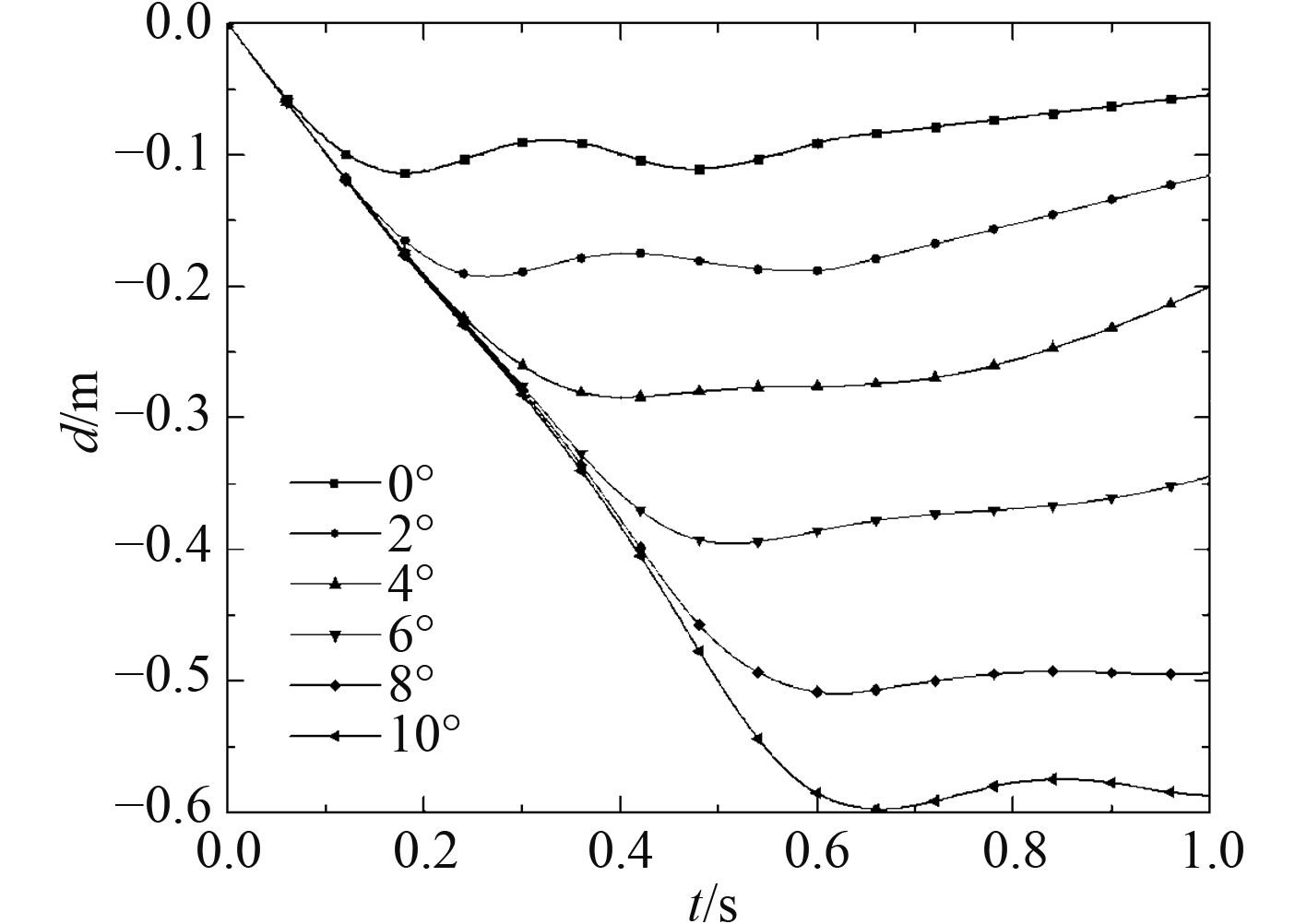
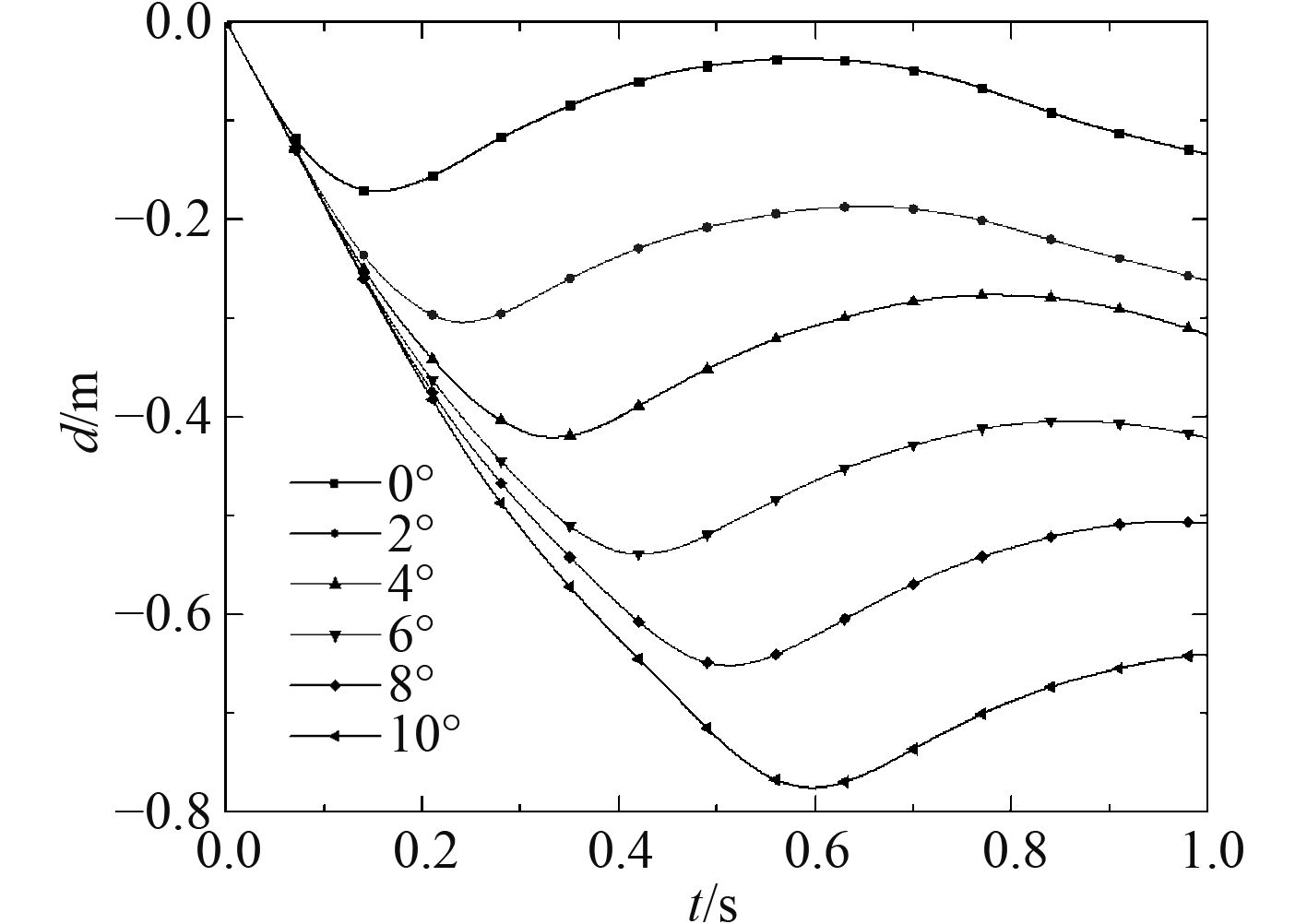
不同角度坠物的深度曲线如图1和图2所示。角度为10°时,相同时间内,甲板的位移最大,坠物对甲板下结构威胁最大。最大冲击深度随角度增大呈线性增长,坠物角度每增加2°时,导管架撞深增幅约为0.1 m左右,说明跌落角度对于大型结构的影响较大。对于吊运的导管架甲板结构,在不同角度下发生跌落也有所不同,角度小于6°时,导管架平台甲板结构左右损伤差异不大,主要以最下一甲板的桁材的压溃为主,分布比较平均;随着角度增加,管架平台甲板结构左右损伤差异增大,先接触的一侧损伤更为严重。因此在吊升中应注意在保证作业设备(吊机、钢丝绳等)正常运转的同时,还需注意对拆解模块摆动的控制及平台六自由度运动的补偿,以尽量减少事故发生后带来的严重后果。
|
图 1 不同角度下导管架跌落深度曲线 Fig. 1 Drop depth curve of jacket under different angles |
|
图 2 不同角度下导管架平台甲板跌落深度曲线 Fig. 2 Drop depth curve of jacket platform deck at different angles |
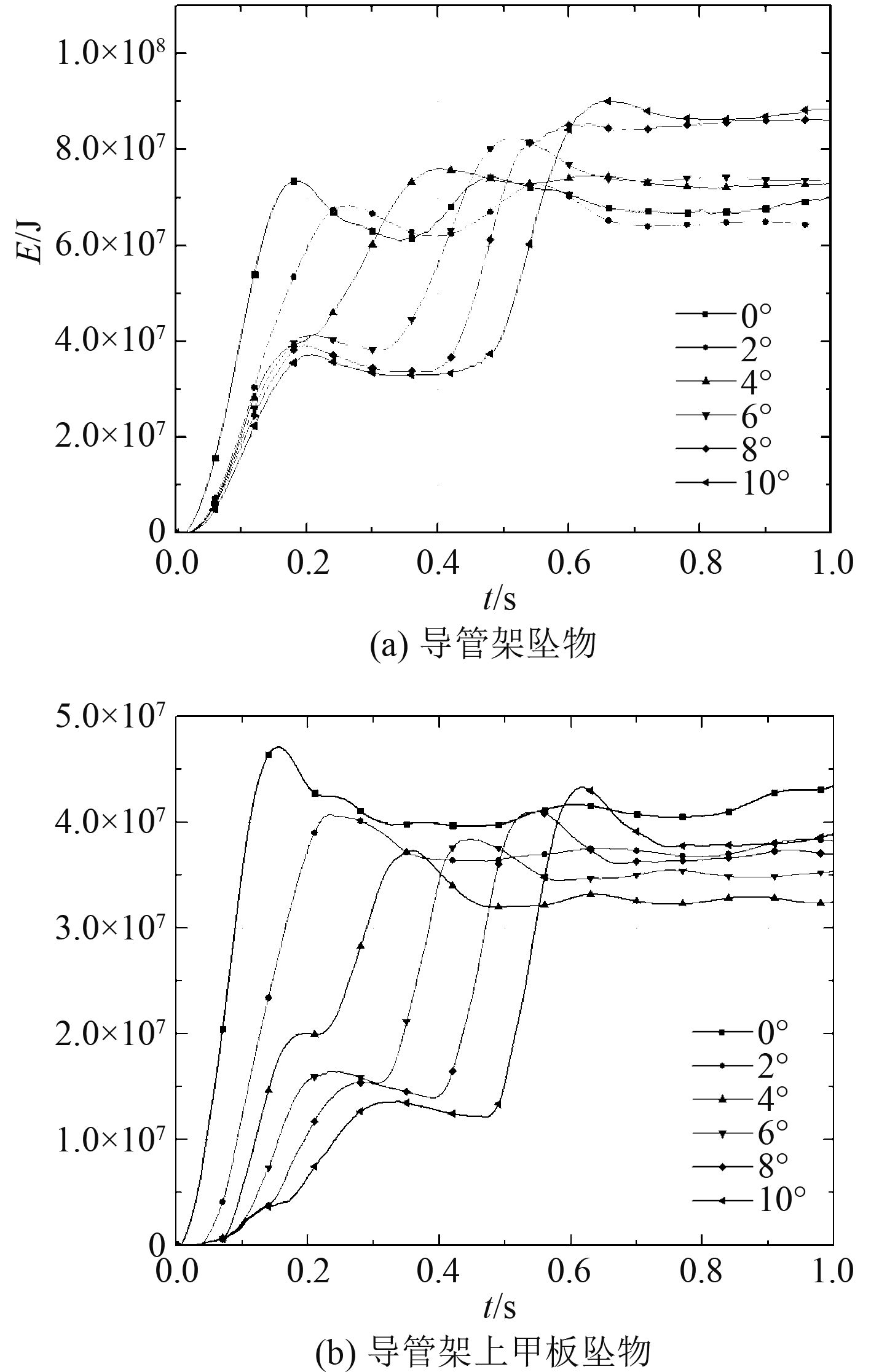
图3和图4为不同场景的板架吸能变化和坠物动能变化曲线。在导管架跌落中,坠物角度为2°时,甲板变形能最小6.43×107 J,当角度逐渐增大时,甲板变形能随之增大;当坠物角度为10°时,甲板吸能达最大值为8.86×107 J。当角度为8°,10°时,导管架在0.6 s时基本停在甲板上,随后动能慢慢减小,伴随有倾倒趋势;其他角度下跌落后,导管架在接触甲板后均迅速弹起,且角度越小,回弹越快;坠物角度为10°时,导管架动能在1 s时最小为6.11×107 J,甲板此刻吸收的变形能也较其他角度大。
|
图 3 板架变形能时历曲线 Fig. 3 Time history curve of energy absorption |

|
图 4 坠物动能时历曲线 Fig. 4 Time history curve of jacket deck kinetic energy |
在甲板模块跌落中,甲板吸收能量变化趋势基本相同,甲板变形能在坠物0°跌落时最大为4.71×108 J,在10°跌落时最小为4.34×108 J。通过查看板架结构的临界变形能及甲板破裂时刻,不难发现平台甲板开始发生失效的时间随角度增大而减小,甲板的临界变形能也随角度增大而减小,可见该场景中随着坠物角度增大,起重平台更容易破裂。除坠物角度为0°工况,甲板坠物的动能在接触后均是有所增加随后才开始减少,这是因为在考虑角度的跌落场景中,坠物在接触甲板后其重心还在下降中,而初始接触区域的结构并不能完全吸收坠物的动能,进而阻止其运动。
2.3 冲击力情况图5为导管架不同角度跌落下的冲击力时历曲线。总体上看,冲击力在接触的一瞬间迅速增大,角度越小,增速越快。角度为0°时,冲击力峰值最大为1.28×108 N,冲击力峰值随着倾斜角度的增大而减小,但其非线性程度却随角度增大显得更加剧烈。当导管架呈10°跌落时,跌落冲击力非线性程度最为剧烈,在整个过程中都不断反复加载卸载,对甲板的威胁最大。

|
图 5 冲击力-时历曲线(导管架) Fig. 5 Impact force-time history curve(jacket)curve(deck) |
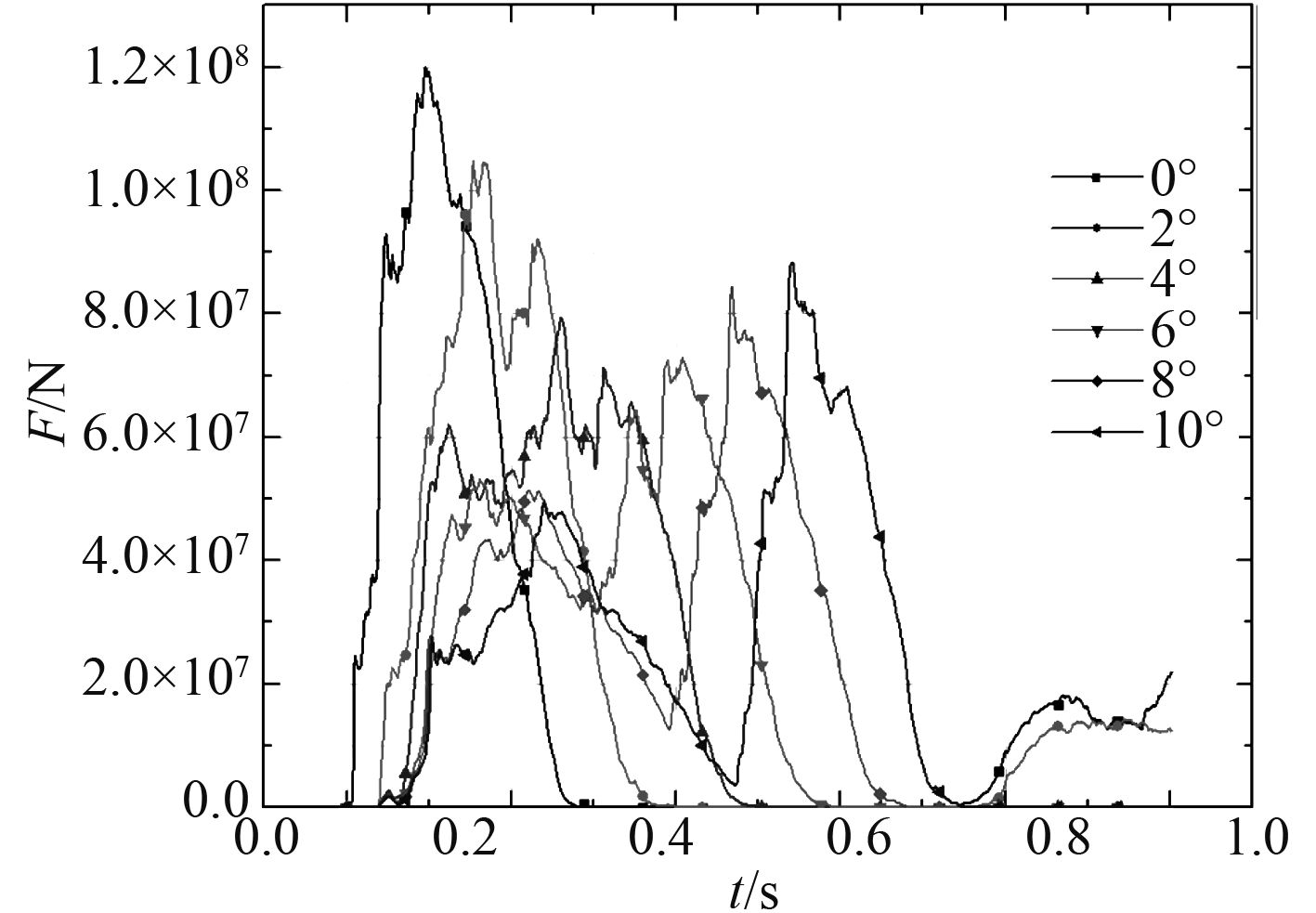
图6为导管架平台甲板不同角度跌落下的冲击力时历曲线。角度为0°时,冲击力峰值最大为1.20×108 N,最小是6°时的峰值7.29 ×107 N。随着倾斜角度的增大,冲击力峰值开始减小,当角度大于6°后,峰值开始回升。
|
图 6 冲击力-时历曲线(上甲板) Fig. 6 Impact force-time history curve(deck) |
半潜式起重平台中的甲板结构包括甲板板、纵骨和横梁(桁材)。现实中坠物可能跌落到甲板的任意位置,但都会和以上结构接触,即物体跌落在甲板面上(两纵骨之间)、物体跌落在纵骨面上、物体跌落在横梁面(舱壁面)上。本文根据甲板构件的不同选取3种典型的跌落场景,在分析时认为细杆坠物为竖直下落,集装箱坠物箱角处与甲板呈45°接触。
|
|
表 4 跌落位置敏感性分析工况 Tab.4 Working conditions of sensitivity analysis for drop positions |
不同角度坠物的深度曲线如图7和图8所示。可以看出,细杆在相同高度下的跌落时甲板位移基本保持在同一水平,10 m,20 m,30 m分别在0.043 m,0.055 m,0.062 m附近。跌落在纵骨上时,细杆都会对甲板面造成破坏并穿透,并且甲板板架骨材首先发生破裂继而甲板面被全部穿透。而撞击点在横梁上及横梁和骨材交汇处时,横梁首先因为压溃而破裂,甲板只是产生了很大的塑性变形,但是并没有发生破裂。

|
图 7 不同角度下细杆跌落深度曲线 Fig. 7 Drop depth curve of thin rod under different angles |

|
图 8 不同角度下集装箱跌落深度曲线 Fig. 8 Drop depth curve of container at different angles |
集装箱跌落在纵骨上时,最大应力出现在纵骨上,当进一步接触时,纵骨首先达到最大塑性失效应变,产生破裂。集装箱跌落在横梁上时,最大应力值首先出现在纵骨、横梁与甲板平面的交汇点处,直到接触处纵骨彻底毁坏,继而板架结构按照集装箱的截面形式进一步破坏。集装箱跌落在横梁与纵桁交汇处上时情况与跌落在横梁上类似。
综上,不同跌落场景中,坠物跌落在纵骨上破坏形式最为严重,甲板的临界变形能比其他情况小的多,坠物跌落在骨材上时,首先出现破坏的点都在骨材的腹板上,坠物跌落在纵骨上时,甲板面两边的骨材腹板上的应力值也很大。
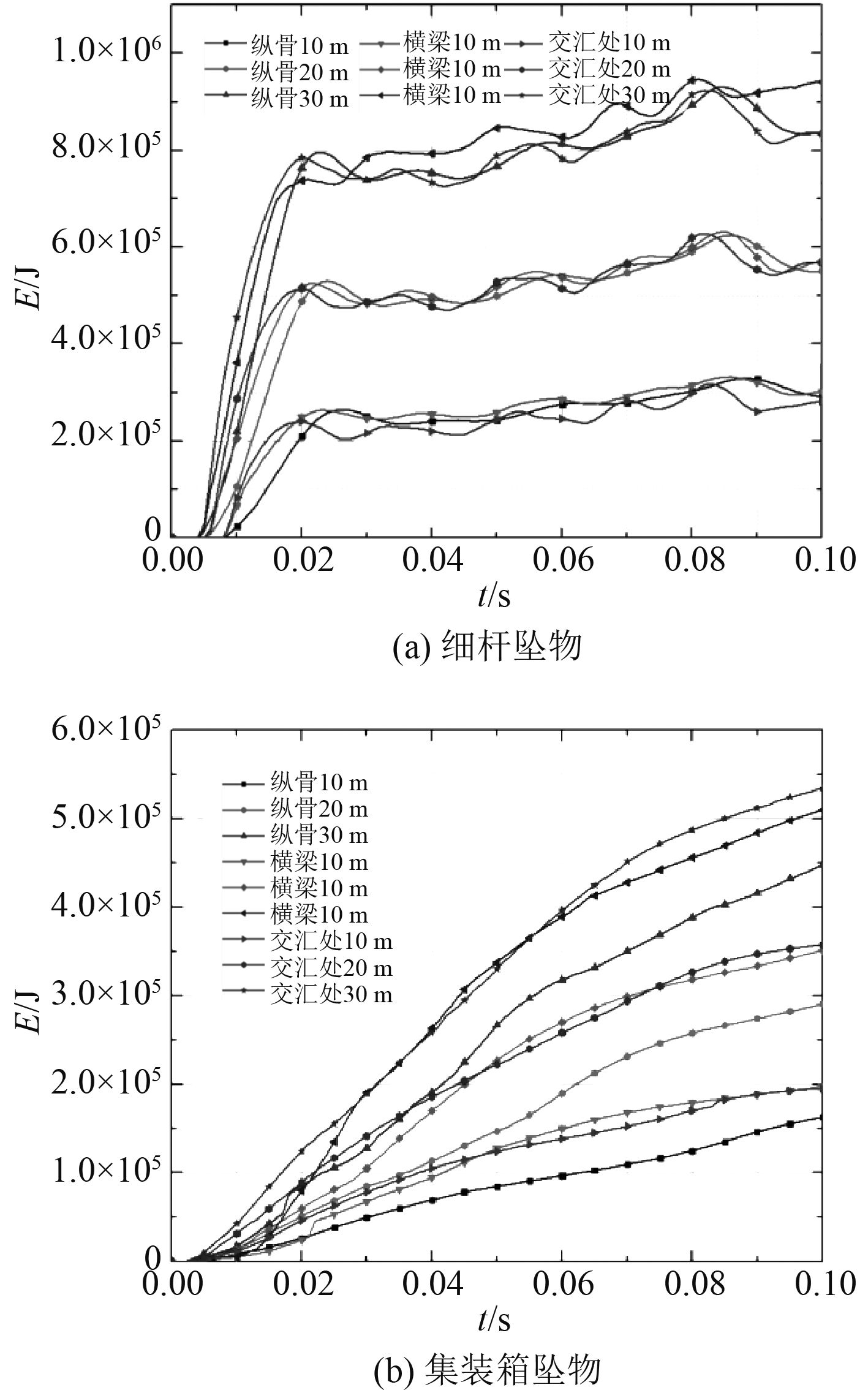
3.2 结构吸能情况板架变形能、坠物动能时历曲线如图9和图10所示。在细杆跌落中,坠物跌落在横梁上时甲板吸收的变形能最大,坠物动能下降接近0,在0.02 s后,少量的板架变形能又开始改变为细杆的动能,细杆会发生反弹运动,其他2种场景同样会发生类似情况。对比同样的高度,可以看出跌落在纵骨上时坠物的动能下降最小,这对于甲板结构是最不利的。
|
图 9 板架变形能时历曲线 Fig. 9 Time history curve of energy absorption |
|
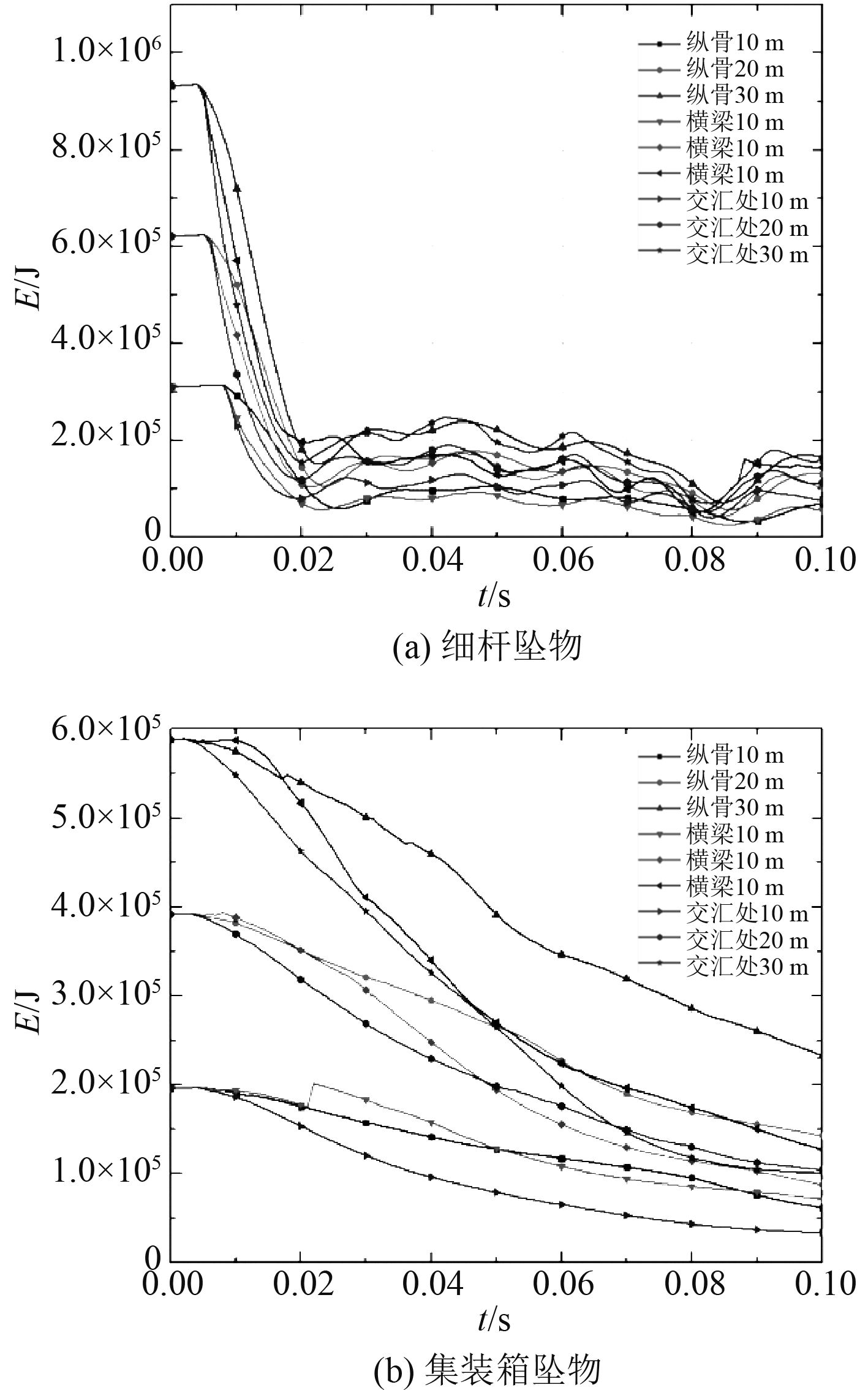
图 10 坠物动能时历曲线 Fig. 10 Time history curve of jacket deck kinetic energy |
集装箱跌落到横梁上时,坠物动能消耗最快,并且从集装箱的运动上顶中可以看出,首次碰撞结束后,集装箱还会发生反弹,因此,集装箱的动能会有小幅回升,板架变形能会有小幅下降。另2种情况能量转化方式基本相同。最后坠物的动能将被全部消耗,坠物静止在甲板面上。可见跌落接触下部支撑结构越强,箱型坠物撞击后越容易发生反弹。
3.3 冲击力情况图11为细杆不同角度跌落下的冲击力时历曲线,跌落在横梁纵桁交汇上时,冲击力在瞬间急速上升,最大冲击力达6.48×106 N,远高于另外2种情况,随后冲击力的下降也更快,相比另外2种场景,结束后冲击力依旧处于较高的水平上,说明该场景是3种跌落场景中最剧烈的。对比不同场景的冲击力加载、卸载持续时间,发现跌落在纵骨上时最短,此时甲板最容易被坠物击穿而破裂。

|
图 11 冲击力-时历曲线(细杆) Fig. 11 Impact force-time history curve(thin rod) |
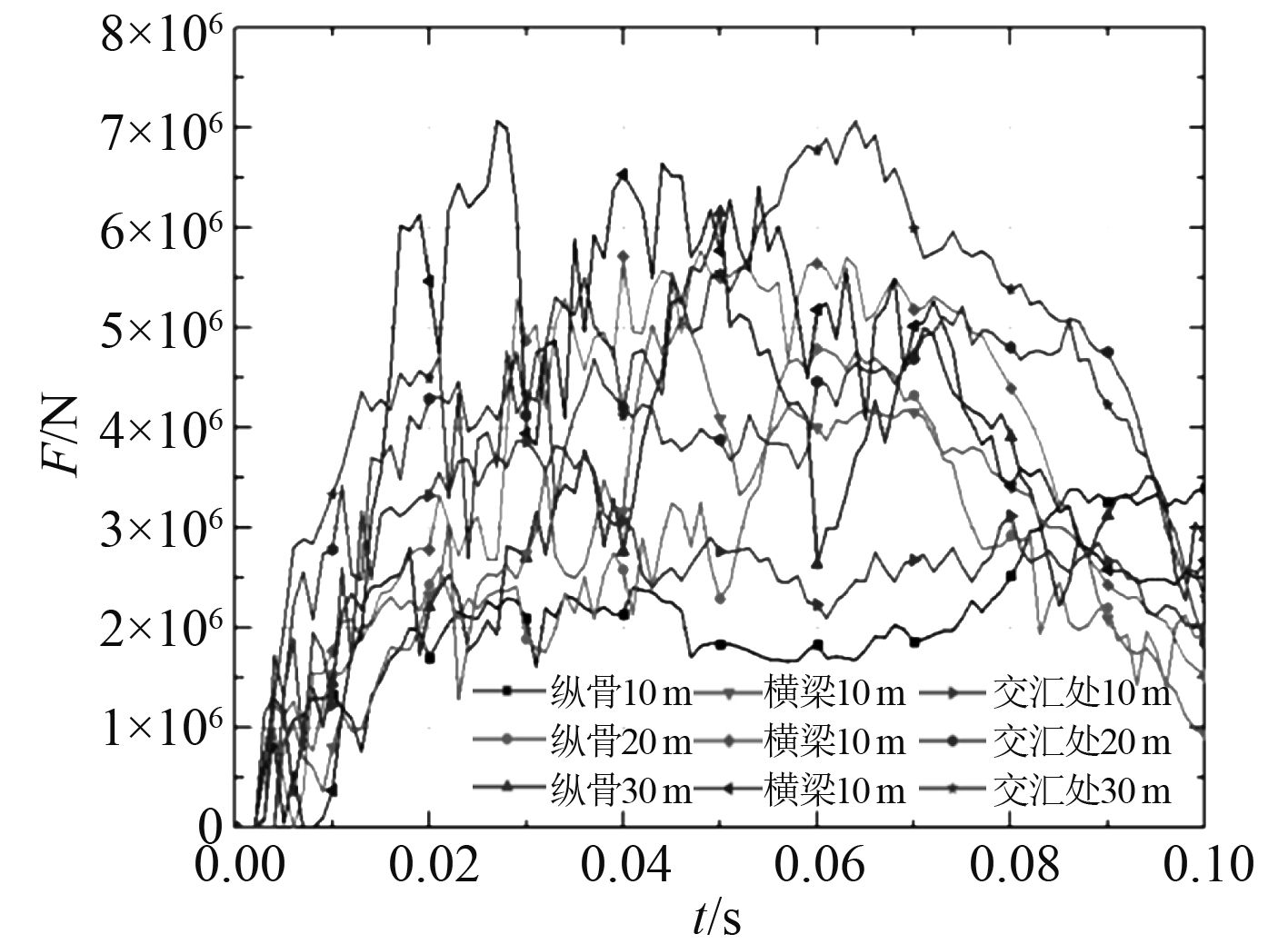
图12为集装箱不同角度跌落下的冲击力时历曲线,可以看出该过程具有强烈的非线性。坠物撞击到横梁交汇处上时,冲击力最大,相对于其他情况来说,冲击力在一个相对较长的时间内在一个较高的水平内波动,而其他2种情况,尤其是坠物撞击到纵骨上时,冲击力峰值点较为显著。
|
图 12 冲击力-时历曲线(集装箱) Fig. 12 Impact force-time history curve(container) |
综上分析,跌落点下方支撑构件越强,坠物动能消耗越迅速,冲击力在一个较高的水平内波动时间越长,对下方构件安全威胁越小。
4 结 语本文以半潜式起重平台甲板为研究对象,运用非线性有限元软件Ls-dyna对不同跌落参数下的结构抗冲击性能进行分析,详细研究了不同跌落角度、跌落区域及接触形式对结构的影响,得到以下主要结论:
1)当跌落角度为0°时,甲板的变形程度最低,不同坠物跌落时的甲板变形分别为0.06 m和0.13 m,10°时均对甲板造成了最为严重的损伤,且坠物向一侧倾倒的趋势最大。
2)不同坠物跌落在甲板纵骨上时甲板破裂的临界变性能最小,吸能最小,甲板吸能分别为9.47×105 J和5.36×108 J,跌落在横梁纵桁交汇处时临界变性能最大,吸能最大,甲板板吸能分别为8.38×105 J和4.50×106 J。
3)坠物在接触到下部结构时会产生向重心反向的滑动,甲板吸能随角度增加而增加,跌落冲击点下构件的局部刚度越强,损伤变形越小。
4)细长型坠物容易穿透甲板,对细长型坠物须严格控制吊升高度;横向跨距过大的坠物在大角度下会对甲板造成严重局部损伤,在吊运时应注意尽量水平调运,以防倾倒。
| [1] |
杨慧, 陈国明, 李新宏, 等. 国内外海底油气管道废弃处置规范[J]. 油气储运, 2017, 36(11): 1326-1331. |
| [2] |
李雪飞, 张锡斌, 任登龙, 等. 浅议海上油气生产设施弃置需要关注的问题[J]. 海洋开发与管理, 2015, 32(4): 8-11. DOI:10.3969/j.issn.1005-9857.2015.04.002 |
| [3] |
JUNG B G, JO S W, NOH S H, et al. Experimental and numerical studies on nonlinear impact response of deck structures subjected to dropped objects[C]// ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering. 2016.
|
| [4] |
夏侯命胜, 郭兴乾, 蒋镇涛, 等. 考虑坠物载荷的钻台结构设计研究[J]. 船舶, 2018, 29(5): 111-119. |
| [5] |
刘伟, 李清泉. 钻铤坠落对钻台甲板的损伤分析[J]. 上海船舶运输科学研究所学报, 2017, 40(2): 36-41. DOI:10.3969/j.issn.1674-5949.2017.02.007 |
| [6] |
XIANG G, BIRK L, YU X, et al. Numerical study on the trajectory of dropped cylindrical objects[J]. Ocean Engineering, 2017, 130(jan. 15): 1-9. |
| [7] |
XIANG G, BIRK L, YU X, et al. Study of the trajectory and landing points of dropped cylindrical object with different longitudinal center of gravity[J]. International Journal of Offshore & Polar Engineering, 2017, 27(3): 274-282. |
| [8] |
孙晓东. 海洋平台甲板落物分析研究及应用[J]. 广东化工, 2015, 42(8): 106-107. DOI:10.3969/j.issn.1007-1865.2015.08.049 |
| [9] |
王醍, 张延昌, 任慧龙, 等. 钻铤坠物冲击下的平台甲板塑性失效分析[J]. 船舶, 2014, 25(4): 27-37. DOI:10.3969/j.issn.1001-9855.2014.04.006 |
| [10] |
周世博, 章文俊, 李泽华, 等. 基于SAPSO-BP网络模型的海洋平台落物碰撞损伤分析[J]. 中国安全生产科学技术, 2019, 15(2): 64-69. |
| [11] |
余峙伟, 朱永梅, 马青丽, 等. 撞击载荷下水下管汇动力响应研究[J]. 江苏科技大学学报(自然科学版), 2019, 33(2): 49-55. |
| [12] |
刘昆, 包杰, 王自力, 等. 自升式平台直管结构碰撞模型试验与仿真分析[J]. 舰船科学技术, 2015, 37(S1): 103-109. |
 2021, Vol. 43
2021, Vol. 43
