2. 中国船舶集团有限公司第七一三研究所,河南 郑州 450000;
3. 河南省水下智能装备重点实验室,河南 郑州 450000
2. Seventh thirteen Institute of China Shipbuilding Industry Corporation, Zhengzhou 450000, China;
3. Key Laboraory of Underwater Intelligent Equipment in Henan Province, Zhengzhou 450000, China
水下无人航行器需要自主完成多种人类无法完成的任务,在复杂环境中的任务规划更具挑战性。目前智能的自主任务规划受到了广泛的关注,而路径规划是实现任务规划的必要前提以及重要组成部分。
路径规划的任务就是在已知的约束条件下找出一条从当前位置到目标位置的最优或次优的可行路径。路径规划方法又可分为经典算法和智能算法。智能算法中有遗传算法、粒子群优化算法、神经网络算法等。大多数论文认为经典算法中有3类主要方法:细胞分解法、人工势场法以及路线图方法[1]。
人工势场法因其表达简洁,原理简单,对硬件要求低,规划速度快等优点而广泛应用于机器人导航与避障中。Khatib首次将人工势场法引入实时路径规划中[2]。人工势场法是构造一个势力场,将在势力场中的航行器看作电子,目标位置对其产生吸引力以保证朝着目标位置前进,障碍物对其产生斥力以保证避开障碍物。然而,人工势场法在路径规划的应用中如果障碍物距离目标点过近、U型障碍物等复杂问题时则会出现无法到达目标不可达等问题。为了克服这些问题,研究人员尝试去改进传统的人工势场法。S. S. Ge等[3]提出当目标附近存在障碍物而使目标不可达时,利用航行器与目标之间的距离来构造新的斥力函数来确保目标位置是全局最小。朱华健等[4]提出通过直接寻找一系列势能极小点来构成航行器的行进路径可解决航行器目标不可达以及震荡问题。林欣等[5]提出利用决策树改进人工势场法,根据斥力增益系数、合力偏转角度和速度对不同障碍分布做出合理的决策。本文提出一种基于速度矢量判断旋转方向的改进人工势场法,在水下无人航行器的局部路径规划中实现安全快速的避障。
1 人工势场法原理人工势场中水下无人航行器受到由障碍物产生的斥力场以及目标物产生的引力场的影响,水下航行器所受到的引力以及斥力的合力方向即为航行器的移动方向,这一运动方向使得航行器避过障碍物并朝着目标位置移动。
目标位置所形成的引力势场可表示为:
| $ {U}_{att}\left(X\right)=\frac{1}{2}{k}_{att}|X-{X}_{d}{|}^{2}\text{。} $ | (1) |
式中:
| $ {F}_{att}=-\nabla {U}_{att}=-{k}_{att}|x-{x}_{d}|\text{。} $ | (2) |
当航行器到达目标位置时引力为0。
1.1 传统人工势场法缺陷1)容易陷入局部极小值。当水下无人航行器所受引力与斥力大小相等、方向相反时,航行器所受合力为0,此时航行器陷入了局部极小值点。在局部极小值点周围的各个位置的合力都指向局部极小值,导致航行器在局部极小值点周围振荡,无法自行走出该区域。
2)传统人工势场法引力部分与水下无人航行器和目标点位置距离成正比,当水下无人航行器距离目标点较远时,引力部分过大,可能导致水下无人航行器与障碍物相撞。
3)当航行器离目标点比较远时,引力将变的特别大,相对较小的斥力在甚至可以忽略的情况下,航行路径上可能会碰到障碍物。
4)水下无人航行器在三维空间中,通常将航行器和障碍物看作在同一水平面内。采用水平面二维人工势场法避障,且使用二维平面固定左旋转方向或者右旋转方向进行避障,如图1和图2所示。对于障碍物长宽比悬殊、复杂海底巡航,扁平型UUV编队协同等特殊情况,且需要航行器快速绕过障碍物时二维平面固定速度旋转方向人工势场法不能很好满足实际工程的全部需求。
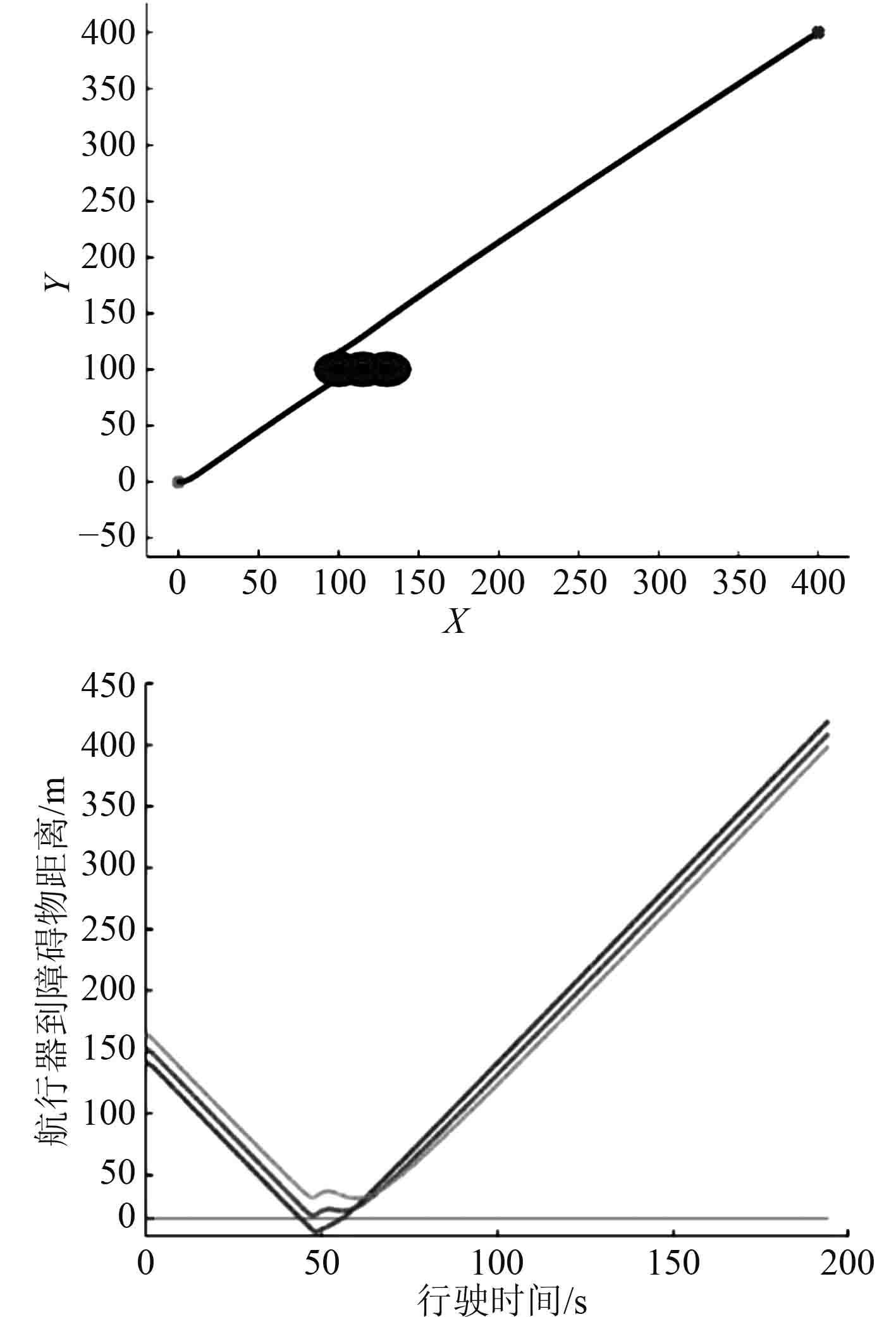
|
图 1 固定速度左旋转避障 Fig. 1 Left-turn obstacle avoidance at fixed speed |
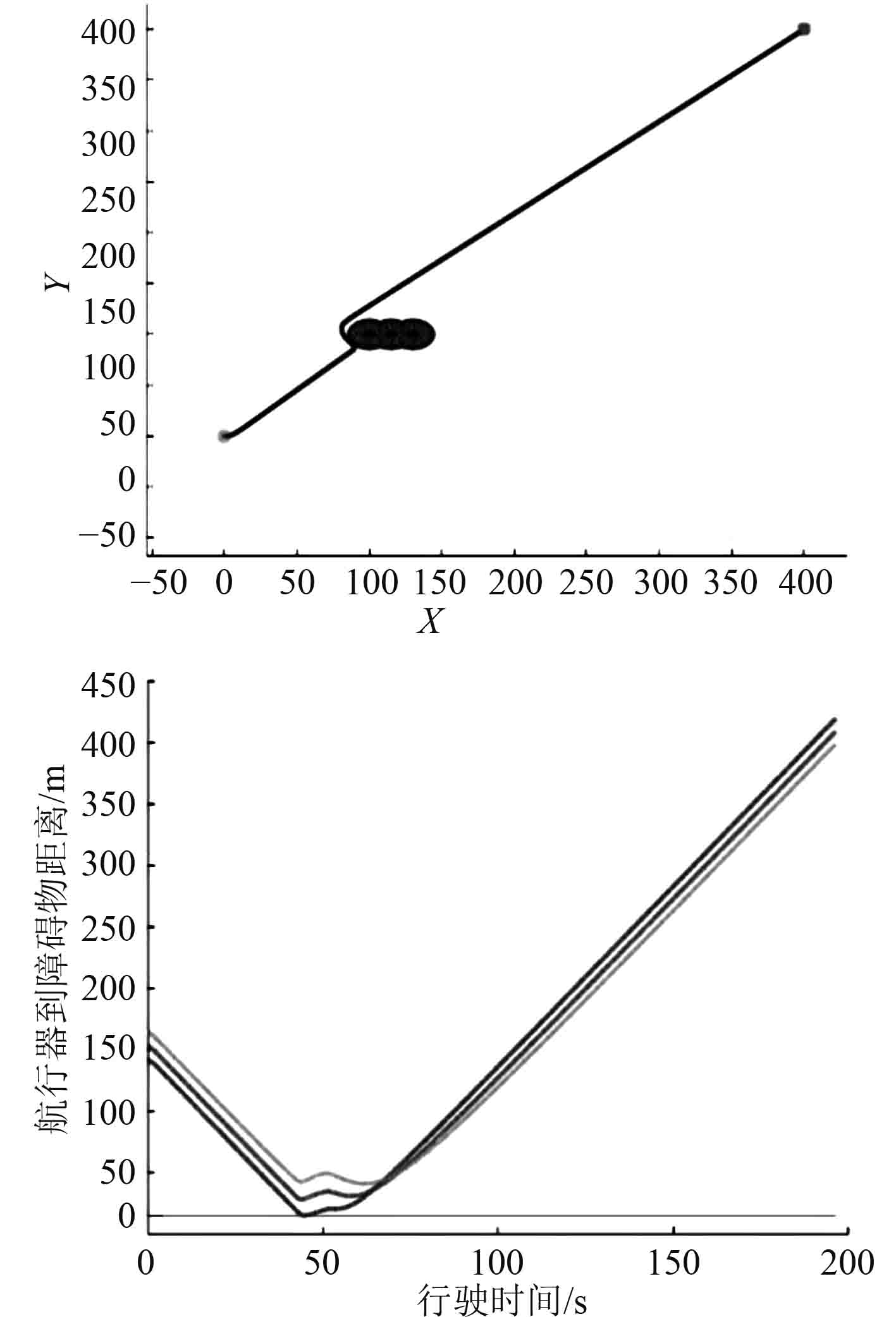
|
图 2 固定速度右旋转避障 Fig. 2 Right-turn obstacle avoidance at fixed speed |
针对传统人工势场法的缺陷,Khatib提出的FIRAS函数是障碍物形成的斥力势场常用的表达方法:
| $ {U_{rep}}(X) = \left\{ {\begin{array}{*{20}{l}} \dfrac{1}{2}{k_{rep}}{{\left( {\dfrac{1}{{\rho \left( {X,{X_{obs}}} \right)}} - \dfrac{1}{{{\rho _0}}}} \right)}^2},&\rho \left( {X,{X_{obs}}} \right) \leqslant {\rho _0}\text{,}\\ 0,&{\rho \left( {X,{X_{obs}}} \right) > {\rho _0}}\text{。} \end{array}} \right. $ | (3) |
式中:
| $\begin{split} {F_{{\rm{rep }}}} = &- \nabla {U_{{\rm{rep }}}} = \\ &\left\{\!\!\!\! {\begin{array}{*{20}{l}} {k_{rep}}{{\left( {\dfrac{1}{{\rho \left( {X,{X_{obs}}} \right)}} - \dfrac{1}{{{\rho _0}}}} \right)}^2}\times\\ \qquad\dfrac{1}{{{\rho ^2}\left( {X,{X_{obs}}} \right)}} \dfrac{{\partial \rho \left( {X,{X_{obs}}} \right)}}{{\partial X}},\!\!\!\!\!\!\!\!&X - {X_{obs}} \leqslant {\rho _0}\text{,}\\ 0,\!\!\!\!\!\!\!\!&{X - {X_{obs}} > {\rho _0}}\text{。} \end{array}} \!\!\!\!\!\!\!\!\!\right.\end{split} $ | (4) |
航行器所受合力可以表示为:
| $ F = {F_{a{\rm{ }}t{\rm{ }}t}} + {F_{r{\rm{ }}e{\rm{ }}p}}\text{,} $ | (5) |
合力
采用式(4)的传统斥力势场,当目标点在碍航物附近时,UUV 无法到达目标点。因此引入新的斥力函数在原有的斥力场的基础上,加入了目标和物体距离的影响。强化目标点附近引力场,弱化目标点附近斥力场,改进势场如下:
| $ {U_{rep}}(X) \!=\! \left\{\!\!\!\!\! {\begin{array}{*{20}{l}} \dfrac{1}{2}{k_{rep}}{{\left( {\dfrac{1}{{\rho \left( {X,{X_{obs}}} \right)}} \!-\! \dfrac{1}{{{\rho _0}}}} \right)}^2}\!\times\\ \qquad{\rho ^2}\left( {X,{X_{obs}}} \right),&\!\!\!\!\!\!\!\!\rho \left( {X,{X_{obs}}} \right) \!\leqslant \!{\rho _0}\text{,}\\ 0,&\!\!\!\!\!\!\!\!{\rho \left( {X,{X_{obs}}} \right)\! > \!{\rho _0}}\text{。} \end{array}} \!\!\!\!\!\!\!\!\!\!\right. $ | (6) |
当水下无人航行器越靠近目标点时,斥力势能越小,引力势能越大。这可解决当目标点周围出现障碍物的局部极小问题。
针对水下无人航行器固定旋转方向的缺陷问题提出基于速度矢量判定的旋转方法。
叉积是2个三维向量之间的叉积生成一个与这2个向量都垂直的新向量。对于A,B两个向量:
| $ \begin{split} &{ A} = {x_1}\hat i + {x_2}\hat j + {x_3}\hat kn\text{,}\\ &{ B} = {y_1}\hat i + {y_2}\hat j + {y_3}\hat kn\text{,} \end{split} $ | (7) |
二者的叉积为:
| $\begin{split} { C} =& { A} \times { B} = \left| {\begin{array}{*{20}{l}} {\hat i}&{\hat j}&{\hat k}\\ {{x_1}}&{{x_2}}&{{x_3}}\\ {{y_1}}&{{y_2}}&{{y_3}} \end{array}} \right| = \left( {{x_2}{y_3} - {y_2}{x_3}} \right)\hat i -\\ &\left( {{x_1}{y_3} - {y_1}{x_3}} \right)\hat j + \left( {{x_1}{y_2} - {y_1}{x_2}} \right)\hat k \text{。}\end{split} $ | (8) |
在三维环境中,采用速度矢量a与障碍物与当前位置矢量b的叉积得到垂直于二者的向量c,通过向量c与速度矢量a的又一次叉积得到旋转矢量d,通过旋转矢量d判断UUV在障碍物的一侧(左侧、右侧、上侧、下侧),进而选择近的一侧作为旋转方向,使速度方向旋转至合力方向离开障碍物。
2 仿真结果及分析本文利用 Matlab 软件针对传统人工势场法的缺陷和水下航行器二维平面固定旋转方向的问题采用改进人工势场法进行仿真,以下仿真结果均是在静态障碍物的前提下进行的。水下无人航行器采用尾十字舵和单主推驱动,仿真中记录机器人重心的轨迹和距离障碍物的距离。仿真结果表明,改进后的人工势场法具有更强的环境适应性,避障更加快速安全,达到了预期的避障效果。
由图3和图4可以看出在距离目标点很远的情况下,航迹上有多个障碍物,由于存在障碍物势力场范围,UUV仍然能够进行安全避障。
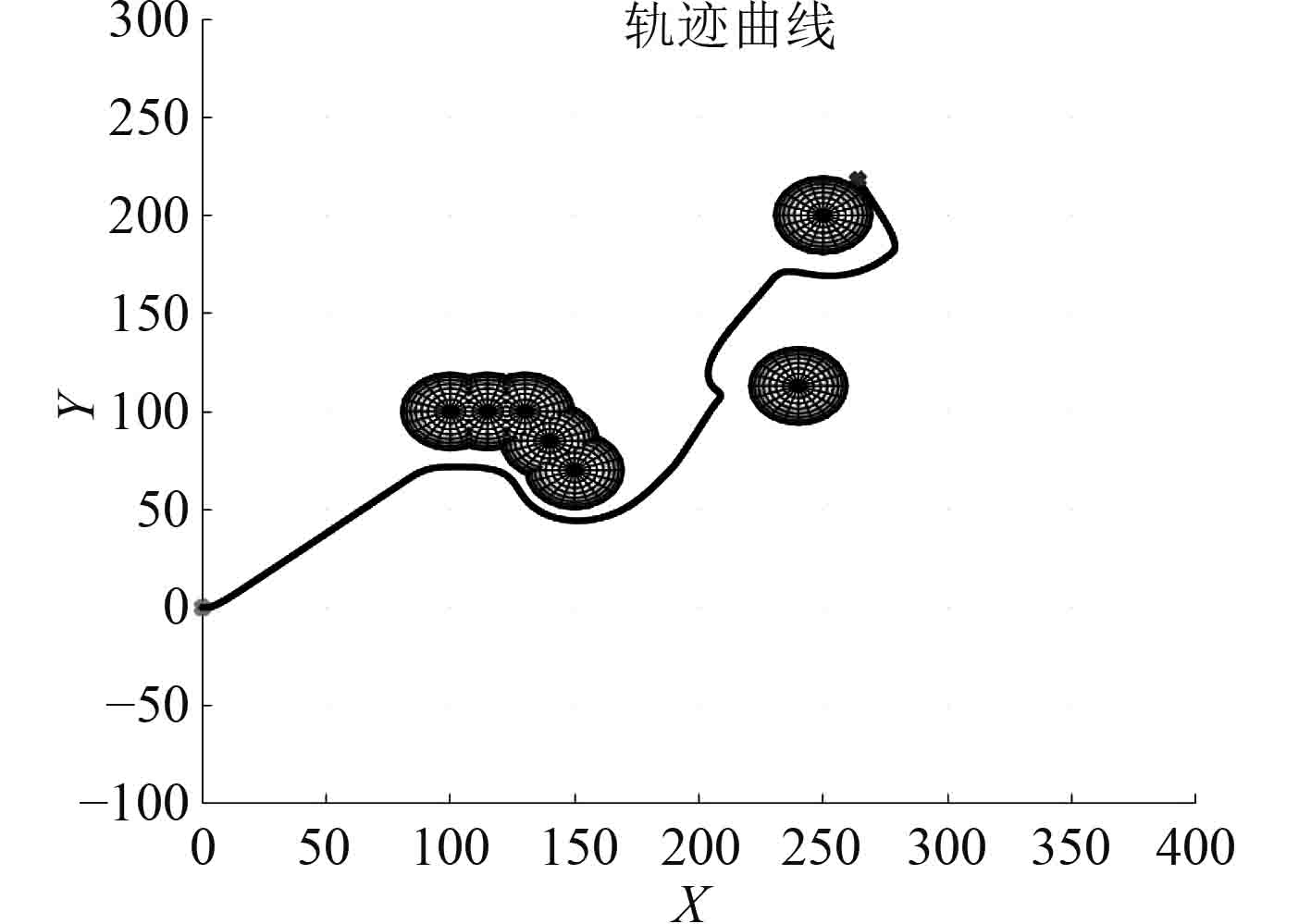
|
图 3 障碍物无斥力场范围时航行器轨迹曲线与航行器距障碍物距离 Fig. 3 When the obstacle has no repulsion field range, the trajectory curve of the aircraft and the distance between the aircraft and the obstacle |
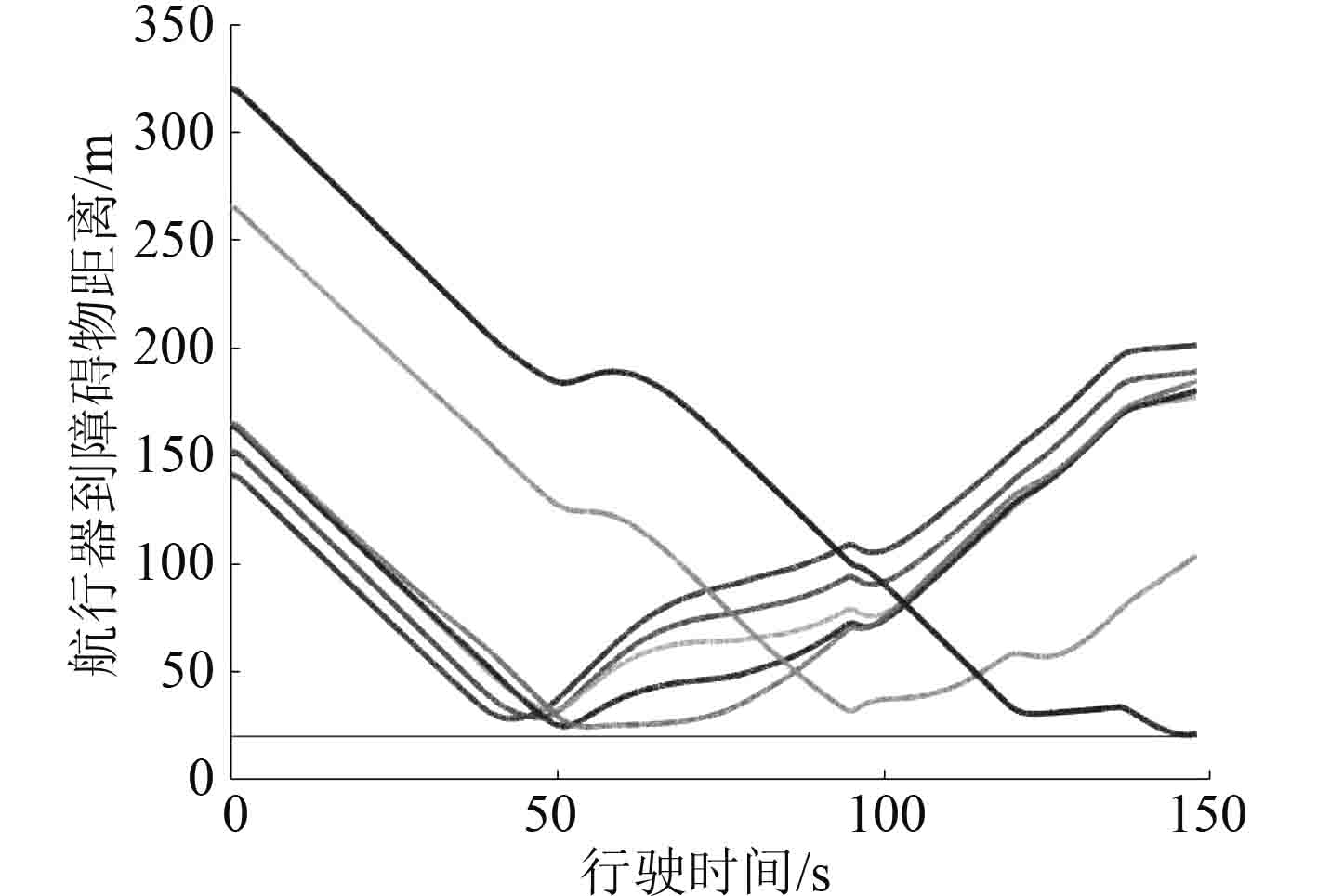
|
图 4 障碍物有势力范围航行器轨迹曲线与航行器距障碍物距离 Fig. 4 When the obstacle has a range of influence, the trajectory curve of the aircraft and the distance between the aircraft and the obstacle |
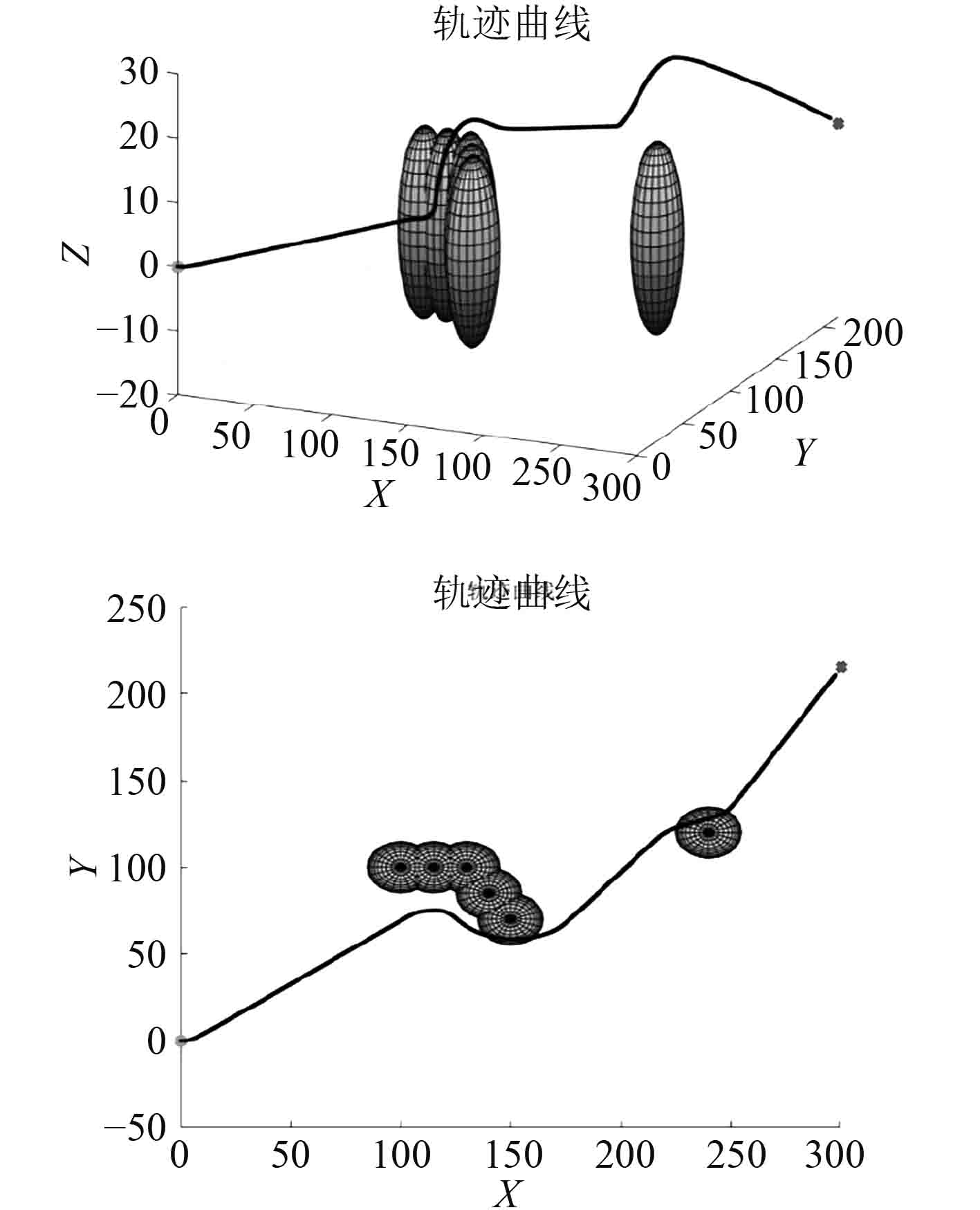
图5和图6显示目标距离障碍物很近时,由于强化了目标点附近的水下无人航行器并没有停止在障碍物周围,同时UUV能够安全穿过障碍物到达目标点。
|
图 5 目标点附近存在障碍物航行器轨迹曲线 Fig. 5 The trajectory curve of the aircraft when there is an obstacle near the target point |

|
图 6 目标点附近存在障碍物时航行器距障碍物距离 Fig. 6 The distance between the aircraft and the obstacle when there is an obstacle near the target point |
由图7和表1可以看出,三维环境中,在不同障碍物和特殊目标点的情况下,给定相同的引力和斥力系数和障碍物斥力场范围,水下航行器会根据实时速度判断障碍物在航行器的左侧,右上侧或者右侧,进而选择最近的一侧作为旋转方向,并不停调整旋转方向进行避障。因而航行器有更短的航行距离,能更快到达目标点。

|
图 7 基于速度矢量判断航行器三维空间航行轨迹 Fig. 7 The three-dimensional space navigation trajectory of aircraft based on velocity vector judgment |
|
|
表 1 改进人工势场法对照试验 Tab.1 Improved artificial potential field method control test |
本文针对 UUV 在未知环境自主航行中的局部路径规划问题,提出一种改进人工势场算法,根据障碍物的形状,目标点的远近,选择合理的障碍物斥力范围和引力斥力系数,再根据速度矢量判定速度旋转方向,这种改进的人工势场法解决了传统人工势场法在三维平面内固定旋转方向的避障缺陷,能很好地应对复杂障碍物和特殊目标点,保持和障碍物的距离,快速且安全到达目标点。但这种方法同样具有局限性,基于速度矢量判断方法会使水下无人航行器控制变得更加复杂,增加航行的控制难度。因此未来在航行器中因增加避障策略器,在不同障碍物和目标点选择不同的避障策略。
| [1] |
ANAVATTI S. G., FRANCIS S. L., GARRATT M., 自主车辆路径规划模块的现状与挑战[C]//2015先进机电一体化、智能制造和工业自动化国际会议(ICAMIMIA), 泗水, 2015,205-214.
|
| [2] |
KHATIB O., 机械手和移动机器人的实时避障[C] //1985年IEEE机器人与自动化国际会议, 美国密苏里州圣路易斯, 1985: 500-505.
|
| [3] |
S. S. GE, Y. J. CUI. 一种新的用于移动机器人路径规划的势场函数[J], 机器人与自动化学报, 2000,16,(5), 615−620. S. S. GE, Y. J. CUI. 一种新的用于移动机器人路径规划的势场函数[J], 机器人与自动化学报, 2000,16(5), 615−620. |
| [4] |
H. ZHU, J. WANG, J. LI,,移动机器人路径规划的一种新的势场方法[C]//2013年第25届中国决策与控制会议 (CCDC), 贵阳, 2013: 2811−2814.
|
| [5] |
X. LIN, Z. WANG, X. CHEN. 基于决策树的改进人工势场法路径规划[C]//2020年第27届圣彼得堡综合导航系统国际会议 (ICINS), 俄罗斯圣彼得堡, 2020: 1−5.
|
 2021, Vol. 43
2021, Vol. 43
