2. 武汉第二船舶设计研究所,湖北 武汉 430205;
3. 华中师范大学,湖北 武汉 430079;
4. 武汉理工大学 汽车工程学院,湖北 武汉 430070
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China;
3. Central China Normal University, Wuhan 430079, China;
4. School of Automobile Engineering, Wuhan University of Technology, Wuhan 430070, China
水下航行器得到了越来越多的应用。此类航行器在水下工作时,运动速度较低,导致其舵效很低[1],这就需要依靠其他的惯性调节系统来调节其运动姿态,因此,水下航行器,尤其是大型的水下航行器,一般都设计有多个压载水舱以及对应的压载水系统控制方案。压载水系统是低速水下航行器调整运动姿态的重要装置,作为一个惯性调节系统,它根据传感器监测到的航行器实时运动状态,发出相应指令,由压载水系统控制水舱注、排水以改变自身质量、质心位置,将惯性力与力矩作用于航行器来实现航行器位置和姿态的调整[2-5]。
传统方式下的低速水下航行器运动姿态惯性调节系统的设计过程费时费力,需要大量投入,故开发相关的参数化软件非常重要,能够在系统方案的早期设计阶段对不同的航行器运动姿态调节系统进行快速评估[6]。针对当前相应软件的开发比较分散、不够系统化的背景,本文采用多领域建模的方法,建立水下航行器六自由度运动模型以及惯性调节系统中水、气、控制器动力学模型,实现了航行器空间运动与其惯性调节系统的耦合动力学联合仿真。
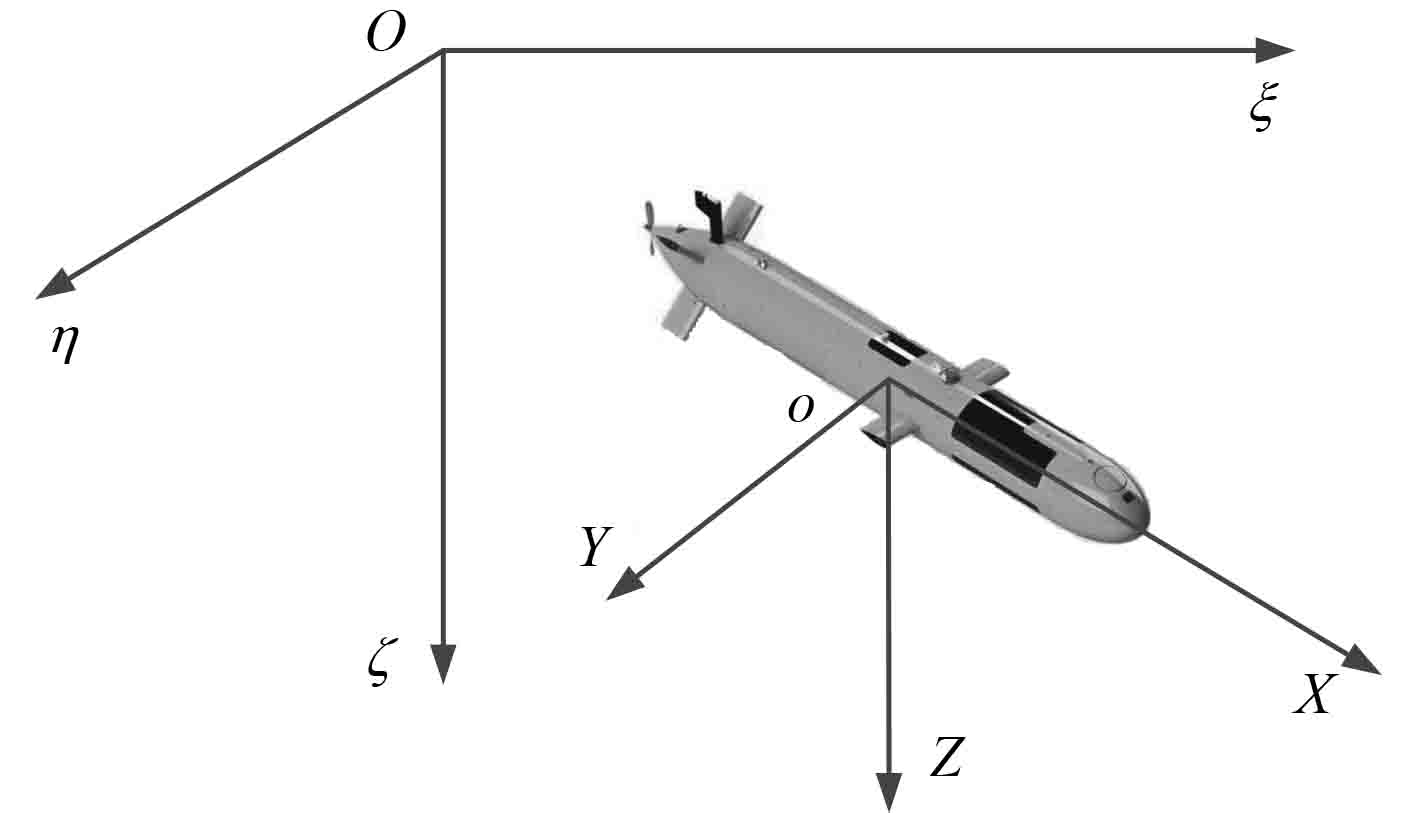
1 水下航行器六自由度运动模型的建立 1.1 水下航行器六自由度运动方程水下航行器运动过程中的2种坐标系(固定坐标系和运动坐标系),如图1所示。
|
图 1 两种运动坐标系 Fig. 1 Two kinds of movement coordinates |
固定坐标系固结在地球表面上,其不随时间和航行器运动而变化。通常取t =0时刻,航行器质心所在的位置为固定坐标系的原点E,
水下航行器的运动可以用在运动坐标系中的速度向量
在上述坐标系定义下的水下航行器六自由度运动方程如下[7-8]:
轴向方程
| $\begin{split} m(\dot u - rv + wq) =& \dfrac{1}{2}\rho {L^4}(X_{qq}'{q^2} + X_{rr}'{r^2} + X_{rp}'rp) + \\ &\dfrac{1}{2}\rho {L^3}\left(X_{\dot u}'\dot u + X_{vr}'vr + X_{wq}'wq\right) +\\ &\dfrac{1}{2}\rho {L^2}\left(X_{uu}'{u^2} + X_{vv}'{v^2}\right) + \\ &\dfrac{1}{2}\rho {L^2}{u^2}\left(X_{{\delta _r}{\delta _r}}'{\delta _r}^2 + X_{{\delta _s}{\delta _s}}'{\delta _s}^2 + X_{{\delta _b}{\delta _b}}'{\delta _b}^2\right) + \\ &{F_{xp}} + {F_x} \text{,} \\[-10pt]\end{split} $ | (1) |
式中:
横向方程
| $\begin{split} m(\dot v - wp + ur) =& \dfrac{1}{2}\rho {L^4}\left(Y_{\dot r}'\dot r + Y_{\dot p}'\dot p + Y_{pq}'pq\right) + \\ &\dfrac{1}{2}\rho {L^3}\Biggr(Y_{\dot v}'\dot v + Y_r'ur + Y_p'up + Y_{wp}'wp +\\ &Y_{v\left| r \right|}'\dfrac{v}{{\left| v \right|}}{({v^2} + {w^2})^{\frac{1}{2}}}\left| r \right|\Biggr) + \\ &\dfrac{1}{2}\rho {L^2}\left(Y_v'uv + Y_{vw}'vw + Y_{v\left| v \right|}'{({v^2} + {w^2})^{\frac{1}{2}}}\right) +\\ &\frac{1}{2}\rho {L^2}\left(Y_{{\delta _r}}'{u^2}{\delta _r}\right) + {F_y} \text{,} \\ \\[-18pt]\end{split} $ | (2) |
垂向方程
| $\begin{split} m(\dot w - qu + pv) = &\dfrac{1}{2}\rho {L^4}\left(Z_{\dot q}'\dot q + Z_{rr}'{r^2} + Z_{rp}'rp\right) + \\ &\dfrac{1}{2}\rho {L^3}\Bigg(Z_{\dot w}'\dot w + Z_q'uq + Z_{vr}'vr + \\ & Z_{vp}'vp + Z_{w\left| q \right|}'\dfrac{w}{{\left| w \right|}}{\left({v^2} + {w^2}\right)^{\frac{1}{2}}}\left| q \right|\Bigg) +\\ &\dfrac{1}{2}\rho {L^2}\Bigr(Z_*'{u^2} + Z_w'uw + \\ &Z_{w\left| w \right|}'w{({v^2} + {w^2})^{\frac{1}{2}}} + Z_{vv}'{v^2}\Bigr) +\\ &\dfrac{1}{2}\rho {L^2}\left(Z_{{\delta _s}}'{u^2}{\delta _s} + Z_{{\delta _b}}'{u^2}{\delta _b}\right) \text{,} \\ \end{split} $ | (3) |
横倾方程
| $ \begin{split}{I}_{x}\dot{p}\!+\!({I}_{x}\!-\!{I}_{y})qr\!=\!&\dfrac{1}{2}\rho {L}^{5}\bigg({K}_{\dot{p}}'\dot{p}+{K}_{\dot{r}}'\dot{r}+{K}_{\left|p\right|p}'p\left|p\right|+{K}_{qr}'qr\bigg)+\\ &\dfrac{1}{2}\rho {L}^{4}\left({K}_{\dot{v}}'\dot{v}+{K}_{p}'up\right) +\dfrac{1}{2}\rho {L}^{3}\Bigg({K}_{v}'uv+\\ &{K}_{vw}'vw+{K}_{\left|v\right|v}'v({{v^2} +{w^2})^{\frac{1}{2}}}\Bigg)+\\ &\frac{1}{2}\rho {L}^{3}\left({K}_{{\delta }_{r}}'{u}^{2}{\delta }_{r}\right)-mgh\mathrm{cos}\theta \mathrm{sin}\phi +{M}_{x}\text{,}\\[-12pt]\end{split}$ | (4) |
纵倾方程
| $\begin{split} {I_y}\dot q + ({I_x} - {I_z})rp =& \dfrac{1}{2}\rho {L^5}\left(M_{\dot q}'\dot q + M_{rr}'{r^2} + M_{rp}'rp\right) + \\ &\dfrac{1}{2}\rho {L^4}\bigg(M_{\dot w}'\dot w + M_{vr}'vr + M_{vp}'vp + \\ &M_{\left| w \right|q}'{({v^2} + {w^2})^{\tfrac{1}{2}}}q + M_q'uq\bigg) +\\ &\frac{1}{2}\rho {L^3}\bigg(M_*'{u^2} + M_w'uw + M_{w\left| w \right|}'{({v^2} + {w^2})^{\frac{1}{2}}} + \\ &M_{vv}'{v^2}\bigg) + \dfrac{1}{2}\rho {L^3}\left(M_{{\delta _s}}'{u^2}{\delta _s} + M_{{\delta _b}}'{u^2}{\delta _b}\right) -\\ & mgh\sin \theta + {M_y} \text{,} \\ \\[-12pt]\end{split} $ | (5) |
偏航方程
| $\begin{split} {I_z}\dot r + ({I_y} - {I_x})pq = &\dfrac{1}{2}\rho {L^5}\left(N_{\dot p}'\dot p + N_{\dot r}'\dot r + N_{pq}'pq\right) + \dfrac{1}{2}\rho {L^4}\bigg(N_{\dot v}'\dot v +\\ & N_p'up + N_r'ur + N_{wp}'wp\bigg) + N_{\left| v \right|r}'{({v^2} + {w^2})^{\frac{1}{2}}}) +\\ & \dfrac{1}{2}\rho {L^3}\bigg(N_v'uv + N_{vw}'vw + N_{\left| v \right|v}'v{({v^2} + {w^2})^{\frac{1}{2}}}\bigg) + \\ &\frac{1}{2}\rho {L^3}\left(N_{{\delta _r}}'{u^2}{\delta _r}\right) + {M_z}\text{。} \\ \\[-18pt]\end{split} $ | (6) |
以上各式右侧为航行器的惯性水动力、黏性水动力及舵水动力的一般表示形式。
式中:
为了确定船舶在海洋空间中的位置和姿态,还需要补充6个运动微分方程:
| $\dot \psi = q\frac{{\sin \varphi }}{{\cos \theta }} + r\frac{{\cos \varphi }}{{\cos \theta }}\text{,}$ | (7) |
| $\dot \varphi = p + q\tan \theta \sin \varphi + r\tan \theta \cos \varphi \text{,}$ | (8) |
| $\dot \theta = q\cos \varphi - r\sin \varphi \text{,}$ | (9) |
| $\begin{split} \dot \xi =& u\cos \psi \cos \theta + v(\cos \psi \sin \theta \sin \varphi - \sin \psi \cos \varphi ) + \\ & w(\cos \psi \sin \theta \cos \varphi + \sin \psi \sin \varphi ) \text{,} \\ \end{split}$ | (10) |
| $\begin{split} \dot \eta =& u\sin \psi \cos \theta + v(\sin \psi \sin \theta \sin \varphi + \cos \psi \cos \varphi ) + \\ &w(\sin \psi \sin \theta \cos \varphi - \cos \psi \sin \varphi )\text{,} \\ \end{split} $ | (11) |
| $\dot \zeta = - u\sin \theta + v\cos \theta \sin \varphi + w\cos \theta \cos \varphi \text{。}$ | (12) |
以上方程表征了航行器在水下的各向运动,作为对航行器运动姿态进行预报和控制的重要依据。
1.2 海浪干扰力的计算航行器在近水面运动时,不可避免受到海浪和海流的影响而产生摇荡,由于受到1阶波浪力和2阶波浪力的作用,存在低频慢变的倾侧与漂移和波频摇荡2种运动响应。
1阶波浪力呈高频周期振荡形式,在其作用下航行器主要做摇荡运动,即垂荡、纵摇以及横摇运动等。计算波浪的1阶摇荡力的近似公式估算法有海勒默等,理论计算方法主要有细长体法、切片法、三维面元法等,模拟时可以运用数值解法。2阶波浪力呈小幅值长周期形式,通常在同周期内为常值,主要与波高及深度有关,被称为波吸引力。对于近水面运动,当海浪为长波,航行器顺着海浪方向运动时,趋于随浪逐流,其深度变化较大;在海浪为短波时,航行器的垂直位置几乎不受浪涌的影响。
因此,航行器在水下受到的波浪力通常包括波动的1阶波浪力和低频变化的2阶波浪力。此外,由于风浪流的存在,航行器对流速度与无浪条件下的对流速度存在差异,而航速也会影响到航行器的动浮力。对于航行器的六自由度运动来说,动浮力通常会引起深度和纵倾的变化;低频的2阶波浪力会产生深沉和纵摇运动,而1阶波浪力通常会对6个自由度都产生影响。
于是,海浪、风浪作用下的外部干扰力
| ${X_w} = {X_{wf}}\text{,}$ | (13) |
| ${Y_w} = {Y_{wf}}\text{,}$ | (14) |
| ${Z_w} = {Z_{wu}} + \;{Z_{ws}}{\rm{ + }}{Z_{wf}}\text{,}$ | (15) |
| ${K_w} = {K_{wf}}\text{,}$ | (16) |
| ${M_w} = {M_{wf}}\text{,}$ | (17) |
| ${N_w} = {N_{wu}} + {N_{ws}} + {N_{wf}}\text{。}$ | (18) |
式中:下角标f表示1阶波浪力;下角标s表示2阶波浪力;下角标u表示动浮力。
艇体风浪中的动浮力为:
| ${{\rm{Z}}_{wu}} = {U_w}^2{\cos ^2}\psi \,{C_z}\text{,}$ | (19) |
| ${N_{wu}} = {U_w}^2{\cos ^2}\psi \,{m_z}\text{。}$ | (20) |
式中:
航行器受到的海浪低频2阶波浪力简化为恒值力和力矩,其形式可表示为:
| ${{\rm{Z}}_{ws}} = {Z_s}{{\rm{e}}^{{b_w}({\zeta _R} - \zeta )}}\text{,}$ | (21) |
| ${N_{ws}} = {N_s}{{\rm{e}}^{{b_w}({\zeta _R} - \zeta )}}\text{。}$ | (22) |
式中:
1阶波浪力通常采用多个正弦波叠加的方式进行逼近,正弦波参数包括频率和相位差。1阶波浪力也随着深度的变化而衰减,衰减系数与2阶波浪力相同。故所受的1阶波浪力的模型可表示为:
| ${X_{wf}} = {e^{bw\left( {{\zeta _R} - \zeta } \right)}}\sum\limits_{i = 1}^4 {\alpha _x^i\sin \left[ {{\omega _i}t + {\phi _i}} \right]} \text{,}$ | (23) |
| ${Y_{wf}} = {e^{bw\left( {{\zeta _R} - \zeta } \right)}}\sum\limits_{i = 1}^4 {\alpha _y^i\sin \left[ {{\omega _i}t + {\phi _i}} \right]} \text{,}$ | (24) |
| ${Z_{wf}} = {e^{bw\left( {{\zeta _R} - \zeta } \right)}}\sum\limits_{i = 1}^4 {\alpha _z^i\sin \left[ {{\omega _i}t + {\phi _i}} \right]}\text{,} $ | (25) |
| ${K_{wf}} = {e^{bw\left( {{\zeta _R} - \zeta } \right)}}\sum\limits_{i = 1}^4 {\alpha _K^i\sin \left[ {{\omega _i}t + {\phi _i}} \right]} \text{,}$ | (26) |
| ${M_{wf}} = {e^{bw\left( {{\zeta _R} - \zeta } \right)}}\sum\limits_{i = 1}^4 {\alpha _M^i\sin \left[ {{\omega _i}t + {\phi _i}} \right]} \text{,}$ | (27) |
| ${N_{wf}} = {e^{bw\left( {{\zeta _R} - \zeta } \right)}}\sum\limits_{i = 1}^4 {\alpha _N^i\sin \left[ {{\omega _i}t + {\phi _i}} \right]}\text{。} $ | (28) |
式中:
基于以上数学公式的推导,在Matlab/Simulink中建立航行器的六自由度运动学模型。其中,利用双环PID控制水下航行器压载水系统的注、排水,以在航行器受到冲击力产生运动姿态及位置改变后,依靠惯性调节系统回到初始状态。
2 运动姿态惯性调节系统动力学建模 2.1 基于AMESim的运动姿态惯性调节系统模型建立 2.1.1 水系统建模水系统部分的模型主要由水舱、阀门、泵组和大水舱等元件构成。其中,水舱元件能接通气系统部分。水系统模型根据需求,配合气系统模型完成注水、排水、循环工况。
图2为水系统部分的模型。水舱元件内部有水和空气,上方接入气系统,下方接入水系统。当与高压空气连通时,依靠高压空气和泵组进行排水;若与排气口相连通,则依靠泵组进行注水并排除水舱内多余的空气;如果都不连通,则水在泵通路内自循环,阀门起到调节不同工况的作用。

|
图 2 水系统模型 Fig. 2 Water system modeling |
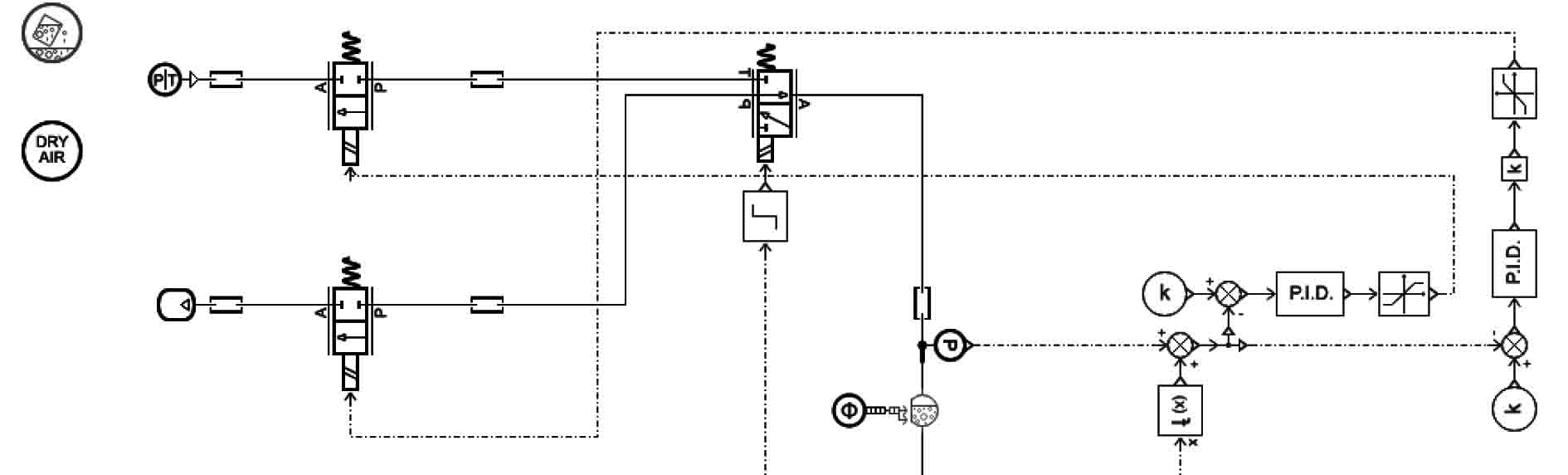
气系统部分的模型主要由压缩空气、排气口、水舱供气阀、水舱排水阀、三通阀和水舱等元件构成,水舱元件连通水系统部分。气系统可以配合水系统,通过控制各阀开关或开度来实现注水、排水和循环工况。
图3为气系统部分的模型。水舱供气(排气)阀模型下端接阀门开度控制信号,以水舱内外压差为控制目标,利用PID控制器进行调节。当水舱需要排水时,水舱供气阀打开,排气阀关闭,通过高压气体促使水从水舱流向泵组,从而排向大水舱;当水舱需要注水时,水舱排气阀打开,供气阀关闭,泵组将从大水舱流出的水泵向水舱,并把舱内多余的空气排出至排气口。三通阀在压载水系统内起到按工况连通相应阀组的作用,即排水工况下连通水舱供气阀,注水工况下连通水舱排气阀。
|
图 3 气系统模型 Fig. 3 Air system modeling |
通过AMESim与Matlab/Simulink软件建立“航行器—压载水系统”的联合仿真模型,其中AMESim用于压载水系统的建模,根据系统不同工况,输出相应的力与力矩;Matlab/Simulink用于航行器运动学建模,接收AMESim内由水舱注水、排水引起的力及力矩变化,计算整个航行器的运动状态,并输出位置信号给AMESim压载水系统,以实现调节。
3 基于多领域联合的低速水下航行器深度调节系统仿真设定工况:迎浪,航行器初始深度30 m,航速0.5 m/s,阀门切换时间5 s,仿真时间600 s,利用惯性调节系统使得航行器最终能维持在初始深度。仿真结果如图4~图6所示。

|
图 4 典型工况下的位移曲线(m) Fig. 4 Movement curve under typical condition |
|
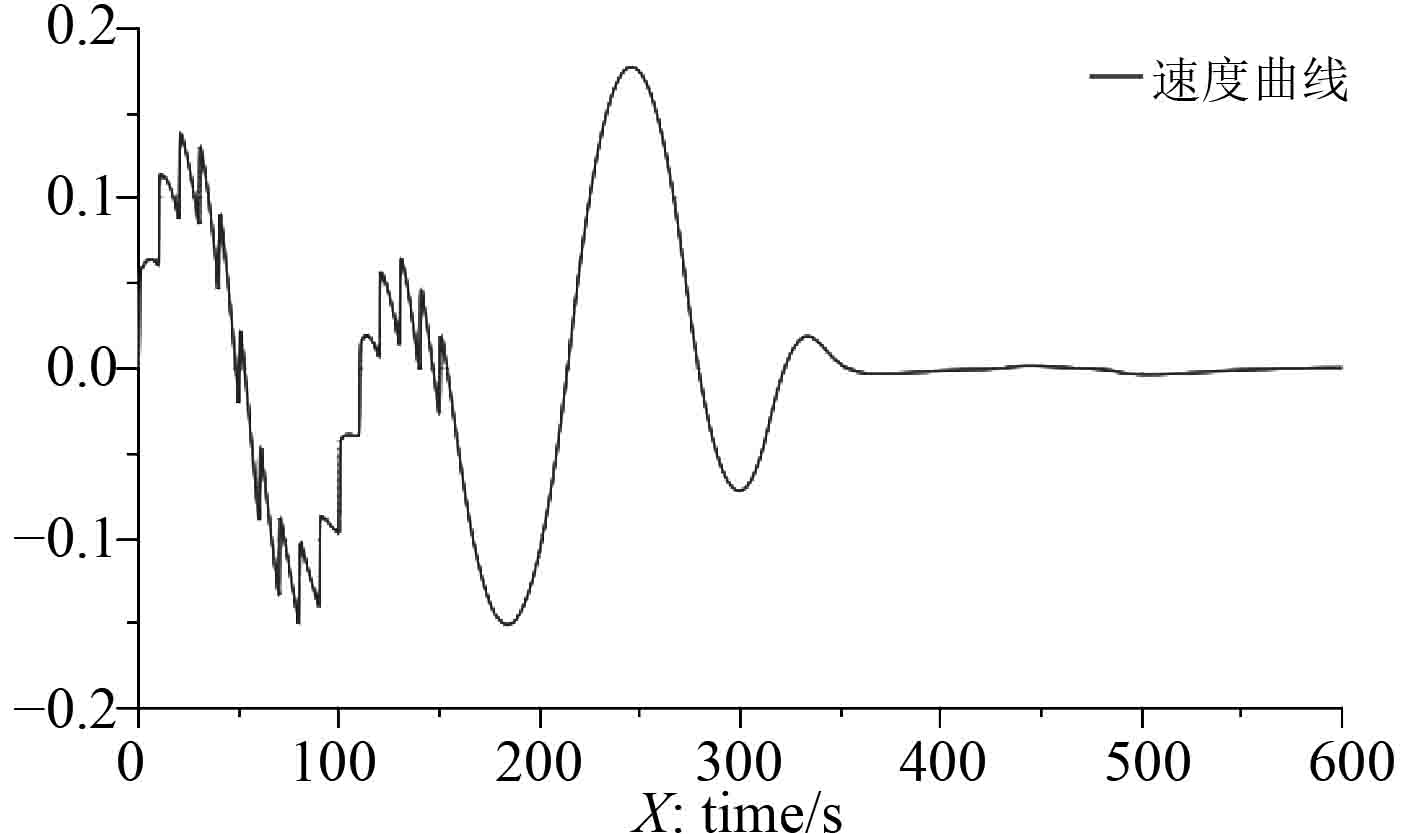
图 5 典型工况下的速度曲线(m/s) Fig. 5 Speed curve under typical condition |
|
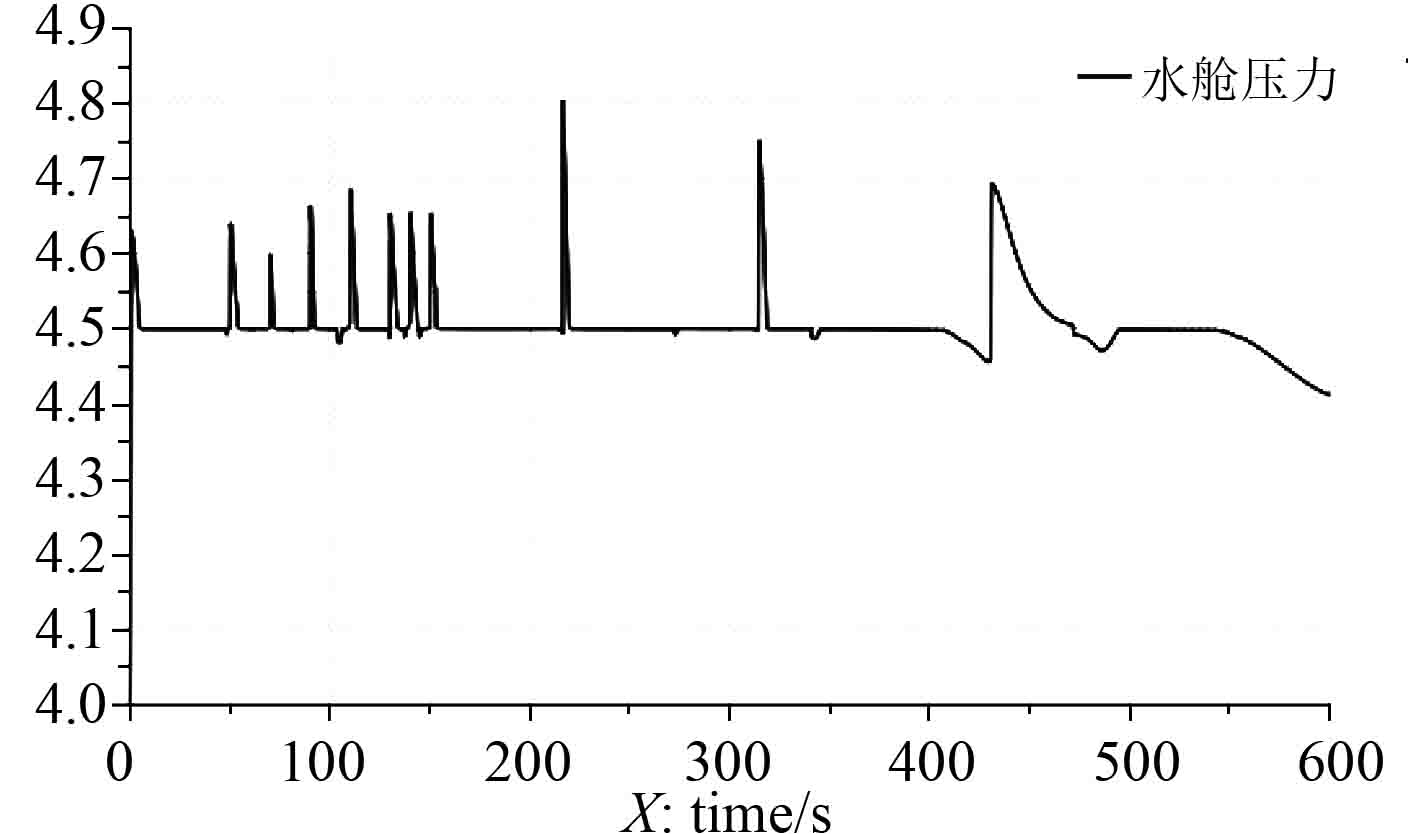
图 6 典型工况下的水舱压力曲线(bar) Fig. 6 Tank pressure curve under typical condition |
本文基于Matlab开发了水下航行器惯性调节系统多领域参数化建模与仿真软件系统,用来模拟水下低速航行器与其惯性调节系统的耦合动力学特性。以某小型水下航行器为例,在设定工况下,通过双环PID控制惯性调节系统,适时改变航行器的运动姿态,使其能够在受到海浪和外部冲击后,短时间内维持到初始深度并将水舱压差控制在安全范围内,验证了系统的有效性。
| [1] |
葛晖, 徐德民, 周秦英. 基于变质心控制的低速水下航行器动力学建模[J]. 机械科学与技术, 2007(3): 327-331. GE Hui, XU De-min, ZHOU Qin-ying. Dynamic modeling of a low speed underwater vehicle based on moving mass control[J]. Mechanical Science and Technology for Aerospace Engineering, 2007(3): 327-331. DOI:10.3321/j.issn:1003-8728.2007.03.014 |
| [2] |
周军. 变质量水下航行器均衡系统自动控制技术研究[D]. 北京: 中国舰船研究院, 2016. ZHOU Jun. The research of auto-control technique of balance system used to variable mass autonomous underwater vehicles[D]. Beijing: China Ship Research and Development Academy, 2016. |
| [3] |
刘西踩. 船舶压载水系统建模仿真研究[D]. 大连: 大连海事大学, 2013. LIU Xi cai. Ships ballast water system modeling and simulation research[D]. Dalian: Dalian Maritime University, 2013. |
| [4] |
马士虎, 刘增荣. 潜艇均衡系统仿真研究初探[J]. 舰船科学技术, 2002, 24(2): 42-44. MA Shi hu, LIU Zeng rong. The pilot study for the submarine ballanced system emulator[J]. Ship Science and Technology, 2002, 24(2): 42-44. |
| [5] |
穆为磊, 邹振兴, 孙海亮,等. 潜器浮力调节系统的低功耗控制策略[J]. 西安交通大学学报, 2018, 52(12): 44-49. MU Wei lei, ZOU Zhen xing, SUN Hai liang, et al. A control strategy with low power consumption for buoyancy regulation system of submersibles[J]. Journal of Xi’an Jiaotong University, 2018, 52(12): 44-49. |
| [6] |
马元. 自主式水下航行器运动控制系统的设计[D]. 青岛: 中国海洋大学, 2014. MA Yuan. A design of motion control system for autonomous underwater vehicle[D]. Qingdao: Ocean University of China, 2014. |
| [7] |
戴君锐, 向先波, 于曹阳. 六自由度水下航行器操纵性仿真及性能评估[J]. 华中科技大学学报(自然科学版), 2015, 43(S1): 452-456. DAI Jun rui, XIANG Xian bo, YU Cao yang. Maneuverability Simulation and performance evaluation of six degrees of freedom underwater vehicle[J]. Journal of Huazhong University of Science and Technology (NATURAL SCIENCE EDITION), 2015, 43(S1): 452-456. |
| [8] |
侯大力. 水下航行器动力学仿真[D]. 济南: 山东大学, 2014. HOU Da li. The dynamic simulation of underwater vehicle[D]. Jinan: Shandong University, 2014. |
 2021, Vol. 43
2021, Vol. 43
