2. 哈尔滨工程大学船舶工程学院,黑龙江 哈尔滨 150001
2. Colleg of Shipbuilding Engineering, Harbin EngineeringUniversity, harbin 150001, China
中国船级社《海上高速船入级及建造规范》[1]中对气垫船的定义如下:系指船舶不论在静止或运动时,其全部重量或大部分重量能被连续产生的气垫所支承的船舶。气垫船在航行过程中就犹如在船体与水面之间加入了一个流动的空气层,减小了水对船体的阻力,从而使船可以在水面上高速行驶或者在海滩等界面登陆,可使航速高达60~80 km/h,可以完成多种使命,在军用和民用领域都有着十分广阔的发展潜力和应用前景,尤其适用于登陆作战中作为登陆输送工具使用。
由于气垫船任务使命的特殊性,使得其对自身重量的控制较常规船严格,这就要求其结构尺寸不能过大,也就使得船体刚度较常规船型弱,再加上高转速发动机、高转速空气螺旋桨等高速振动源的作用,气垫船激励频率与激励幅值较常规船型大,使得气垫船的振动问题更为突出。在航行中产生剧烈的振动不仅会影响舒适性和工作效率,而且较高的振动幅值和频率更易在应力过大部位产生疲劳破坏,从而影响结构的强度和航行安全[2]。因此准确计算预报气垫船的振动性能尤其重要。但通常计算方法只考虑单一激振力下的响应[3],之后结合《舰船通用规范》[4]等相关规范要求进行校核,这与实际情况并不完全相符。本文采用有限元建模软件MSC.Patran对气垫船进行有限元建模,考虑多种激振力在同一位置处的瞬态响应,运用MSC.Nastran进行瞬态计算分析得到速度时历,根据GB/T 16301-2008规范[5]得到振动速度的均方根值,更符合实际情况且与实测值具有可比性。
1 气垫船振动分析 1.1 气垫船结构振动特性分析气垫船的甲板面相对而言较为广阔,同时具有较大舱室空间,气垫船内部大体为铝合金材质的箱体作为支撑结构,其设有燃油舱、淡水舱、舷侧气道、装载甲板等结构,铝合金的箱体四周为柔性围裙,气垫位于船底,一般采用稳定围裙将气垫分为不同的气室。甲板上方安装布置有空气螺旋桨等,船体左右两侧或左中右分别设有垫升风机。
气垫船在垫升状态高速航行时,船体与水面脱离,气垫的橡胶面与水面的接触势必会带来强烈的气垫-波浪之间的砰击作用,造成船体结构的剧烈振动。气垫船的激励源很多,船上的推进主机、垫升主机、垫升风扇以及空气螺旋桨等振动源都会产生不同频率的激励,再加上气垫受波浪砰击产生的振动,以及各种轴系传导力的过程中会产生不同程度的振动,诸多因素使得气垫船的振动非常复杂[6]。而气垫船由于质量要求,通常采用较薄的铝合金材料,使得结构本身振动频率不高,诸多振动源会使得船体结构产生较大的结构动静应力。所以气垫船的振动,成为气垫船在设计和建造过程中不能忽视的问题。
1.2 气垫船振动源参数结合气垫船运行及工作原理,船上高频振动源主要包括推进主机、空气螺旋桨、推进主机、风机等[7],本文选取垫升主机基座和推进主机基座这一典型结构进行振动特性分析计算,对其影响较大的激振源有推进主机(3个)、空气螺旋桨(3个)、垫升主机(2个)。由于风机离基座较远对基座响应值影响小,所以计算时不予考虑。振动源的组成、质量、偏心距等参数如表1所示。
|
|
表 1 振动源基本参数 Tab.1 Basic parameters of vibration sources |
不同频率下的转子动量可由下式计算:
| $\mathop P\limits^ \to = mv\cos wt\mathop i\limits^ \to - mv\sin wt\mathop j\limits^ \to \text{,} $ | (1) |
| $\frac{{{\rm{d}}\mathop p\limits^ \to }}{{{\rm{d}}t}} = {F_X}\mathop i\limits^ \to + ({F_y} - mg)\mathop j\limits^ \to \text{,} $ | (2) |
在得到转子动量之后,可根据下式计算转子动态激振力幅值:
| ${F_x} = {F_y} = me \times {(2\text{π} n)^2} \text{。} $ | (3) |
振动源在测试时激励源频率如表2所示。
|
|
表 2 振动源在测试时激励源频率 Tab.2 Excitation frequency of vibration sources in test |
气垫船的振动计算有限元模型依据详细设计图纸来建模,前后处理及分析运算均运用大型商用有限元软件MSC/Patran 和Nastran来完成。
根据CCS《船上振动控制指南》[7]的相关规定,在计算船舶局部结构的振动问题时,梁、板、板架等并不能作为孤立结构,对于短舱内部结构,依照推进主机基座和垫升主机基座的结构图纸对主机基座进行有限元建模,在推进主机重心位置建立MPC点并与推进主机基座相连,将推进主机重量施加到MPC点上。对于其他设备,如甲板上布置的空气螺旋桨桨叶、空气螺旋桨的桨轴等其他结构均在其重心位置建立MPC并施加对应的重量;在垫升主机重心位置建立MPC点与垫升主机基座相关联,将垫升主机重量施加到MPC点上,对于其他设备(空气螺旋桨、桨塔、推进主机等)均在其重心位置进行配重,以达到与实船重量分布相同,将上述设备按照重心位置进行配载,使桨塔与发动机短舱结构有限元模型的重心位置与实船的重心位置一致。
计算基座处的局部响应,模型范围取为31剖面~船尾(约1/2船长),这样在保证计算精度的同时节约计算时间,而且模拟了垫升主机及推进主机的基座的边界条件,消除了由于边界条件设置不准确使得计算结果失真。根据文献[8-9]边界条件在31剖面处取为简支。该计算模型包括127119个单元,62000个节点。计算模型如图1所示。

|
图 1 气垫船局部振动有限元模型 Fig. 1 Finite element model of local vibration of hovercraft |
为有效地研究气垫船基座的振动问题,针对实船进行振动测试试验,试验振动频率响应的测试区域选为垫升主机基座和推进主机基座,与有限元分析位置相同,即左舷推进主机和垫升主机的基座处,实船测点布置位置如图2所示。H1,H2,H5,H6测点分别对应的有限元模型节点编号为Node173275,173316,1063297,1063185。

|
图 2 气垫船局部振动测点布置 Fig. 2 Arrangement of local vibration measuring points for hovercraft |
考虑到测试时气垫船处于稳定航行状态,激振力的频率和大小不变,激振力方向随时间不断变化,因此采用瞬态响应分析计算气垫船的局部响应。建立各激振力随时间变化的场函数,得到方向随时间不断变化的激振力,施加到模型上。阻尼根据经验取0.05,时间步长取为0.001 s,步数3100步。
根据上述要求,在有限元模型上施加激振力的场函数并递交计算,基座上4个测点的加速度、速度时历曲线部分结果如图3~图10所示。

|
图 3 H1点处横向速度响应曲线 Fig. 3 Lateral velocity response curve at H1 point |
|
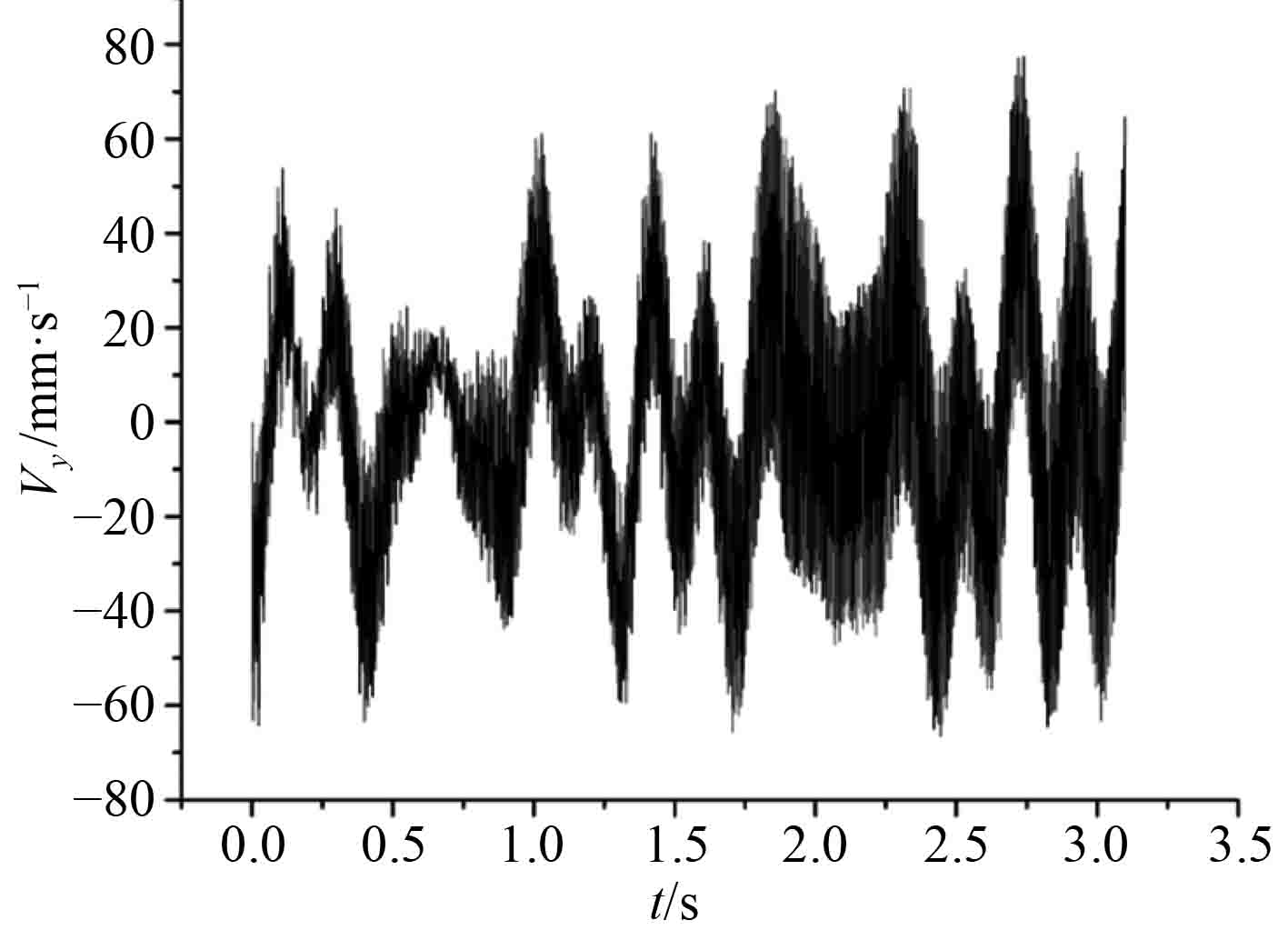
图 4 H5点处横向速度响应曲线 Fig. 4 Lateral velocity response curve at H5 point |

|
图 5 H1点处垂向速度响应曲线 Fig. 5 Vertical velocity response curve at H1 point |
|
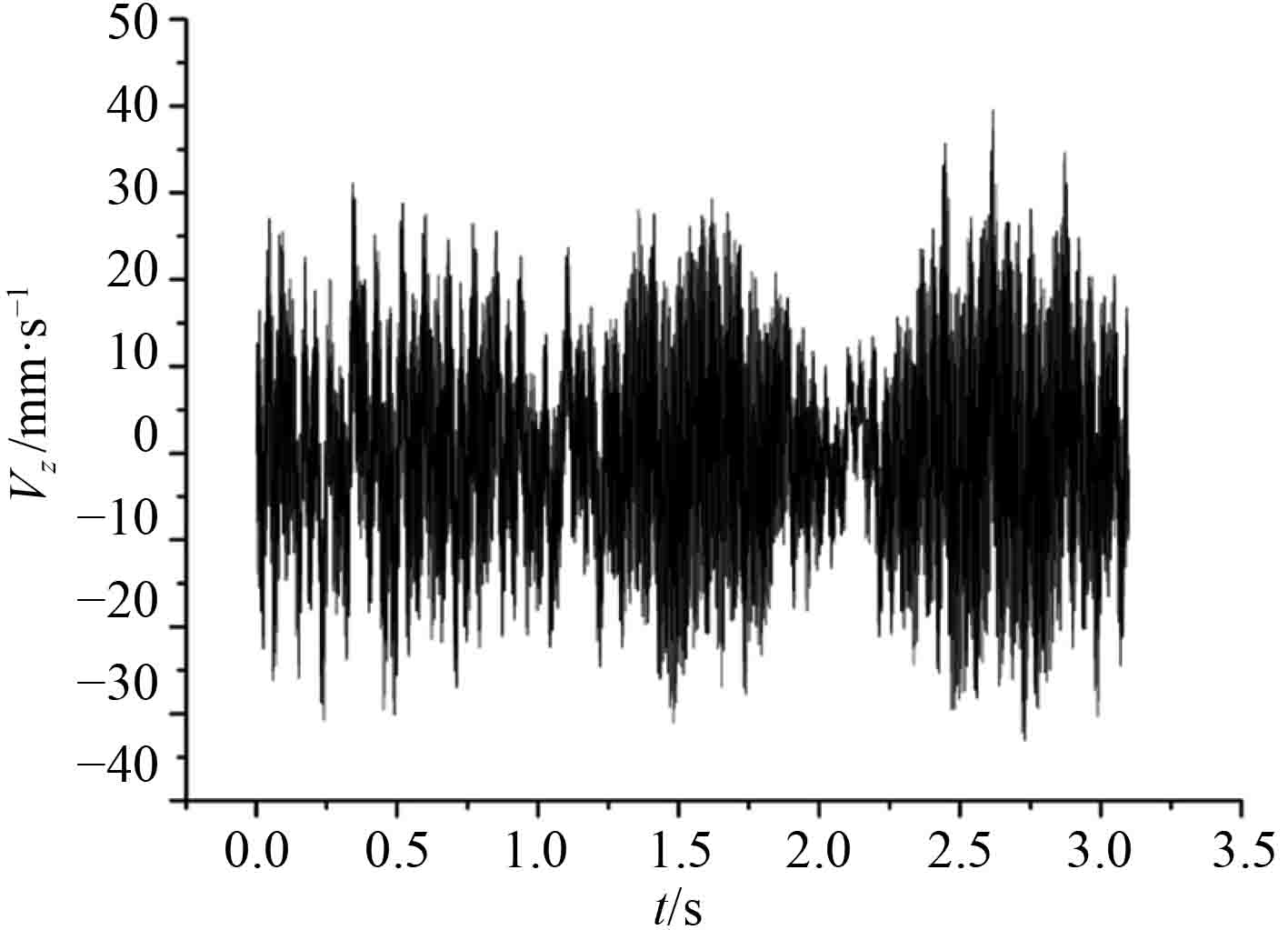
图 6 H2点处垂向速度响应曲线 Fig. 6 Vertical velocity response curve at H2 point |
|
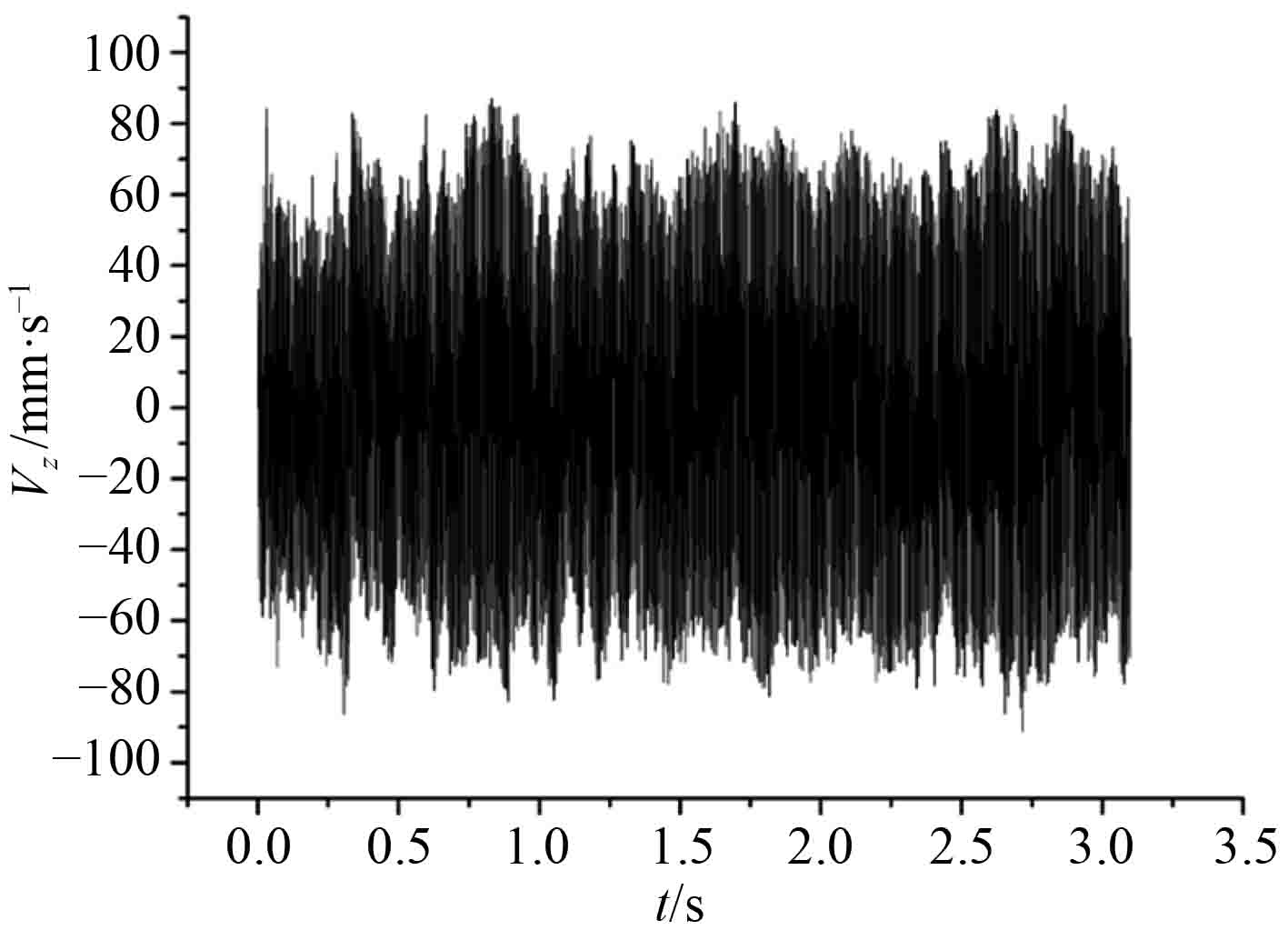
图 7 H5点处垂向速度响应曲线 Fig. 7 Vertical velocity response curve at H5 point |
|
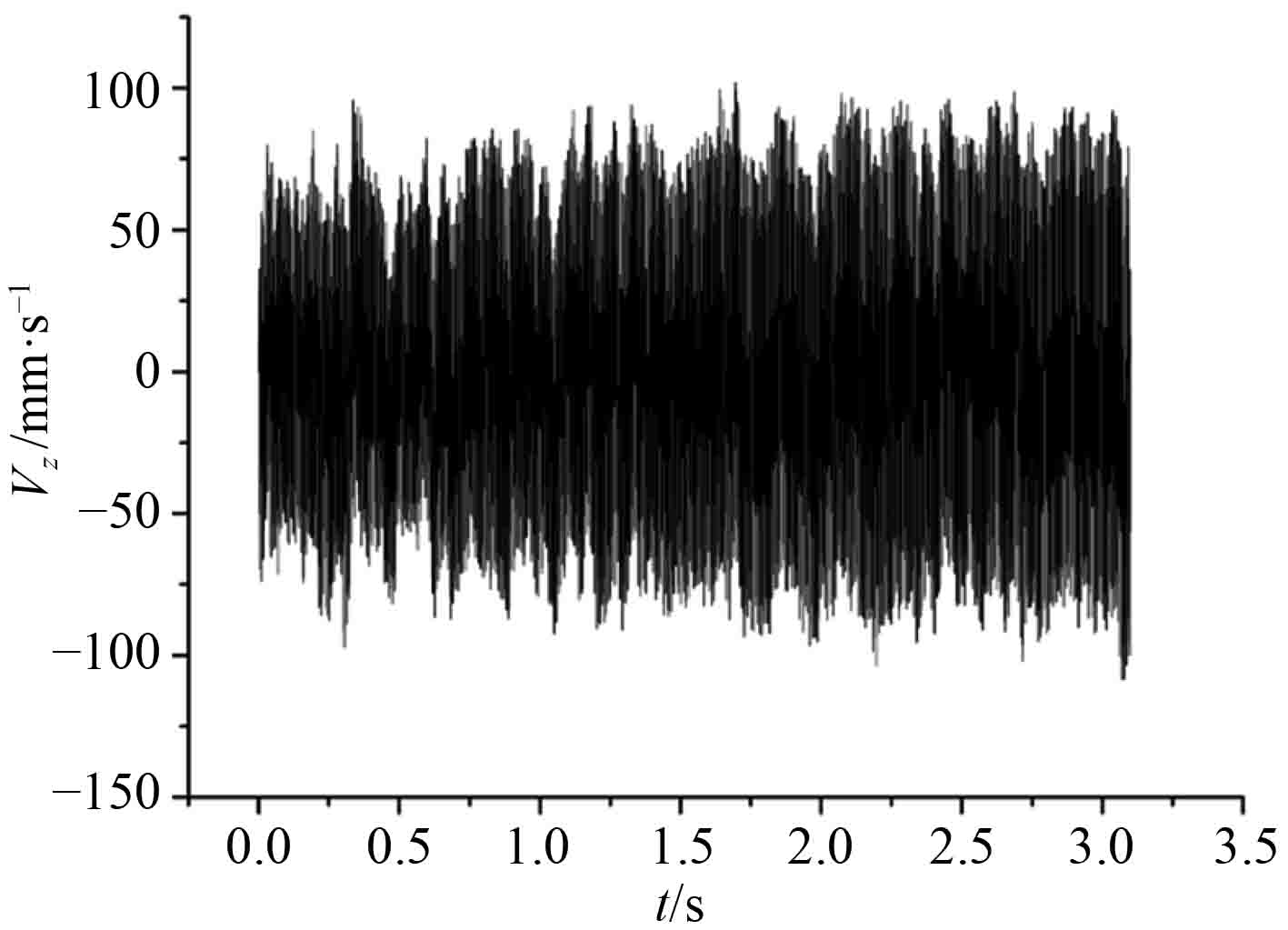
图 8 H6点处垂向速度响应曲线 Fig. 8 Vertical velocity response curve at H6 point |
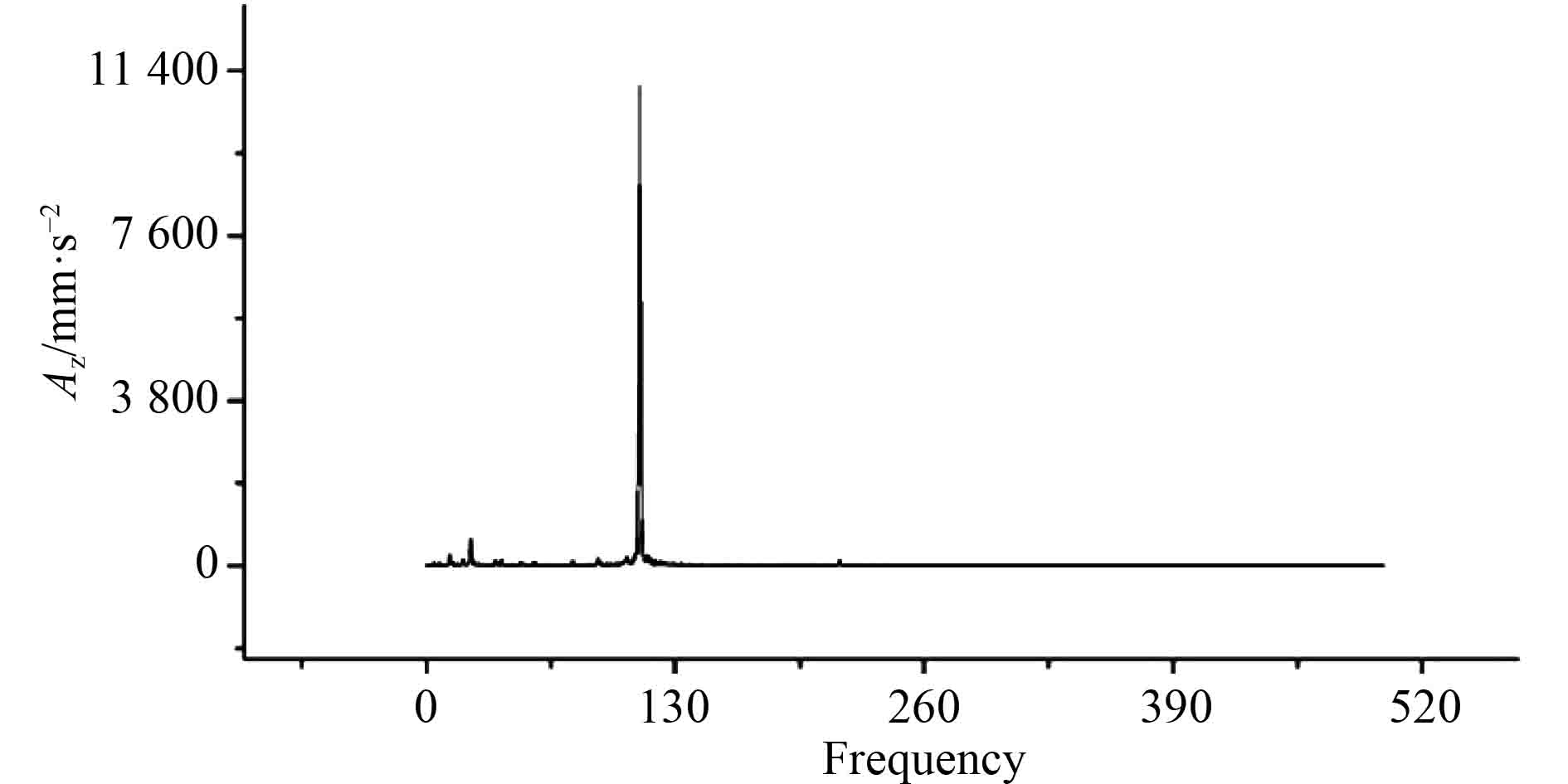
|
图 9 H2点垂向加速度频率响应曲线 Fig. 9 Frequency response curve of vertical acceleration of H2 point |
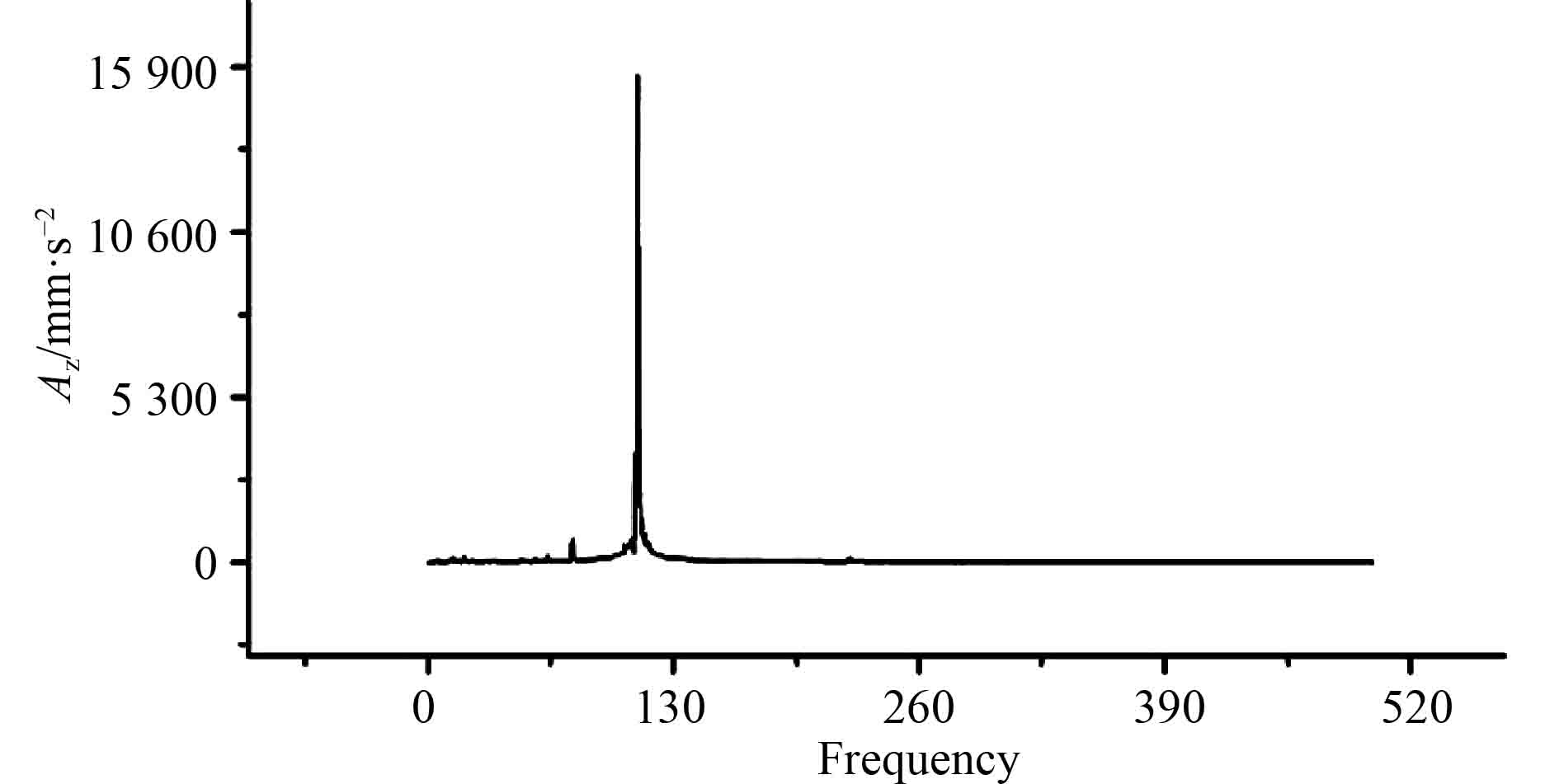
|
图 10 H6处垂向加速度频率响应曲线 Fig. 10 Frequency response curve of vertical acceleration of H6 point |
计算各测点在所有主要激振力共同作用下的瞬态响应值,参照GB/T 16301-2008标准,对测点在激振力下的响应计算数据按照如下公式处理,得到振动速度的均方根值。
| $V = \sqrt {\frac{1}{T}\int\nolimits_0^T {{V^2}(t){\rm{d}}t} }\text{。} $ | (4) |
其中:
根据式(4)对所得时历曲线进行处理,得到速度的均方根值,推进主机基座和垫升主机基座垂向速度频率响应、横向速度频率响应以及垂向加速度的测试值和计算值如表3~表5所示。
|
|
表 3 垂向速度响应值对比 Tab.3 Comparison of vertical velocity response values |
|
|
表 4 横向速度响应值对比 Tab.4 Comparison of lateral velocity response values |
|
|
表 5 垂向加速度响应值对比 Tab.5 Comparison of vertical acceleration response values |
计算值是参照GB/T 16301-2008标准,对测点在各个激振力共同作用下的瞬态响应计算数据按照均方根公式,得到速度的有效值。因此,计算值是考虑了不同激振源共同作用对测点响应的影响。由于在计算过程只考虑了几个主要激振源,而实际上还有其他不可预估的激振源,再加上厂商提供的主要激振源计算数据有限,也会影响激振力计算的准确性,进而影响计算结果。
1)从垂向速度的测量值和计算值的结果来看,垫升主机基座位置(H1,H2)的测量值和计算值偏差不大。从空间位置来看,垫升主机基座距离推进主机和空气螺旋桨较远,这2种激振源对垫升主机基座响应的影响较小,因此垫升主机基座响应主要来源于垫升主机激振源。垫升主机激振力估算准确,则计算结果就会与实测结果接近。推进主机基座位置(H5,H6)的测量值和计算值偏差较大。在估算推进主机和空气螺旋桨激振力时,只考虑了由于机械不平衡引起的激振力,而空气螺旋桨在工作时产生了不均匀的压力场,由此引起的激振力估算困难,在计算时未予施加,也可能导致计算值与测试值偏差较大[10]。从测量结果来看,H5与H6的测量值也相差很大,若测试结果准确,则可能是H6基座处的局部刚度过小。H5,H6位置处的响应值从测试结果和计算结果来看均大于H1,H2处的响应值,是由于发动机短舱处的存在推进主机和空气螺旋桨2种激振源且短舱处的刚度要小于垫升机舱处的刚度。
2)从横向速度的测量值和计算值的结果来看,H1位置的测量值稍大于计算值,H5位置的测量值与计算值较为接近,整体结果吻合较好。H1位置和H5位置的测量值均稍大于计算值,可能是计算时主要激振力估算稍小,也可能是其他激振力引起的基座处响应增加。
3)加速度计算值是由对测点在各个激振力共同作用下的瞬态响应计算得到。通过对时域内的响应进行傅里叶变换(FFT)得到加速度的频率响应曲线。计算时激振源频率只有12 Hz,111 Hz和112 Hz 3种。因此傅里叶变化后响应峰值应该在3种频率或其倍频附近[11]。测试时,实船激振源有很多,H2,H6测点在48.5 Hz附近都存在一个峰值,此时应有一较大的激振力,推测为由于周围流场不均匀引起的作用在空气螺旋桨桨叶上的激振源频率。H2点处在138.5 Hz与175.5 Hz存在两个大的峰值,推测可能为垫升主机实际频率。H6测点109.5 Hz存在大的峰值,此值为推进主机的频率。计算值在空气螺旋桨的倍频处存在较小的峰值,可能是空气螺旋桨激振力估算偏小。计算值在主机激振力频率存在最大峰值,理论上是合理的。
4 结 语本文以有限元法入手,考虑对典型结构影响较大的振动源,将多个激振力同时施加在有限元模型上,得到测点的速度时历,结合规范得到速度的均方根计算值,所得结论如下:
1)计算值与测试值吻合较好,同时施加多个主要振动源的激振力并基于此得到时历速度,该方法可应用于船体振动分析;
2)在计算过程只考虑了几个主要激振源,而实际上还有其他不可预见的激振源,再加上主要激振源计算数据有限,也会影响激振力计算的准确性,进而影响计算结果,因而确定振动源,并获得准确的振动数据,对气垫船振动评估尤为重要。
| [1] |
中国船级社. 海上高速船入级及建造规范[S]. 北京: 人民交通出版社, 2015.
|
| [2] |
徐伟. 全垫升式气垫船总振动计算方法研究[D]. 大连: 大连理工大学, 2018.
|
| [3] |
李建彰. 全垫升气垫船结构强度评估及局部振动分析[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [4] |
中国人民解放军总装备部. 舰船通用规范 1组[S], GJB 4000-2000, 2000.
|
| [5] |
中国国家标准化管理委员会. 船舶机舱辅机振动烈度的测量和评价[S], GB-T 16301-2008, 2008.
|
| [6] |
孙迪. 全垫升式气垫船总振动简化分析方法研究[D]. 大连: 大连理工大学, 2020.
|
| [7] |
尤矢勤, 恽良. 气垫船的振动问题[J]. 舰船科学技术, 1990(6): 1-11. |
| [8] |
中国船级社. 钢质海船入级及建造规范[S]. 北京: 人民交通出版社.
|
| [9] |
曲鹏. 小型气垫船结构强度有限元分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [10] |
王绍明, 姚征. 全垫升气垫船内部流场的数值模拟与改进[J]. 船舶力学, 2007(2): 179-184. DOI:10.3969/j.issn.1007-7294.2007.02.003 |
| [11] |
姚熊亮. 船体振动[M]. 哈尔滨: 哈尔滨工程大学出版社, 2004.
|
 2021, Vol. 43
2021, Vol. 43
