2. 上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240
2. The Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
船体梁极限强度是船体结构抵抗整体崩溃的最大能力,准确评估船体梁极限强度对于船体设计有着重要意义。目前,船体梁极限强度的计算方法主要有3类:非线性有限元法、逐步崩溃法以及理想结构单元法。其中,逐步崩溃法(Smith法)的核心思想是将船体舱段横剖面分为板单元、加筋板单元和硬角单元,根据各类单元的载荷-端缩曲线,通过力平衡准则迭代找到每一曲率下的中和轴位置,计算得到整个舱段的弯矩-曲率曲线,从而得出船体梁的极限弯矩[1]。Smith法具有操作简单、耗时短、准确性较高的优点,被多种规范采纳,作为计算船体梁极限强度的重要方法之一。
符合实际情况的单元载荷-端缩曲线是确定剖面中和轴准确位置的基础,对Smith法的计算精度有着重要的影响。确定载荷-端缩曲线的方式通常有3种[2]:解析求解;数值计算;模型试验。目前的HCSR规范中规定的载荷-端缩曲线并未考虑侧向载荷的作用,而侧向载荷是船体结构所受的常见载荷之一,比如货物、设备的重力以及水压力,且侧向载荷与轴向载荷的联合作用,会对加筋板的载荷-端缩曲线产生明显影响[3],因此对载荷-端缩曲线进行修正有着重要意义。
Paik等[4]研究了加筋板在轴向载荷、面内弯矩以及侧向载荷联合作用下的极限强度,并将计算结果和试验结果进行了对比,证实了提出公式的有效性。Shanmugam[5]对受单轴压缩和侧向载荷联合作用下的加筋板极限强度进行了模型试验研究和数值计算,得出对于此联合作用下的加筋板,板柔度系数
对于仅受轴向压缩的加筋板的极限强度,Zhang和Khan[6]提出一种半解析的经验公式形式(见式(1)),并给出了梁柱柔度系数
| $ \frac{{{\sigma _u}}}{{{\sigma _{Yeq}}}}{\rm{ = }}\frac{1}{{{\beta ^{{Z_1}}} \cdot \sqrt {1.0 + {\lambda ^{{Z_2}}}} }}{\text,} $ | (1) |
| $ \frac{{{\sigma _u}}}{{{\sigma _{Yeq}}}}{\rm{ = }}\frac{1}{{{\beta ^{0.28}} \cdot \sqrt {1.0 + {\lambda ^{3.2}}} }}{\text。} $ | (2) |
式中,带板柔度系数
| $ \beta {\rm{ = }}\frac{b}{{{t_p}}}\sqrt {\frac{{{\sigma _{Yeq}}}}{E}}{\text,} $ | (3) |
梁柱柔度系数
| $ \lambda {\rm{ = }}\frac{a}{{\pi r}}\sqrt {\frac{{{\sigma _{Yeq}}}}{E}}{\text。} $ | (4) |
式中,
| $ r = \sqrt {\frac{I}{{b{t_p} + {b_f}{t_f} + {h_w}{t_w}}}} {\text,} $ | (5) |
| $\begin{split} I \!=& \frac{{b{t_p}^3}}{{12}} \!+\! b{t_p}{\left( {{z_0} \!-\! \frac{{{t_p}}}{2}} \right)^2} \!+\! \frac{{{h_w}^3{t_w}}}{{12}} \!+\! {h_w}{t_w}{\left( {{z_0} \!-\! \frac{{{h_w}}}{2} \!-\! {t_p}} \right)^2} \!+ \\ &\frac{{{b_f}{t_f}^3}}{{12}} \!+\! {b_f}{t_f}{\left( {{t_p} \!+\! {h_w} \!+\! \frac{{{t_f}}}{2} \!-\! {z_0}} \right)^2}{\text,} \end{split}$ | (6) |
| $ {z_0} = \frac{{0.5bt_p^2 + {h_w}{t_w}({t_p} + 0.5{h_w}) + {b_f}{t_f}({t_p} + {h_w} + 0.5{t_f})}}{{b{t_p} + {b_f}{t_f} + {h_w}{t_w}}}{\text。} $ | (7) |
对于受轴向压缩和侧向载荷的钢制加筋板,Xu[7]提出一种经验公式形式(见式(8)),设定3种侧向压力,即0 MPa(对应0 m水压),0.1 MPa(对应10 m水压)和0.2 MPa(对应20 m水压),计算了1296个加筋板算例,拟合得到了不同种类加筋板对应的
| $ \frac{{{\sigma _{xu}}}}{{{\sigma _{Yeq}}}} = \frac{1}{{\sqrt {\left( \begin{gathered} {X_0} + {X_1}\lambda + {X_2}\beta + {X_3}\lambda \beta + {X_4}{\lambda ^2} + {X_5}{\beta ^2} + \\ {X_6}{\lambda ^2}{\beta ^2} + {X_7}{\lambda ^3} + {X_8}{\beta ^3} + {X_9}{\lambda ^3}{\beta ^3} + {X_{10}}{\lambda ^4} \\ \end{gathered} \right)} }} \leqslant \frac{1}{{{\lambda ^2}}}{\text。} $ | (8) |
目前学者采用的有限元模型大部分为加筋板板架,考虑了相邻结构对加筋板的影响,而Smith法中基本假设之一是各单元无相互作用且变形独立[8],因此,本文采用单个加筋板作为研究对象,减少相邻单元对加筋板载荷-端缩曲线的影响,使得到的载荷-端缩曲线修正公式更适用于Smith法。另一方面,目前学者得到的载荷-端缩修正公式大多仅针对临界应力进行修正,而侧向载荷还会同时影响临界应变,本文将从临界应力和临界应变2个方面入手,对HCSR规定的T型加筋板梁柱屈曲状态下的载荷-端缩曲线进行修正。
1 计算模型介绍 1.1 模型参数本文选择T型加筋板作为研究对象,共建立192个T型加筋板模型,材料采用理想弹塑性模型,加强筋建立在短边中心处,加筋板参数如表1所示(若无特别说明,其余章节中参数符号含义均与表1相同)。
|
|
表 1 加筋板模型各参数含义以及算例参数值汇总 Tab.1 Parameter meaning and value of stiffened plate model |
等效屈服强度
| $ {\sigma _{{\rm{Y}}eq}}{\rm{ = }}\frac{{{\sigma _{{\rm{Y}}p}}b{t_p} + {\sigma _{{\rm{Y}}s}}({b_f}{t_f} + {h_w}{t_w})}}{{b{t_p} + {b_f}{t_f} + {h_w}{t_w}}}{\text。} $ | (9) |
Do [9]统计出船体加筋板的长宽比通常在5~6之间,因此在设计模型参数时,取加筋板长宽比为5。Zhang[6]统计了12个油船和10个散货船的设计数据,总结出典型船体板柔度系数及梁柱柔度系数的分布范围,其中板柔度系数多分布在1~2.5之间,而梁柱柔度系数多分布在0.25~0.95之间。本文通过调整加筋板几何参数,得到4种不同的板柔度系数:1.1731,1.4664,1.9552,2.3234,以及分布在[0.3067,1.0240]之间的一系列梁柱柔度系数,与船体加筋板统计得到的分布范围基本一致。
1.2 载荷与边界条件边界条件是影响加筋板载荷-端缩曲线的重要因素,实际情况中,加筋板的边界条件介于简支与固支之间,类似弹性支座,计算时采用简支边界更为保守[10]。
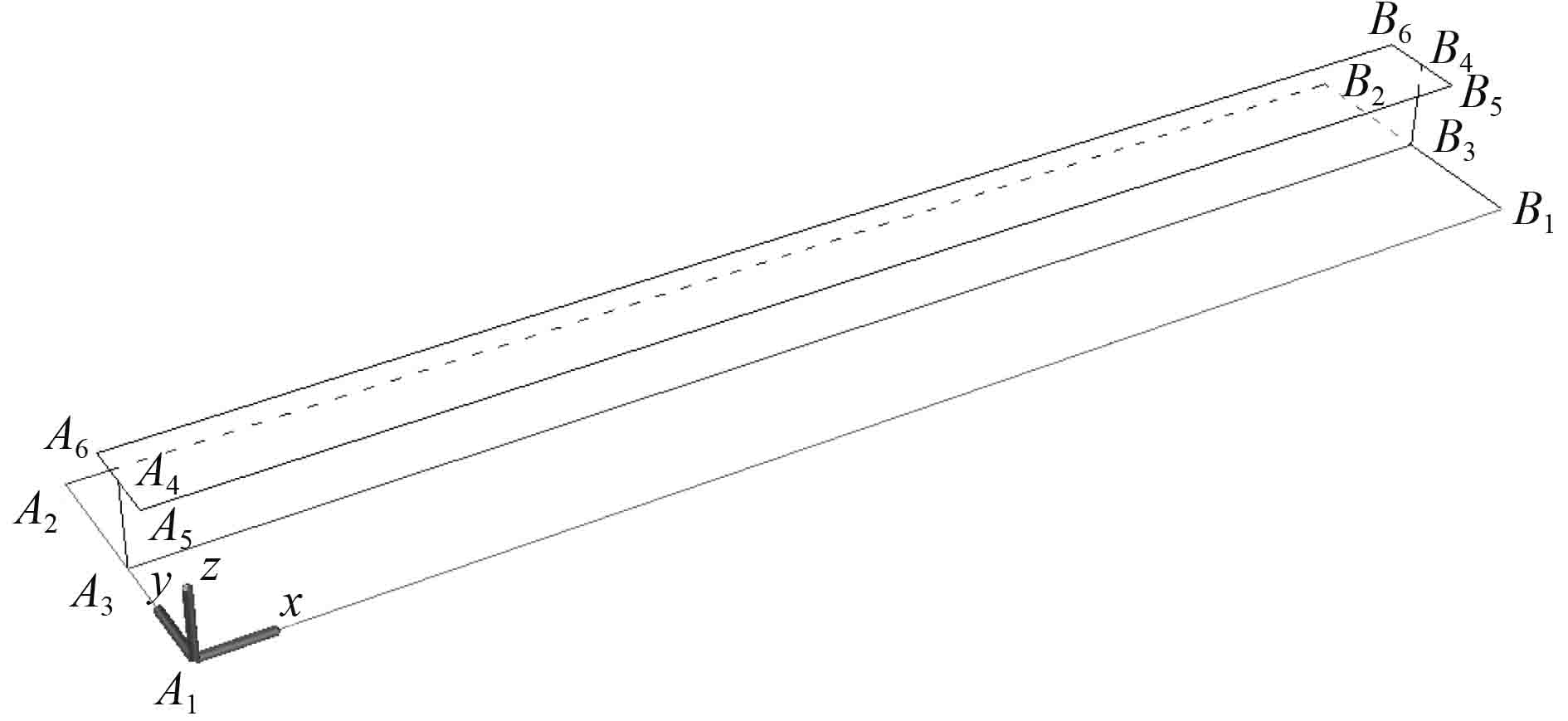
综合考虑Smith法的基本假设和船体板的实际情况,对加筋板施加边界条件(见表2),加筋板各点编号如图1所示。其中Ui代表沿i方向的平动自由度,Ri代表绕i轴的转动自由度,‘0’代表对应自由度被约束。
|
|
表 2 加筋板边界条件 Tab.2 The boundary condition of stiffened plate model |
|
图 1 加筋板节点编号示意图 Fig. 1 Diagram of stiffened plate node number |
考虑Smith法中各单元应保持相互独立,以及船体加筋板具有连续性,在加筋板的A1-B1,A2-B2边上应保持Rx=Rz=0。由于加筋板为轴向压缩,应约束y方向上的位移,因此在A1-B1,A2-B2边施加对称边界条件(Uy=0,Rx=Rz=0)。在短边(A1-A2,A3-A4,A5-A6,B1-B2,B3-B4,B5-B6)上施加轴向压缩位移载荷,并约束y方向与z方向的位移,以及x方向的转角。
为对比不同侧向载荷对加筋板载荷-端缩规律的影响,对每一个模型,依次施加大小为0,0.05 MPa,0.1 MPa,0.15 MPa,0.2 MPa的均布侧向载荷,分别对应0 m,5 m,10 m,15 m,20 m深度的水压,侧向载荷方向由无加强筋一侧指向有加强筋一侧,施加范围为整个带板面。
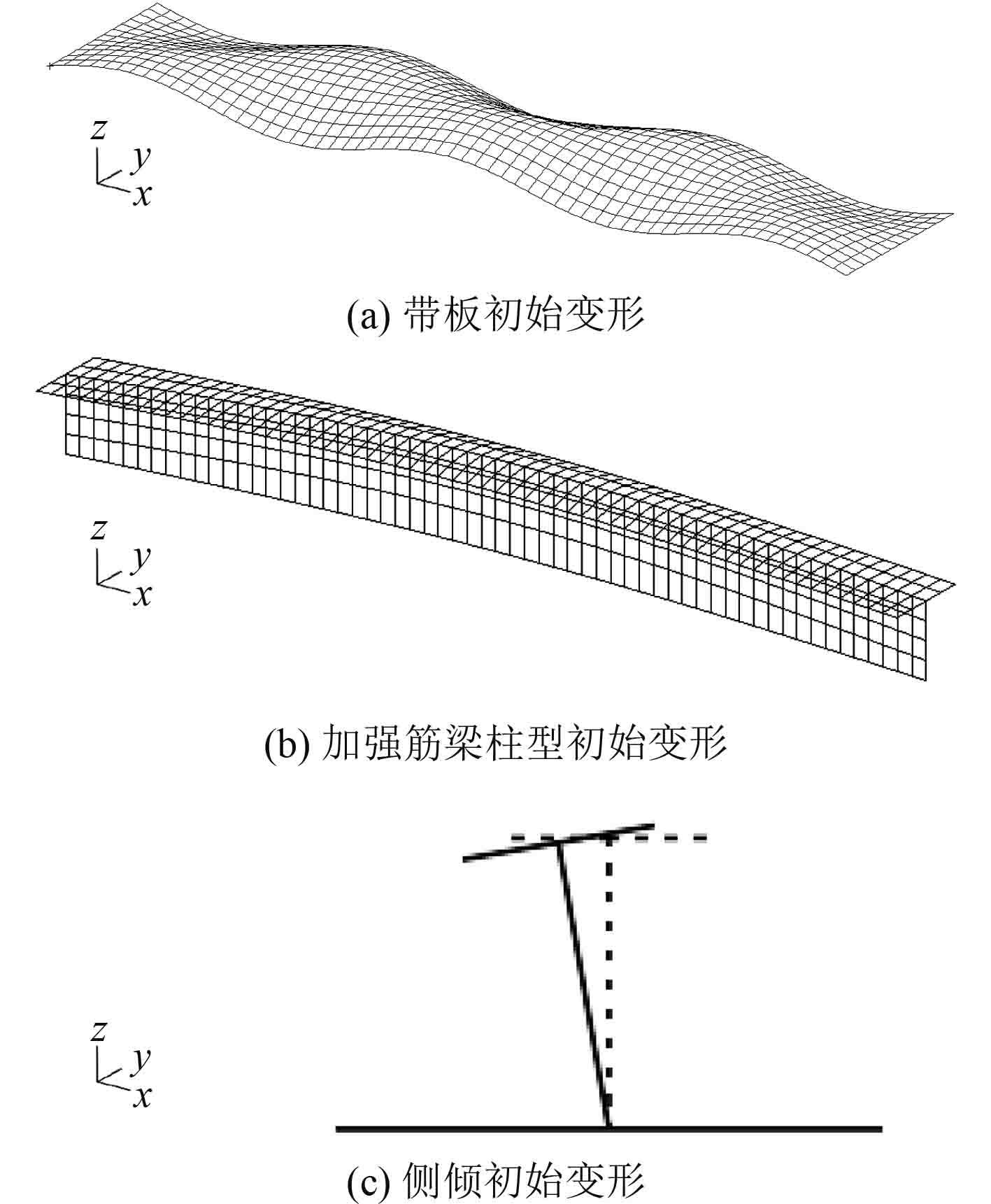
1.3 初始缺陷初始缺陷会对加筋板的破坏模式和临界载荷产生显著影响,在梁柱屈曲破坏模式中,通常采用3种初始缺陷[4]:对带板单元节点施加式(10)所示的带板屈曲和梁柱屈曲型初始变形,对加强筋单元节点施加式(11)所示的梁柱屈曲型初始变形,以及如式(12)所示的侧倾初始变形。
| $ {w_{op}} = {A_0}\sin \left( {\frac{{m\text{π} x}}{a}} \right)\sin \left( {\frac{{\text{π} y}}{b}} \right){\rm{ + }}{B_0}\sin \left( {\frac{{\text{π} x}}{a}} \right)\sin \left( {\frac{{\text{π} y}}{b}} \right){\text,} $ | (10) |
| $ {w_{oc}} = {B_0}\sin \left( {\frac{{\text{π} x}}{a}} \right)\sin \left( {\frac{{\text{π} y}}{b}} \right){\text,} $ | (11) |
| $ {w_{os}} = \frac{{{C_0}z}}{{{h_w}}}\sin \left( {\frac{{\text{π} x}}{a}} \right){\text。} $ | (12) |
式中,
采用MSC Patran软件对加筋板模型添加初始缺陷,初始变形示意图如图2所示。
|
图 2 加筋板初始变形示意图(变形放大10倍) Fig. 2 Diagram of initial distortion of stiffened plate model (Deformation magnified 10 times) |
采用参数化建模方法,利用MSC Patran建立加筋板模型,施加初始变形场;利用Abaqus设置边界条件,计算模型在不同侧向载荷作用下的支反力-位移曲线,从而得到不同侧向载荷作用下模型的载荷-端缩曲线。将非线性有限元法计算得到的临界载荷和临界端缩量换算为临界应力和临界相对应变,并以无侧向载荷时的临界应力和临界相对应变作为标准值,进行无因次化处理,计算结果如图3和图4所示。

|
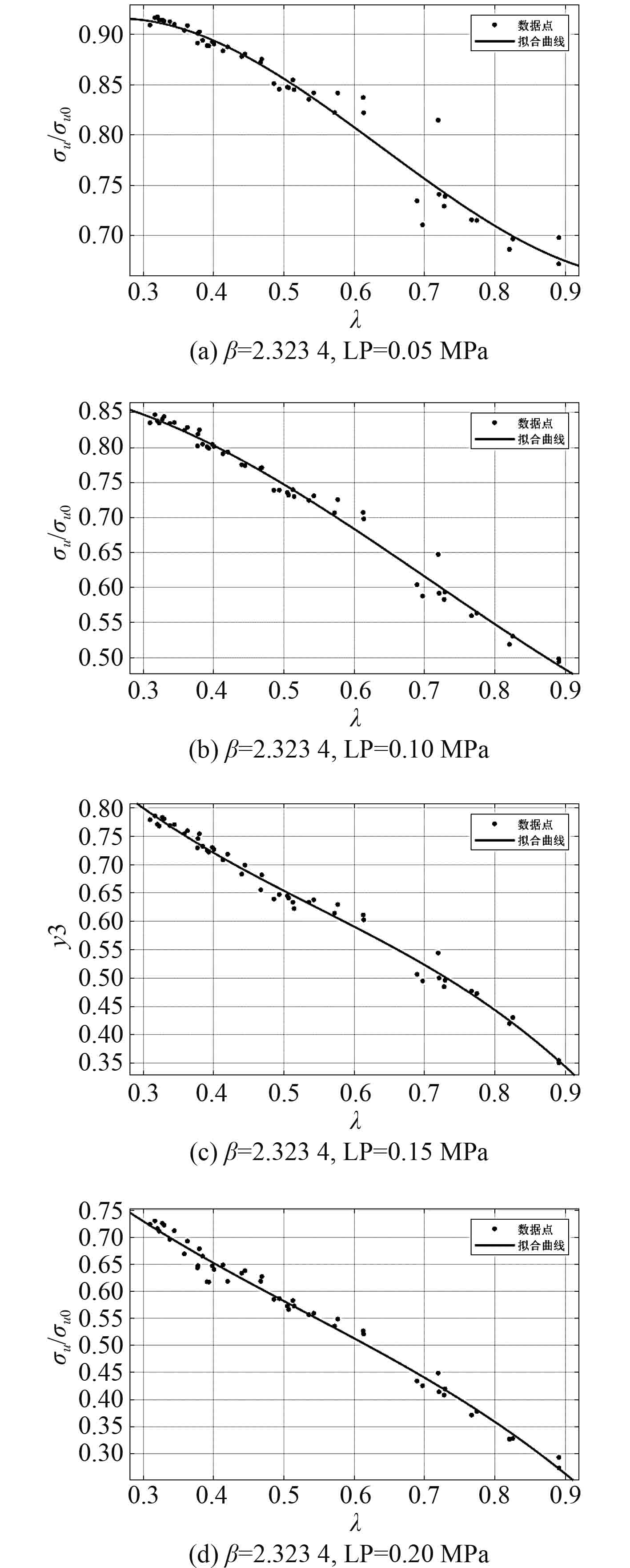
图 3 不同侧向载荷作用下无因次化临界应力有限元法计算结果 Fig. 3 Dimensionless critical stress results of stiffened plate model under different lateral loads by finite element method |

|
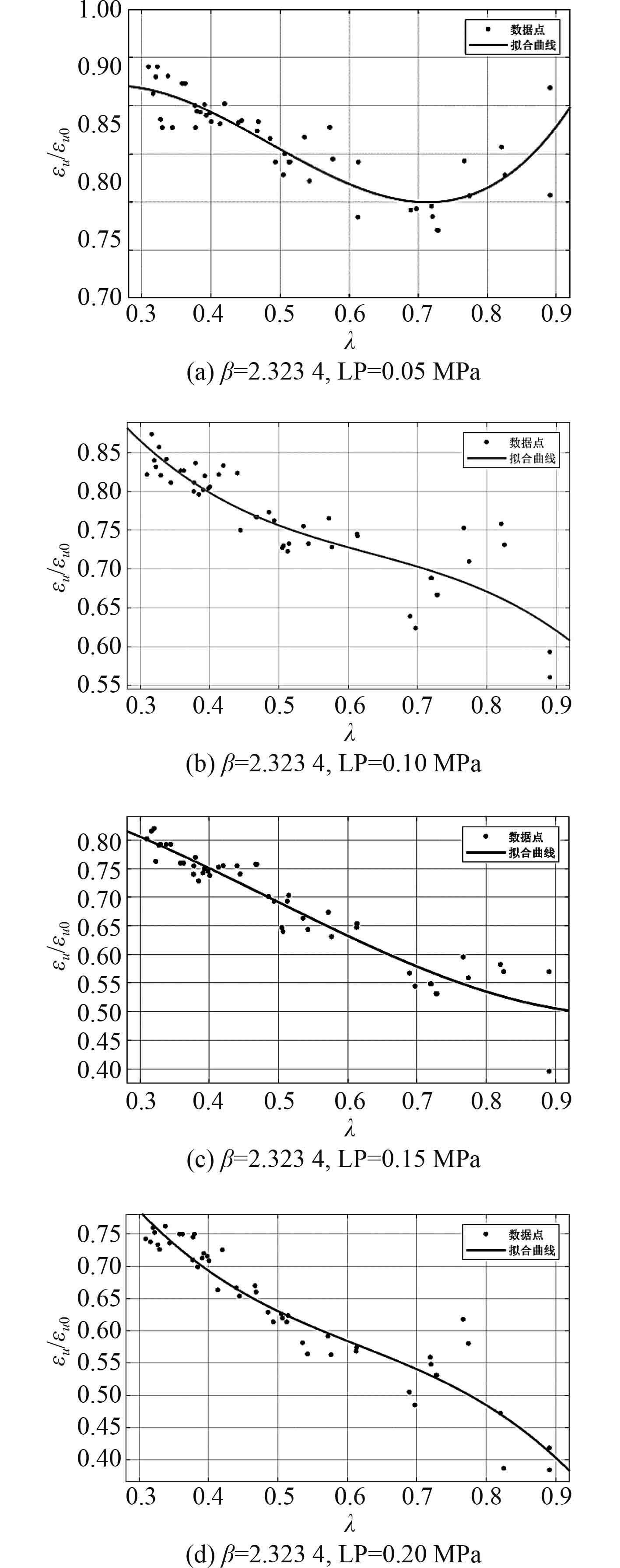
图 4 不同侧向载荷作用下无因次化临界应变有限元法计算结果 Fig. 4 Dimensionless critical strain results of stiffened plate model under different lateral loads by finite element method |
固定板柔度系数
|
图 5 σu/σu0关于λ拟合公式示意图 Fig. 5 Diagram of the fitting formula about σu/σu0 and λ |
|
图 6 εu/εu0关于λ拟合公式示意图 Fig. 6 Diagram of the fitting formula about εu/εu0 and λ |
对临界应力和临界应变分别采用式(13)和式(14)进行拟合。不同
|
|
表 3 不同板柔度系数和侧向载荷对应的临界应力拟合修正公式系数 Tab.3 Coefficients of critical stress fitting correction formula corresponding to different plate slenderness ratio and lateral loads |
|
|
表 4 不同板柔度系数和侧向载荷对应的临界应变拟合修正公式系数 Tab.4 Coefficients of critical strain fitting correction formula corresponding to different plate slenderness ratio and lateral loads |
| $ \frac{{{\sigma _u}}}{{{\sigma _{u0}}}}\left( \lambda \right) = {p_1}{\lambda ^3} + {p_2}{\lambda ^2} + {p_3}\lambda + {p_4}{\text,} $ | (13) |
| $ \frac{{{\varepsilon _u}}}{{{\varepsilon _{u0}}}}\left( \lambda \right) = {p_5}{\lambda ^3} + {p_6}{\lambda ^2} + {p_7}\lambda + {p_8}{\text。} $ | (14) |
将板柔度系数

|
图 7 临界应力修正公式系数p1~p4关于β和LP拟合结果 Fig. 7 The fitting results of coefficients of the critical stress correction formula about β and LP |

|
图 8 临界应变修正公式系数p5~p8关于β和LP拟合结果 Fig. 8 The fitting results of coefficients of the critical strain correction formula about β and LP |
|
|
表 5 p1~p8关于β和LP的拟合公式参数表 Tab.5 Coefficients of fitting formula about p1~p8 corresponding to β and LP |
| $ \begin{split} {p_i}(\beta ,LP) = &{p_{00}} + {p_{10}} \cdot \beta + {p_{01}} \cdot LP + {p_{20}} \cdot {\beta ^2} +\\ &{p_{11}} \cdot \beta \cdot LP + {p_{02}} \cdot L{P^2} + {p_{30}} \cdot {\beta ^3} + \\ &{p_{21}} \cdot {\beta ^2} \cdot LP +{p_{12}} \cdot \beta \cdot L{P^2} + {p_{03}} \cdot L{P^3} {\text。} \end{split} $ | (15) |
对于组成船体梁横剖面的普通加筋板单元的梁柱屈曲,HCSR中描述其的载荷-端缩曲线方程如下式[2]:
| $ {\sigma _{CR1}}{\rm{ = }}\varPhi {\sigma _{C1}}\frac{{{A_s} + 10{b_{E1}}{t_p}}}{{{A_s} + 10{b_E}{t_p}}}{\text。} $ | (16) |
式中,
| $ \varPhi {\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {{\rm{ - 1}}},&{\varepsilon < - 1}{\text,}\\ \varepsilon ,&{{\rm{ - 1}} \leqslant \varepsilon \leqslant {\rm{1}}}{\text,}\\ {\rm{1}},&{\varepsilon > 1}{\text。} \end{array}} \right. $ | (17) |
| $ \varepsilon = \frac{{{\varepsilon _E}}}{{{\varepsilon _Y}}}{\text。} $ | (18) |
| $ {\varepsilon _Y} = \frac{{{\sigma _{Yeq}}}}{E}{\text。} $ | (19) |
式中:
| $ {\sigma }_{C1}=\left\{\begin{array}{cc}\dfrac{{\sigma }_{E1}}{\varepsilon },& {\sigma }_{E1}\leqslant \dfrac{{\sigma }_{Yeq}}{2}\varepsilon {\text,} \\ {\sigma }_{Yeq}\left(1-\dfrac{{\sigma }_{Yeq}\varepsilon }{4{\sigma }_{E1}}\right),& {\sigma }_{E1}>\dfrac{{\sigma }_{Yeq}}{2}\varepsilon {\text。}\end{array}\right. $ | (20) |
式中:
| $ {\sigma _{E1}} = {{\text{π}} ^2}E\frac{{{I_E}}}{{{A_E}{l^2}}}{10^{ - 4}}{\text。} $ | (21) |
式中:
| $ {b_{E1}} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{b}{{{\beta _E}}}},&{{\beta _E} > 1.0} {\text,}\\ b,&{{\beta _E} \leqslant 1.0} {\text,} \end{array}} \right. \;\; {\beta _E} = {10^3}\dfrac{b}{{{t_p}}}\sqrt {\frac{{\varepsilon {\sigma _{Yp}}}}{E}}{\text。} $ | (22) |
式中:
| $ {b_E} = \left\{ {\begin{array}{*{20}{c}} {\left( {\dfrac{{2.25}}{{{\beta _E}}} - \dfrac{{1.25}}{{\beta _E^2}}} \right)b},&{{\beta _E} > 1.25}{\text,} \\ b,&{{\beta _E} \leqslant 1.25} {\text。} \end{array}} \right. $ | (23) |
根据此载荷-端缩曲线方程,可以通过相对应变
按照给出的修正公式形式和修正公式系数,对HCSR规定的加筋板梁柱屈曲载荷-端缩曲线进行修正,修正公式如下式:
| $ {\sigma _{CR1}}{\rm{(}}\varepsilon '){\rm{ = }}{f_1}(LP,\beta ,\lambda )\Phi {\sigma _{C1}}\frac{{{A_s} + 10{b_{E1}}{t_p}}}{{{A_s} + 10{b_E}{t_p}}}{\text。} $ | (24) |
式中:
| $ \begin{split} {p_i}(\beta ,LP) = &{p_{00}} + {p_{10}} \cdot \beta + {p_{01}} \cdot LP + {p_{20}} \cdot {\beta ^2} + \\ &{p_{11}} \cdot \beta \cdot LP + {p_{02}} \cdot L{P^2} + {p_{30}} \cdot {\beta ^3} + \\ &{p_{21}} \cdot {\beta ^2} \cdot LP +{p_{12}} \cdot \beta \cdot L{P^2} + {p_{03}} \cdot L{P^3} {\text。} \end{split} $ | (25) |
为验证修正公式的有效性,分别采用修正公式和非线性有限元法计算8个加筋板模型,加筋板几何参数如表6所示。材料采用理想弹塑性模型,屈服极限为315 MPa,弹性模量为206000 MPa,加强筋设立在短边中心处,初始缺陷、边界条件和载荷按照2.2节与2.3节设置。
|
|
表 6 加筋板算例几何参数(mm) Tab.6 Geometric parameter values of stiffened plate model |
将修正公式和非线性有限元法的计算结果进行比较,如表7所示。表中数据为无因次化临界应力和无因次化临界应变,LP1~LP4依次代表施加0.05 MPa,0.1 MPa,0.15 MPa,0.2 MPa的侧向载荷。从表中可以看出,按照修正公式得到的计算结果与按照非线性有限元法计算结果的相对误差在10%以内,说明本文得到的修正公式有效。
|
|
表 7 修正公式与有限元法计算结果对比 Tab.7 Comparison of the results by the modified formula and the finite element method |
为计入侧向载荷对Smith法中加筋板单元载荷-端缩规律的影响,采用数值仿真方法,计算192块T型加筋板模型在不同侧向载荷和纵向压缩载荷作用下的载荷-端缩曲线,根据计算结果拟合得到临界应力和临界应变的修正公式,对HCSR规定的T型加筋板梁柱屈曲状态下的载荷-端缩曲线进行了修正,得到以下结论:
1)侧向载荷对T型加筋板梁柱屈曲状态下的载荷-端缩曲线具有显著影响,较大的侧向载荷(
2)对于柔度系数较小(
3)当
| [1] |
SMITH C S. Influence of local compressive failure on ultimate longitudinal strength of a ship's hull[J]. Proc. int. sym. on Practical Design in Shipbuilding, 1977. |
| [2] |
朱青淳, 王福花, 王晓宇. 纵骨多跨梁柱屈曲载荷-端缩曲线的修正[J]. 中国造船, 2014(1): 52-59. |
| [3] |
陈彦廷, 于昌利, 桂洪斌. 船体板和加筋板的屈曲及极限强度研究综述[J]. 中国舰船研究, 2017, 12(1): 54-62. |
| [4] |
PAIK J K, KIM B J. Ultimate strength formulations for stiffened panels under combined axial load, in-plane bending and lateral pressure: a benchmark study[J]. 2002, 40(1): 45-83.
|
| [5] |
SHANMUGAM N E, DONGQI Z, CHOO Y S, et al. Experimental studies on stiffened plates under in-plane load and lateral pressure[J]. Thin Walled Structures, 2014, 80: 22-31. DOI:10.1016/j.tws.2014.02.026 |
| [6] |
ZHANG S, KHAN I. Buckling and ultimate capability of plates and stiffened panels in axial compression[J]. Marine Structures, 2009, 22(4): 791-808. DOI:10.1016/j.marstruc.2009.09.001 |
| [7] |
XU M C, SONG Z J, ZHANG B W, et al. Empirical formula for predicting ultimate strength of stiffened panel of ship structure under combined longitudinal compression and lateral loads[J]. Ocean Engineering, 2018, 162(aug. 15): 161-175. |
| [8] |
IACS, 2018. Common structural rules for bulk carriers and oil tankers[S]. International Association of Classification Societies, London, UK, 2018.
|
| [9] |
KIM D K. A technical review on ultimate strength prediction of stiffened panels in axial compression[J]. Ocean Engineering, 2018, 170: 392-406. DOI:10.1016/j.oceaneng.2018.10.022 |
| [10] |
XU M C, YANAGIHARA D, FUJIKUBO M, et al. Influence of boundary conditions on the collapse behaviour of stiffened panels under combined loads[J]. Marine Structures, 2013, 34(DEC.): 205-225. |
 2021, Vol. 43
2021, Vol. 43
