2. 武汉第二船舶设计研究所,湖北 武汉 430205
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China
机电设备运转产生的振动噪声对舰船的辐射噪声控制、仪器仪表工作和船员身心健康等造成不利影响。浮筏隔振是当前舰船针对设备振动最有效的控制措施,其振动控制特性也得到相关科技人员的广泛研究[1-9]。
在浮筏隔振系统声学性能的研究中,主要采用理论与数值仿真方法[1-6]、理论与试验方法[7-9]等手段。而在理论、数值仿真及验证试验的研究中,往往仅考虑运转设备,而忽视了弹性安装的非运转设备对运转设备在浮筏隔振系统中的振动传递特性影响。这会降低浮筏隔振系统声学性能的估算精度,是理论结果与工程结果之间误差的一个重要原因。
本文首先针对运转设备、非运转设备、筏架、基座和上下层减振器等浮筏隔振系统组件,考虑其自身易于通过试验获取的导纳和阻抗矩阵,分别建立了导纳方程和阻抗方程,并组装形成了含非运转设备的浮筏隔振系统三向振动传递模型。然后,试验验证了在振动传递模型中考虑非运转设备的必要性。最后,根据对比工况的试验结果分析了非运转设备对浮筏隔振系统振动传递特性的影响规律。
1 浮筏隔振系统动力学模型典型浮筏隔振系统主要由被隔振设备、上层减振器、筏架(中间构架)、下层减振器和基座结构等组成,如图1所示。其中,针对特定的运行工况,设备分为运转设备和非运转设备。1)对结构件(设备、筏架和基座)建立导纳方程,对减振元件(上下层减振器)建立阻抗方程;2)利用阻抗导纳综合法,构建浮筏隔振系统的多点三向振动传递物理模型;3)通过代入运转设备的机脚振动速度给出含非运转设备的浮筏隔振系统三向振动传递模型。其中,定义

|
图 1 含非运转设备的典型浮筏隔振系统 Fig. 1 A typical floating raft isolation system with non-operating equipment |
以运转设备减振器为例,并将其简化为如图2所示的力学模型。其中,

|
图 2 减振器简化模型 Fig. 2 Simplified model of damper |
定义
| $\left[ {\begin{array}{*{20}{c}} {{ Z}_{11}^j}&{{ Z}_{12}^j} \\ {{ Z}_{21}^j}&{{ Z}_{22}^j} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{ V}_j^s} \\ {{ V}_j^f} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{ F}_j^s} \\ { - { F}_j^f} \end{array}} \right]{\text{。}}$ | (1) |
类似推导可得,下层减振器和非运转设备减振器的阻抗方程如下:
| $\left[ {\begin{array}{*{20}{c}} {{ Z}_{11}^x}&{{ Z}_{12}^x} \\ {{ Z}_{21}^x}&{{ Z}_{22}^x} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{ V}_x^f} \\ {{ V}_x^t} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{ F}_x^f} \\ { - { F}_x^t} \end{array}} \right],$ | (2) |
| $\left[ {\begin{array}{*{20}{c}} {{ Z}_{11}^J}&{{ Z}_{12}^J} \\ {{ Z}_{21}^J}&{{ Z}_{22}^J} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{ V}_J^s} \\ {{ V}_J^f} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{ F}_J^s} \\ { - { F}_J^f} \end{array}} \right]{\text{。}}$ | (3) |
定义运转设备导纳矩阵为
| ${ Y}_{jj}^s{ F}_j^s = {{ V}_{0j}} - { V}_j^s{\text{,}}$ | (4) |
定义非运转设备导纳矩阵为
| ${ V}_{JJ}^s{ F}_J^s = - { V}_J^s{\text{。}}$ | (5) |
定义筏架对应运转设备和非运转设备上层减振器安装点的导纳矩阵分别为
| $\left[ {\begin{array}{*{20}{c}} {{ Y}_{jj}^f}&{{ Y}_{jJ}^f}&{{ Y}_{jx}^f} \\ {{ Y}_{Jj}^f}&{{ Y}_{JJ}^f}&{{ Y}_{Jx}^f} \\ {{ Y}_{xj}^f}&{{ Y}_{xJ}^f}&{{ Y}_{xx}^f} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{ F}_j^f} \\ {{ F}_J^f} \\ { - { F}_x^f} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{ V}_j^f} \\ {{ V}_J^f} \\ {{ V}_x^f} \end{array}} \right]{\text{。}}$ | (6) |
定义基座导纳矩阵为
| ${ Y}_{xx}^t{ F}_x^t = { V}_x^t{\text{。}}$ | (7) |
若已知运转设备的振动速度向量
| $\left[ {\begin{array}{*{20}{c}} {{ I} + { Y}_{JJ}^s{ Z}_{11}^J}&0&{{ Y}_{JJ}^s{ Z}_{12}^J}&0&0 \\ {{ Y}_{jJ}^f{ Z}_{21}^J}&{{ I} + { Y}_{jj}^f{ Z}_{22}^j}&{{ Y}_{{\rm{j}}J}^f{ Z}_{22}^J}&{{ Y}_{jx}^f{ Z}_{11}^x}&{{ Y}_{jx}^f{ Z}_{12}^x} \\ {{ Y}_{JJ}^f{ Z}_{21}^J}&{{ Y}_{Jj}^f{ Z}_{22}^j}&{{ I} + { Y}_{JJ}^f{ Z}_{22}^J}&{{ Y}_{Jx}^f{ Z}_{11}^x}&{{ Y}_{Jx}^f{ Z}_{12}^x} \\ {{ Y}_{xJ}^f{ Z}_{21}^J}&{{ Y}_{xj}^f{ Z}_{22}^j}&{{ Y}_{xJ}^f{ Z}_{22}^J}&{{ I} + { Y}_{xx}^f{ Z}_{11}^x}&{{ Y}_{xx}^f{ Z}_{12}^x} \\ 0&0&0&{{ Y}_{xx}^t{ Z}_{21}^x}&{{ I} +{ Y}_{xx}^t{ Z}_{22}^x} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{ V}_J^s} \\ {{ V}_j^f} \\ {{ V}_J^f} \\ {{ V}_x^f} \\ {{ V}_x^t} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ { - { Y}_{jj}^f{ Z}_{21}^j{ V}_j^s} \\ { - { Y}_{Jj}^f{ Z}_{21}^j{ V}_j^s} \\ { - { Y}_{xj}^f{ Z}_{21}^j{ V}_j^s} \\ 0 \end{array}} \right]{\text{。}}$ | (8) |
上述振动传递动力学模型中的结构件导纳矩阵和减振元件阻抗矩阵均可直接试验获取,从而避免了模型搭建过程中的矩阵求逆,有利于提高该动力学模型的计算浮筏隔振系统振动传递特性的精度。
2 验证试验 2.1 试验台架方案验证试验台架包括两型设备(电机、水泵)、水泵管路及其附件、两层减振器、公共筏架和基座等,如图3所示。其计算模型采用右手螺旋坐标系,以水泵进口方向为X向正向,以垂向上为Z向正向。电机和水泵分别通过4个减振器平置安装在筏架上侧,而筏架则通过4个下层减振器弹性安装在基座上,基座通过螺栓固定在实验室刚性地基上。水泵管路通过软管连接到远端,从而隔离其对基座振动响应的干扰。

|
图 3 试验台架示意图 Fig. 3 Schematic diagram of test bench |
电机和水泵各自4个减振器的安装方式一致,水泵的额定流量为22.5 t/h,试验台架的其他参数如表1所示。
|
|
表 1 试验台架参数 Tab.1 Conditions of test |
试验工况如表2所示。
|
|
表 2 试验工况 Tab.2 Conditions of test |
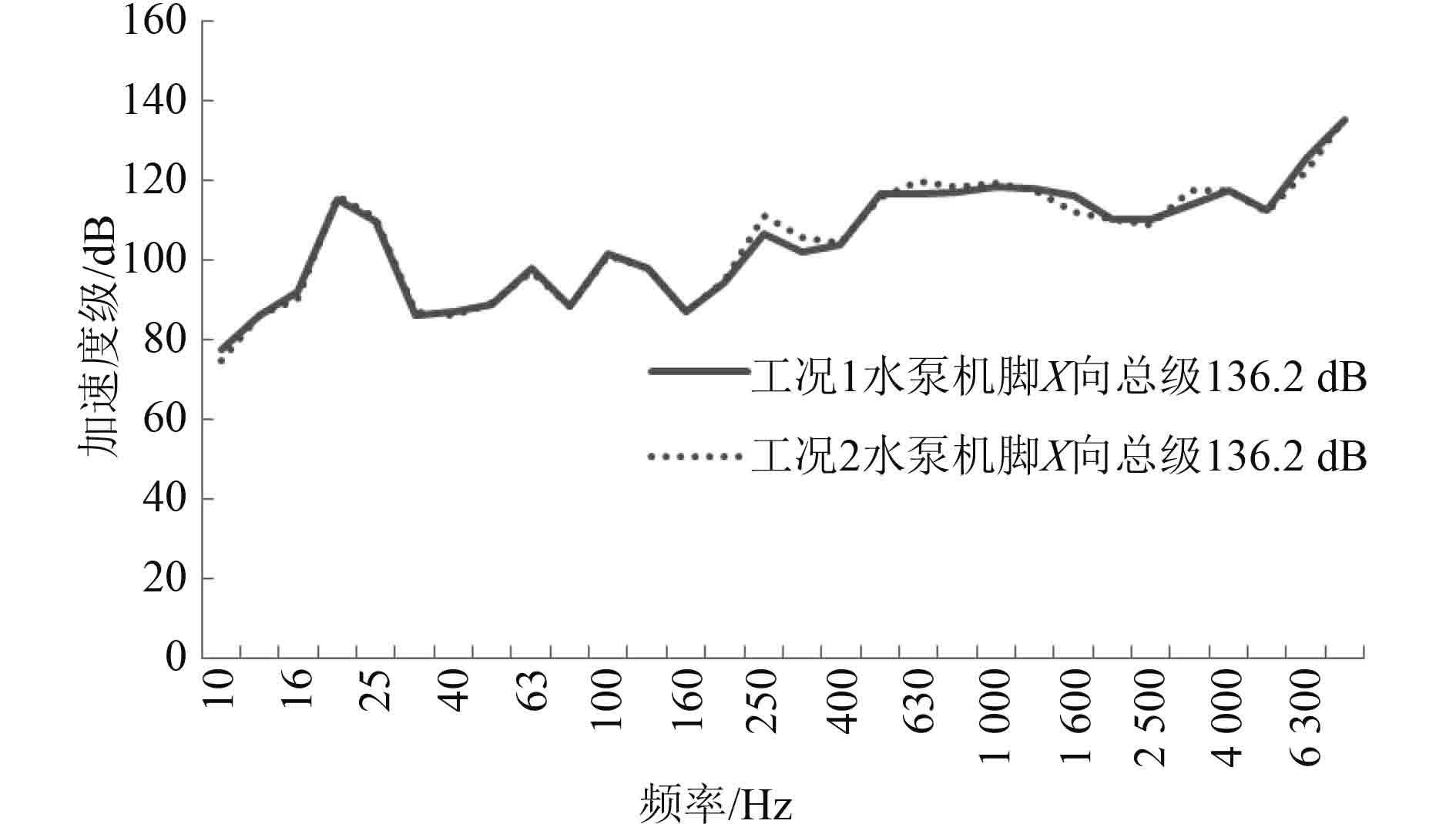
工况1和工况2为是否安装非运转设备(电机)对运转设备(水泵)隔振效果影响的对比工况。水泵机脚和基座的振动响应试验结果如图4~图9所示。
|
图 4 水泵机脚振动响应(X向) Fig. 4 The vibration response of pump seat (X direction) |
|
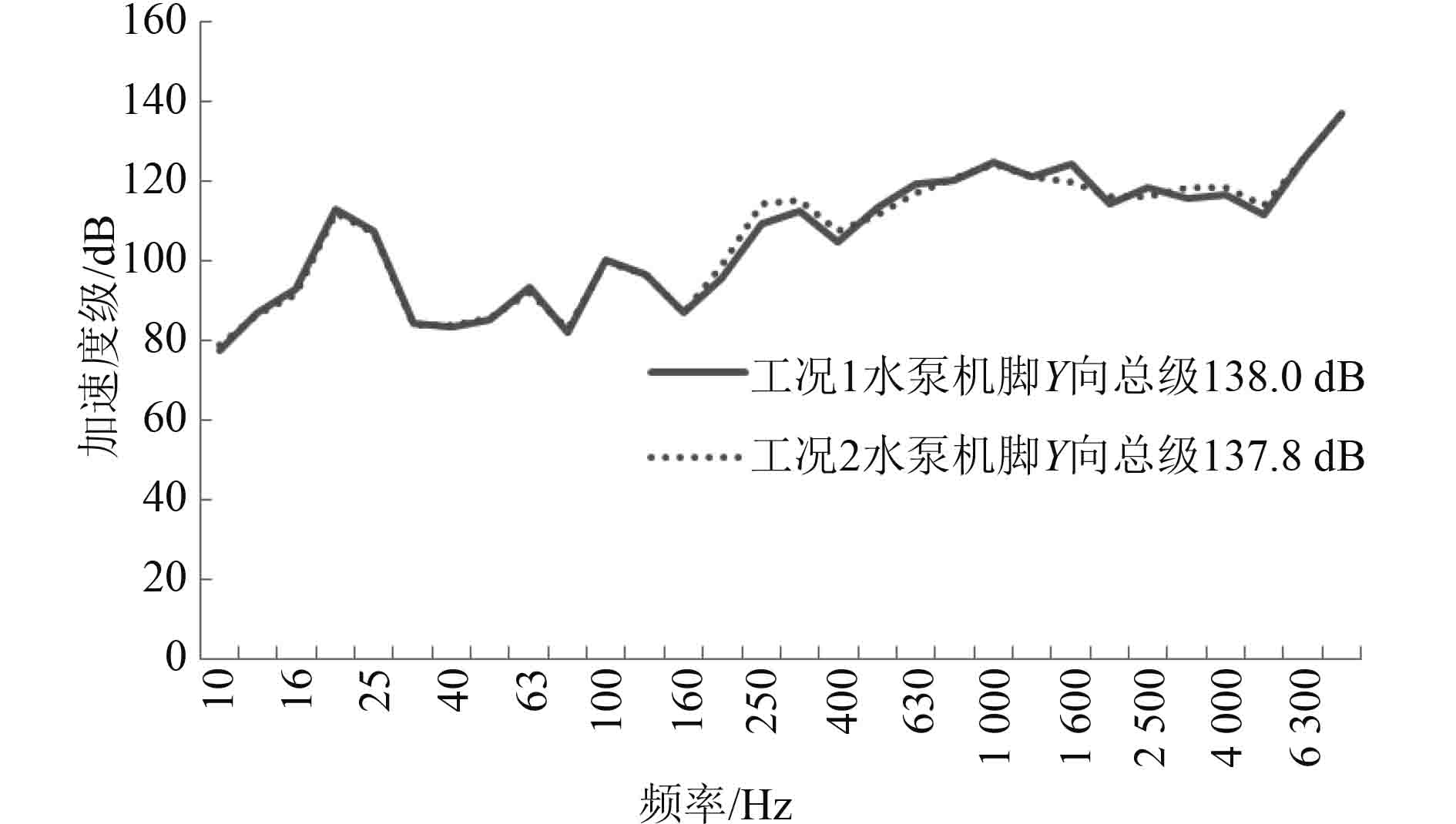
图 5 水泵机脚振动响应(Y向) Fig. 5 The vibration response of pump seat(Y direction) |
|
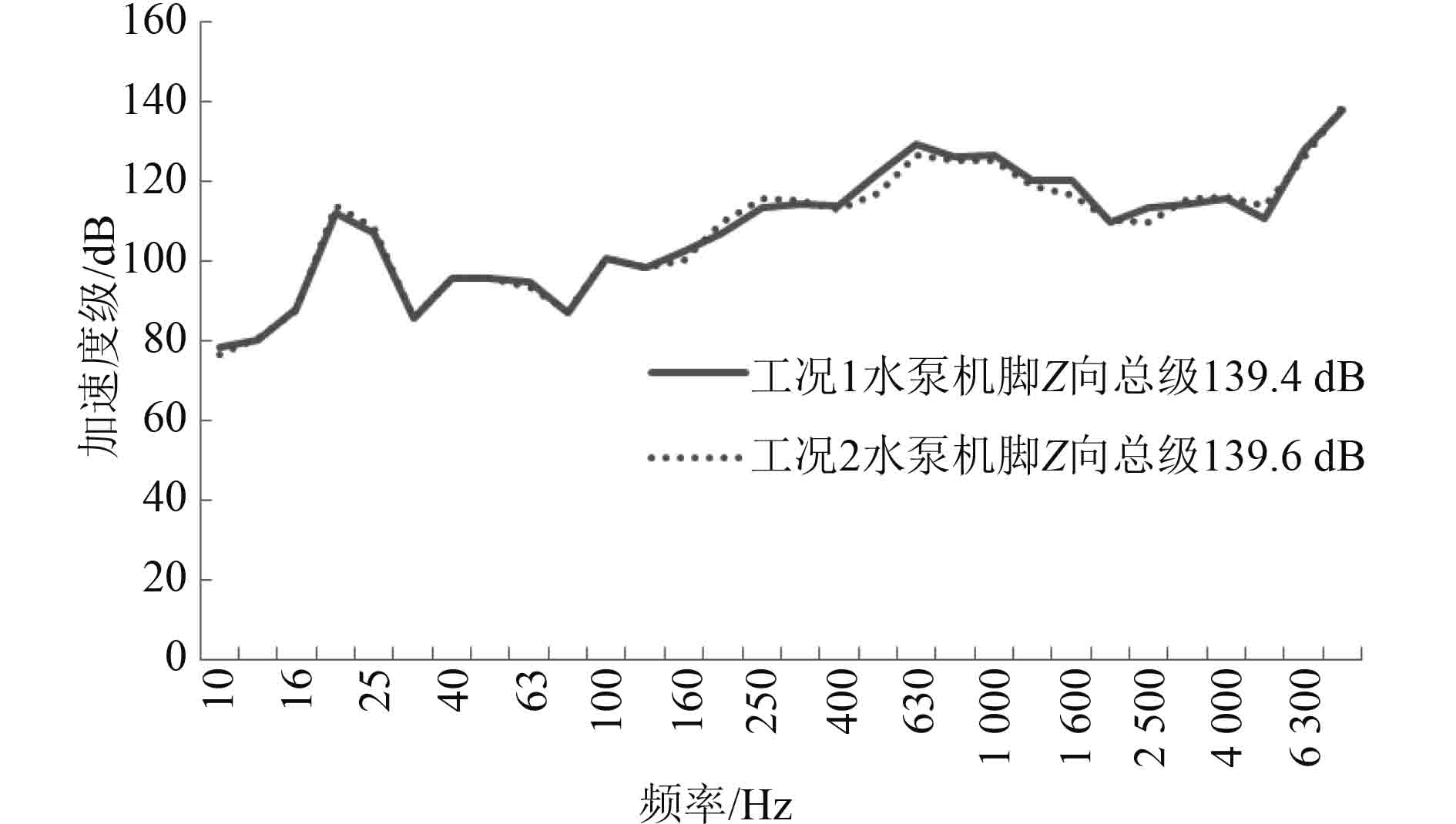
图 6 水泵机脚振动响应(Z向) Fig. 6 The vibration response of pump seat(Z direction) |

|
图 7 基座振动响应(X向) Fig. 7 The vibration response of base structures(X direction) |

|
图 8 基座振动响应(Y向) Fig. 8 The vibration response of base structures(Y direction) |

|
图 9 基座振动响应(Z向) Fig. 9 The vibration response of base structures(Z direction) |
从图4~图6可以看出,是否安装电机对水泵机脚三向振动的影响很小(差值约0.2 dB),可以忽略。
从图7~图9可以看出,试验台架增装电机后,基座XYZ三向振动分别降低了3.7 dB,0 dB和5.2 dB。说明对于本试验台架安装的隔振装置来说,弹性安装的电机及其下安装的减振器耗散了水泵经由筏架传递到基座X向和Z向的振动能量,特别是在16~40 Hz,50~80 Hz和400~500 Hz频段,即增装电机后基座的前3阶响应峰均得到了有效控制,且其他频段响应无明显增大现象。
图10和图11分别为基座的响应时频图。可以看出:1)试验台架增装电机后,基座Y向振动响应整体变化不明显,在14~19 Hz频段出现响应谷,与图8的趋势一致;2)基座Z向在除13~15 Hz频段外,振动响应整体降低,与图9的趋势一致。这说明增装非运转设备可改变浮筏隔振系统原有的整体模态,且配置得当时可有效消耗运转设备的振动能量,提升隔振系统的声学性能。

|
图 10 基座响应时频图(Y向) Fig. 10 Time-frequency image for vibration response of base structure (Y direction) |

|
图 11 基座响应时频图(Z向) Fig. 11 Time-frequency image for vibration response of base structure (Z direction) |
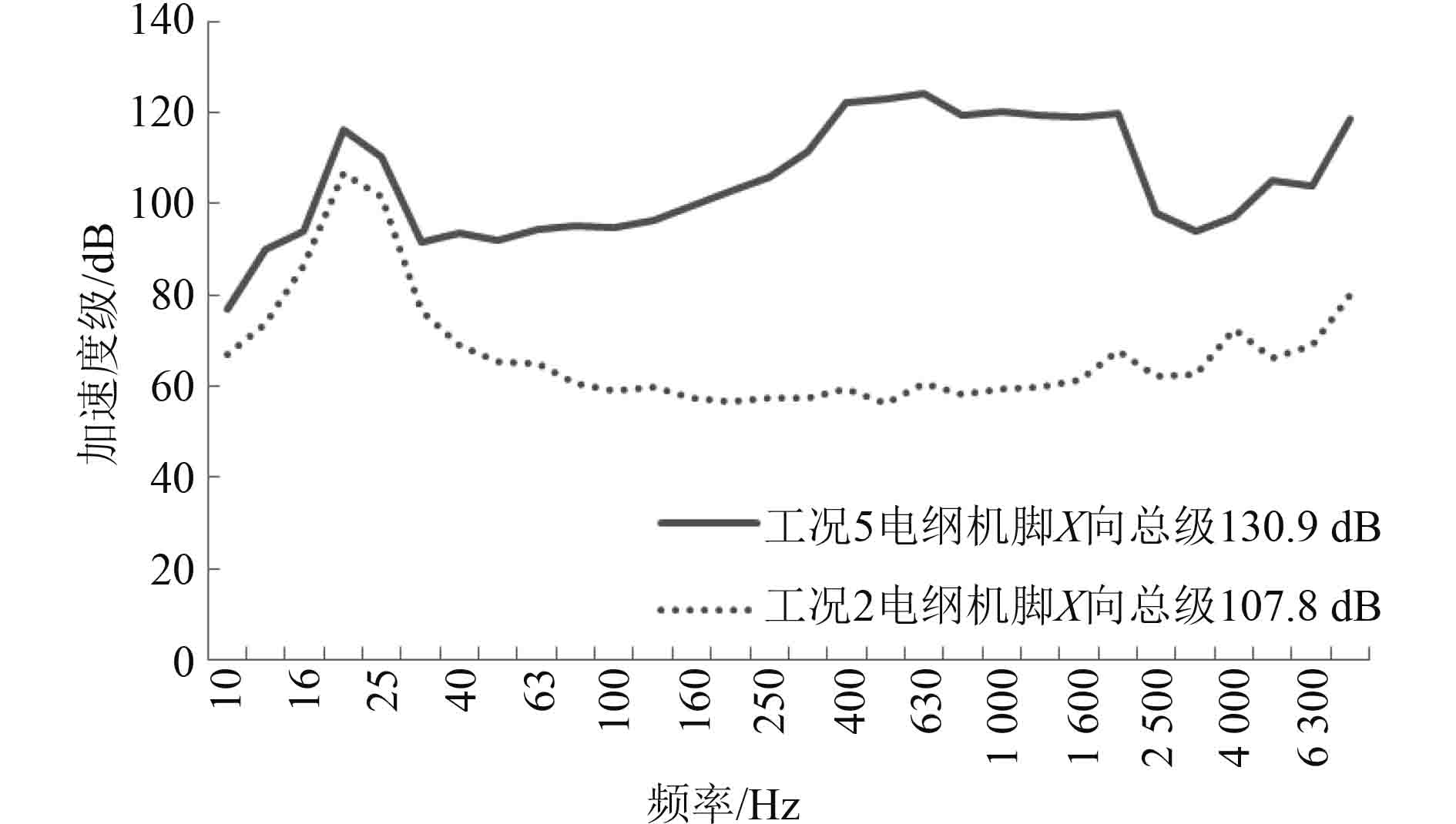
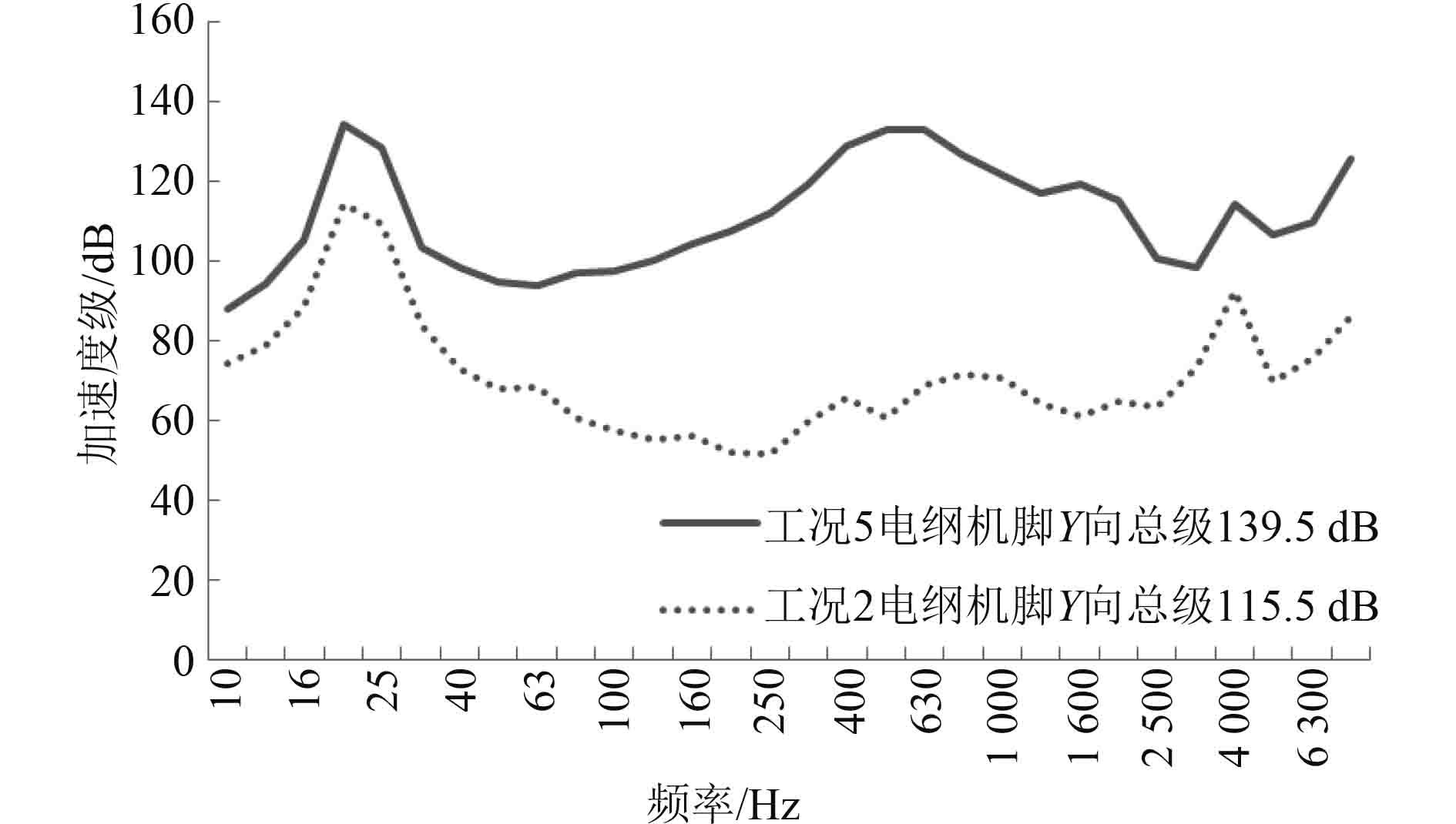
图12~图14为电机正常运行和被动激励时的机脚三向振动响应对比。可以看出,电机被动激励时的三向振动响应明显低于其正常运转的响应。这说明在配置得当的情况下,弹性安装的非运转设备(电机)既能有效消耗水泵的振动能量,又不会对自身造成损害。
|
图 12 电机机脚振动响应(X向) Fig. 12 The vibration response of motor seat (X direction) |

|
图 13 电机机脚振动响应(Y向) Fig. 13 The vibration response of motor seat (Y direction) |
|
图 14 电机机脚振动响应(Z向) Fig. 14 The vibration response of motor seat (Z direction) |
本文建立了含非运转设备的浮筏隔振系统三向振动传递模型,并通过试验验证了在振动传递模型中考虑弹性安装非运转设备的必要性。得出如下结论:
1)非运转设备对浮筏运转设备机脚振动的影响可忽略;
2)增装非运转设备可改变浮筏隔振系统原有的整体模态,对应的模态频率应避开各设备的运转频率;
3)将非运转设备与运转设备进行整体匹配隔振设计可提升隔振系统的声学性能;
4)当非运转设备的安装频率处于浮筏运转设备的共振频段内时,需校核其振动响应是否超过自身限值。
| [1] |
余永丰, 庞天照, 关珊珊, 等. 大型浮筏隔振系统筏架耦合振动研究[J]. 噪声与振动控制, 2010(5): 56-59. DOI:10.3969/j.issn.1006-1355.2010.05.013 |
| [2] |
张树桢, 陈前. 浮筏隔振系统的非共振响应分析[J]. 振动工程学报, 2014, 27(3): 326-332. DOI:10.3969/j.issn.1004-4523.2014.03.003 |
| [3] |
李增光. 浮筏及双层隔振装置隔振性能计算与分析[J]. 噪声与振动控制, 2015(6): 65-68. |
| [4] |
孙红灵. 弹性基础隔振系统的简化性能指标和有源控制力[J]. 声学学报, 2016, 41(2): 227-235. |
| [5] |
杨明月. 分布参数双层隔振系统的主被动控制机理研究[D]. 济南: 山东大学, 2015.
|
| [6] |
赵建学, 俞翔, 柴凯, 等. 双层隔振系统隔振性能分析[J]. 中国舰船研究, 2017(5): 56-59. |
| [7] |
温华兵, 昝浩, 陈宁, 等. 惯容器对隔振系统动态性能影响研究[J]. 实验力学, 2015, 30(4): 483-5490. DOI:10.7520/1001-4888-14-179 |
| [8] |
叶珍霞. 基座设计对隔振效果的影响分析与优化方法研究[J]. 舰船科学技术, 2019, 41(9): 48-51. DOI:10.3404/j.issn.1672-7649.2019.09.009 |
| [9] |
张森森, 商超, 戴俊, 等. 浮筏隔振系统三向振动传递特性研究[J]. 舰船科学技术, 2019, 41(11): 77-80. DOI:10.3404/j.issn.1672-7649.2019.11.015 |
| [10] |
原春晖. 机械设备振动源特性测试方法研究[D]. 武汉: 华中科技大学, 2006.
|
 2021, Vol. 43
2021, Vol. 43
