2. 中国船级社温州办事处,浙江 温州 330302
2. China Classification Society Wenzhou Office, Wenzhou 330302, China
双体船在快速性、耐波性、操纵性上都具有独特的优势,甲板面积大、高速低阻等特点,使其成为近年来发展最快的高性能船舶之一,现已广泛应用于军用、民用船舶[1]。相对于常规船舶,双体船由于片体间存在兴波干扰,所以双体船型线和片体间距对其快速性影响显著。在相同排水量下,双体船比常规船舶的湿表面积更大,这就使得其在低速航行时,具有较大的摩擦阻力。但在高速航行时,适宜的片体间距能够产生有利的兴波干扰,有效降低船舶兴波阻力。因此,双体船在不同片体间距下,其阻力性能有较大的差异。在船型保持不变的情况下,进一步优化片体间距是提高双体船阻力性能的有效方法之一。
近年来,国内外学者对双体船做了大量研究工作。邓芳等[2]通过Maxsurf建立双体船模型,运用Hullspeed细长体理论,得到了兴波阻力与不同片体中心距、长宽比之间的变化规律。Moraes等[3]运用细船体理论和Shipflow研究了2种不同船型的高速双体船兴波阻力随片体间距变化的规律。杜友威等[4]以某穿浪双体船为参考船型,研究了阻力及片体干扰之间的变化规律。陈京普等[5]自行开发了基于改进的Dawson法的数值预报程序,用于双体船、三体船的阻力预报,并分别以一艘小水线面双体船、一艘三体船验证了程序的可靠性和准确性。李广年等[6]基于Isight优化平台,以最小兴波阻力为目标,对非对称双体船的侧体布局进行了优化分析。李豪杰等[7]对一艘36 ft的水翼双体船进行了实船试验及CFD仿真分析,研究了水翼对双体船阻力的影响以及不同配置情况下的优化情况,得到了最佳的双体船水翼配置形式。马建等[8]分析了片体瘦削系数、片体间距和尾扰流板深度对穿浪双体船剩余阻力的影响,提出了一种基于模型试验的穿浪双体船总阻力预报方法。
综上,研究人员提出了各种方法用于双体船阻力性能预报,针对降阻问题,或优化型线,或优化片体间距,较少有相关研究综合考虑二者的耦合作用对双体船阻力性能的影响。本文以某双体船为对象,运用数值模拟技术,结合Lackenby变形方法,优化双体船的船体型线。在此基础上,进一步优化片体间距,与型线优化的船型相比,阻力性能得到了进一步改善。
1 数学模型 1.1 控制方程该双体船在粘流中做匀速运动,不考虑升沉和纵倾,满足如下质量守恒方程及N-S方程:
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 {\text,}$ | (1) |
| $ \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_j}}} + \mu \frac{\partial }{{\partial {x_j}}}\left(\frac{{\partial {u_i}}}{{\partial {x_j}}}\right) + {f_i}{\text。}$ | (2) |
式中:ui,uj分别为i方向和j方向的速度分量;xi,xj分别为i方向和j方向的位移分量;fi为xi方向上的体积力分量;μ为动力粘性系数。
1.2 湍流模型湍流模型采用k-ω(SST-Menter)湍流模型。其中,湍流动能k方程和特殊耗散率ω方程分别为:
| ${v_t} = \frac{k}{\omega }{\text,}$ | (3) |
| $\frac{{\partial k}}{{\partial t}} + \left({U_j} - {\sigma _k}\frac{{\partial {v_t}}}{{\partial {x_j}}}\right)\frac{{\partial k}}{{\partial {x_j}}} - \frac{1}{{{R_k}}}{\nabla ^2}k + {s_k} = 0 {\text,}$ | (4) |
| $\frac{{\partial \omega }}{{\partial t}} + \left({U_j} - {\sigma _\omega }\frac{{\partial {v_t}}}{{\partial {x_j}}}\right)\frac{{\partial \omega }}{{\partial {x_j}}} - \frac{1}{{{R_k}}}{\nabla ^2}\omega + {s_\omega } = 0 {\text。}$ | (5) |
式中:k,ω的初值为k0=1.1×10−7,ω0=9.0,用以抵消湍流耗散的环境湍流值;σk,σω为常数,σk=σω=0.5;sk,sω为用户自定义值。
1.3 双体船阻力计算与常规船舶相比,双体船在静水中航行所受到的阻力还包括片体间的干扰阻力,忽略空气阻力和附体阻力,双体船总阻力应为:
| $ {R_t} = {R_f} + {R_r} + {R_\xi } = {R_f} + {R_r} + {R_{w1 \leftrightarrow 2}} + \Delta {R_v}{\text{。}} $ | (6) |
式中:Rt为总阻力;Rf为摩擦阻力;Rr为剩余阻力;Rξ为干扰阻力。干扰阻力Rξ应包括两片体间的兴波干扰阻力Rw1↔2和粘性干扰阻力ΔRv。
假定1+αk为考虑片体间粘性干扰下的形状因子,只与船体形状有关。则双体船的总阻力系数为:
| ${C_t} = {\rm{(1}} + \alpha k{\rm{)}}{C_f} + {C_{w1}} + {C_{w2}} + {C_{w1 \leftrightarrow 2}}{\text{。}}$ | (7) |
式中:Ct为总阻力系数;Cf为摩擦阻力系数;CW为兴波阻力系数。
由1957ITTC公式可得摩擦阻力系数为:
| ${C_f} = \frac{{0.075}}{{{{({\rm{lg}}Re - 2)}^2}}}{\text{。}}$ | (8) |
式中:Re为雷诺数,Re=uL/ν;其中u为船速,L为船长,ν为运动粘性系数。
Couser等[9]给出了双体船形状修正因子计算公式如下:
| ${\rm{1}} + ak = 3.03{(L/{D^{1/3}})^{ - 0.4}}{\text,}$ | (9) |
因此可以得出双体船的粘性阻力为:
| ${R_v} = 0.5(1 + \alpha k)\rho {v^2}s{C_f}{\text。}$ | (10) |
其中:ρ为流体密度;s为船体湿表面积。
2 双体船船型优化 2.1 船型建立某高速双体客船的三维模型如图1所示。该船体在总体布局上关于中纵剖面对称,但就单个片体而言却是非对称的,片体的主要船型参数如表1所示,其设计航速us=20 kn(Fr=0.572)。对该双体船采用Lackenby法进行变形优化,保证排水量变化满足δΔ=±5%以内。浮心纵向位置最大偏移量δxb=−0.01Lpp,棱形系数最大改变量为δCp=−0.05,得到优化船型。

|
图 1 某双体船船体几何形状 Fig. 1 The hull geometry of a catamaran |
|
|
表 1 片体的主要参数 Tab.1 The main parameters of the slice |
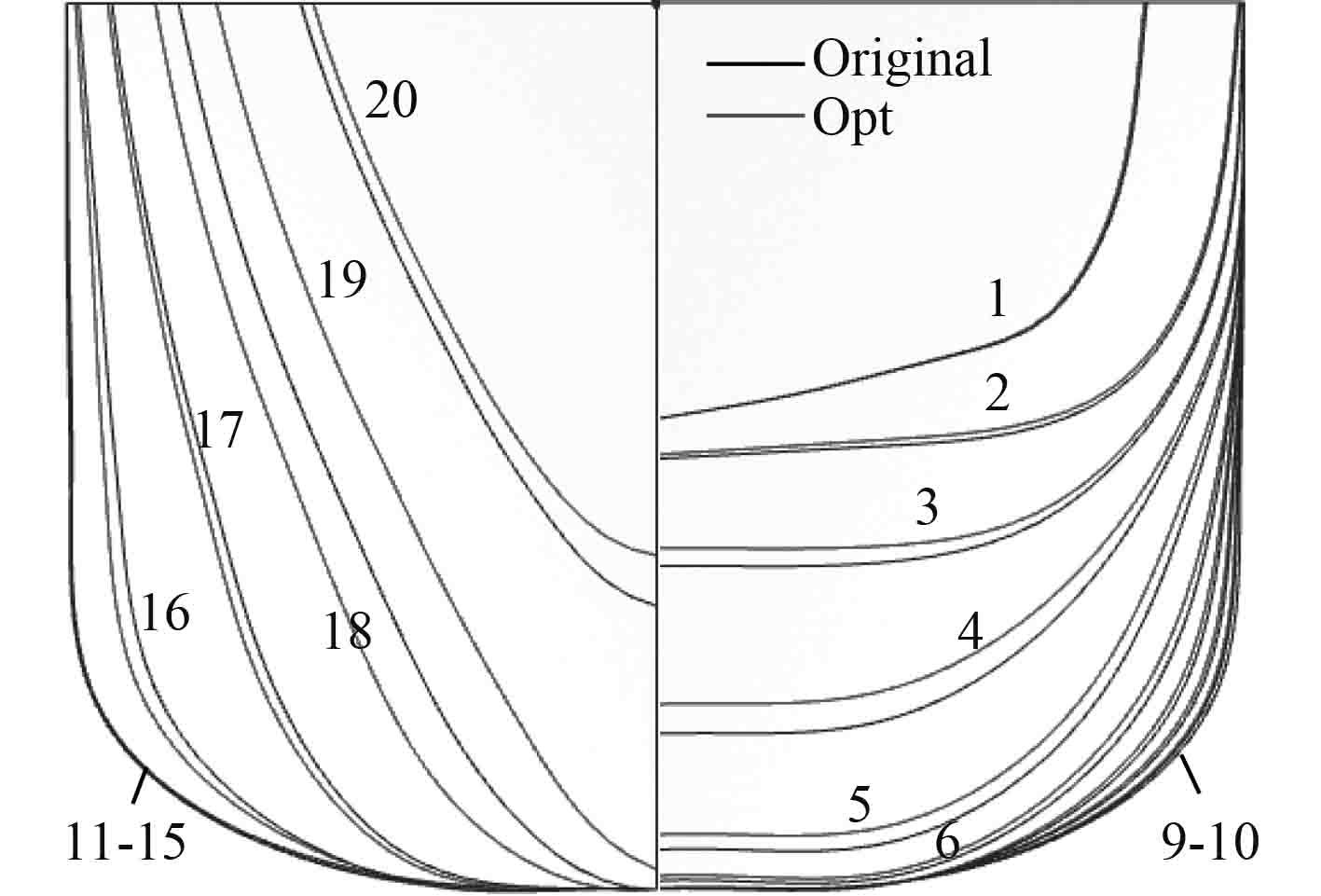
优化船浮心纵向位置向后偏移,平行中体无明显变化,首尾部均有不同程度地收缩,首部紧缩程度更加明显,排水体积相对原始船减少4.8%。变形前后双体船左舷侧船体型线对比如图2所示。
|
图 2 优化前后型线对比 Fig. 2 Optimal hull of profile before and after |
数值计算中模型缩尺比α=3,根据相似定律,船模设计航速um=5.94 m/s(Fr=0.572),计算不考虑纵倾和升沉。
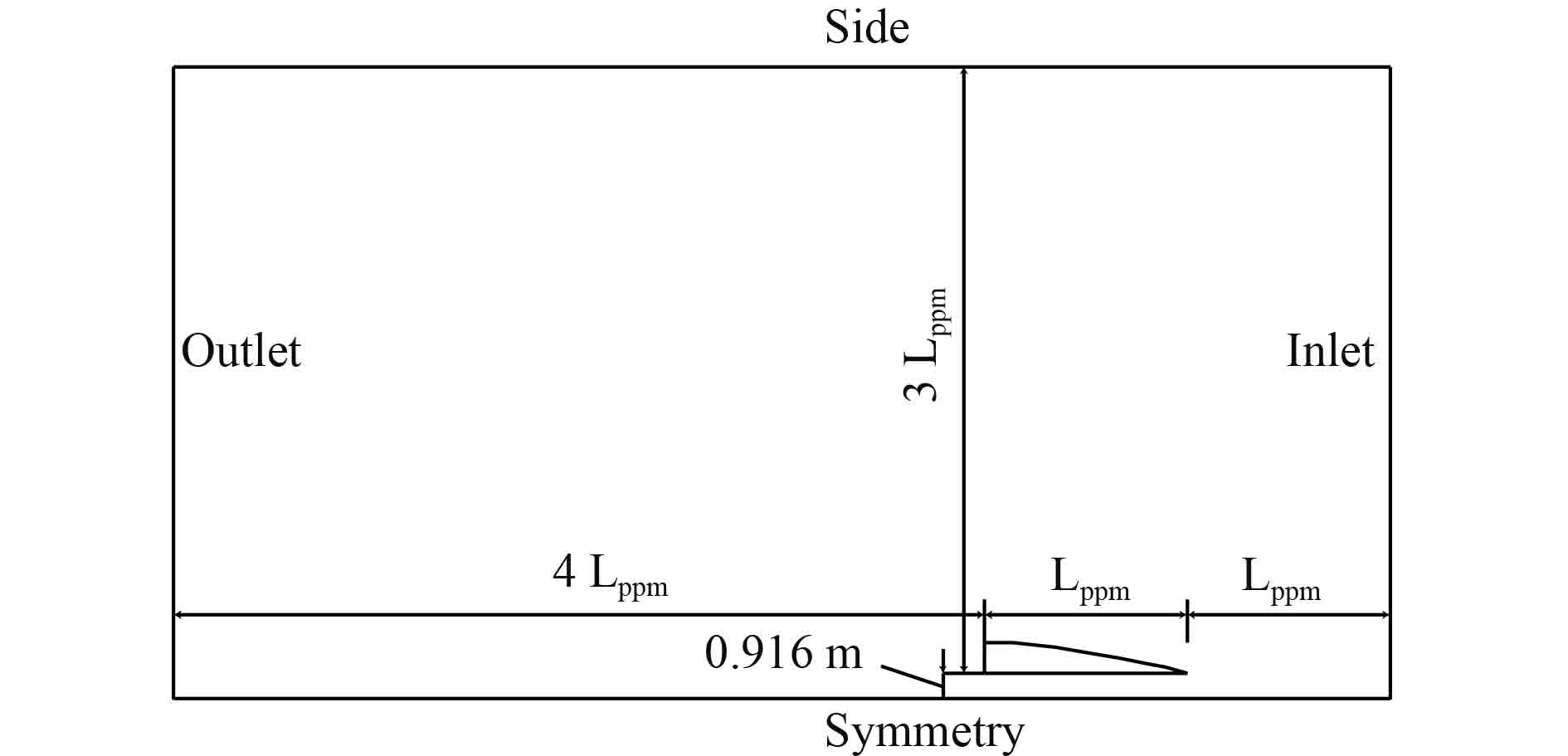
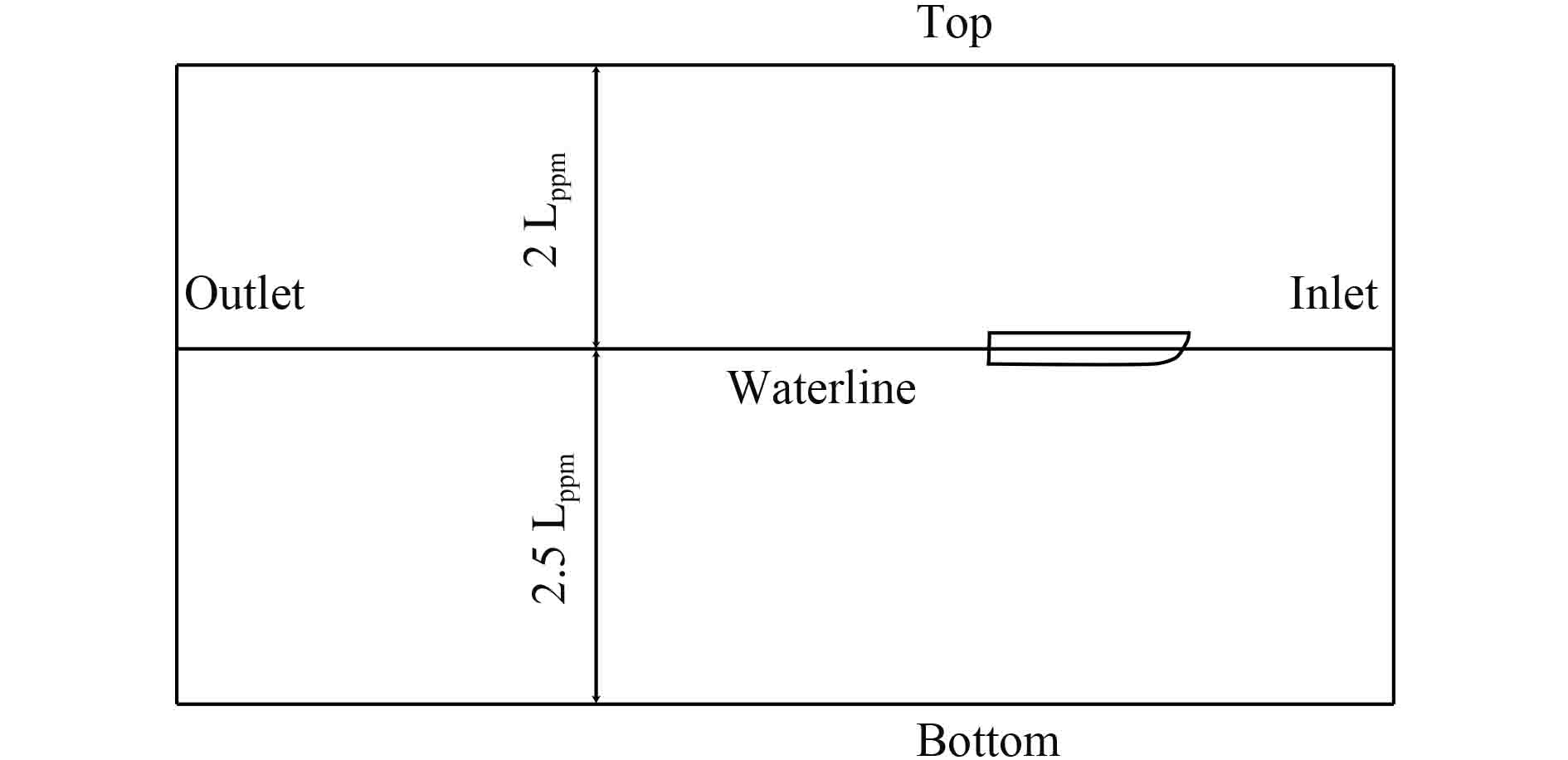
2.2 数值计算 2.2.1 计算域与边界条件船模关于中纵剖面对称,计算只需考虑左侧片体。计算域采用长方体区域,其中入口边界距船首约Lppm(Lppm为船模的垂线间长),出口边界距船尾约4Lppm,水面以上、船体以下分别约为2Lppm,2.5Lppm,对称面距船体为0.916 m,另一边界距船体约为3Lppm。
出口边界定义为压力出口,船身均为壁面,其他边界条件均定义为速度入口。
|
图 3 计算域尺寸(俯视) Fig. 3 The size of domain(plan view) |
|
图 4 计算域尺寸(主视) Fig. 4 The size of domain(front view) |
切割体网格是近十年新发展起来的一种网格划分技术,其生成简单、网格质量高、优良的复杂表面适应性等特点,受到了广大CFD学者的关注[10]。本文采用切割体网格与近壁面的棱柱层网格相结合的方式进行计算域的网格离散,近壁处理方式采用壁面函数方法,网格应布置于对数率层之内,即y+值应满足30<y+<300,网格数量接近200万,该网格数量能够达到计算精度要求。离散后的网格如图5和图6所示。

|
图 5 自由液面处网格 Fig. 5 Grid at free surface |

|
图 6 船身网格 Fig. 6 Grid on hull |
优化前后双体船模型在设计航速下的Rf,Rr如表2所示。通过Lackenby法使优化船的浮心纵向位置向船后偏移,使得船首形状相对瘦小,有利于降低船体阻力。Rf在高速双体船总阻力的占比较低,Rr占比高达85%以上。优化后,Cr相对于原始船减小了13%。
|
|
表 2 优化前后阻力计算结果 Tab.2 The results of calculation before and after optimization |
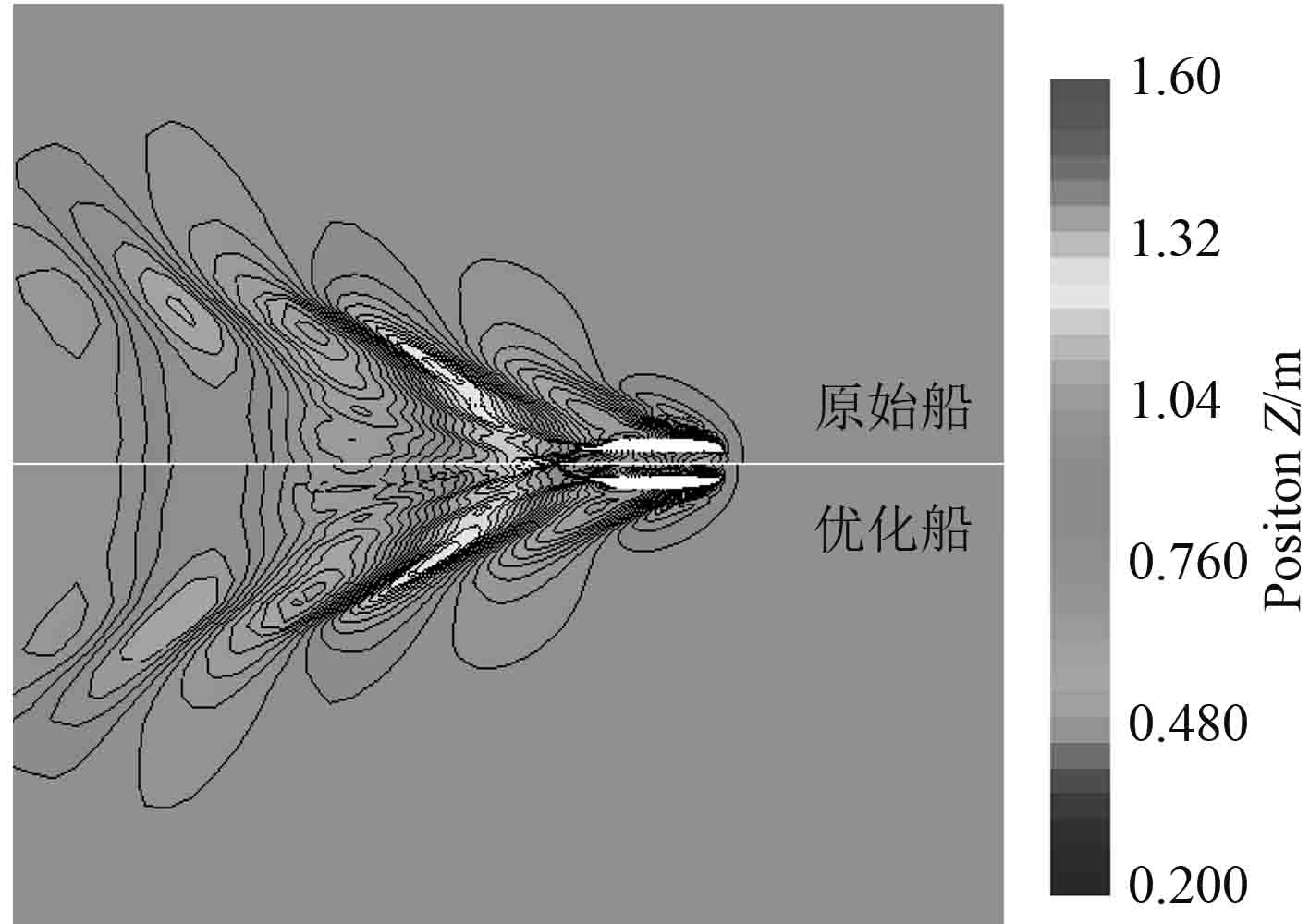
优化前后双体船的波高图如图7所示。通过对比二者,可以发现优化船型的兴波分布相对于原始船有所改善,优化船型波峰有所削弱。
|
图 7 优化前后波形对比图 Fig. 7 The waveforms before and after optimization |
在前文优化船型的基础上,分析片体间距对双体船阻力的影响,对其进行片体布局优化。首先定义片体间距比λ为片体间距sp与片体型宽B之比,即λ=sp/B。考虑λ=0.4~1.6时的双体船阻力。
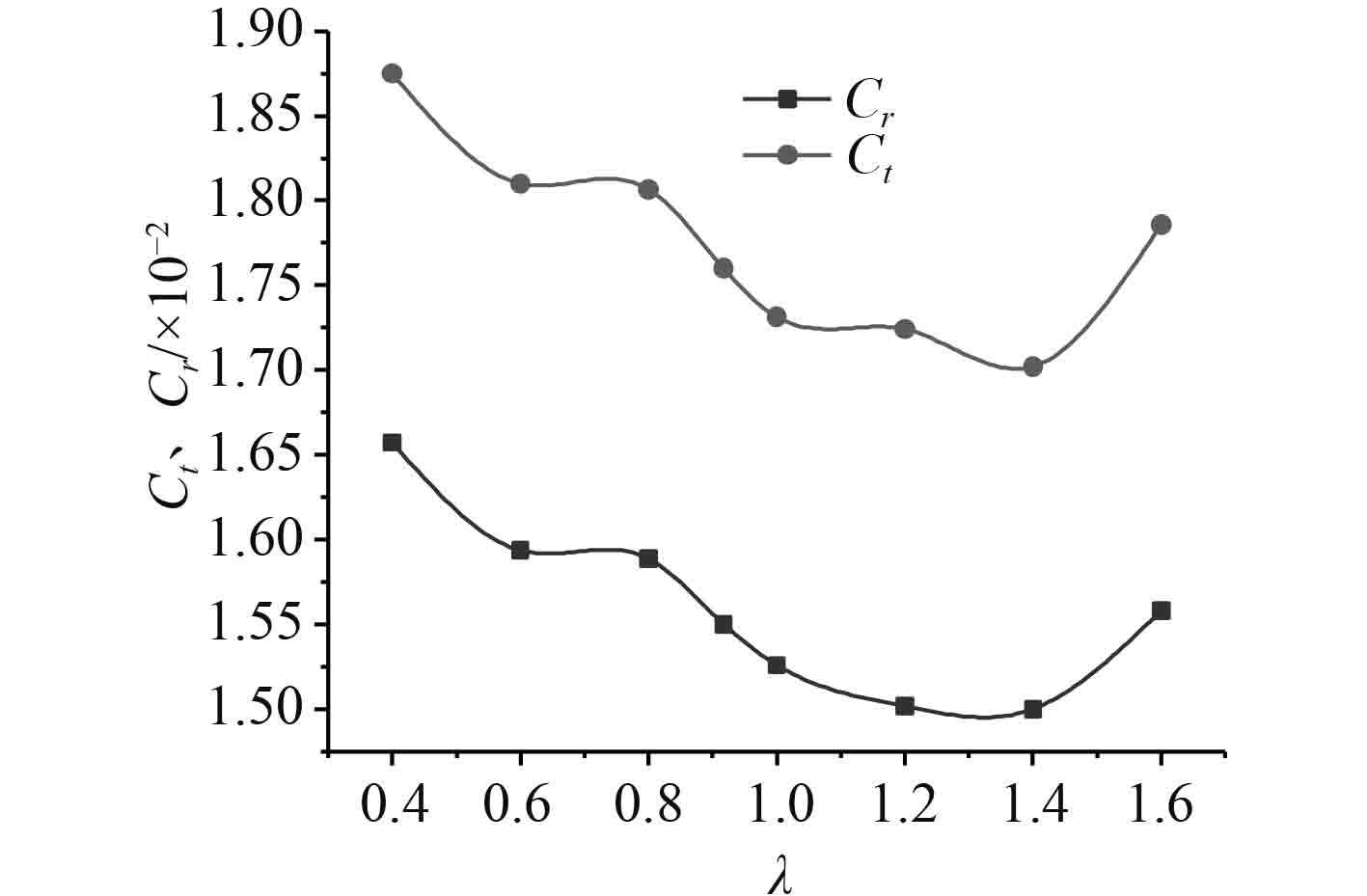
由图8所示,Cr和Ct在不同片体间距下的变化趋势基本一致。当λ=0.4~1.4之间时,Cr总体呈现下降趋势,且在λ=1.4处出现谷值;在λ=0.4~0.6以及λ=0.8~1.0区间,Cr呈现较大幅度地下降,而在λ=0.6~0.8之间,Cr基本保持不变;在λ=1.0~1.4区间内,下降趋势相对较为平缓。当λ>1.4时,Cr急剧增大。相对于λ=0.4而言,λ=1.4时的Cr和Ct分别降低了9.47%和9.23%;相对于型线优化后船型而言,λ=1.4时的Cr和Ct分别降低了3.23%和3.30%。图9给出了不同λ下的波形图。
|
图 8 不同λ下的Cr、Ct Fig. 8 Cr and Ct under different λ |

|
图 9 不同λ下的波形图 Fig. 9 The waveforms under different λ |
本文以某双体船为研究对象,运用数值模拟技术,结合Lackenby变形方法,改进船体型线,再优化片体间距。计算结果表明,本研究提出的预报方法及优化方案能够有效地应用于双体船设计,并得到如下结论:
1)以该高速双体船为例,在保证一定排水量变化范围内,通过Lakenby法使浮心纵向位置相对于船舯后移,变形后的船体艏部相对瘦小,使得船体阻力减小。在设计航速v=20 kn(Fr=0.572)下,剩余阻力系数减小约13%,总阻力系数减小12%。
2)在优化船型的基础之上,进一步优化片体间距,在设计工况下双体船剩余阻力的随片体间距变化趋势与总阻力变化趋势基本一致,存在最佳片体间距比使得船体阻力达到最优值。仅从阻力性能角度出发,该双体船片体间距比λ=1.4时阻力性能最优,与型线优化后的船型相比,Cr和Ct分别降低了3.23%,3.30%。
本文研究了型线优化及片体间距优化对双体船阻力优化的耦合作用,为双体船的设计优化提供了一定的技术支持。考虑船体运动、多航速下的阻力优化将是下一步的研究方向。
| [1] |
王骏. 高性能船舶研究现状及发展趋势[J]. 船舶物资与市场, 2020(8): 7-9. WANG J. Research status and development trend of high performance ship[J]. Marine Equipment/Materials & Marketing, 2020(8): 7-9. |
| [2] |
邓芳, 邓魏彬. 双体船阻力性能计算及船型设计优化[J]. 青岛科技大学学报(自然科学版), 2015, 36(1): 72-76. DENG F, DENG W B. Resistance calculation and hull design and optimization of catamaran[J]. Journal of Qingdao University of Science and Technology(Natural Science Edition), 2015, 36(1): 72-76. |
| [3] |
MORAES H B, VASCONCELLOS J M, LATORRE R G. Wave resistance for high-speed catamarans[J]. Ocean Engineering, 2004, 31: 2253-2282. DOI:10.1016/j.oceaneng.2004.03.012 |
| [4] |
杜友威, 李彪, 周新院. 基于阻力分析的穿浪双体船船型设计及优化[J]. 舰船科学技术, 2019, 41(13): 31-34+44. DU Y W, LI B, ZHOU X Y. Ship design and optimization of wave-piercing catamaran based on resistance performance analysis[J]. Ship Science and Technology, 2019, 41(13): 31-34+44. |
| [5] |
陈京普, 朱德祥, 何术龙. 双体船/三体船兴波阻力数值预报方法研究[J]. 船舶力学, 2006(2): 23-29. CHEN J P, ZHU D X, HE S L. Research on numerical prediction method for wave-making resistance of catamaran/trimaran[J]. Journal of Ship Mechanics, 2006(2): 23-29. DOI:10.3969/j.issn.1007-7294.2006.02.004 |
| [6] |
李广年, 赵连恩, 陈庆任, 等. 非对称双体船兴波问题与侧体布局优化分析[J]. 中国造船, 2013, 54(4): 55-62. LI G N, ZHAO L E, CHEN Q R, et al. Wave-making problem and optimal solution of piece hull arrangement for asymmetric catamaran[J]. Shipbuilding of China, 2013, 54(4): 55-62. DOI:10.3969/j.issn.1000-4882.2013.04.007 |
| [7] |
LI H J, PUTR A A M F, SUN K, et al. Boat trial validation and resistance prediction of a 36-foot hydrofoil catamarans using CFD[J]. Journal of Ship Mechanics, 2020, 24(6): 740-753. |
| [8] |
马健, 张再夫, 李惠敏. 穿浪双体船剩余阻力影响因素分析及总阻力预报方法[J]. 船舶力学, 2011, 15(Z1): 32-39. MA J, ZHANG Z F, LI H M. Influencing factors of residual resistance and a prediction method of total resistance about wave-piercing catamaran[J]. Journal of Ship Mechanics, 2011, 15(Z1): 32-39. |
| [9] |
COUSER P, WELLICOME J F, MOLLAND A F. An improved method for the theoretical prediction of the wave resistance of transom-stern hulls a slender body approach[J]. International Shipbuilding Progress, 1998, 45(444): 1-18. |
| [10] |
王硕, 苏玉民, 庞永杰, 等. 高速滑行艇CFD精度研究[J]. 船舶力学, 2013, 17(10): 1107-1114. WANG S, SU Y M, PANG Y J, et al. Study on the accuracy in the hydrodynamic prediction of high-speed planning crafts of CFD method[J]. Journal of Ship Mechanics, 2013, 17(10): 1107-1114. DOI:10.3969/j.issn.1007-7294.2013.10.002 |
 2021, Vol. 43
2021, Vol. 43
