0 引　言

水下弹射筒口气泡及其载荷特性是潜射装置关注的重要内容之一。相关研究表明，在水下弹射发射过程中，导弹离筒后，混合气体进入水中在筒口形成气泡，筒口气泡在导弹运动过程中会经历膨胀、收缩、破碎等过程，会对导弹运动及相邻设备产生显著的力学载荷扰动^[1-2]。

王亚东等^[3]采用计算流体力学方法，对潜射导弹弹射离筒后筒口气泡的发展变化过程进行了数值研究分析，给出了筒口附近典型位置压强变化情况。邓佳等^[4]对水下同心筒发射的筒口气泡进行了数值研究，获得了筒口气泡的形态变化过程和气泡内部压强变化规律。卢丙举等^[5]从横向流载荷出发，研究了水下弹射的横向动力学特性。为降低和抑制发射过程中的力热载荷，胡晓磊等^[6]研究了同心筒发射燃气流流动特点和筒口导流板结构对弹体的影响。潘登等^[7]对鱼雷发射箱在使用扇形孔导流隔板和无导流隔板时内流场变化情况进行数值模拟，分析导流隔板对发射箱内流场的影响。

本文结合一筒多弹水下弹射筒口气泡载荷抑制需求，采用多相流数值计算方法，对水下弹射筒口导流条件下筒口气泡发展变化状态和载荷特性进行研究分析，为相关研究和工程应用提供参考。

1 理论模型与求解方法 1.1 控制方程

围绕水下弹射涉及的气液两相流动，采用VOF模型^[8]进行求解计算。VOF模型是一种欧拉-欧拉模型，通过求解单独的动量方程并处理穿过求解区域内各种流体的体积分数来模拟多相流动。该模型假设相与相之间不能互相穿插，需要通过计算各相的体积分数来确定交界面。具体的控制方程包括：

1）体积分数的连续方程：

$\dfrac{\partial }{{\partial t}}\left( {{\alpha _m}} \right) + {\vec \upsilon _m} \cdot \nabla {\alpha _m} = \dfrac{{{S_{{\alpha _m}}}}}{{{\rho _m}}}\text{，} $

(1)

2）动量方程：

$\begin{split}\dfrac{\partial }{{\partial t}}({\rho _m}{\vec \upsilon _m}) + &\nabla \cdot \left( {{\rho _m}{{\vec \upsilon }_m}{{\vec \upsilon }_m}} \right) = - \nabla p + \nabla \cdot \\ & \left[ {\mu _m}\left( \nabla {{\overset {\rightharpoonup } {\upsilon } }_m} + \nabla \overset{\rightharpoonup} {\upsilon } _m^T \right) \right] + {\rho _m}\overset{\rightharpoonup} {g} + \overset{\rightharpoonup} {F} \text{，}\end{split} $

(2)

3）能量方程：

$\dfrac{\partial }{{\partial t}}\left( {\rho E} \right) + \nabla \cdot \left[ {\overset{\rightharpoonup} {\upsilon } \left( {\rho E + p} \right)} \right] = \nabla \cdot \left( {{k_{eff}}\nabla T} \right) + {S_h} \text{，}$

(3)

其中： ${\overset{\rightharpoonup} {\upsilon } _m}$ 为质量平均速度； ${S_{{\alpha _m}}}$ 为质量输送源项，在不考虑相与相之间转移的情况下，右端项为0； ${\alpha _m}$ 为第 $m$ 相的体积分数； $\overset{\rightharpoonup} {F} $ 为体积力； $\ {\mu _m}$ 为混和物的粘度； ${k_{eff}}$ 为有效传导率； $\ \rho $ 为密度，二者均被各相共享； ${S_h}$ 为热源项，包括辐射热和体积热。

为采用雷诺平均方法求解流动控制方程，采用Realizable k-ε湍流模型封闭流动脉动产生的雷诺应力和输运项。为此，引入带湍动能及其耗散率的输运方程，其方程为：

$\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M}\text{，}$

(4)

$\begin{split}\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} = &\frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _t}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}S\varepsilon - \\ &\rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + {C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b}\text{。}\end{split}$

(5)

其中： ${C_2}$ 和 ${C_{1\varepsilon }}$ 为常数； ${G_k}$ 为速度梯度引起的湍动能； ${G_b}$ 为由浮力引起的湍动能； ${Y_M}$ 为可压速湍流脉动膨胀的耗散率； ${\sigma _k}$ ， ${\sigma _\varepsilon }$ 为湍动能及耗散率的普朗特数。

1.2 数值计算方法

水下弹射时，导弹在发射筒内向上运动，两相流动区域相应产生显著变化。研究主要采用动网格技术^[9-10]，对流动控制方程进行求解计算。在运动网格中计算流场时，通用变量 $\phi $ 在任意控制体 $V$ 上的守恒方程可以表示为：

$\begin{split}\frac{{\rm d}}{{{\rm d}t}}\int_V {\rho \varphi {\rm d}V} + &\int_{\partial V} {\rho \varphi (\vec u - {{\vec u}_g}) \cdot {\rm d}\vec A} = \\ &\int_{\partial V} {\Gamma \nabla \varphi \cdot {\rm d}\vec A} + \int_V {{S_\varphi }{\rm d}V}\text{，} \end{split}$

(6)

式中： $\vec u$ 为流体速度矢量； ${\vec u_g}$ 为网格运动速度； $\Gamma $ 为耗散系数； ${S_\varphi }$ 为 $\varphi $ 的源项； $\partial V$ 为控制体 $V$ 的边界。上式中第一项为对时间的导数项，通过一阶向后差分可以表示为

$\frac{{\rm d}}{{{\rm d}t}}\int_V {\rho \varphi {\rm d}V} = \frac{{{{(\rho \varphi V)}^{n + 1}} - {{(\rho \varphi V)}^n}}}{{\Delta t}}\text{，}$

(7)

${V^{n + 1}} = {V^n} + \frac{{{\rm d}V}}{{{\rm d}t}}\Delta t\text{，}$

(8)

$\frac{{{\rm d}V}}{{{\rm d}t}} = \int_{\partial V} {{{\vec u}_g} \cdot {\rm d}\vec A} = \sum\limits_j^{{n_f}} {{{\vec u}_{gj}} \cdot {{\vec A}_j}} \text{，}$

(9)

${\vec u_{gj}} \cdot {\vec A_j} = \frac{{\delta {V_j}}}{{\Delta t}}\text{。}$

(10)

式中： $n$ 和 $n + 1$ 分别为当前及下一个时间步； ${\rm d}V/{\rm d}t$ 为控制体的体积对时间的导数; ${\rm d}V/{\rm d}t$ 为满足网格守恒定律； ${n_f}$ 为控制体 $V$ 上面的数量； ${\vec A_j}$ 为第 $j$ 个面的法向矢量； $\delta {V_j}$ 为控制体 $V$ 第 $j$ 个面在 $\Delta t$ 时间步长内扫描形成的体积。

在研究分析中，以商用计算流体力学软件Fluent作为工具对流动模型进行求解计算。并采用自定义函数UDF在弹体表面进行压强积分获得弹体承受的流体作用力，进而解算弹射过程中的弹体运动速度。

2 计算模型设置 2.1 计算模型与导流结构

为获得水下弹射筒口两相流动状态和导流结构对筒口附近力学载荷的抑制特性，以国内外均有关注的一筒多弹水下发射装置为对象，建立计算分析模型。计算模型包括发射筒、筒口结构、导弹、部分艇体以及外场计算区域，如图1所示。计算模型中结构壁面均采用无滑移绝热边界，来流迎风面设置为速度入口，来流迎风面以外的计算域外场设置为压强出口，并依据水深环境指定随深度变化的压强值。

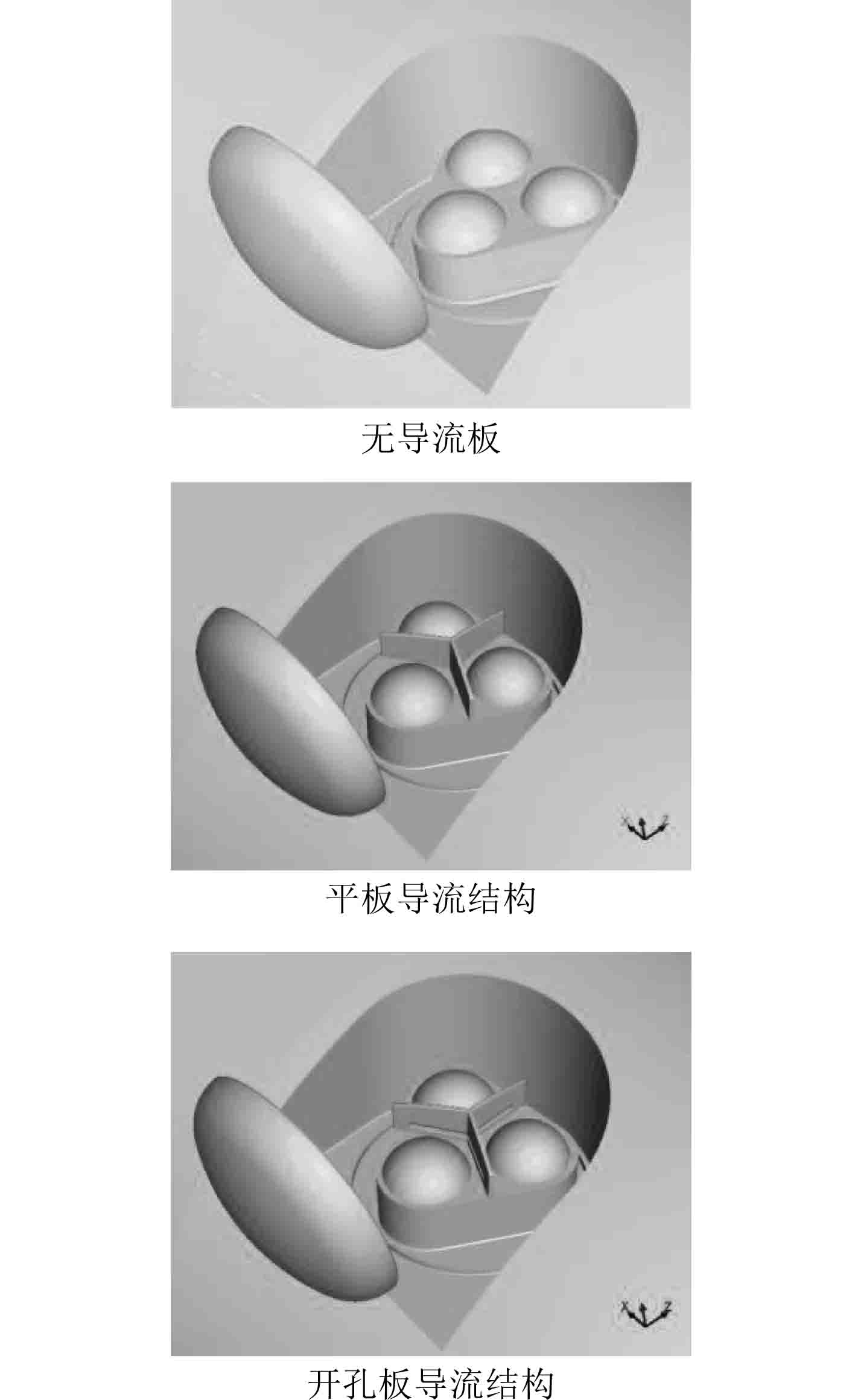
为对比和考察筒口导流结构对水下弹射筒口气泡及作用载荷的抑制作用，分别对3种形式的筒口结构进行研究分析，如图2所示。一是无导流板模型结构，二是平板导流结构，三是开孔导流结构。对于开孔导流结构，为便于建模分析，采用矩形孔形式。

2.2 计算网格与模型校验

计算采用结构化网格模型，在流动梯度较大的筒口及壁面附近区域区域进行网格加密。未添加导流板计算模型在筒口附近的网格如图3所示。

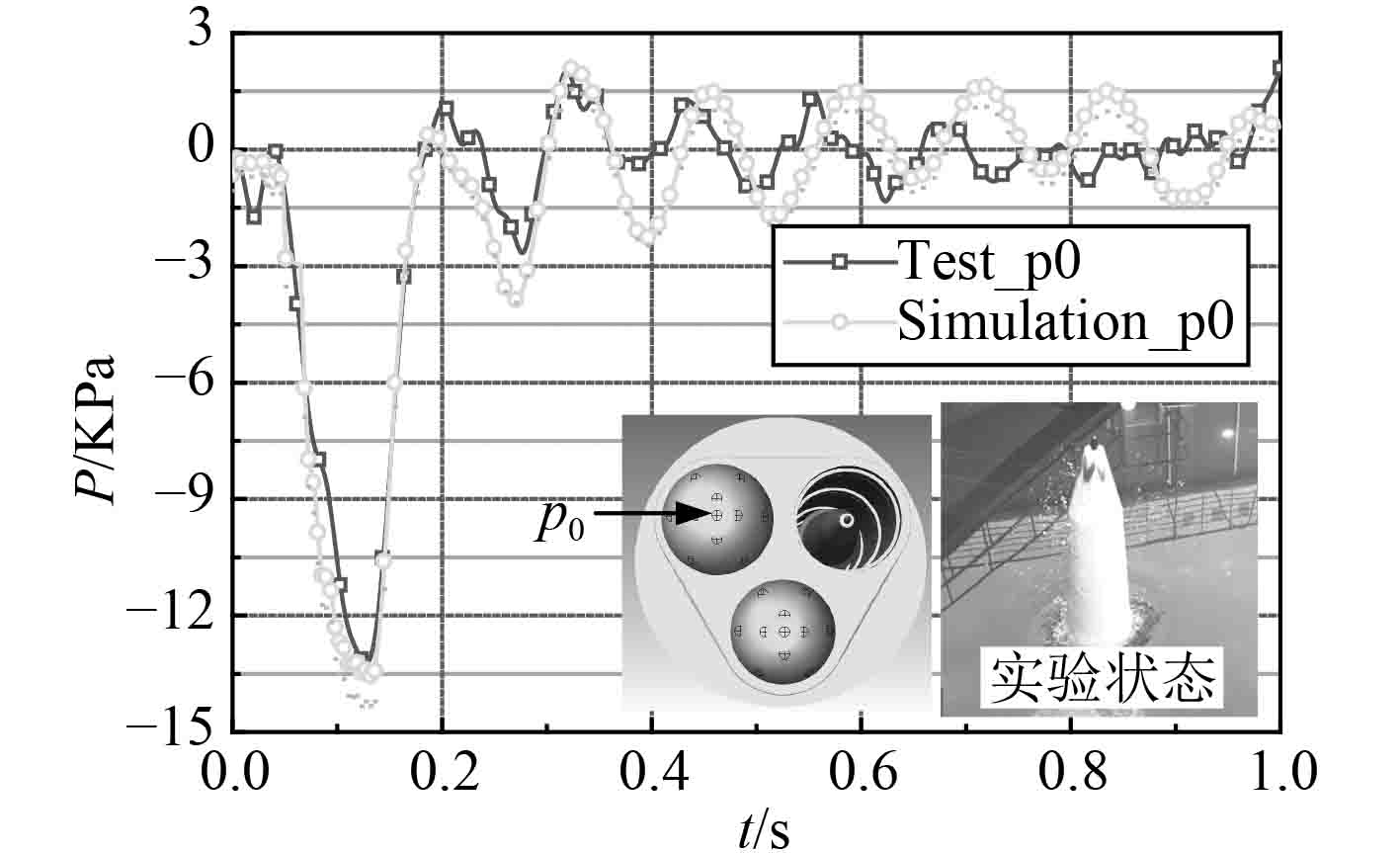
为校验计算模型的有效性，结合模拟弹水池弹射模型，建立相应的计算分析模型和测点压强监测，获得计算结果与实验测量结果对比如图4所示，图中以弹体离筒时刻作为时间零点。从图中可以看出，计算模型与实验结果在弹体离筒初期的压强冲击载荷吻合良好，在后期也具有良好的规律一致性，表明研究采用的方法和模型可用于水下弹射两相流动和气泡载荷特性分析。

3 计算结果分析 3.1 不同结构下的载荷特性

针对不同导流结构形式的计算模型，设置弹射筒口所处水深分别为30 m和100 m，通过数值计算获得水下弹射过程中的两相流动和典型载荷状态。

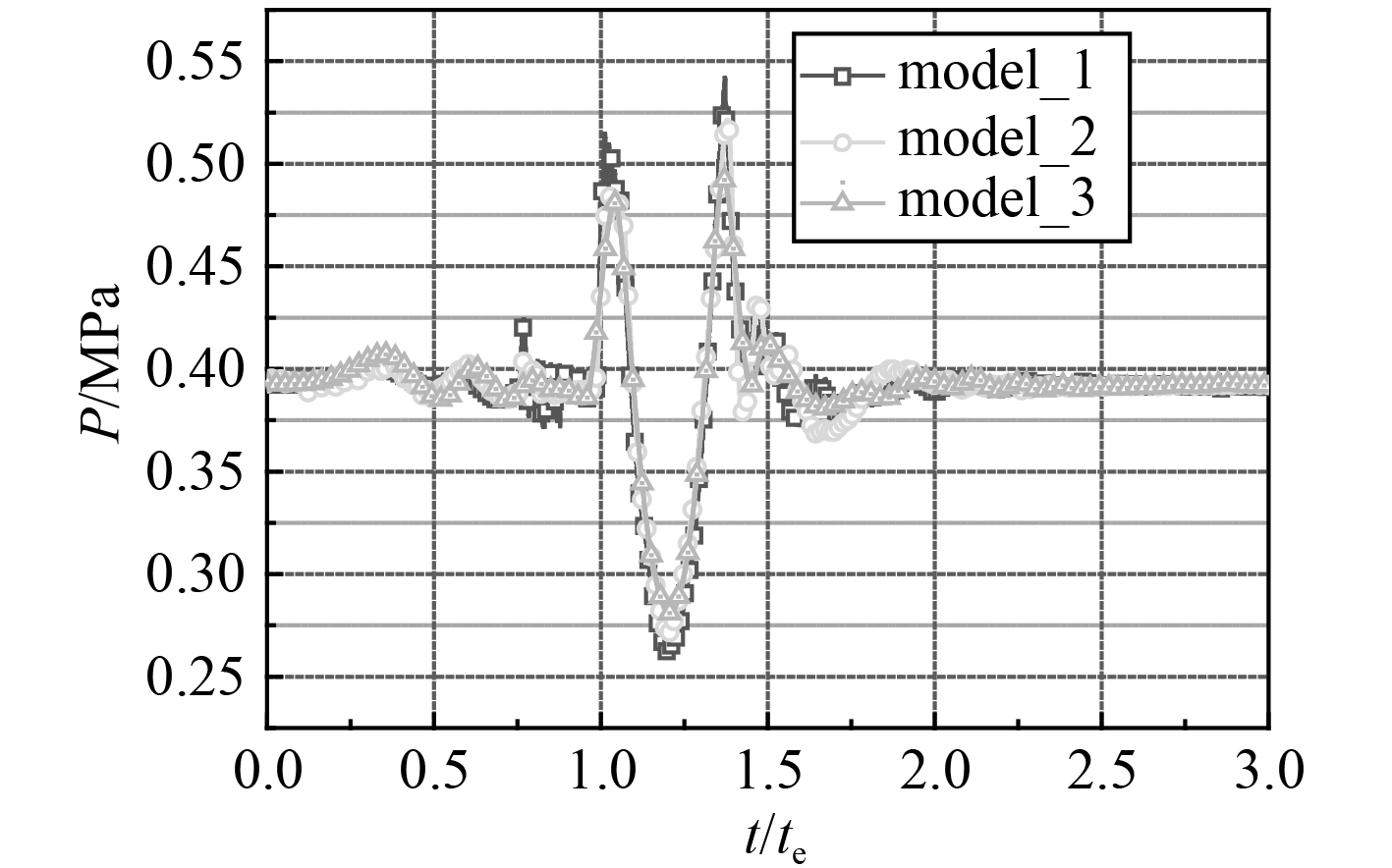
图5给出了筒口水深30 m条件下，发射筒相邻水密膜中心测点p₀压强随时间的变化曲线。为便于后续比较，以离筒时刻的时间t_e对横轴进行无量纲处理。从图中可以看出，3种结构模型获得的测点压强具有相近的变化规律，即在弹体筒内运动阶段，测点压强小幅变化；弹体离筒时，由于筒内高压弹射气体与水环境连通，在相邻设备表面产生显著的压强冲击；受筒口气泡发展变化影响，相邻设备经历了一个完整的正负压交替作用过程；此后相邻设备受到的压强载荷逐渐减小。对于3种模型结构，无导流板结构模型（model_1）对应的测点受到的正负压冲击幅值大于其它两种结构。对于平板导流结构模型（model_2），测点受到的正负压冲击减小，其振荡最大幅值相对模型1降低约8%。在开孔板导流结构模型（model_3）中，测点受到的正负压交变载荷进一步减小，其振荡幅值相对模型1降低约21%。

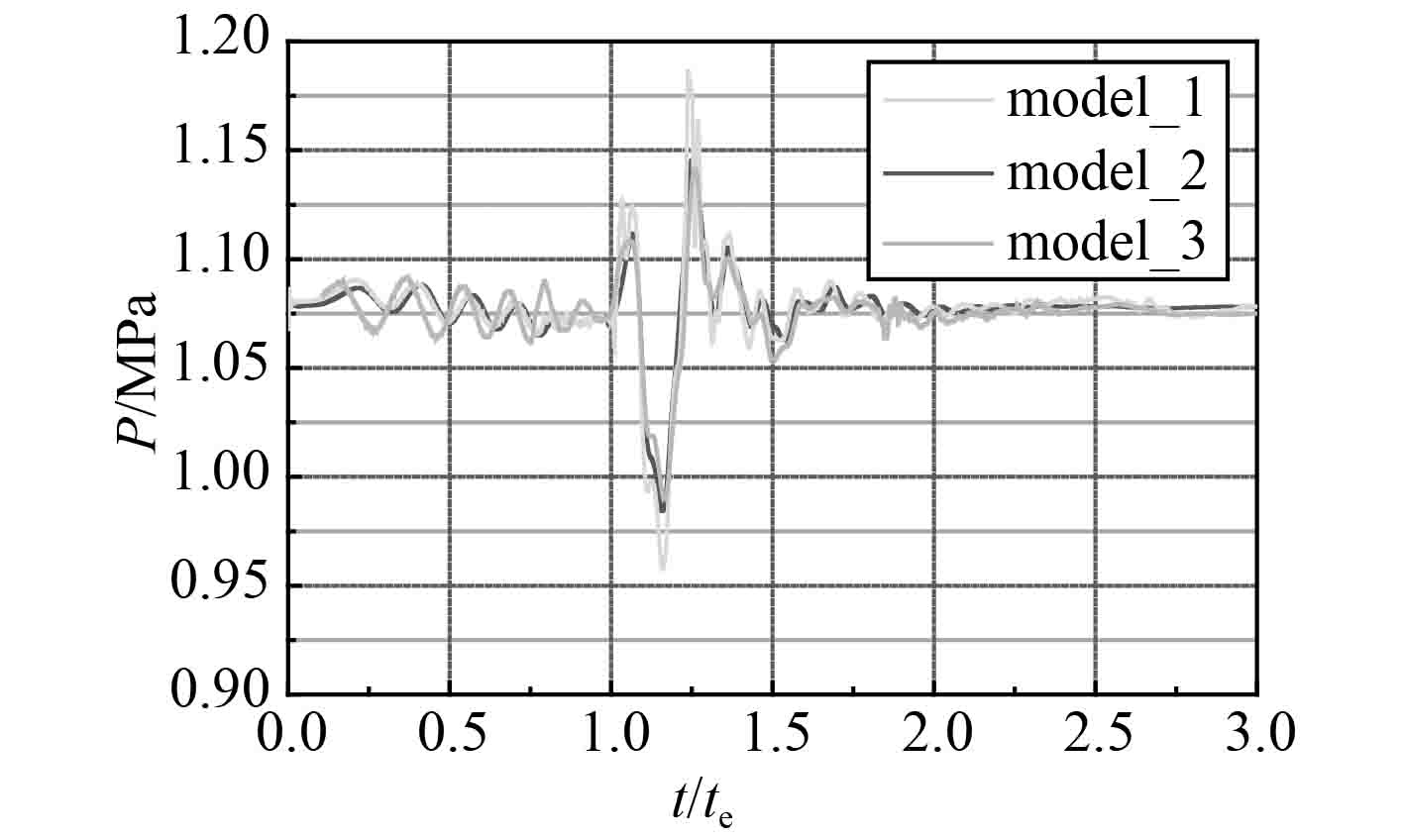
图6给出了筒口水深100 m条件下，发射筒相邻水密膜中心测点p₀压强随时间的变化曲线。可以看出，尽管弹射水深增加，相邻设备承受的载荷变化规律与30 m水深类似。对于3种模型结构，同样是无导流板结构模型对应的测点压强承受的载荷幅值最大；平板导流结构模型使测点最大振荡幅值降低约30%；开孔板导流结构模型使测点最大振荡幅值降低约33%。

3.2 筒口气泡状态

为研究并明确导流结构引起筒口附近载荷变化的原因，这里结合筒口气泡发展状态，对导流结构的作用进行深入分析。

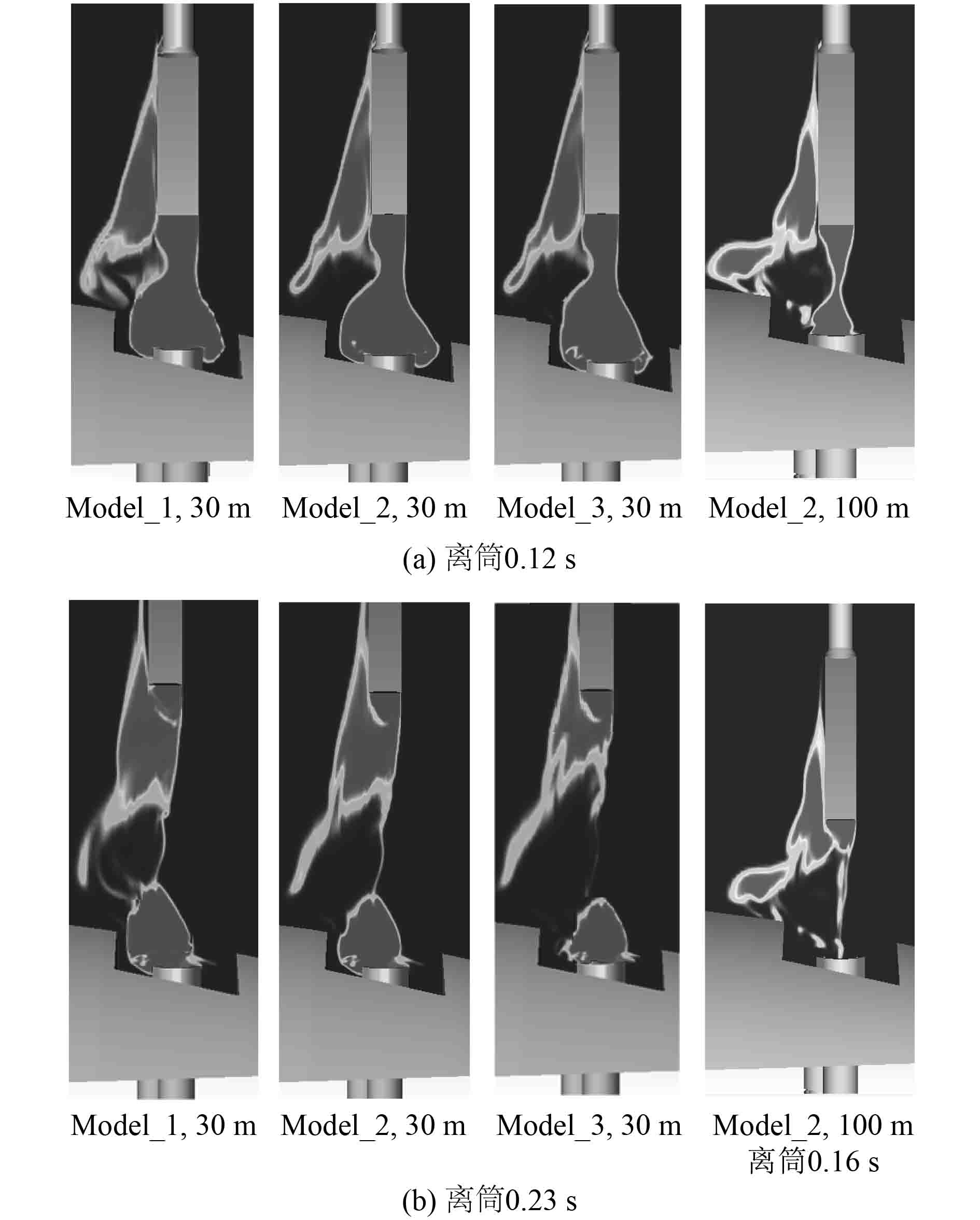
图7给出了不同结构模型弹体离筒初期筒口气泡的发展状态对比。可以看出，在30 m水深时，弹体离筒0.12 s时，3种筒口结构对应的筒口气泡形态基本一致，即筒内工质压强高于环境压强，筒口气泡呈现显著的膨胀状态，在模型2和模型3中，气泡尺寸均超过了导流板的尺寸。在弹体离筒0.23 s，弹射工质气体分离为随弹底运动的气泡和滞留筒口的气泡，由于气泡内压强因过度膨胀低于环境压强，筒口气泡出现收缩状态。对于带开孔导流板的模型3，气体在膨胀并穿过开孔时，气液两相界面的不稳定性增加，部分穿过开孔的气泡破碎为小气泡，在筒口主气泡收缩时，气泡尺寸减小。事实上，筒口气泡压强向外传播过程中，主要受到2种因素影响，一是压强直接通过水介质传播时，随着传输距离增加载荷会逐渐下降；二是筒口气泡膨胀收缩变化引起交变压强载荷。导流板的存在，在一定程度上能够增加筒口气泡载荷传递至相邻发射筒口的距离，因此平板导流在此时能够产生一定的效果；而气泡膨胀尺寸超过导流板，又限制了这一抑制作用。开孔导流板随对压强载荷的传播具有一定遮挡效应外，使筒口气泡在膨胀通过开孔时增加了不稳定性并破碎为小气泡，在一定程度上抑制了筒口气泡的膨胀收缩变化，进一步抑制了交变载荷的幅值。

对比30 m和100 m水深状态，可以看出，水深环境增加后，尽管弹射时采用比较接近的筒内外压强差，但深水环境下筒口气泡显著小于浅水环境。在0.12 s时，100 m水深下的筒口气泡尺寸与导流板尺寸接近，导流板对压强冲击的抵制作用增加。同样由于筒口气泡缩小，穿过开孔导流板的气体显著减少，因此开孔对载荷的抑制作用减小。在0.16 s时，100 m水深下的筒内气体已被倒灌水介质压缩进入发射筒内。可见在不同水深环境下，筒口导流结构对压强载荷的抑制作用有着较大差异。在浅水环境下，筒口气泡尺寸较大，开孔导流结构上的开孔对载荷抑制的贡献较大；在深水环境下，筒口气泡尺寸小，主要通过导流结构对压强传播路径的阻隔起到载荷抑制作用。

4 结　语

围绕水下弹射筒口气泡载荷抑制问题，利用数值计算方法对无导流、平板导流和开孔板导流下的测点载荷进行了对比分析，研究结果表明导流结构对发射筒口气泡载荷具有一定的抑制作用，主要体现在如下两方面：

1）导流结构能够在一定程度下改变筒口附近压强载荷传播路径，对相邻设备承受的压强载荷起到一定的抑制作用。当发射水深较深时，筒口气泡尺寸减小，抑制效果增加。

2）开孔导流板能够在筒口气泡膨胀并穿过孔板过程中，因相间界面非稳定性增加而破碎脱落，对筒口气泡膨胀收缩过程产生的交变载荷幅值产生抑制作用。