随着机器人技术的迅猛发展,机器人在军事领域上的应用越来越广泛。波音公司为美国海军研制了以机械臂为主体、基于潜艇鱼雷发射管的UUV回收系统,并于2006年初完成海试[1]。舰艇通过发射管进行小型UUV的布放、回收以及物资输送,具有很强的隐蔽性,应用前景广阔。目前国内在这方面的研究尚处于空白阶段,因此基于发射管的回收机械臂具有较好的实用价值和研究意义。
机械臂装载在发射管内,因此其体积、外形及重量有着严格限制。在机械臂的设计过程中,动力学求解得到的机械臂动态过程中各关节的力与力矩可为驱动校核、优化机械臂结构等工作提供参考。Pratheep V G[2]在Solidworks中建立了机械臂的三维模型并在Matlab下进行运动控制仿真。袁凯[3]和鲍俊维[4]分别设计了六功能和五功能的中等负载水下机械臂,并利用牛顿-欧拉法建立了机械臂动力学模型。王懿[5]基于迭代Newton-Euler矢量力学方法和Morison方程建立了静水条件下考虑流体阻力的六自由度机械臂动力学模型,通过Matlab软件仿真分析了流体阻力对机械臂关节控制力矩最大影响。
本文针对舰艇的回收打捞需求,对机械臂进行结构设计,建立虚拟样机模型得到相应的动力学参数;规划回收轨迹求解机械臂的关节驱动力矩;最后对比分析浮力、负载重量、负载空间尺寸对机械臂的动力学特性的影响。
1 机械臂的结构设计与三维模型 1.1 机械臂的总体结构设计基于发射管的回收机械臂在待机时能回缩在发射管内,伸展后能完成“抓取-对齐-回收”任务。其中,机械臂待机时的回缩功能可通过改装机械臂的安装平台来实现,但机械臂需要具备折叠功能,并保证折叠后的包络圆直径要小于发射管的管径。总体参数为:折叠后的包络圆直径不大于300 mm,最大伸展长度为2 m,负载为10 kg、长度800 mm的圆柱状负载。
自由度是衡量机械臂运动灵活性的主要技术指标,同时也衡量着机械臂结构的复杂程度[6]。常见的结构紧凑水下机械臂自由度较少,而自由度较多的水下机械臂结构尺寸较大,美国Schilling Robotics公司的Orion4R机械臂(见图1)和Titan4机械臂(见图2)。基于发射管的回收机械臂对灵活性要求较高,需要六自由度来确保能够以多种姿态抓取不同位置的物体并完成回收。另外,由于旋转关节相比移动关节灵活性较高、占地空间较小而且工作空间更大,回收机械臂的6个关节选择旋转关节。根据Pieper法则[7],机械臂相邻的3个关节轴线平行或交于同一点时,机械臂逆运动学有封闭解。因此本文设计的回收机械臂第4、第5和第6关节轴线交于一点。此时机械臂的前3个关节控制末端夹爪的位置;后3个关节控制末端夹爪的姿态,可视为由定位机构和定向机构组成。

|
图 1 Orion4R机械臂 Fig. 1 Orion4R manipulator |

|
图 2 Titan4机械臂 Fig. 2 Titan4 manipulator |
为了实现机械臂能够在发射管内伸缩的功能需求,机械臂采用可折叠方案,以保证机械臂折叠后具有较小的包络圆直径及足够大的臂长。目前主流的折叠结构分为两折叠式和三折叠式,如图3所示。两折叠式机械臂的结构方案伸展距离有限,多数应用于工业、协作等对于工作范围要求不大的场合;三折叠型机械臂有更长的臂展,但在同等的包络圆直径下臂截面较小,承载能力不高。考虑到回收机械臂空间尺寸的限制和承载能力,回收机械臂采用两折叠型,连接臂从常见的圆筒形改为便于折叠的单板结构。

|
图 3 两折叠型与三折叠型机械臂 Fig. 3 Two fold and three fold manipulators |
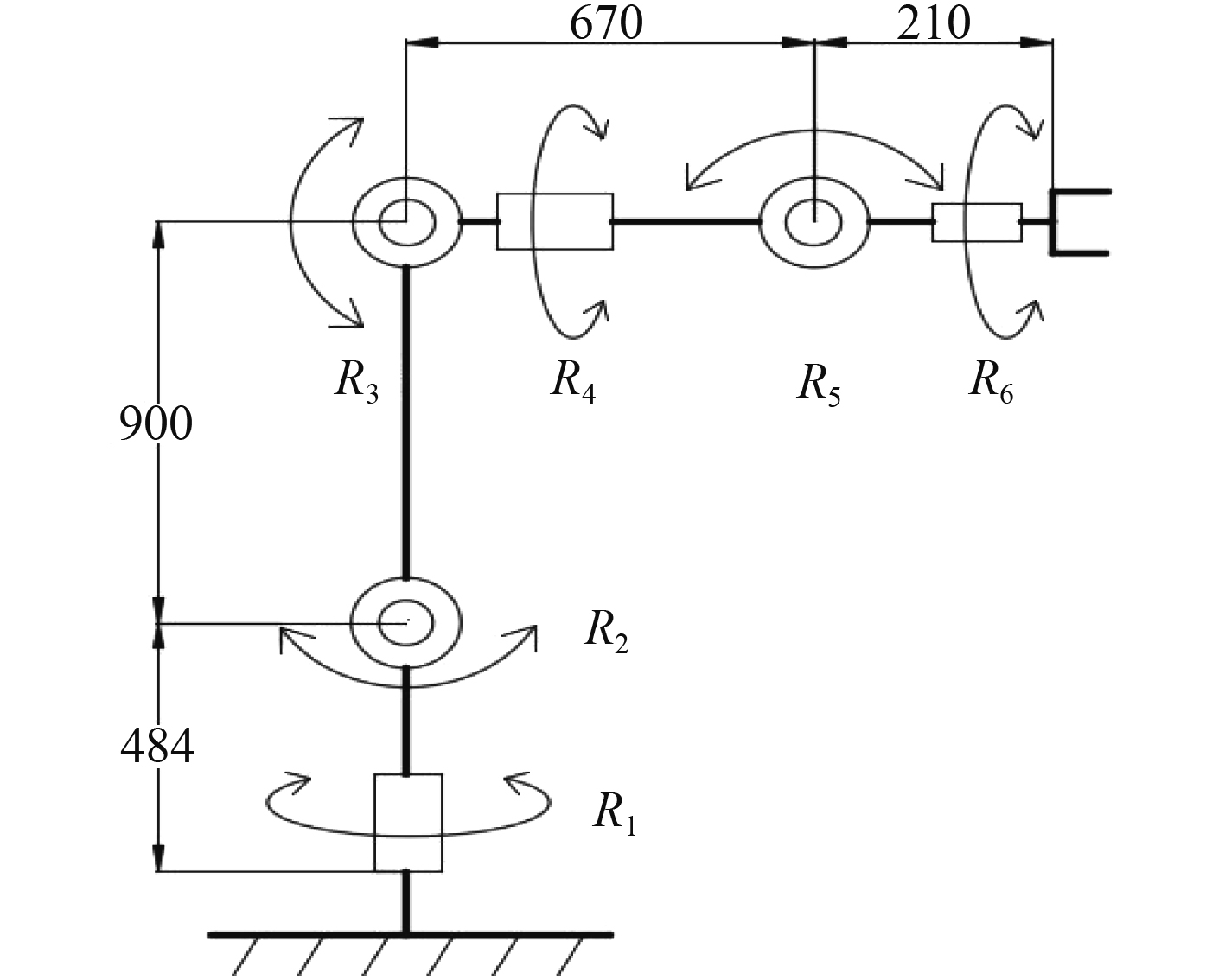
通过分配臂长-驱动校核-改进臂长分配的动态优化过程,确定回收机械臂结构简图如图4所示。选择合适的电机、材料后用Solidworks三维设计软件绘制的三维模型如图5所示。
|
图 4 回收机械臂的结构简图 Fig. 4 Structure diagram of recovery manipulator |

|
图 5 机械臂的虚拟样机模型 Fig. 5 Virtual prototype model of manipulator |
建立三维模型后,利用Solidworks软件中的质量评估功能[8]获取机械臂6个连杆的质量及动力学参数。
质量:46.5 kg,44.9 kg,14.2 kg,5.3 kg,3.5 kg,2.7 kg。
关节坐标系下的连杆质心:
质心坐标系下的惯性张量:
| $\begin{split}&\left[ {\begin{array}{*{20}{c}} {4.4}&0&0 \\ 0&{4.17}&{0.51} \\ 0&{0.51}&{0.37} \end{array}} \right]\quad \left[ {\begin{array}{*{20}{c}} {0.35}&0&{0.37} \\ 0&{5.06}&0 \\ {0.37}&0&{5.04} \end{array}} \right]\text{,}\\ & \left[ {\begin{array}{*{20}{c}} {0.37}&0&0 \\ 0&{0.04}&{ - 0.01} \\ 0&{ - 0.01}&{0.36} \end{array}} \right]\quad \left[ {\begin{array}{*{20}{c}} {0.17}&0&0 \\ 0&{0.17}&0 \\ 0&0&{0.01} \end{array}} \right]\text{,}\\ & \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \\ 0&{0.01}&{ - 0.01} \\ 0&{ - 0.01}&{0.02} \end{array}} \right]\quad \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 0&{0.02}&0 \\ 0&0&0 \end{array}} \right]\text{。}\end{split} $ |
牛顿一欧拉法建立动力学方程原理是在建立连杆间的速度传递关系,得到各旋转关节的角度和角速度后,利用牛顿方程与欧拉方程求解各个连杆的惯性力与惯性力矩(式(1)和式(2)),最后通过连杆质心处的力平衡与力矩平衡方程求解关节的力与力矩。
| $F = m\;\mathop {{v_C}}\limits^ \cdot \text{,}$ | (1) |
| $N = {\;^C}I\;\mathop \omega \limits^ \cdot + \omega \otimes {\;^C}I\;\omega \text{。}$ | (2) |
其中:
为求解连杆质心速度与加速度,根据正运动学建立的连杆间的变换关系,从连杆1到连杆6向外递推:
| $\begin{split} &i = 1 \to 6 \text{,} \\ & ^{i + 1}{\omega _{i + 1}} = {}_i^{i + 1}R{\;^i}{\omega _i} + \mathop {{\theta _{i + 1}}}\limits^ \cdot \;\mathop {{e_3}}\limits^ \to \text{,} \\ & \mathop {^{i + 1}{\omega _{i + 1}}}\limits^ \cdot = {}_i^{i + 1}R{\;^i}\mathop {{\omega _i}}\limits^ \cdot + {}_i^{i + 1}R{\;^i}{\omega _i} \otimes \mathop {{\theta _{i + 1}}}\limits^ \cdot \;\mathop {{e_3}}\limits^ \to + \mathop {{\theta _{i + 1}}}\limits^{ \cdot \cdot } \;\mathop {{e_3}}\limits^ \to \text{,} \\ & ^{i + 1}{v_{i + 1}} = {}_i^{i + 1}R\;{(^i}\mathop {{\omega _i}}\limits^ \cdot \otimes {\;^i}{P_{i + 1}}{ + ^i}{\omega _i} \otimes {(^i}{\omega _i}{ \otimes ^i}{P_{i + 1}}) + \mathop {^i{v_i}}\limits^ \cdot ) \text{,} \\ & \mathop {^{i \!+\! 1}{v_{{C_{i \!+\! 1}}}}}\limits^ \cdot = \mathop {^{i \!+\! 1}{\omega _{i \!+\! 1}}}\limits^ \cdot { \otimes ^{i \!+\! 1}}{P_{{C_{i \!+\! 1}}}}{ \!+\! ^{i + 1}}{\omega _{i \!+\! 1}} \otimes {(^{i \!+\! 1}}{\omega _{i \!+\! 1}}{ \otimes ^{i \!+\! 1}}{P_{{C_{i \!+\! 1}}}}) \!+\! \mathop {^{i \!+\! 1}{v_{i \!+\! 1}}}\limits^ \cdot \text{。} \end{split} $ | (3) |
其中:
通过连杆质心上的力和力矩平衡方程可得:
| $ \begin{split} &^i{f_i} = {}_{i + 1}^iR{\,^{i + 1}}{f_{i + 1}}{ + ^i}{F_{{c_i}}}\text{,}\\ &^i{n_i} = {}_{i + 1}^iR{\;^{i + 1}}{n_{i + 1}}{ + ^i}{N_C}_{_i}{ + ^i}{p_{{C_i}}}{ \otimes ^i}{F_{{C_i}}}{ + ^i}{p_{i + 1}} \otimes {}_{i + 1}^iR{\;^{i + 1}}{f_{i + 1}}\text{。} \end{split}$ | (4) |
其中:
最后,在力和力矩平衡方程式(4)中令
至此,动力学方程的推导已完成。输入机械臂连杆质量、动力学参数(质心、惯性张量)和关节的运动轨迹(角度、角速度、角加速度)即可求解关节驱动力矩。
3 机械臂工作过程的动力学仿真 3.1 回收过程轨迹规划机械臂的轨迹规划分为笛卡尔空间规划与关节空间规划,规划的方法有线性、多项式插值和样条插值等[9]。回收过程属于常规的点到点运动,可采用关节空间轨迹规划;多项式轨迹规划能满足插值结果连续、平滑的要求,同时回收机械臂起点和终点的速度和加速度及路径点都可确定,因此采用七次多项式[10]进行插值。
在七次多项式下,关节角、角速度、角加速度设置如下:
| $\begin{split} & \theta (t) = {c_0} + {c_1}t + {c_2}{t^2} + {c_3}{t^3} + {c_4}{t^4} + {c_5}{t^5} + {c_6}{t^6} + {c_7}{t^7} \text{,} \\ & \mathop \theta \limits^ \cdot (t) = {c_1} + 2{c_2}t + 3{c_3}{t^2} + 4{c_4}{t^3} + 5{c_5}{t^4} + 6{c_6}{t^5} + 7{c_7}{t^6} \text{,} \\ &\mathop \theta \limits^{ \cdot \cdot } (t)\! = \!2{c_2} + 6{c_3}t\! +\! 12{c_4}{t^2}\! +\! 20{c_5}{t^3}\! +\! 30{c_6}{t^4} \!+\! 42{c_7}{t^5} \text{。} \end{split} $ | (5) |
七次多项式的工作轨迹有8个系数,需要8组方程来确定。在确定回收机械臂起点
| $\left[\!\!\! {\begin{array}{*{20}{c}} {{\theta _0}} \\ {\mathop {{\theta _0}}\limits^ \cdot } \\ {\mathop {{\theta _0}}\limits^{ \cdot \cdot } } \\ {{\theta _1}} \\ {{\theta _2}} \\ {{\theta _m}} \\ {\mathop {{\theta _m}}\limits^ \cdot } \\ {\mathop {{\theta _m}}\limits^{ \cdot \cdot } } \end{array}} \!\!\!\right] \!=\! \left[\!\!\! {\begin{array}{*{20}{c}} 1\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0 \\ 0\!\!&\!\!1\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0 \\ 0\!\!&\!\!0\!\!&\!\!2\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0 \\ 1\!\!&\!\!{{t_1}}\!\!&\!\!{t_1^2}\!\!&\!\!{t_1^3}\!\!&\!\!{t_1^4}\!\!&\!\!{t_1^5}\!\!&\!\!{t_1^6}\!\!&\!\!{t_1^7} \\ 1\!\!&\!\!{{t_2}}\!\!&\!\!{t_2^2}\!\!&\!\!{t_2^3}\!\!&\!\!{t_2^4}\!\!&\!\!{t_2^5}\!\!&\!\!{t_2^6}\!\!&\!\!{t_2^7} \\ 1\!\!&\!\!{{t_m}}\!\!&\!\!{t_m^2}\!\!&\!\!{t_m^3}\!\!&\!\!{t_m^4}\!\!&\!\!{t_m^5}\!\!&\!\!{t_m^6}\!\!&\!\!{t_m^7} \\ 0\!\!&\!\!1\!\!&\!\!{2{t_m}}\!\!&\!\!{3t_m^2}\!\!&\!\!{4t_m^3}\!\!&\!\!{5t_m^4}\!\!&\!\!{6t_m^5}\!\!&\!\!{7t_m^6} \\ 0\!\!&\!\!0\!\!&\!\!2\!\!&\!\!{6{t_m}}\!\!&\!\!{12t_m^2}\!\!&\!\!{20t_m^3}\!\!&\!\!{30t_m^4}\!\!&\!\!{42t_m^5} \end{array}} \!\!\!\right]{\kern 1pt} \,\left[ \begin{gathered} {c_0} \\ {c_1} \\ {c_2} \\ {c_3} \\ {c_4} \\ {c_5} \\ {c_6} \\ {c_7} \\ \end{gathered} \right]\text{,}$ | (6) |
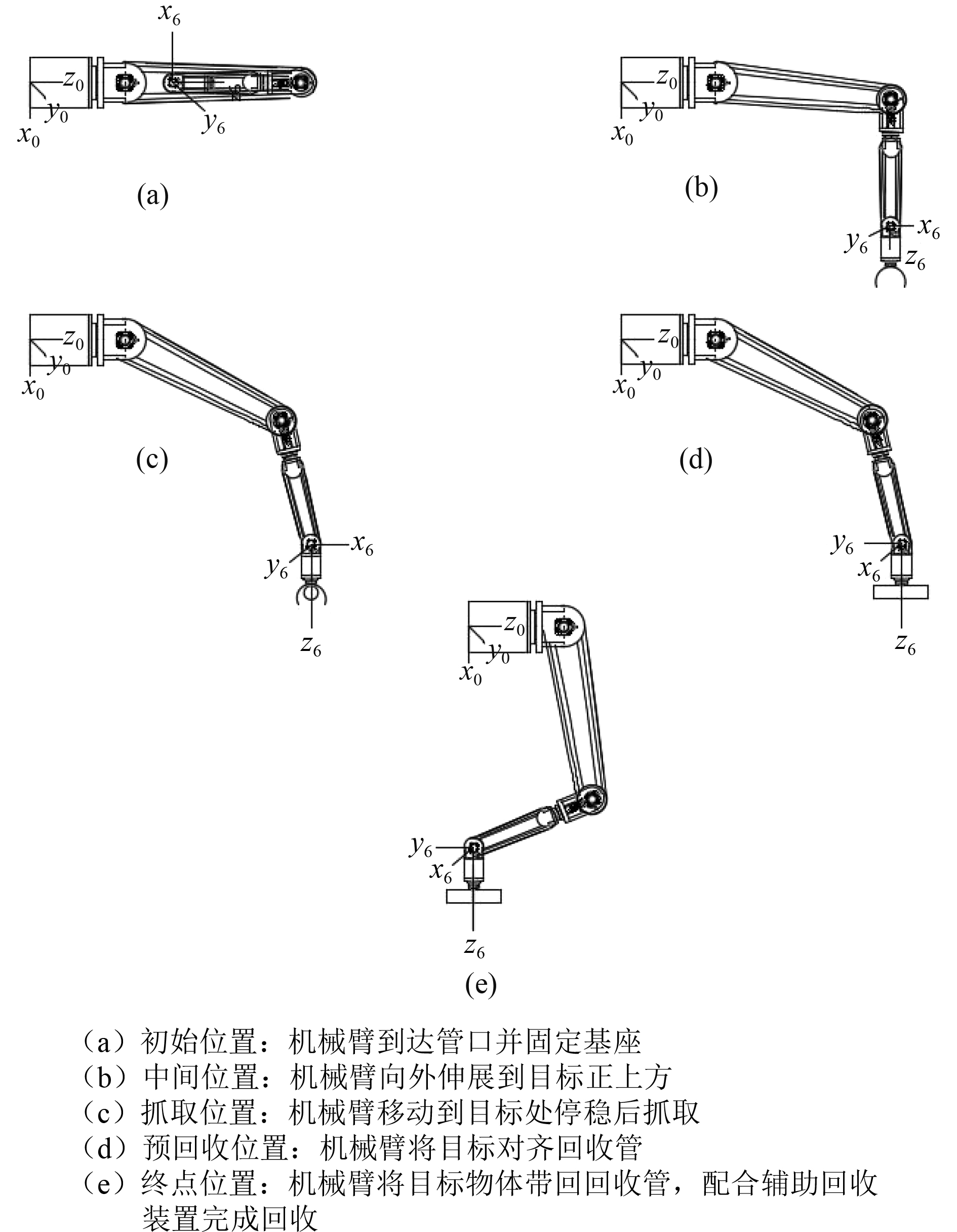
回收机械臂的工作过程如图6所示。
|
图 6 机械臂回收过程 Fig. 6 End pose at intermediate point |
根据末端坐标系与基坐标系的关系确定各路径点的位姿矩阵,并由逆运动学方程转化关节角,选取关节角最接近的一组解,结果如表1所示。
|
|
表 1 各路径点关节角 Tab.1 Joint angle of each path point |
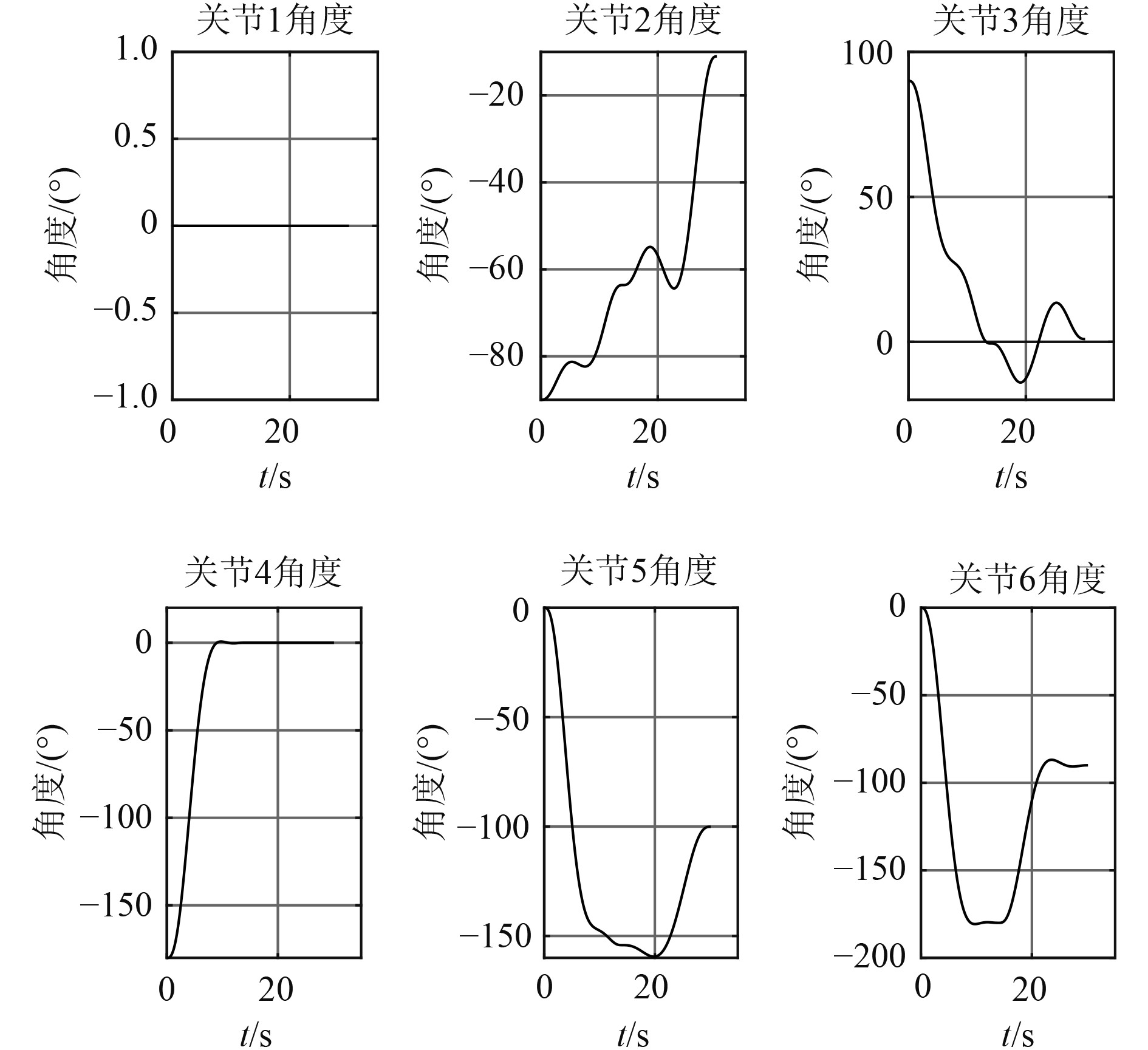
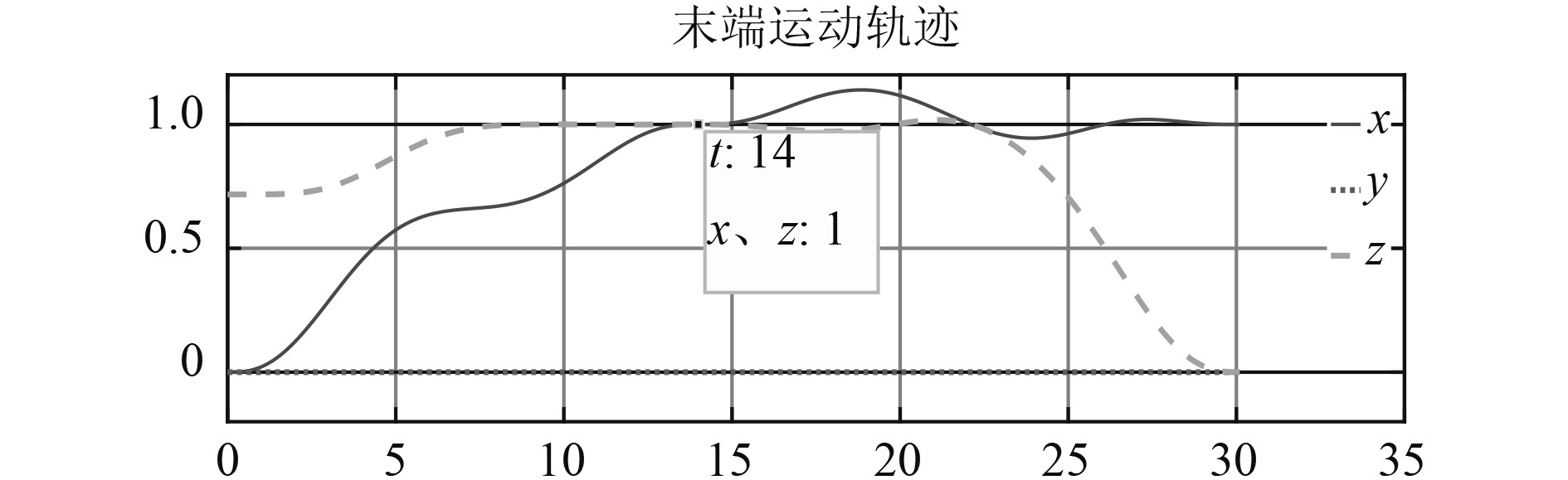
舰艇在回收水面或水下目标时,往往处于超低速或静止状态,因此在仿真时不考虑舰艇运动的影响。本次仿真设定目标回收物位于机械臂基坐标系右方1 m、下方1.2 m处;回收管轴线在基坐标系下方1 m处,管口与机械臂底座对齐。由于机械臂在回收过程的起点、抓取点及终点处均为静止状态,分别对抓取过程(a)~(c)和回收过程(d)~(e)的工作轨迹进行规划。设定起点和终点角速度、角加速度分别为0 m/s和0 m/s2,抓取过程和回收过程的运动时间分别为14 s和16 s,采用七次多项式插值后得到的各关节角度、末端运动轨迹和关节角速度如图7~图9所示。
|
图 7 回收过程中各关节的角度变化曲线 Fig. 7 The angle curve of each joint |
|
图 8 回收过程中末端运动轨迹 Fig. 8 The trajectory of the end in the recycling process |
|
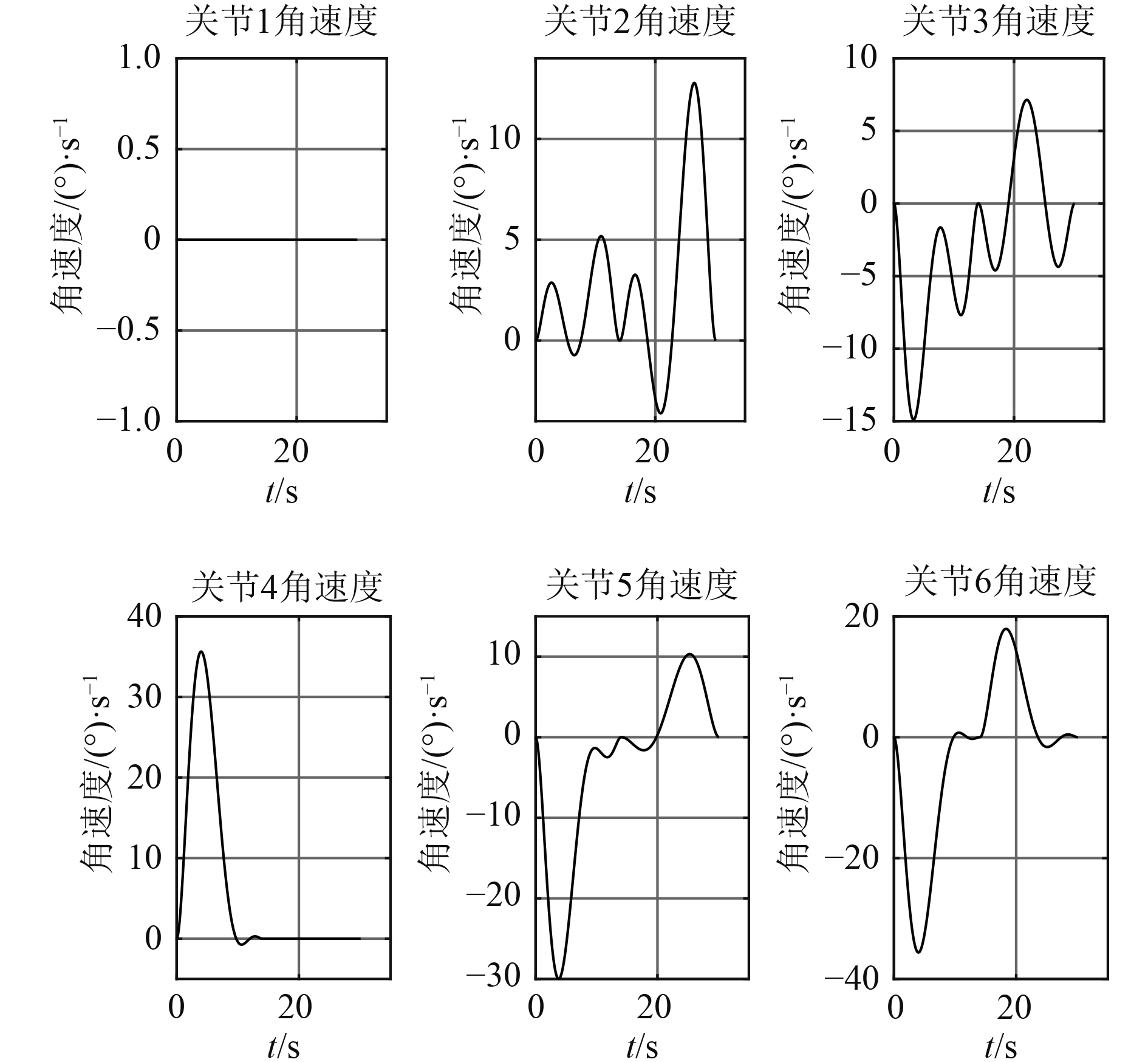
图 9 回收过程中各关节的角速度变化曲线 Fig. 9 Angular velocity curve of each joint |
轨迹规划的结果显示,机械臂在0 s时处于折叠状态;在0~14 s期间伸展并运动到目标物处。在14 s时,机械臂的角速度及角加速度都为零,说明机械臂已停稳在目标物处。14~30 s期间机械臂重新启动,开始抓取目标物、完成目标物轴线与回收管道轴线对齐并移动到回收点处的任务。机械臂在工作过程中角度的变化曲线平滑无断点,角速度无突变情况,运动的稳定性基本满足要求。
3.2 动力学方程的求解在得到机械臂的运动规律后,结合获取的动力学参数,通过建立的动力学方程即可求解关节实时力矩。下面分别将浮力、目标负载的重量和空间尺寸作为变量进行动力学仿真,分析其对回收机械臂动力学特性的影响。
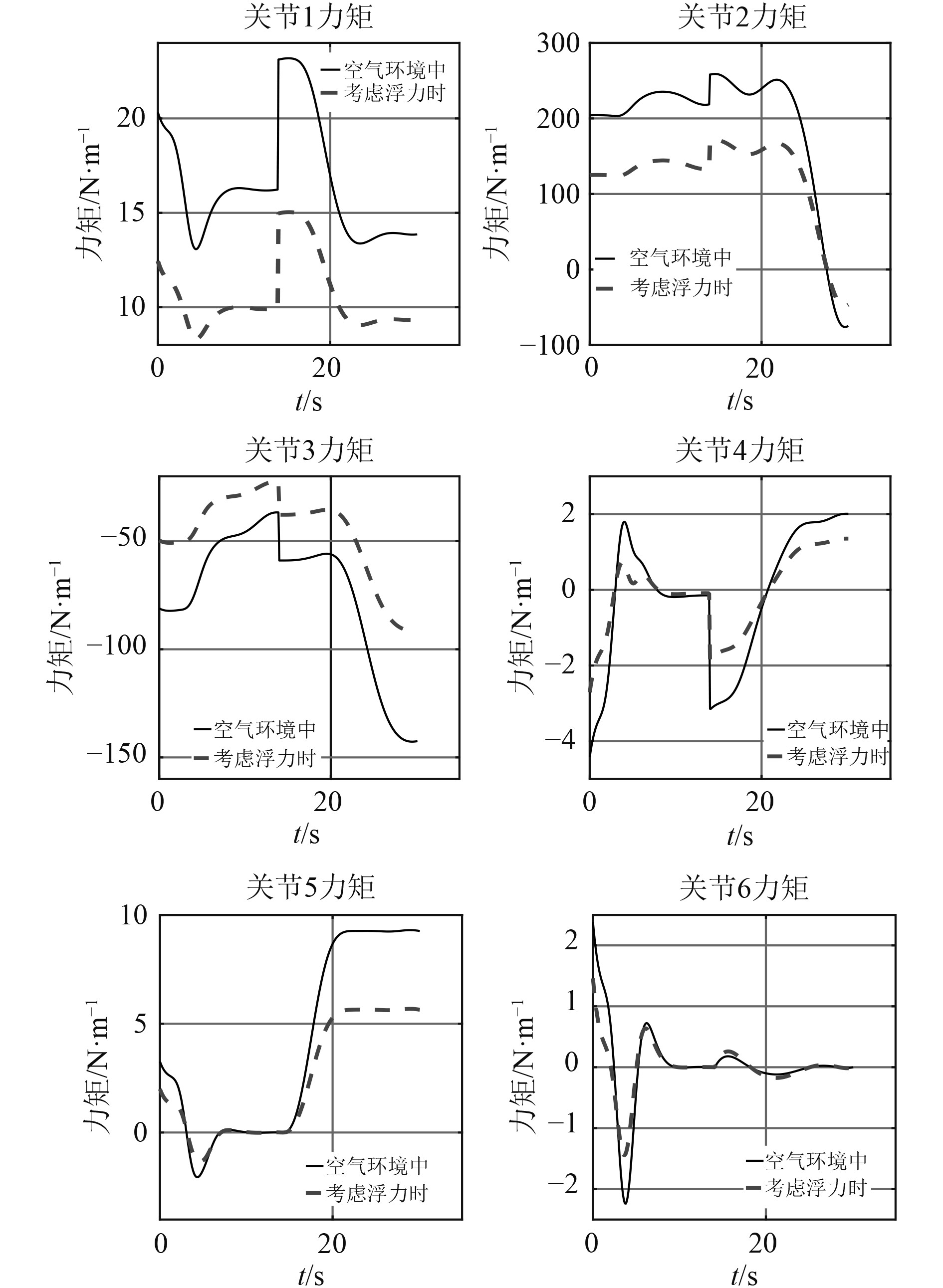
在考虑重力因素时,设定回收机械臂基坐标系{0}处的质心加速度g=9.8 m/s2,这等价于机械臂以加速度9.8 m/s2向上做加速运动,这个假想的加速度与重力作用在连杆上的效果相同。另外,在同时考虑重力与浮力因素时,根据回收机械臂与水的密度比,设定基坐标系质心加速度g1=6.6 m/s2,求解结果如图10所示。
|
图 10 考虑浮力下的力矩对比曲线 Fig. 10 Driving torque curve considering buoyancy |
从图10可看出,在考虑浮力时关节所需的驱动力矩较小,这是因为浮力抵消了回收机械臂部分重量,减小了关节处的重力力矩。浮力对关节力矩的影响较大。例如在0 s时,浮力可减小关节2约40%驱动力矩。
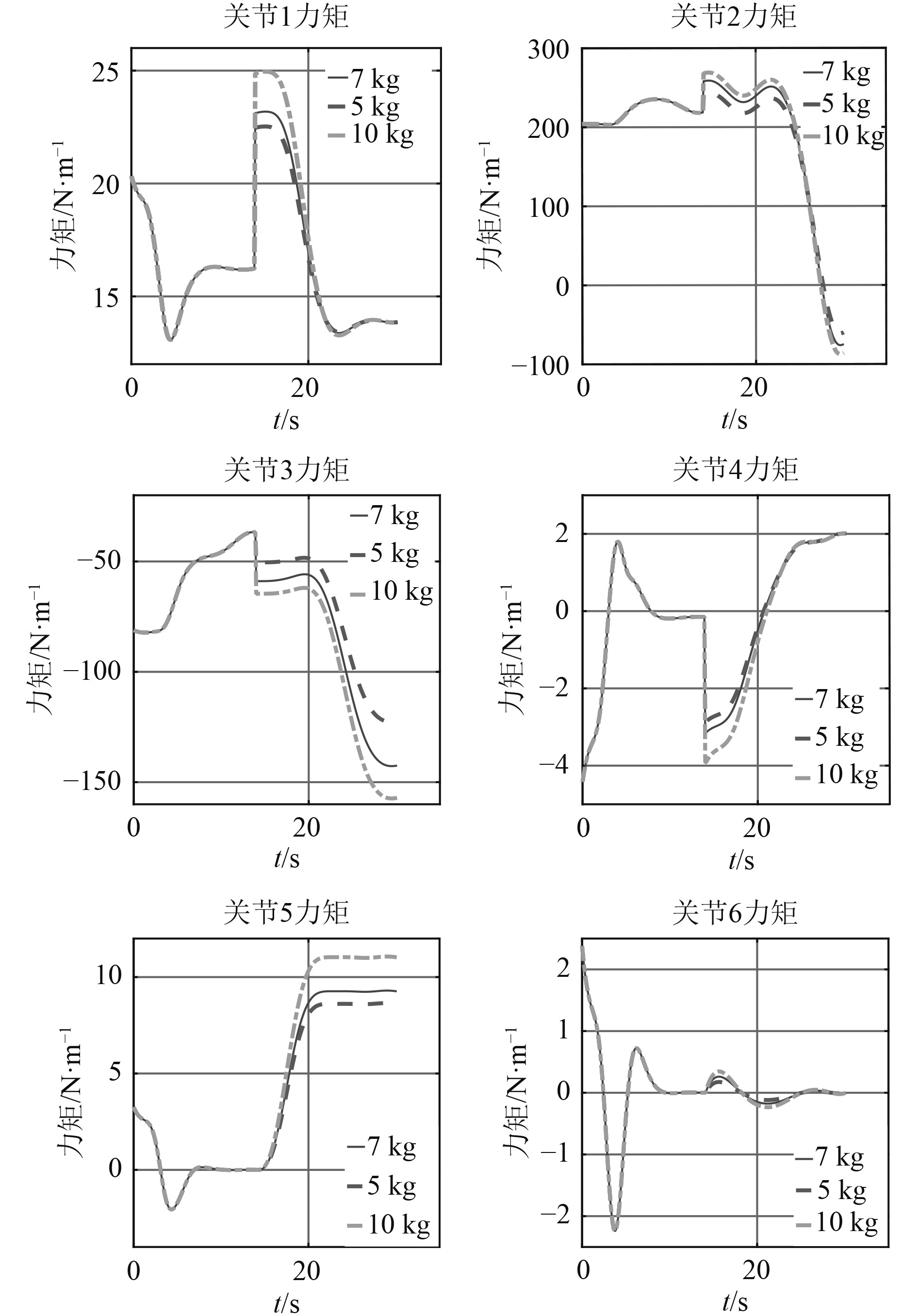
此外,分别在5 kg,7 kg,10 kg的负载重量下按照相同的运动轨迹进行回收机械臂动力学的求解,结果对比如图11所示。
|
图 11 不同负载重量下的力矩对比曲线 Fig. 11 Driving torque curve considering load |
从图11可看出,回收机械臂在14 s时抓取回收物,因此在14 s前各个重量下的力矩曲线相同。负载的重量与关节所需驱动力矩呈正相关关系,负载重量越大,关节所需驱动力矩越大,负载重量不影响关节力矩曲线的趋势。
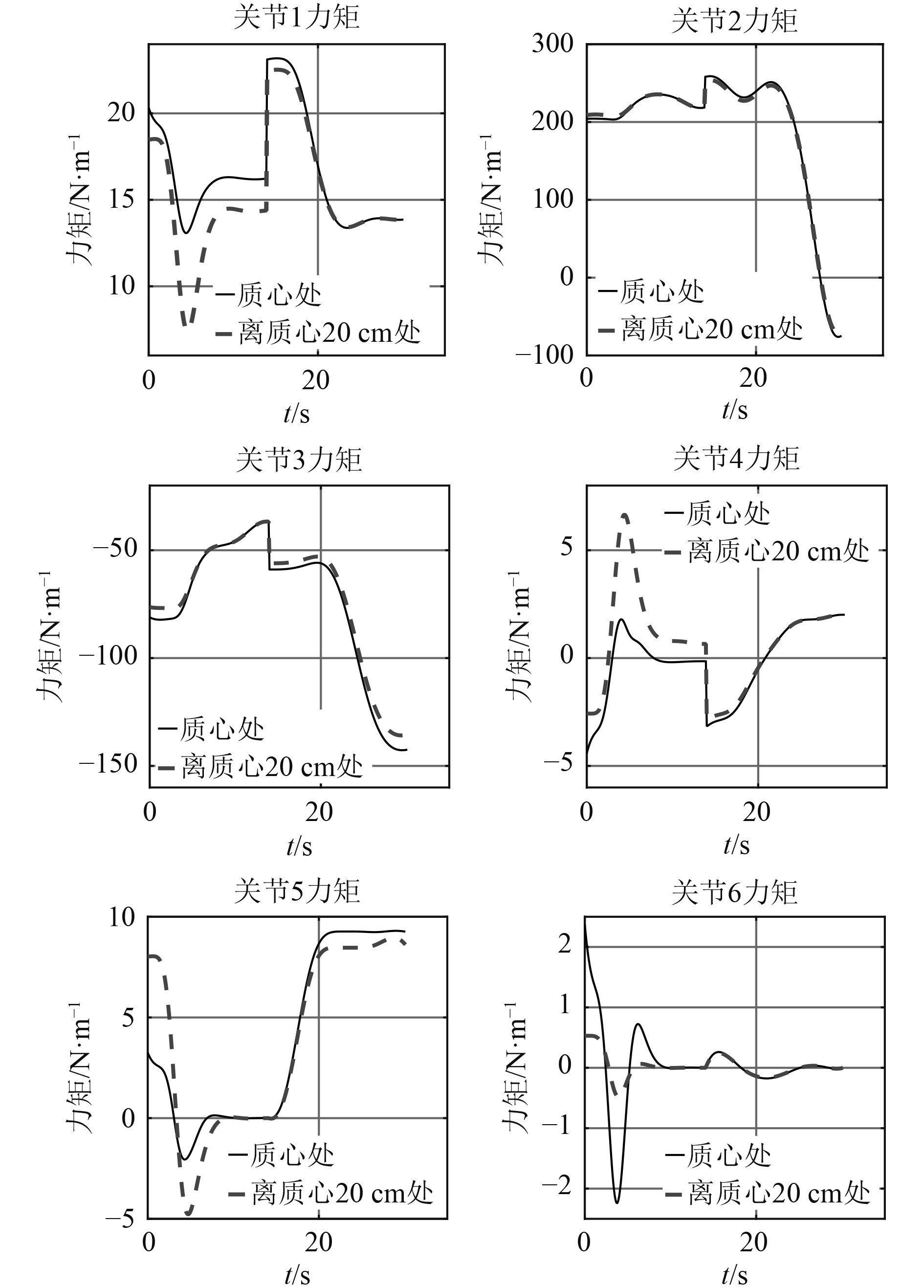
为研究不同尺寸的回收物对驱动力矩的影响,现假设手爪夹在离质心20 cm,此时产生的额外力矩为2 N/m,绕x轴顺时针转动。计算关节力矩时,需在牛顿-欧拉法中“内推”部分末端连杆的力矩平衡中加上额外力矩再进行迭代,得到的关节力矩对比曲线如图12所示。
|
图 12 考虑夹持位置下的力矩对比曲线 Fig. 12 Driving torque curve considering load size |
在14 s时回收机械臂夹取负载时姿态如图13所示,此时额外力矩与关节2、关节3和关节6的旋转平面垂直,关节1和关节4的旋转平面与额外力矩不垂直。因此关节1和关节4的力矩曲线在14 s时的力矩不同,关节2、关节3和关节6的力矩曲线在14 s时相同。
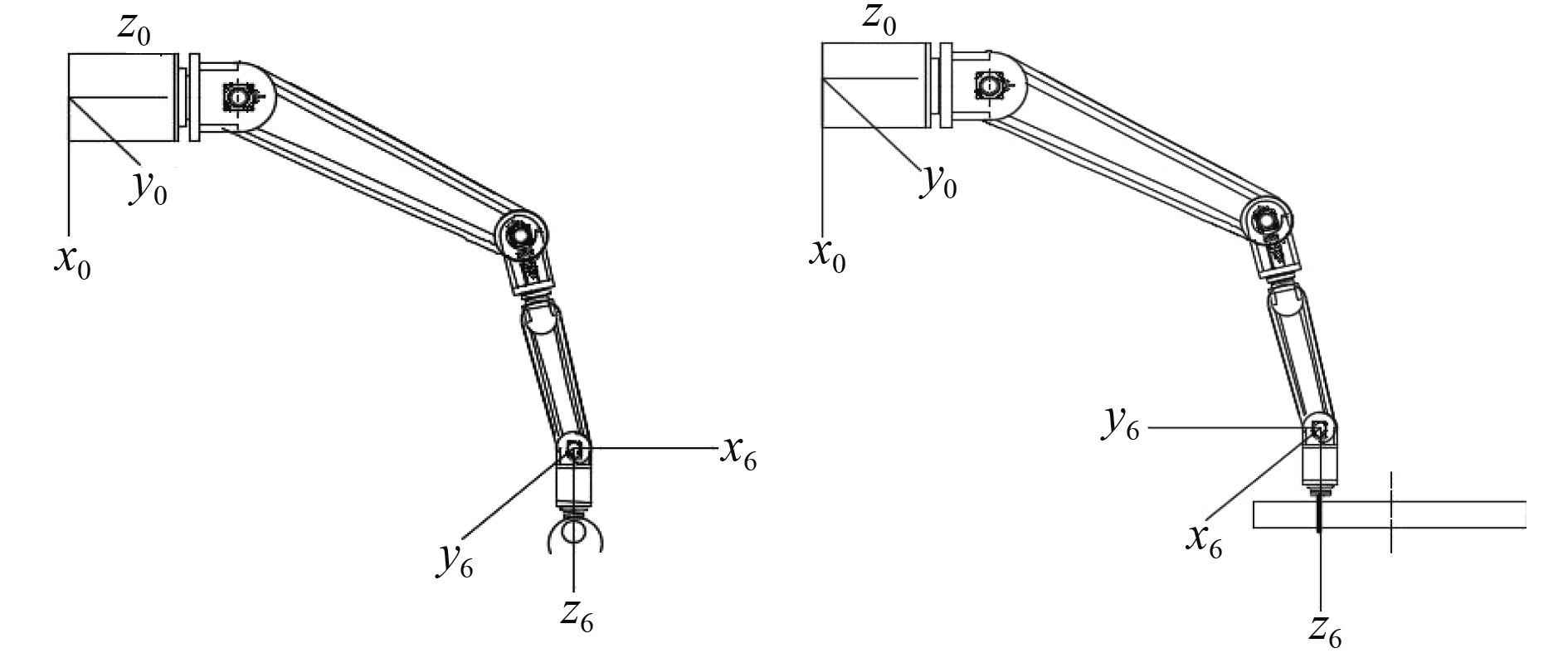
|
图 13 机械臂在抓取和回收时的姿态 Fig. 13 manipulator attitude in grasping and retrieving |
在14 s后,回收机械臂夹取负载并进行姿态变换,将负载轴线与回收管的轴线对齐。此时不同夹持位置产生的额外力矩与关节1、关节4和关节6的旋转平面垂直,与关节2、关节3和关节5的旋转平面不垂直。因此夹持位置对于关节1和关节4的影响逐渐减小;对关节2、关节3和关节5的影响逐渐增大。由于6号回转关节与柱状负载的轴线相垂直,因此夹持位置对6号回转关节的驱动力矩无影响。
4 结 语本文建立了基于发射管的回收机械臂三维模型,完成了回收轨迹规划与动力学仿真。轨迹规划结果表明回收机械臂能灵活完成打捞回收的动作;动力学仿真结果表明回收机械臂能抓取回收规定的负载,且浮力、负载的重量和空间尺寸均对关节驱动力矩有一定影响,在进行动力学分析时不可忽视。
本文进行的动力学仿真为后续驱动校核与控制系统设计等工作提供一定的参考。研究中,回收机械臂在水中运动时水动力仅考虑了浮力因素,且动力学参数由三维模型设计软件计算得到,没有考虑关节摩擦和弹性以及实际加工装配误差等因素,因此仿真结果与真实应用情况存在一定差异。下一步需要进行动力学参数辨识,并加入水阻力、附加质量力等因素,提高动力学仿真的精度。
| [1] |
杨迪. 潜艇布放与回收UUV时的水动力性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [2] |
V G PRATHEEP, M CHINNATHAMBI, E B PRIYANKA, et al. Design and analysis of six DOF robotic manipulator[J]. IOP Conference Series: Materials Science and Engineering, 2021, 1055(1). DOI:10.1088/1757-899X/1055/1/012005 |
| [3] |
袁凯. 水下电动机械臂设计及运动控制方法研究[D]. 济南: 山东大学, 2020.
|
| [4] |
鲍维俊. 水下液压机械手设计与分析[D]. 杭州: 杭州电子科技大学, 2016.
|
| [5] |
王懿, 张爱霞, 郭瑞岩, 等. 六自由度水下机械臂动力学模型及流阻影响研究[J]. 北京理工大学学报, 2020, 40(11): 1143-1149. |
| [6] |
陈赛旋. 协作机器人零力控制与碰撞检测技术研究[D]. 合肥: 中国科学技术大学, 2018.
|
| [7] |
PIEPER D, ROTH B. The kinematics of manipulators under computer control[C]//Proceedings of the Second In-ternational Congress on Theory of Machines and Mechanisms, Zakopane, Poland, 1969, 2: 159−169.
|
| [8] |
郭锐. 六自由度水下机械臂系统设计及试验[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [9] |
Introduction to robotics: Mechanics and control: John J. Craig[J]. Automatica, 1987, 23(2): 263−264.
|
| [10] |
姜立. 多关节机器人运动学与轨迹规划及仿真研究[D]. 长春: 吉林大学, 2016.
|
 2021, Vol. 43
2021, Vol. 43
