船舶液位监控系统是实现船舶自动化的一个重要系统,关系到船舶在装卸货及航行中的安全问题。船舶在装卸货物的过程中,船体会发生一定程度的倾斜,为了保证船舶的平衡,需要对压载水舱内的液位进行调节。工作人员根据压载水舱的液位以及船舶的吃水状态计算出相应的配载,手动控制或者自动控制压载水泵和阀门的开启状态,对压载舱进行压水和排水[1]。液位监控系统自动化的应用节省了劳动力,提高了船员操作效率。高精度的液位监测系统则是船舶装卸和航行安全的重要保证。因此,液位监测系统的首要问题是如何使测量的液位更精确、更可靠。
在液位监测的过程中,由于环境的不确定因素干扰以及单传感器自身的局限性,使得测量的液位值往往不完整或带有较大的不确定性,甚至含有异常噪声点。针对液位测量的误差,本文提出一种基于卡尔曼滤波的多传感器融合算法,对液位测量值进行滤波,提高液位测量的精度,获得了稳定可靠的输出值。
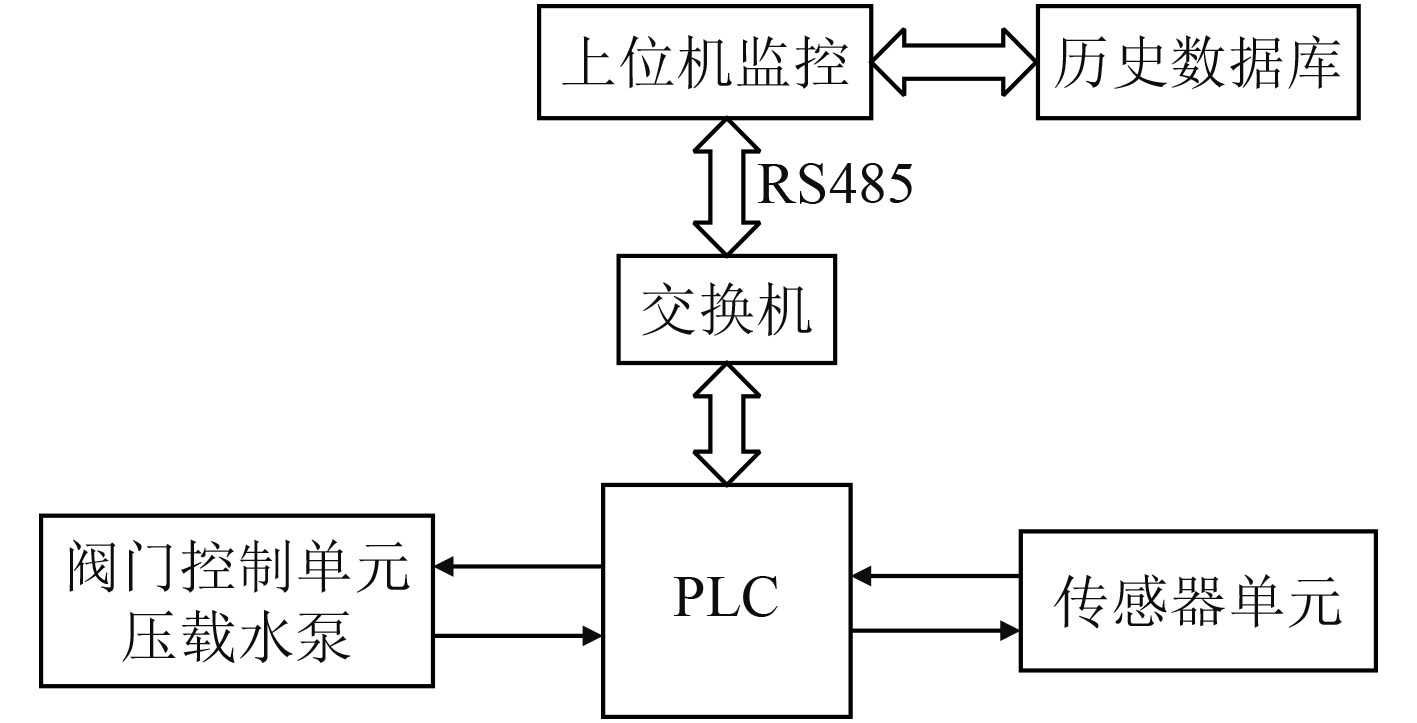
1 液位监控系统 1.1 液位监控系统的结构船舶液位监控系统主要由信号采集单元、下位机PLC、阀门控制单元、上位机监控软件以及历史数据库组成。信号采集单元中的传感器用于对舱内液位、吃水深度、压力、温度等参数进行采集。本系统的PLC选用西门子S7-1200,用于对多个传感器采集的信号进行运算处理,根据不同的数据类型输出相应的信号。阀门控制单元根据PLC发出的命令,由阀门和压载泵完成对应的动作。上位机选用组态王6.55进行开发,采用TCP/IP协议通过交换机与下位机进行通讯,并动态监控整个系统。历史数据库由MySQL数据库设计开发,采用ODBC协议与上位机连接。图1为系统的结构图。
|
图 1 液位监控系统结构简图 Fig. 1 Structure diagram of liquid level monitoring system |
船舶液位监控系统实时监测各压载舱内液位的高度以及吃水深度,通过监测舱内液位的变化从而调控压载系统的进排水量。因此,只有保证船舶吃水和压载舱内液位等参数的精度及可靠,才能确保船舶实现准确、安全及平稳的控制。
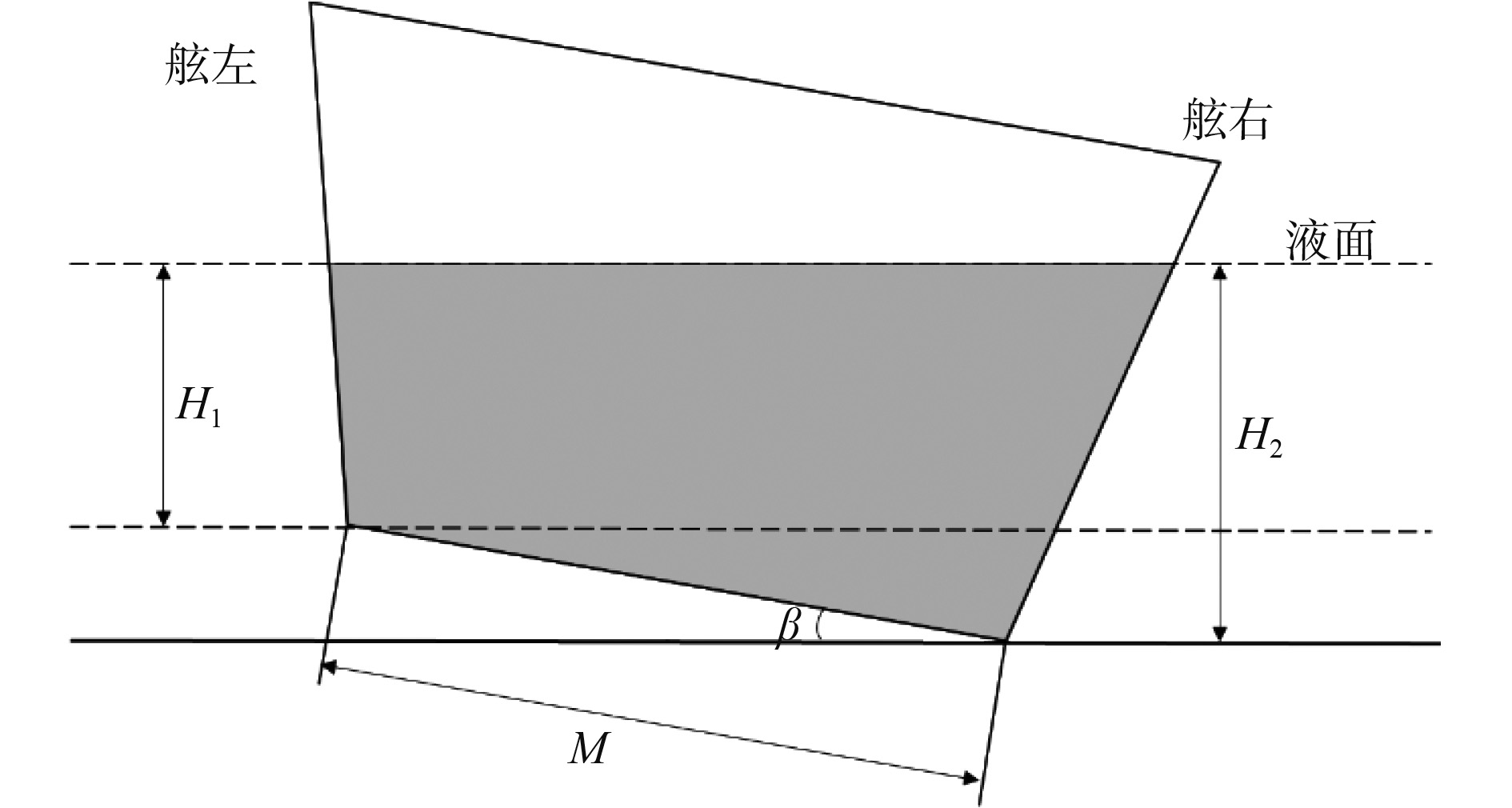
船舶吃水测量的方法由传感器的安装方位决定。本文采用六角吃水测量法,将传感器分别安装在船舶左右两舷的首中尾6个角,左右吃水的测量由安装在船舯左右舷底部压载舱底的传感器测得,首尾吃水的测量由安装在首尖舱和隔离空舱底的传感器测得[2]。船舶的横倾角通过船左右吃水差得出,方法如图2所示。
|
图 2 船舯左右吃水横倾角计算 Fig. 2 Calculation of the yaw angle around the ship |
图中
| $\beta = \arcsin \left( {\frac{{\left| {{H_2} - {H_1}} \right|}}{M}} \right)\text{。}$ | (1) |
船舶纵倾角度的计算方法同理。从上述公式可看出船舶横纵倾角度计算的真实值取决于船舷吃水测量的精度。
2 液位监测的误差分析船舶液位监测过程中,对液位的测量会不可避免地出现误差,改进测量方法消除误差则是液位监测系统中重要的一环。对测得的数据比较分析后发现,液位测量误差的来源有2个方面,一是传感器设备产生的误差,二是测量环境的不确定因素带来的误差。
传感器在传感器单元中,受到供电电路的电磁、电缆信号等干扰,可能会产生静态性偏差、零点漂移及灵敏度漂移等问题,因而传感器的初始标定值存在一定的误差,需要对传感器进行预处理,作二次标定以补偿其新增不确定度[3]。
2.1 传感器标定针对液位传感器的预处理流程如图3所示,包括标定、转换、分值滤波和微值滤波几个过程。

|
图 3 数据的预处理过程 Fig. 3 Data preprocessing |
图中
对传感器在不同情况下测得的几组数据进行标定[4]。在实验水舱中,采用雷达液位计对0.5 m高的液位进行测量,其电流输出值为5 mA;对0.8 m高的液位进行测量,输出值为5.6 mA。标定公式如下式:
| $Cv{S_n} = \frac{1}{2}{X_{IN}} - 2\text{。}$ | (2) |
对标定后的转换值
通过对传感器进行预处理,可将测量误差降至最低,也能减少部分测量过程中的随机误差,且对传感器输出值进行标定,也能及时检测传感器故障,提高传感器测量输出数据的可靠性。
2.2 波动液位的卡尔曼滤波环境的因素则是由于船舶受到风浪的干扰以及在装卸货物时船体的倾斜导致液面的波动幅度较大,使得测得的误差较大。
考虑到液面的波动是无法避免的,因此,需要对测得的液位信号进行滤波,将影响液位监测的液面波动、观测噪声等滤除,实时获得精确可靠的液位监测。在中央处理单元采用滤波程序对采集的数据进行处理,本文采用卡尔曼滤波器对传感器测量结果进行滤波,卡尔曼滤波是基于贝叶斯定理,利用递归迭代进行滤波的方法,主要用来预测和更新。
由卡尔曼滤波原理,随机线性离散系统的方程为:
| $x(k + 1) = { A}x(k) + \Gamma w(k)\text{,}$ | (3) |
| $y(k) = { H}x(k) + v(k)\text{。}$ | (4) |
式中:
压载系统对舱内液位高度进行调节,操控压载泵和阀门对水舱内进水,记采样时间为
| $s(k + 1) = s(k) + \dot s(k){t_0} + 0.5{t_0}^2a(k)\text{,}$ | (5) |
| $\dot s(k + 1) = \dot s(k) + {t_0}a(k)\text{,}$ | (6) |
定义在采样时刻
| $\left[ {\begin{array}{*{20}{c}} {s(k + 1)} \\ {\dot s(k + 1)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{{t_0}} \\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {s(k)} \\ {\dot s(k)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {0.5{t_0}^2} \\ {{t_0}} \end{array}} \right]w(k)\text{,}$ | (7) |
观测方程为:
| $y(k) = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {s(k)} \\ {\dot s(k)} \end{array}} \right] + v(k)\text{。}$ | (8) |
式中:
液位的预测过程为:
| $\hat X(k + 1|k) = { A}\hat X(k|k)\text{,}$ | (9) |
| $P(k + 1|k) = { A}P(k|k){{ A}^{\rm T}} + \varGamma Q{\varGamma ^{\rm T}}\text{。}$ | (10) |
根据液位的预测方程,将液位的初始状态以及初始协方差输入卡尔曼滤波器后,可不断得到液位变化的真实值,滤波效果理想[7]。
虽然传感器测得的液位高度经过卡尔曼滤波后能够得到一个较为稳定、精确的值,但在实际船舶液位监测的过程中,传感器测得的液位数据在传输交换过程中不仅有可能出现时滞,且单个传感器在液位测量的过程中可能会出现故障或者受到干扰导致得到的液位测量值与真实值相差较大。因而在本实验系统中需采用多传感器测量液位[8],以减少信息处理过程中可能出现的偏差,提高液位估计精度,在对舱内液位建模时还需将液位监测系统作为时滞系统进行处理。
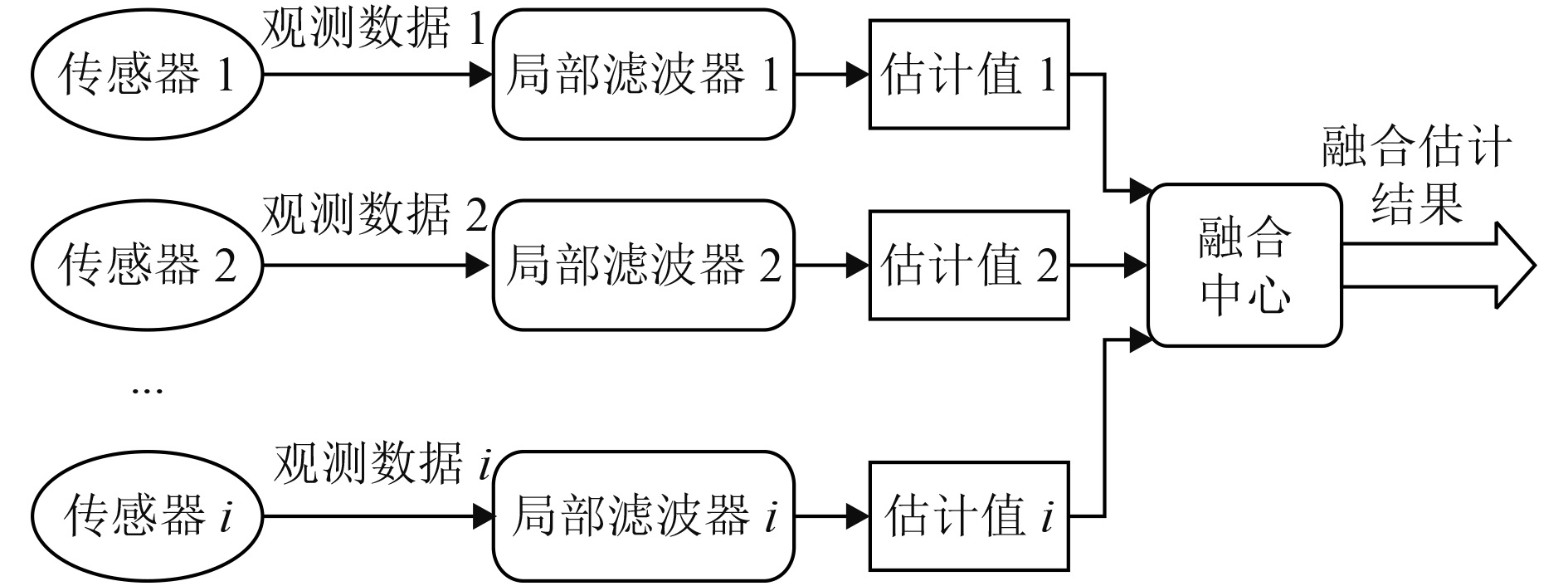
3 液位监测系统中的多传感器融合算法多传感器融合算法作为智能测量的关键技术之一,其融合方式有多种,本文采用分布式融合算法,如图4所示。首先单个传感器测得的数据经过局部滤波器进行处理,得出各个传感器的状态估计值,然后采用最小二乘估计对估计状态进行融合。分布式融合估计改变了全局最优估计的数据处理结构,将整个系统分成几个小系统进行处理,提高了计算机实时并行处理速度[9]。
|
图 4 分布式融合算法结构图 Fig. 4 Structure diagram of distributed fusion algorithm |
考虑传感器测量的液位值在观测中存在一步随机时滞的非理想情况[10],多传感器线性离散系统模型如下:
| $x(k + 1) = Ax(k - r) + w(k)\text{,}$ | (11) |
| $ {y}_{i}(k)={h}_{i}(k)x(k)+{v}_{i}(k),i=1,2,\cdots ,L\text{。}$ | (12) |
式中:
采用二维随机变量
| $P({\varepsilon _{ki}} = 1) = E\left[ {{\varepsilon _{ki}}} \right] = {p_k}\text{,}$ | (13) |
| $P({\varepsilon _{ki}} = 1) = 1 - E\left[ {{\varepsilon _{ki}}} \right] = 1 - {p_k}\text{,}$ | (14) |
假设系统状态
对系统状态扩展,状态扩展形式:
| $X(k + 1) = { A}X(K) + { \varGamma} (K)w(k)\text{,}$ | (15) |
| ${y_i}(k) = {{ H}_i}X(k) + {v_i}(k)\text{。}$ | (16) |
式中:
卡尔曼滤波的过程主要为预测与更新,在
1)第
预测过程:
| ${\hat X_i}(k + 1|k) = { A}{\hat X_i}(k|k)\text{,}$ | (17) |
| ${P_{ii}}(k + 1|k) = { A}{P_{ii}}(k|k){{ A}^{\rm T}} + { \varGamma} Q{{ \varGamma} ^{\rm T}}\text{,}$ | (18) |
卡尔曼增益:
| ${K_i} = {P_{ii}}(k + 1|k){H_i}^{\rm T}{\left[ {{H_i}{P_{ii}}(k + 1|k){H_i}^{\rm T} + {R_i}} \right]^{ - 1}}\text{,}$ | (19) |
新息:
| $e = {y_i}(t) - {H_i}{\hat X_i}(k + 1|k)\text{,}$ | (20) |
更新过程:
| ${\hat X_i}(k + 1|k + 1) = {\hat X_i}(k + 1|k) + {\varepsilon _{ki}}{K_i}e\text{,}$ | (21) |
| ${P_{ii}}(k + 1|k + 1) = {P_{ii}}(k + 1|k) - {\varepsilon _{ki}}{K_i}{H_i}{P_{ii}}(k + 1|k)\text{。}$ | (22) |
2)任意2个传感器之间的估计误差互协方差
预测互协方差:
| ${P_{ij}}(k + 1|k) = { A}{P_{ij}}(k|k){{ A}^{\rm T}} + { \varGamma} Q{{ \varGamma} ^{\rm T}}\text{,}$ | (23) |
更新互协方差:
| ${P_{ij}}(k + 1|k + 1) = ({ I} - {\varepsilon _{ki}}{K_i}{H_i}){P_{ij}}(k + 1|k){({ I} - {\varepsilon _{kj}}{K_j}{H_j})^{\rm T}}\text{。}$ | (24) |
式中:
3)多传感器分布式加权最优融合估计
矩阵加权最优融合估计值
| ${\hat X_0}(k|k) = \sum\nolimits_{i = 1}^l {{a_i}} (k){\hat X_i}(k|k)\text{,}$ | (25) |
式中,
| $\left[ {{a_1}(k), \cdots ,{a_L}(k)} \right] = {({e^{\rm T}}{P^{ - 1}}(k|k)e)^{ - 1}}{e^{\rm T}}{P^{ - 1}}(k|k)\text{,}$ | (26) |
| ${ P}(k|k) = {({P_{ij}}(k|k))_{nL * nL}}\text{。}$ | (27) |
式中:
最优融合误差阵:
| ${P_0}(k|k) = {({e^{\rm T}}{P^{ - 1}}(k|k)e)^{ - 1}}\text{。}$ | (28) |
在实验中将液位的初始高度以及液位变化的初始速度赋值给初始状态,给出估算的初始协方差,输入并启动最优卡尔曼滤波器即可得到稳定且精确的真实液位值[13]。
4 实验仿真及结果分析在实验室内模拟船舶的压载舱设计实验水舱,实现液位监测系统的功能并采集水舱进出水时液位的数据,进行算法处理,输出液位的精确值[14]。船舶装卸货物时,压载舱根据船舶的倾斜角度调节相应压载舱的舱内液位。在本文实验中,将调节压载水前的液位高度作为初始高度值,将水泵抽水的速率转换成液位上升高速度。对一侧水舱内的液位的测量采用2个雷达液位计进行观测,在水舱晃动的情况下分别做进水处理和无进出水处理。
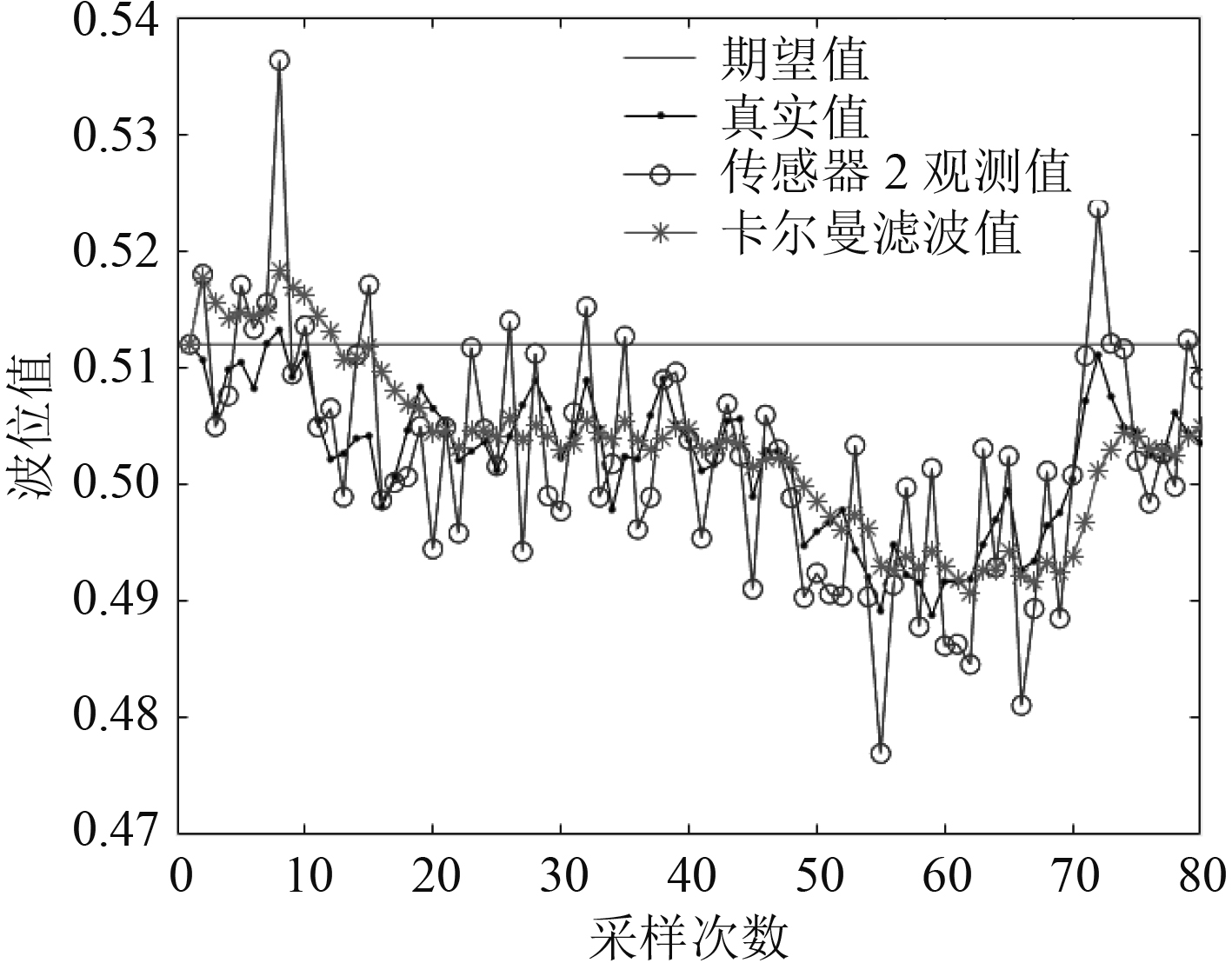
在Matlab中进行仿真,首先在实验水舱液位不变的情况下,只对其做晃动处理,取80个采样点。液位高度初始值为0.512 m,且由式(17)~式(22)可求得单传感器的局部状态最优卡尔曼估计值,如图5和图6所示,即单传感器在不同位置测得的数据的卡尔曼滤波。由式(25)得到分布式的矩阵加权最优融合估计,如图7所示。

|
图 5 传感器1的液位测量值与滤波值 Fig. 5 Sensor 1 level measurement and filtered value |
|
图 6 传感器2的液位测量值与滤波值 Fig. 6 Sensor 2 level measurement and filtered value |
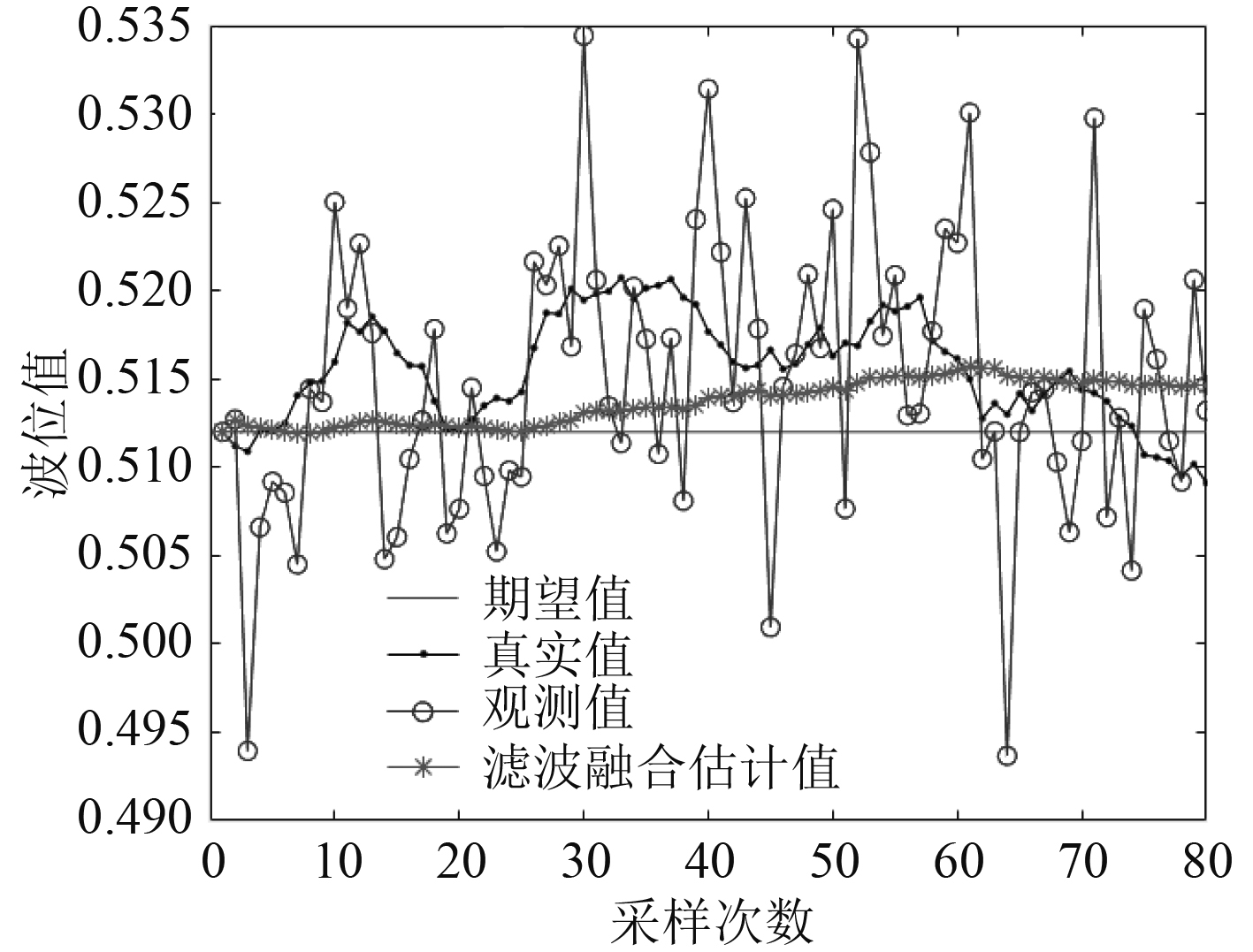
|
图 7 分布式加权融合卡尔曼滤波 Fig. 7 Distributed weighted fusion Kalman filtering |
由图5~图7可得,传感器测得的实时液位值上下波动,与实际值的误差较大,而雷达液位计经过卡尔曼滤波器处理过的估计值趋于真实值,且较为稳定;而单传感器测得的数据过于片面,不能全面表现出整个舱内的液位。从滤波融合估计值来看,波动基本处于实际液位值0.512 m的±4 mm左右,能准确表达舱内液位的状态。
在实验水舱进水时对水舱做晃动处理,取100个采样点,液位高度初始值为0.512 m,仿真结果如图8~图10所示。
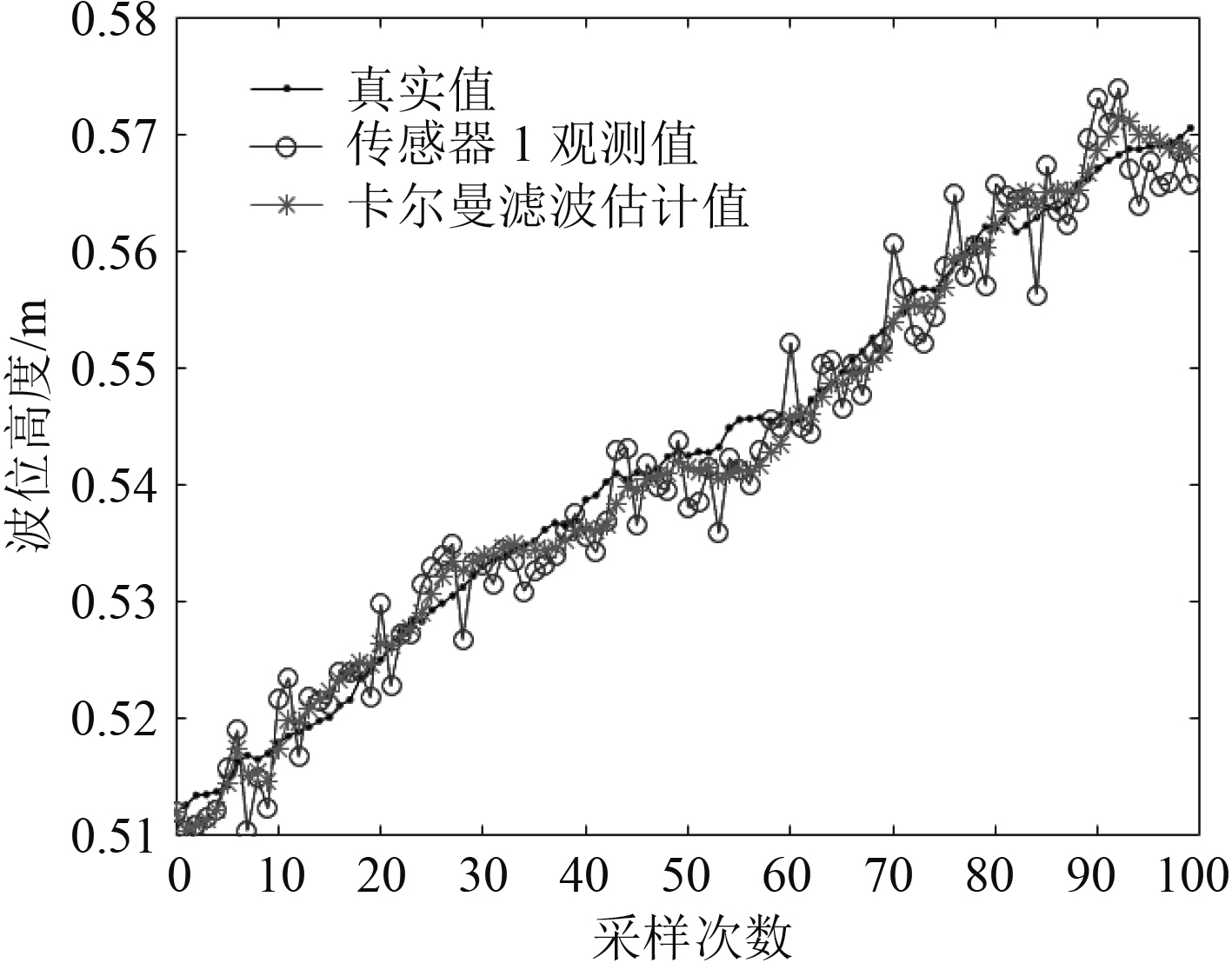
|
图 8 传感器1的测量值与滤波值 Fig. 8 Sensor 1 measured and filtered values |
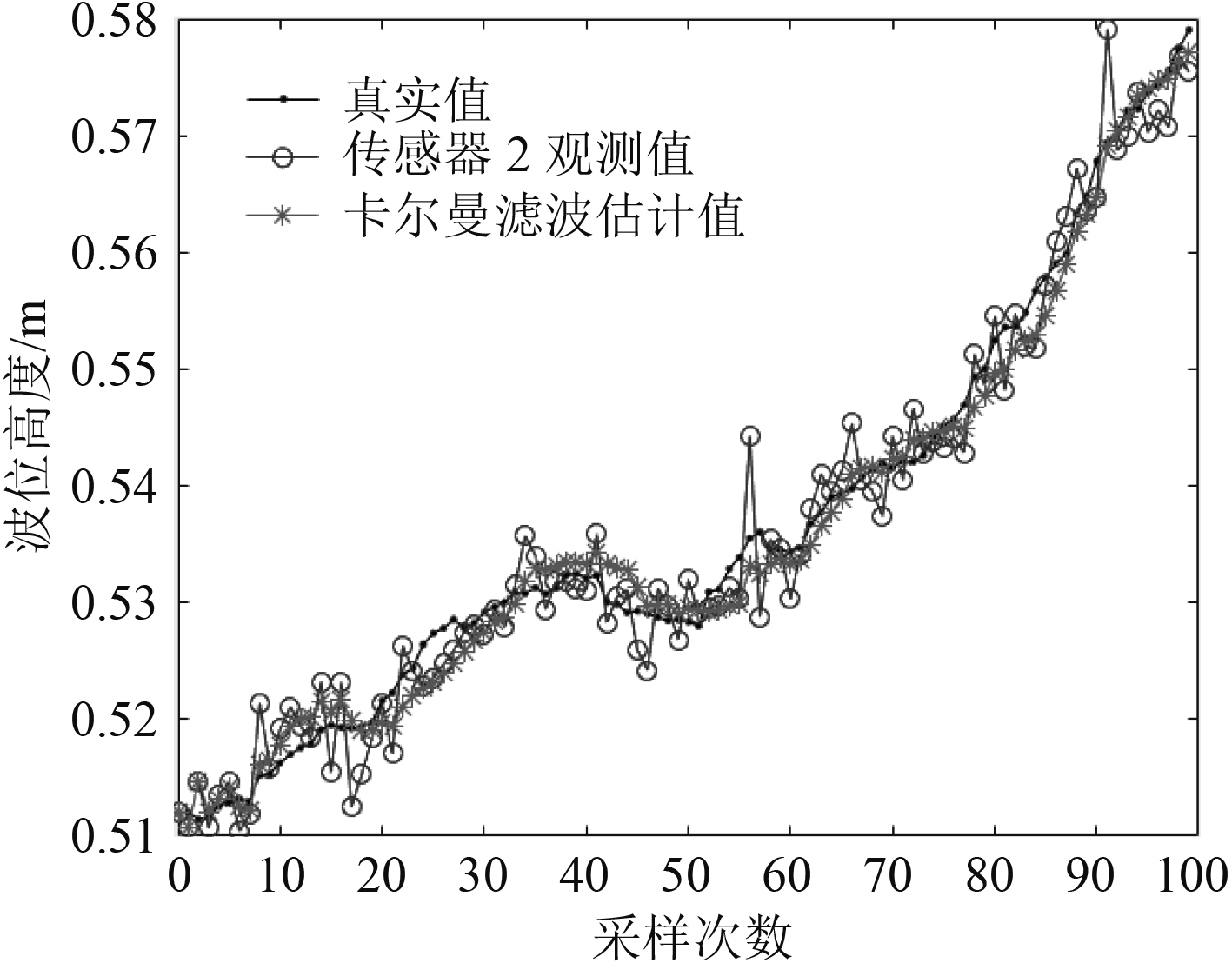
|
图 9 传感器2的测量值与滤波值 Fig. 9 Sensor 2 measured and filtered values |
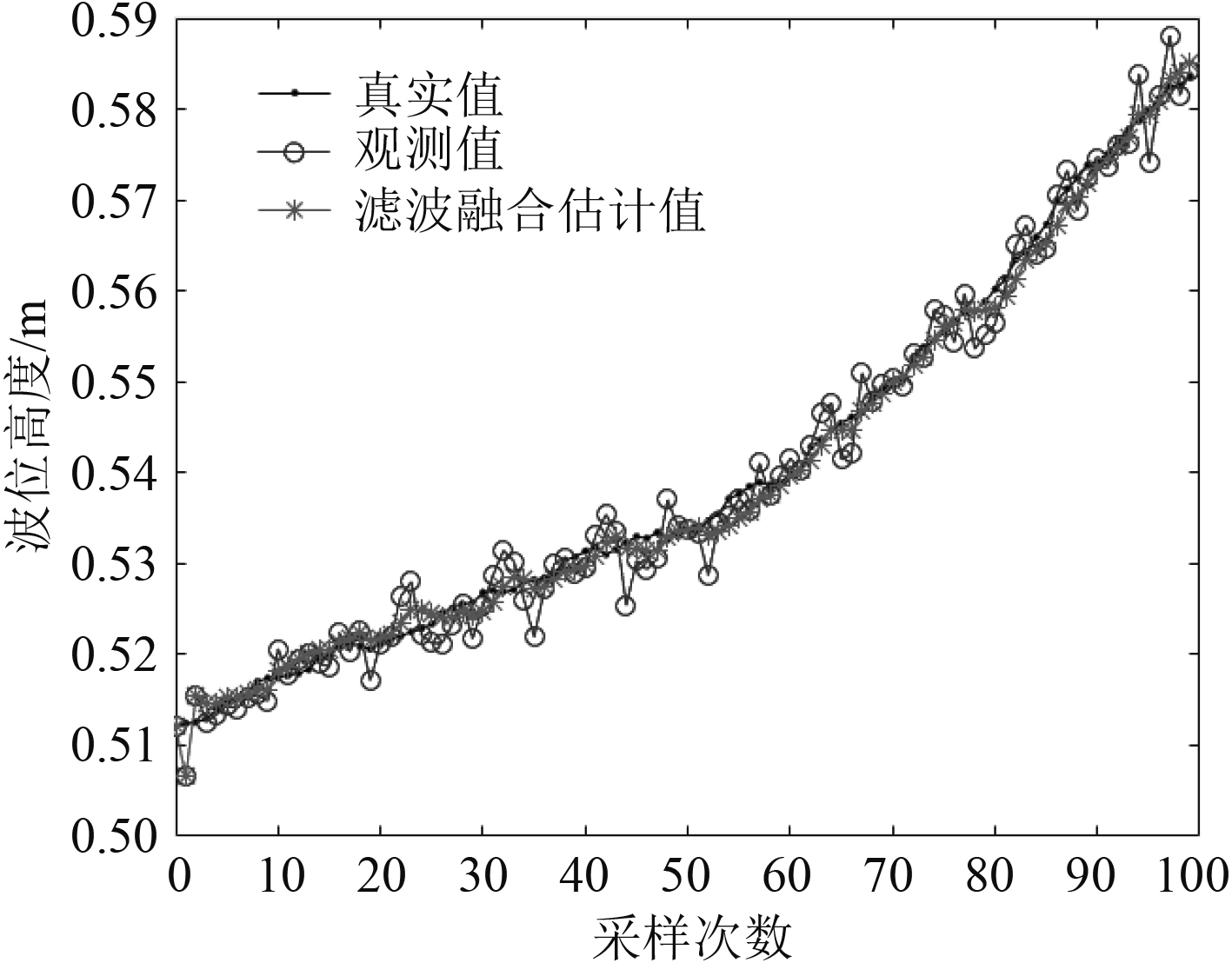
|
图 10 分布式加权融合卡尔曼滤波 Fig. 10 Distributed weighted fusion Kalman filtering |
由图10可见,液位波动的测量值经过最优融合卡尔曼滤波器处理后表示的更加稳定,输出值趋于真实值,最大波动不超过6 mm,且运行一段时间后输出基本趋于平稳。因此,可看出滤波融合的效果良好。同时,经过多次测量比较,采用本系统测量的液位值平均误差在0.5%以内,满足系统设计要求,可见采用分布式最优加权融合卡尔曼滤波器的滤波效果良好。表1为试验所用的100组数据计算的误差。
|
|
表 1 液位测量精度比较 Tab.1 Comparison of liquid level measurement accuracy |
由表1可得,本文实验中液位监测的方法虽然在测量前对传感器进行了预处理,可测量后的误差仍然较大。在单传感器测量下,采用卡尔曼滤波产生的误差较小,而多传感器滤波融合后的误差最小。由此可见,多传感器融合算法具有较高的精度。因此,在精度要求高的液位监控系统中可考虑采用本文提出的多传感器融合方法。
5 结 语本文针对船舶液位监测过程中液位测量易出现的误差,且考虑到单传感器测量数据容易产生偏差,提出一种在时滞系统下的基于卡尔曼滤波的多传感器融合算法,给出了多传感器分布式加权最优融合估计和最优融合误差。对液位变化过程进行建模,使用此方法对传感器测得值进行处理,提高液位输出值的精确度和稳定性。通过仿真和实验证明,本文采用的对测量数据的处理方法使得到的液位输出值相比于常用方法更加精确可靠,具有一定的实用性。
| [1] |
周少华, 周根明, 郭霆, 等. 浮船坞沉浮自动控制系统的设计和实现[J]. 船舶工程, 2013, 35(5): 55-58. |
| [2] |
施海涛. 船舶液位遥测与阀门遥控系统的设计与实现[D]. 镇江: 江苏大学, 2016.
|
| [3] |
王莉娜, 赵先龙, 阮锐, 等. 压力传感器的自动标定技术[J]. 海洋测绘, 2007(4): 78-80. DOI:10.3969/j.issn.1671-3044.2007.04.023 |
| [4] |
姚健. 液位遥测在船舶配载中的应用研究[D]. 大连: 大连海事大学, 2019.
|
| [5] |
陶峰. 船用高精度液位遥测及控制系统的设计[D]. 镇江: 江苏科技大学, 2016.
|
| [6] |
TIAN TIAN, SHULI SUN, HONGLEI LIN. Distributed fusion filter for multi-sensor systems with finite-step correlated noises[J]. Information Fusion, 2019, 46: 128-140. DOI:10.1016/j.inffus.2018.05.002 |
| [7] |
孙甲冰. 多传感器离散随机系统的分布式融合估计研究[D]. 济南: 山东大学, 2011.
|
| [8] |
郭颜萍, 胡桐, 李志乾, 等. 船舶相对风的融合算法研究[J]. 舰船科学技术, 2020, 42(5): 34-39. DOI:10.3404/j.issn.1672-7649.2020.05.007 |
| [9] |
宋琳, 蔡云泽, 高建喜, 等. 多传感器时滞系统数据丢失时滤波融合算法[J]. 控制工程, 2010, 17(S2): 104-107+123. |
| [10] |
Z. LI, M. LIU AND B. LI, Research on fusion filtering algorithm for lost observation system[C]//2019 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 2019: 257−261.
|
| [11] |
吕楠. 时滞系统的分布式融合滤波[D]. 哈尔滨: 黑龙江大学, 2008.
|
| [12] |
YI Chun-lei, ZHANG Kun-fan, PENG Neng-ling. A multi-sensor fusion and object tracking algorithm for self-driving vehicles[J]. Proceedings of the Institution of Mechanical Engineers, 2019, 233(9): 2293-2300. DOI:10.1177/0954407019867492 |
| [13] |
KAPALE S, BHARAKAD A. Liquid level estimation in dynamic condition using Kalman filter[J]. International Journal of Engineering Research & Applications, 2016, 6(8): 12-16. |
| [14] |
刘庆华, 仲海啸, 陶峰, 等. 卡尔曼滤波融合新算法及其船舶高精度液位测量的应用[J]. 中国造船, 2016, 57(2): 192-200. DOI:10.3969/j.issn.1000-4882.2016.02.021 |
 2021, Vol. 43
2021, Vol. 43
