无人艇作为海上移动平台,受风、浪、流等作用会产生六自由度运动,包括3个方向的平动和3个方向的转动。对于旋转运动,船体不同位置与旋转中心的距离不等,旋转运动产生的线速度不同,而船体任意点的合速度是平动速度与转动速度的矢量和,故实际海上航行无人艇船体各点的合速度矢量均不相等。无人艇的许多作业场景依赖于观测无人艇自身某一局部位置的位姿信息,例如,无人艇的布放和回收、多无人艇对接、无人艇靠离码头、艇载传感器位姿补偿(如摄像头、测扫声呐、避障声呐、对底声呐、激光雷达等)等。为此,如何获取船体任意位置的实时位姿状态成为无人艇智能化发展中信息感知关键技术的重要挑战之一。
船体任意位置实时位姿状态获取,通常需要若干个惯导传感器数据的融合处理。司帆等[1]为克服机翼挠曲变形对机载导弹对准产生的影响,根据主、子惯导的惯性器件输出,得到子惯导所处位置的高精度实时姿态信息。王林等[2]针对单轴与双轴旋转惯导的信息融合问题,设计联合旋转调制策略,实现了单轴旋转惯导定位误差的预测与补偿,提高了系统的导航定位可靠性。刘镇波等[3]提出一种基于分布式IMU的相对姿态估计方法,能够在系统无高精度惯导及变形统计特性未知的情况下,获取机载关键位置精确的相对姿态。这些研究着重关注多个物理传感器的数据融合测算传感器所在局部位置的实时位姿,虽然精度较高,但却不能满足任意多个测点的位姿实时观测需求。随着无人艇全船布置设备增多,有限个惯导传感器扩容却显著增加了传感系统的复杂度及投资成本。
当前,数字孪生技术的迅速发展为上述需求提供了新的解决思路。数字孪生是一种集成了多物理量、多尺度、多概率的仿真过程,以数字化方式创建物理实体的虚拟模型,通过虚实交互与数据融合实现物理实体的全生命周期服务[4-5]。这个概念最早被提出是用于描述产品的生产制造和实时虚拟化呈现,随后该理念被推广应用到工业产品、大型装备的实时运行监测[6]。数字孪生通常包括物理空间的实体、信息空间的虚拟孪生体、物理空间和信息空间之间的数据和信息交互接口三部分[7-9]。目前,已有多位学者对数字孪生在船舶领域的应用进行了初步研究。李凯等[10]基于数字孪生提出数字化舰船的总体框架,并探索基于数字孪生的产品设计、辅助决策、健康管理等潜在应用场景。陶飞等[11]提出将数字孪生与船舶工业结合,参照数字孪生五维模型,探讨基于数字孪生的船舶设计、制造、运维、使用等全生命周期一体化管理理念。然而,由于缺乏系统的数字孪生理论支撑和应用准则指导,目前在船舶领域数字孪生的研究多集中于理论探讨,鲜有实际应用报道。
因此,面向无人艇任意位置实时姿态估计需求,本文设计基于数字孪生的无人艇虚实结合三维交互系统,通过刚体运动学建立无人艇物理空间时序数据与信息空间几何信息的跨空间融合方法。基于单套状态感知设备获取的信息,无人艇实现在信息空间实时映射来自物理空间的航行状态,并可实时估算船体任意位置的位姿状态。
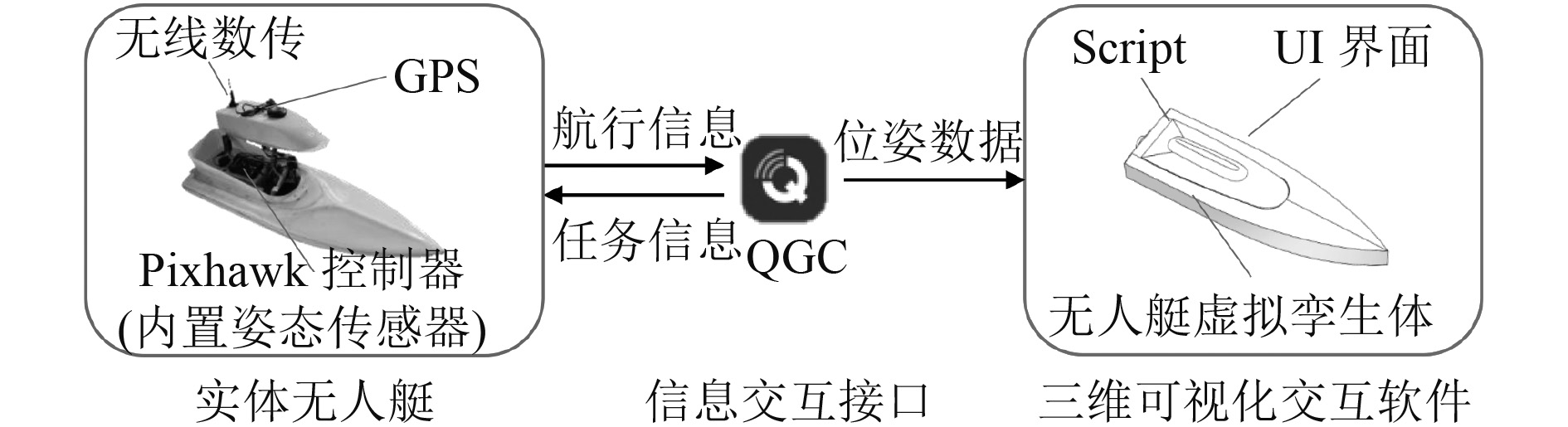
1 无人艇虚实结合三维交互系统架构 1.1 系统总体框架如图1所示,无人艇虚实结合三维交互系统由实体无人艇、三维可视化交互软件以及物理空间与信息空间的交互接口组成。无人艇是系统在物理空间的实体对象,搭载了姿态传感器、位置传感器等传感设备,能够感知航行信息并实时传递给上位机。三维可视化软件是系统进行无人艇姿态三维可视化显示和姿态信息虚实交互的部分,由无人艇虚拟孪生体、UI界面和Script组成。信息交互接口主要由地面站软件(QGroundControl,QGC)组成,QGC在系统中发挥数据中介作用,一方面向无人艇发送任务信息,并接收无人艇传回的航行信息;另一方面从无人艇传回的航行信息中提取位姿数据,发送给三维可视化交互软件。
|
图 1 无人艇虚实结合三维交互系统总体构架 Fig. 1 Framework of the unmanned surface vehicles' virtual reality fusion three-dimensional interactive system |
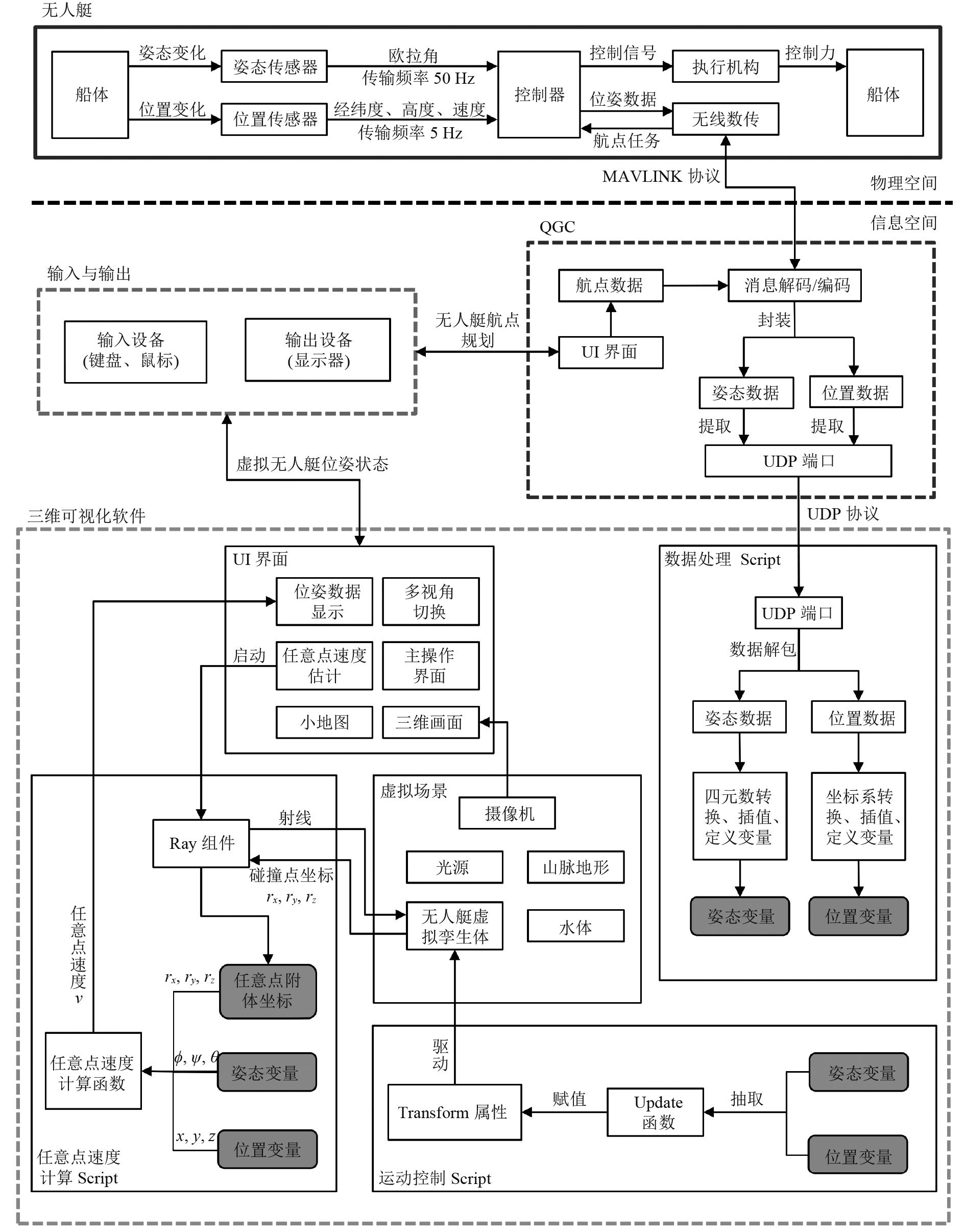
无人艇虚实结合三维交互系统能够把实体无人艇传感器感知到的位置、姿态等信息实时映射为信息空间中无人艇虚拟孪生体的运动信息。从无人艇传感器实时数据的输入到三维可视化软件中无人艇虚拟孪生体运动的输出,信息流需要跨越多个软硬件平台。如图2所示,在物理空间、信息空间以及数据交互接口中,均设有数据的传递、转化模块,各模块共同组成了系统的信息流传输机制。
|
图 2 无人艇虚实结合三维交互系统数据传输机制 Fig. 2 The unmanned surface vehicles' virtual reality fusion three-dimensional interactive system structure |
无人艇与上位机通过无线数传以MAVLINK协议方式通信,上位机中安装有二次开发的QGC软件,在QGC软件中解析MAVLINK消息包提取传感器数据,并用UDP封装姿态数据(横滚角、首向角、俯仰角)和位置数据(经度、纬度、相对海拔、速度)。通过本地UDP套接字,将封装好的数据发送至特定端口。同时,在Unity3D数据处理Script中创建Socket对象,监听该端口,实时接收位姿数据。数据处理Script把接收到的UDP数据解包,并对位姿数据进行预处理后分别赋予位置变量和姿态变量。运动控制Script和任意点速度计算Script分别调用这些变量实现无人艇虚拟孪生体的三维动态显示和实时位姿状态估计功能。
2 虚拟无人艇及交互设计 2.1 虚拟无人艇孪生体及虚拟场景建立精确的无人艇虚拟孪生体模型是三维可视化交互软件实现无人艇数字孪生的基础。本文用SolidWorks建立实体无人艇1∶1三维模型,再用3Dmax转换为可供导入Unity3D的.fbx文件。为了获得逼真的三维仿真效果,在三维可视化交互软件中构建与真实环境相似的虚拟场景,例如基于Terrain组件建立山脉,利用法线贴图、菲涅尔效应、漫反射着色器以及折射着色器等模拟水体,采用Skybox及光源模拟天空和光线。
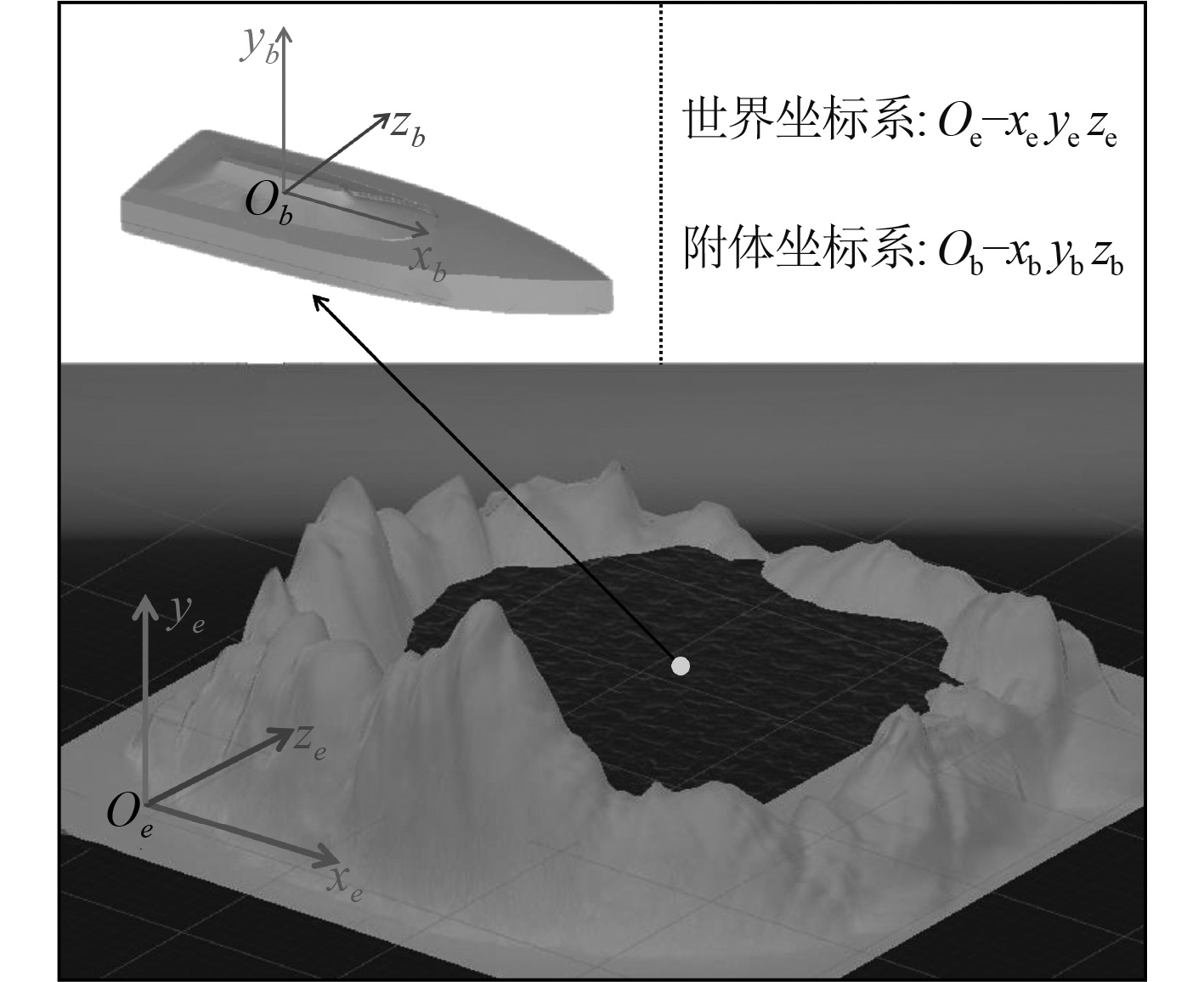
如图3所示,虚拟场景导入无人艇虚拟孪生体,把附体坐标系的坐标原点设置在无人艇质心位置,xb轴正方向指向船首,zb轴正方向指向左舷,yb轴正方向竖直向上。无人艇虚拟孪生体初始位置位于虚拟场景中央,满足航行试验需求。
|
图 3 虚拟场景及场景中的无人艇虚拟孪生体 Fig. 3 Virtual scene and twin USV inside |
三维可视化交互软件使用QGC传回的位姿数据来驱动无人艇虚拟孪生体。对于位置数据,将GPS测量得到的经纬度信息经坐标变换转化到虚拟场景的世界坐标系;对于姿态数据,将欧拉角形式姿态信息转换为四元数,避免万向节死锁问题。
无人艇位姿数据采样率取决于无人艇的控制周期和传感器自身固有属性,本文中位置和姿态数据采样率分别为5 Hz和50 Hz。而虚拟场景中流畅的画面通常要求帧率在30FPS以上,为此,对坐标系转换后的位置数据进行线性插值和球面插值补帧,使得无人艇在虚拟场景中的动态画面流畅且过渡平滑。
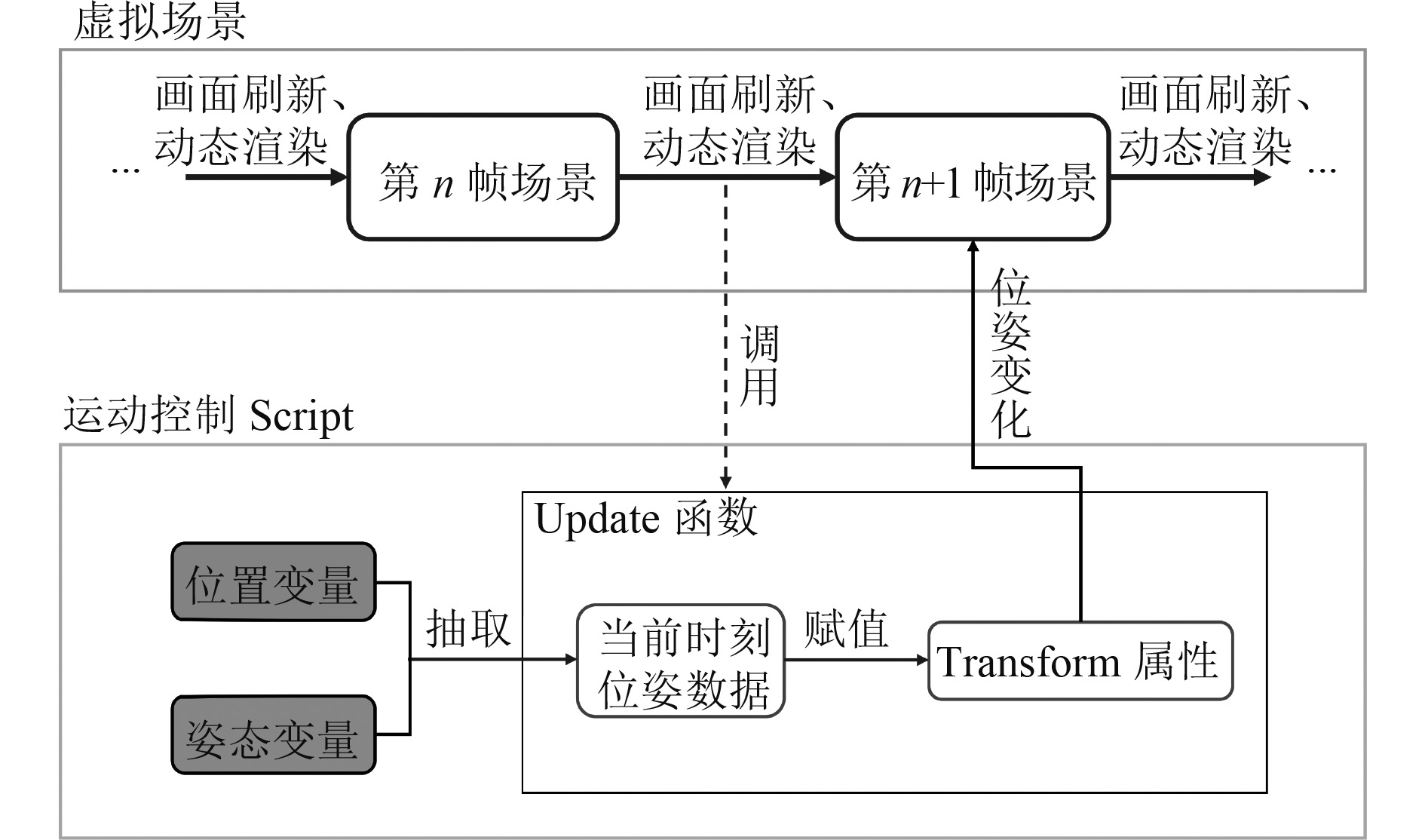
真实位姿数据驱动无人艇虚拟孪生体动态画面刷新原理如图4所示。在运动控制Script中,在每一帧画面刷新时调用一次Update函数,经差值优化的位姿变量赋值给无人艇虚拟孪生体Transform属性,更新无人艇虚拟孪生体在下一帧动画中的位姿状态,结合Unity3D图形引擎进行动态渲染,产生动态画面。
|
图 4 位姿数据驱动无人艇虚拟孪生体原理 Fig. 4 The principle of position and attitude data driving twin USV |
本系统实体无人艇为基于Pixhawk的小型喷水推进无人艇(总长0.66 m,型宽0.20 m),由控制系统、动力系统、感知系统、通信系统等构成,各系统部件沿中纵剖面布置在无人艇两舷。感知系统主要由GPS和惯导组成。
3.2 实体无人艇监控系统实体无人艇监控系统由无人艇和上位机组成,如图5所示。上位机运行QGC软件,通过3DR 433 MHz数传与无人艇通信,实现向无人艇发送指令,同时接收无人艇传回各种状态。本系统上位机可规划无人艇的航行任务、航路、下达指令;接收无人艇的实时状态反馈,在QGC和三维可视化交互软件界面实时显示无人艇的航行状态、地图轨迹等信息。

|
图 5 无人艇监控硬件系统 Fig. 5 USV monitoring hardware system |
根据实体无人艇的位姿时序数据,结合虚拟孪生体几何模型数据,本文实现了虚实结合跨空间数据融合,可估算船体任意位置的实时速度。
将无人艇视为刚体,虚拟孪生体质心是旋转中心,也是附体坐标系原点
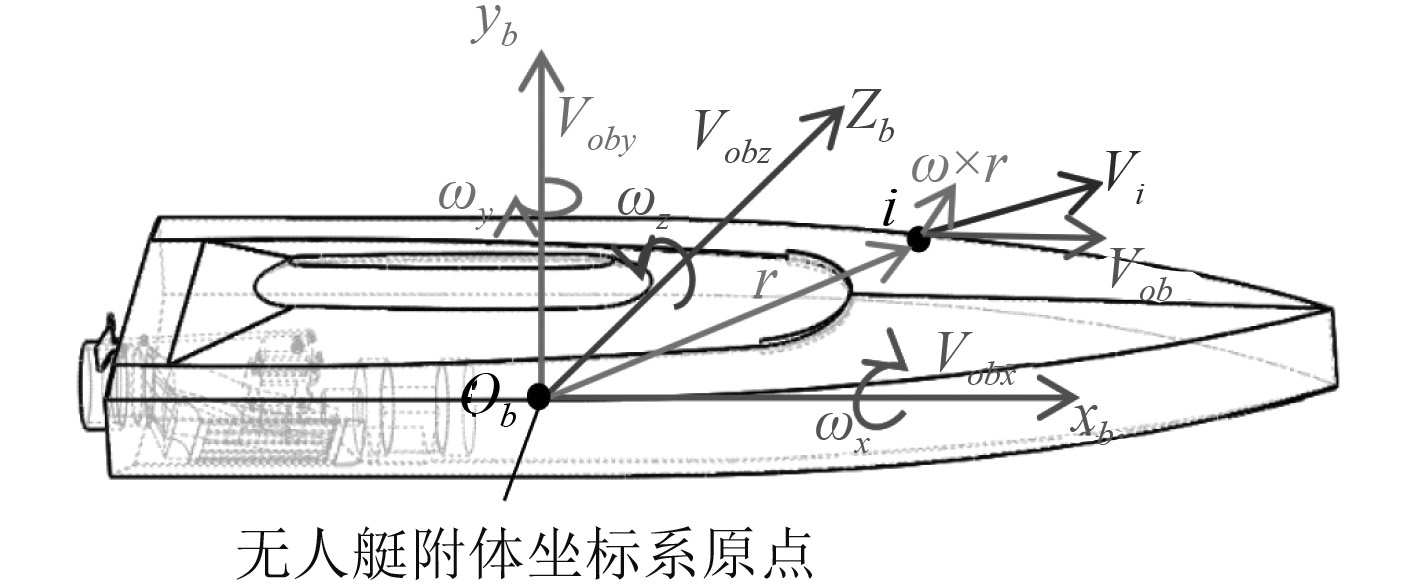
|
图 6 任意点i的速度分析 Fig. 6 Velocity analysis of arbitrary point i |
1)无人艇绕
| ${\omega } = \frac{{{\Theta }\left( {{t_0}} \right) - {\Theta }\left( {{t_0} - {\rm{\Delta }}t} \right)}}{{{\rm{\Delta }}t}} = \left[ {\begin{array}{*{20}{c}} {\dot \phi } \\ {\dot \psi } \\ {\dot \theta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\omega _x}} \\ {{\omega _y}} \\ {{\omega _z}} \end{array}} \right]\text{,}$ | (1) |
2)无人艇平移运动是前进、横漂、起伏3个方向的叠加,即
某一时刻
| $ \left\{\begin{array}{l}\beta =\psi +{\mathrm{tan}}^{-1}\dfrac{{b}_{2}-{b}_{1}}{{a}_{2}-{a}_{1}}-\dfrac{\text{π} }{2},{a}_{2}-{a}_{1}>\rm{0}\text{,} \\ \beta =\psi +{\mathrm{tan}}^{-1}\dfrac{{b}_{2}-{b}_{1}}{{a}_{2}-{a}_{1}}-\dfrac{3\text{π} }{2}\rm{,}{a}_{2}-{a}_{1}<0 \text{,}\end{array}\right.$ | (2) |
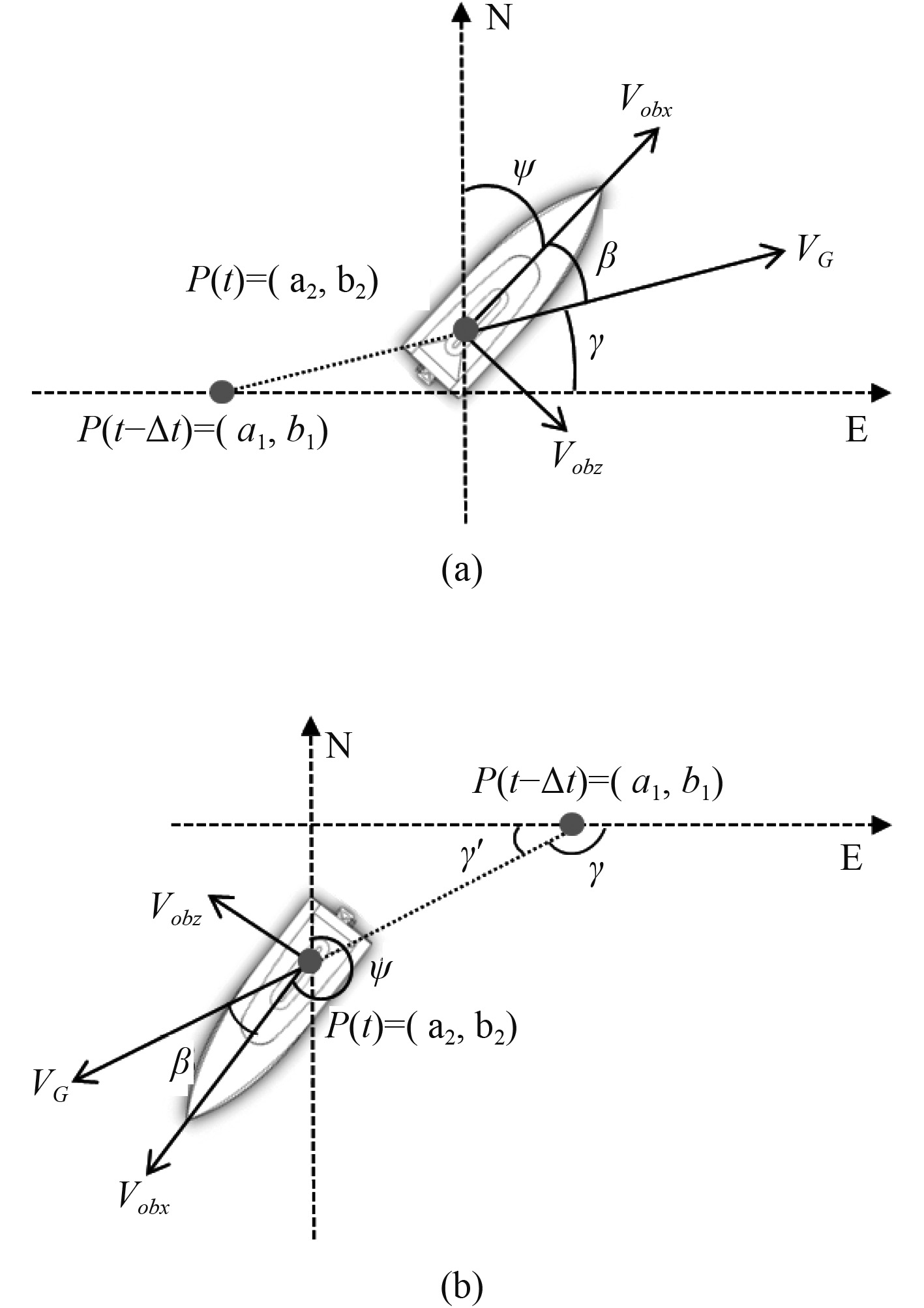
|
图 7 首向角与航向角分析 Fig. 7 Analysis of heading angle and course angle |
根据公式
| $\left\{ {\begin{array}{*{20}{l}} {{V_{ix}}\left( t \right) \!=\! {v_G} \!\cdot\! \cos \beta \!+\! \dfrac{{\psi (t) \!-\! \psi \left( {t \!-\! {\rm{\Delta }}t} \right)}}{{{\rm{\Delta }}t}} \cdot {r_z} \!+\! \dfrac{{\theta \left( t \right) \!-\! \theta \left( {t \!-\! {\rm{\Delta }}t} \right)}}{{{\rm{\Delta }}t}} \cdot {r_y}} \text{,}\\ {{V_{iy}}\left( t \right) = \dfrac{{\phi \left( t \right) - \phi \left( {t - {\rm{\Delta }}t} \right)}}{{{\rm{\Delta }}t}} \cdot {r_z} + \dfrac{{\theta \left( t \right) - \theta \left( {t - {\rm{\Delta }}t} \right)}}{{{\rm{\Delta }}t}} \cdot {r_x}} \text{,}\\ {{V_{iz}}\left( t \right) \!=\! {v_G} \!\cdot\! \sin \beta \!+\! \dfrac{{\phi \left( t \right) \!-\! \phi \left( {t \!-\! {\rm{\Delta }}t} \right)}}{{{\rm{\Delta }}t}} \!\cdot\! {r_y} \!+\! \dfrac{{\psi \left( t \right) \!-\! \psi \left( {t \!-\! {\rm{\Delta }}t} \right)}}{{{\rm{\Delta }}t}} \cdot {r_x}} \text{,} \end{array}} \right.$ | (3) |
按照矢量求和方法可计算i点合速度值
| $ \begin{split} {v_i} \!&\!\! \sqrt {{{\left( {{{\dot x}_{ie}} \!+\! \dot \psi {r_z} + \dot \theta {r_y}} \right)}^2} \!+\! {{\left( {{{\dot y}_{ie}} \!+\! \dot \phi {r_z} \!+\! \dot \theta {r_x}} \right)}^2} \!+\! {{\left( {{{\dot z}_{ie}} \!+\! \dot \phi {r_y} \!+\! \dot \psi {r_x}} \right)}^2}}\!= \\ & f(\phi ,\psi ,\theta ,{x_{ie}},{y_{ie}},{z_{ie}},{r_x},{r_y},{r_z})\text{。}\\[-10pt] \end{split}$ | (4) |
其中,
进行本文开发的无人艇虚实结合三维交互系统及任意位置速度估计功能的湖试。以某一段直角转弯航路为例分析,航行轨迹如图8所示。

|
图 8 试验航行轨迹 Fig. 8 Experimental navigation trajectory |
如图9所示,三维可视化交互软件速度估计界面,鼠标点击无人艇虚拟孪生体任意位置可计算该点实时速度。在无人艇船体上任取四点作为速度估计观测点,取

|
图 9 无人艇速度估计界面及试验点位置分布 Fig. 9 Speed estimate UI for USV and experimental point layout |
受限于本试验无人艇尺寸,4个试验点与无人艇质心
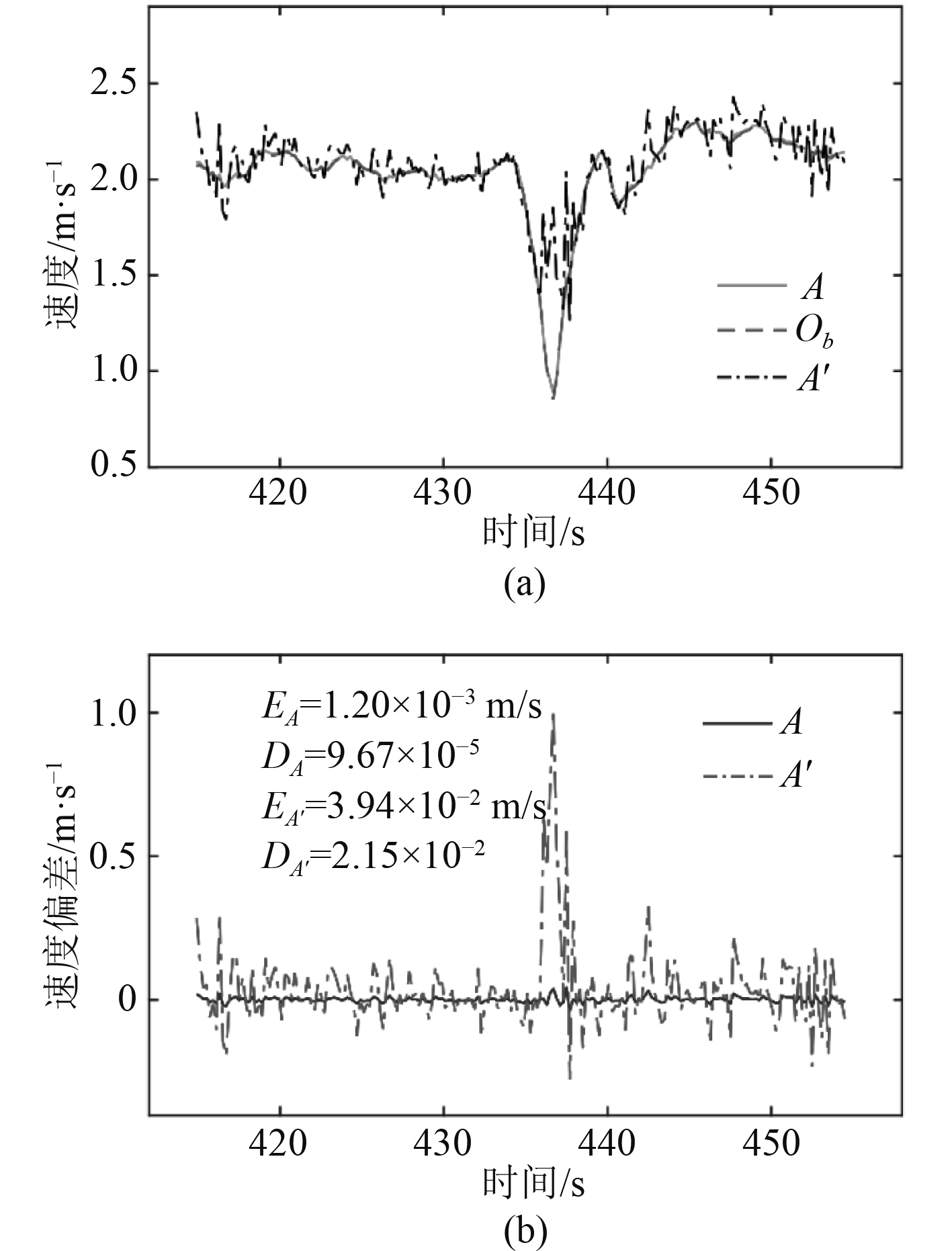
|
图 10
航行过程A点、A′点与
|

|
图 11
航行过程B点、B′点与
|
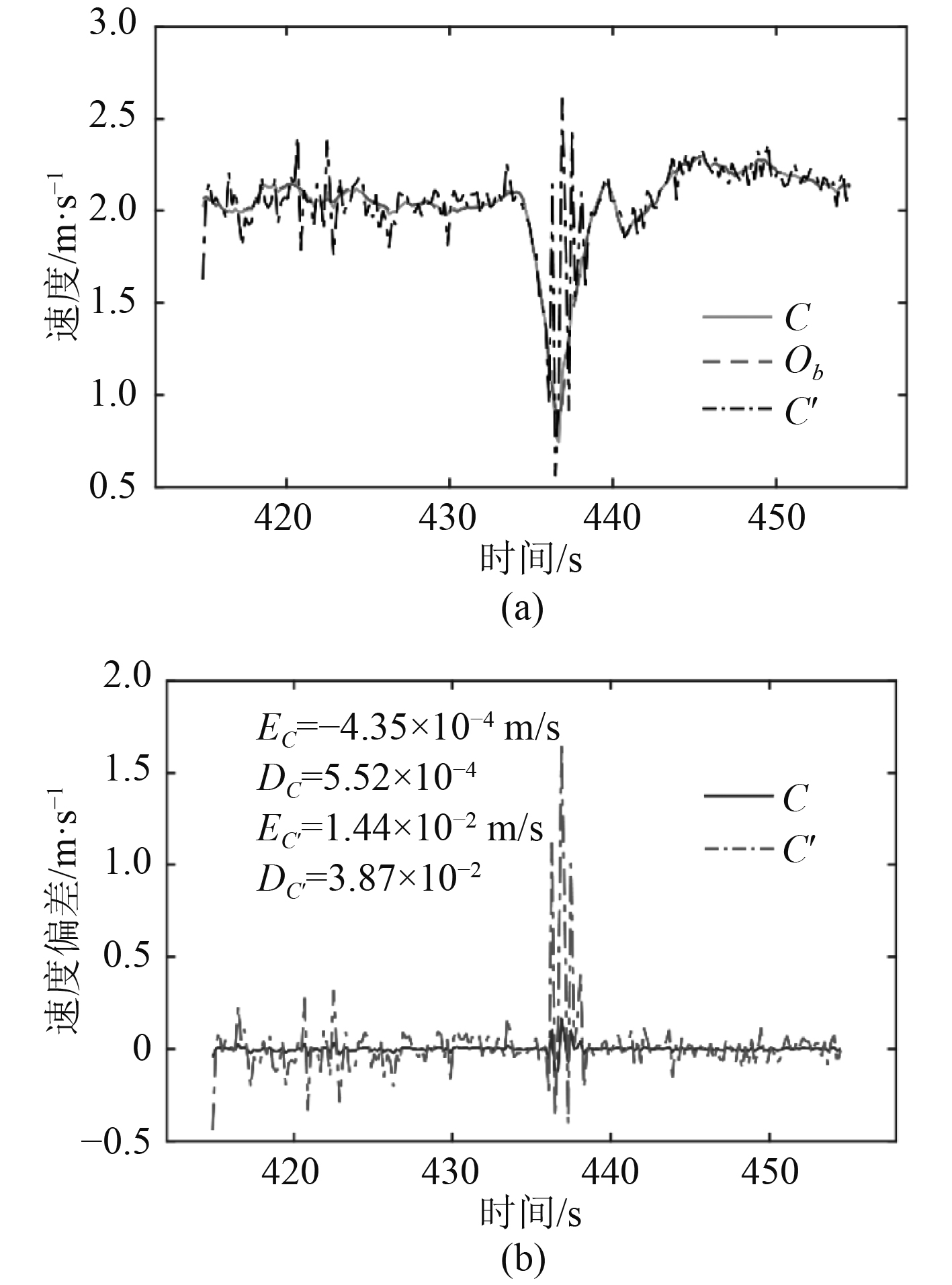
|
图 12
航行过程C点、C′点与
|
|
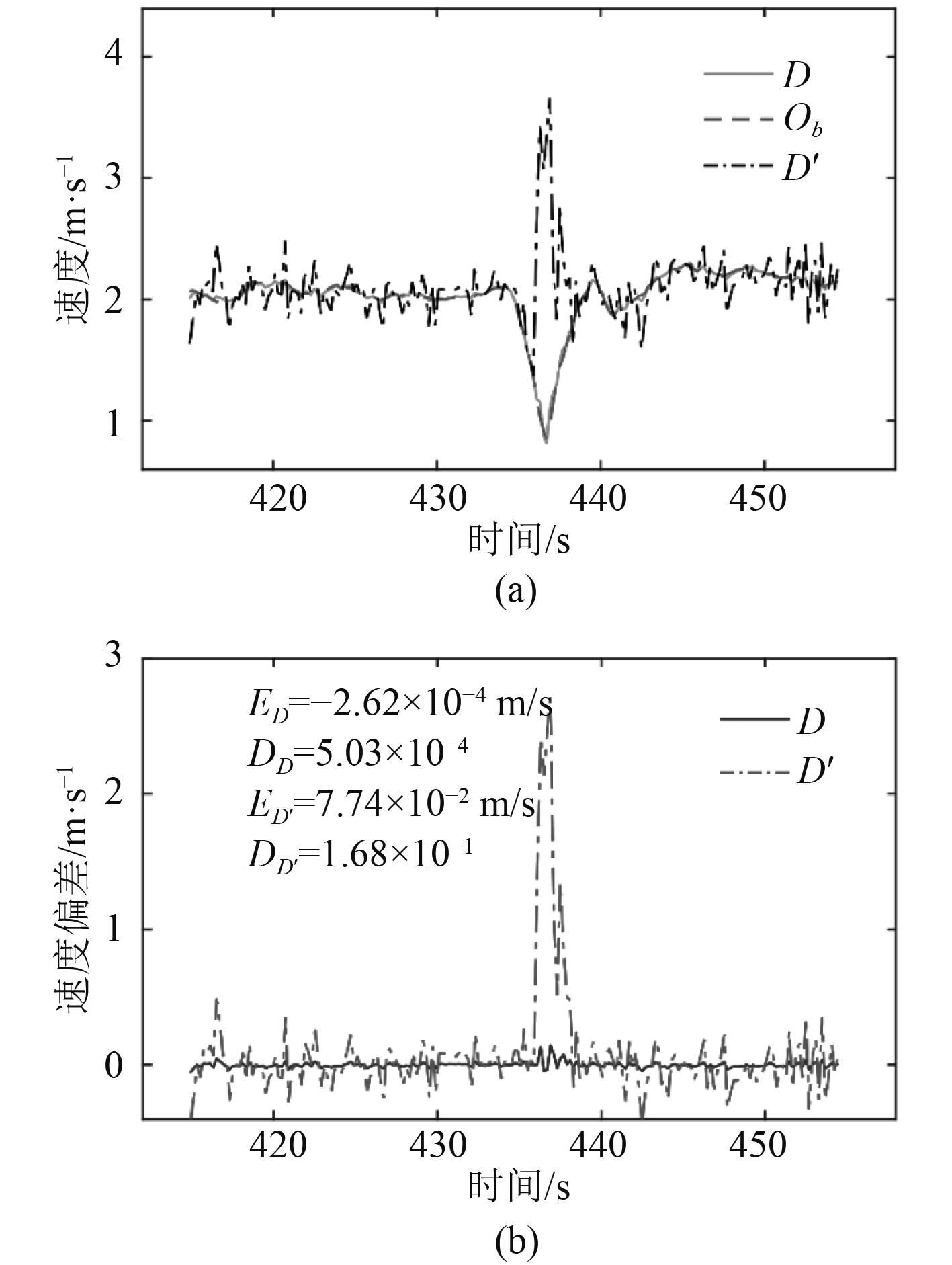
图 13
航行过程D点、D′与
|
无人艇在415~435 s和435~455 s两个时间段内直线航行,为降低转弯过程轨迹跟踪误差,无人艇自主程序控制会在435~440 s时间段降速完成直角转弯过程。由图10~图13可见,试验点A-D的实际速度均与无人艇质心
本文建立基于数字孪生的无人艇虚实结合三维交互系统,实现了在信息空间真实映射物理空间无人艇航行状态,并可在信息空间估计无人艇任意位置速度。该系统以自研无人艇为物理空间实体对象,使用Unity3D在信息空间搭建了无人艇虚拟孪生体,利用QGC软件建立物理空间与虚拟空间的交互接口。利用虚实结合跨空间姿态数据融合原理,将物理空间实时观测位姿信息与信息空间无人艇几何模型信息融合。基于有限数量的传感器实现了对无人艇全船任意位置的实时姿态估计。通过湖试验证了本系统的三维交互与速度估计功能。当无人艇角速度增大导致姿态变化较大时,无人艇局部位置的合速度将与质心位置的偏差明显增加,且随着与质心间距增加,这种偏差效应更加显著。
本文建立的无人艇虚实结合三维交互系统有助于船舶智能感知技术发展,但在信息空间估计数据服务于物理空间方面仍需进一步探究.
| [1] |
司帆, 谷雨, 赵剡, 等. 基于相对惯性导航的机载导弹二次传递对准[J]. 航空兵器, 2017(6): 41-48. |
| [2] |
王林, 吴文启, 魏国, 等. 双航海惯导联合旋转调制协同定位与误差参数估计[J]. 中国惯性技术学报, 2017, 25(5): 599-605. |
| [3] |
刘镇波, 李四海, 王珏, 等. 基于分布式IMU的相对姿态估计方法[J]. 弹箭与制导学报, 2014, 34(5): 21-25. DOI:10.3969/j.issn.1673-9728.2014.05.006 |
| [4] |
陶飞, 刘蔚然, 刘检华, 等. 数字孪生及其应用探索[J]. 计算机集成制造系统, 2018, 24(1): 1-18. TAO F, LIU W, LIU J, et al. Digital twin and its potential application exploration[J]. Computer Integrated Manufacturing Systems, 2018, 24(1): 1-18. |
| [5] |
苗田, 张旭, 熊辉, 等. 数字孪生技术在产品生命周期中的应用与展望[J]. 计算机集成制造系统, 2019, 25(6): 1546-1558. MIAO T, ZHANG X, XIONG H, et al. Applications and expectation of digital twin in product lifecycle[J]. Computer Integrated Manufacturing Systems, 2019, 25(6): 1546-1558. |
| [6] |
刘大同, 郭凯, 王本宽, 等. 数字孪生技术综述与展望[J]. 仪器仪表学报, 2018, 39(11): 1-10. |
| [7] |
GRIEVES M, VICKERS J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems[J]. Transdisciplinary Perspectives on Complex Systems, 2017, 85-113. |
| [8] |
GRIEVES M. Digital twin: Manufacturing excellence through virtual factory replication[J]. White paper, 2014, 1-7. |
| [9] |
GRIEVES M. Virtually perfect: Driving innovative and lean products through product lifecycle management[M]. Space Coast Press, 2011.
|
| [10] |
李凯, 钱浩, 龚梦瑶, 等. 基于数字孪生技术的数字化舰船及其应用探索[J]. 船舶, 2018, 29(6): 101-108. |
| [11] |
陶飞, 刘蔚然, 张萌, 等. 数字孪生五维模型及十大领域应用[J]. 计算机集成制造系统, 2019, 25(1): 1-18. |
| [12] |
LorenzMeier. PX4/Firmware at v1.8. 0[EB/OL]. (2018-06-19) [2019-03-28]. https://github.com/PX4/Firmware/tree/v1.8.0.
|
| [13] |
中国船级社. 无人水面艇检验指南[S]. 北京: 中国船级社, 2018.1. China Classification Society. Survey guide for unmanned surface vehicles[S]. Beijing: China Classification Society, 2018.1. |
 2021, Vol. 43
2021, Vol. 43
