0 引　言

组合导航系统是将2种或者2种以上的非相似导航系统的输出进行综合处理,获得更高的导航精度与可靠性^[1-2]。最常见的组合导航系统是以惯导为核心的惯性基组合导航系统^[3-4]。捷联惯导（Strapdown Inertial Navigation，SINS）具有用数字平台代替实体平台，结构简单，体积小，重量轻等特点，成为研究的热门^[5]。然而SINS却存在导航精度随时间发散的问题，无法仅仅依靠自身校正误差^[6]。这就是SINS需要与其他导航设备进行组合导航的原因，常见的基于捷联惯导的组合系统可以应用在陆用导航（GPS、罗兰C、里程计）、水下导航（多普勒计程仪、基线系统）、航空航天以及无人系统导航等领域^[7-9]，然而，实现惯性基组合导航的关键技术就是组合滤波方法^[10]。

在现代滤波技术中，1995年由S.J.Julier和J.K.Uhlmann提出的无迹卡尔曼滤波算法（Unscented Kalman Filter，UKF）一直是研究的热点，该算法通过UT变换可以不忽略泰勒展开的高阶项，从而在非线性系统中有较高的估计精度和稳定性，受到了广泛的关注^[11]。在捷联惯性基组合导航的实际应用中，估计的精度与实时性都是需要考虑的问题，UKF不太大的计算量与较高的精度导致其成为了一种可行非线性的滤波方法，这也是其成为研究热点的原因之一。

在捷联惯性基组合导航实际应用中，捷联惯导自身比较稳定，不易受到干扰，而环境情况复杂多变，使得量测量难以避免的会被污染、干扰，这会对UKF的精度造成较大的影响，甚至导致滤波器的发散，进而影响到组合导航的效果。比如在城市中使用SINS/GPS系统，可能存在卫星受到信号遮挡、信号受到干扰的情况；在水下使用SINS/DVL系统，可能存在水流速或者水底地形的变化导致的测速异常等问题。如何提高滤波的抗干扰能力，提升组合导航系统的稳定性是UKF在实际应用中必须要解决的问题。传统的鲁棒方法是通过增加量测噪声矩阵的权重以削弱野值对滤波的影响，但是这样会牺牲滤波一定的估计精度^[12]。文献[13]对鲁棒滤波在初始对准动基座中的应用进行了研究，文献[14]对改进的Huber鲁棒滤波进行了研究，通过文献[15]使用支持向量回归的方法提高组合导航系统的鲁棒性。

针对捷联惯性基直接法组合导航系统实际使用中出现的量测量中出现野值的问题，本文提出一种基于一类支持向量机辅助的适用于捷联惯性基组合导航的鲁棒UKF算法（Support Vector Machine - Adaptive UKF，SVM-UKF）。本方法首先使用一类支持向量机（Support Vector Machine，SVM）建立滑动窗，来辨别滤波中的新息是否为异常，对于正常新息不予处理，对于异常的新息采用指数加权的方法得到新的“正确”新息以替代野值新息，这样不但可以修正量测值，还可以提高该情况下滤波的估计精度，提高系统的鲁棒性，根据江试实验数据，对SINS/GPS系统使用SVM-UKF与常规UKF，RUKF滤波组合导航的精度进行比较。实验结果表明，在量测量有野值污染的情况下，SVM-UKF具有更高的估计精度。

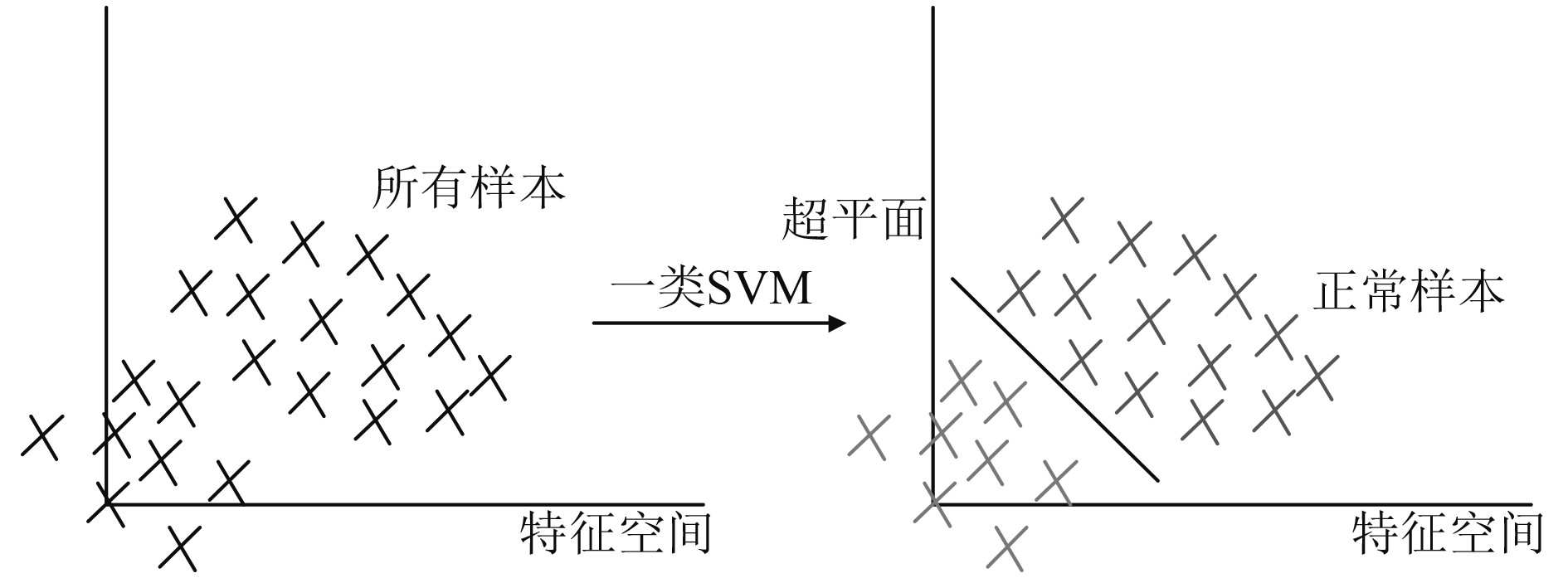
1 基于一类SVM的野值识别与处理

对于量测量中野值的辨别，一类SVM具有适用于小样本，非线性等特点，只需要正常工作的小样本数据就可以进行模型的训练，非常适用于野值的辨识。一类SVM本质是通过在特征空间中寻找超平面对正常样本与异常样本进行分离，如图1所示。

1.1 训练方法

一类SVM的在线训练流程如下：

1）构建新息样本滑动窗

选取n个连续的不含野值的新息数据组作为训练信息样本滑动窗 $X = {[{x_{1,}}{x_{2,}}\cdots,{x_n}]^{\rm{T}}}$ ,式中 $x$ 表示新息。规范化训练新息滑动窗中每一个向量 $x$ 。对规范化后的新息滑动窗进行主元分析得到目标向量矩阵 $Y$ ：

$Y= X{P_{PC}} = {[{y_1},{y_2},\cdots,{y_n}]^{\rm{T}}} \in {R^{n \times l}}\text{。}$

(1)

式中： ${P_{PC}} = [{p_1},{p_2},\cdots,{p_n}] \in {R^{N \times l}}$ 表示主元矩阵； $y$ 为支持向量； $l$ 为特征空间的维数。

2）训练一类SVM模型

根据新息样本滑动窗训练得到的目标向量矩阵 ${{Y}}$ ，训练一类SVM模型为：

$\mathop {\min }\limits_\alpha {\alpha ^{\rm{T}}}H\alpha \text{，}$

(2)

约束条件为：

$0 \leqslant {\alpha _i} \leqslant \frac{1}{{nv}}, \sum\limits_{i = 1}^n {{\alpha _i}} = 1\text{，}$

(3)

式中： $\alpha = {[{\alpha _1},{\alpha _2},\cdots,{\alpha _n}]^{\rm{T}}}$ 表示优化权值向量； ${H_{ij}} = $ $ K({y_i},{y_j})$ ， ${y_i},{y_j} \in Y$ ， $K({y_i},{y_j}) = {e^{ - {{\left\| {{x_i} - {x_j}} \right\|}^2}/2{\sigma ^2}}}$ 为核函数； $v \in \{ 0,1\} $ 是置信水平，用来表示允许训练新息样本出现错误被分类的程度。

3）计算偏移量

$b = \frac{1}{{{n_s}}}\sum\limits_{i = 1}^{{n_s}} {\sum\limits_{j = 1}^n {{\alpha _j}K({y_i},{y_j}} } )\text{。}$

(4)

式中： $b$ 为偏移量； ${n_s}$ 为 $y$ 的个数。设定置信水平 $v$ 的值，将新息样本滑动窗中的新息按从大到小的顺序排列，若验证数据样本的大小为 $n$ ，则取第 $v \times n$ 个新息值为阈值 ${J_n}$ 。

1.2 检测方法与野值处理

1）计算目标向量

将待检测新息数据 ${x'}$ ，加入到新息样本滑动窗 $X$ 中得到新样本，对 ${x'}$ 进行规范化，根据式（1）得到目标向量：

$y = {x'}{P_{PC}} \in {R^{1 \times l}}\text{。}$

(5)

2）计算距离检测量

本文采用文献[16]提出的使用一类SVM模型的相反数作为检测量的方法，计算距离检测量为：

$F(t) = - \sum\limits_{i = 1}^n {{\alpha _i}K({y_i}} y) + b\text{。}$

(6)

2）野值的识别与处理

1）新息的野值识别

若 $F(t) < {J_n}$ ，则新加入的新息 ${x'}$ 为正常值；若 $F(t) > $ $ {J_n}$ ，则可以认定新息 ${x'}$ 为野值，证明相对应的量测值为野值。

2）野值处理

传统的处理方法大多为将野值剔除，如果有数量较多的野值，剔除的方法有可能造成滤波的估计精度下降甚至发散。本文采用指数加权的方法，通过对滑动窗内正常的新息进行赋权，估计出野值新息处的“正确”新息，以替代野值新息。按照时间轴距离野值越近的新息权值越高，越远的新息权值越低，目的是使得越靠近野值的正常新息越能在对野值新息的估计中占有更大的比重。

权值系数应满足

$\sum\limits_{i = 0}^{n - 1} {{\beta _i}} = 1\text{，}$

(7)

权值系数因子为 $d = [(1 - r)/(1 - {r^{n - 2}})]$ ，其中 $r$ 为遗忘因子，根据经验通常取0.95～0.99。

这样可以得到滑动窗内所有权值系数计算公式

${\beta _i} = d{r^{i - 1}}\text{，}$

(8)

通过权值系数可以估计出“正确”新息替代野值新息

${x_n} = {x_{n - 1}}{\beta _1} + {x_{n - 2}}{\beta _2} + \cdots + {x_1}{\beta _{n - 1}}\text{。}$

(9)

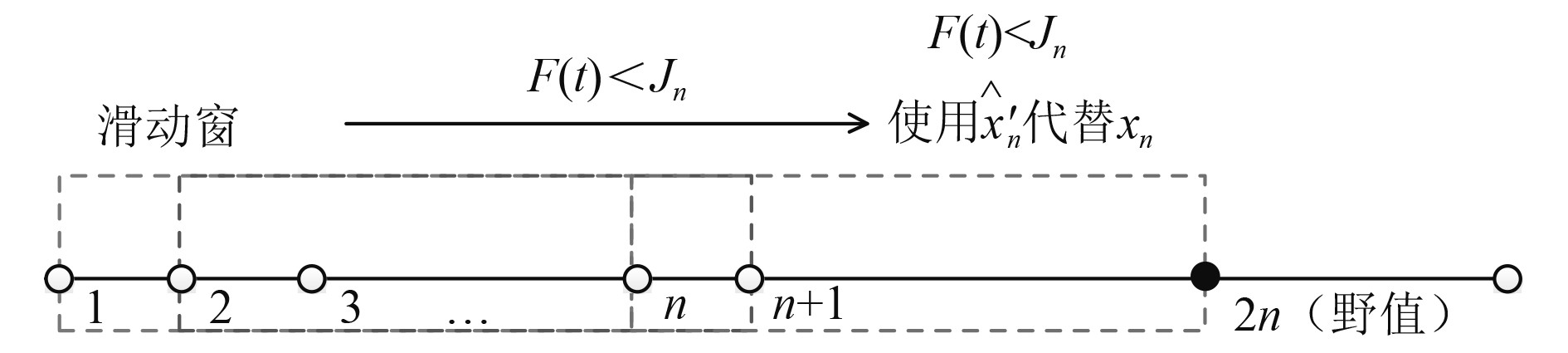
这样通过指数加权就可以消除量测值野值对滤波效果影响。与传统的直接对量测值野值进行剔除的方法相比，该方法不影响滤波的量测更新，避免了滤波由于缺少量测更新造成的估计精度急剧下降甚至发散的情况。野值识别与处理的示意图如图2所示。

1.3 SVM-UKF算法

对于捷联惯性基松组合下的直接法组合导航，状态量为 $\hat x_{k - 1}^{} = {\left[ {{{\hat \varphi }_{k - 1}},{{\hat p}_{k - 1}},\hat v_{k - 1}^{},\hat \varepsilon _{k - 1}^{},\hat \nabla _{k - 1}^{}} \right]^{\rm{T}}}$ ， ${\hat \varphi _{k - 1}}$ 表示 $k - 1$ 时刻姿态估计值， ${\hat p_{k - 1}}$ 表示 $k - 1$ 时刻位置估计值， $\hat v_{k - 1}^{}$ 表示 $k - 1$ 时刻速度估计值， $\hat \varepsilon _{k - 1}^{}$ 表示 $k - 1$ 时刻陀螺漂移， $\hat \nabla _{k - 1}^{}$ 表示 $k - 1$ 时刻加速度计零偏，采用捷联惯导基本方程，该方程为非线性模型：

${x_k} = f({x_{k - 1}}) + {w_{k - 1}}\text{，}$

(10)

${y_k} = h({x_k}) + {r_k}\text{，}$

(11)

式中， ${x_k}$ 表示 $k$ 时刻的状态量， ${y_k}$ 表示 $k$ 时刻的量测量， ${w_{k - 1}} \sim N(0,{Q_{K - 1}})$ 为系统噪声， ${r_{k - 1}} \sim N(0,{R_{K - 1}})$ 为量测噪声， $f( \bullet )$ 表示捷联惯导基本方程， $h( \bullet )$ 为量测模型，对 $h( \bullet )$ 进行离散化处理可以得到 $H( \bullet )$ 。

SVM-UKF算法流程如下：

1）时间更新

定义状态量 $\hat x_{k - 1}^{} = {\left[ {{{\hat \varphi }_{k - 1}},{{\hat p}_{k - 1}},\hat v_{k - 1}^{},\hat \varepsilon _{k - 1}^{},\hat \nabla _{k - 1}^{}} \right]^{\rm{T}}}$ ，

使用UT变化构造sigma点 ${\chi _{k - 1}}\left( i \right) = sigma ( {{\hat x}_{k - 1}}, $ $ {P_{k - 1}} )$ ，

通过系统模型更新得到 $\chi _{k/k - 1}^{}\left( i \right)$ ，

状态预测均值与协方差为：

${\hat x_{k/k - 1}} = \sum\limits_{i = 0}^{2n} {w\left( i \right){\chi _{k/k - 1}}\left( i \right)}\text{，} $

(12)

$\begin{split} {P_{k/k - 1}} =& \sum\limits_{i = 0}^{2n} {w\left( i \right)\left( {{\chi _{k/k - 1}}\left( i \right) - {{\hat x}_{k/k - 1}}} \right)} \times \\ & {{{\left( {{\chi _{k/k - 1}}\left( i \right) - {{\hat x}_{k/k - 1}}} \right)}^{\rm T}}} + {Q_{k - 1}} \text{。} \end{split} $

(13)

2）量测更新

计算新息并代入滑动窗：

$re{s_k} = {\hat y_k} - h{\hat x_k}\text{，}$

(14)

若新息为野值，使用指数加权计算替代值后代入量测更新：

$re{s_k} = re{s_{k - 1}}{\beta _1} + re{s_{k - 2}}{\beta _2} + \cdots + re{s_1}{\beta _{k - 1}}\text{，}$

(15)

若新息为正常值，直接进入量测更新：

${{{y}}_{{k}}}{\rm{ = }}{{{H}}_{{k}}}{{{x}}_{{k}}}{\rm{ + }}{{{\eta }}_{{k}}}\text{，}$

(16)

${{{x}}_{{k}}}{\rm{ = }}{{{x}}_{{{k/k - 1}}}}{\rm{ + }}{{{K}}_{{k}}}{{re}}{{{s}}_{{k}}}\text{，}$

(17)

${{{P}}_{{k}}}{\rm{ = }}[{{{I}}_{{n}}}{\rm{ - }}{{\rm{K}}_{{k}}}{{{H}}_{{k}}}]{{{P}}_{{{k/k - 1}}}}\text{，}$

(18)

${{{K}}_{{k}}}{\rm{ = }}{{{P}}_{{{k/k - 1}}}}{{H}}_{{k}}^{\rm{T}}{[{{H}}_{{k}}^{}{{{P}}_{{{k/k - 1}}}}{{H}}_{{k}}^{\rm{T}}{\rm{ + }}{{{R}}_{{k}}}]^{ - 1}}\text{。}$

(19)

2 实验及分析

通过实验对所研究的SVM-UKF方法估计效果进行评价。实验采用位置作为量测量SINS/GPS松组合方式。

实验采用激光陀螺捷联惯导与GPS组合实验数据来比较3种算法的估计效果。该实验中采用激光捷联惯导系统的输出数据，激光陀螺漂移约为0.01^° /h，加速度计零偏约为5×10⁻⁵ g。惯导IMU更新率为200 Hz，GPS接收机更新率为1 Hz，水平速度误差小于0.1 m/s，位置误差小于2 m。

初始速度姿态位置由激光捷联惯导提供。

$\begin{split} {P_0} = &{\rm{Diag}}([[1;1;1]*glv.{\rm{deg}}; \\ &0.1;0.1;0.1; \\ &10/{R_\lambda };10/{R_\lambda };10{)^2} \text{，} \end{split} $

$glv.deg = {\rm{ 0}}{\rm{.0175}}\text{，}$

${R_0} = {\rm{diag}}{(1;1;1{\rm{)}}^2}\text{，}$

${Q_0} = {\rm{diag}}{([web;wdb;{0_{3 \times 1}}])^2}\text{，}$

${R_\lambda } = {\rm{6378137}}\text{，}$

$web = [0.29 \times {10^{ - 4}};0.29 \times {10^{ - 4}};0.29 \times {10^{ - 4}}]\text{，}$

$wdb = [0.97 \times {10^{ - 4}};0.97 \times {10^{ - 4}};0.97 \times {10^{ - 4}}]\text{。}$

实验过程共10000 s，本文选取5800～6700 s的900 s数据进行研究，该段中航行轨迹见图3，五角星表示船的初始位置，圆点表示船的末端位置。在GPS输出中每隔60 s加入800 m的位置误差模拟GPS出现野值，以未加入野值的SINS/GPS组合导航系统的结果作为参考基准，由于航海更关注位置与航向，因此给出组合导航的位置与航向估计效果如图4～图6所示。

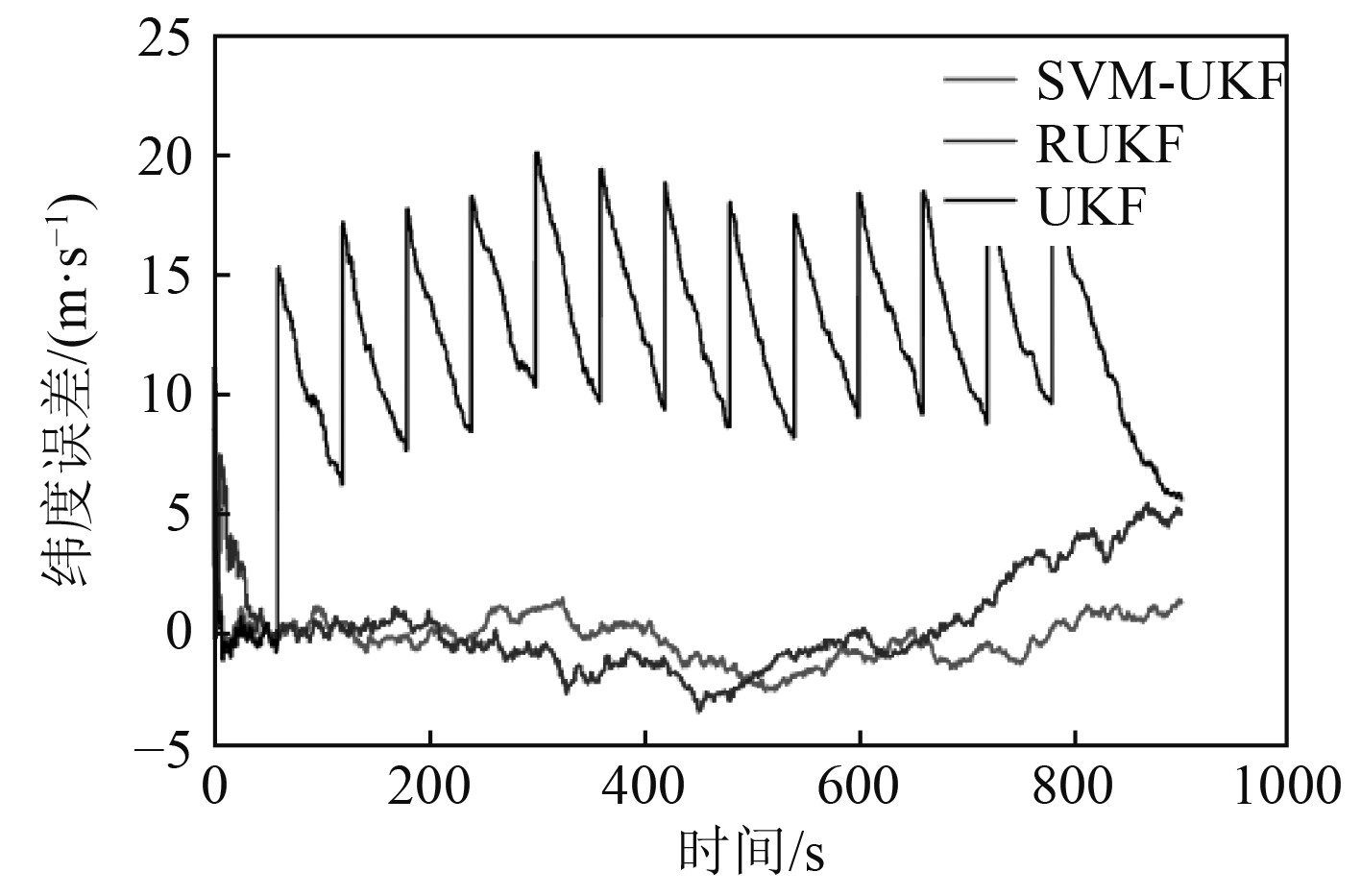
图4与图5表示了位置的估计结果，可以看到UKF受到野值的干扰已经发散，RUKF与SVM-UKF则表现出较好的估计效果。表1给出了不同算法的位置、航向、东向、北向速度的RMSE统计数据结果。由表1可以看出，RUKF方法的位置误差为4.968 m，航向误差5.43′，北向速度估计误差0.08/s，东向速度估计误差0.07 m/s，SVM-UKF方法的更好，位置误差和航向误差分别为2.474 m和3.34′，北向、东向速度估计误差为0.04 m/s与0.06 m/s。

根据实验结果，可以得出结论。在位置估计中，虽然RUKF有一定的鲁棒性，但野值以及鲁棒算法还是影响了滤波器的估计精度，SVM-UKF的估计效果比RUKF提高50.2%。分析航向的估计结果可以发现，RUKF虽然具有一定的鲁棒性，由于受到野值的干扰，SVM-UKF的估计效比RUKF提高38%。在速度估计方面，北向速度的估计精度SVM-UKF比RUKF提高了50%，东向速度的估计精度SVM-UKF比RUKF提高了14.2%。

3 结　语

捷联惯性基组合导航中，量测值存在野值的情况时有发生，这个问题都会导致UKF的估计精度下降。针对这些问题，本文提出了一种基SVM-UKF算法。通过使用一类支持向量机训练滑动窗，按照新息是否为进行分类，对于异常的新息采用指数加权的方法进行估计，使用新的估计值替换野值。进行了船载实验对SINS/GPS系统进行算法的性能检验。通过与UKF，RUKF相比较，证明了算法的有效性，得到结果：在实验中，SVM-UKF对比于RUKF，位置估计精度、航向估计精度分别提高了50.2%与38%，北向、东向速度对比于RUKF分别位置估计精度，航向估计精度提高了50%与14.2%。