2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074;
4. 中国地质大学(武汉) 海洋学院,湖北 武汉 430074
2. China Ship Development and Design Center, Wuhan 430064, China;
3. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology (HUST), Wuhan 430074, China;
4. College of Marine Science and Technology, China University of Geosciences, Wuhan 430074, China
随着人类社会经济的发展,石油、天然气、煤等常规能源已经不能满足人们的长远需求。核能作为人类最具希望的未来能源,它的合理开发利用成为人们关注的热点。海上浮式核电平台的开发,可以很好地解决海洋工业发展所需的能源需求[1]。海上核电平台船在船尾通过单点系泊方式系泊在海洋中时,主机舱内排出的温排水会随着水流方向流向核反应堆舱外,这会使核反应堆冷却水系统进水口的海水温度升高,从而影响冷却效果。因此,研究海上核电平台船的温排水在船体外域流场扩散的影响因素,减小温排水对核反应堆冷却水温度场的影响,对核电平台的安全运行具有重要意义。
当前,研究者们主要是采用数值模拟的方法来计算水流场和温度场[2-3]。Ardalan等[4]运用CFD方法并采用k−ε湍流模型,对在均匀、稳定的环境中,以45°排放角度的热盐流出物进行数值模拟,发现将发电厂的温污水和海水淡化厂的含盐污水混合形成热含盐污水,可以更好地改善排放系统性能的结论。Chen等[5]使用RANS方程和标准湍流模型,模拟了在规则波中的中等深度处水平排放浮力圆形射流的流场变化情况,给出了不同动量比下射流振荡的机理,并发现射流扩散过程中最关键的因素是波高与水深的比值。田力荣等[6]运用了三维数值模拟方法研究了在不同洋流速度和进、出水口布置方式下,浮式核电站周围海域温度尤其是循环冷却水进水口的温度场,得到了在底进侧排的布置方式下,冷却水进水口温升为零,而在底进底排的布置方式下,随着洋流速度的增大,温排水射流扩散范围会更广,进水口温升更大的结论。孙玉贤[7]选取了RNG k-ε紊流模型作为数学计算模型,采用有限体积法对同流环境中的浮力射流的控制方程进行了离散,结合压力—速度耦合算法(SIMPLE算法),求解出单孔浮射流和三孔浮射流的水力特性并进行了试验研究和对比验证。李慧子[8] 采用有限体积法结合Reynolds平均法对海上核电平台船的温排水在船体外域流场中的温度扩散规律进行了三维数值模拟。卿晓霞等[9]采用有限体积法,研究了江水源热泵系统尾水在江河水域中排放的温度扩散规律。该数值仿真模型得到的计算值与实际测量温度的相对误差在1.73%以内,说明所采用的方法能够很好地对江河流域的温度场进行数值模拟。目前,针对海上核电平台船外域温度场的扩散问题,还缺乏深入的探讨。本文通过不同环境水流速度、不同排水角度和不同排水口形状条件下的温排放进行数值计算,找到浮式核电平台主机舱温排水的排水口的最佳设计参数。
1 数值模拟方法数值方法是通过求解质量守恒方程、动量守恒方程及能量守恒方程来得到近似的物理解。Reynolds平均法(也称RANS方法)是目前工程上使用最为广泛的湍流数值模拟方法。该方法假设湍流运动物理量的值可以看作由瞬时脉动值和时间平均值叠加而成,其湍流时均流动的控制方程[10]为:
连续方程
| $\frac{{\partial \rho }}{{\partial t}} + {\rm{div}}(\rho u) = 0{\text,}$ | (1) |
动量方程(Navier-Stokes方程)
| $\begin{split}\frac{{\partial \left( {\rho \bar u} \right)}}{{\partial t}} + {\rm{div}}(\rho \bar u\bar u) =& {\rm{div}}(\mu grad \bar u) - \frac{{\partial \bar p}}{{\partial x}} + \\ &\left[ { - \frac{{\partial \left( {\rho \overline {u{'^2}} } \right)}}{{\partial x}} - \frac{{\partial \left( {\rho \overline {u'v'} } \right)}}{{\partial y}} - \frac{{\partial \left( {\rho \overline {u'w'} } \right)}}{{\partial z}}} \right] + {S_u}{\text,}\end{split}$ | (2) |
| $\begin{split}\frac{{\partial \left( {\rho \bar v} \right)}}{{\partial t}} + {\rm{div}}(\rho \bar v\bar u) =& {\rm{div}}(\mu grad \bar v) - \frac{{\partial \bar p}}{{\partial y}} + \\ &\left[ { - \frac{{\partial \left( {\rho \overline {u'v'} } \right)}}{{\partial x}} - \frac{{\partial \left( {\rho \overline {v{'^2}} } \right)}}{{\partial y}} - \frac{{\partial \left( {\rho \overline {v'w'} } \right)}}{{\partial z}}} \right] + {S_v}{\text,}\end{split}$ | (3) |
| $\begin{split}\frac{{\partial \left( {\rho \bar w} \right)}}{{\partial t}} \!+\! {\rm{div}}(\rho \bar w\bar u) \!=& {\rm{div}}(\mu grad \bar w) - \frac{{\partial \bar p}}{{\partial z}} +\\ &\left[ { - \frac{{\partial \left( {\rho \overline {u'w'} } \right)}}{{\partial x}} \!-\! \frac{{\partial \left( {\rho \overline {v'w'} } \right)}}{{\partial y}} \!-\! \frac{{\partial \left( {\rho \overline {w{'^2}} } \right)}}{{\partial z}}} \right] \!+\! {S_w}{\text,}\end{split}$ | (4) |
能量方程
| $\begin{split}\frac{{\partial \left( {\rho \bar T} \right)}}{{\partial t}} \!+\! {\rm{div}}(\rho \bar u\bar T) \!=& {\rm{div}}(\Gamma grad \bar T) +\\ &\left[\! { - \frac{{\partial \left( {\rho \overline {u'T'} } \right)}}{{\partial x}}\! \!-\!\! \frac{{\partial \left( {\rho \overline {v'T'} } \right)}}{{\partial y}}\! \!-\! \!\frac{{\partial \left( {\rho \overline {w'T'} } \right)}}{{\partial z}}} \!\!\right] \!\!+\! {S_T}{\text。}\end{split}$ | (5) |
其中:
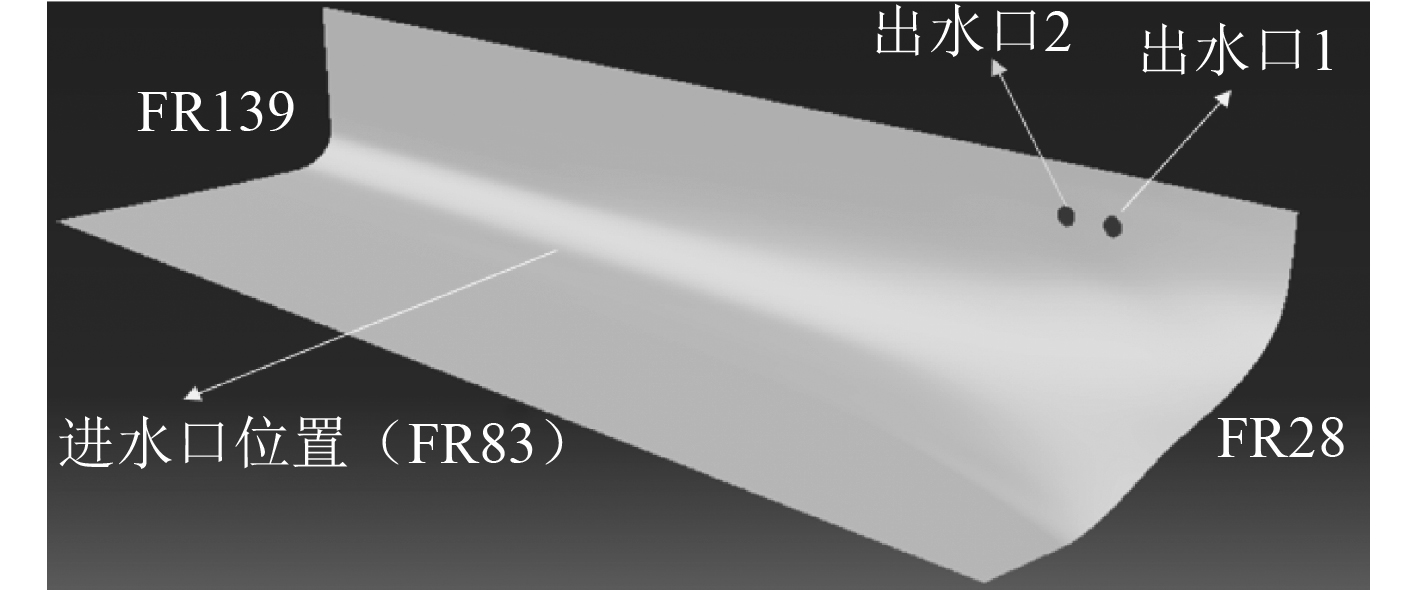
本文研究对象为海上核电平台船,船体主要尺度参数如表1所示。由于船体左右对称,并且主要是研究在出水口与进水口之间的船体表面及其外流域的温度场,所以只取其水下部分的船体左舷和沿船长方向FR28-FR139(肋位)之间的部分建立计算模型。定义:首垂线与基平面的交点为坐标原点;沿船长方向船尾指向船首为x轴正方向;船体左舷指向右舷为y轴正方向;船底沿吃水方向往上为z轴正方向。出水口(直径750 mm)位于FR42-FR48范围内,中心位置高度为6.32 m;进水口(直径1100 mm)中心位置位于FR83处,高度位置为6.32 m。船体表面模型如图1所示。
|
|
表 1 船体主要尺度参数 Tab.1 Principal dimensions of ship |
|
图 1 船体表面模型 Fig. 1 Ship surface model |
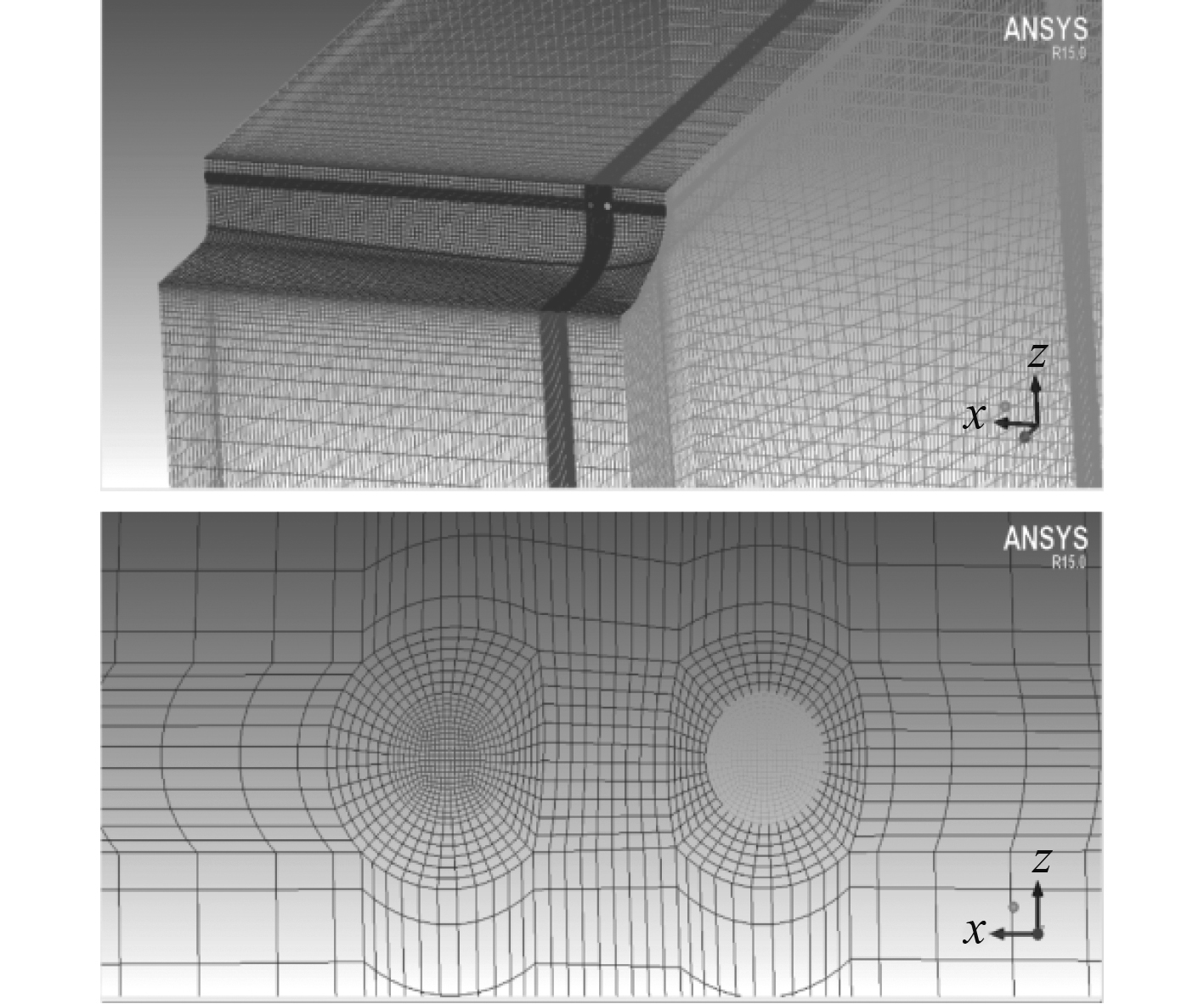
计算域的横向长度约为船宽的5倍,计算域的垂向长度约为吃水的5.5倍。采用六面体网格离散流体计算域,出水口处采用了O-Block网格划分方法,如图2所示,整体网格的质量在0.65以上。计算边界条件如表2所示。
|
图 2 计算域及出水口网格分布 Fig. 2 Grid of calculation domain and outfall |
|
|
表 2 边界条件设置 Tab.2 Boundary conditions setting |
海上浮式核电站正常工作时漂浮在水面上,在系泊系统的作用下船体位置一般不会发生较大的改变,但由于环境水流流速会不断发生变化,从而会对船体周围流域的温度场产生一定的影响。为了探讨环境水流流速对温度场的影响,本文选取多个不同的水流速度进行分析,具体计算工况如表3所示。
|
|
表 3 不同流速计算工况 Tab.3 Calculation conditions of different flow velocities |
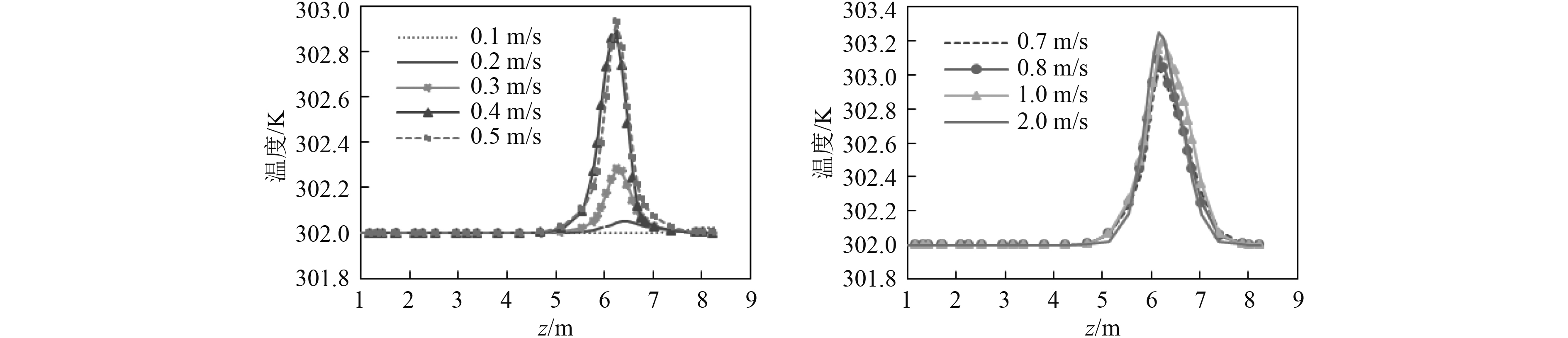
按表3中计算工况对环境水流入口的流速进行改变,得到船体表面温度云图和船体进水口表面温升曲线如图3和图4所示。当环境水流流速为0.1 m/s时,进水口表面最高温升为0.024 K,出水口的温排水对进水口表面附近流域的温度场影响很小。温排水主要沿着出水口的流速方向扩散,这是由于温排水与环境水流存在温差,密度会有所不同,在浮力的作用下,温排水沿重力方向发生了扩散,这种沿重力方向扩散的现象在环境水流流速很小的情况下尤为明显。当环境水流流速增大至0.4 m/s时,进水口表面最高温升为0.871 K,较之前流速为0.1 m/s,0.2 m/s,0.3 m/s时有了较大的提升,并且随着水流速度的不断增大,温排水沿着环境水流的流速方向扩散趋势越来越明显,进水口表面最高温升也越来越大。此时由于水流流速较大,浮力的影响越来越小以至于忽略不计,并且温排水沿出水口流速方向的扩散趋势也被减弱。当环境水流流速为2.0 m/s时,进水口表面最高温升最高为1.248 K。从图4可以看出,随着水流流速的增大,最高温升的增长速度不断变缓。表明当流速超过某一范围,流速的增大已经不能使得进水口附近流域的温度场发生较大变化。

|
图 3 不同水流流速下的温度场变化 Fig. 3 Temperature field variation at different flow velocities |
|
图 4 不同水流流速下进水口表面温度沿z轴变化 Fig. 4 The inlet surface temperature changes along the z axis at different flow velocities |
假设最开始的温排水垂直出射时排水角度为0°,排水方向(即出水口流速方向)向船尾方向偏移为正,向船首方向偏移为负。环境水流流速为0.5 m/s,具体计算工况如表4所示。
|
|
表 4 不同排水角度计算工况 Tab.4 Calculation conditions of different drainage angles |
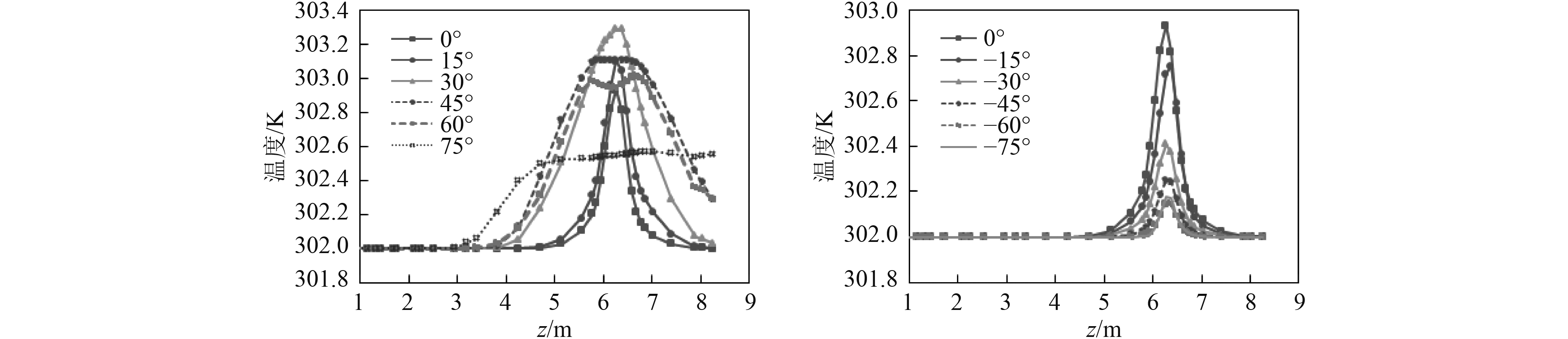
按表4的计算工况对出水口温排水的流速方向进行改变,得到船体表面温度云图和船体进水口表面温升曲线如图5~图7所示。当排水方向向船尾偏移时,随着排水角度的增大,温排水扩散的范围更广,这是因为当排水角度为正时,排水口排出的温排水流速在沿船长方向上(即x方向上)有一个与环境流速相反方向的速度分量,导致了在出水口附近的流体有一个激烈的碰撞,温排水与环境水流的混合更加充分均匀,扩散范围也就更广。当排水角度大于0°且小于60°时,进水口表面的温升比不改变排水角度时要大,其中排水角度为30°时,温升值最大为1.291 K;当排水角度超过60°时,进水口表面的温升比不改变排水角度时要小,其中排水角度为75°时,温升值最小为0.571 K。当排水方向向船首偏移时,随着排水角度的增大,温排水往外(即y轴负方向)扩散的趋势越明显,温度云图上具体表现为,温度较高的流体离船表面越来越远。总体来看,排水角度为负时,进水口表面的温升都比排水角度为0°时要小。当排水角度在−60°~0°之间时,随着排水角度绝对值值不断增大,温升越来越小,其中排水角度为−60°时,温升值最小为0.146 K;当排水角度为−75°时,温升值为0.178 K,比60°时稍大。

|
图 5 不同排水角度(正)下的温度场变化 Fig. 5 Temperature field variation at different drainage angles (positive) |

|
图 6 不同排水角度(负)下的温度场变化 Fig. 6 Temperature field variation at different drainage angles (negative) |
|
图 7 不同排水角度进水口表面温度沿z轴变化 Fig. 7 The inlet surface temperature changes along the z axis at different drainage angles |
正常圆形排水孔直径为750 mm,在保证排水孔面积和温排水质量流速相等的前提下,另外选取方形和三角形作为排水孔的形状,模拟不同排水孔形状下,船体周围流体温度场的变化。图8为3种排水孔计算模型的网格划分情况,其中方形排水孔和圆形排水孔采用O-Block网格划分,三角形排水孔采用Y-Block网格划分,模型其他部分网格的划分情况保持不变。

|
图 8 三种排水孔计算模型的网格划分 Fig. 8 Grid generation of three different outfalls |
分别对排水形状为圆形、方形和三角形3种情况进行计算,得到的船体表面温度云图和船体进水口表面温升曲线如图9和图10所示。观察三者的温度云图可以发现在出水口附近流域处,排水孔形状为圆形和方形时温度场的差别不大,但形状为三角形时的温度场改变较大;在离出水口一段距离后,三者的温度场几乎一样。排水孔形状为圆形时进水口表面最高温升值最大,为0.931 K;方形次之,最高温升值为0.846 K;三角形最高温升值最小,为0.556 K。

|
图 9 不同排水孔形状下的温度场变化 Fig. 9 Temperature field variation at different outfalls |

|
图 10 不同排水孔形状下进水口表面温度沿z轴变化 Fig. 10 The inlet surface temperature changes along the z axis at different outfalls |
本文开展了海上核电平台船的温排水在船体外域流场中的温度扩散数值仿真。针对不同环境水流速度、不同排水角度和不同排水口形状条件下的温排放进行了数值计算,得到如下结论:
1)当环境水流流速较小时,温排水主要沿着出水口的流速方向和重力方向扩散,此时进水口表面温升较小;当环境水流流速较大时,温排水主要沿着环境水流的流速方向扩散,此时进水口表面温升较大。
2)当排水方向向船尾偏移时,由于温排水与环境水流混合的更加充分,温排水扩散范围较广,此时船舶周围流域的流场和温度场在趋于稳定后呈现一种周期性的变化。在排水角度小于60°时,进水口表面的温升比不改变排水角度时要大。当排水方向向船首方向偏移时,温排水向外扩散的趋势更加明显,此时进水口表面的温升比不改变排水角度时要小。
3)在出水口附近流域处,排水孔形状为三角形时的温度场有所不同。而离出水口一段距离后,圆形、方形和三角形3种情况下的温度场差别不大。此外,排水孔形状为圆形时进水口表面温升最大,方形次之,三角形最小。
| [1] |
兰志刚, 李新仲, 肖钢, 等. 海上浮式核电站温排水对海洋生态环境的影响[J]. 海洋科学, 2016, 40(6): 84-88. DOI:10.11759/hykx20151008004 |
| [2] |
熊立众, 孙江龙. 轮缘推进器水动力性能数值分析[J]. 舰船科学技术, 2021, 43(3): 83-88. XIONG L Z, SUN J L. Numerical analysis of hydrodynamic performance of rim driven propeller[J]. Ship Science and Technology, 2021, 43(3): 83-88. |
| [3] |
王小川, 杨立, 薛蒙. 潜艇排气集水箱内部流场及温度场的数值模拟[J]. 舰船科学技术, 2010, 32(4): 109-112. WANG X C, YANG L, XUE M. Numerical simulation of the flow field and temperature field inside the water-collecting box of submarine[J]. Ship Science And Technology, 2010, 32(4): 109-112. DOI:10.3404/j.issn.1672-7649.2010.04.027 |
| [4] |
ARDALAN H, VAFAEI F. CFD and experimental study of 45°inclined thermal-saline reversible buoyant jets in stationary ambient[J]. Process, 2019(6): 219. DOI:10.1007/s40710-019-00356-z |
| [5] |
Y. L. CHEN, S. C. Hsiao. Numerical modeling of a buoyant round jet under regular waves[J]. Ocean Engineering, 2018(161): 154-167. |
| [6] |
田力荣, 方园, 杨继飞, 等. 浮动式核电站温排水热扩散模拟研究[J]. 汽轮机技术, 2019, 61(4): 271-274. DOI:10.3969/j.issn.1001-5884.2019.04.009 |
| [7] |
孙玉贤. 同流中热水浮射流的数值模拟及试验研究[D]. 西安: 西安理工大学, 2009.
|
| [8] |
李慧子, 刘安涟, 刘毅. 温排水对船体外域水流温度场影响计算[J]. 中国舰船研究, 2019, 14(S1): 82-89. |
| [9] |
卿晓霞, 张景尧, 周健, 等. 江水源热泵系统尾水排放试验模型的数值模拟[J]. 中南大学学报(自然科学版), 2016, 52(5): 703-707. |
| [10] |
P. ROLLET-MIET, D. LAURENCE, J. FERZIGER. LES and RANS of turbulent flow in tube bundles[J]. International Journal of Heat and Fluid Flow. 1999, 20(3): 241−254.
|
 2021, Vol. 43
2021, Vol. 43
