自升式平台是海洋作业平台中应用最广泛的一类平台,其依靠桩腿站立于海底,桩腿承担着平台主体的重量和外部环境载荷,对整个平台的安全性起着至关重要的作用。自升式平台桩腿的形式并不唯一,对比于其他形式的桩腿,桁架式桩腿[1]结构的细长比更小,所遭受的水动力载荷更小,加上其桁架式结构形式具有较高的强度,因而具有较高的安全性和材料利用率,在大型自升式平台中应用更为普遍。桁架式桩腿由3根带齿条的竖向弦杆和多根撑管组成,其横向尺寸远远小于其纵向尺寸。
在整条桩腿中,弦杆发挥着举足轻重的作用。例如,平台的升降操作需要依托弦杆来完成,平台在作业工况和自存工况下,弦杆是主要的承力构件,进而关系到整座平台的安全性。因此,对弦杆所遭受的水动力载荷进行[2]研究,是保证整座平台安全性的重要工作之一。
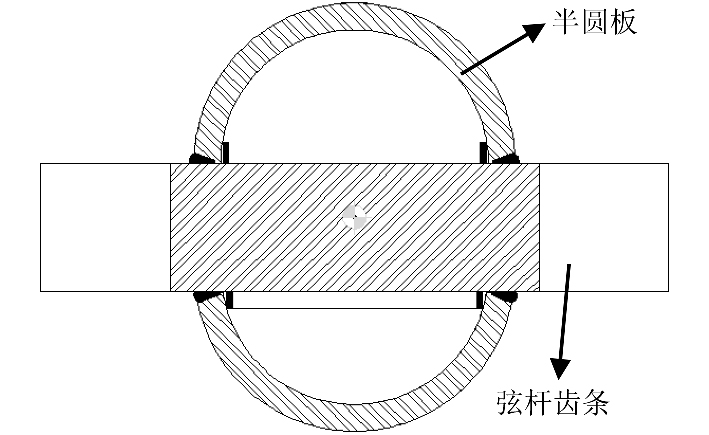
弦杆的结构形式与圆柱形的撑杆不同,其剖面呈不规则的几何形式,如图1所示。
|
图 1 桁架式桩腿弦杆剖面示意图 Fig. 1 Chord section geometry |
弦杆由2块半圆板和1块齿条板焊接而成,沿着弦杆的轴向,齿条的尺寸呈一定的几何规律改变。本文对带有复杂齿条结构的弦杆绕流流场进行分析,以得到弦杆的水动力特性。
根据学者们的大量研究[3-4],钝体的结构形式发生些许改变,构件周围的流场特性将随之发生较大的改变。对于弦杆而言,矩形齿条的存在使得弦杆周围的流场特性与以往学者们所研究的钝体周围的流场特性完全不同。国内外学者针对圆柱绕流、方柱绕流以及波浪圆柱绕流等[5-11]进行了大量的研究,但对于弦杆形式的钝体绕流,却鲜有论文和专著公开发表,而自升式平台桩腿的现行设计分析中,也很少考虑涡激振动的影响,为平台的生产作业埋下了安全隐患。基于此,本文以自升式平台典型桁架式桩腿的弦杆为切入点,针对其绕流机理进行研究,为桩腿的安全可靠设计提供理论依据。
1 控制方程假设海水为黏性不可压缩流体,分析过程中海水温度保持恒定,忽略温度的变化影响,则弦杆绕流流场的控制方程为N-S方程[12],包括质量守恒方程和动量守恒方程。
质量守恒定律:单位时间内流体微团中的质量增加等于同一时间间隔内流入该微团的静质量,即
| $\nabla \cdot V = 0\text{,} $ | (1) |
动量守恒定律:流体微团的动量变化率等于作用在该流体微团上的所有外力之和,则有:
| $\rho \left( {\frac{{\partial V}}{{\partial t}} + V \cdot \nabla V} \right) = - \nabla p + \mu {\nabla ^2}V + \rho g\text{,}$ | (2) |
自升式平台工作于海洋中,大部分桩腿结构位于海平面以下,弦杆遭遇波浪和海流的共同作用,其周围水质点的速度波动范围较大,加上弦杆结构本身的特征尺寸达到0.5 m左右,因而弦杆周围流场的雷诺数Re可达到105以上,弦杆周围绕流流场往往处于湍流状态。
处于湍流状态的流体微团,可假设随时间变化的物理量始终围绕某一平均值上下脉动,即可认为:瞬时值=时均值+脉动值。将此概念应用于动量方程(2)中的速度项,湍流瞬时速度
| $\frac{{\partial \overline {{u_i}} }}{{\partial t}} + \overline {{u_j}} \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} = {\bar f_i} - \frac{1}{\rho }\frac{{\partial \bar p}}{{\partial {x_i}}} + \nu {\nabla ^2}\overline {{u_i}} - \frac{{\partial \overline {u_i'u_j'} }}{{\partial {x_j}}}\text{。}$ | (3) |
式中:
由于Reynolds应力是未知量,因此,对湍流问题的求解还需建立Reynolds应力输运方程以及选择适当的湍流模型。
| $\left\{ \begin{split} \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = &\frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} + {G_b} -\\ &\rho \varepsilon - {Y_M} + {S_k} \text{,} \\ \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) =& \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) +{C_{1\varepsilon }}\frac{\varepsilon }{k}( {G_k} +\\ &{C_{3\varepsilon }}{G_b} ) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} - {R_\varepsilon } + {S_\varepsilon } \text{。} \\ \end{split} \right.$ | (4) |
其中:
| ${C_{1\varepsilon }}{\rm{ = }}1.42 - \frac{{\eta \left( {1 - \eta /{\eta _0}} \right)}}{{1 + \beta {\eta ^3}}}{\rm{ = }}1.42 - \frac{{\eta \left( {1 - \eta /4.377} \right)}}{{1 + 0.012{\eta ^3}}}\text{,}$ |
| ${C_{2\varepsilon }}=1.68\text{,}$ |
| $\eta {\rm{ = }}{\left( {2{E_{ij}} \cdot {E_{ij}}} \right)^{1/2}}\frac{k}{\varepsilon }\text{,}$ |
| ${E_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\text{,}$ |
| ${\mu _{eff}}{\rm{ = }}\mu + {\mu _t}{\rm{ = }}\mu + \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }{\rm{ = }}\mu + 0.0845\rho \frac{{{k^2}}}{\varepsilon }\text{。}$ |
式中:
RNG
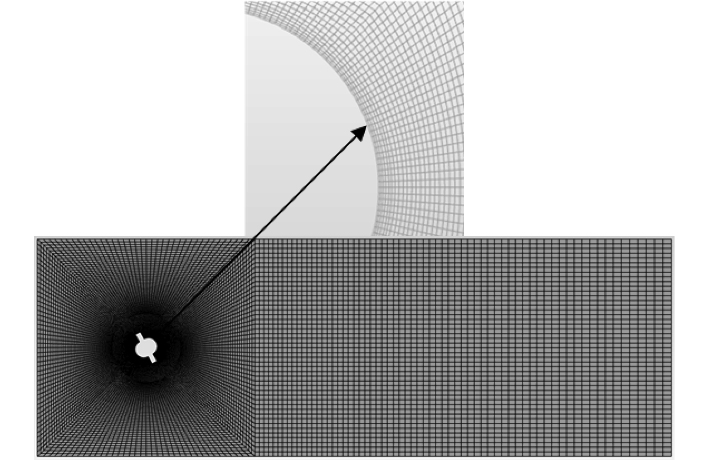
以某300 ft自升式钻井平台为例,令弦杆的特征尺寸为D,则齿条板的厚度T=0.25D,齿高H=0.303D,分析流域范围及弦杆附近网格分别如图2和图3所示。

|
图 2 流场建模范围及边界条件 Fig. 2 Model range and boundary conditions |
|
图 3 流场网格 Fig. 3 Mesh division diagram |
弦杆齿条板与来流流速的夹角称为流向,为得到不同流向对弦杆绕流流场的影响结果,在分析中,对同一较高Re下,对0°,15°,30°,45°,60°,75°,90°共7个流向的弦杆绕流流场进行分析。
数值求解中,压力项选择PRESTO!格式离散,Momentum项选择QUICK格式离散,对湍动能和耗散率项则选用具有绝对稳定性能的2阶迎风格式,然后选用具有无条件稳定性的全隐式积分方案在时间域上离散控制方程,最后采用SIMPLEC算法求解所得到的代数方程组。
3 分析结果为探究齿条对弦杆绕流流场的影响,首先分别给出相同绕流流场下、不带齿条结构和带齿条结构(0°流向)的流场分析结果以作对比,如图4和图5所示。

|
图 4 不带齿条结构的流场分布图 Fig. 4 Flow field without rack structure |

|
图 5 带齿条结构的流场分布图 Fig. 5 Flow field with rack structure |
根据对比可知:
1)二者绕流流场物理量的整体分布相似,在钝体的迎流面一侧形成低速高压区,在背流面一侧形成低速低压区,在钝体两侧形成高速低压区,在尾流区生成湍动能;
2)在相同的外界流场中,不带齿条结构的绕流流场的压力分布云图、速度分布云图和湍动能分布云图均呈规则的S形分布,而带齿条结构的绕流流场,在0°来流条件下,各压力云图呈现出尾巴状,二者间的区别较大;
3)在0°来流条件下,通过压力云图的对比分析可以发现,与不带齿条结构的尾流流场相比,带齿条结构的尾流流场的低压区集中于弦杆尾部附近,集中低压区的面积更大;
4)在0°来流条件下,齿条结构具有一定的导流作用,使得钝体绕流流场的速度梯度、压力梯度降低,延迟涡激振动的发生。
由此可见,齿条的存在,使得钝体绕流流场发生了较大的改变,而钝体绕流流场特性又直接影响到钝体所遭受的水动力载荷。水动力载荷是自升式平台的控制载荷之一,对于小尺度结构物所遭受的水动力载荷,可采用半理论、半经验的Morison方程进行计算,应用该公式的关键是弦杆拖曳力系数Cd的选取,以及规范中提及但实际工程中很少有设计者考虑的升力系数Cl,水动力系数Cd和Cl大小选取的准确性直接影响到平台桩腿所遭受水动力载荷分析的准确性,从而最终影响到桩腿结构级结构形式的设计。
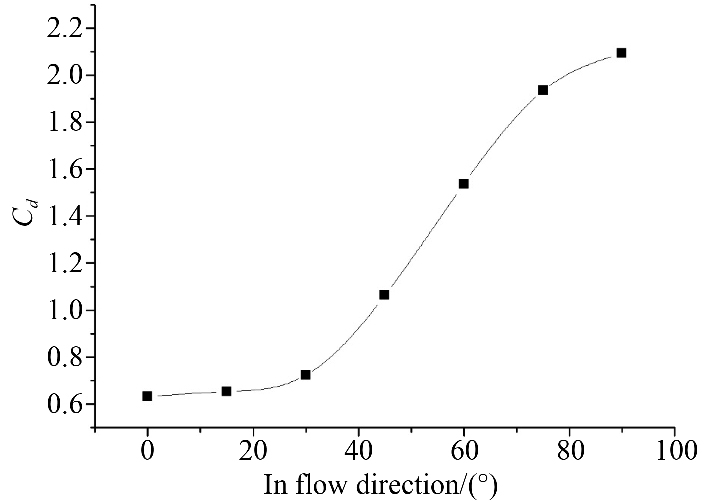
同时,齿条与来流方向的夹角同样会影响到钝体绕流流场特性。图6为不同来流方向下弦杆拖曳力系数Cd的分析结果。
|
图 6 不同流向下的水动力系数Cd Fig. 6 Hydrodynamic coefficient Cd under different inflow directions in flow direction |
由图6可知:
1)随着弦杆齿条与来流速度之间夹角的角度增加,拖曳力系数Cd也随之增加;
2)在来流角度小于30°以前,拖曳力系数Cd的增加较为缓慢;
3)来流角度一旦大于30°,拖曳力系数Cd迅速增加,在90°时达到最大;
4)在0°来流下,拖曳力系数最小,即Cdmin=0.63,在90°来流下,拖曳力系数最大,即Cdmax=2.1,最大值与最小值之间相差达到了3倍以上。
一般地,自升式平台包含3条桩腿,每条桩腿包含3根弦杆,各弦杆的齿条板方向并不相同,因而相同的流场中,不同方位的弦杆会产生不同的流向角。故在实际工程中,从桩腿所遭受水动力载荷最小的角度考虑,建议平台的安放方位应使得弦杆在常年中大部分时间里处于最接近于顺流向方向。
90°来流下,弦杆的水动力系数较大,因此单独分析弦杆在该流向下、不同Re下的Cd和Cl值,如表1所示。
|
|
表 1 不同Re下的Cd时均值和Cl最大值 Tab.1 Cd and Cl under different Re in 90 ° inflow direction |
由表1可知:
1)在所分析的Re区间内,当Re较低时,Cd值较大,但无Cl值,说明此时的流动状态处于层流状态;
2)随着Re的增加,Cd值逐渐降低,降低到在2.5上下浮动;
3)当Re=370,Cl值开始出现,Cl=0.321,说明此时弦杆尾流产生了明显的涡激振荡,而在所有计算的Re范围内,此时的Cd值最小;
4)与Cd值变化趋势不同的是,随着Re的增加,Cl值逐渐增加,最大值已经超过了1;
5)无论是弦杆的Cd时均值、还是Cl时历幅值,均远大于相同情形下圆柱形结构的相应值。
由此可见,与常规钝性体相比,弦杆的齿条结构的对其绕流流场的影响非常大,导致其水动力系数Cd和Cl值均比较大,即带有齿条的弦杆所遭受的拖曳力更大,高雷诺数下其横流方向的升力同样较大。这表明在相同的特征尺度、相同的环境条件下,弦杆受到的水动力载荷更大、更复杂,这也为自升式平台桩腿的设计提出了更大的挑战。
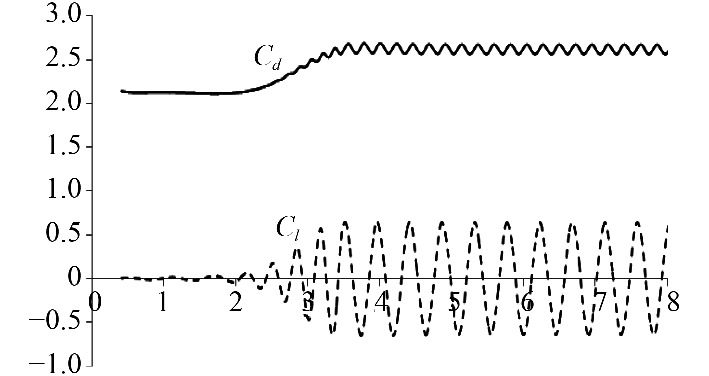
既然Re是决定弦杆尾流场状态的重要因素,而弦杆的尾流场状态又决定了Cd,Cl的时历过程,因此,不同Re数的Cd,Cl的时历规律也不同。图7和图8分别给出了90°来流下,Re=1100,443050的Cd和Cl时历曲线。
|
图 7 Cd和Cl时历曲线 (Re=1110) Fig. 7 Time history curves of Cd and Cl(Re=1110) |
|
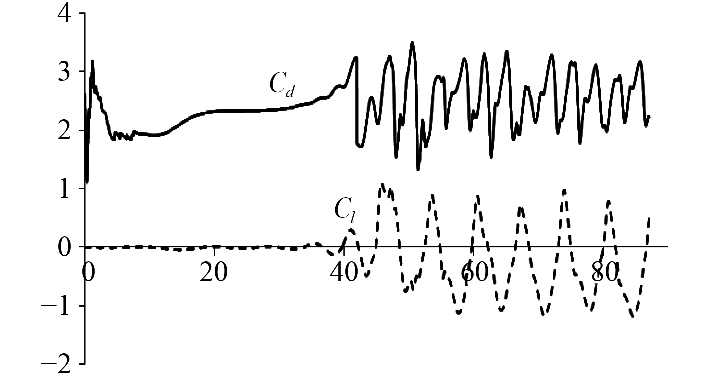
图 8 Cd和Cl时历曲线 (Re=443050) Fig. 8 Time history curves of Cd and Cl(Re=443050) |
1)在Re=1100时,拖曳力系数Cd和升力系数Cl均呈现出有规律的周期性,振荡周期的大小相同,每个振荡周期内的时历过程也基本相同;
2)在Re=1100时,Cd在均值2.619附近上下振荡,振荡幅值较小,Cl在0值上下振荡;
3)在Re=1100时,Cl的振荡周期为Cd的振荡周期的2倍,与圆柱绕流结果相同;
4)在Re=1100时,根据Cl的振荡周期,得到St约为0.11,与圆柱绕流的结果相差较大;
5)在Re=443050时,拖曳力系数Cd和升力系数Cl整体也表现出一定的规律性,但不再具有固定的周期,每个周期内部的时历过程也不相同;
6)在Re=443050时,Cd在均值附近上下振荡,但与Re=1100相比,其振荡幅值明显大得多,Cl同样是在0值上下振荡;
7)在Re=443050时,Cl的振荡周期同样约略为Cd的振荡周期的2倍;
8)在Re=443050时,根据Cl的振荡周期,得到St约为0. 062,与Re=1100的结果相差较大,同样与圆柱绕流的结果相差也较大。
根据前述分析可知,由于齿条的存在,弦杆的绕流流场具有更大的压力差、更剧烈的涡激振荡,从而导致Cd和Cl值更大,且在高雷诺数下,其振荡幅值也较大。故带有齿条的弦杆所遭受的水动力载荷更大,剧烈的载荷振荡可能给弦杆带来较大的疲劳损伤。
为了进一步说明不同Re的弦杆绕流尾流流场特征,图9~图12分别给出了90°流向下,Re分别等于74,370,1110,443050的弦杆绕流流场湍动能的分布云图。
|
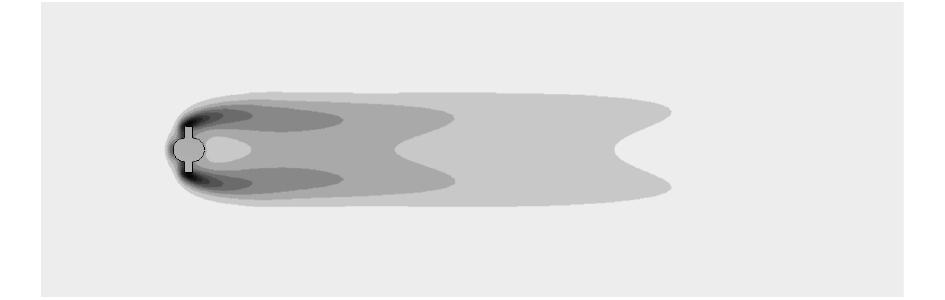
图 9 湍动能分布云图 (Re=74) Fig. 9 Contour of turbulent kinetic energy (Re=74) |

|
图 10 湍动能分布云图 (Re=370) Fig. 10 Contour of turbulent kinetic energy (Re=370) |

|
图 11 湍动能分布云图 (Re=1110) Fig. 11 Contour of turbulent kinetic energy (Re=1110) |

|
图 12 湍动能分布云图 (Re=443050) Fig. 12 Contour of turbulent kinetic energy (Re=443050) |
根据各云图的分析结果,可知:
1)弦杆齿条结构剖面为矩形,故90°来流下,在所计算的Re数范围内,流动分离点始终位于齿条的尖点;
2)当Re=74,弦杆后方过流断面较宽,形成较大的低压区,从而形成较大的Cd值,在此Re下已经有明显的涡生成,但涡并没有脱落;
3)当Re=370,1100,弦杆来流后方尾涡区变窄,生成明显的对称涡,对称涡出现摆动,呈“S”形依次向下游运动,可观察到明显的漩涡交替脱落现象,且Re增大后的涡迹更长;
4)当Re=443050,弦杆后方的尾流场呈完全的湍流状态,涡的形状并不规则,弦杆附近脱落的涡还未长大,就迅速向下游迁移,涡的影响域已经超出计算域;
5)随着Re的增大,脱落的涡与涡之间的距离也增加,高Re的流场,其不稳定的尾流涡的生成、迁移和消失表现为一定的随机性,弦杆绕流流场更加复杂;
6)Re=443050,弦杆后方的尾流场呈完全的湍流状态,能够详细观察到大涡的生成、脱落和迁移,甚至能够观察到较小的涡丝,但由于采用RANS湍流模型进行计算,无法捕捉到小尺度涡的生成、运动和耗散过程。
4 结 语本文对不同Re数下二维弦杆绕流流场进行模拟,根据分析结果可知,RNG
沿弦杆轴向齿条的存在使得弦杆几何形式沿其轴向发生变化,弦杆周围流场呈现出强烈的三维[13-14]效应,因此应进一步研究齿形对弦杆绕流的影响。
| [1] |
朱亚洲, 孙承猛, 林海花, 等. 自升式平台桁架式桩腿结构选型方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 155-161. DOI:10.11918/j.issn.0367-6234.2016.10.023 |
| [2] |
CAO Y, NIE W, HU X, et al. Parameter sensitivity study of dynamic response for jack-ups by FEM analysis[J]. Ocean Engineering, 2016, 124(15): 125-134. |
| [3] |
ALAM, M. M., MEYER, J. P.. Global aerodynamic instability of twin cylinders in cross flow[J]. Journal of Fluids Structure,, 2013, 41: 135-145. DOI:10.1016/j.jfluidstructs.2013.03.007 |
| [4] |
LIN Y F, BAI H L, ALAM M M, et al. Effects of large spanwise wavelength on the wake of a sinusoidal wavy cylinder. J. Fluids. Struct., 2016, 61: 392–409.
|
| [5] |
GUSTAVO R. S. ASSI, PETER W. BEARMAN. Vortex-induced vibration of a wavy elliptic cylinder[J]. Journal of Fluids Structure, 2018, 80: 1–21.
|
| [6] |
谷家扬, 蒋汝斌, 渠基顺. 不同流向下低质量比方形四立柱涡激运动特性研究[J]. 船舶工程, 2015, 37(1): 40-44. |
| [7] |
端木玉, 万德成. 不同长细比圆柱绕流的大涡模拟[J]. 水动力学研究与进展(A辑), 2016, 31(1): 295-302. |
| [8] |
林凌霄, 陈威, 林永水. 单双圆柱涡激振动数值模拟研究[J]. 舰船科学技术, 2020, 42(7): 49-53. LIN Ling-xiao, CHEN Wei, LIN Yong-shui. Numerical simulation of vortex-induced vibration of single or double circular cylinders[J]. Ship Science and Technology, 2020, 42(7): 49-53. DOI:10.3404/j.issn.1672-7649.2020.07.010 |
| [9] |
孙洪源, 黄维平, 李磊, 等. 低长径比浮式圆柱涡激运动实验研究[J]. 船舶力学, 2019, 23(4): 405-411. SUN Hong-yuan, HUANG Wei-ping, LI Lei,et al. Experimental study on vortex induced motions of a floating cylinder with low aspect ratio[J]. Journal of Ship Mechanics, 2019, 23(4): 405-411. |
| [10] |
高云, 张壮壮, 杨斌等. 圆柱体横流与顺流方向涡激振动耦合模型研究[J]. 振动与冲击, 2020, 39(11): 22-30.
|
| [11] |
武磊, 赵伟文, 万德成. 不同浸没长度下串列双立管涡激振动数值模拟[J]. 海洋工程, 2020, 38(3): 52-61. WU Lei, ZHAO Wei-wen, WAN De-cheng. Numerical simulations on vortex-induced vibrations(VIV) of two tandem risers with different submerged lengths[J]. The Ocean Engineering, 2020, 38(3): 52-61. |
| [12] |
王福军. 计算流体动力学分析—CFD软件原理与应用. 北京: 清华大学出版社, 2004.
|
| [13] |
杨春蕾, 朱仁传, 缪国平, 等. 基于RANS和DES法船体绕流模拟及不确定度分析[J]. 上海交通大学学报(自然版), 2012, 46(3): 430-435. |
| [14] |
赵伟文, 万德成. 用SST-DES和SST-URANS方法数值模拟亚临界雷诺数下三维圆柱绕流问题[J]. 水动力学研究与进展(A辑), 2016, 31(1): 1-8. ZHAO Wei-wen, WAN De-cheng. Numerical study of 3D flow past a circular cylinder at subcritical Reynolds number using SST-DES and SST-URANS[J]. J. Chinese Journal of Hydrodynamics(A), 2016, 31(1): 1-8. |
 2021, Vol. 43
2021, Vol. 43
