随着海洋探索的深入,大量的海上结构物被广泛布置以满足海洋资源开发的需求。然而,诸如海洋平台等海上结构物往往需要一个稳定的作业环境保证其安全和正常工作,防波堤应运而生[1-2]。按布置方式,防波堤分为固定式和浮式防波堤2种,随着人类逐渐向深远海迈进,固定式防波堤造价急剧上升,阻断洋流影响海洋生物等劣势越来越明显。与固定式防波堤相比,浮式防波堤因其适应性好、建造维护成本低、对海洋环境影响小等优势得到越来越多的使用。但是,浮式防波堤在作为海洋平台等海上结构物消波减能掩体的同时,会受到严重的波浪砰击载荷,对自身结构安全产生威胁,在浮式防波堤的研究中,既要关注其消波能力的好坏,同时也不可忽视防波堤自身安全性能[3-5]。
波浪砰击问题最早出现在船舶领域,船首出入水时都会受到明显的波浪砰击现象,威胁船舶的安全。关于砰击问题以理论研究、试验研究以及数值模拟为主,最先起源于二维楔形体入水的问题[6]。但理论推导不能将砰击过程中的所有问题充分考虑,试验研究对人力物力消耗过大,因此数值仿真仍是最主流的分析方法。本文基于CFD方法,采用STARCCM+软件,充分考虑流体粘性,对锚链锚泊式浮式防波堤和垂直导桩锚泊式浮式防波堤分别进行数值模拟,深入探究波高以及周期变化下,砰击载荷沿防波堤的分布规律,并对不同锚泊方式下浮式防波堤的砰击载荷以及运动响应进行对比,最终揭示其砰击响应规律。
1 数学模型 1.1 流体控制方程计算流体力学CFD是在计算机科学进步下发展起来的一门介于流体力学、数学以及计算机科学之间的综合学科,建立在流体力学控制方程的基础上。控制方程从本质上讲是物理守恒定律的数学表达式,主要遵循的物理定律包括流体质量守恒定律、动量守恒定律以及能量守恒定律,鉴于本文未考虑温度变化的影响,因此仅考虑前两项,具体表达如下:
1)连续性方程
连续性方程是质量守恒定律在流体力学中的具体表达,对流体采用连续介质模型,密度和速度在时间以及空间上都是连续、可微函数,数学表达式为:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_x})}}{{\partial x}} + \frac{{\partial (\rho {u_y})}}{{\partial y}} + \frac{{\partial (\rho {u_z})}}{{\partial z}} = 0\text{。}$ |
2)运动方程
运动方程是牛顿第二定律即动量守恒定在流体力学中的具体表达,假设流体不可压缩时,数学表达式为:
| $\begin{split} \rho \frac{{D{u_x}}}{{Dt}} = \rho {f_x} - \frac{{\partial p}}{{\partial x}} + \mu \left(\frac{{{\partial ^2}{u_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_x}}}{{\partial {z^2}}}\right)\text{,} \end{split} $ |
| $\begin{split} \rho \frac{{D{u_y}}}{{Dt}} = \rho {f_y} - \frac{{\partial p}}{{\partial y}} + \mu \left(\frac{{{\partial ^2}{u_y}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_y}}}{{\partial {z^2}}}\right)\text{,} \end{split} $ |
| $\begin{split} \rho \frac{{D{u_z}}}{{Dt}} = \rho {f_z} - \frac{{\partial p}}{{\partial z}} + \mu \left(\frac{{{\partial ^2}{u_z}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_z}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_z}}}{{\partial {z^2}}}\right) \text{。} \end{split} $ |
在现实情况中,波浪接触结构物时会发生剧烈运动,因此,在计算模型的选择上采用RNG
| $\begin{split} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = &\frac{\partial }{{\partial {x_j}}}\left[(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {x_j}}}\right] +\\ &{G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k} \text{,} \end{split} $ |
| $\begin{split} \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = &\frac{\partial }{{\partial {x_j}}}\left[(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}})\frac{{\partial \varepsilon }}{{\partial {x_j}}}\right] +\\ &({G_k} + {C_{3\varepsilon }}{G_b}) - C2\sigma \rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon } \text{。} \end{split} $ |
式中:k是由湍动能而产生的;
CDF方法从本质上讲是对一系列的偏微分方程进行求解,但直接求解很困难,因此通常将控制方程在空间上离散。主要的离散方法包括有限元法、有限差分法和有限体积法,本文选择有限差分法求解控制方程。
2 计算模型本文以方箱型浮式防波堤为研究对象,分别对应锚链锚泊以及垂直导桩锚泊2种锚泊方式,以1∶20缩尺比建立数值模型,同时改变波浪周期以及波高,研究砰击载荷沿防波堤的分布规律,并对不同锚泊方式下浮式防波堤的砰击载荷以及运动响应进行对比,最终揭示其砰击响应规律。
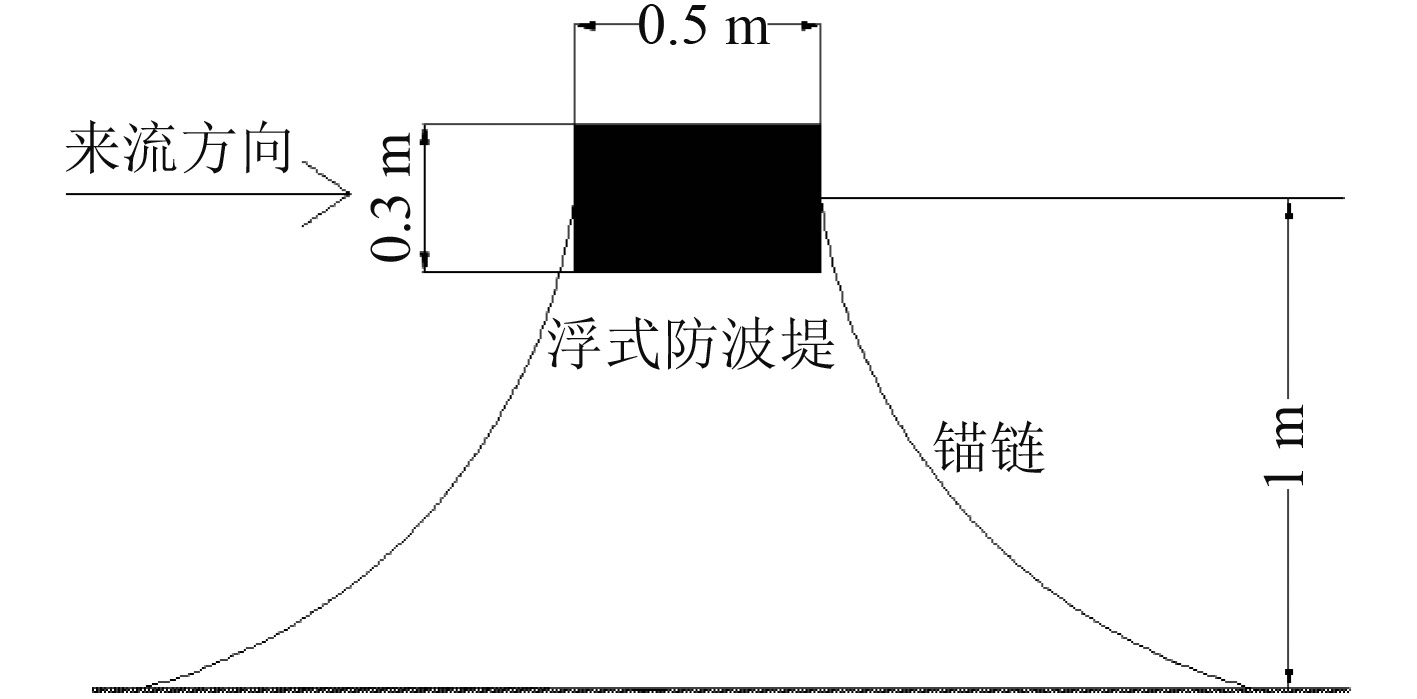
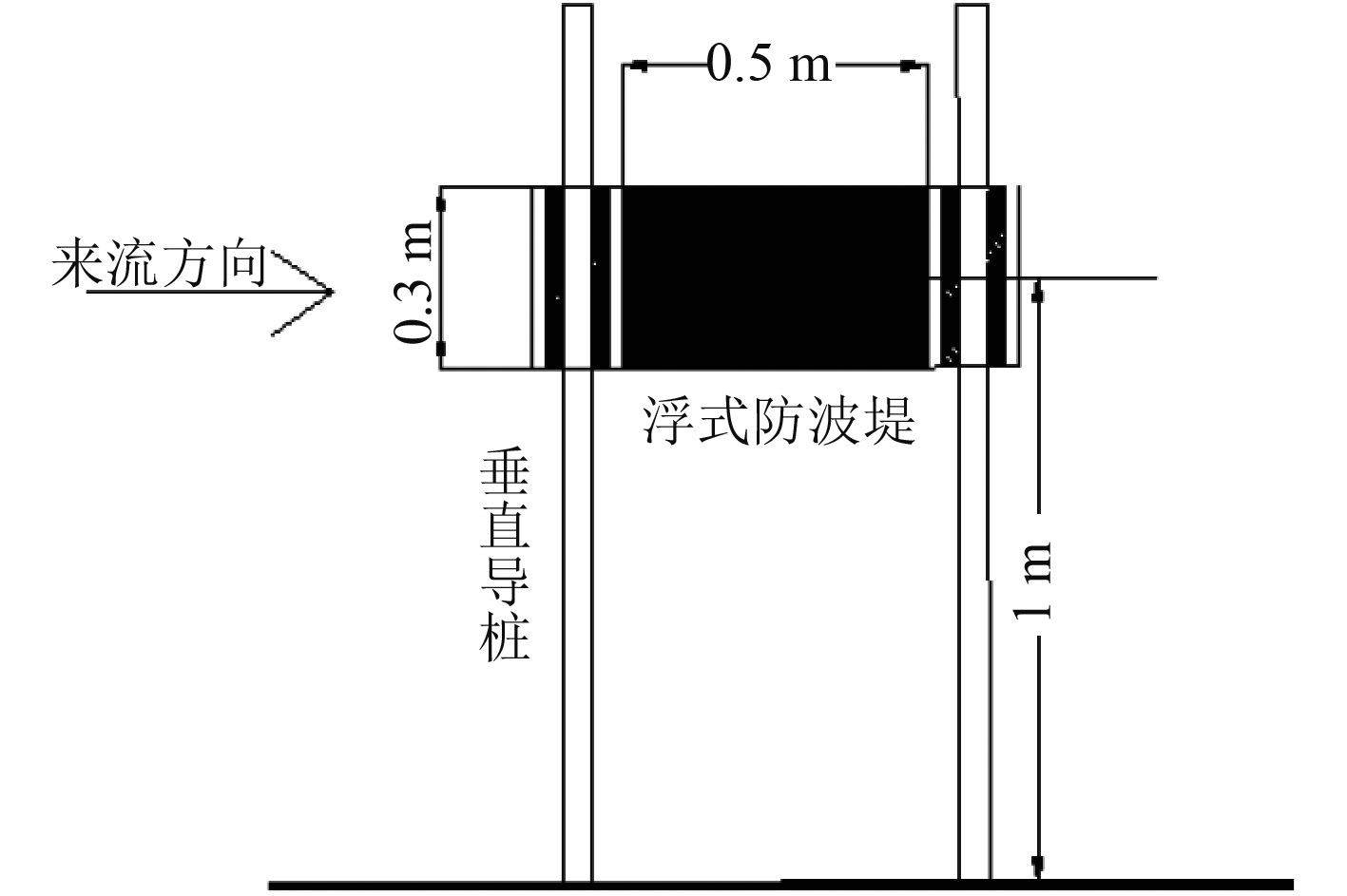
2.1 模型设计浮式防波堤原型堤长30 m,宽10 m,高6 m,吃水为3 m,按照缩尺比1∶20换算后,堤宽0.5 m,堤高0.3 m,吃水0.15 m,鉴于本文进行二维数值计算,因此浮式防波堤的堤长不在考虑范围内。本浮式防波堤分别采用锚链以及垂直导桩进行锚泊,具体锚泊设计如图1所示。
|
图 1a 锚链锚泊式浮式防波堤 Fig. 1a Floating breakwaters moored by chains |
|
图 1b 垂直导桩锚泊式浮式防波堤 Fig. 1b Floating breakwaters moored by vertical piles |
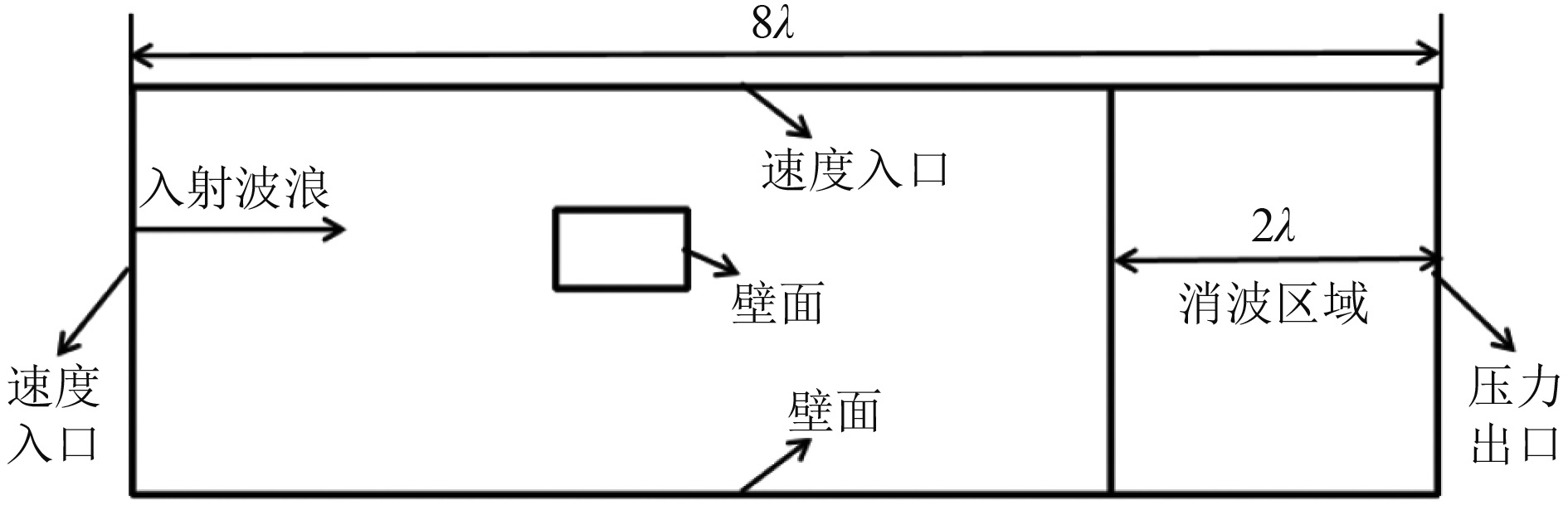
计算域设置的合理性与数值模拟准确性息息相关。参考前人的设置,计算域设置为8λ(λ为入射波波长),为了避免波浪反射影响模拟的准确性,在出口处设置2λ的消波区域。计算域左侧和顶端采用速度入口,右侧为压力出口,底部为壁面,两侧采用对称平面,防波堤表面设为壁面,具体设置如图2所示。
|
图 2 计算模型几何示意图 Fig. 2 Computing model geometric diagram |
波浪传播方向以及波高方向的网格数影响波浪波形,尤其在自由液面附近,波浪的波动剧烈,网格需要进行加密,根据前人的经验,波浪前进方向一个波长内网格设置为80个以上,波高方向网格设置为20个以上,远离自由液面网格逐渐变大。由于波浪砰击浮式防波堤运动剧烈,因此采用重叠网格技术,使重叠网格与浮式防波堤一起运动,对运动区域进行加密,网格尺寸与自由液面处波高方向的网格相同。表1和图3分别为波高0.1 m,周期1.1 s时具体网格划分参数和示意图。
|
|
表 1 模型网格参数 Tab.1 Model mesh parameters |

|
图 3 模型网格示意图 Fig. 3 Schematic diagram of model grid |
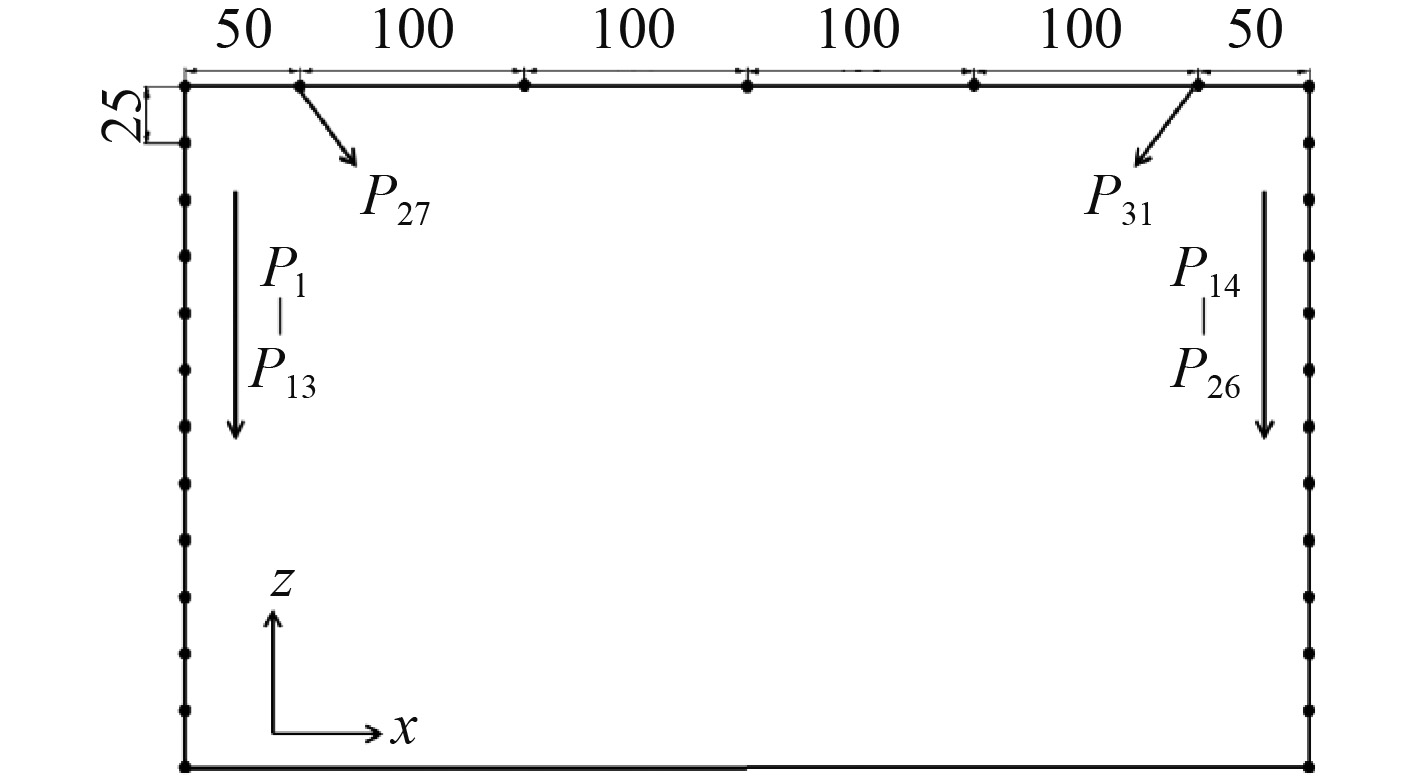
通过在防波堤表面布置测点对砰击载荷随时间变化进行监测。测点具体布置如图4所示,迎浪面处从上至下每25 mm布置一个测点,测点编号为P1~P13,背浪面处从上至下每25 mm布置一个测点,测点编号为P14~P26,防波堤顶端从P27开始每100 m设置一个测点至P31结束。
|
图 4 浮式防波堤测点布置示意图 Fig. 4 Schematic diagram of measuring point of floating breakwater |
试验水深1 m,采用规则波,波高0.1~0.2 m,周期1.1~1.5 s,具体波浪参数如表2所示。
|
|
表 2 波浪参数 Tab.2 Wave parameter |
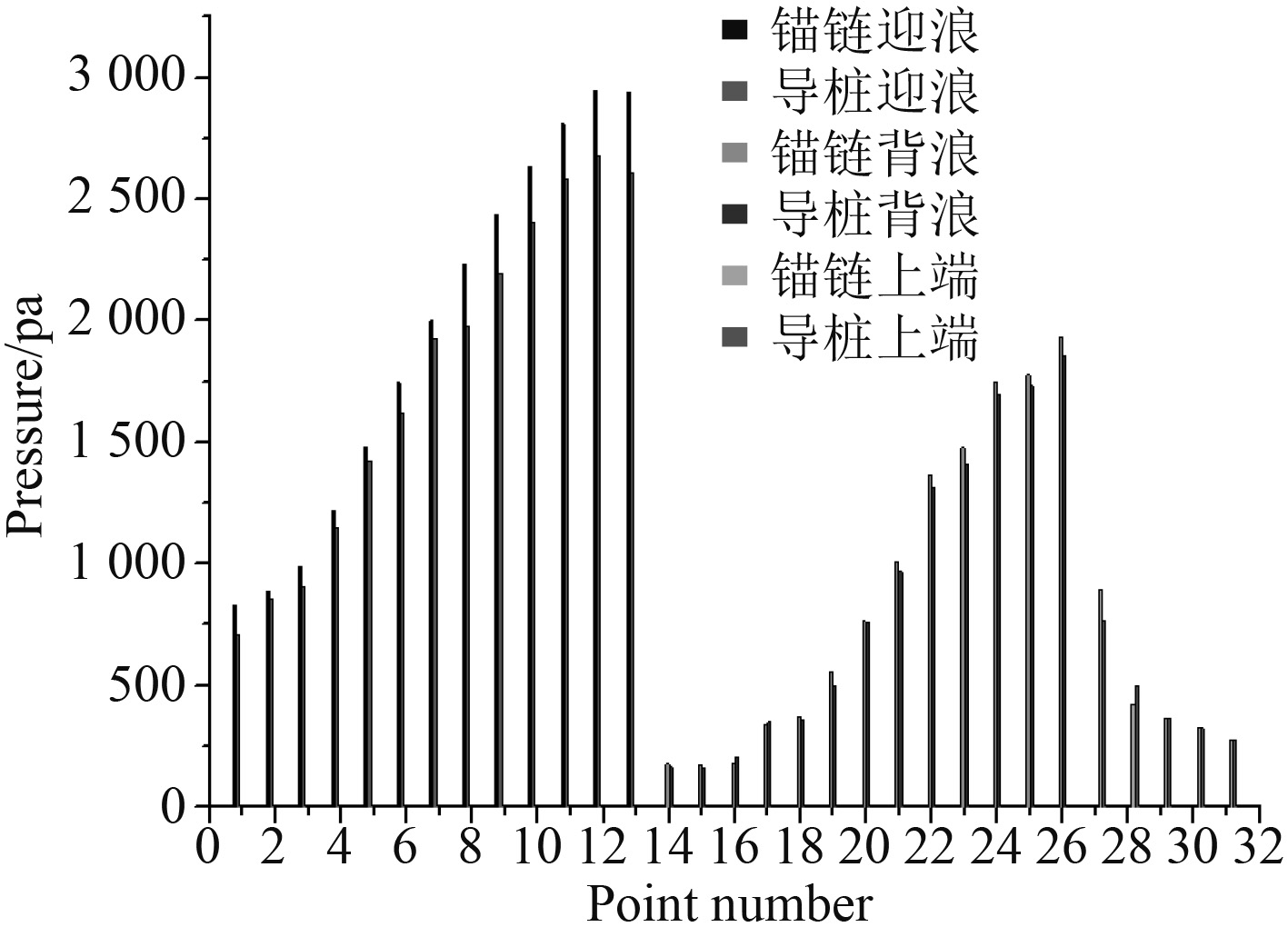
以波高0.2 m,周期1.2 s为例,分析浮式防波堤表面砰击载荷分布规律。表3是不同锚泊方式下不同测点的砰击压力极值,将表格中的数据绘制成条形图,以便更加清晰进行对比。如图5所示,从测点位置看,2种锚泊方式下,浮式防波堤迎浪面的砰击力显著大于背浪面以及防波堤上表面,从趋势上来看,除极个别测点外,2种锚泊方式下迎浪面以及背浪面的砰击压力均随深度的增加而增加,上表面测点的砰击压力沿来流方向逐渐减小。同时,还可以看出,采用锚链锚泊时,浮式防波堤的砰击压力较垂直导桩锚式会增大,这是由于此时的浮式防波堤存在横摇以及横荡,浮式防波堤运动的速度与水质点的速度相叠加,加重水体对浮式防波堤的冲击,造成砰击力的变大。P5~P9测点位于迎浪面自由液面附近,锚链锚泊时,其砰击载荷从1478 Pa增加至2436 Pa,占总体增幅的45%,导桩锚泊时,其砰击载荷从1322 Pa增加至2294 Pa,占总体增幅得51.1%,水线面位置,砰击载荷的变化尤为剧烈。
|
|
表 3 测点极值表 Tab.3 Extreme value table of measuring point |
|
图 5 测点极值图 Fig. 5 Extreme value graph of measuring point |
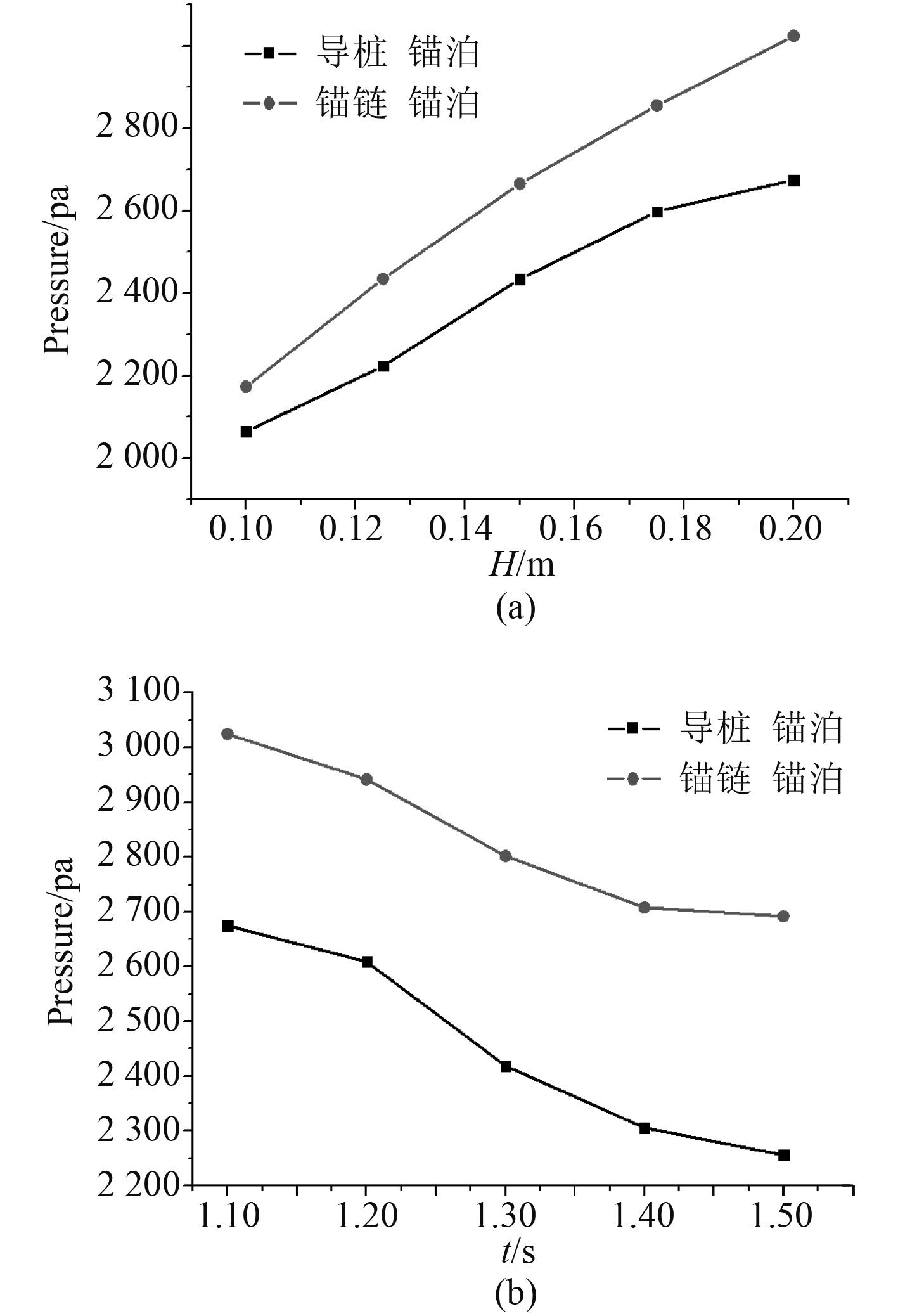
图6(a)为周期1.1 s时最大砰击载荷随波高变化的趋势。可以看出,随着波高的增大,2种锚泊方式下的最大砰击载荷都逐渐增大,这是由于随着波高增大,波浪所具有的的能量也就越大。图6(b)为波高0.2 m时浮式防波堤砰击载荷随周期变化的规律。可以明显看出,2种锚泊方式下的最大砰击载荷随周期的增大而减小。这是由于周期越小,波陡越大,浮式防波堤前端流场越剧烈,因此所造成的砰击载荷也越大。由图6还可以看出,锚链锚泊的浮式防波堤最大砰击载荷大于垂直导桩锚泊的浮式防波堤。同时,从变化幅度看,砰击载荷随波高的增幅明显减小,0.1~0.125 m时,锚链锚泊式浮式防波堤和导桩锚泊式浮式防波堤砰击载荷增幅分别为12%和7.5%,0.175~0.2 m时,增幅分别为5.9%和3.5%。而砰击载荷随周期的增大先减小,后趋于平缓,在1.2~1.3 s时,锚链锚泊式浮式防波堤砰击载荷减小最大为4.8%,导桩锚泊式浮式防波堤为7.2%。
|
图 6 最大砰击载荷变化趋势 Fig. 6 variation trend of maximum slamming load |
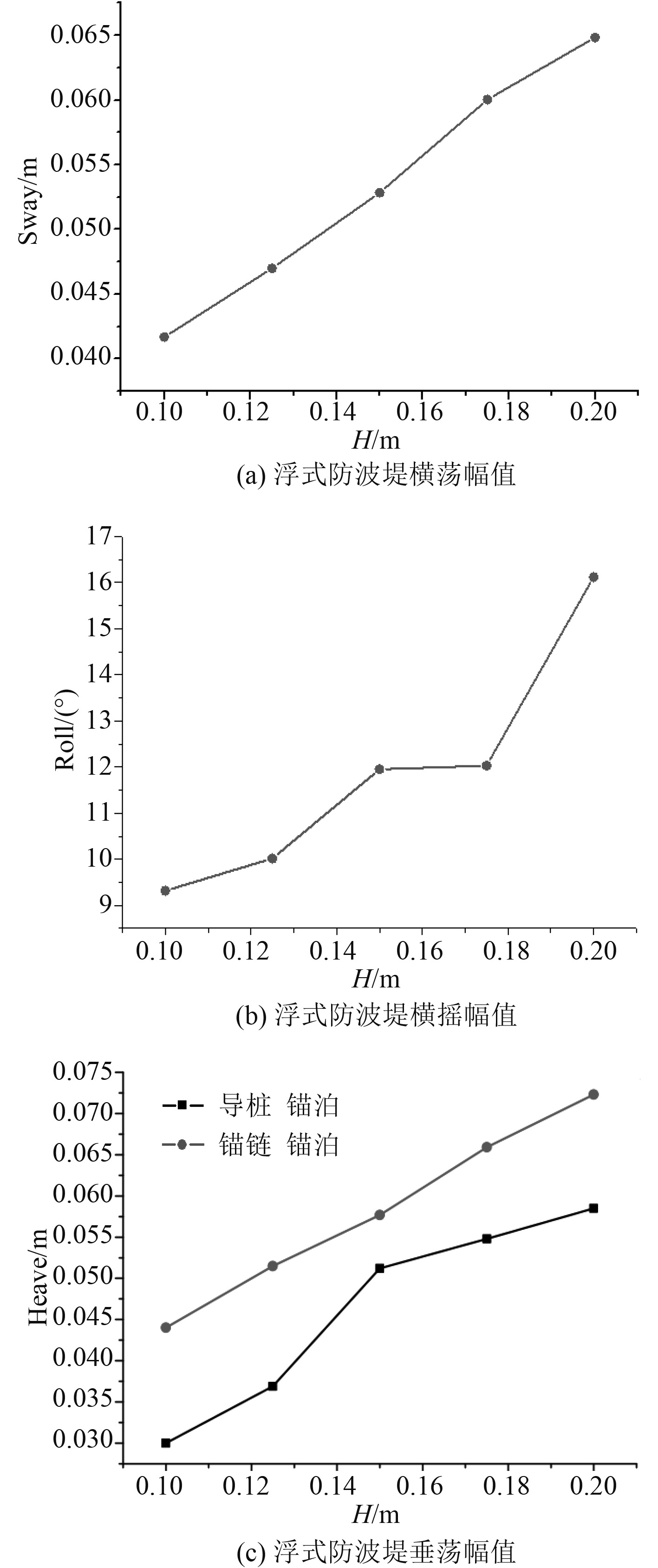
图7为规则波作用下,周期1.1 s时入射波高变化对浮式防波堤运动响应的影响。可以看出,随着波高的增加,2种锚泊方式下浮式防波堤的运动响应均逐渐增大。这是由于波高越大,波浪所具有的能量也就越大,造成的运动也就越激烈。由于垂直导桩锚泊的浮式防波堤仅存在垂荡一个自由度,因此,仅将2种系泊方式下浮式防波堤的垂荡响应进行对比。由图7(c)可以看出,锚链锚泊时,浮式防波堤的垂荡响应较大。0.1~0.2 m范围内,锚链锚泊式浮式防波堤横荡从0.042 m增加至0.065 m,增幅为54.7%;横摇从9.312°增加至16.12°,增幅为73.1%;垂荡从0.044 m增加至0.0724 m,增幅为64.5%,导桩锚泊式浮式防波堤垂荡从0.031增加至0.059,增幅为90.3%。
|
图 7 不同波高下浮式防波堤运动响应 Fig. 7 Motion responses of floating breakwater under different wave heights |
图8为规则波作用下,波高0.2 m时,波浪周期变化对浮式防波堤运动响应的影响。可以看出,锚链锚泊时,浮式防波堤的横荡以及垂荡响应均随周期的增大而增大,而横摇响应随周期的增大而减小。这是由于波浪与浮式防波堤之间存在相位差,短周期时,浮式防波堤由于惯性无法对波浪做出及时的回应,运动滞后于波浪,因此,垂荡和横摇较小。然而,周期越小,波长越短,波陡越大,防波堤前的流场越剧烈因此造成横摇响应越剧烈。与波高变化是趋势相同,锚链锚泊时浮式防波堤垂荡响应较大,但随着周期的增大,垂荡响应之间的差距逐渐减小,且其值都在波幅0.1 m附近,周期1.5 s时,锚链锚泊式浮式防波堤的垂荡为0.101 m,导桩锚泊式浮式防波堤的垂荡为0.102 m。

|
图 8 不同周期下浮式防波堤运动响应 Fig. 8 Motion responses of floating breakwater under different periods |
本文运用CFD方法,基于STAR-CCM+软件,分别以锚链锚泊式浮式防波堤和垂直导桩锚泊式浮式防波堤作为研究对象,分析规则波作用下,浮式防波堤的砰击载荷及其运动响应,并进行比较,得出以下结论:
1)2种锚泊方式下,浮式防波堤所受到的砰击载荷主要集中在迎浪面,在自由液面附近波动表现的尤为剧烈。随着深度的增加,测点所受的砰击载荷变大,0.2~1.2 s时其最大砰击载荷分别为2945 Pa和2677 Pa,位于迎浪面底部附近。
2)浮式防波堤所受的砰击载荷受波高以及周期的影响较为明显,随波高的增大而增大,随周期增大而减小,但趋于平缓。相同情况下,锚链锚泊式浮式防波堤所受砰击载荷较大。
3)2种锚泊方式下,浮式防波堤的运动响应均随入射波高的增大而增大,在0.1~0.2 m范围内,锚链锚泊式浮式防波堤横荡、横摇以及垂荡的增幅分别为54.7%,73.1%和64.5%,导桩锚泊式浮式防波堤垂荡增幅90.3%。浮式防波堤的横摇响应随周期的增大而减小,横荡以及垂荡响应与横摇趋势相反。
| [1] |
高振星. 浮式防波堤的研究及进展[J]. 中国科技论文, 2006, 5(6): 67-70. |
| [2] |
毛伟清. 浮式防波堤的研究[J]. 中国造船, 1994(4): 49-56. |
| [3] |
李芬, 邹早建. 浮式海洋结构物研究现状及发展趋势[J]. 武汉理工大学学报(交通科学与工程版), 2003(5): 100−104.
|
| [4] |
霍发力, 张健, 杨德庆. 工作水深对浮式平台波浪砰击影响的敏感性分析[J]. 上海交通大学学报, 2017(4):410−417.
|
| [5] |
杨秋霞, 冯国庆, 刘玉超, 等. 深海平台砰击载荷的数值分析[J]. 船舶力学(z1).
|
| [6] |
张于维, 王志东, 晋文菊, 等. 二维楔形体砰击载荷研究[J]. 中国舰船研究, 2010, 5(3): 34-37. DOI:10.3969/j.issn.1673-3185.2010.03.008 |
 2021, Vol. 43
2021, Vol. 43
