0 引　言

水下目标安全态势研究受限于结构声辐射、声传播特性研究以及声呐接收设备信号处理技术的研究进展，已有众多学者围绕水下大型复杂结构振动声辐射、水声信道传播理论等重要课题开展了深入研究。周军伟等^[1]、俞孟萨等^[2]、张烈山等^[3]建立了水下航行器声辐射求解方法，在求解效率方面进行了大量开拓性工作，推动了数值仿真方法的工程化应用。射线理论、简正波模型等海洋声场基本理论是复杂海洋环境声传播研究的理论基础，海洋声场边界相互作用、体积效应得以体现于声场传播模型，针对三维声场空间的数值模型已具备应用条件，复杂海洋环境声场建模技术相对完善^[4-6]。因此，基于声呐性能建模原理，分析声呐设备完成既定探测任务时的效能，讨论给定条件下的检测概率和探测距离具备成熟的技术条件。文献[7]将水下航行器近似为各向同性的点声源，给出了一套评估水下航行器声隐身态势的方法，并分析了对其的影响因素。文献[8]将水下航行器声学安全性能评估由数值计算问题变为基于多传感器信息融合的模式识别问题，通过将改进D-S证据理论模型和图像欧氏距离模型相结合，提出了一种新的水下航行器声学安全性能快速评估方法。目前，数值仿真方法是较为成熟的水下航行器辐射噪声求解方法，其有效性与准确性已得到试验验证，且其求解效率也满足工程应用条件^[9]。本文在已有研究成果基础上，通过数值仿真方法，获取水下航行器辐射噪声数据，以被动声呐方程为理论基础，进行浅海环境水下航行器声探测数值建模，分析水下航行器安全态势，对优化舰船声学设计、提高舰船隐身安全性具有十分重要的工程意义。

1 水下航行器线谱声探测理论模型

声呐方程是用于量化声呐性能代数表达式，窄带相干处理的被动声呐方程，如下式：

$S{E_{NB}} = (SL{\rm{ - }}PL{\rm{) - (}}N{L_f}{\rm{ + }}BW{\rm{ - }}AG{\rm{) - }}DT{\text{。}}$

(1)

式中：声源级SL可通过数值仿真方法获取；传播损失PL可通过高斯型声束模型获取。以上2项参数计算方法相对成熟，具体参见文献[5]与文献[9]。NL_f为噪声级，主要考虑风噪声与行船噪声，通过经验公式估算^[10-11]；BW为带宽，可近似表示为10*l gδf，δf为处理带宽；AG为阵增益，DT为检测阈；围绕阵增益、检测阈等参数，总结相对成熟的经验算法或数值模型，建立水下航行器窄带噪声探测模型。

1.1 检测阈计算方法

由于噪声与信号自然起伏的统计特性，导致目标信号的检测信噪比难以明确得出。因此，基于统计检测理论，进行接收机特定信噪比条件下的信号检测概率分析十分必要。对于瑞利衰落信号，单个信号的幅度服从瑞利分布，信号幅度的概率密度函数如下：

${f_S}(A) = \frac{A}{{{a^2}}}\exp \left( - \frac{{{A^2}}}{{2{a^2}}}\right)(A \geqslant 0){\text，}$

(2)

对于瑞利噪声，信号与噪声概率密度函数：

${f_{S + N}}(A) = \frac{{A/{\sigma ^2}}}{{1 + R}}\exp \left( - \frac{{{A^2}/2{\sigma ^2}}}{{1 + R}}\right)(A \geqslant 0){\text，}$

(3)

式中， $\sigma $ 为样本标准差。

$R \equiv \frac{{E({A^2})}}{{2{\sigma ^2}}}{\text，}$

(4)

由此可得检测概率：

${p_d} = \exp \left( - \frac{{A_T^2/2{\sigma ^2}}}{{1 + R}}\right){\text。}$

(5)

从而得到瑞利衰落信号ROC曲线，表征检测阈DT、虚警概率P_fa以及检测概率P_d间的数量关系。其中，虚警指的是由单纯噪声起伏引起的声呐系统错误目标报告。概率密度函数的某个物理观测量在给定范围内的积分与积分变量无关，对于高斯噪声，相干处理后的概率密度函数如式（2）。由噪声引起的阈值超越概率如下式：

${p_{{{f}}a}} = \exp \left( - A_T^2/2{\sigma ^2}\right){\text。}$

(6)

1.2 阵增益计算方法

被动声呐设备拾取压力扰动经信号处理提高信噪比，信号处理方法包括时域和空域滤波，时域滤波通过降低噪声级获得信噪比增益，对空域滤波，通过波束形成技术，滤除部分角度范围内噪声。

波束形成是声呐阵列信号处理的主要内容，包括多元基阵各阵元输出信号的加权、延时以及求和处理，将阵元拾取信号累加，从而形成空间指向性。声呐阵列响应指接收机输出端信噪比，由水听器处声信号经时间与空间滤波获取。对于均匀片状偶极子噪声源，水平线列阵噪声增益为：

${G_N} = \frac{{\int {Q_\Omega ^NB(\Omega ){\rm d}\Omega } }}{{{Q^N}}}{\text。}$

(7)

式中： $B(\Omega ) = \dfrac{{{{\sin }^2}u}}{{{u^2}}}$ ； $u(\theta ,\varphi ) = \dfrac{{\text{π} L}}{\lambda }(\cos\theta \sin\varphi - \sin \psi )$ 。

假定 $Q_\Omega ^N$ 与 $\sin\theta$ 成比例，则

$\begin{split}{G_N} =& \frac{{\displaystyle\int {{\rm d}\theta \displaystyle\int {\rm d} \varphi \left(\frac{{{{\sin }^2}u}}{{{u^2}}}\right){\sin}\theta \cos \theta } }}{{\displaystyle\int {{\rm d}\theta \displaystyle\int {\rm d} \varphi \sin\theta \cos \theta } }} =\frac{N}{\text{π} } = \\ &\frac{{\displaystyle\int {\Delta \varphi (\theta )\sin\theta \cos \theta } {\rm d}\theta }}{\text{π} }{\text，}\end{split}$

(8)

取 $\Delta \varphi /2$ 的近似解，由此可得：

$N \approx \frac{{2\text{π} }}{{kL}}\int_0^{\arccos (\sin \psi )} {(\cos^2\theta - {{\sin }^2}\psi )_{}^{ - 1/2}} \sin\theta \cos \theta {\rm d}\theta {\text。}$

(9)

对于端射情况，阵增益表达式如下：

${G_N} = \frac{2}{\text{π} }\int_0^{\arcsin \sqrt {2\text{π} /kL} } {\sqrt {2\text{π} /kL - {{\sin }^2}\theta } } \sin\theta {\rm d}\theta {\text。}$

(10)

2 水下航行器声学安全态势分析

首先进行水下目标辐射声源级数值仿真、海洋声场传播损失仿真、背景噪声级估算，再经信号处理得接收设备阵列响应，并基于统计检测理论，完成声学安全态势分析。

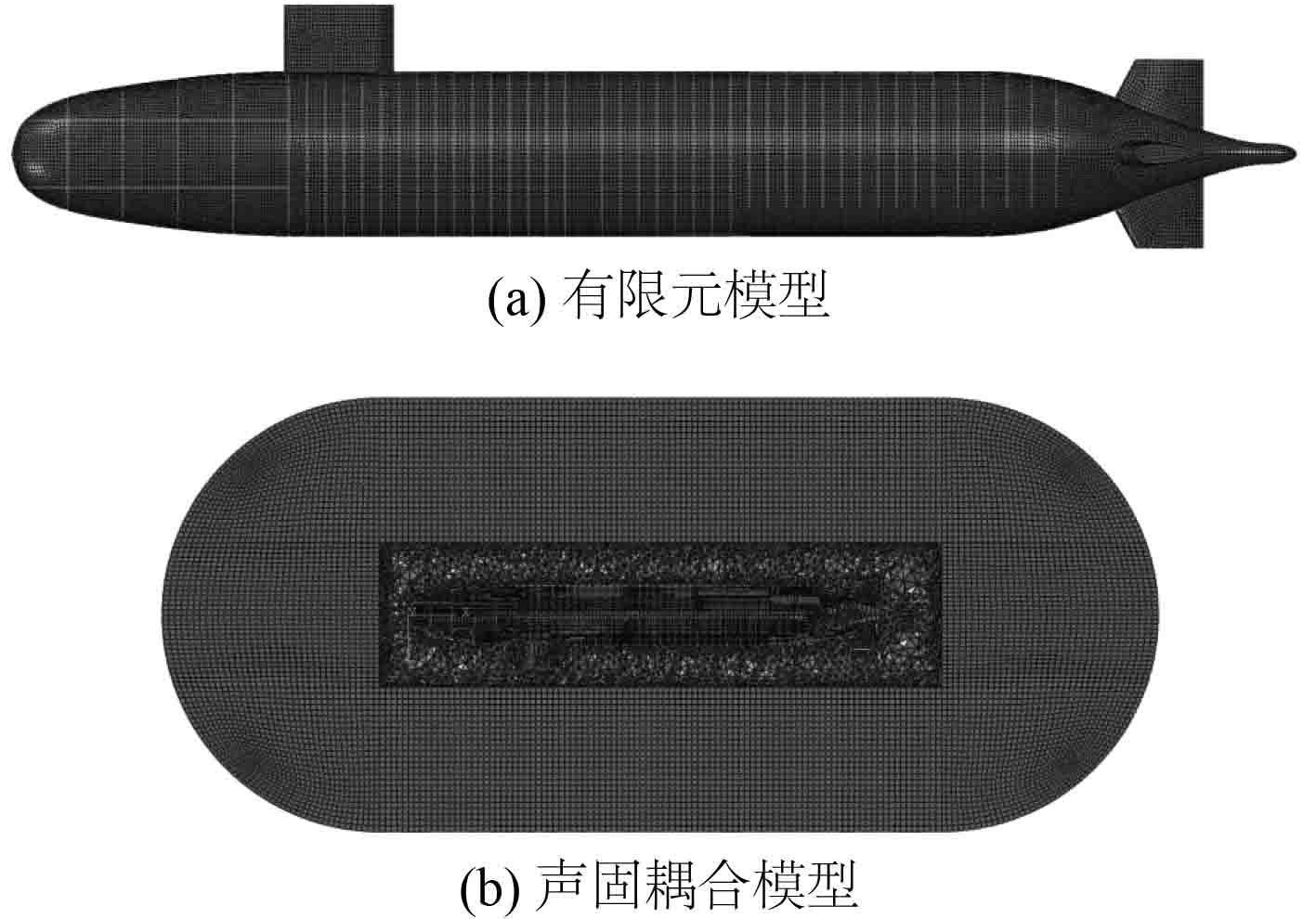
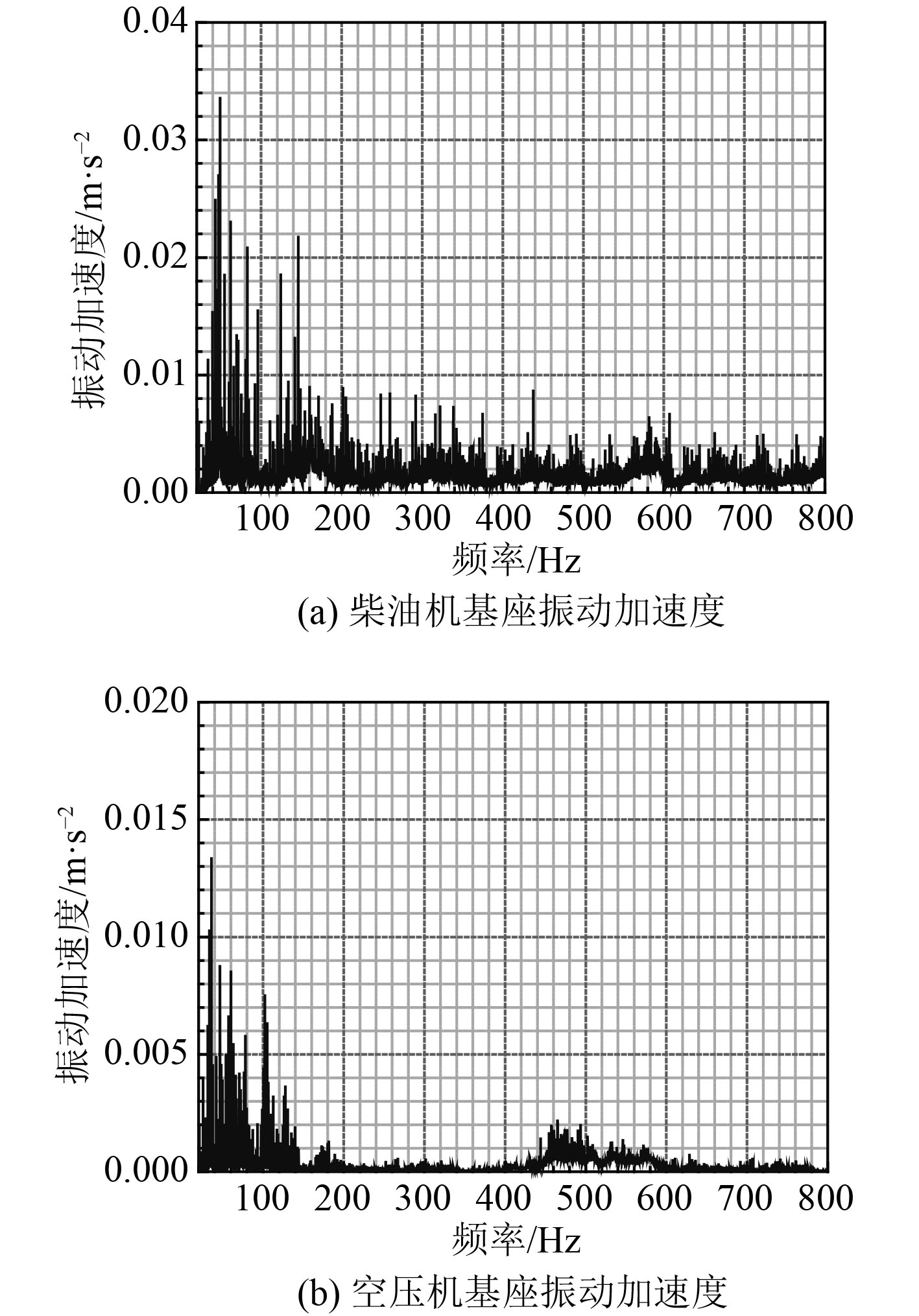
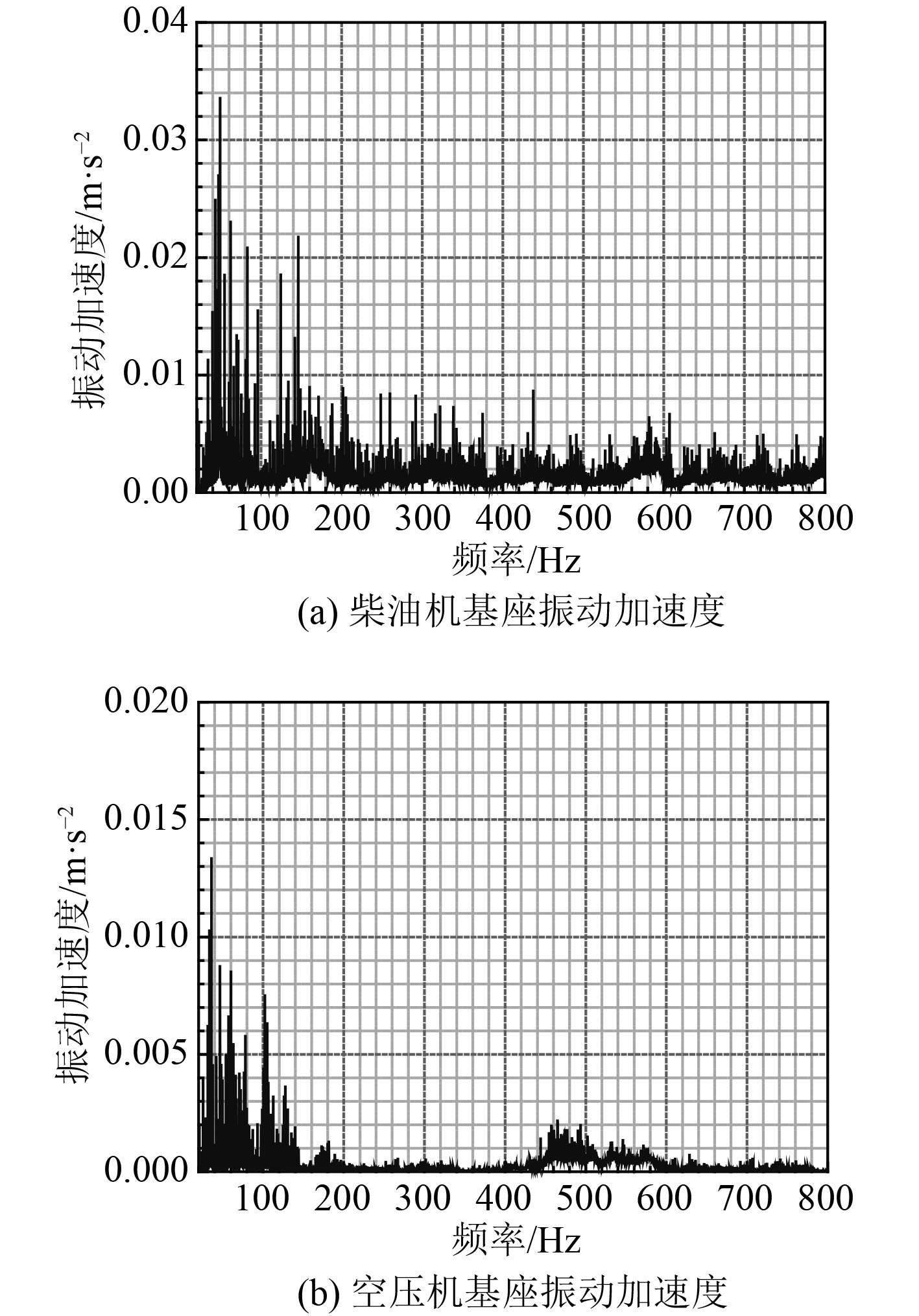
2.1 水下航行器结构声辐射特性分析

基于声固耦合法与边界元法，采用频域分析方法，进行水下航行器辐射噪声仿真计算。计算模型为suboff模型，并考虑基座，舱壁等局部结构，如图1所示。考虑柴油机、空压机等激励源设备，激励载荷频谱曲线如图2所示。激励载荷表征参数为振动加速度，施加于机舱舱筏基座。水平面距模型中心1000 m的圆周范围内设置声压考核点。计算频段20～800 Hz，分析步长 $\Delta f$ =2 Hz。

水下航行器辐射噪声数值仿真结果如图3和表1所示。右舷考核点（ $\theta $ = 0°）辐射噪声水平总体偏大，通过分析该考核点声压响应可知，10～800 Hz频段，考核点声源谱密度级波动较大，并在15 Hz（160.3 dB），40 Hz（150.8 dB），380 Hz（139.8 dB）等频点出现峰值线谱。水下航行器结构声辐射谱密度级总体呈现低频大、高频小的变化趋势，10～800 Hz频段谱密度级在156～162 dB之间，10～100 Hz频段谱密度级在156～163 dB之间，两者十分接近，辐射声能主要集中在10～100 Hz的中低频段。

2.2 水下噪声传播损失计算

对于浅海声场环境，涉及声波和强变异性海底边界之间的交互作用，导致原本高强度的声反射、声散射等计算更加复杂。为模拟海底地形起伏引起的声传播差异，构建海底地形模型如图4所示。模型包括岛弧、海脊、海底平原等典型海底特征结构。

基于水声传播理论进行海洋声场传播损失计算，声源深度50 m，水平范围10 km，最大水深200 m，海底沉积物为黏土，空隙率 $\eta $ =85.8%、密度 $\,\rho $ =1260 kg/m³、声速 $c$ =1505 m/s，厚度d=200 m。θ= 0°时，典型频点传播损失计算结果如图5所示。

2.3 水下航行器探测距离计算

考虑位于海面以下50 m的浅水域水下目标，声探测分析频段为256～500 Hz。接收机为长45 m的水平线列阵，假设位于正横波束方向。声呐滤波器分辨率为0.25 Hz，虚警率为1次/h。接收频段内共形成 $1\;024 \times $ $ 32$ 个波束。背景噪声包含风噪声与行船噪声。依据窄带相干处理的被动声呐方程，以目标初始位置沿垂向在海面的投影为坐标原点，坐标系如图4所示，Y轴正方向为航向。如果探测概率为50%，对应检测阈DT₅₀=13.8 dB，通过筛选频段内各频点对应的探测距离的最大值，绘制 $0 < \theta < \text{π} $ 范围内的目标探测距离分布，如图6所示。图中Z坐标为深度，XY坐标为水平距离。

目标探测距离沿着各个方向角θ的变化幅度较大。以上算例探测距离的主要影响因素包括：

1）海水声吸收效应。海水的黏性以及硼酸、硫酸盐的化学弛豫效应导致声传播过程中，一部分声能转化成热能，引起声衰减。算例分析频率对应多种声吸收系数，从而导致传播损失差异。算例分析频段的声衰减主要由化学弛豫效应引起，盐度与静压是主要影响因素。

2）目标声辐射源级。380 Hz与430 Hz为水下辐射噪声峰值线谱，探测距离提升明显，并对256～500 Hz的频段探测性能造成影响。

对应DT₅₀检测阈，水深30 m的XOY平面探测距离-方向角曲线如图7所示。

由图7可知，对应多数的方向角，256～500 Hz频段与380 Hz峰值线谱的探测距离曲线重合，少数方向角的频段探测距离参照430 Hz峰值线谱取值。其他多数频点难以引起频段探测效能差异。

对于指定方向角，线谱噪声探测距离由特定峰值频点界定。由此可知，水下航行器辐射噪声峰值线谱对接收机探测效能影响显著。因此，针对峰值线谱的减振降噪设计，是优化水下航行器声学性能的关键。

3 结　语

本文基于被动声呐方程，围绕声源级、水声传播损失、阵增益等各项量化声呐性能主要参数，结合数值计算，完成了水下航行器窄带水声探测建模，开展水下航行器安全态势分析。主要结论如下：

1）水下航行器辐射噪声峰值线谱对接收机探测效能影响显著，针对中、低频线谱噪声的减振降噪设计应以控制线谱作为声学优化的重点。

2）目标探测距离沿各个方向角θ的变化幅度较大，探测距离的主要影响因素包括海水的声吸收效应与目标声辐射强度等。

3）随着分析频率的增加，水下航行器结构声源谱密度级呈现总体下降的趋势。