2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
深入探索海洋需要越来越多的水下设备部署。当前以蓄电池为动力源的中小型自主水下机器人,续航能力普遍在10~40 h之间。大型自主水下机器人可携带小型水下设备进行部署、回收;建立水下移动基站,为小型机器人补充能源;能够同时承担多种复合任务,水下设备的作业时间与作业范围能够大大增加。未来大规模水下机器人联网、协同对于高续航的大型自主水下机器人的安全性与自主性要求越来越高。机器人尺寸、重量的增加,其操纵性、机动性必然随之降低,灵活度势必减弱,这些问题使得大型机器人的环境模型更加复杂、机动性约束更加严格、路径选择更加困难,因此需要求解能力更强的全局静态与局部动态路径规划算法。
粒子群优化(PSO)优化算法具有算法简单、收敛迅速等优点,但各粒子间缺少信息交流,“搜索”能力与“收敛”能力难以完美平衡,局部最优解的“陷阱”难以完全避开。在利用PSO算法规划全局路径时,大量文献在粒子群算法中,通过借鉴其他算法进行融合改进,并提高了粒子群算法的性能,取得良好效果。在全局静态路径规划研究中,文献[1]结合随机采样与均匀变异的方法来更新粒子,在高机动救援机器人的路径规划中生成了高质量的最优路径,但在保证收敛的前提下,其搜索能力仍需提高以保证机器人获取更大的安全活动空间;文献[2]提出了环境选择与匹配选择策略,在迭代过程中逐渐减少随机性,收敛速度大大提高,但其落入局部最优的可能性同样增大;文献[3]通过引入模拟退火算法,利用退火算法暂时接受少许劣质解的特性,优化全局搜索能力,提高局部搜索精度,但算法参数量的增加使得计算量、复杂性也同样增加;文献[4]通过差分进化过程,借鉴遗传算法的交叉变异过程,于粒子群算法中生成新的粒子,增加粒子群的信息交互能力,但其过多的变异增加了不必要的计算量;文献[5]在PSO算法中引入同性因子,结合鱼群算法的“跳跃”过程提升了算法的求解能力,较好平衡了搜索与收敛能力,满足AUV在复杂海域航行时的全局路径规划需求,但其过于依赖先验环境,对于实时环境信息融合海图后的动态环境模型缺少验证;在动态规划研究中,文献[6]提出基于改进的双向快速扩展随机搜索树(RRT)算法,优化搜索树之间的连接方式,并设计新的动态步长策略,能够较优规划局部避障路径,但其算法随机性强没有得到改善,路径的平滑连接依旧困难;文献[7]通过基于全局路径规划的引导,通过障碍物运动预测与滚动优化方式进行动态避障,但其对规划结果过于依赖障碍运动预测方式,且存在规划路径远离既定路线的可能;文献[8]改进了速度障碍法并用于动态避障,通过碰撞与避障的时间判定避障动作的始末时间,但其对速度条件过分依赖,如若障碍物速度过慢,可能发生碰撞危险。
基于上述问题,考虑实际海域环境,构建海域环境模型、目标函数以及优化约束条件,通过目标函数加权方式,将多目标函数转化为单目标函数,并通过调整加权权重突出机器人对各目标函数的重视程度;提高算法求解和收敛能力对加权后目标函数优化,得到最优或次优解,从而完成全局静态与局部动态相结合的路径规划任务。
1 基于改进PSO算法的全局静态规划 1.1 障碍物处理与极坐标建立真实海洋环境障碍大小形状各异,为缩短全局规划时间而简化障碍模型。模型简化前后满足以下三点:障碍物“阻挡”效果不发生改变;尽量减少可行路径损失以及方便计算,提高计算效率。分析海岸、船只、浮标、游鱼、暗礁以及漂浮物等动、静态障碍,选取矩形或圆形的障碍物包围方式。对于长宽比小于1.5的障碍物采用圆形包围;长宽比大于1.5的障碍物采用有向包围盒(OBB,即具有方向性的矩形)包围。考虑大型水下机器人航行状态调整缓慢,操纵性与机动性较弱,障碍模型外侧通过增加圆形直径或增加矩形边长的方式,膨胀一个安全阈值
以起始点为极点,起始点与终止点连线为极轴建立极坐标系,顺时针方向为负,逆时针方向为正。以极点为圆心,圆形障碍物的极径为半径建立路径同心圆。规划的路径用路径集合点
矩形障碍物位置由4个顶点确定,全部顶点建立路径同心圆会增加计算量,降低计算效率,选择2个顶点建立路径同心圆既能较好反应障碍信息,又能减少计算量。根据矩形顶点所在位置的极径长短有2种选取方式:极径最长和最短的2个顶点;极径次长和次短的2点。
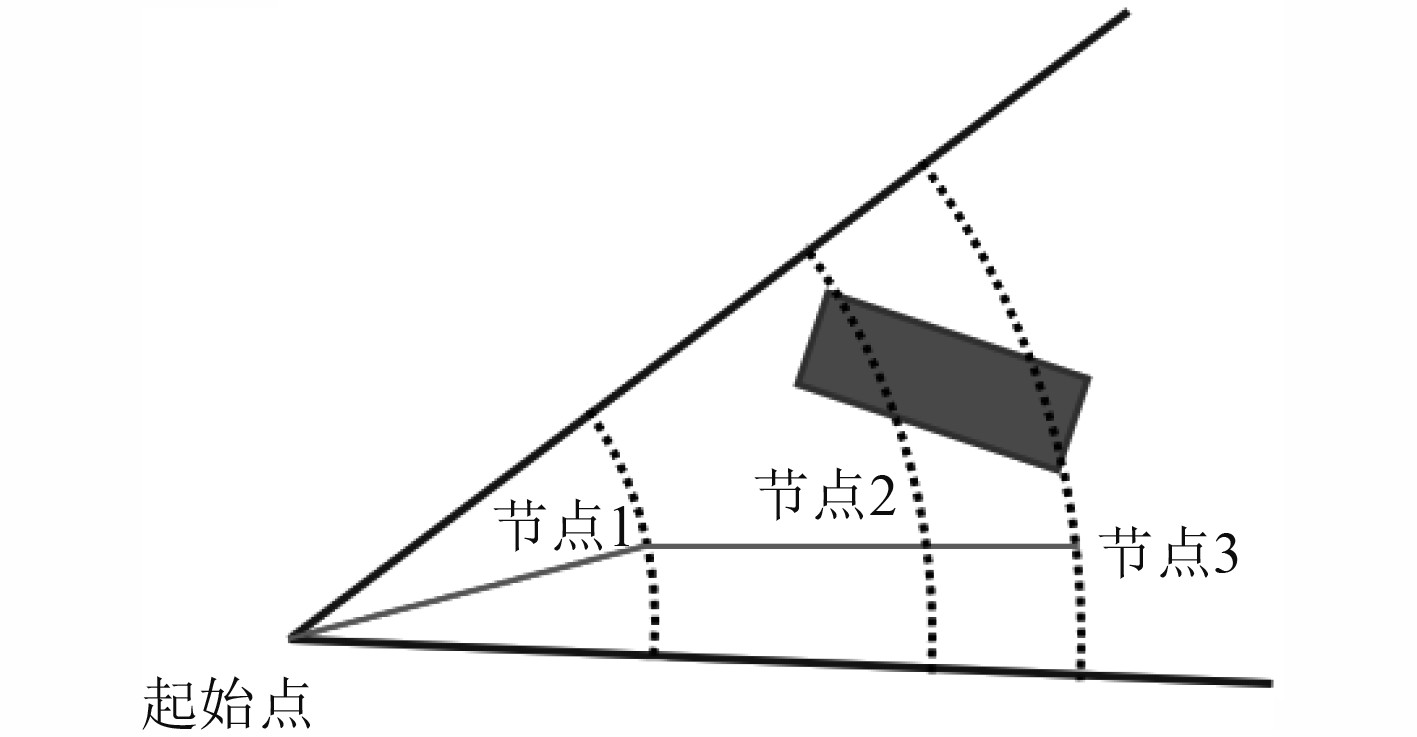
如图1所示,选取极径最长和最短的顶点会出现路径节点之间有障碍物“突出”现象。靠近障碍物调整航向角是对机器人回转性能的巨大挑战,在严格的机动性约束下大型水下机器人不具备此种回转条件的能力。因此,采取图2所示的方式建立路径同心圆。

|
图 1 极径最长和最短顶点建立路径同心圆 Fig. 1 Path concentric circle established by the longest and shortest vertices of polar radius |
|
图 2 极径次长和次短顶点建立路径同心圆 Fig. 2 Path concentric circle established by the second longest and the second shortest vertices of polar radius |
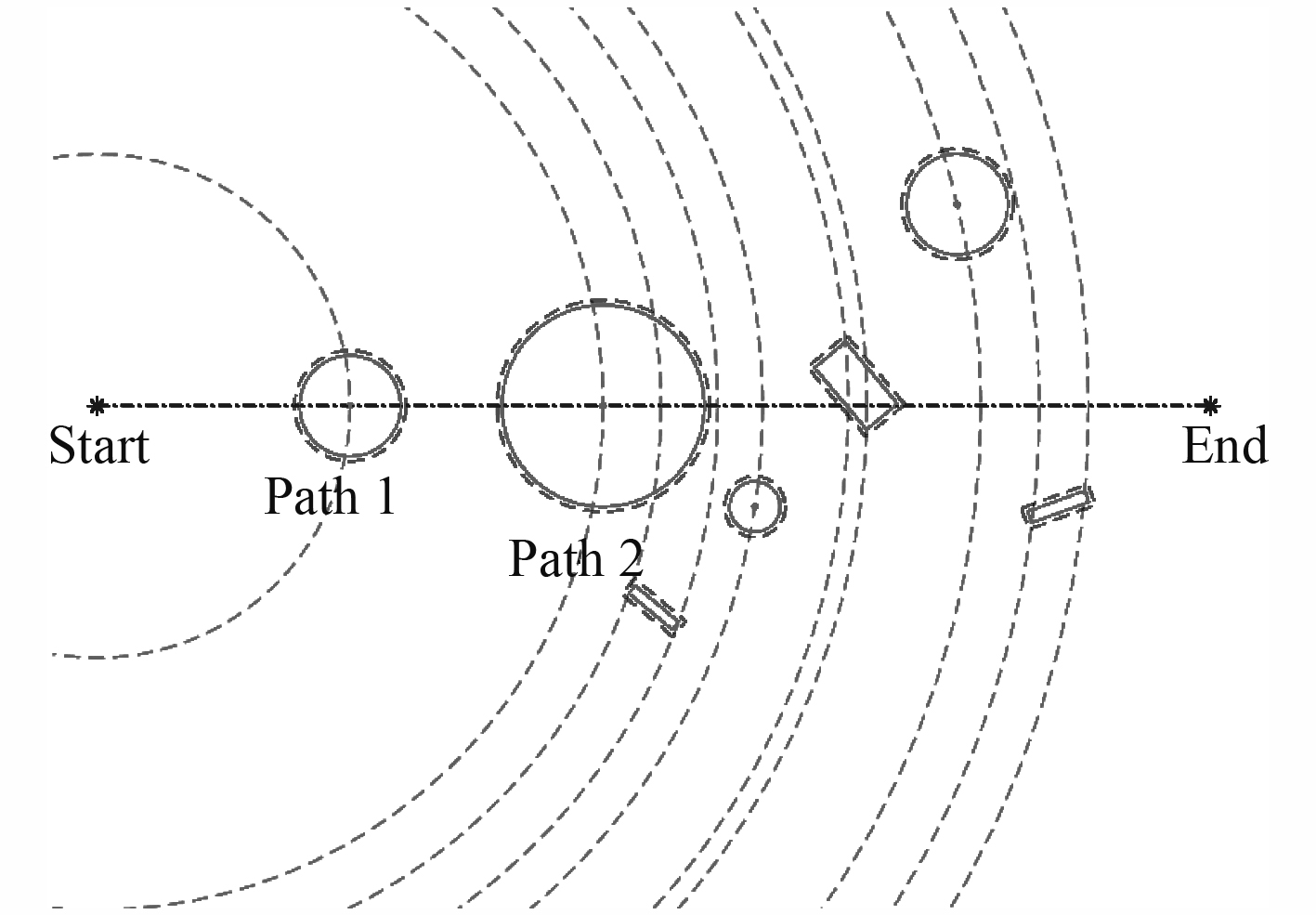
由起始点、障碍物信息建立极坐标,采用弧形虚线表示路径同心圆,同心圆圆心为起始点;圆形、矩形实线表示障碍物;圆形、矩形虚线代表障碍物膨胀安全阈值
|
图 3 极坐标系下的障碍物模型 Fig. 3 Obstacle model in the polar coordinate system |
在自主水下机器人航行过程中,在线获取环境信息有限,由先验知识规划的路径信息十分重要。通常为得到全局最优路径,机器人会根据障碍物模型构建目标函数,将规划问题转化为多目标函数优化问题[9]。在全局路径规划中,需要在工作空间中搜索出一条从起始点到终止点的最优路径。最优路径不仅满足机器人自身速度、加速度以及角速度约束,同时还在满足安全条件下保证路径最短。执行层中的避障问题可以视为机器人在可行区域内的优化搜索,通过多目标函数优化求解找到可行区域的解。
建立路径长度函数
| $ {J_1}={\displaystyle \sum _{i=0}^{n}L({P_i}\text{,}{P_{i+1}})}\text{,} $ | (1) |
其中,L(.,.)为两路径点的欧式距离;
建立路径可行度函数
| $ {J_2}={\displaystyle \sum _{i=0}^{n}{D}_{({i})}} \text{,}$ | (2) |
为防止出现路径点位于障碍内部或阈值区域内的情况,设立危险度函数
| $ {{D}}_{({{i}})}= \left\{ {\begin{array}{*{20}{l}} { + \infty ,}&{{{{P}}_{{{i - 1}}}}{{{P}}_{{i}}} \cap {{OB = }}\emptyset }\text{,}\\ {{{0,}}}&{{{{P}}_{{{i - 1}}}}{{{P}}_{{i}}} \cap {{OB}} \ne \emptyset } \text{。}\end{array}} \right. $ | (3) |
式中:
建立回转可行度函数
| $ {J_3}={\displaystyle \sum _{i=0}^{n}{W}_{({i})}}\text{,} $ | (4) |
建立回转评估函数
| $ {{{W}}_{({{i}})}}{{ = }}\left\{ {\begin{array}{*{20}{l}} {{{0}},}&{{{|}}{\omega _{({{i}})}}{{|}} \leqslant {\omega _{{{l}}({{i}})}}}\text{,}\\ {{{ + }}\infty {{,}}}&{\left| {{\omega _{({{i}})}}} \right| > {\omega _{{{l}}({{i}})}}}\text{。} \end{array}} \right. $ | (5) |
其中:
粒子群算法通过适应度函数来判别粒子优劣,是逼近最优解的决定性因素,适应度函数的选择将直接影响算法性能。在静态障碍环境中,寻求与障碍物不相交、路径长度最短且满足最大回转角限制的可行路径。
采用线性加权方法将
| $ {{Fit(i) = a_1J_1 + a_2J_2}} + {{a_3J_3}}\text{。} $ | (6) |
若路径符合航行条件,则适应度为路径总和;若路径不符合航行条件,则适应度为无穷大。为比较粒子优越性,制定如下粒子择优条件:
1)如
2)如
粒子群算法以其简单、参数少、快速收敛等特性被广泛应用在机器人各领域[10]。PSO 算法是一种随机搜索算法,该算法设计无质量的粒子群来模拟鸟群,鸟群中的粒子仅有2个属性:速度
| $ \left\{ {\begin{array}{*{20}{c}} {{{V}}_{{i}}^{{{t + 1}}}{{ = w}}i{{V}}_{{i}}^{{t}} + c_1r_1({{P}}_{{i}}^{{t}}{{ - X}}_{{i}}^{{t}}) + c_2r_2({G^{{t}}}{{ - X}}_{{i}}^{{t}}}) \text{,}\\ {{{X}}_{{i}}^{{{t + 1}}} = {{X}}_{{i}}^{{t}} + {{V}}_{{i}}^{{{t + 1}}}} \text{,} \end{array}} \right. $ | (7) |
| $ {{1}} \leqslant {{i}} \leqslant {{N}}\text{。} $ |
学习因子
| $ {c}_{1,2}={c}_{1,2\min}+\frac{{run_{\max}}-{run}}{{run_{\max}}} \times ({c}_{1,2\max}-{c}_{1,2\min})\text{。} $ | (8) |
其中,
惯性权重
| $ { w }= { w}_{\max} - \frac{(w_{\max} - w_{\min} ) \times run}{{run_{\max} }}\text{。} $ | (9) |
其中:
粒子最终收敛位置由群体最佳位置和个体历史最佳位置决定[13]。本文定义:如果粒子群经过若干代更新后,所有粒子都未发现比历史最优更优的值,则算法处于轻度收敛状态。引入遗传算法“变异”过程使得最佳位置发生“变异”。由于粒子群陷入局部“陷阱”是逐渐形成的,因此需要结合求解阶段对群体最佳位置进行变动,即采取不同的变异方式引导种群向有利方向继续搜索。
定义粒子
| $ {{d_k = }}\frac{1}{d}\sqrt {\sum\limits_{j = 1}^d {{{(x_{\rm{kj}} - gb_j)}^2}} } \text{。} $ | (10) |
其中:
定义
| $ \gamma (t){\rm{ = rand}}() \times gb(t) \times {\rm{F_{itbest}}}\text{。} $ | (11) |
式中:
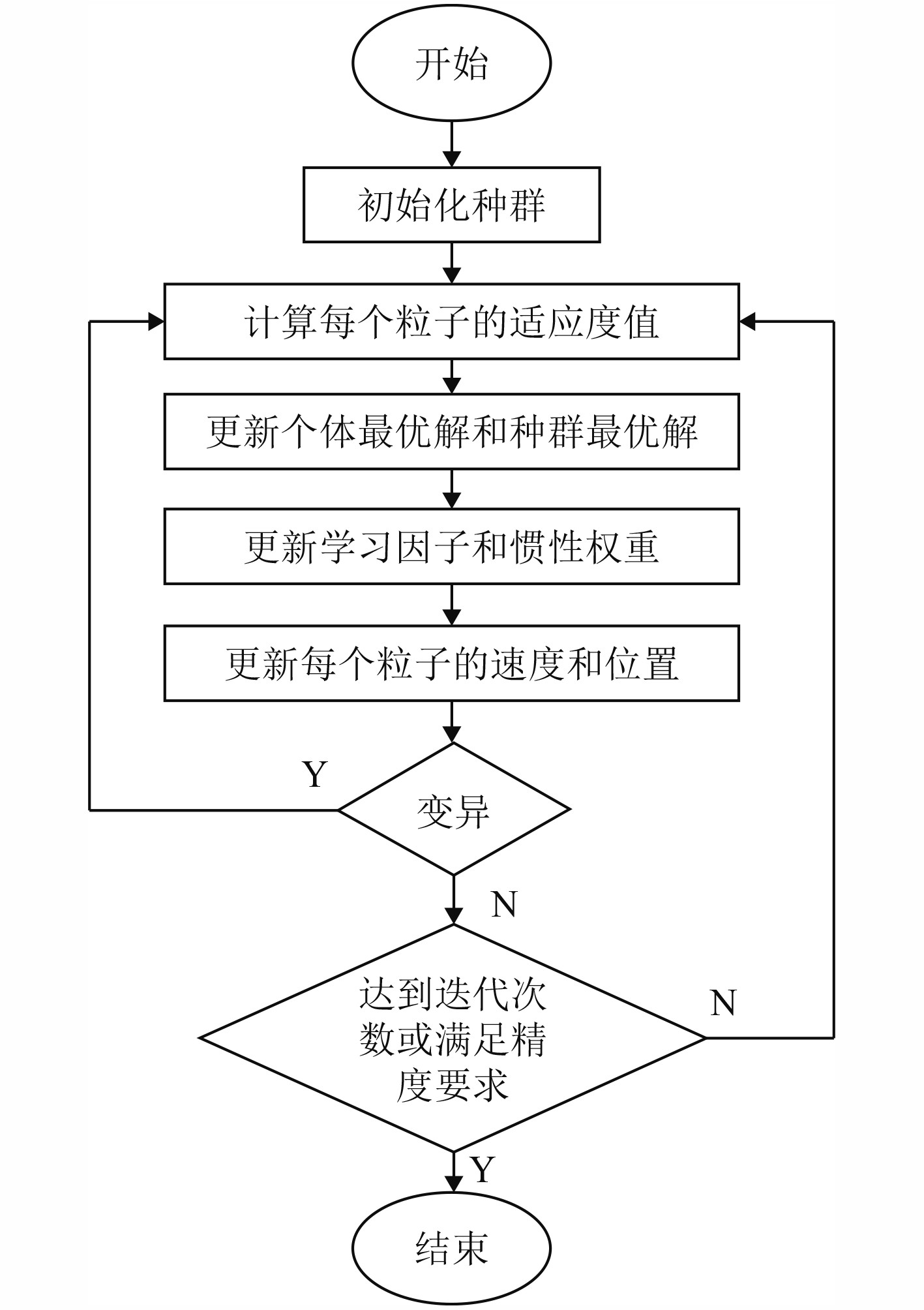
全局路径规划的流程图如图 4 所示。分为如下步骤:
|
图 4 静态环境改进PSO算法流程图 Fig. 4 Flowchart of improved PSO algorithm in static obstacle environment |
1)初始化种群,包括设置粒子的个数、维度,各个粒子的位置、速度,最大迭代次数
2)计算粒子适应度。
3)由粒子择优规则找出个体最优解和群体最优解。
4)更新学习因子与惯性权重,更新粒子的速度和位置。
5)经过指定代数更新后,如若粒子仍未产生新的群体最优解,则根据式(11)判断是否处于轻度收敛状态。若处于轻度收敛状态,则根据式(12)对最优解进行变异并转入第2步;否则转入第6步。
6)判断迭代次数是否达到
机器人航行过程中,遭遇游鱼、漂浮物以及船舶等动态障碍时,可以改变首向绕过障碍,也可调整航速躲避障碍。当机器人遭遇动态障碍阻挡时,如需调整航速为
在局部动态避障的规划中,构建障碍物模型进行避障规划时,由导航精度带来的障碍物位置偏差会导致避障效果不理想,因此选建障碍物相对机器人的速度坐标系。利用机器人搭载的声呐系统采集数据构建障碍物相对机器人的地图系统,其中包括障碍物相对机器人方位
| $ \Delta {{x = }}\upsilon_{{r}}*\Delta {{t*\cos(}}\vartheta_r{{)*\cos(}}\psi_{{r)}}\text{,} $ | (12) |
| $ \Delta {{y = }}\upsilon_{{r}}*\Delta {{t*\cos(}}\vartheta _r{{)*\sin(}}\psi_{{r)}}\text{,} $ | (13) |
假定在时间
| $ {(x_{21}},{y_{21})=}({x_1-}\Delta {x},{y_1-}\Delta {y})\text{,} $ | (14) |
障碍物运动速度为:
| $ \upsilon_o = \sqrt {{{(x_1 - \Delta x - x_2)}^2} + {{(y_1 - \Delta y - y_2)}^2}} /\Delta t\text{,} $ | (15) |
障碍物运动方向为:
| $ \psi _o = {{\arctan ((y_{21} - y_2)} /{(x_{21} - x_2)}})\text{。} $ | (16) |
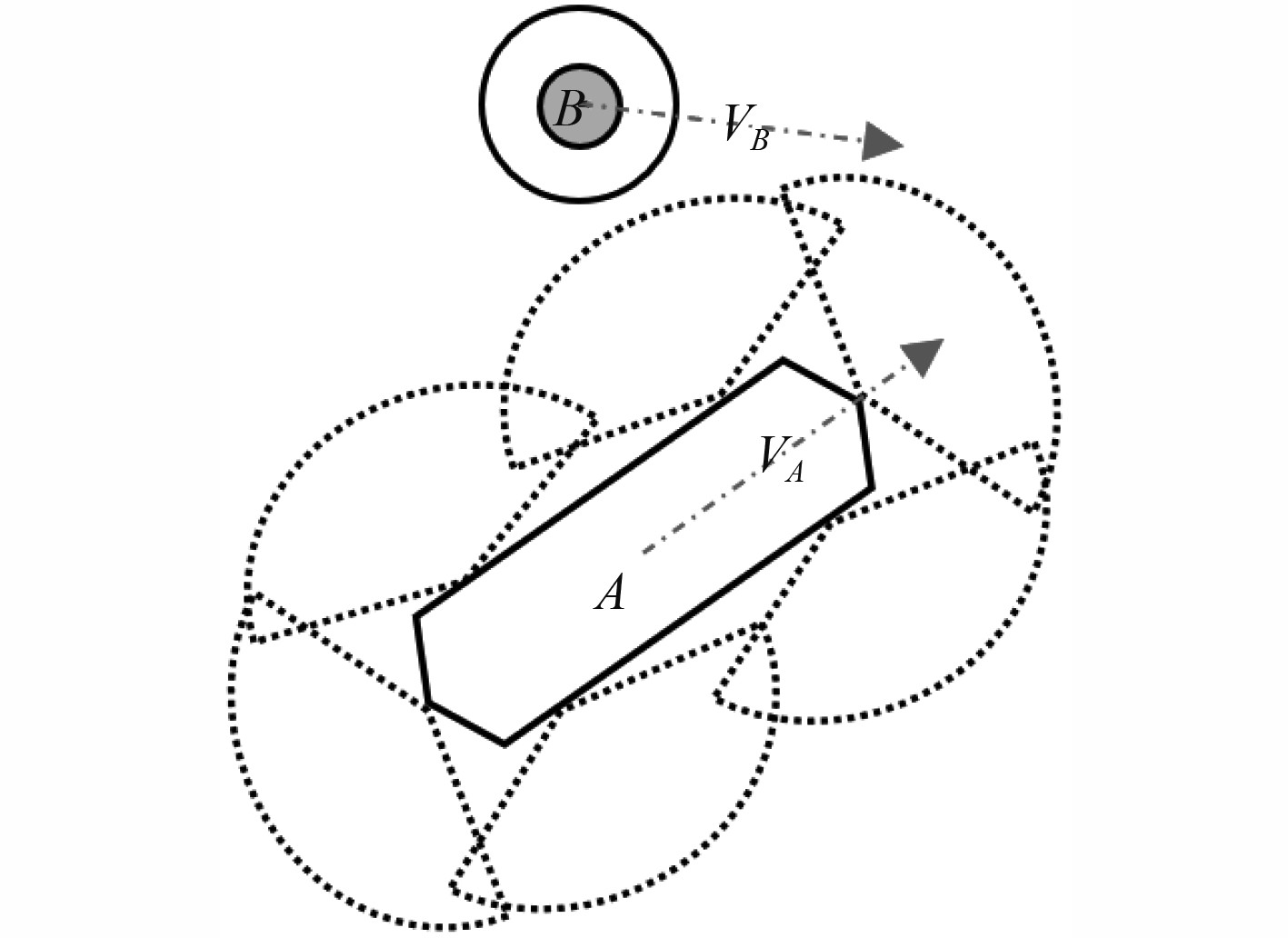
根据声呐图像的障碍物轮廓,对障碍物长宽比判别后进行包围处理。如图5所示,机器人A与障碍物B均按照固定航向与航速运动。
|
图 5 机器人与障碍物运动情况 Fig. 5 The motion of vehicle and obstacle |
将机器人A视为质点,并结合机器人尺寸与安全阈值对障碍物B进行膨胀处理。计算A相对B的相对速度
| $ \lambda {{(P,V) = \{ P + tV|t}} \geqslant {{0\} }}\text{,} $ | (17) |
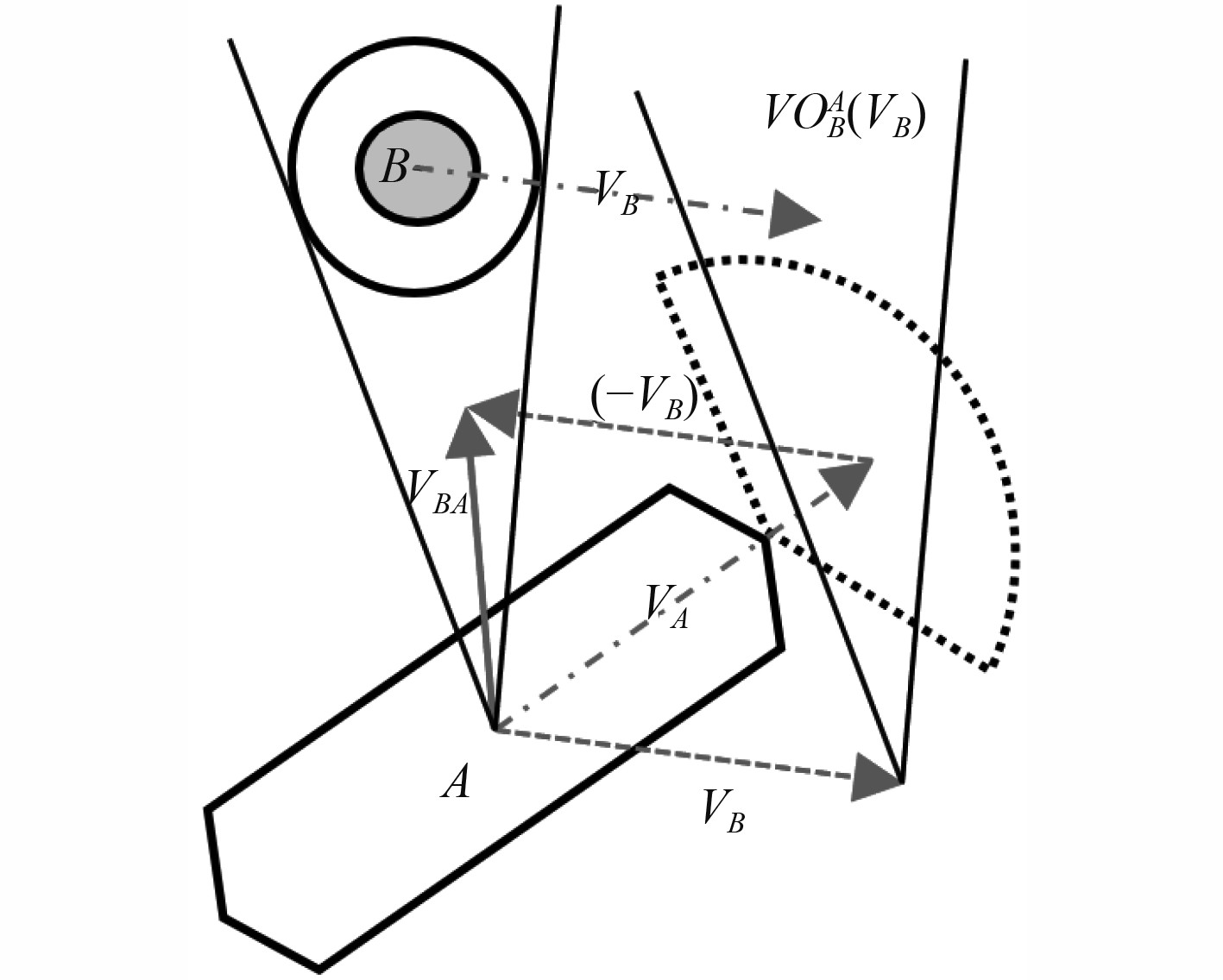
当从A点发出沿
|
图 6 碰撞条件判定 Fig. 6 Determination of collision condition |
由速度障碍法,定义碰撞范围为:
| $ {{VO}}_{{B}}^{{A}}({V_B})=\{{V_A|}\lambda ({P_A,V_A}-{V_B)}\cap ({B}\oplus -{A})\ne \varnothing \}\text{,} $ | (18) |
| $ {{A}} \oplus {{B = \{ a + b|a}} \in A,b \in B{{\} }} - {{A = \{ }} - {{a|a}} \in A{{\} }} \text{。} $ | (19) |
如不改变机器人A的航行状态,机器人将在某一时刻
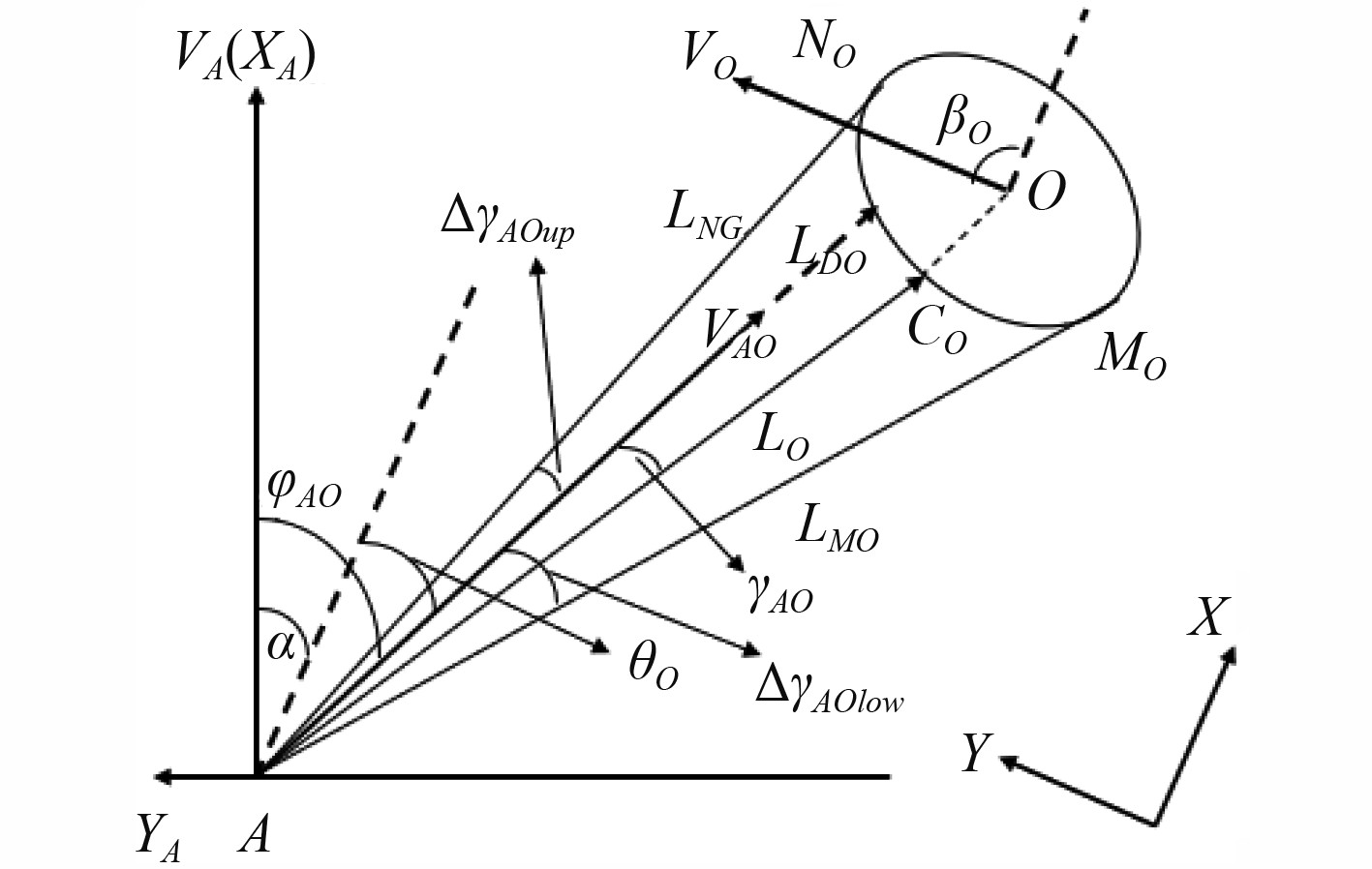
建立机器人-障碍物相对速度坐标系如图7所示。
|
图 7 机器人-障碍物相对速度坐标系 Fig. 7 Relative velocity coordinate system of vehicle-obstacle |
设全局坐标系
机器人在时间区间
| $ {\rm{ - \text{π} }} \leqslant \Delta \gamma_{AO{{i}}} \leqslant \Delta \gamma_{AOlow}\text{,} $ | (20) |
| $ \Delta \gamma_{AO{\rm{up}}} \leqslant \Delta \gamma _{AO{{i}} }\leqslant {\rm{\text{π }}}\text{。} $ | (21) |
假设
| $ \Delta \gamma _{{AOi }}\!=\!\gamma_{{AOi}}*\Delta {{t \!= }} \!-\! \frac{{\sin \varphi_{AOi}}}{{V_{{AOi}}}}\Delta V_A \!+\! \frac{{\cos \varphi_{ AOi}}}{{V_{{AOi}}}}\Delta V_{A*}\Delta \alpha \!-\! \Delta \theta_{{Oi}}\text{。} $ | (22) |
其中,
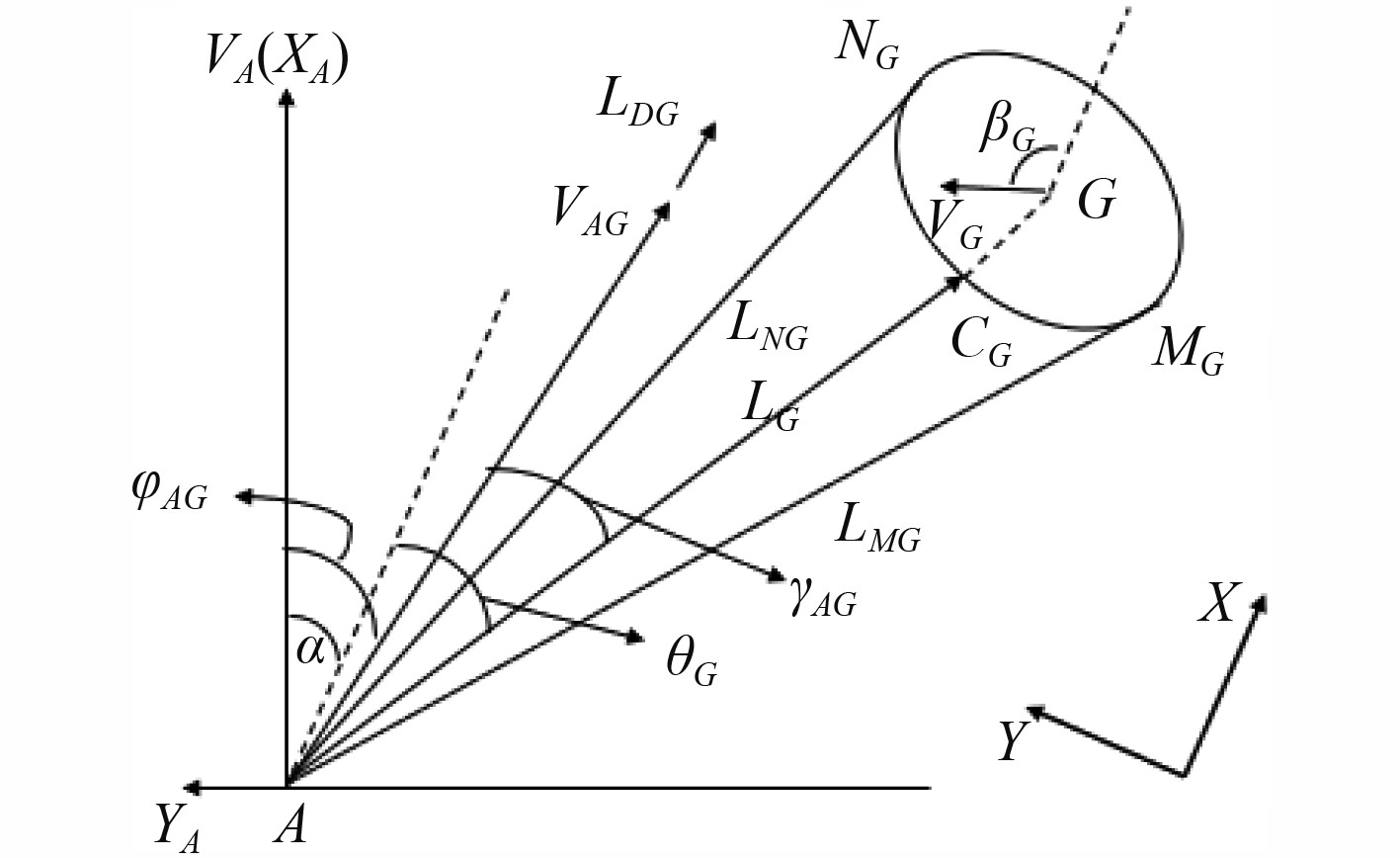
建立机器人-目标区域相对速度坐标系如图8所示,定义与机器人-障碍物相对速度坐标系相同。
|
图 8 机器人-目标点相对速度坐标系 Fig. 8 Relative velocity coordinate system of vehicle-target |
假设机器人子路径终点位于可行区域G内,
| $ {{J_{G1} }}= |\gamma_{{AG }}+\frac{{\sin \varphi_{AG}}}{{V_{AG}}}\Delta V_A - \frac{{\cos \varphi_{AG}}}{{V_{AG}}}V_A\Delta \alpha + \Delta \theta_ G{\rm{|}}\text{,} $ | (23) |
为了减少偏航时间,使机器人尽快回归正常航线,建立最小时间函数。具体表示为在避障前航线方向上,当机器人航向分量在此方向速度最大时,能使偏航时间最短,则
| $ {{J_{G2} }}=\frac{{\Delta V_{AG\max }}}{{V_{AG}}} - \frac{{\cos \varphi_ {AG}}}{{V_{AG}}}V_A - \frac{{V_A\sin \varphi_{\rm{AG}}}}{{V_{AG}}}\Delta \alpha \text{,} $ | (24) |
利用线性加权方法分别将目标函数
| $ {{F_{(i)} }}=\varpi_1 {{J_{G1} + }}\varpi_2 {{J_{G2}}}\text{。} $ | (25) |
其中,
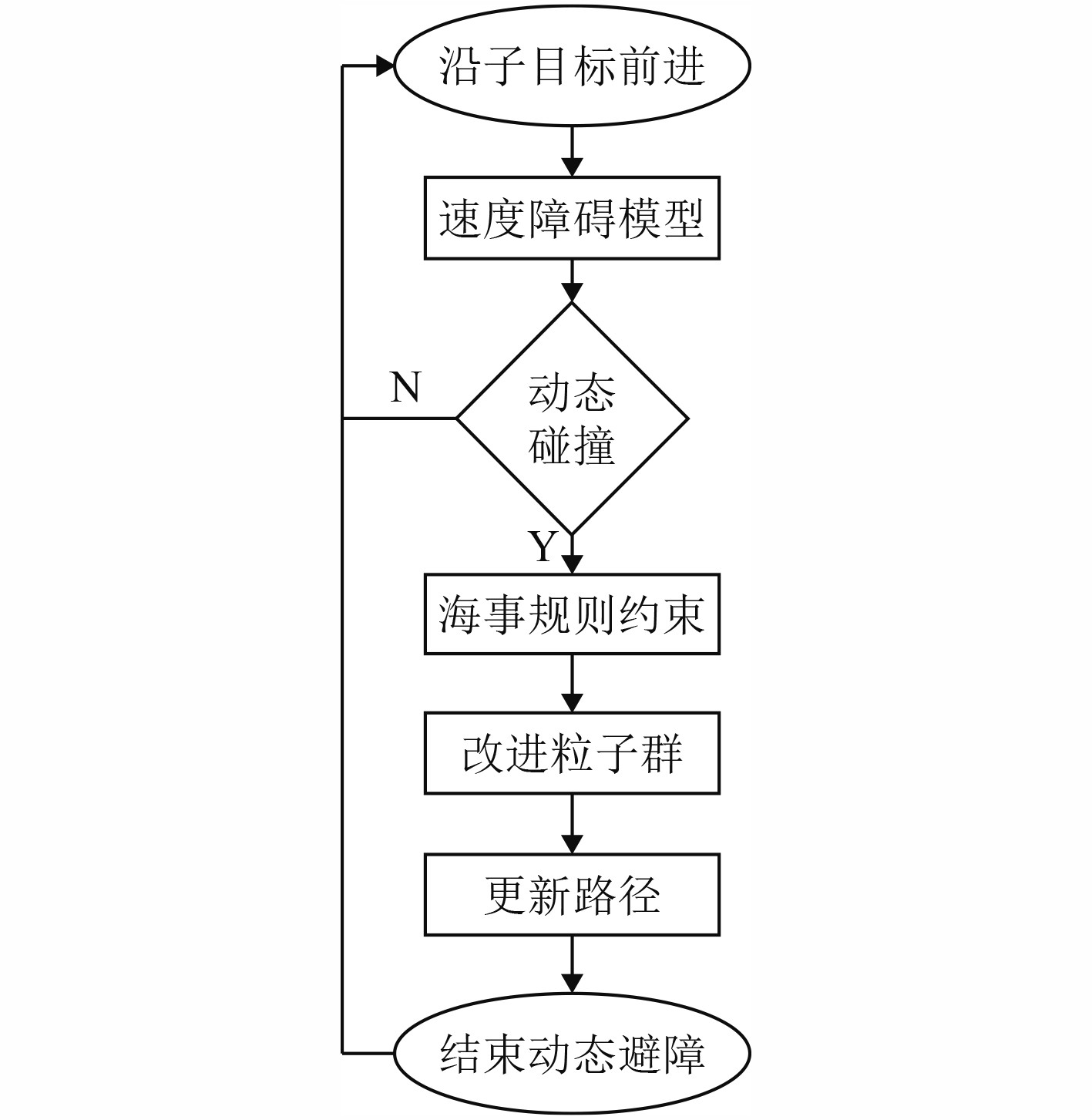
动态障碍环境下路径规划于路径节点间进行规划,由当前路径点向下一个路径点航行过程中进行避障操作,其算法具体流程如图9所示。
|
图 9 动态环境改进PSO算法流程图 Fig. 9 Flowchart of improved PSO algorithm in dynamic obstacle environment |
根据建立的环境模型与适应度函数,分别采用遗传算法,传统粒子群算法和改进粒子群算法对机器人全局静态路径规划进行仿真实验。实验结果对比表明,本文的改进粒子群算法在全局静态规划中有更好的路径规划结果。最后,验证局部动态环境下路径规划效果。
为满足算法的稳定性并保证收敛,选取线性递减惯性权重,其中
|
|
表 1 实验结果 Tab.1 The result of experiment |
|
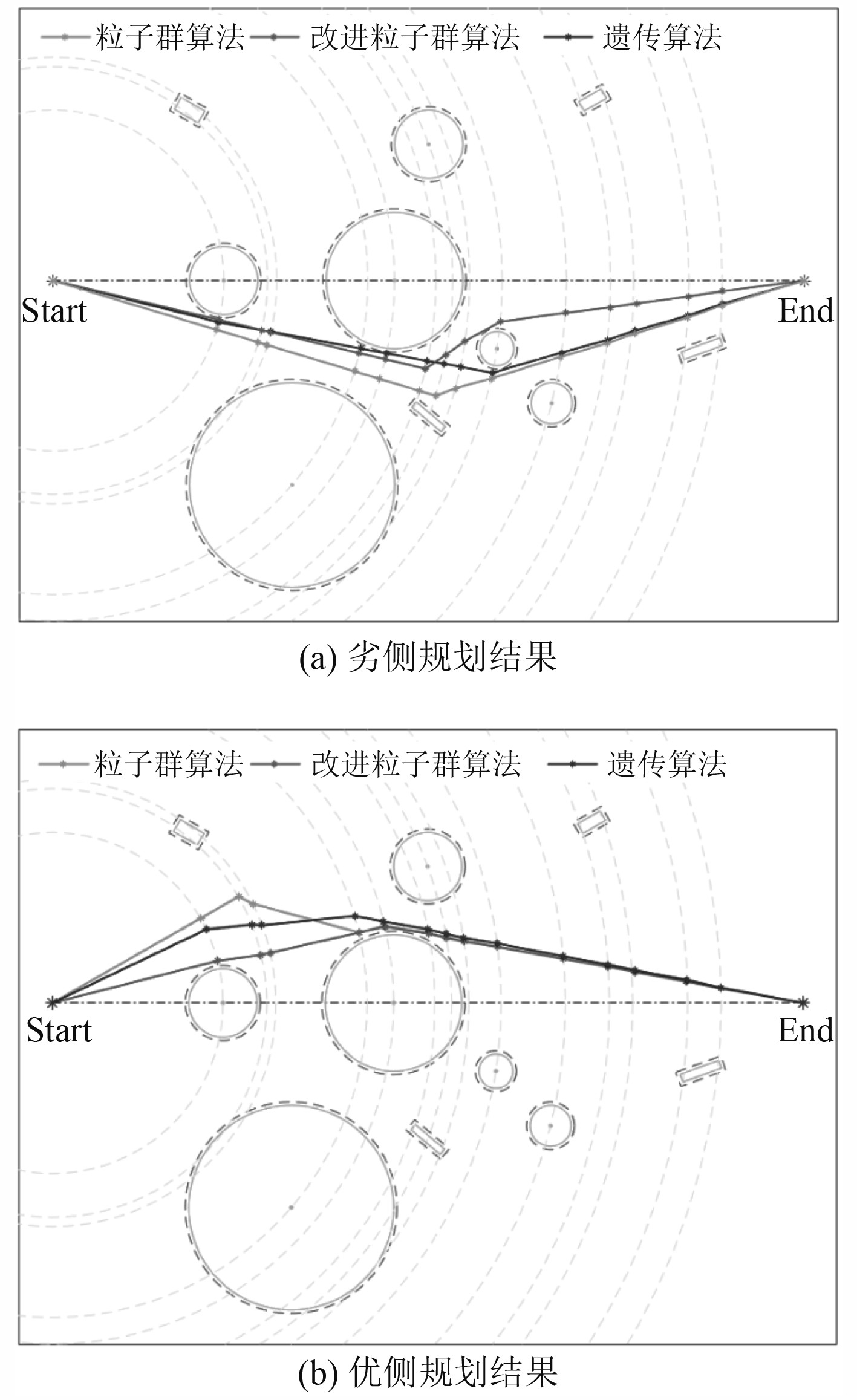
图 10 同侧路径规划结果 Fig. 10 The result of path planing in the same side |
|
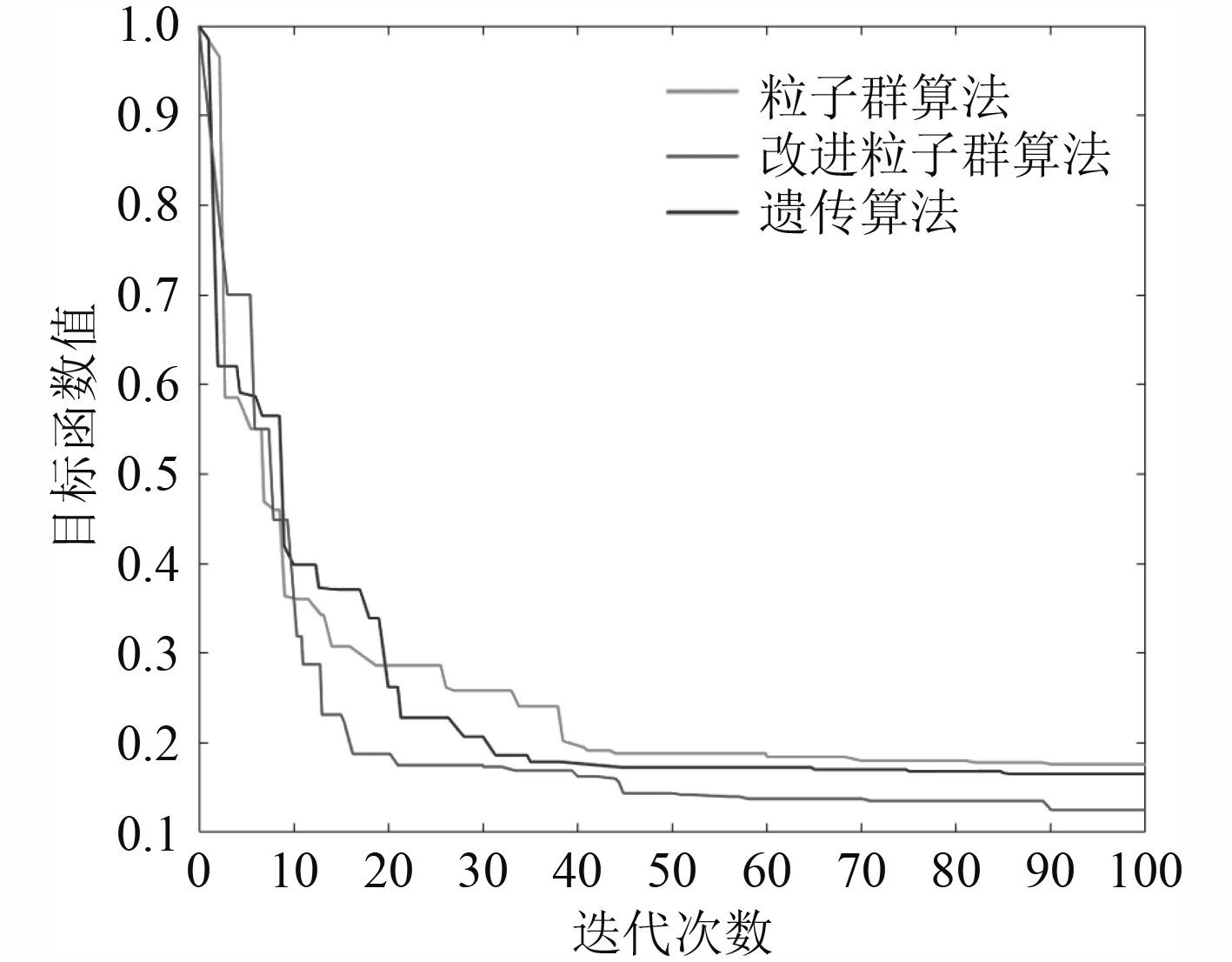
图 11 目标函数值的迭代曲线 Fig. 11 Iterative curve of objective function value |
分析表1,由20次实验结果所得路径长度平均值升序排序,分别为改进粒子群算法、遗传算法和粒子群算法。如图10所示,同侧实验结果比较表明,3种方法都能够完成全局静态路径规划任务,且机器人航行全程无危险;与遗传算法、传统粒子群算法相比,改进粒子群算法的规划效果更好,规划路径长度更短。
图11为选取某次实验的函数值迭代曲线。结果表明,改进粒子群算法的收敛效果和求解能力优于传统 PSO 算法和遗传算法,且算法的跳出局部最优解的能力优于二者。改进后的粒子群算法在前期搜索效果弱于传统粒子群算法和蚁群算法的情况下,能够利用粒子的“变异”加快搜索速度,快速逼近最优解。在后期收敛中,由于“变异”粒子的引入,能够避免陷入局部最优解。由以上分析可知,改进的粒子群算法在做机器人全局静态路径规划时,具有较强的搜索和收敛能力。
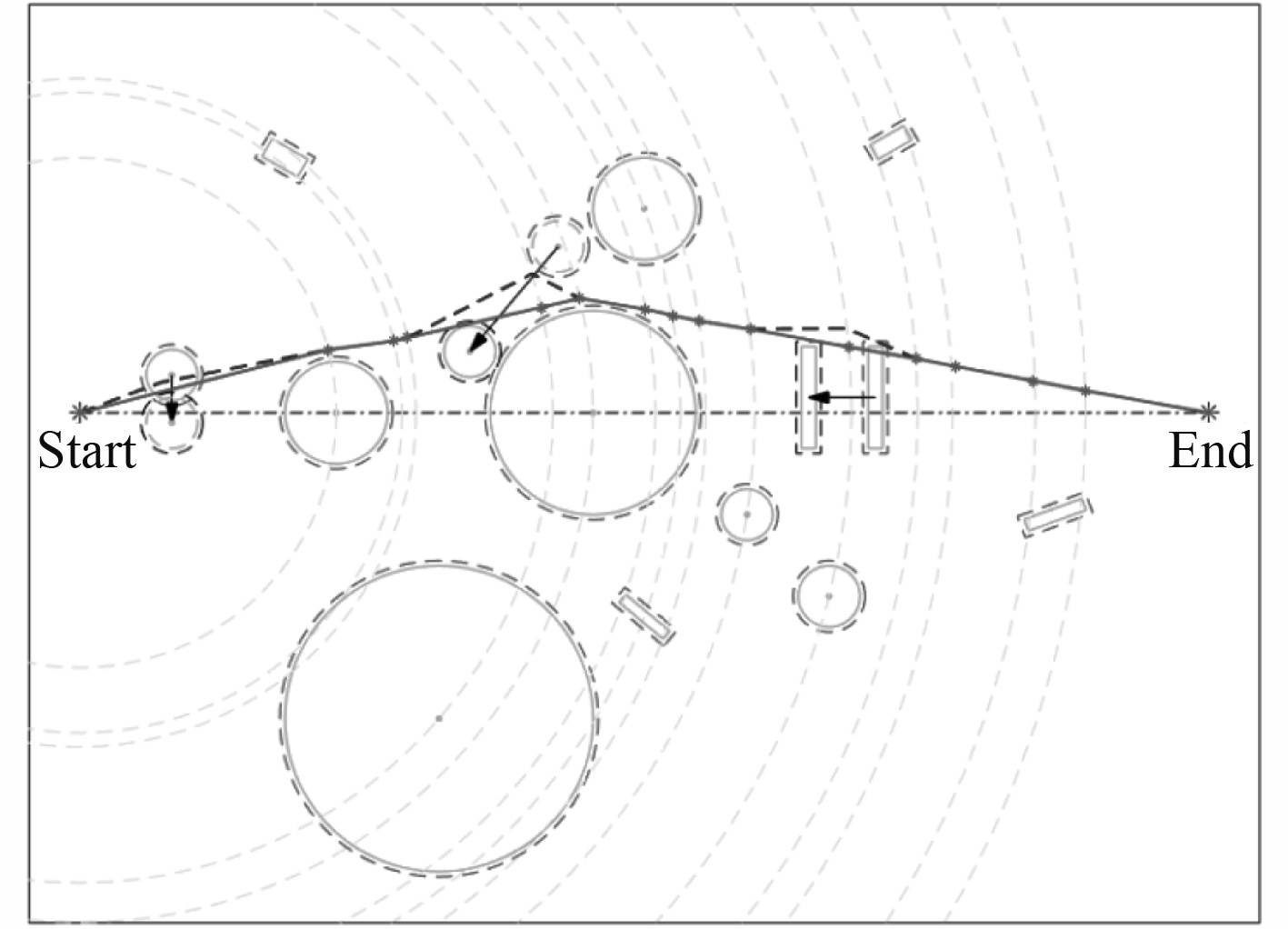
同时,本文验证了局部动态路径规划能力。图12为全局静态最优规划路径中,加入局部动态障碍后所得到的最终规划结果。结果表明,针对不同的局部动态障碍,机器人能够安全、高效的进行躲避,且避障动作小、路径损失少,能够在全局路径的基础上规划出最优避障路径。
|
图 12 动态环境下规划结果 Fig. 12 The result of path planing in dynamic obstacle environment |
本文依据大型自主水下机器人路径规划需求,在严格的机动性约束条件下构建了路径长度、路径可行度和回转可行度函数;通过引入最优位置变异过程增强了算法在全局静态路径规划过程中的求解能力;面对局部动态规划,引入速度障碍法以获得碰撞范围和安全区域。实验结果表明,全局静态与局部动态相融合的路径规划方法,在全局静态规划中路径更短、求解能力更强,局部动态规划能够规划出最优避障路径,高效且稳定。
| [1] |
ZHANG Y, GONG D W, ZHANG J H. Robot path planning in uncertain environment using multi-objective particle swarm optimization[J]. Neurocomputing, 2013, 103(MAR. 1): 172-185. |
| [2] |
DI L, ZHENG Z, XIA M, et al. Robot path planning based on an improved Multi-objective PSO method[C]// International Conference on Computer Engineering. 2016.
|
| [3] |
NIE Z, YANG X, GAO S, et al. Research on autonomous moving robot path planning based on improved particle swarm optimization[C]// 2016 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2016.
|
| [4] |
PANDA A, MALLIPEDDI R, DAS S. Particle swarm optimization with a modified learning strategy and blending crossover[C]// 2017 IEEE Symposium Series on Computational Intelligence (SSCI). IEEE, 2017.
|
| [5] |
张岳星, 王轶群, 李硕, 等. 基于海图和改进粒子群优化算法的AUV全局路径规划[J]. 机器人, 2020, 42(1): 120-128. |
| [6] |
向金林, 王鸿东, 欧阳子路, 等. 基于改进双向RRT的无人艇局部路径规划算法研究[J]. 中国造船, 2020, 61(1): 157-166. DOI:10.3969/j.issn.1000-4882.2020.01.016 |
| [7] |
董蛟, 刘忠, 张建强, 等. 欠驱动USV实时自主避障路径规划算法[J]. 电光与控制, 2020, 27(5): 10-13+51. DOI:10.3969/j.issn.1671-637X.2020.05.003 |
| [8] |
张洋洋, 瞿栋, 柯俊, 等. 基于速度障碍法和动态窗口法的无人水面艇动态避障[J]. 上海大学学报(自然科学版), 2017, 23(1): 1-16. |
| [9] |
LI D, ZHENG Z, MENG X, et al. Robot path planning based on an improved multi-objective PSO method[C]//International Conference on Computer Engineering, Information Science & Application Technology. Paris, France: Atlantis Press, 2016: 496501.
|
| [10] |
DADGAR M, JAFARI S, HAMZEH A. A PSO-based multi-robot co-operation method for target searching in unknown environments[J]. Neurocomputing, 2016, 177: 62-74. DOI:10.1016/j.neucom.2015.11.007 |
| [11] |
POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33-57. DOI:10.1007/s11721-007-0002-0 |
| [12] |
MAC TT, COPOT C, TRAN D T, et al. A hierarchical global path planning approach for mobile robots based on Multi-objective particle swarm optimization[J]. Applied Soft Computing, 2017. |
| [13] |
TRELEA IC. The particle swarm optimization algorithm: convergence analysis and parameter selection[J]. Information Processing Letters, 2003, 85(6): 317-325. DOI:10.1016/S0020-0190(02)00447-7 |
| [14] |
刘振, 周先存. 基于独立权重和分级变异策略的粒子群算法[J]. 吉林大学学报(理学版), 2017(2). |
| [15] |
PAOLO FIORINI Z S. Motion planning in dynamic environments using velocity obstacles[C]// International Journal of Robotics Research. 1998.
|
| [16] |
祖迪. 动态环境下移动机器人自主规划方法研究[D]. 沈阳: 中国科学院沈阳自动化研究所, 2007.
|
 2021, Vol. 43
2021, Vol. 43
