2. 船舶振动噪声重点实验室,武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
气囊隔振系统正逐步应用于船舶动力模块集成隔振,为船舶的机械噪声高效治理提供了技术途径[1]。由于气囊隔振系统需要承载动力设备重量以及维持高精度姿态平衡,对系统的可靠性要求高,目前国内对船舶气囊隔振系统的可靠性研究比较少,对此类隔振系统开展可靠性研究可以为隔振系统设计优化及运行维护提供理论支撑。
施亮等[2]建立了气囊隔振装置的对中姿态响应计算模型,分析了气囊漏气、元器件失效等故障模式对隔振装置控制性能的影响。吕志强等[3]对气囊浮筏隔振装置姿态控制进行研究,分析了气囊漏气对筏架姿态控制性能的影响。张国富等[4]从结构和力学的角度对城市轨道车辆使用的空气弹簧进行疲劳寿命分析,并推测了空气弹簧关键结构部位的失效率对其可靠性影响程度。孙微等[5]对整星隔振系统进行结构的可靠性分析,将可靠性设计理论与灵敏度分析方法相结合,研究了设计参数的改变对结构可靠性的影响。
本文以某船舶气囊隔振系统为研究对象,建立可靠性网络模型及可靠性计算方法,在此基础上对影响隔振系统可靠性的因素进行分析,为气囊隔振系统的可靠性设计优化提供依据。
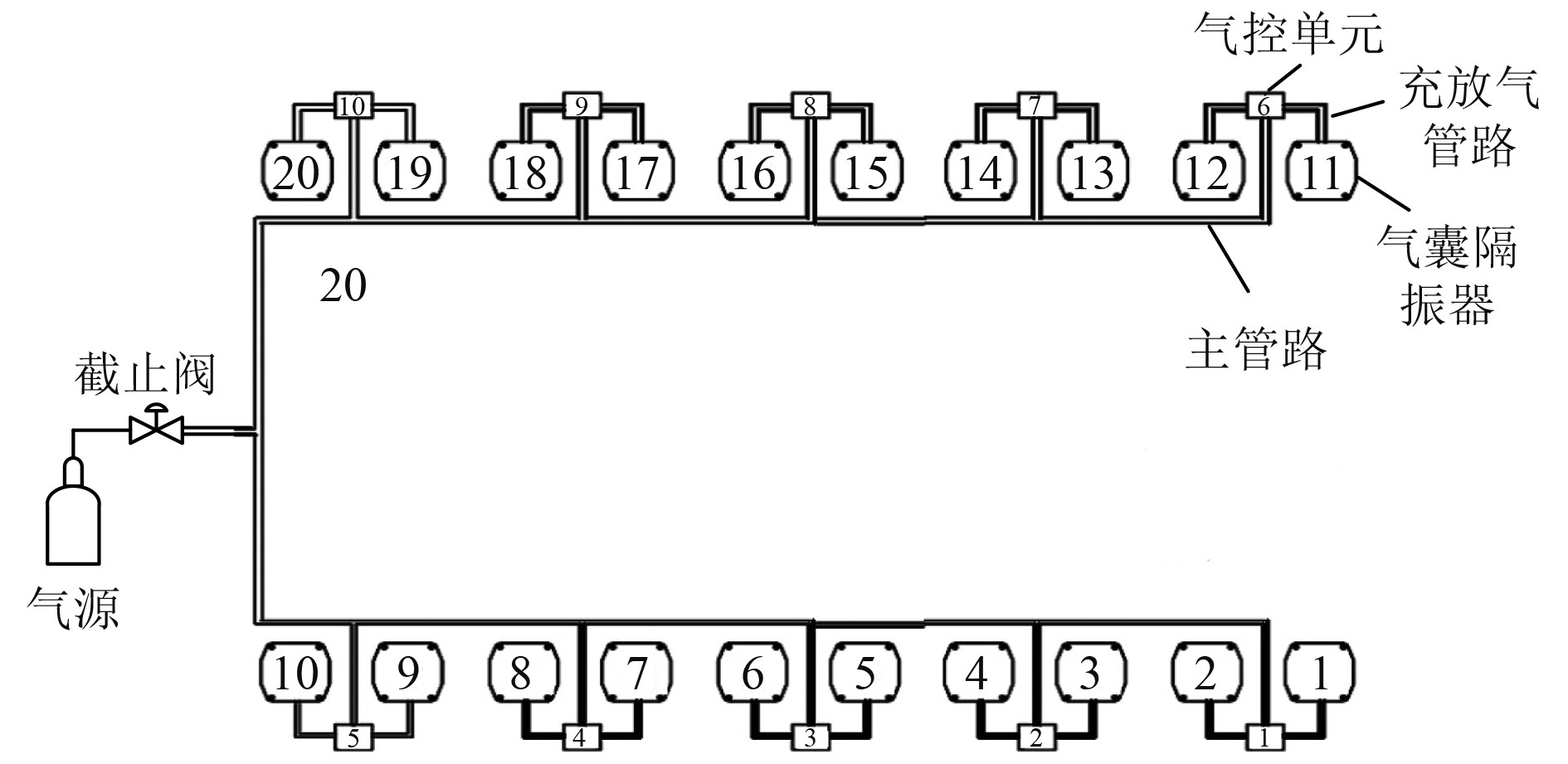
1 气囊隔振系统的可靠性分析模型 1.1 系统结构及工作原理气囊隔振系统由气囊隔振器、充放气管路、气控单元以及主管路组成,管路与其他部件之间用接口连接,如图1所示。
|
图 1 气囊隔振系统 Fig. 1 Air-spring mounting system |
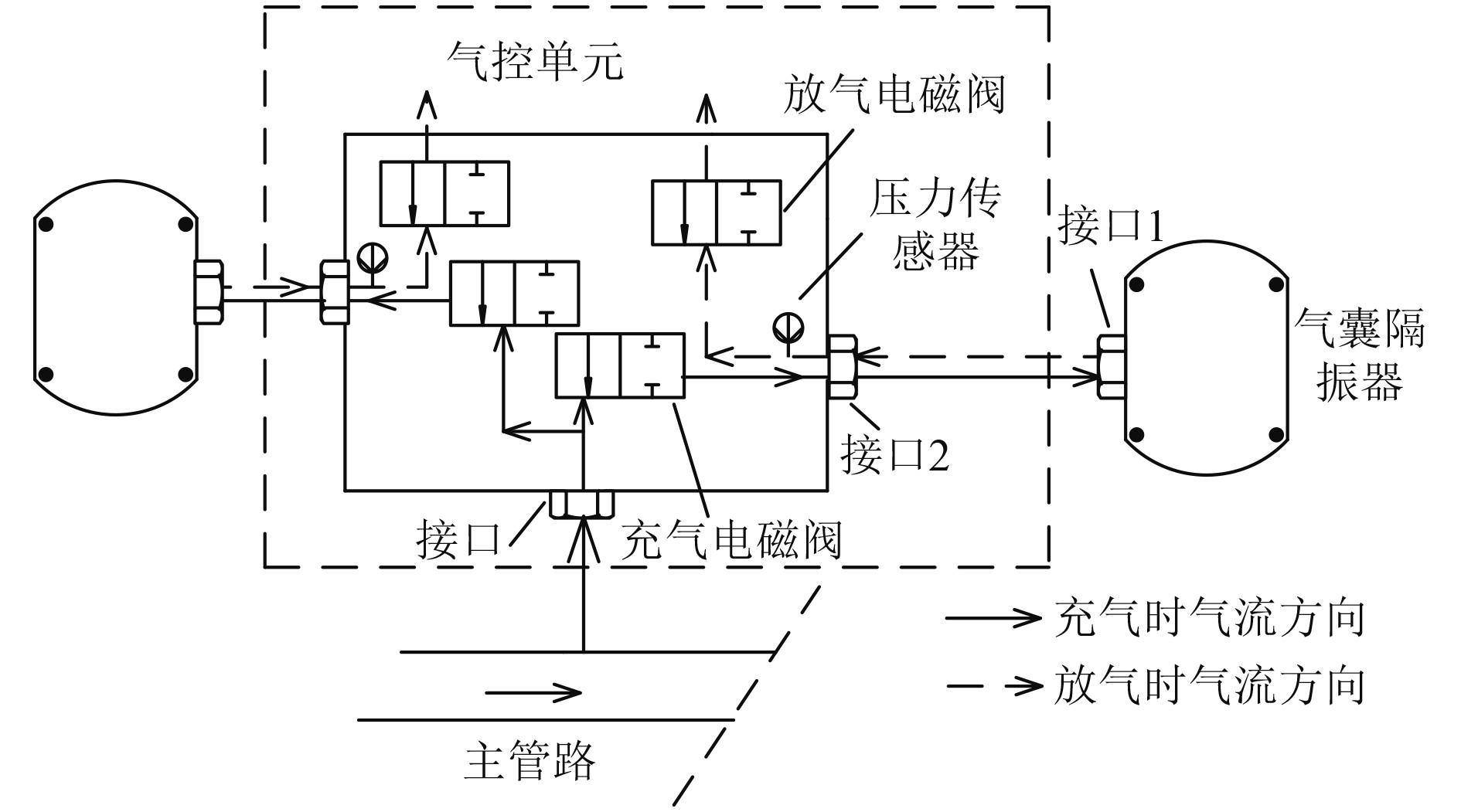
气囊隔振器分布在船舶动力模块底层,承载动力设备重量。气控单元主要是对气囊隔振器进行充放气操作以及监测气囊内压力。气囊隔振器和气控单元通过充放气管路连接,气控单元连接着主管路。图2为隔振系统的工作原理,在隔振系统充气工作过程中,气体通过主管路进入到气控单元,此时充气电磁阀打开,气体由气控单元进入气囊隔振器内,完成对气囊的充气。在隔振系统放气过程中,气体从气囊内经过管路进入到气控单元,此时放气电磁阀打开,气体直接从气控单元排出。
|
图 2 气控单元工作原理图 Fig. 2 Schematic diagram of pneumatic unit |
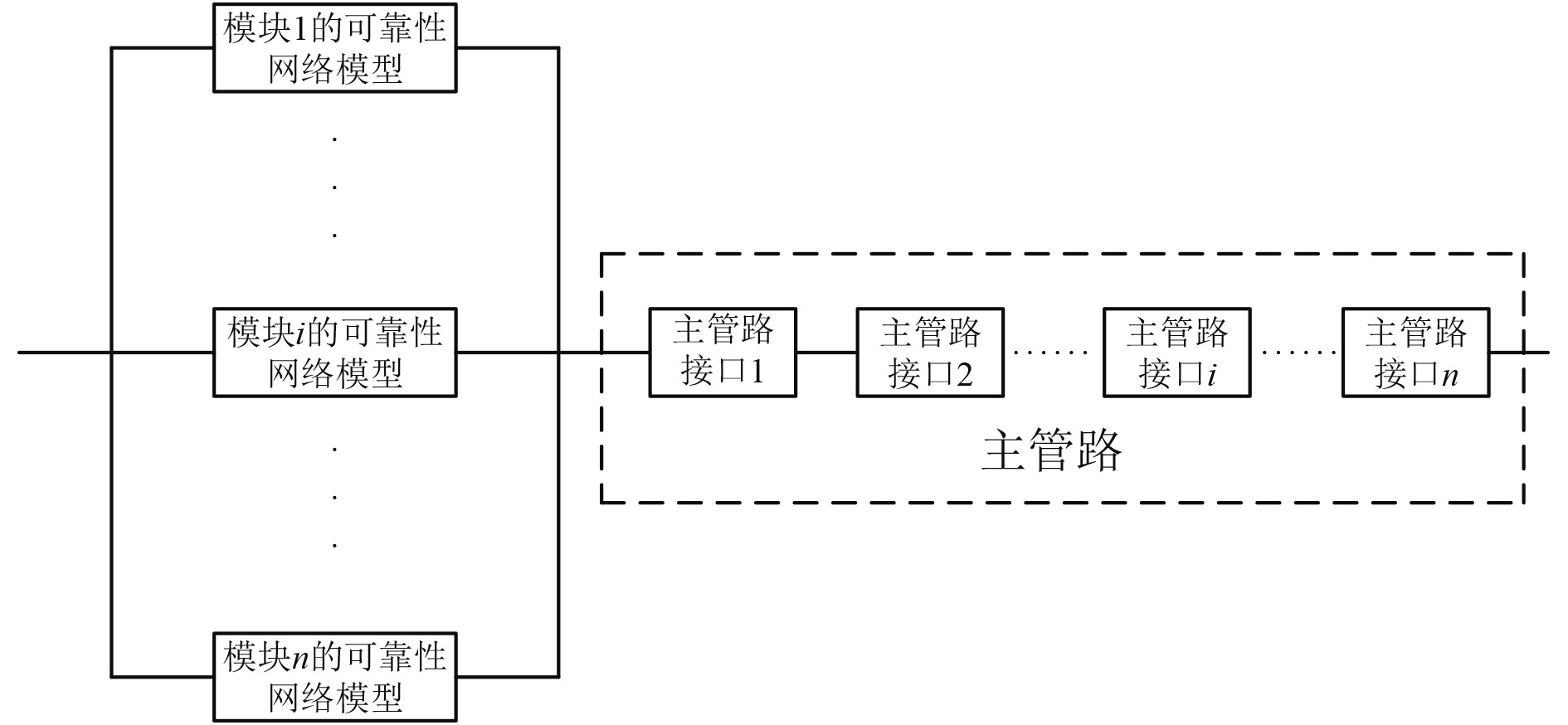
根据船舶气囊隔振系统的结构特点,建立可靠性网络模型,将其划分为
|
图 3 隔振系统可靠性网络模型 Fig. 3 Reliability network model of air-spring mounting system |
|
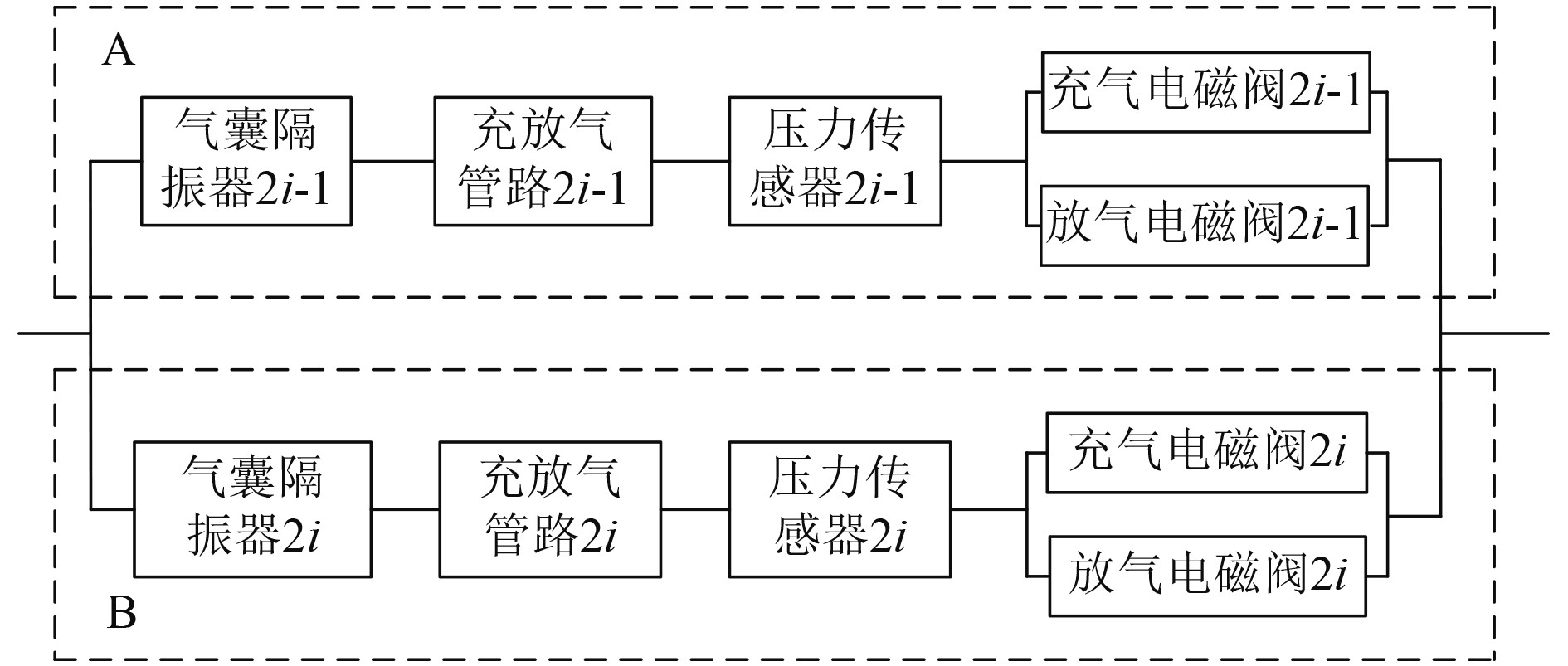
图 4 可靠性模块的可靠性网络模型 Fig. 4 Reliability network model of reliability module |
对于可靠性模块,A和B两部分的部件连接方式相同,且两部分中相同部件的失效率相同,则有A和B两部分的可靠度相同,因此对可靠性模块进行可靠性分析时,只需分析B部分的可靠度即可,并可以在此分析结果的基础上对隔振系统的可靠度进行研究。
1.3 系统可靠度计算模型由
隔振系统的每个可靠性模块由相同的两部分组成,且这两部分是相互独立的,故隔振系统总共具有
| $ {R}_{S}=\left(\begin{array}{c}2n\\ k\end{array}\right){R}_{2i}^{k}·{F}_{2i}^{2n-k}·{R}_{Z}{\text{。}}$ | (1) |
式中:
设定
假设B部分中各部件的可靠度与不可靠度分别为
| ${R_{2i}} = {R_1}R_2^2{R_3}\left( {1 - {F_4}{F_5}} \right){\text{。}}$ | (2) |
式中:
B部分中每个部件的可靠度
| ${R_j} = {e^{ - {\lambda _j}t}}{\text{。}}$ | (3) |
其中:
主管路可靠度
| ${R_Z}{\rm{ = }}\prod\limits_{i = 1}^n {{r_i}}{\text{。}} $ | (4) |
其中:
| ${R_Z} = {r^n} = {e^{ - n{\lambda _0}t}}{\text{。}}$ | (5) |
分析单一部件对隔振系统可靠度的影响,即当单一部件的失效率为0时,隔振系统可靠度发生的变化。
假设
假设可靠性模块中气囊隔振器的失效率
| $ {R}_{2i}={R}_{2}^{2}{R}_{3}·\left(1-{\displaystyle \prod _{j=4}^{5}{F}_{j}}\right){\text{,}}$ | (6) |
将式(6)代入式(1)中得到
同理,假设
定义
| ${\alpha _j} = \frac{{\left| {{R_S} - {R_S}\left( {{\lambda _j} = 0} \right)} \right|}}{{{R_S}}}{\text{,}}(j = 0 \sim 5){\text{。}}$ | (7) |
由式(7)可以得到单一部件对隔振系统可靠度的具体影响程度。
2 隔振系统可靠度影响因素分析 2.1 单一部件对隔振系统可靠度影响分析现有大型气囊隔振系统由10个可靠性模块组成,即
以隔振系统运行10个月为例,对其进行可靠度分析如表1所示。
|
|
表 1 隔振系统各部件可靠度 Tab.1 Reliability of each component of air-spring mounting system |
由式(2)得到可靠性模块中B部分的可靠度
该隔振系统具有的B部分有16个能正常工作,该系统就能正常工作,则有:
| ${R_S} = \left( \begin{gathered} 20 \\ 16 \\ \end{gathered} \right) \!\times\! {0.755\;2^{16}} \!\times\! {\left( {1 - 0.755\;2} \right)^4} \times {0.830\;1^{10}}{\rm{ = 0}}{\rm{.726\;2}}{\text{。}}$ |
即10个月后隔振系统正常工作的概率为73%。
|
|
表 2 单一部件对隔振系统可靠度的影响因子 Tab.2 The impact factor of a single component |
由表2可知:1)在隔振系统的可靠性网络模型中,所有的主管路接口串联连接,且失效率在所有部件中最大,因此主管路接口对隔振系统可靠度的影响因子最大;2)充放气管路具有2个接口,且与其他部件串联连接,其失效率仅次于主管路接口,故充放气管路对隔振系统可靠度的影响较大;3)气囊隔振器的失效率在所有部件中是最低的,因此对隔振系统可靠度影响较小,为0.0009;4)充、放气电磁阀是并联连接,即使其失效率大于压力传感器与气囊隔振器,它们对隔振系统可靠度的影响却最小。
2.2 运行前维护对系统可靠度的影响分析在隔振系统的所有部件中,管路的可靠度与检修维护措施关联很大,因此在隔振系统运行前对其进行维护,如检查管路的气密性、更换接口的密封垫片等,可以提高隔振系统的可靠度。经验表明,检修维护后管路的失效率下降约50%。
隔振系统运行18个月后管路可靠度如表3所示。
|
|
表 3 检修维护后管路可靠度 Tab.3 Pipeline reliability after overhaul and maintenance |
其余部件可靠度可根据式(3)计算,由式(2)得到可靠性模块中B部分的可靠度
与2.1计算结果相比可得到:系统运行前对管路进行检修维护后,即使系统运行18个月时间,其可靠度仍然高于未维护时隔振系统运行10个月时的可靠度,说明运行前对管路的检修维护可以很好延长隔振系统的正常运行时间。
2.3 气囊隔振器数量对系统可靠度的影响分析不同气囊隔振器数量的隔振系统可靠度具有差别。对比分析气囊隔振器数量分别为8,20,32的三型隔振系统可靠度,每型隔振系统可以在20%隔振器失效时满足设备承载力要求,即三型隔振系统的正常工作B部分数量分别为7,16,26,隔振系统可正常工作。因为可靠度取0~1,故对隔振系统可靠度的分析也是取0~1。现对三型隔振系统可靠度随时间的变化进行分析。
由表4和图5可知,由于承载余量的不同,三型隔振系统的可靠度具有差别。每型气囊隔振系统可靠度随运行时间的下降速度不同,Ⅰ型气囊隔振系统可靠度下降速度最慢,Ⅱ型气囊隔振系统可靠度下降速度最快;在系统运行9000多小时之前,Ⅰ型气囊隔振系统可靠度低于其他气囊隔振系统,但运行10500多小时之后,Ⅰ型气囊隔振系统高于其它气囊隔振系统。对于三型隔振系统,Ⅲ型气囊隔振系统正常运行的时间高于其他气囊隔振系统。
|
|
表 4 三型隔振系统的可靠度随时间的变化 Tab.4 Reliability variation with time of three air-spring mounting system |

|
图 5 三型隔振系统的可靠度随时间的变化 Fig. 5 Reliability variation with time of three air-spring mounting system |
本文建立船舶气囊隔振系统的可靠性网络模型,对影响气囊隔振系统可靠度的因素进行讨论:
1)气囊隔振系统的各个部件对其可靠度的影响程度不同。气体管路是对隔振系统可靠度影响程度大的部件,分析表明,在系统运行前对其进行检修维护,能够大幅提高隔振系统可靠度,延长隔振系统的运行时间。
2)对于不同规模的隔振系统,由于承载余量的不同,在运行前期,大型气囊隔振系统表现出更高可靠度,但随时间下降较快。随着运行时间延长,小型隔振系统的可靠度会逐渐高于大型气囊隔振系统。
| [1] |
何琳, 徐伟. 舰船隔振技术及其进展[J]. 声学学报, 2013, 38(2): 128-136. |
| [2] |
施亮, 何琳, 徐伟, 等. 船舶主机气囊隔振装置的对中可控性[J]. 海军工程大学学报, 2011(5): 27-30+35. DOI:10.3969/j.issn.1009-3486.2011.05.006 |
| [3] |
吕志强, 施亮, 赵应龙. 气囊浮筏隔振装置姿态控制问题[J]. 噪声与振动控制, 2013(1): 40-44. |
| [4] |
张国富, 方宇. 城市轨道车辆空气弹簧系统使用寿命及可靠性评价方法[D]. 上海: 上海工程技术大学, 2013: 55−71.
|
| [5] |
孙微, 方勃. 整星隔振系统的可靠性分析及其优化设计[D]. 哈尔滨: 哈尔滨工业大学, 2008: 19−29.
|
| [6] |
WILLIAM M GOBLE. Control Systems Safety Evaluation & Reliability[M]. 北京: 中国电力出版社, 2008: 110−123.
|
| [7] |
BILLINTON R., ALLAN R. N. Reliability evaluation of engineering systems: concepts and techniques[M]. New York: Plenum Press, 1983.
|
| [8] |
DHILLON B. S. Reliability engineering in systems design and operation[M]. New York: Van Nostrand Reinhold, 1983.
|
| [9] |
HENLEY E. J., Kumamoto H. Probabilistic risk assessment: reliability engineering, design, and analysis, Piscataway[M]. NJ: IEEE Press, 1992.
|
| [10] |
Shooman M. L. Probabilistic reliability: An engineering approach[M]. 2nd Ed., Malabar, FL: Robert E. Krieger Publishing, 1990.
|
 2021, Vol. 43
2021, Vol. 43
