2. 海军研究院,北京 100071
2. Naval Research Academy, Beijing 100071, China
钢丝绳隔振器是美国20世纪70年代末研制成功的一种非线性隔振器材[1],因其固有频率低、可靠性高、使用寿命长等优点被广泛运用到舰载设备、弹药运输、航空设备和机械设备的隔振缓冲装置中[2]。钢丝绳隔振器在工作时能够产生干摩擦并消耗大量的能量,能有效隔离振动和冲击。迄今为止,大量学者通过理论和实验方法研究了钢丝绳隔振器的力学特性。
刘广璞[3]通过静态和动态实验发现与线性隔振器材相比,钢丝绳隔振器能够吸收更多的能量。Vaiana[4]和班书昊[5]分别研究了钢丝绳隔振器的水平和三向刚度。万叶青[6]和王红霞[7]分别研究了线圈数目、钢丝绳直径、绳环参数、绳环的水平倾斜角度和激励振幅、频率对钢丝绳隔振器迟滞特性的影响规律。王勇[8]用锤击法对小型钢丝绳隔振器进行空载和有预载的冲击实验,用双线性模型来描述力-位移曲线。Pablo[9]基于Duffing的数学模型使用谐波平衡法建立了冲击响应的数学模型。Bo Cen[10]采用数值模拟方法研究简化的钢丝绳隔振器的垂向静刚度,但钢丝绳弹性模量是仿真所得需进行实验验证。Shaowu Tu[11]运用Bo Cen中简化的有限元方法分析了钢丝绳隔振器的直径比、节距和钢丝绳弯曲半径对隔振器力学性能的影响。
上述学者主要通过实验探究钢丝绳隔振器的力学特性,仿真研究较少,主要原因是钢丝绳隔振器的非线性特性较强。当探究钢丝绳直径、钢丝绳结构形式、线圈数目、极限位移和隔振器高宽比等参数对隔振器性能的影响时,如果都用实验来探究,成本较高且花费时间较多,因此对钢丝绳隔振器的仿真研究尤为重要。本文通过建立一个简化的球形钢丝绳隔振器有限元模型,基于Abaqus有限元软件对其进行数值仿真研究,与实验结果对比误差在9%以内,验证了仿真方法的有效性,为球形钢丝绳隔振器力学特性的研究提供参考
1 钢丝绳拉伸实验及压缩仿真 1.1 钢丝绳弹性模量测定实验 1.1.1 实验方法GGQ25-62L球形钢丝绳隔振器所用钢丝绳结构为6
钢丝绳直径为6.4 mm,芯股和侧股直径分别为2.4 mm和2 mm,试样在两夹具之间的距离为80 mm。实验试样及试样装夹如图1和图2所示,实验所用钢丝绳试样足以代表绳股的特性,无任何缺陷。

|
图 1 钢丝绳试样 Fig. 1 Wire rope sample |

|
图 2 钢丝绳拉伸实验图 Fig. 2 Wire rope tensile experiment diagram |
实验时发现钢丝绳在夹具夹头处易发生应力集中的情况,在测量钢丝绳最小破断力时总是在夹具夹头处发生钢丝绳断裂现象,因此,为减小应力集中对实验结果的影响,在两夹头处裹上一层橡胶圈,可减小应力集中对实验结果的影响。
实验步骤如下:
1)先测定绳股的最小破断拉力,即为绳股即将拉断时的值,通过实验测得。
2)将绳股装夹时先处于松弛状态,缓慢调整实验机使绳股处于绷直状态,然后对实验机调零。先给绳股施加最小破断力10%的载荷(F10%),记录此时的位移。
3)测定钢丝绳初始状态的弹性模量,继续对试样施加载荷至不超过钢丝绳最小破断力的30%(F30%),同时记录绳股F30%时对应的位移。
4)测定绳股稳定状态或完全稳定状态的弹性模量时,继续对试样施加载荷至不超过绳股最小破断力的50%(F50%),记录绳股最小破断力F50%时对应的位移,然后将载荷降至绳股最小破断力的5%(F5%),记录F5%时对应的位移。
采用上述实验方法和步骤分别对芯股和侧股进行实验,求得单根绳股实际弹性模量。
1.1.2 实验结果钢丝绳实际弹性模量根据GB/T 24191-2009《钢丝绳实际弹性模量测定方法》中的规定来计算,实际弹性模量计算公式为:
| ${E_{10 - 30}} = {L_0}\frac{{\left( {{F_{30\% }} - {F_{10\% }}} \right)}}{{{A_{0\left( {{x_2} - {x_1}} \right)}}}}{\text{。}}$ | (1) |
式中:L0为钢丝绳绳股试样长度;A0为绳股横截面积;F30%为30%钢丝绳最小破断力;F10%为10%钢丝绳最小破断力;X2为30%钢丝绳最小破断力时对应的位移;X1为10%钢丝绳最小破断力时对应的位移。由式(1)计算钢丝绳实际弹性模量结果如表1所示。
|
|
表 1 绳股实际弹性模量 Tab.1 Actual elastic modulus of wire rope |
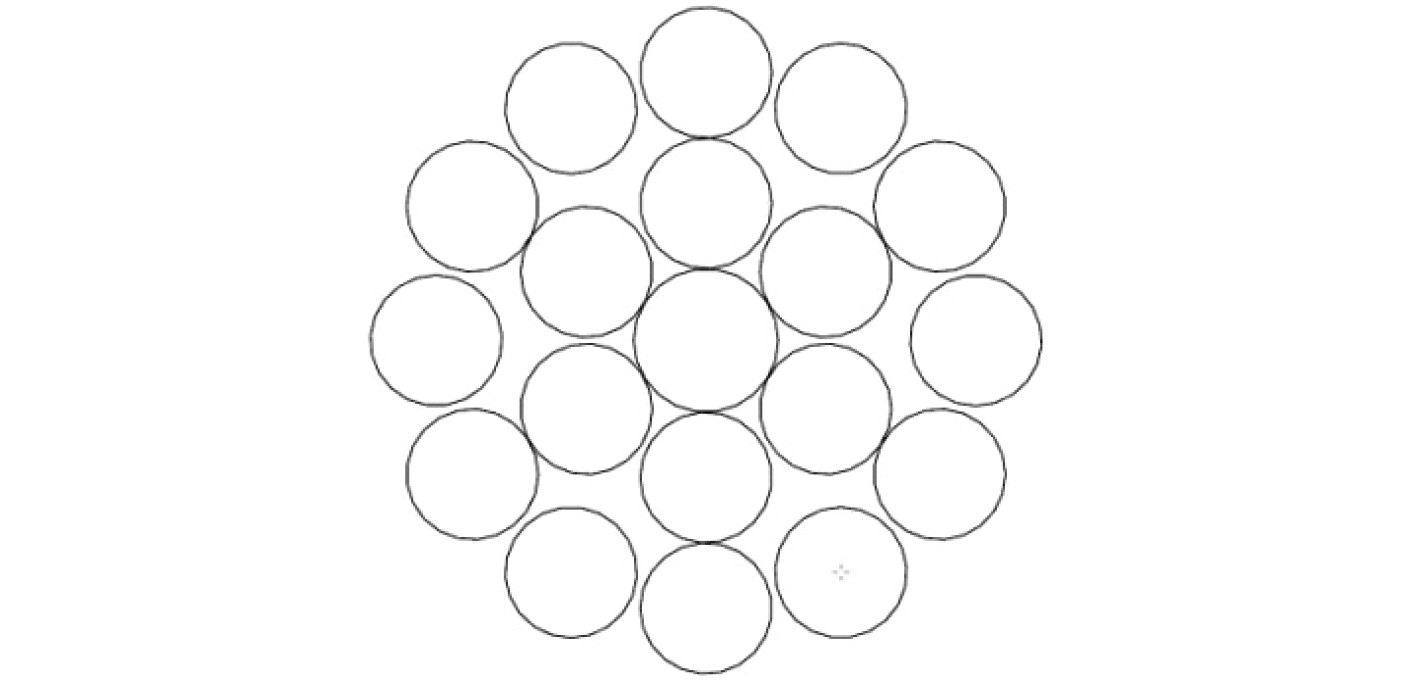
钢丝绳在压缩时出现失稳现象,无法得到其弹性模量,因此通过仿真获得其压缩时弹性模量。钢丝绳单根绳股截面如图3所示,共有1+6+12根钢丝,将6
|
图 3 绳股截面图 Fig. 3 Wire rope cross section |
仿真时将钢丝绳本构模型定义为双线性随动硬化模型[10],其弹性模量和切线模量如下考虑:
1)双线性随动硬化模型采用Hill屈服准则,在一个方向加载-卸载作用后各个方向上的强化效果不同与钢丝绳在弯曲时的复杂受力相吻合。将钢丝绳拉伸实验得到的弹性模量作为隔振器简化模型第一阶段的弹性模量。
2)双线性随动硬化模型中塑性段模拟的是钢丝绳股与股、丝与丝分离的这一过程,因此将压缩仿真时的弹性模量作为隔振器简化模型第二阶段的切线模量,将钢丝绳压缩时丝与丝分离时的应力作为钢丝绳隔振器的初始软化载荷。
3)在简化的有限元仿真模型中只考虑了芯股和侧股之间的干摩擦阻尼。
1.2.1 钢丝绳的建模及边界条件设置实验所用的钢丝绳芯股和侧股直径分别为2.4 mm和2 mm,其中芯股芯丝直径为0.56 mm,芯股侧丝直径为0.46 mm;侧股芯丝直径为0.44 mm,侧股侧丝直径为0.39 mm。钢丝的材料为304不锈钢,其具有加工性能好、韧性高等特点,弹性模量为190 GPa,切线模量为1.8 GPa,屈服应力为320 MPa,密度为7 850 kg/m3,泊松比为0.3。
钢丝在压缩过程中会承受张力和压缩载荷,因此钢丝绳相邻的丝与丝之间的接触定义为自接触,使用自接触可以自动定义相互作用面,该方法计算结果准确,并节省了大量的计算时间。钢丝的塑性定义为Kinematic-Hardening,选用罚函数法,切向摩擦系数为0.115[12],具有硬接触行为。钢丝绳划分的网格为六面体网格,网格大小为0.12,六面体网格具有在弯曲载荷作用下不易自锁且能获得更精确的位移。采用Abaqus/Explicit算法,此算法适用于复杂的接触问题,并且能够较好模拟高度非线性的准静态问题。
在UG中建立钢丝绳三维模型并导入Abaqus中,在钢丝绳的两端分别建立参考点,钢丝绳的2个端面分别耦合到参考点RP1和RP2,在参考点上施加边界条件和载荷。一端参考点RP1完全约束,限制其6个方向的自由度;另一端参考点RP2只允许轴向的移动,其余5个自由度被限制。边界条件如图4所示。在加载端施加位移载荷,压缩速度为20 mm/min。

|
图 4 边界条件设置 Fig. 4 Boundary condition setting |
通过仿真分别求得芯股和侧股压缩时的弹性模量和软化载荷。在压缩时,钢丝之间接触变松,钢丝相互分离,钢丝中间部分应力较大。对于简化的模型,等效应变εE为总变形量ΔL0与初始钢丝绳长度的比值,等效σE由拉伸和压缩时的力F决定,等效应变和等效应力的表达式如下:
| ${\varepsilon _E} = \Delta {L_0}/{L_0} = \left| {L - {L_0}} \right|/{L_0}{\text{,}}$ | (2) |
| ${\sigma _E} = 4F/\text{π} {d^2}{\text{。}}$ | (3) |
式中:L0为绳股初始长度,d为绳股直径。
运用式(2)和式(3)求得钢丝绳等效应力和等效应变,通过等效应力-应变关系求得钢丝绳单根绳股等效弹性模量,仿真所得的结果如表2所示。
|
|
表 2 芯股和侧股仿真结果 Tab.2 Core wire rope and side wire rope simulation results |
本文研究的钢丝绳隔振器是GGQ25-62L球形钢丝绳隔振器,其为全金属结构,可靠性高,使用寿命长。钢丝绳隔振器的垂向刚度决定了其承载能力,在准静态载荷的作用下,通过实验测定其力-位移曲线,用插值法求得球形钢丝绳隔振器的垂向刚度。图5为钢丝绳隔振器进行的准静态压缩实验。

|
图 5 隔振器压缩实验 Fig. 5 Vibration isolator compression experiment |
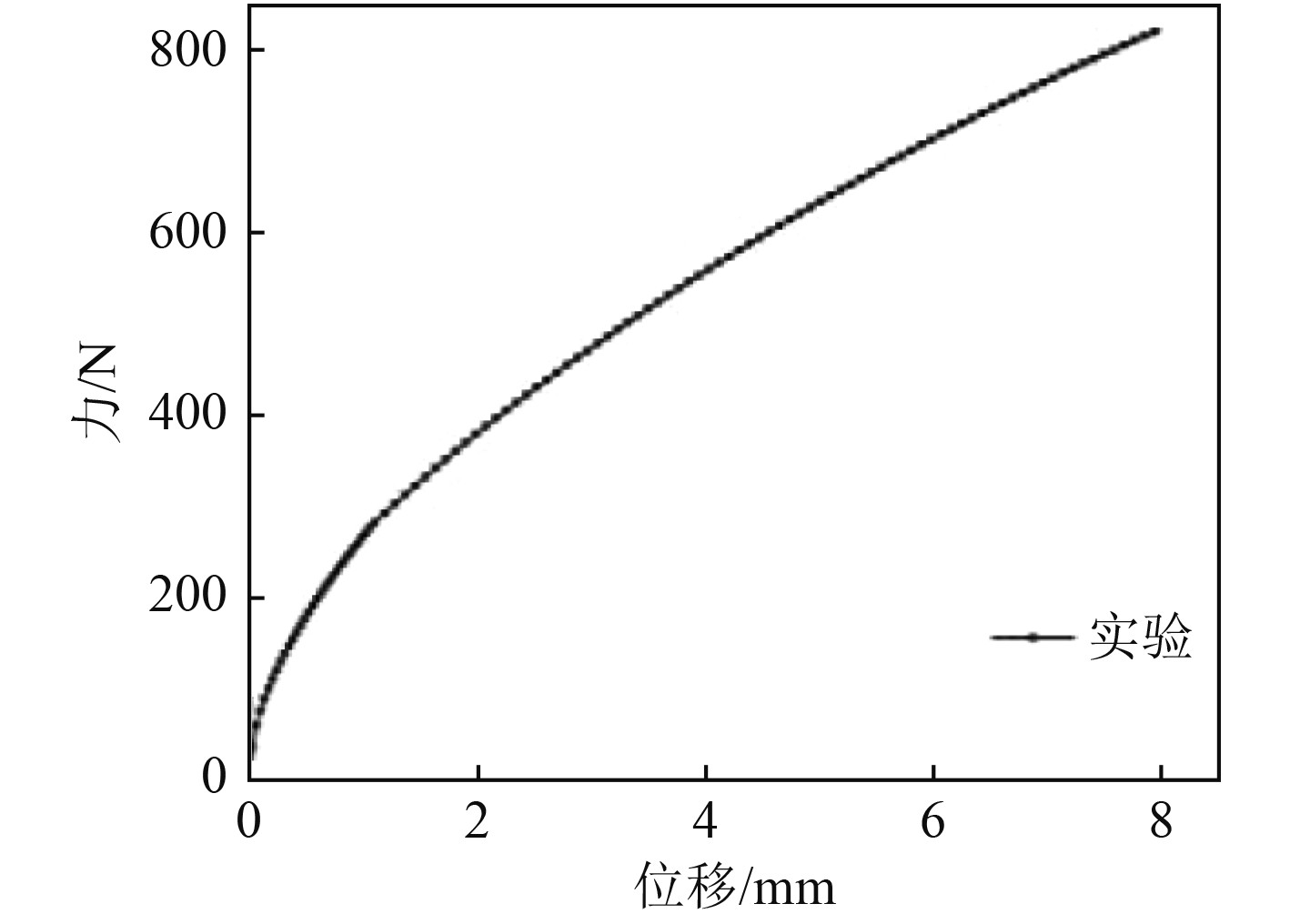
首先,对钢丝绳隔振器进行垂向的循环加载实验以消除钢丝绳隔振器本身的内应力,电子万能实验机的加载速度为20 mm/min,测试位移从0逐渐加载到8 mm并逐渐卸载到初始位置,通过循环加载实验使得钢丝绳隔振器各部分之间的稳定接触条件,特别是中心股和侧股之间丝与丝的接触。在循环加载实验后对GGQ25-62L球形钢丝绳隔振器进行准静态压缩实验,得到垂向的力-位移曲线,如图6所示。
|
图 6 隔振器压缩时力-位移曲线 Fig. 6 Force-displacement curve during compression of vibration isolator |
分析图6可知,球形钢丝绳隔振器压缩时初始阶段刚度较大,约为306.49 N/mm,在垂向位移约为0.15 mm时刚度明显降低,约为77.16 N/mm,在垂向位移约为8 mm时,力的大小为827.43 N。实验结果表明钢丝绳隔振器具有明显的非线性软化迟滞特性,这主要是由于钢丝绳隔振器在压缩载荷下钢丝绳的复杂变形引起的,根据刚度软化这一特性可以将其简化为双线性模型。钢丝绳由于相互缠绕而具有一定的刚度,使得钢丝绳隔振器在加载的第1阶段具有线性弹性,随着载荷的进一步加大,钢丝绳的弯曲压缩载荷大于钢丝绳隔振器的极限载荷,导致钢丝绳隔振器进入第2阶段的变形,钢丝绳隔振器的股与股、丝与丝之间相互滑移和分离导致垂向刚度小于初始刚度。球形钢丝绳隔振器在压缩时刚度软化的过程中钢丝绳各股之间产生内摩擦,并与钢丝绳的运动方向相反,从而消耗大量的能量,当钢丝绳隔振器具有适当的软化刚度和良好的稳定性时,其具有良好的隔振和隔冲性能。
2.2 球形钢丝绳隔振器准静态压缩仿真GGQ25-62L球形钢丝绳隔振器所选用的钢丝绳结构为6
|
|
表 3 绳股的材料属性 Tab.3 Material properties of the wire rope |
将表3所得的材料参数输入球形钢丝绳隔振器有限元模型中进行有限元仿真。钢丝绳隔振器有限元模型如图7所示。实体模型中上下甲板简化为上中心点RP1和下中心点RP2,将钢丝绳的两端分别耦合到RP1和RP2,RP2被完全固定,RP1只能沿隔振器的垂向运动,在RP1上施加位移载荷,位移载荷为20 mm/min,加载位移为8 mm。

|
图 7 有限元模型 Fig. 7 Finite element model |
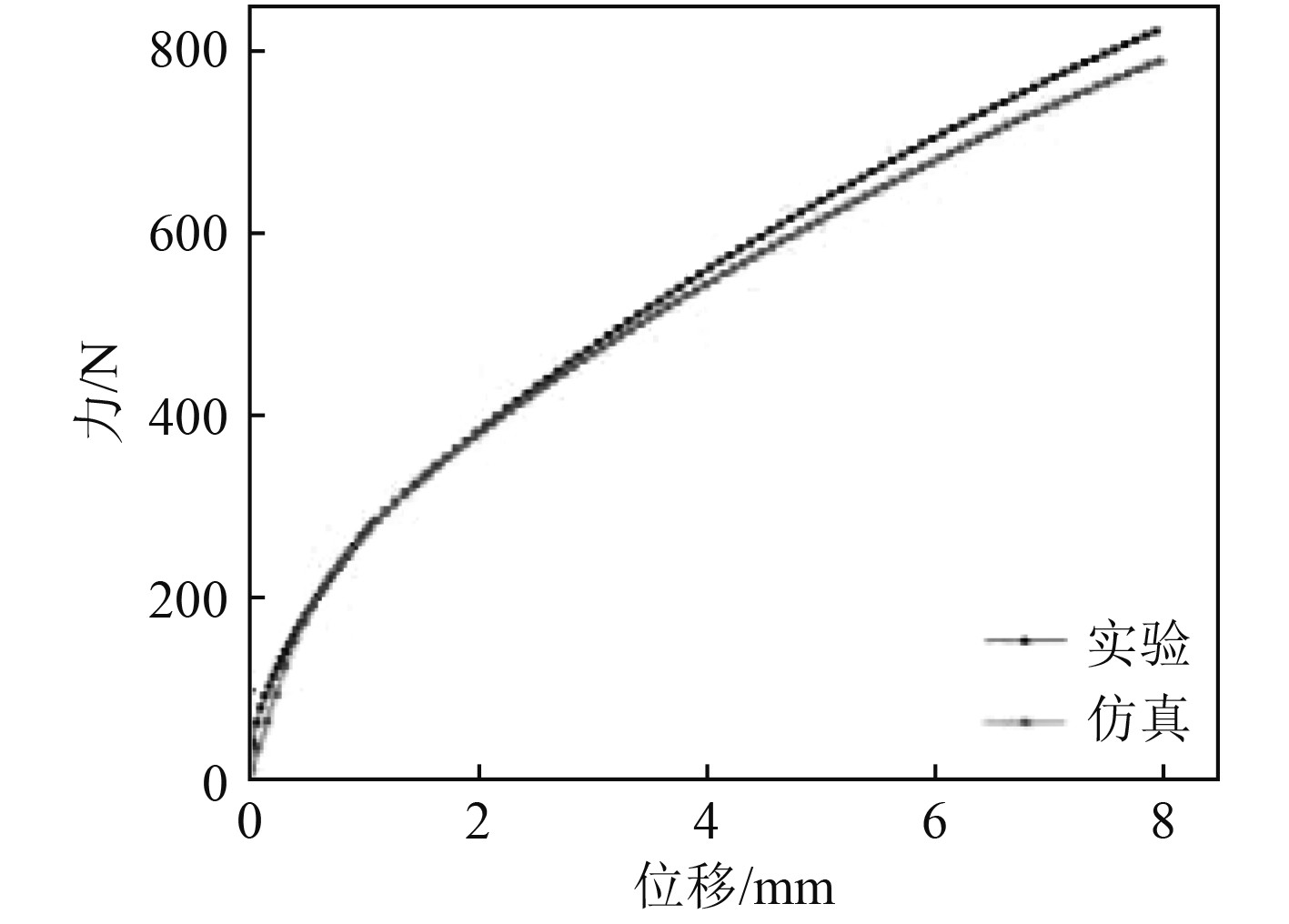
钢丝绳隔振器仿真和实验的力-位移曲线如图8所示,在初始阶段仿真的刚度与实验相比较小,在0.5 mm之后,仿真曲线和实验曲线吻合较好。
|
图 8 钢丝绳隔振器压缩力-位移曲线 Fig. 8 Compression force-displacement curve of wire rope vibration isolator |
由表4可知,第1阶段的钢丝绳隔振器的刚度明显大于软化后第2阶段钢丝绳隔振器的刚度,仿真所得的钢丝绳隔振器的第1阶段和第2阶段的钢丝绳隔振器的刚度分别为285.30 N/mm和70.81 N/mm,实验所得钢丝绳隔振器第1阶段和第2阶段的刚度分别为306.49 N/mm和77.16 N/mm,误差在9%以内。在加载到8 mm时,钢丝绳隔振器有限元分析所得载荷为794.97 N,实验载荷为827.43,误差为3.92%,仿真和实验对比结果验证了此仿真方法的有效性。由于钢丝绳和钢丝绳隔振器结构参数变化较多,对其进行实验会花费许多时间和成本,因此可通过有限元仿真进一步探究钢丝绳和钢丝绳隔振器的结构参数对隔振器力学性能的影响。
|
|
表 4 钢丝绳隔振器的仿真与实验结果对比 Tab.4 Comparison of simulation and experimental results of wire rope vibration isolator |
本文通过对球形钢丝绳隔振器建立一个新的建模方法并通过实验来验证,主要得出了以下结论:
1)在球形钢丝绳隔振器准静态压缩的过程中,采用所简化的模型和计算方法得到的结果和实验结果吻合较好,在隔振器最大位移为8 mm时力的误差在4%以内。
2)实验结果表明球形钢丝绳隔振器有明显刚度软化现象,采用Kinematic-Hardening能够较好的模拟球形钢丝绳隔振器压缩时刚度软化这一特性。
3)通过对球形钢丝绳隔振器实验与仿真结果刚度的对比分析,K1和K2误差在9%以内,所提出的仿真方法能够较好模拟球形钢丝绳隔振器的力学特性,为用仿真方法探究钢丝绳隔振器的几何参数对其性能的影响提供参考。
| [1] |
龚宪生, 骆意, 王红霞. 钢丝绳隔振器弹性元件空间曲线模型分析[J]. 重庆大学学报, 2014, 37(2): 7-13+21. |
| [2] |
曹晓政, 姜文涛, 李倩, 等. 车载电子设备隔振的随机振动分析[J]. 云南电力技术, 2018, 46(6): 68-71. DOI:10.3969/j.issn.1006-7345.2018.06.019 |
| [3] |
刘广璞, 王福明, 樊文欣. 钢丝绳隔振器动态特性试验研究[J]. 华北工学院测试技术学报, 1999, 13(3): 180-184. |
| [4] |
VAIANA, N., SPIZZUOCO, M., &SERINO, G. (2017). Wire rope isolators for seismically base-isolated lightweight structures: Experimental characterization and mathematical modeling[J]. Engineering Structures, 140, 498–514.
|
| [5] |
班书昊, 李晓艳, 蒋学东, 等. 钢丝绳隔振器的非线性动力学模型[J]. 力学与实践, 2012, 34(1): 66-69. |
| [6] |
万叶青, 范立民, 齐煜. 钢丝绳隔振器非线性特性分析[J]. 振动与冲击, 2007, 26(7). DOI:10.3969/j.issn.1000-3835.2007.07.031 |
| [7] |
王红霞. O型钢丝绳隔振器特性研究[D]. 重庆: 重庆大学, 2015.
|
| [8] |
王勇, 黄映云. 锤击法测评小型钢丝绳隔振器冲击特性[J]. 船舶工程, 2007, 29(4): 79-81. DOI:10.3969/j.issn.1000-6982.2007.04.017 |
| [9] |
TAPIA-GONZÁLEZ, P. E., & LEDEZMA-RAMÍREZ, D. F. Experimental characterisation of dry friction isolators for shock and vibration[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2017, 36(1), 83–95.
|
| [10] |
CEN, B., LU, X., & ZHU, X. Research of numerical simulation method on vertical stiffness of polycal wire rope isolator[J]. Journal of Mechanical Science and Technology, 2018, 32(6), 2541–2549.
|
| [11] |
TU, S., LU, X., & ZHU, X. Effect of structure parameters on polycal wire rope isolator stiffness-damping characteristics[J]. Shock and Vibration, 2019: 1–10.
|
| [12] |
ERDONMEZ. C, IMRAK. C. E.. A finite element model for independent wire rope core with double helical geometry subjected to axialloads[J]. Sadhana, 2011, 36(6): 995-1008. DOI:10.1007/s12046-011-0053-1 |
 2021, Vol. 43
2021, Vol. 43
