2. 上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
工程船舶和大型海洋工程装备平台上通常配有直升机平台,直升机起降过程中甲板板架结构会产生较大的冲击载荷。滚装船作为专门运输车辆的船舶,其甲板结构需承受来自轿车或大型载重卡车的轮胎作用力。大多数研究通常将这类通过轮组向甲板传递的载荷称为轮印载荷。由于轮印载荷具有作用位置不确定以及局部重载的特点,所以研究其等效简化处理对于甲板结构的设计和强度校核计算具有重要意义。
针对轮印载荷的等效简化处理,国内一些学者已经进行了广泛的研究分析。汤雅敏等[1]以直升机平台甲板为研究对象,基于数值仿真方法,分别采用轮胎动态冲击、轮胎准静态压载等处理方式模拟轮印载荷,分析平台甲板的响应特点;张文强等[2]将轮印载荷等效为一定矩形区域内的均布压力,研究了多轮印载荷作用下车辆甲板板厚的设计方法。
目前已有研究和规范对轮印载荷大多采用了在接触面积内施加一定均布载荷的处理方式[3],但并未考虑车辆轮胎作为一种超弹性的橡胶材料,其结构具有强非线性,因此直接采用平面压力载荷的处理方式往往计算精度不高[4]。轮胎与加筋板的接触过程中应力为不均匀分布,并且接触应力的具体分布形式非常复杂,受诸多因素的影响,如轮胎的类型(子午胎,斜交胎),轮胎的结构材料(几何尺寸,橡胶),具体加载条件(胎压,车辆荷载)。因此合理的模拟真实轮胎结构与甲板之间的实际接触是轮印载荷等效简化处理研究的关键。基于此本文构建载重子午线轮胎的有限元模型,利用商业有限元分析软件(Abaqus2017),以轮胎—铝合金甲板结构作为研究对象,基于能量法提出轮印载荷等效简化处理的方法。该简化方法是通过乘以补偿系数β的圆形均布压力代替实际轮印载荷,进而将复杂的非线性接触问题转化为线弹性问题,将轮印载荷通过等效处理实现了极大程度的简化。最后结合实际工程算例,从加载区域、加筋板的最大应力值、加筋板上应力状态分布这3个方面对简化等效模型进行验证,并与基于规范的计算结果进行对比,从而为此类甲板的设计以及强度计算提供理论参考。
1 研究对象 1.1 铝合金甲板鉴于铝合金材料具有强度高、质量轻、易加工以及耐腐蚀等优良性能,可以很好实现船舶轻量化以及高速化的建造目标,受到造船业的青睐。
本文以某型船的装载甲板作为研究对象,铝合金材料的弹性模量
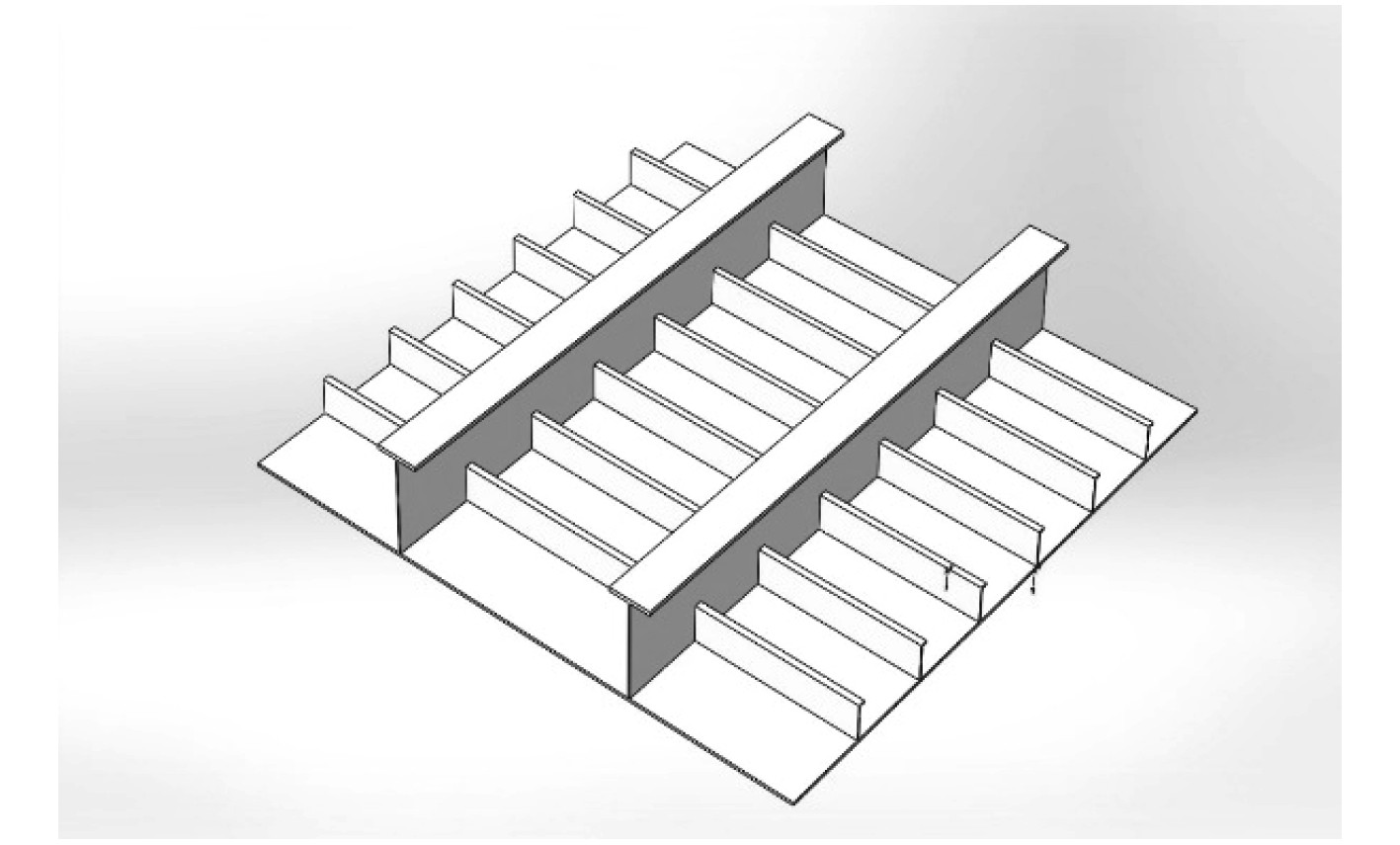
|
图 1 加筋板三维示意图 Fig. 1 3D schematic diagram of stiffened plate |
子午线轮胎能够承受较大的内压压力,且胎面不易变形,具有良好的地面抓力以及稳定性,基于此本文以子午线轮胎作为研究对象。橡胶作为轮胎的主要组成成分,它是一种超弹性材料,所以关于轮胎的接触是一种高度非线性问题。
1.2.1 轮胎材料本构橡胶材料的应力-应变特性具有高度的非线性,是一种几乎不可压缩的超弹性材料。模拟其本构关系是进行有限元仿真分析的关键。其中,Yeoh 模型拟合精度高,稳定性好,选择该模型模拟橡胶力学特性时其应变能本构方程表示为:
| $W = {C_{10}}({I_1} - 3) + {C_{20}}{({I_1} - 3)^2} + {C_{30}}{({I_1} - 3)^3}{\text{,}}$ | (1) |
式(1)代表材料的应力-应变关系。在小变形情况下,
基于Yeoh模型下橡胶各部分材料参数如表1所示。
|
|
表 1 橡胶材料参数 Tab.1 Rubber material parameters |
本文选用的是315/70R15NHS载重型子午线轮胎。该轮胎的名义断面宽度为 308 mm,R代表该轮胎结构为子午线轮胎,轮辋的名义直径为0.2032 m,NHS代表该汽车为重型载重汽车轮胎。该轮胎包含5个组成部分,分别为胎面、带束层、帘布层、胎侧、三角胶、钢圈,其结构示意图如图2所示。
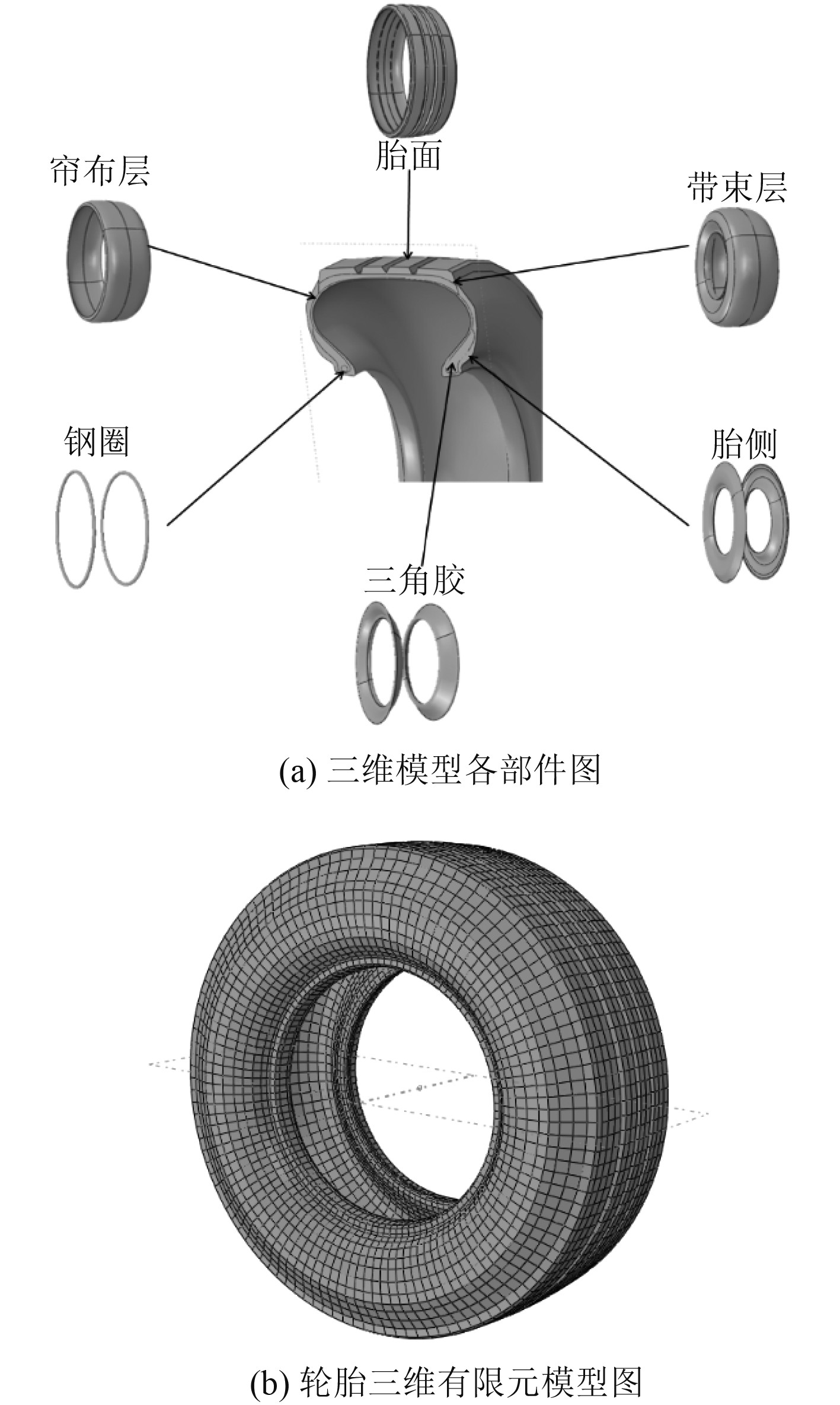
|
图 2 轮胎基本组成结构图 Fig. 2 The basic structure of the tire |
|
|
表 2 子午线轮胎参数 Tab.2 Tire parameters |
由于本文主要研究轮印载荷下铝合金加筋板的压力分布及其等效简化,所以只在线弹性阶段进行考虑。考虑边界效应,选取铝合金甲板板格作为研究对象,利用Abaqus软件建立轮胎—加筋板结构有限元模型,轮胎的接触中心与加筋板模型中心处于同一位置,并以此为坐标原点。同时定义沿纵骨方向为x轴方向以及垂直纵骨方向为y轴方向。轮胎作用位置如图3所示。
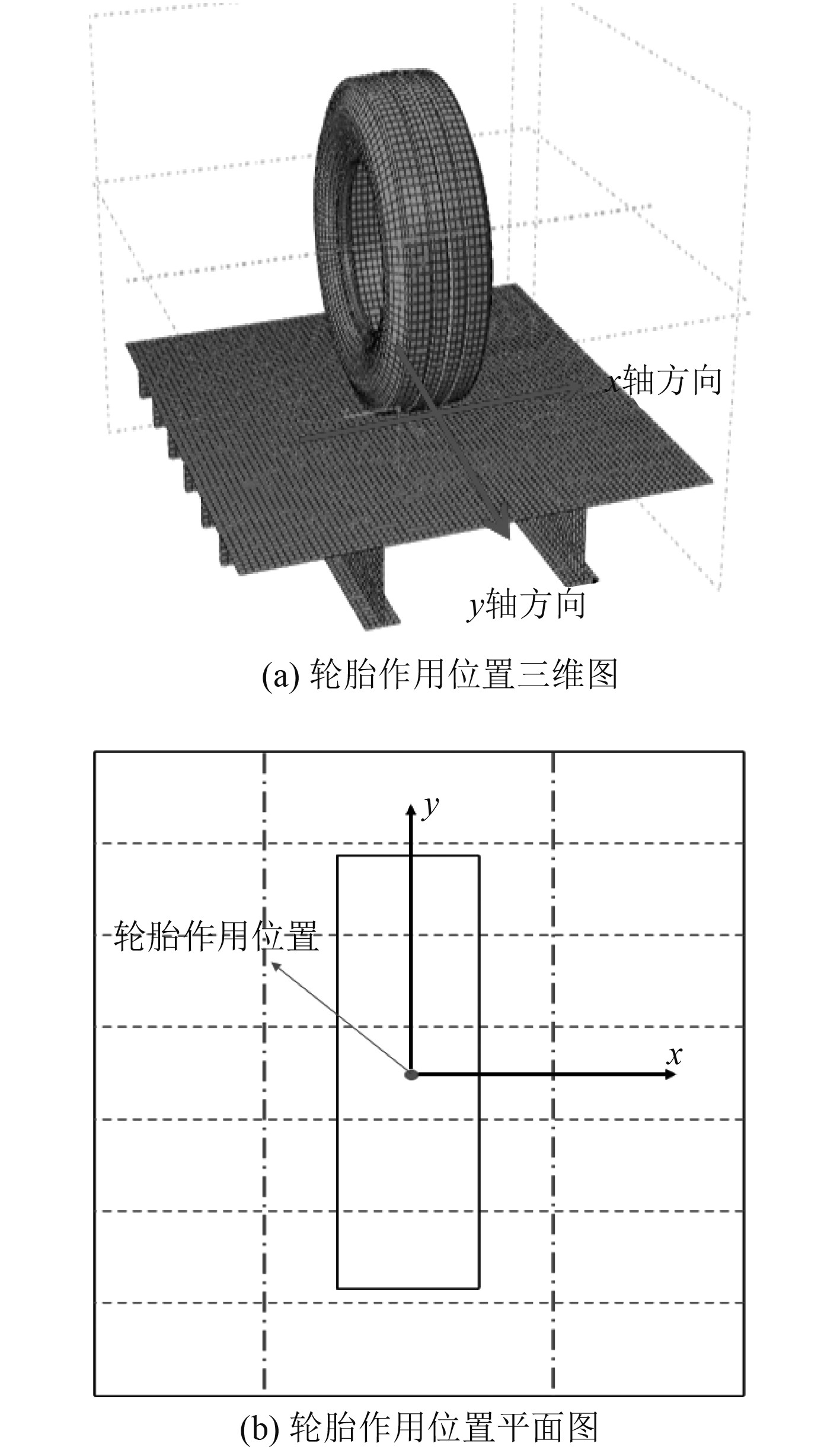
|
图 3 轮胎作用位置示意图 Fig. 3 Schematic diagram of the role of the tire |
接触主要有2处,其中一处是轮胎的外圆面与加筋板的接触,另外一处是轮辋与轮胎之间的接触。轮胎与加筋板之间的接触通过在二者间建立接触对来实现。由于轮毂以及轮辋的刚度相对于轮胎很大,同时轮胎与轮辋的接触边界条件对于轮胎加筋板之间的接触作用影响很小。因此可以通过限制轮辋处单元的自由度来简化两者之间的接触关系,并在轮胎中心参考点和轮辋边界处设置耦合约束。这样轮载便可以通过参考点作用在轮胎上。
考虑到实际甲板模型中周围强框架约束以及支撑作用,因此可以将板格四周简化为刚性固定约束。
2.2 轮胎—加筋板载荷施加对于轮胎—加筋板模型主要考虑以下2种载荷:1)充气压力,即胎压,在轮胎内表面定义均匀分布的法向载荷。2)轮印载荷,即加筋板受轮胎垂向荷载作用。在轮胎轮辋的中心点施加集中力载荷。
2.3 轮胎—加筋板接触分析轮胎的不同加载工况将会影响加筋板上接触应力的分布,因此随机选取胎压0.4 MPa,轮载30 kN(工况1);胎压0.6 MPa,轮载15 kN(工况2);胎压0.7 MPa,轮载20 kN(工况3);胎压0.8 MPa,轮载25 kN(工况4)这4组工况,探究轮印载荷下加筋板接触区域的分布形式,如图4~图7所示。

|
图 4 工况1下加筋板接触应力分布 Fig. 4 Contact stress distribution under case 1 |

|
图 5 工况2下加筋板接触应力分布 Fig. 5 Contact stress distribution under case 1 |

|
图 6 工况3下加筋板接触应力分布 Fig. 6 Contact stress distribution under case3 |

|
图 7 工况4下加筋板接触应力分布 Fig. 7 Contact stress distribution under case 4 |
通过不同工况下轮胎-加筋板接触应力的分布形式可以看出:轮印载荷下加筋板上接触区域的外轮廓可以近似地看成圆,现有规范多将轮印载荷简化处理为矩形区域内的均布载荷,与实际存在一定偏差。基于此,本文提出将轮印载荷简化处理为圆形区域内的均布载荷,接下来就等效简化过程以及合理性分析展开论述。
3 轮印载荷的等效简化计算由不同工况下的接触应力云图可知,轮印载荷下加筋板的接触应力分布形式较为复杂,受胎压、轮载等因素的影响。现有研究及规范通常将轮印载荷简化为矩形区域内的均布压力。但这种简化方法没有考虑胎压因素的影响,这就导致了使用该方法分析的结果与实际结构的力学行为存在较大差异,无法准确预测加筋板的结构响应。因此,本文提出一种同时考虑胎压和轮载影响的等效简化计算方法,并结合实际工况算例验证此方法的合理性。
3.1 等效简化的基本原理基于能量法可知,对弹性体所做的外力功
| $\partial W = \partial U{\text{,}}$ | (2) |
以能量法作为理论依据,认为实际轮印载荷对加筋板结构的能量与圆形均布载荷输入的能量相等,提出均布加载补偿系数的概念。即
| ${W_{tl}} = {W_y}{\text{。}}$ | (3) |
其中:
根据有限元仿真方法求解
| ${W_{tl}} = \mathop{{\oiint}}\limits_s {T\delta {\rm{d}}s} + {\mathop{{\oiiint}}\limits_{{\!\!V}} } {F\delta {\rm{d}}V}{\text{。}} $ | (4) |
其中:
实际分析时并不将加筋板本身内部结构的影响考虑在内,认为体力做功为0,因此:
| ${W_{tl}} = \mathop{{\oiint}}\limits_s {T\delta {\rm{d}}s} {\text{,}}$ | (5) |
圆形均布载荷对加筋板结构做功可表示为:
| ${W_y} = \mathop{{\oiint}}\limits_{{S'}} {PW{\rm{d}}{S'}} = \beta {P_0}\mathop{{\oiint}}\limits_{{S'}} W {\rm{d}}{S'}{\text{。}}$ | (6) |
其中:
将式(5)和(6)代入式(3)求得
圆形均布加载补偿系数
| ${W_{tl}} = \sum {\sigma \delta {\rm{d}}s} {\text{,}}$ | (7) |
求解圆形均布载荷对加筋板结构做功关键在于加载的圆形区域大小。由于不同轮载和胎压工况下,等效均布压力加载半径
| $a = \sqrt {\frac{F}{{\text{π} {P_0}}}} {\text{,}}$ | (8) |
其中:F为轮载;
等效圆形均布压力对加筋板所做的功可以表示为:
| ${W_y} = K\int_0^a {2\text{π} r{P_0}\omega {\rm{d}}r}{\text{,}} $ | (9) |
将(7)式和(9)式代入(3)式,最终可得到等效压力系数的表达式为:
| $\beta = \frac{{\displaystyle\sum {\sigma \delta {\rm{d}}s} }}{{\displaystyle\int_0^a {2\text{π} r{P_0}\omega {\rm{d}}r} }}{\text{。}}$ | (10) |
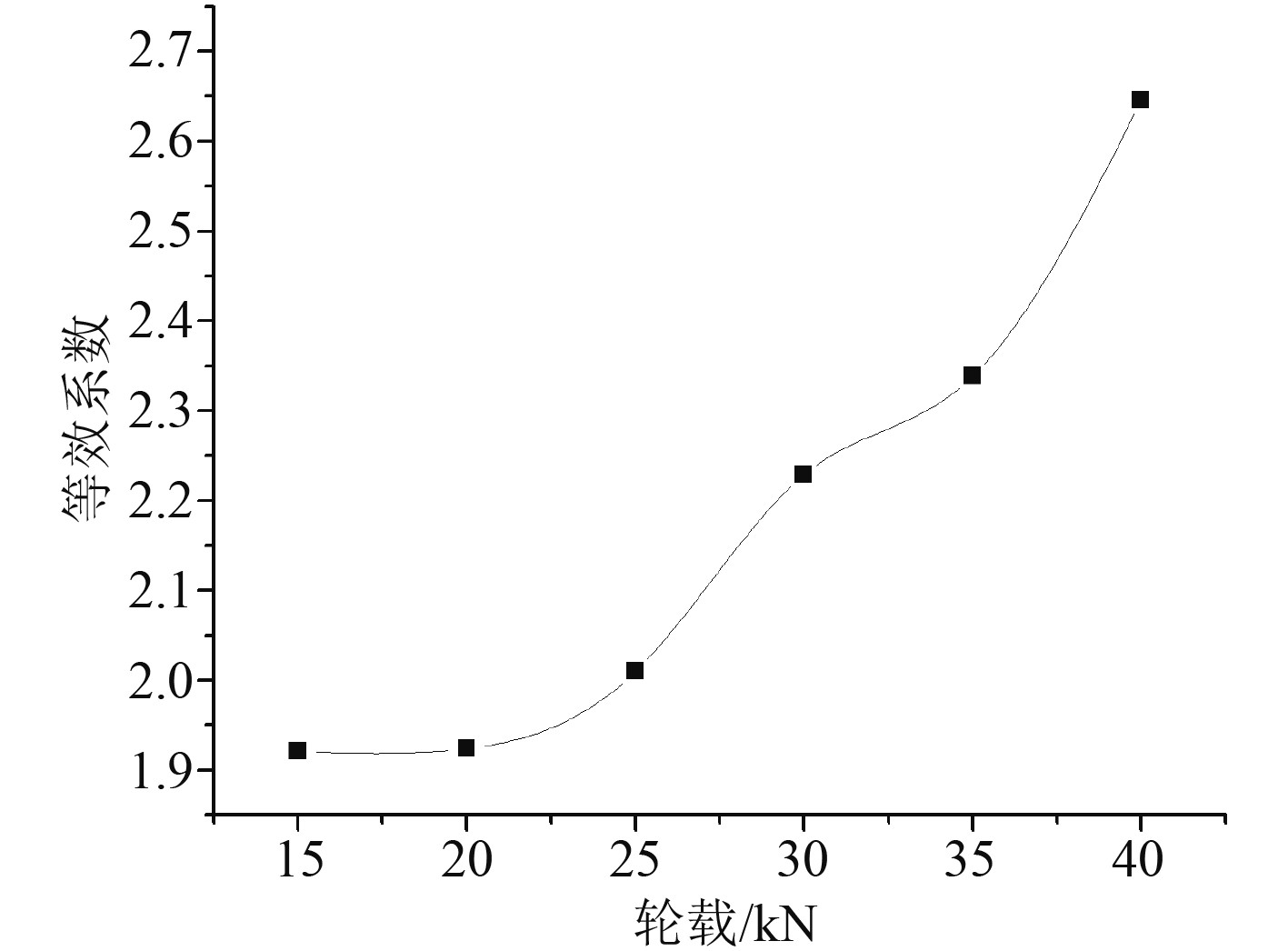
由式(10)可计算当轮载为30 kN时,不同胎压下的加载补偿系数如图8所示。当胎压0.8 MPa,不同轮载下的加载补偿系数如图9所示。
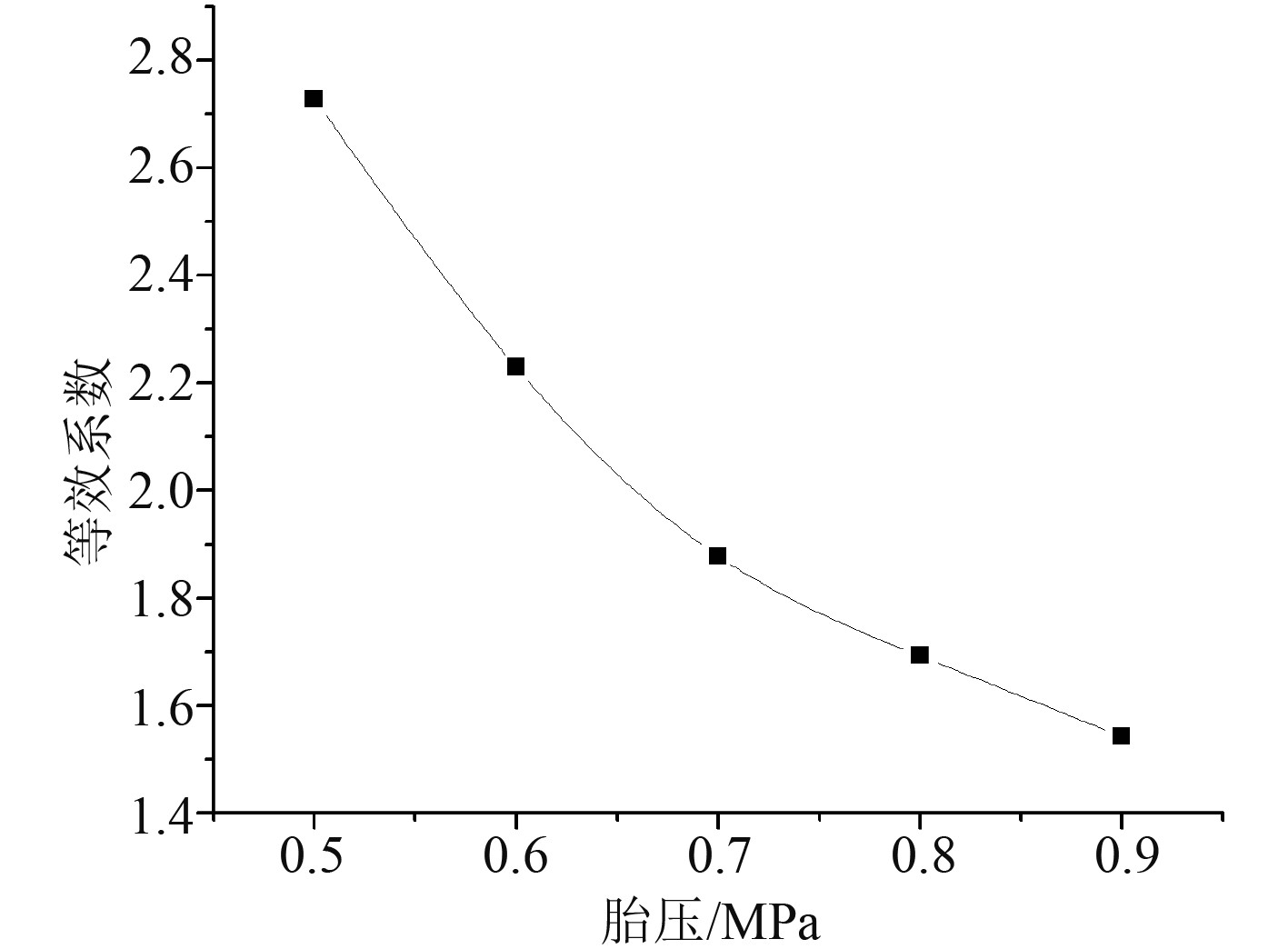
|
图 8 不同胎压下加载补偿系数 Fig. 8 coefficient under different tire pressures |
|
图 9 不同轮载下加载补偿系数 Fig. 9 coefficient under different wheel loads |
由图8和图9可知,圆形均布加载补偿系数
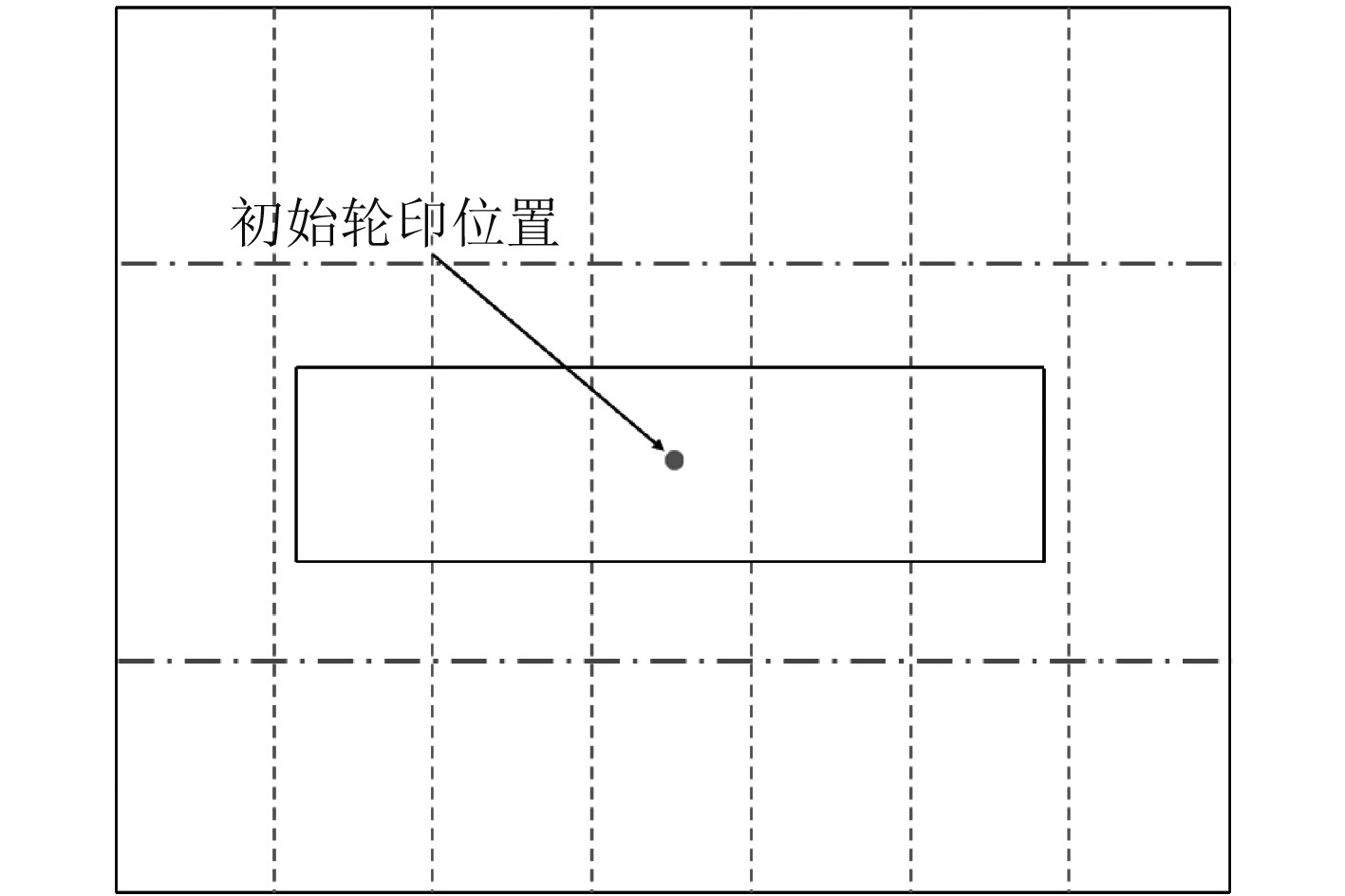
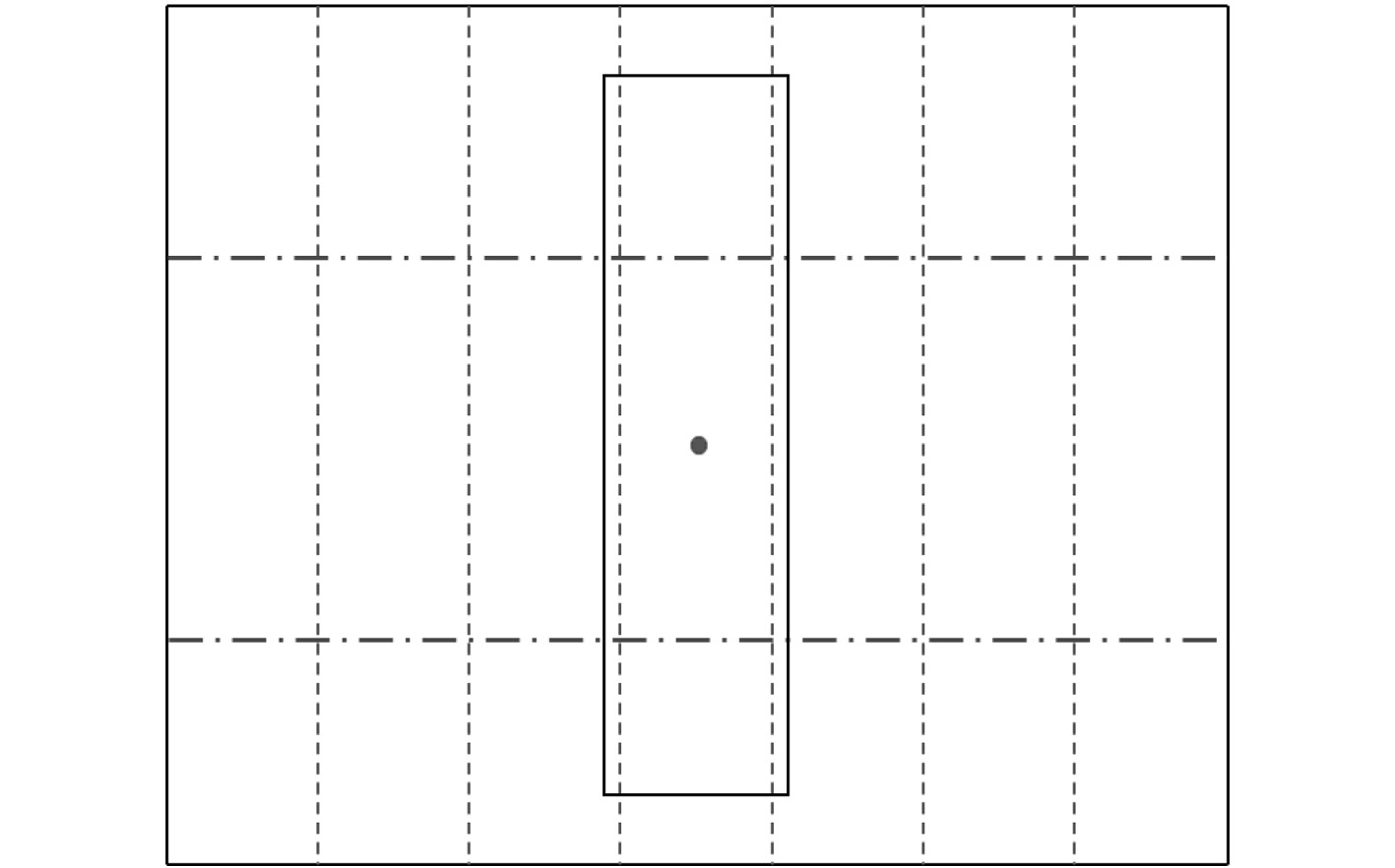
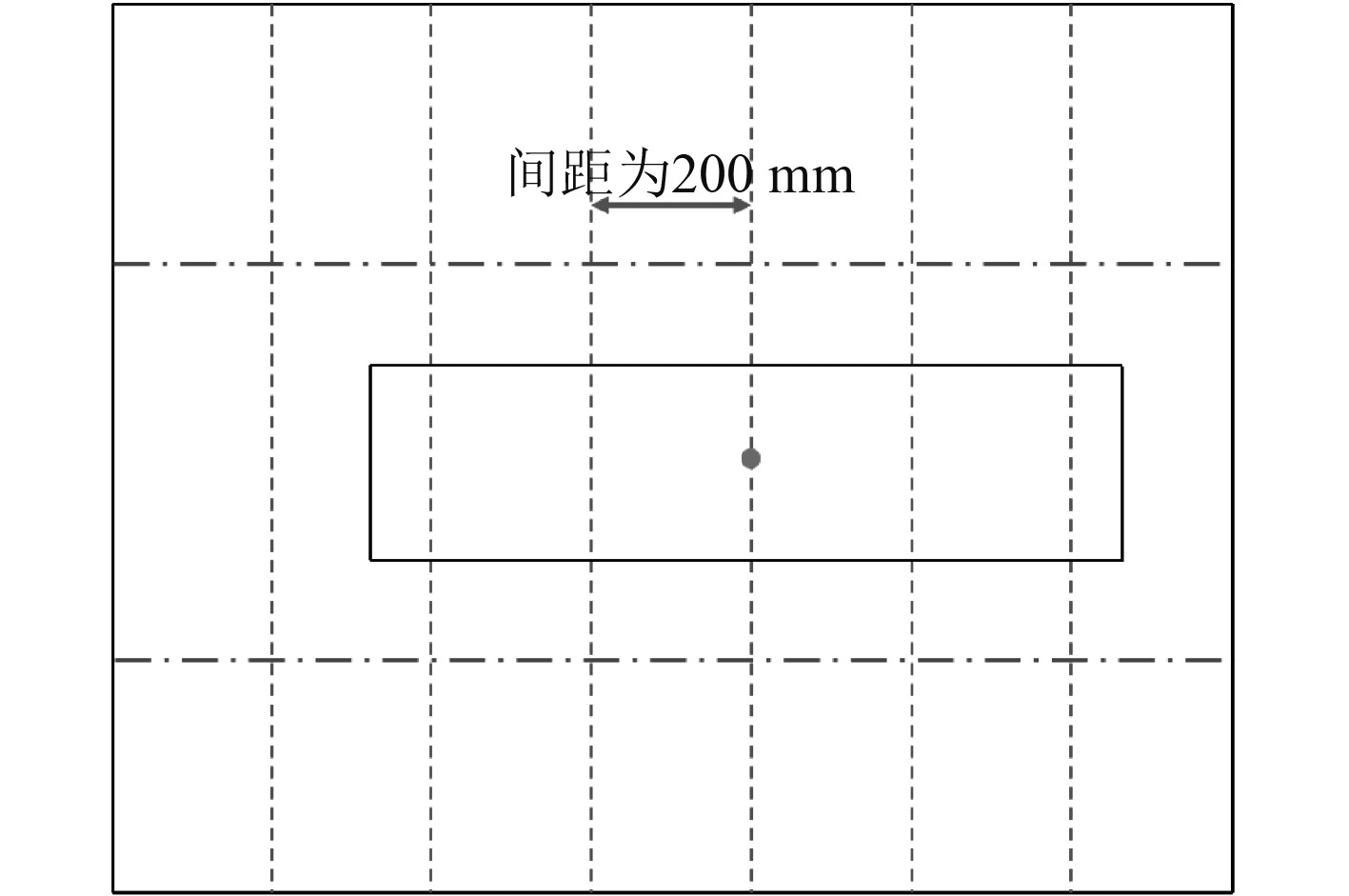
为探究轮印位置对加载补偿系数的影响,本文在初始轮印位置基础上做了如下随机变动作为计算工况:轮胎转动90°(工况1),轮胎前移100 mm(工况2),轮胎前移200 mm(工况3),如图10~图13所示。
|
图 10 初始轮印位置 Fig. 10 Initial wheel position |
|
图 11 工况1下轮印位置 Fig. 11 Case 1 under the wheel printing position |
|
图 12 工况2下轮印位置 Fig. 12 Case 2 under the wheel printing position |

|
图 13 工况3下轮印位置 Fig. 13 Case 3 under the wheel printing position |
加载工况统一选取轮载30 kN,胎压0.8 MPa,不同轮印位置下加载补偿系数β的值如表3所示。
|
|
表 3 不同轮印位置下加载补偿系数 Tab.3 Load compensation coefficient under different wheel positions |
通过表3的数据可知,当轮印位置发生变化后,相应的圆形均布加载补偿系数几乎没有变化。因为当胎压、轮载加载工况一定时,轮印位置的改变并不影响轮胎对加筋板的做功情况,所以可以认为轮印位置对加载补偿系数β没有影响。
3.4 加筋板结构参数对补偿系数加筋板结构参数[6]主要包括面板厚度以及加筋板纵骨高度。加载工况统一选取轮载30 kN,胎压0.7 MPa,轮印位置选择初始位置。
3.4.1 面板厚度以初始计算模型的板厚值6 mm作为参考,增加3组计算模型,板厚分别为4 mm,5 mm,7 mm。计算不同面板厚度下的加载补偿系数β值,如表4所示。
|
|
表 4 不同面板厚度下加载补偿系数 Tab.4 Load compensation coefficient under different panel thickness |
以初始计算模型的纵骨高度值70 mm作为参考,增加3组计算模型,纵骨高度值分别为60 mm,65 mm,75 mm。计算不同纵骨高度下的加载补偿系数β值,如表5所示。
|
|
表 5 不同纵骨高度下加载补偿系数 Tab.5 Load compensation coefficient at different longitudinal bone heights |
通过不同加筋板结构参数下的加载补偿系数可知,纵骨高度值对加载补偿系数β没有影响,而加筋板面板厚度对加载补偿系数β有一定影响,呈正相关。这是因为随着面板厚度增加,加筋板结构的相对刚度有所增强,导致轮胎作用能量增加,因此加载补偿系数β值有所提高。
4 轮印载荷简化等效模型的合理性研究分析简化等效模型提出的意义在于可以使用基于补偿系数β的圆形均布载荷代替实际轮胎对加筋板结构的压力,这样可以将复杂的非线性接触分析问题转化为线弹性问题。通过对比实际轮胎接触压力、规范下的均布加载压力、等效圆形均布压力下加筋板结构响应的差异,验证所提出简化等效模型的合理性。
4.1 加载区域的对比分析船级社规范和英国民用航空局CAP437 指导性文件[7]中提到可将轮印载荷简化为均布载荷(作用范围为 0.3 m×0.3 m)。以轮载30 kN,胎压0.6 MPa实际加载工况为例,按照
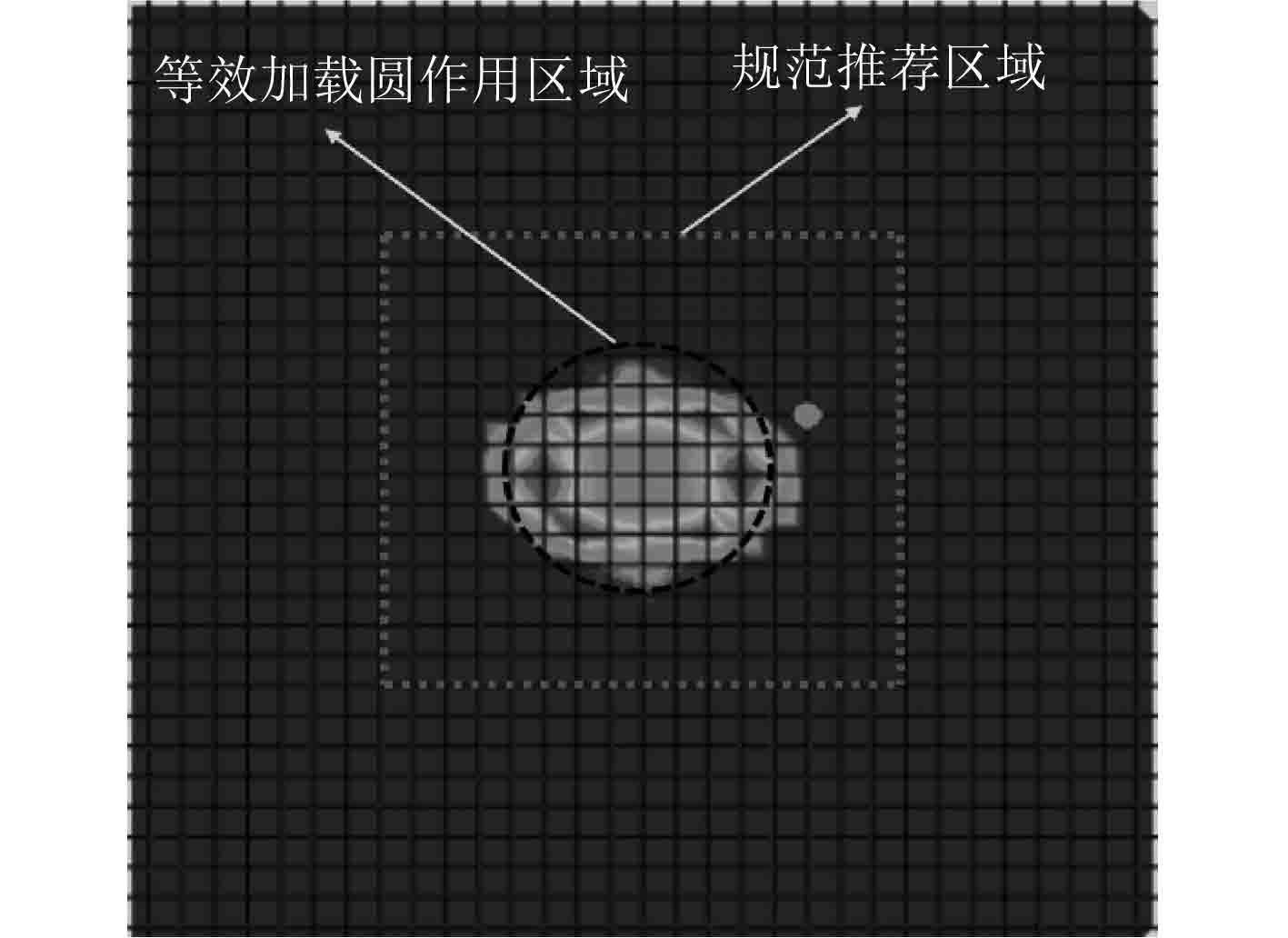
这4组加载工况对应的加载区域如图14~图17所示,实际接触应力云图上的虚线方框表示规范推荐加载区域。虚线圆框表示等效圆形均布载荷加载区域。接触应力云图显示实际工况的接触区域。
|
图 14 工况1加载区域对比分析图 Fig. 14 Comparative analysis of loading area |
|
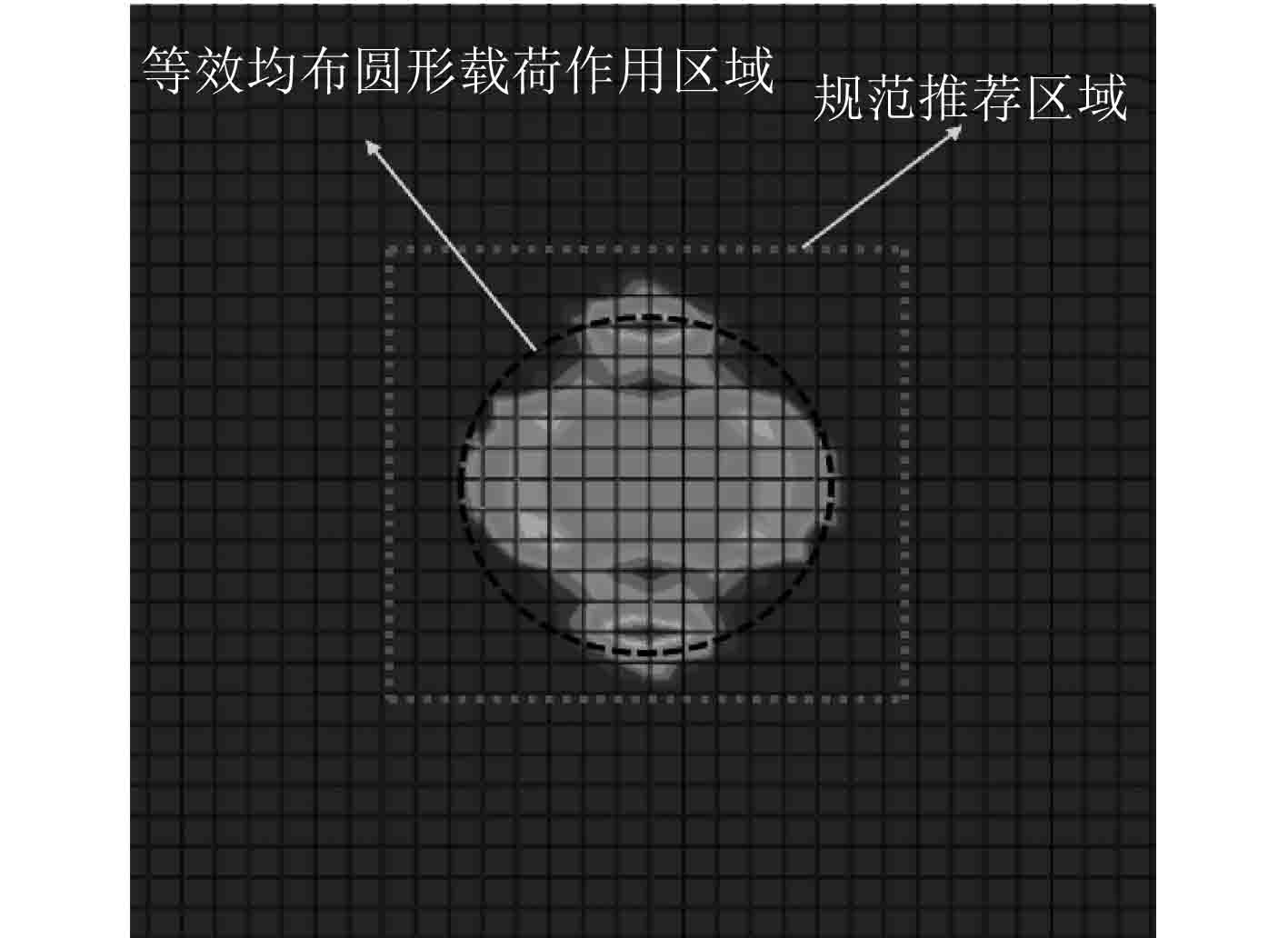
图 15 工况2加载区域对比分析图 Fig. 15 Comparative analysis of loading area |
|
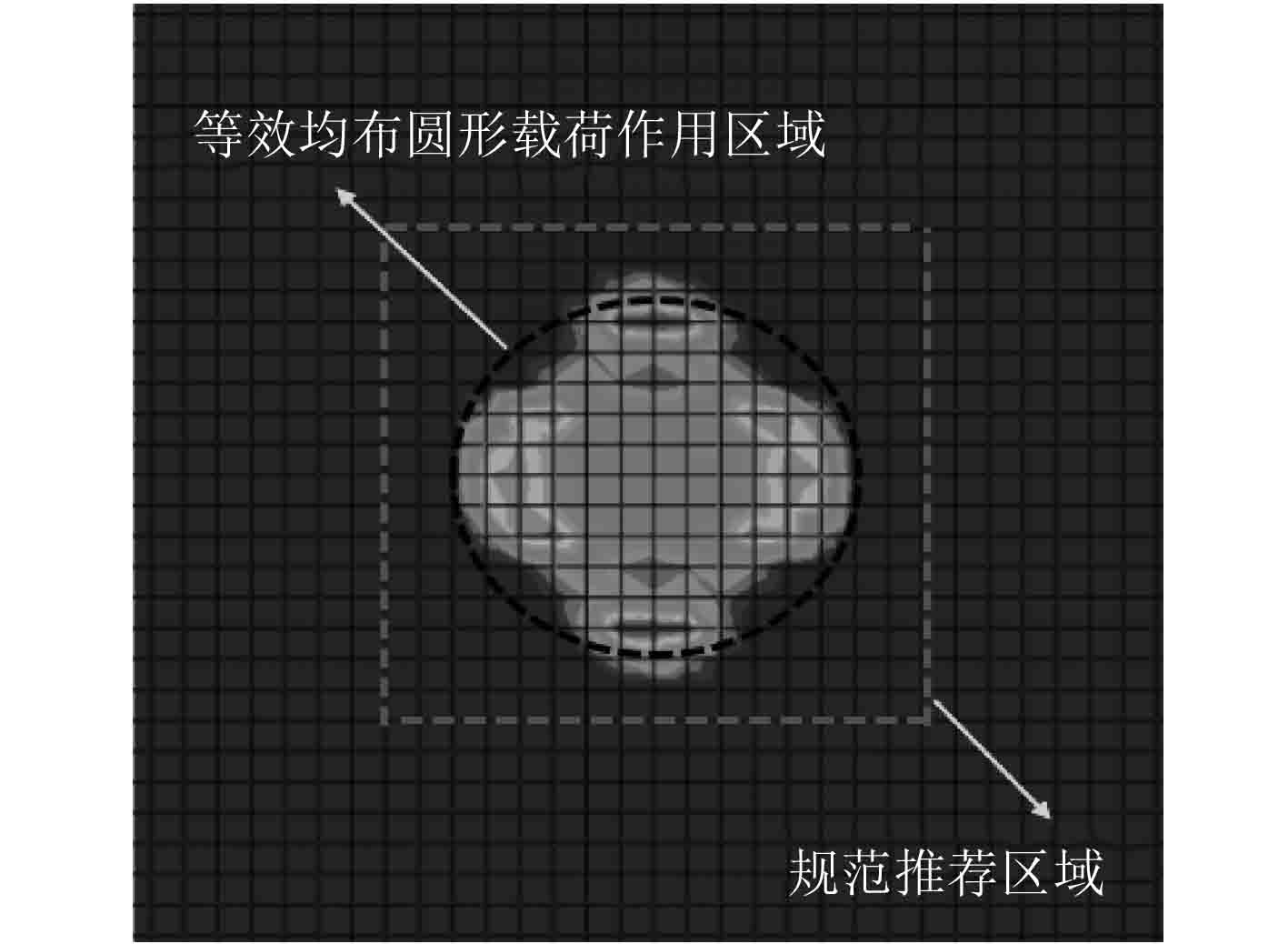
图 16 工况3加载区域对比分析图 Fig. 16 Comparative analysis of loading area |
|
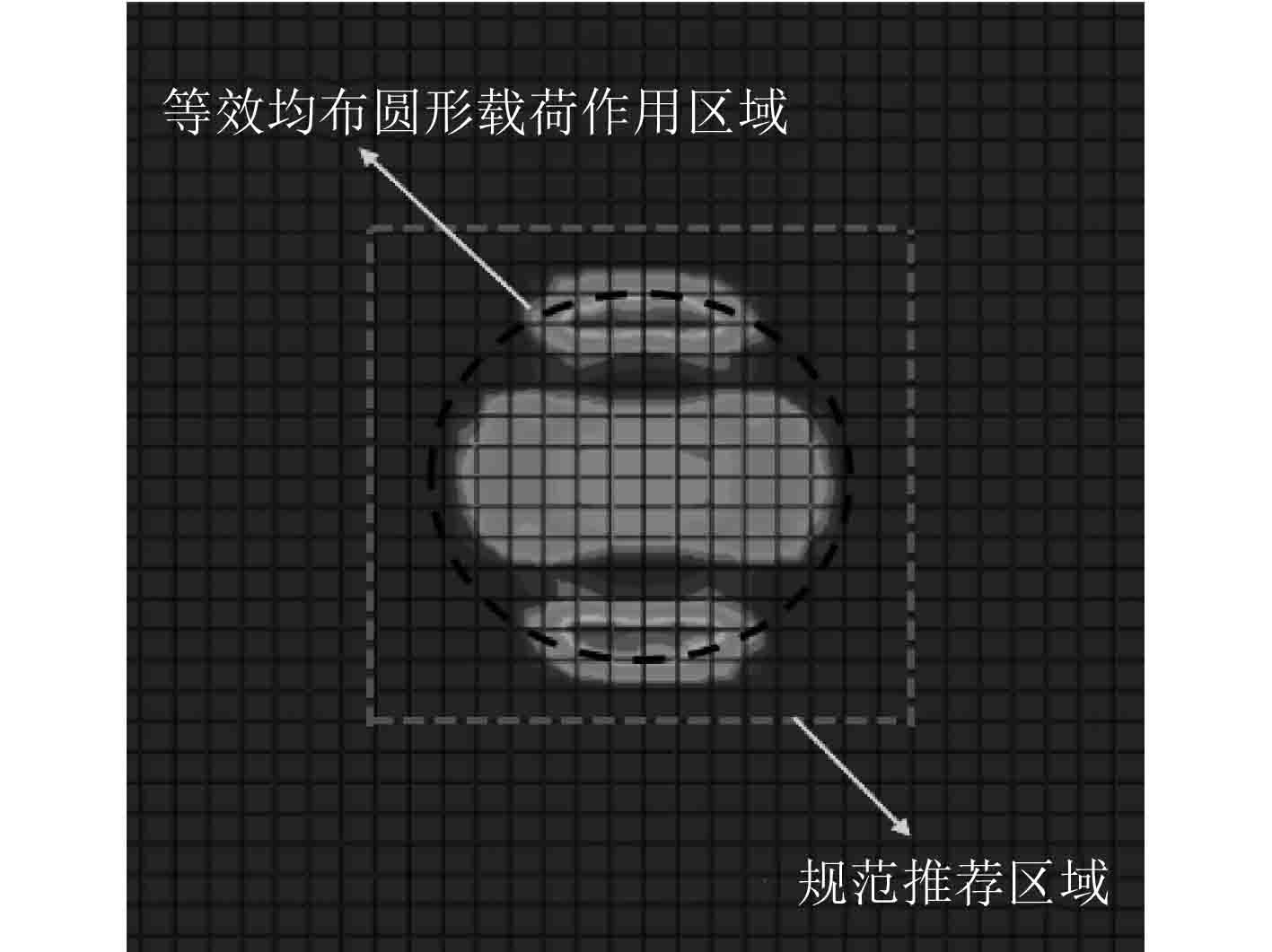
图 17 工况4加载区域对比分析图 Fig. 17 Comptive analysis of loading area |
通过随机选取4组工况下的加载区域对比分析图可知,简化等效模型下的圆形均布载荷作用区域与实际轮胎的加载区域相近,而规范推荐的加载区域与实际压力范围存在明显偏差。因此从载荷作用区域角度分析,简化等效模型是合理的而且要比规范具有更高的精度。
4.2 加筋板上最大应力值分析加筋板的最大应力值是甲板结构设计以及强度校核的重要指标。本文随机选取8组工况,对比分析在这3种载荷处理方式下加筋板的最大应力值。具体计算工况为:胎压为0.6 MPa,轮载分别为15 kN(工况1),25 kN(工况2),30 kN(工况3),35 kN(工况4);轮载为30 kN,胎压分别为0.5 MPa(工况5),0.6 MPa(工况6),0.7 MPa(工况7),0.8 MPa(工况8)。将各种工况相对应的处理方式下加筋板最大应力值(MPa)结果汇总如表6所示。
|
|
表 6 结果汇总 Tab.6 Summary of results |
从随机选取的8组计算工况可以发现,与实际计算结果相比简化等效模型方法的误差范围仅为1.5%~5.46%,而规范均布载荷作用下的最大应力值误差范围却高达25.79%~59.94%,在加筋板最大应力值预测这项指标上预测精度平均提升了33.99%。因此对于加筋板最大应力的计算,简化等效模型方法是合理的,同基于规范的计算相比有更高的精度。
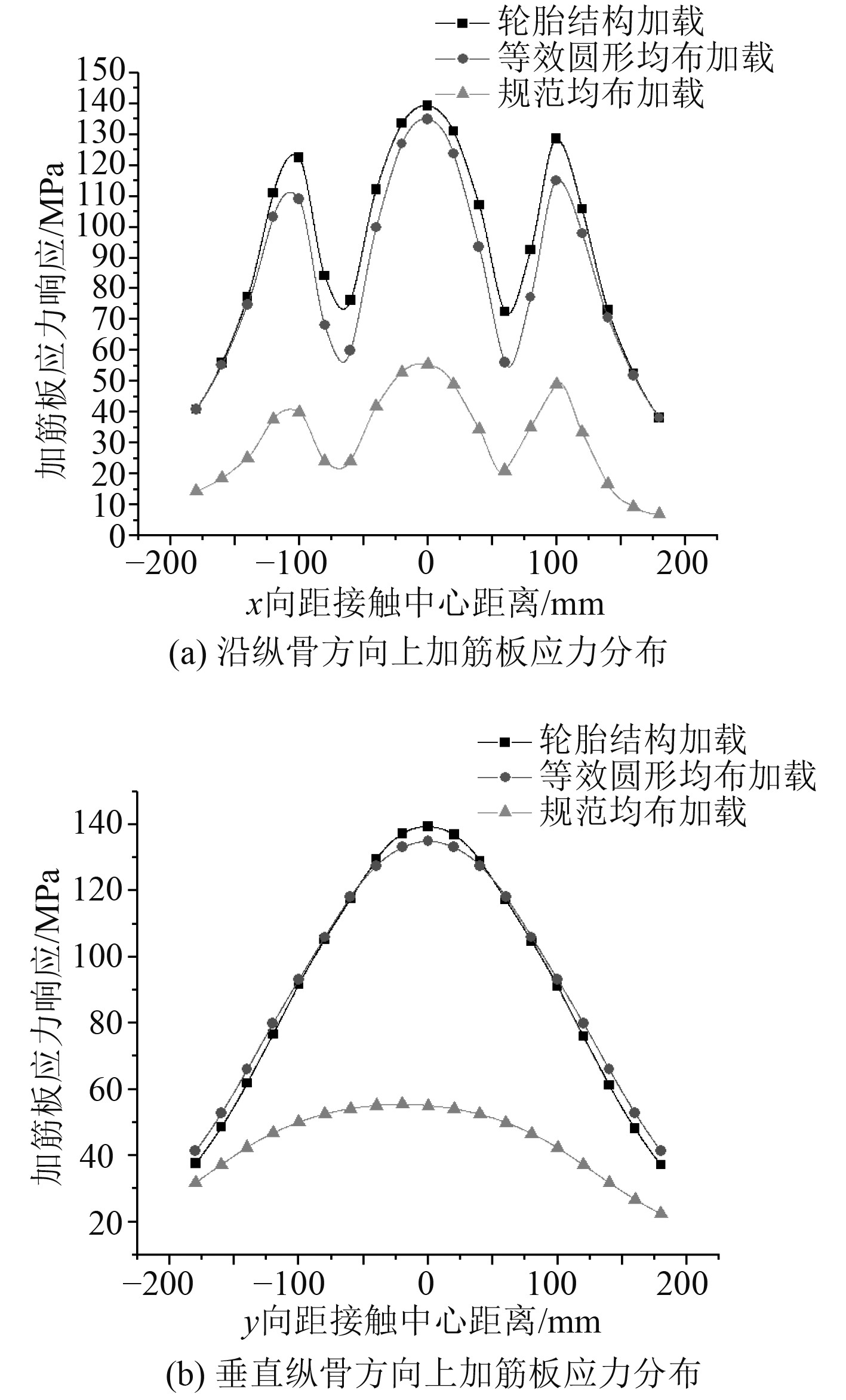
4.3 加筋板上应力分布对比分析以轮胎接触中心作为原点,取沿纵骨方向(x轴方向)以及垂直纵骨方向(y轴方向)这2个方向,随机选取:胎压0.6 MPa,轮载15 kN(工况1);胎压0.6 MPa,轮载25 kN(工况2);胎压0.7 MPa,轮载30 kN(工况3)这3组工况,对比分析各种工况在这3种不同载荷处理方式下加筋板上的的应力分布情况,如图18~图20所示。
|
图 18 18工况1下的加筋板应力分布曲线 Fig. 18 Stress distribution curve of stiffened plate under case 1 |
|
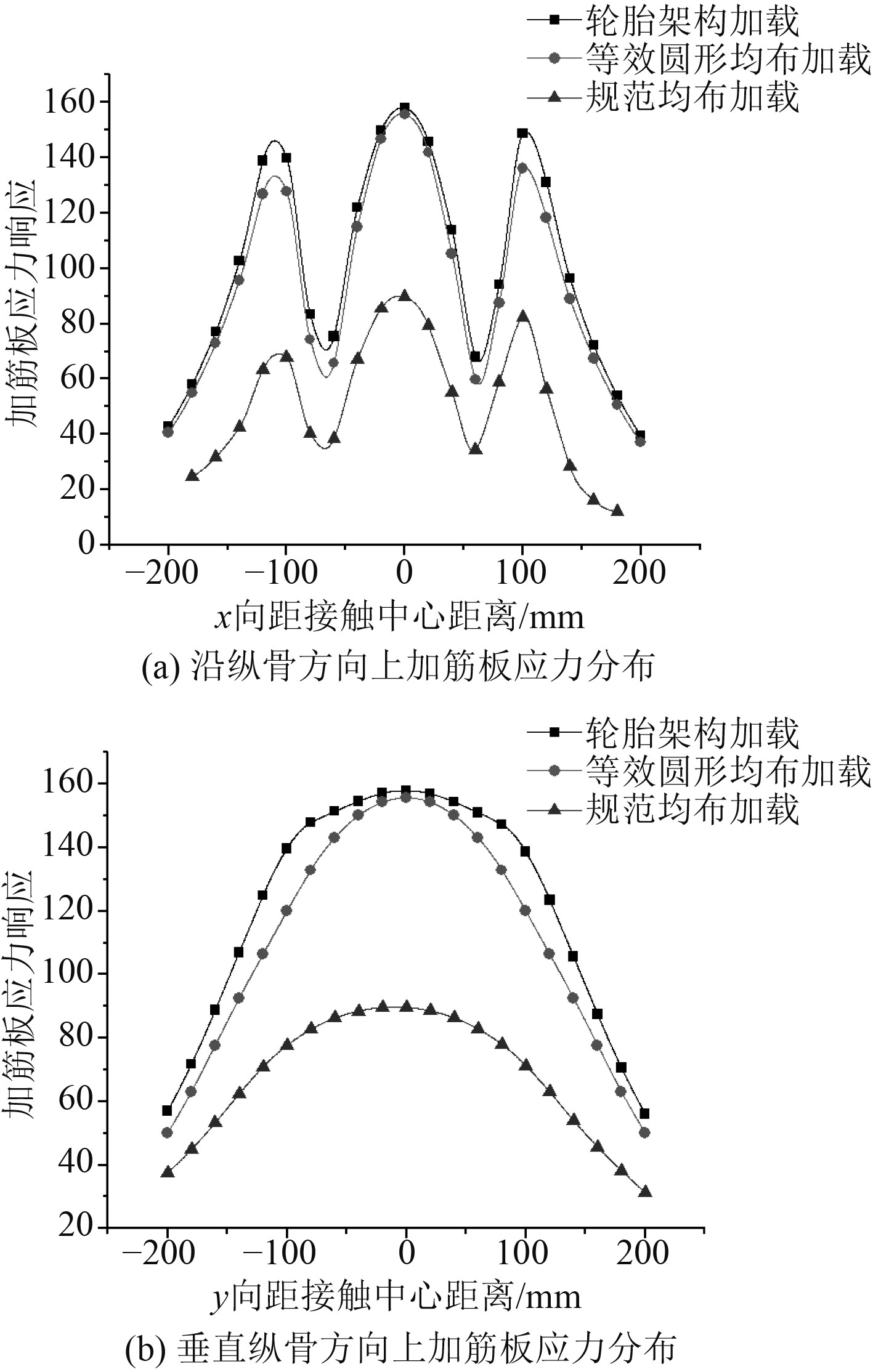
图 19 工况2下的加筋板应力分布曲线 Fig. 19 Stress distribution curve of stiffened plate under case 2 |
|
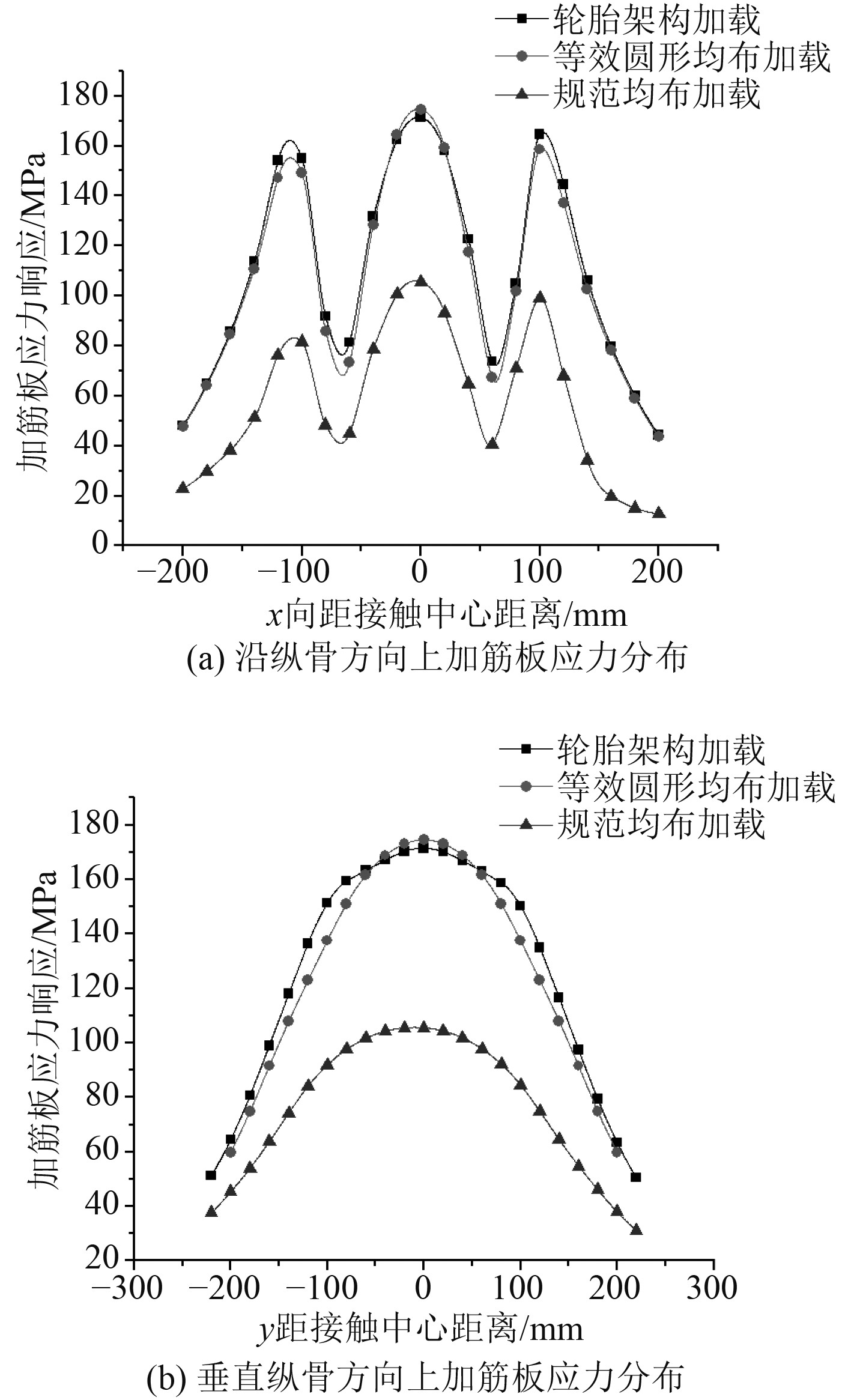
图 20 工况3下的加筋板应力分布曲线 Fig. 20 Stress distribution curve of stiffened plate under case 3 |
在这3种载荷处理方式下,简化等效模型下的应力曲线与实际计算结果几乎一致,但是规范计算的应力曲线与实际计算结果存在明显差异。因此从加筋板上的应力分布来看,简化等效模型是合理的,同基于规范的计算相比有更高的精度。
通过多组工况的计算结果,以及从加载区域、加筋板最大应力值、加筋板应力状态分布情况这3个方面的综合分析,可以验证轮印载荷的简化等效模型是有效的,同时相对于规范有较高的精度。
5 结 语本文通过有限元仿真分析,建立了子午线轮胎与铝合金加筋板的有限元模型,基于能量法提出了等效圆形载荷补偿
1)轮印载荷通过等效简化模型可以处理为
2)轮印位置对等效圆形补偿系数
3)加筋板结构参数中的面板厚度与系数
4)轮印载荷的等效简化模型实现了将复杂的非线性接触计算简化为线弹性计算,同规范相比有更高的精度,对此类铝合金甲板的结构设计以及强度校核具有重要的参考价值。
| [1] |
汤雅敏, 张延昌. 轮印载荷下夹层板直升机平台结构响应特性[J]. 船舶工程, 2019, 4(41): 23-29. TANG Y M, ZHANG Y C. Response characteristic of sandwich plates under different forms of patch loading[J]. Ship Engineering, 2019, 4(41): 23-29. |
| [2] |
张文强, 刘俊. 多轮印载荷下车辆甲板板厚设计研究[J]. 船舶工程, 2016, 38(12): 5-9. |
| [3] |
LLOYD'S REGISTER. Rules and regulations for the classification of naval ships[S]. London: Lloyd's Register, 2015.
|
| [4] |
STAINBACK J. Structural analysis of helicopter flightand hangar decks[R]. Bethesda, MD: Naval SurfaceWarfare Center, Carderock Division, 2001.
|
| [5] |
柳帅蒙. 载重轮胎接地压力模型研究[D]. 西安: 长安大学, 2015.
|
| [6] |
刘 聪, 程远胜. 加筋板轮印载荷分布特性的试验与数值分析[J]. 海洋工程, 2017, 35(4): 84-93. LIU C, CHENG Y S, et al. Experiment and numerical analyses on wheel load distribution on stiffened plate[J]. The Ocean Engineering, 2017, 35(4): 84-93. |
| [7] |
The UK Civil Aviation Authority. CAP 437 Standards for Offshore Helicopter Landing Areas[S]. 2013.
|
 2021, Vol. 43
2021, Vol. 43
