潜水器一般可分为载人潜水器(Human Occupied Vehicles,HOVs)、有缆遥控水下机器人(Remotely Operated Vehicles,ROVs)和水下自治机器人(Autonomous Underwater Vehicles,AUVs)[1],而载人潜水器,特别是深海载人潜水器,是海洋开发的前沿与制高点之一。目前中国、美国、法国、俄罗斯、日本拥有世界上仅有的几艘深海载人潜水器,其中我国比较典型的载人潜水器是“蛟龙”号,“蛟龙”号是目前世界上下潜最深的作业型载人潜水器[2-7]。2012年,“蛟龙”号成功实现了下潜深度7062 m的六自由度运动、悬停定位通信、探测、感知和取样作业[8]。
载人潜水器相对其他潜器而言,其外形较大且复杂,其动力学模型高度非线性耦合,因此对其数学模型的试验验证更有意义。目前国内外研究未有在公开文献对载人潜水器动力学模型进行试验验证,本文以“蛟龙”号载人潜水器为研究对象,选取大洋38航次第3航段中的第149次和第151次试验数据进行仿真计算,通过与试验结果反馈对比,验证其六自由度模型。
1 载人潜水器运动仿真数学模型 1.1 运动学模型研究载人潜水器的六自由度运动时,通常采用通用坐标系,建立2个坐标系:一个定义为惯性坐标系,其固定于地球,又称地球坐标系;另一个定义为随体坐标系,其固定于潜水器,又称潜水器坐标系,2种坐标系均采用右手系。
通过惯性坐标系与潜水器坐标系的转换,可得到载人潜水器的空间运动学模型[9]:
| $\left[ \begin{gathered} {\dot \xi } \\[-2pt] {\dot \eta } \\[-2pt] {\dot \zeta }\\[-2pt] {\dot \phi } \\[-2pt] {\dot \theta }\\[-2pt] {\dot \psi } \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{T}}&{\rm{0}} \\[-2pt] {\rm{0}}&{{W}} \end{array}} \right]\left[ \begin{gathered} u \\[-2pt] v \\[-2pt] w \\[-2pt] p \\[-2pt] q \\[-2pt] r \end{gathered} \right]{\text{。}}$ | (1) |
其中:
| ${{T}} = \left( {\begin{array}{*{20}{c}} {{\rm{c}} \theta {\rm{c}} \psi }&{ - {\rm{c}} \phi {\rm{s}} \psi + {\rm{s}} \phi {\rm{s}} \theta {\rm{c}} \psi }&{{\rm{s}} \phi {\rm{s}} \psi + {\rm{c}} \phi {\rm{s}} \theta {\rm{c}} \psi } \\ {{\rm{c}} \theta {\rm{s}} \psi }&{{\rm{c}} \phi {\rm{c}} \psi {\rm{ + }}{\rm{s}} \phi {\rm{s}} \theta {\rm{s}} \psi }&{ - {\rm{s}} \phi {\rm{c}} \psi + {\rm{c}} \phi {\rm{s}} \theta {\rm{s}} \psi } \\ { - {\rm{s}} \theta }&{{\rm{s}} \phi {\rm{c}} \theta }&{{\rm{c}} \phi {\rm{c}} \theta } \end{array}} \right){\text,}$ | (2) |
| ${{W}} = \left[ {\begin{array}{*{20}{c}} 1&{{\rm{s}} \phi {\rm{t}} \theta }&{{\rm{c}} \phi {\rm{t}} \theta } \\ 0&{{\rm{c}} \phi }&{ - {\rm{s}} \phi } \\ 0&{{{{\rm{s}} \phi } / {{\rm{c}} \theta }}}&{{{{\rm{c}} \phi }/ {{\rm{c}} \theta }}} \end{array}} \right]{\text。}$ | (3) |
其中,s(.)=sin(.),c(.)=cos(.),t(.)=tan(.)。
1.2 动力学模型可以把载人潜水器看作为一个刚体,对其进行受力分析,采用刚体运动动量定理和动量矩定理,可得到潜水器空间六自由度方程[10]。
其中,外力和外力矩包括螺旋桨推力、水动力、重力和浮力及力矩等,而环境引起的干扰力可由具体的作业环境进行分析,对于外力和外力矩建模可参考文献[11],其中纵向、横向和转首模型如下:
| $\begin{split} \sum\limits_{\rm{i}} {{X_i}} =& \frac{1}{2}\rho {L^4}\left[ {X_{qq}^{'}{q^2} + X_{rr}^{'}{r^2} + X_{pr}^{'}pr} \right] + \frac{1}{2}\rho {L^3}X_{\dot u}^{'}\dot u +\\ &\frac{1}{2}\rho {L^3}\left[ {X_{\dot u}^{'}\dot u + X_{vr}^{'}vr + X_{wq}^{'}wq} \right] + \frac{1}{2}\rho {L^2} [ X_{uu}^{'}{u^2} +\\ &X_{vv}^{'}{v^2} \!+\! X_{ww}^{'}{w^2} \!+\! X_{uw}^{'}uw ] \!-\! \left( {W \!-\! B} \right)\sin \theta \!+\! {X_T} {\text,} \end{split} $ | (4) |
| $\begin{split} \sum\limits_{\rm{i}} {{Y_i}} =& \frac{1}{2}\rho {L^4}\Bigr[ Y_{\dot r}^{'}\dot r + Y_{\dot p}^{'}\dot p + Y_{r\left| r \right|}^{'}r\left| r \right| + Y_{p\left| p \right|}^{'}p\left| p \right| + Y_{pq}^{'}pq +\\ & Y_{qr}^{'}qr \Bigr] + \frac{1}{2}\rho {L^3}\Bigr[ Y_{\dot v}^{'}\dot v + Y_p^{'}up + Y_r^{'}ur + Y_{vq}^{'}vq + \\ &Y_{wp}^{'}wp + Y_{wr}^{'}wr \Bigr] + \frac{1}{2}\rho {L^3}\Biggr[ Y_{v\left| r \right|}^{'}\frac{v}{{\left| v \right|}}\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 / 2}}}} \right|\left| r \right| +\\ & Y_{vww}^{'}v{w^2} \Biggr] + \frac{1}{2}\rho {L^2} \left[ {Y_0^{'}{u^2} + Y_v^{'}uv + Y_{vw}^{'}vw} \right] + \\ &\frac{1}{2}\rho {L^2}Y_{v\left| v \right|}^{'}v\left| {{{\left( {{v^2} \!+\! {w^2}} \right)}^{\frac{1}{2}}}} \right| \!+\!\left( {W \!-\! B} \right)\cos \theta \sin \phi \!+\! {Y_T}{\text,}\\[-15pt] \end{split} $ | (5) |
| $\begin{split} \sum\limits_{\rm{i}} {{N_i}} = &\frac{1}{2}\rho {L^5}\Bigr[ N_{\dot r}^{'}\dot r + N_{\dot p}^{'}\dot p + N_{pq}^{'}pq + N_{qr}^{'}qr{\rm{ + }}N_{r\left| r \right|}^{'}r\left| r \right| + \\ &N_{p\left| p \right|}^{'}p\left| p \right| \Bigr] + \frac{1}{2}\rho {L^4}\Bigr[ N_{\dot v}^{'}\dot v + N_{wr}^{'}wr + N_{wp}^{'}wp + N_{vq}^{'}vq +\\ & N_{vww}^{'}v{w^2} \!+\! N_r^{'}ur \!+\! N_p^{'}up \Bigr] \!+\! \frac{1}{2}\rho {L^4}N_{\left| v \right|r}^{'}\left| {{{\left( {{v^2} \!+\! {w^2}} \right)}^{{1 / 2}}}} \right|r \!+\\ & \frac{1}{2}\rho {L^3}\left[ {N_0^{'}{u^2} + N_v^{'}uv + N_{vw}^{'}vw} \right] + \frac{1}{2}\rho {L^3}N_{v\left| v \right|}^{'}v\Bigr| \Bigr( {v^2} +\\ & {w^2} \Bigr)^{{1 / 2}} \Bigr| + \left( {{x_G}W - {x_C}B} \right)\cos \theta \sin \phi + {N_T} {\text。}\\[-15pt] \end{split} $ | (6) |
由式(4)~式(6)看出,其水动力模型高度非线性耦合,载人潜水器外形复杂。水动力系数的来源是某风洞和旋臂水池中的模型试验,水动力学系数参考文献[12]。
2 大洋试验与仿真计算在大洋38航次第3航段中,“蛟龙”号下潜了10次,成功率100%,超额、圆满地完成了航段潜水器科学调查任务,充分验证了“蛟龙”号超深渊区复杂海底地形环境下各系统功能性能和取样作业能力。
本文选取“蛟龙”号载人潜水器在第149次和第151次下潜数据进行试验验证。
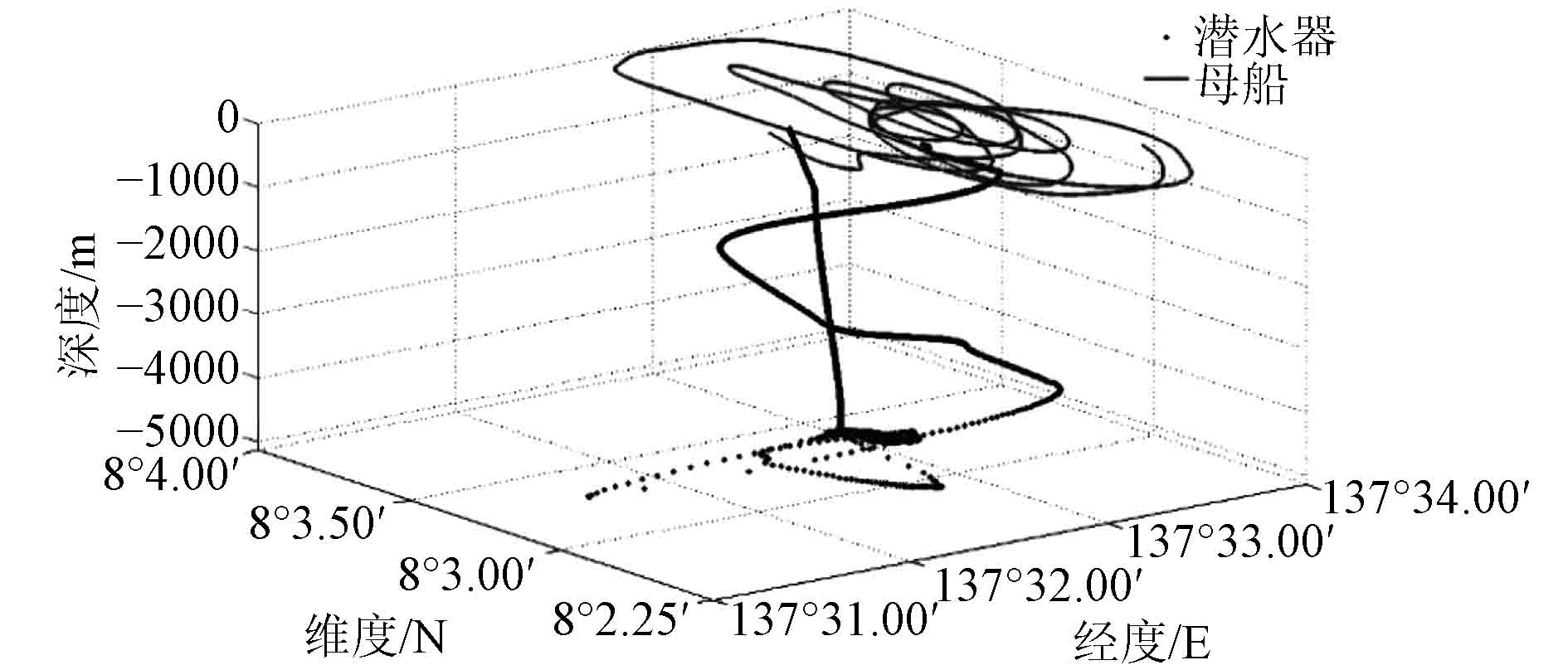
2.1 第149潜次运动仿真与试验验证“蛟龙”号和母船在第149次的轨迹如图1所示。从图中可见,该潜次的无动力下潜运动轨迹比较稳定,因此采用六自由度模型对该阶段运动进行仿真计算,并结合海试数据,对仿真结果进行反馈验证。
|
图 1 “蛟龙”号与母船运动轨迹 Fig. 1 Trajectories of Jiaolong and its mother ship |
在07:32进行下潜,对下潜的前3000 s进行仿真计算。
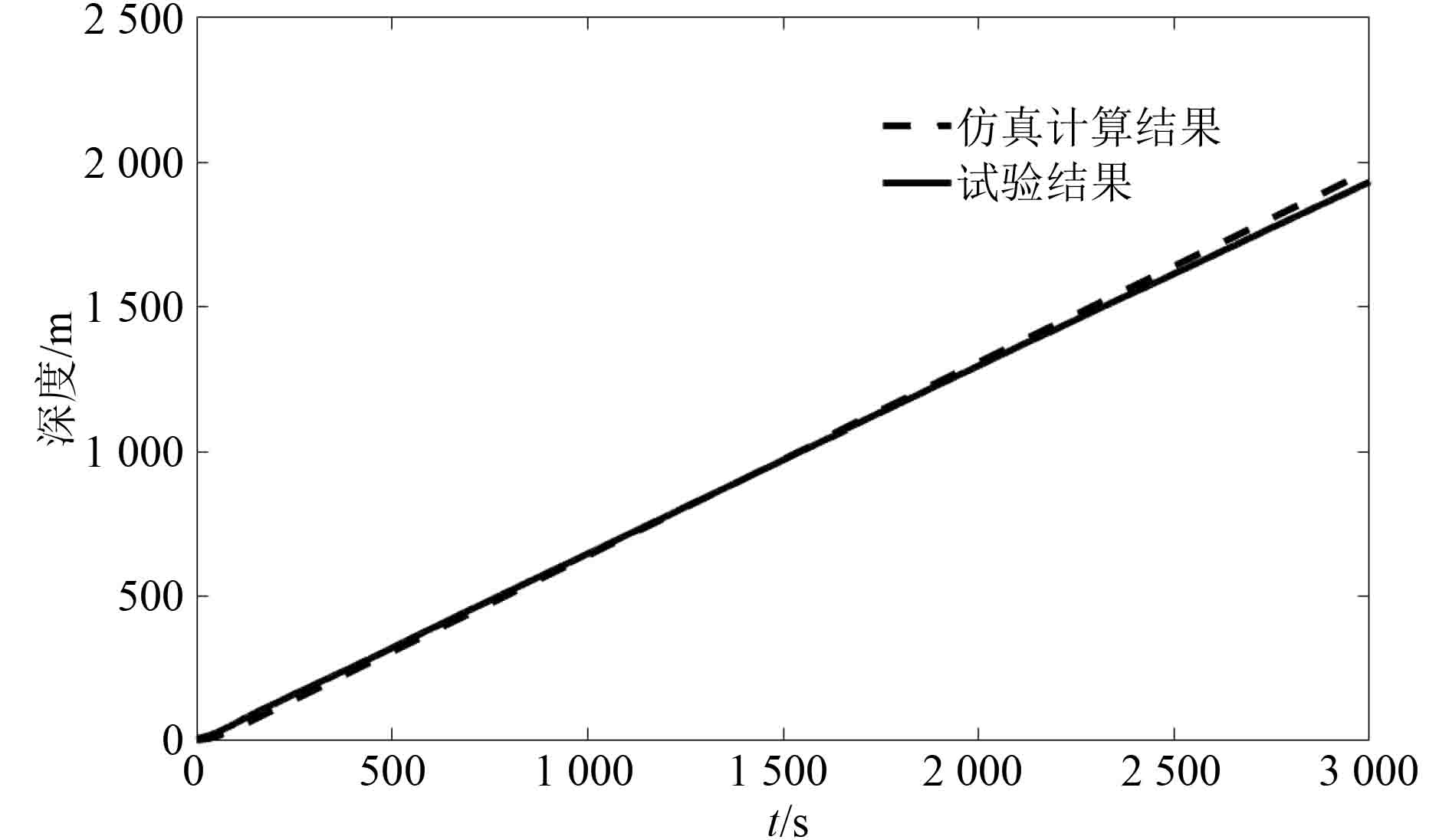
试验下潜的深度和模型仿真计算的下潜深度如图2所示。
|
图 2 潜水器下潜深度 Fig. 2 Depth of submersible |
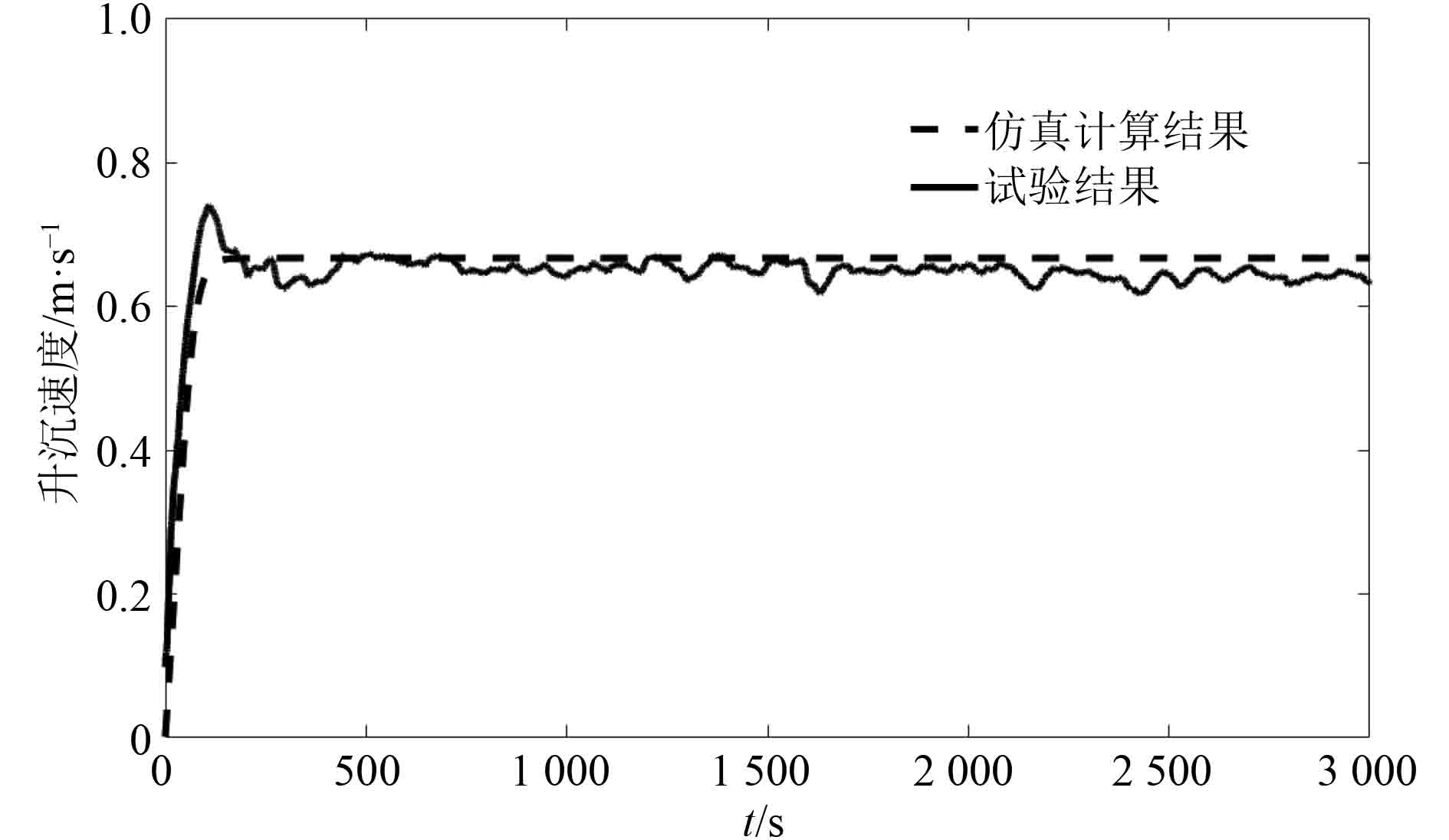
试验结果和模型仿真计算的升沉速度如图3所示。
|
图 3 潜水器升沉速度 Fig. 3 Submergence speed of submersible |
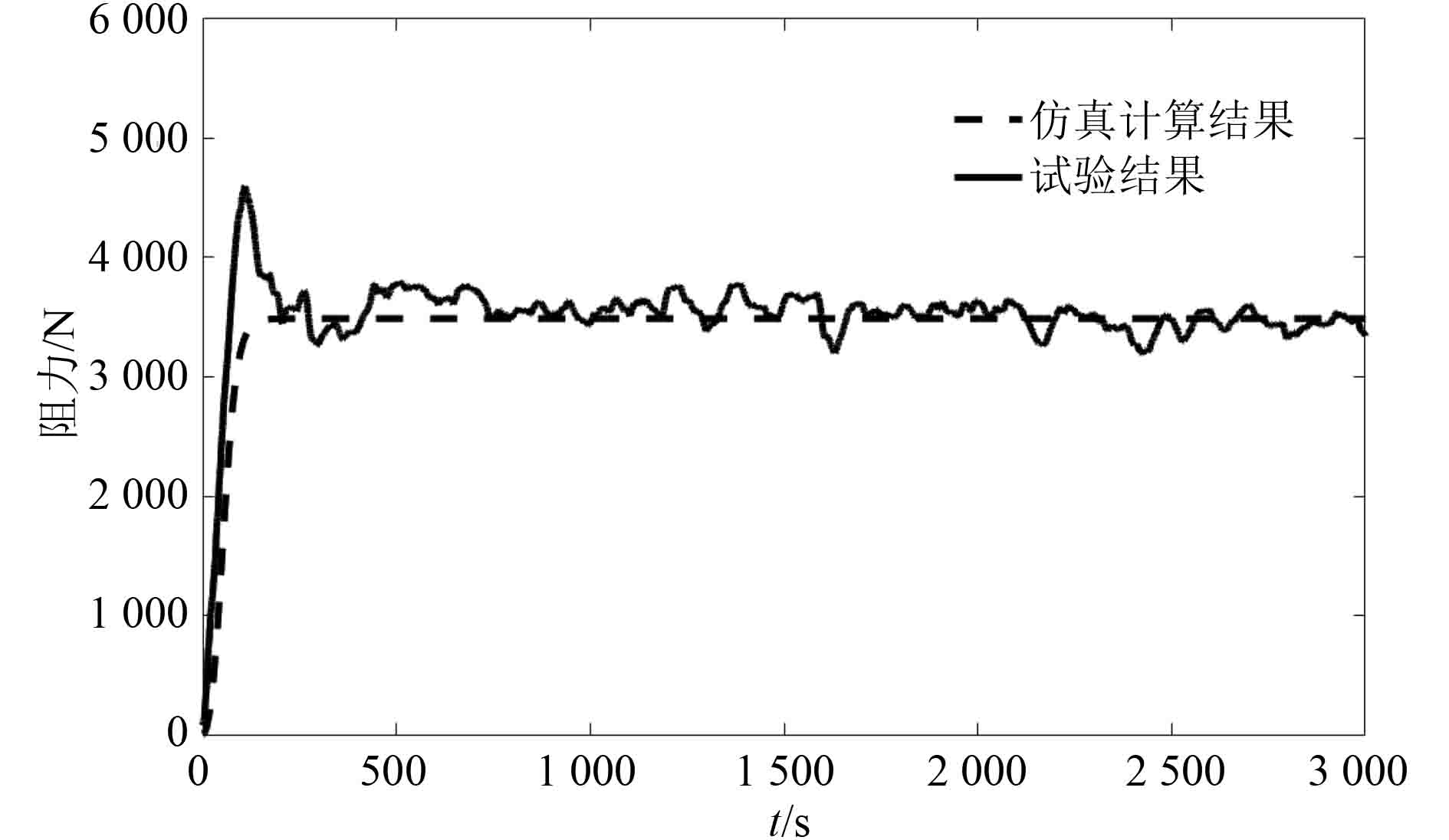
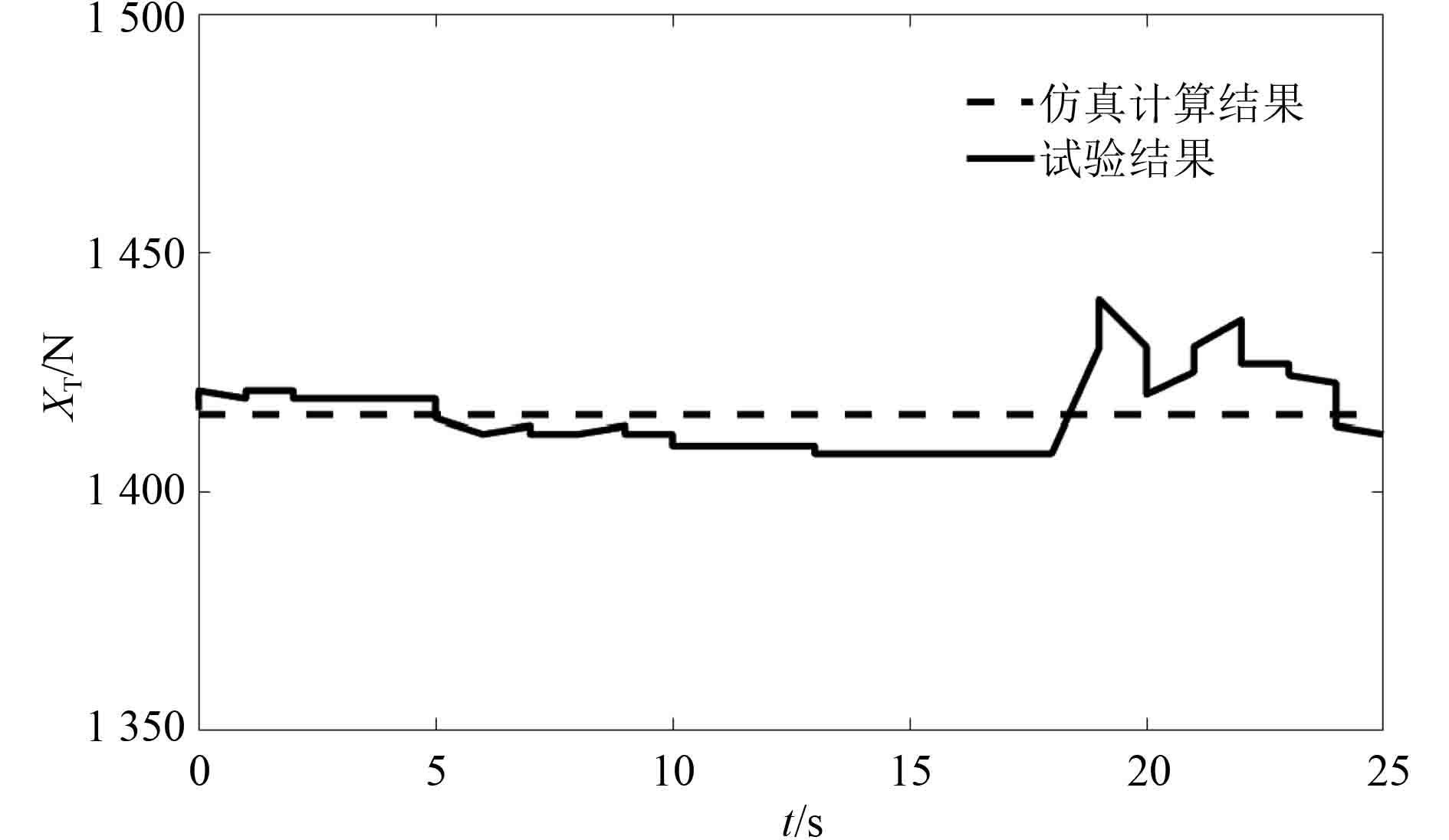
试验结果和模型仿真计算的阻力如图4所示。
|
图 4 潜水器下潜阻力 Fig. 4 Submergence resistance of submersible |
通过仿真计算结果和试验结果对比,可以看出:在t=2 000 s时下潜深度误差为8.1 m,在t=3000 s时达到下潜过程的最大误差37.6 m;仿真的下潜加速过程与试验的下潜过程误差很小,在t=150 s时达到稳定速度,潜水器下潜稳定后,升沉速度最大偏差为0.046 m/s。
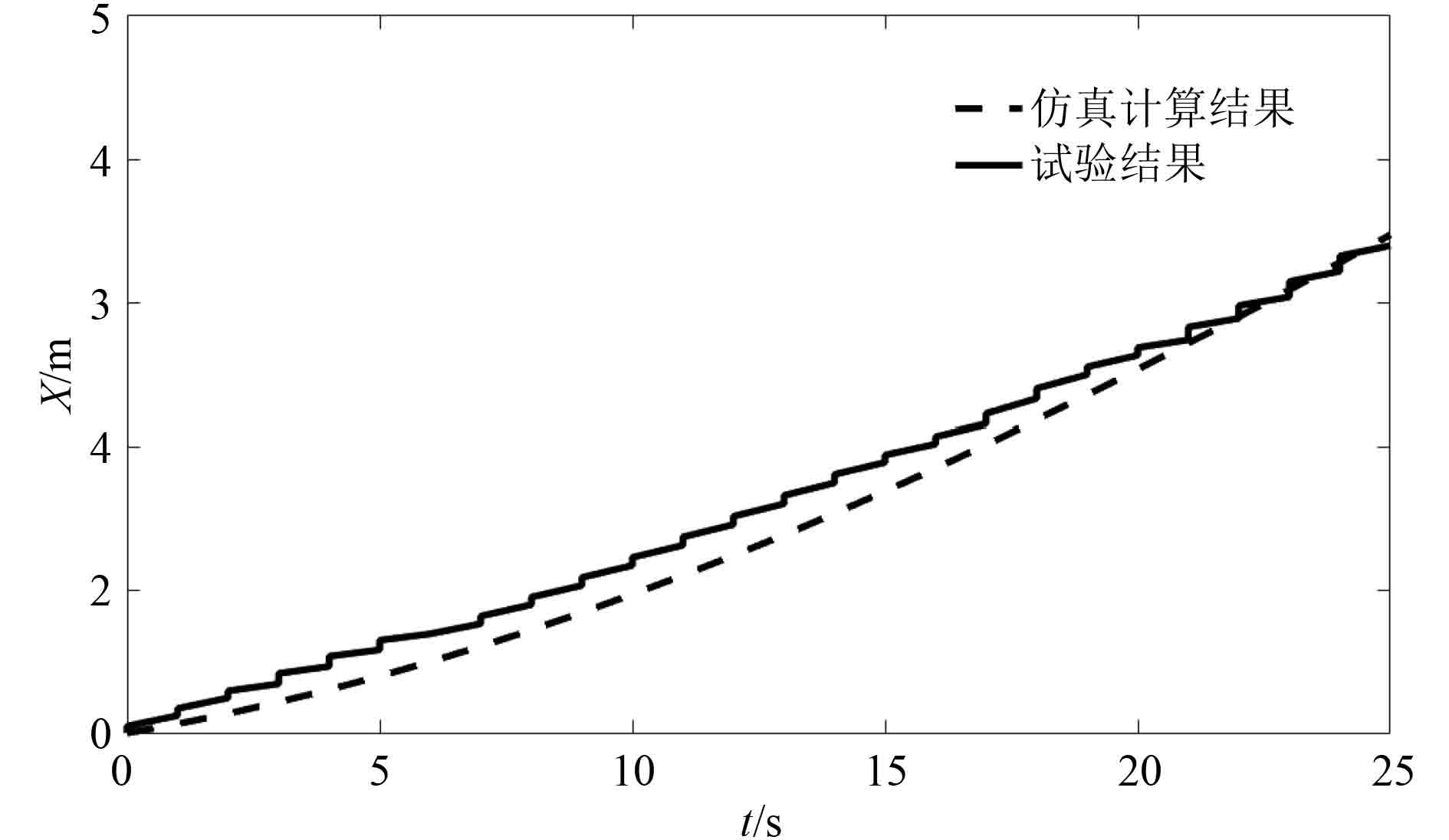
2.2 第151潜次运动仿真与试验验证“蛟龙”号在近海底时进行了前进/后退操作航行,采用手动控制方法。因此,选取该潜次推力基本稳定的作业区间作为潜水器模型验证数据。模型仿真结果与实际结果对比如图5~图8所示。
|
图 5 潜水器X位置 Fig. 5 X position of submersible |
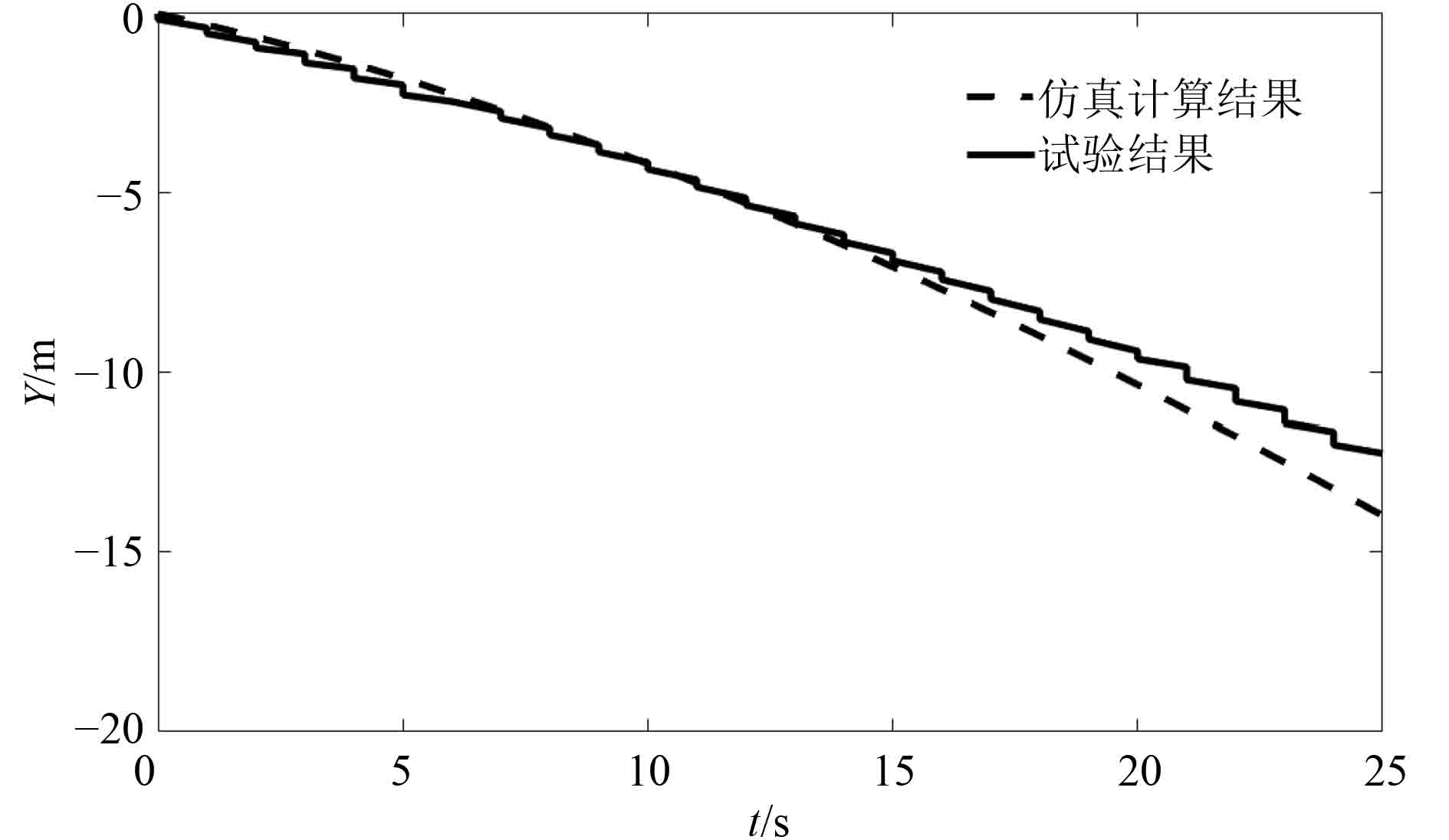
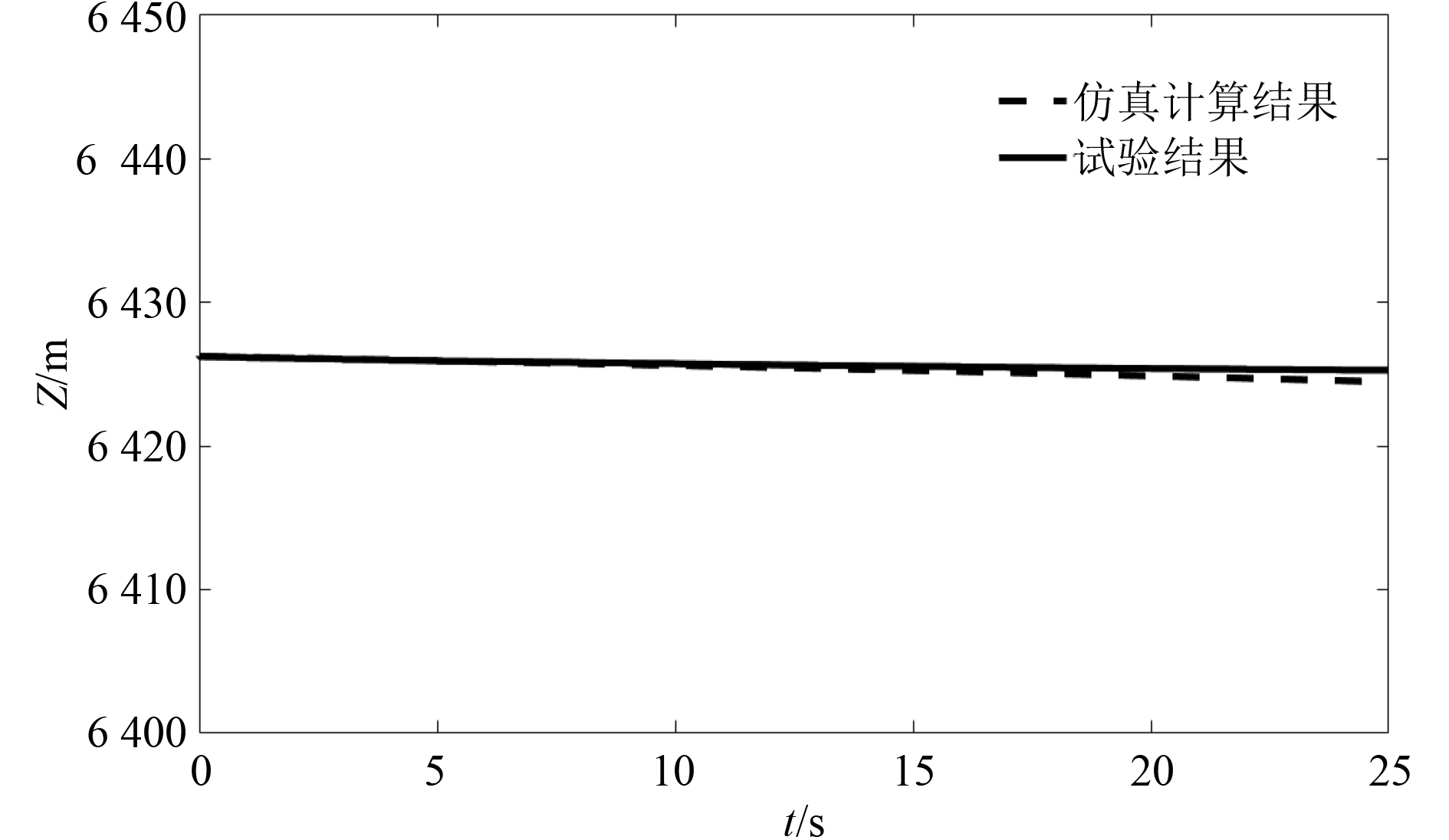
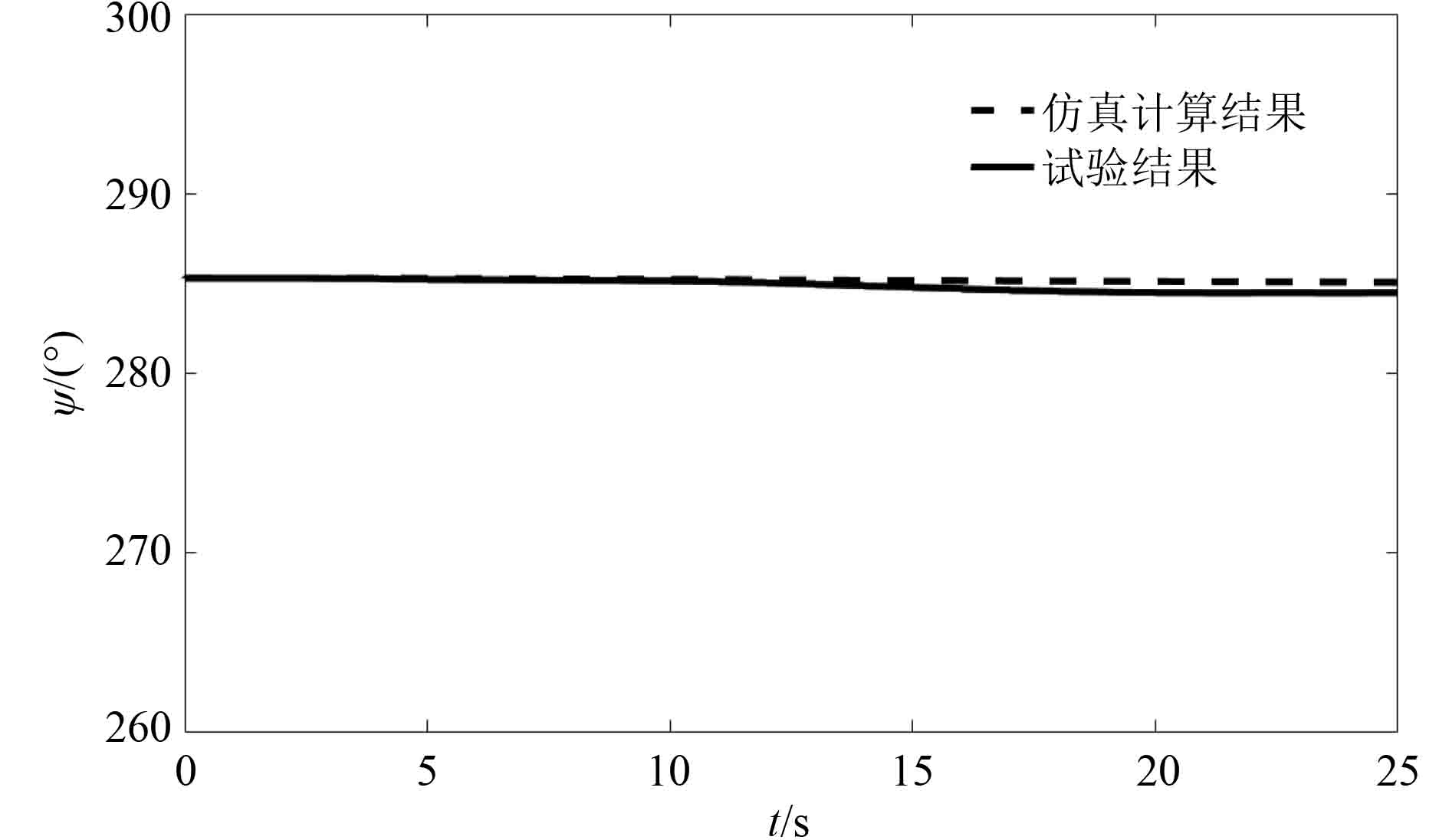
通过仿真计算结果与试验结果对比,惯性坐标系下的载人潜水器位置的仿真计算结果与试验结果的误差很小,X位置最大偏差为0.25 m,Y位置最大偏差为1.6 m,Z位置最大偏差为0.61 m;航向角仿真结果和试验结果的误差也很小,保持在285°附近,航向角最大偏差为0.55°。引起误差原因是实际的推力是手动控制,不断变化的,而仿真推力值是恒定的,实际的推力和仿真的推力比较如图9所示。
|
图 6 潜水器Y位置 Fig. 6 Y position of submersible |
|
图 7 潜水器Z位置 Fig. 7 Z position of submersible |
|
图 8 潜水器航向角 Fig. 8 Heading angle of submersible |
|
图 9 推进器推力 Fig. 9 Thruster thrust |
本文以“蛟龙”号载人潜水器为研究对象,采用数学描述和约束模型试验相结合的方法,得到载人潜水器六自由度数学模型,并选取大洋38航次第3航段中的第149次和151次试验数据进行仿真计算,通过模型仿真计算结果与“蛟龙”号载人潜水器在太平洋试验结果的对比可以看出:试验结果与仿真计算结果的偏差很小,从而验证了六自由度数学模型的有效性。研究结果可为复杂外形深海潜器的运动仿真、控制调试和航行监测提供参考,具有一定的工程价值。
| [1] |
刘涛, 王璇, 王帅, 等. 深海载人潜水器发展现状及技术进展[J]. 中国造船, 2012, 53(3): 233-243. |
| [2] |
BOWEN A D, YOERGER D R, TAYLOR C, et al. The Nereus hybrid underwater robotic vehicle for global ocean science operations to 11, 000 m depth[C] // Proceedings of IEEE/MTS Oceans, 2008.
|
| [3] |
BARRIE B. W, ROBERT S. B. A Replacement for the Alvin Submersible[J]. Marine Technology Society Journal, 2004, 38(2): 85-91. DOI:10.4031/002533204787522721 |
| [4] |
KOHNEN W. Human exploration of the deep seas: fifty years and the inspiration continues[J]. Marine Technology Society Journal, 2009, 43(5): 42-62. DOI:10.4031/MTSJ.43.5.30 |
| [5] |
SAGALEVITCH A M. From the bathyscaph trieste to the submersible mir[J]. Marine Technology Society Journal, 2009, 43(5): 79-86. DOI:10.4031/MTSJ.43.5.3 |
| [6] |
SAGALEVITCH A M. 25th anniversary of the deep manned submersibles Mir-1 and Mir-2[J]. Oceanology, 2012, 52(6): 817-830. DOI:10.1134/S0001437012060100 |
| [7] |
OGURA S, KAWAMA I, SAKURAI T, et al. Development of oil filled pressure compensated lithium-ion secondary battery for DSV Shinkai 6500[C]// Oceans. IEEE, 2008.
|
| [8] |
崔维成, 刘峰, 胡震, 等. 蛟龙号载人潜水器的7 000米级海上试验[J]. 船舶力学, 2012, 16(10): 1131-1143. |
| [9] |
魏延辉. UVMS系统控制技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2017.
|
| [10] |
孙元泉. 潜艇和深潜器的现代操纵理论与应用[M]. 北京: 国防工业出版社, 2001.
|
| [11] |
谢俊元. 深海载人潜水器动力学建模研究及操纵仿真器研制[D]. 无锡: 江南大学, 2009.
|
| [12] |
张华. 7 000米载人潜水器空间大机动及特殊工况运动的水动力特性研究. CSSRC, 2004, ZQXW-Q001-A-C-009.
|
 2021, Vol. 43
2021, Vol. 43
