2. 喷水推进技术重点实验室,上海 200011
2. Science and Technology on Water Jet Propulsion Laboratory, Shanghai 200011, China
喷水推进是一种广泛应用在中高速船舶、具有时代特征的先进推进方式[1]。与传统螺旋桨推进相比具有很多优点,但是在喷水推进船设计阶段,只能通过相似换算将模型实验数据换算为实尺度喷水推进船的推力和阻力,从而实现快速性预报。在此过程中尺度效应对快速性预报的准确性具有重大影响。因此研究尺度效应对喷水推进器进出口流场的影响对喷水推进船的快速性预报具有重要意义。
1 研究对象以某喷水推进船为研究对象,该喷水推进船安装两台混流式喷水推进泵,设计航速Vs为32 kn,喷泵设计转速ns为372 r/min,设计流量Qs为30 m3/s。

|
图 1 喷水推进船 Fig. 1 Water jet propulsion ship |
船模航速可以根据傅汝德相似得出:
| ${{\rm{V}}_{0\lambda }}{\rm{ = }}\frac{{{V_{\rm{s}}}}}{{\sqrt \lambda }}\text{,}$ | (1) |
在满足进速系数相等且假定伴流无尺度作用时,叶轮转速满足以下相似关系:
| ${{{n}}_{{m}}}{{ = }}{{{n}}_{{s}}}\sqrt \lambda \text{,}$ | (2) |
喷泵流量和转速满足的相似公式如下:
| $ \frac{{{Q_{\rm{s}}}}}{{{Q_\lambda }}}{\rm{ = }}{\left( \lambda \right)^3} \cdot \frac{{{{{n}}_{{e}}}}}{{{{{n}}_\lambda }}}\text{。} $ | (3) |
根据以上相似关系式可以求出不同缩尺比的船速及喷泵参数如表1所示。
|
|
表 1 不同缩尺比喷泵参数 Tab.1 Parameters of pump with different scale ratio |
由此可以得到不同缩尺比下喷泵的参数,进而可以对不同缩尺比下的喷泵进行数值模拟。
3 叶轮和导叶体模拟方法叶轮和导叶体是喷水推进系统重要水动力部件,在数值模拟喷水推进船自航状态时对于叶轮和导叶的数值模拟通常采用滑移网格法、旋转坐标系法、虚拟盘、力源法4种方法[5],其中滑移网格法和旋转坐标系法需要对叶轮和导叶体全部划分网格,对计算机性能要求较高,且耗时较长。而力源法没有考虑水流的旋转,与实际流场相差较大,因此决定采用虚拟盘方法对叶轮和导叶体进行数值模拟。
喷水推进器叶轮的扭矩系数和的推力系数定义如下:
转矩系数
| ${{{K}}_{{Q}}}{{ = }}\frac{{{Q}}}{{\rho {{{n}}^{{2}}}{D^5}}}\text{。}$ | (4) |
式中:Q为转子转矩,N·m;ρ为水的密度,kg/m3;n为转速,r/min;D为喷泵特征直径,m。
根据相似关系,不同缩尺比的喷泵的转矩系数相等。
推力系数
| ${{{K}}_{{T}}}{{ = }}\frac{{{T}}}{{\rho {{{n}}^{{2}}}{D^4}}}\text{。}$ | (5) |
式中:T为喷水推进器产生的推力。
与螺旋桨推进船不同,喷水推进船喷水推进器产生的推力要大于叶轮旋转产生的轴向力,因此在计算喷水推进器的推力系数时,推力T取喷水推进器产生的推力,也就是船舶的阻力值,因此不同缩尺比喷泵的KT是不同的,需要具体计算如表2所示。
|
|
表 2 不同缩尺比转子扭矩系数和推力系数 Tab.2 Torque and thrust coefficients of propeller with different scale ratios |
数值计算时只计算一半船体和1台喷泵,采用两相流计算,计算域的长度为6 L(L为船长,船首之前计算域长度为2 L),宽度为L,高度为1.3 L(水线以上部分高度为0.3 L)。

|
图 2 计算域 Fig. 2 Calculation domain |
在Star CCM中划分网格,并且在划分网格时将其分为船体域、叶轮域、导叶体域3个部分,叶轮域和船体域采用Trim网格,导叶体域采用多面体网格。在水线面附近和喷口以后区域网格进行加密。

|
图 3 计算模型划分网格 Fig. 3 Mesh of computing model |
计算模型入口设为速度入口,速度为船速;计算域出口设为压力出口;计算域2个侧面设为对称边界;计算域底部设为壁面;计算域顶部设为对称边界;在叶轮域添加虚拟盘,并设定好不同缩尺比下叶轮的KT,KQ和转速。

|
图 4 转子域虚拟盘 Fig. 4 Virtual disk of propeller domain |
计算得到不同缩尺比喷口处流量与相似换算得到的流量误差如表3所示。
|
|
表 3 喷口处流量计算误差 Tab.3 Calculation error of flow rate at nozzle |
进口形状采用椭圆形,其位置取在进口流道与船底板切点前方1D处,椭圆的长半轴由流线追踪法确定,椭圆的短半轴由质量守恒确定,从而得到不同缩尺比下椭圆的形状,进而可以计算出边界层影响系数α。对不同缩尺比下椭圆的长半轴和短半轴无因次化如表4所示。
|
|
表 4 进口计算结果 Tab.4 Results at inlet |
对椭圆的长半轴和短半轴无因次化后可以看出,不同缩尺比下椭圆的长半轴基本在1附近,而椭圆的短半轴会随着缩尺比的增加而不断增加,无因次化后的椭圆面积也会随着缩尺比的增加而不断增加,即缩尺比越大,获流区也会相应增加。不同缩尺比的边界层影响系数相差不大。
定义喷水推进船实泵产生的推力如下:
| ${T_s}{\rm{ = }}{\rho _s}{Q_s}\left( {{V_{\rm{j}}}_s - {\alpha _s}{V_{0s}}} \right)\text{。}$ | (6) |
式中:Fs为实泵产生的推力;ρs为实船航行时水的密度;Vjs为实泵喷口速度;αs为实船边界层影响系数。
定义缩尺比为λ的模型泵产生的推力如下:
| ${T_\lambda }{\rm{ = }}{\rho _\lambda }{Q_\lambda }\left( {{V_{\rm{j}}}_\lambda - {\alpha _\lambda }{V_{0\lambda }}} \right)\text{。}$ | (7) |
式中:Fλ为模型泵产生的推力;ρλ为实船航行时水的密度;Vjλ为模型泵喷口速度;αλ为实船边界层影响系数;V0λ为模型船航速。
由以上2个公式可得:
| $\frac{{{T_{\rm{s}}}}}{{{T_\lambda }}}{\rm{ = }}\frac{{{\rho _s}{Q_s}\left( {{V_{\rm{j}}}_s - {\alpha _s}{V_{0s}}} \right)}}{{{\rho _\lambda }{Q_\lambda }\left( {{V_{\rm{j}}}_\lambda - {\alpha _\lambda }{V_{0\lambda }}} \right)}}{\rm{ = }}\frac{{{\rho _s}{Q_s}{V_{0s}}\left( {\dfrac{{{V_{\rm{j}}}_s}}{{{V_{0s}}}} - {\alpha _s}} \right)}}{{{\rho _\lambda }{Q_\lambda }{V_{0\lambda }}\left( {\dfrac{{{V_{\rm{j}}}_\lambda }}{{{V_{0\lambda }}}} - {\alpha _\lambda }} \right)}}\text{,}$ | (8) |
由喷泵相似换算式(3),上式可以转化为:
| ${T_{\rm{s}}}{\rm{ = }}{{\rm{T}}_\lambda }\frac{{{\rho _s}}}{{{\rho _\lambda }}}\frac{{{n_{\rm{s}}}}}{{{n_\lambda }}}{\lambda ^{7/2}}\dfrac{{\left( {\dfrac{{{V_{\rm{j}}}_s}}{{{V_{0s}}}} - {\alpha _s}} \right)}}{{\left( {\dfrac{{{V_{\rm{j}}}_\lambda }}{{{V_{0\lambda }}}} - {\alpha _\lambda }} \right)}}\text{,}$ | (9) |
定义无因次系数
| ${{C = }}\left( {\frac{{{V_{\rm{j}}}}}{{{V_0}}} - \alpha } \right)\text{,}$ | (10) |
则式(9)可以转化为:
| ${{\rm{F}}_{\rm{s}}}{\rm{ = }}{F_\lambda }\frac{{{\rho _s}}}{{{\rho _\lambda }}}\frac{{{{\rm{n}}_{\rm{s}}}}}{{{n_\lambda }}}{\lambda ^{7/2}}\frac{{{C_{\rm{s}}}}}{{{C_\lambda }}}\text{。}$ | (11) |
式中:Cs为实船C值;Cλ为缩尺比为λ时C值。
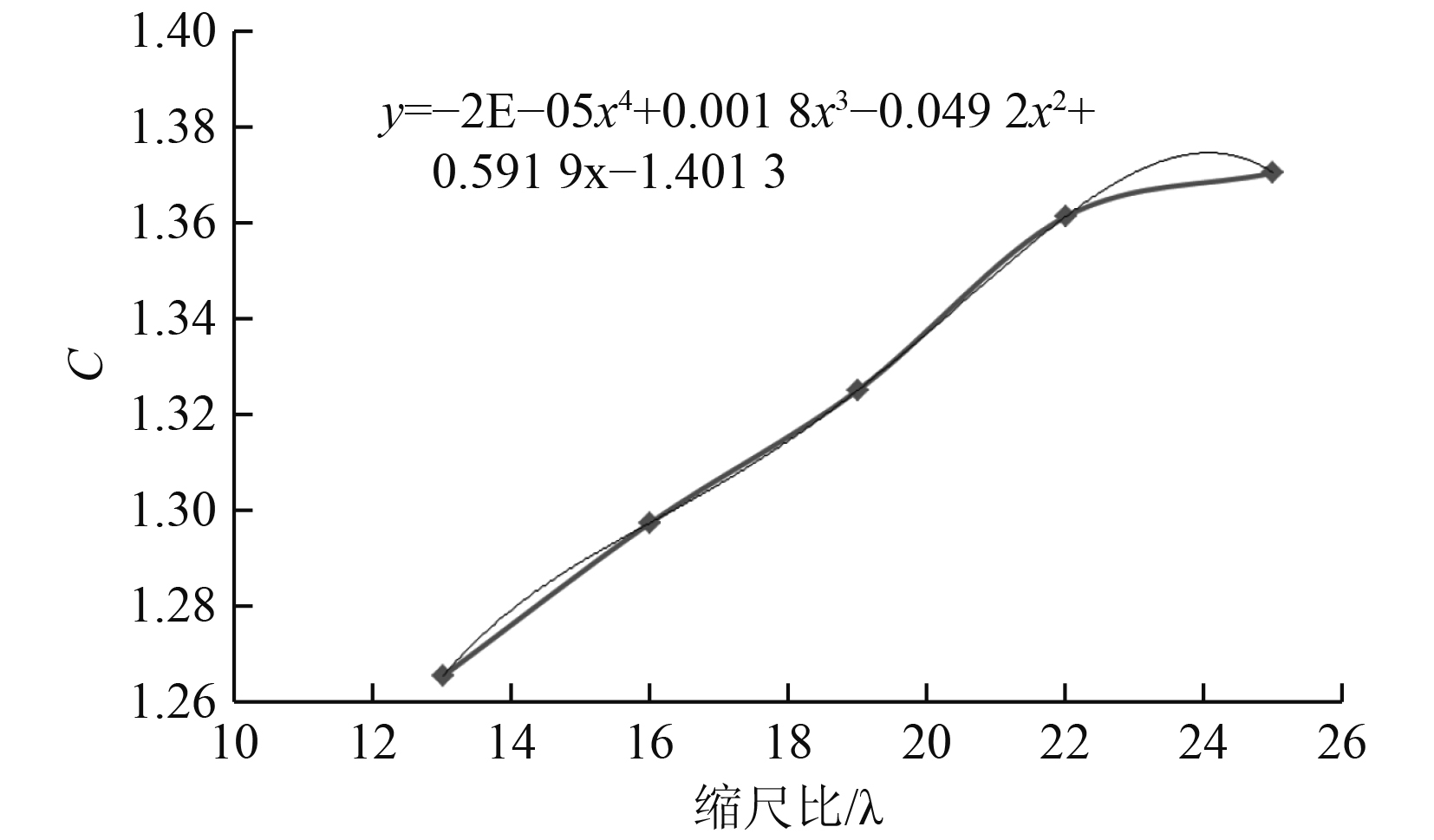
由上式可以看出,在将实验测量的缩尺比为λ的喷水推进泵产生的推力换算为实泵产生的推力时,其不仅与功率和缩尺比有关,与无因次系数C也有关系。根据以上计算结果,不同缩尺比的喷水推进泵无因次系数C值如表5所示。
|
|
表 5 不同缩尺比下C值 Tab.5 C of different scale ratio |
将以上数据绘制成图5。可以看出,随着缩尺比的增加,C值也不断增加,但是增加的速度会逐渐变缓,C值与缩尺比λ的关系可以用四次多项式拟合。通过拟合出的关系式就可以计算出缩尺比为1时的C值,进而换算出实泵产生的推力。
|
图 5 不同缩尺比C值 Fig. 5 C of different scale ratio |
将缩尺比为λ喷水推进器进口速度Vin无因次化,不同缩尺比下Vin/V0云图如图6所示。

|
图 6 不同缩尺比Vin/V0云图 Fig. 6 Vin/V0 contour of different scale ratio |
可以看出,进口Vin/V0云图分布大部分区域都小于1,即进口的速度分布中大部分区域都小于船速。缩尺比对进口的速度分布影响不大。
4.3.2 出口将缩尺比为λ喷水推进器出口速度Vjλ无因次化,不同缩尺比Vjλ/V0λ云图如图7所示。

|
图 7 不同缩尺比Vjλ/V0λ云图 Fig. 7 Vjλ/V0λ contour of different scale ratio |
受导流帽影响,喷口Vjλ/V0λ云图中间区域数值较小,而边侧区域速度相对较高。缩尺比对出口的速度影响不明显。
定义出口不均匀度系数如下式:
| $\zeta {\rm{ = }}\frac{1}{Q}\int {\left| {u - \overline U } \right|} {\rm d}A\text{。}$ | (12) |
式中:Q为截面流量;u为截面上任一点的速度;
不同缩尺比喷水推进出口不均匀度系数如表6所示。可以看出,不同缩尺比下喷水推进出口不均匀度基本相同。
|
|
表 6 不同缩尺比下出口不均匀度 Tab.6 Non-uniformity at nozzle of different scale ratio |
通过以上计算分析得出以下结论:
1)将模型尺度喷水推进装置推力换算到实泵时,引入了无因次系数C,该系数会随着的缩尺比的增加而不断增加。可以通过计算不同缩尺比时C值,拟合出一个C值与缩尺比的曲线,进而求出实泵的C值,然后通过相似换算即可得出实泵产生推力。
2)在缩尺比较大时,缩尺比对喷水推进进口和出口速度分布以及出口不均匀度影响不大。
| [1] |
金平仲. 船舶喷水推进[M]. 北京: 国防工业出版社, 1988.
|
| [2] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2010.
|
| [3] |
Final report and recommendation to the 21th ITTC[C]// The 21th International Towing Tank Conference. Bergen and Trondheim, Norwegian: ITTC, 1996.189−209.
|
| [4] |
Waterjet propulsion performance prediction-waterjet inlet duct, pump loop and waterjet system tests and extrapolation[C]//Final Recommendation of the Specialist Committee on Validation of Waterjet Test Procedures to the 24th ITTC. Edinburgh. UK: ITTC, 2005: 7.5-02-05-032.
|
| [5] |
沈志荣. 船桨舵相互作用的重叠网格技术数值方法研究[D]. 上海: 上海交通大学, 2014.
|
 2021, Vol. 43
2021, Vol. 43
